中2数学 1学期の計算 第10回 全32問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
① $-8-2\times7$
答え $-22$
\begin{eqnarray*} &&-8-2\times7\\ &=&-8-14\\ &=&-22 \end{eqnarray*}② $\cfrac{17}{6}+\cfrac{1}{4}-4$
答え $-\cfrac{11}{12}$
\begin{eqnarray*} &&\cfrac{17}{6}+\cfrac{1}{4}-4\\ &=&\cfrac{34}{12}+\cfrac{3}{12}-\cfrac{48}{12}\\ &=&-\cfrac{11}{12} \end{eqnarray*}③ $-1^6\times(-1)^7$
答え $1$
\begin{eqnarray*} &&-1^6\times(-1)^7\\ &=&-1\times(-1)\\ &=&1 \end{eqnarray*}④ $8a-3b-9a-9b$
答え $-a-12b$
\begin{eqnarray*} &&8a-3b-9a-9b\\ &=&8a-9a-3b-9b\\ &=&-a-12b \end{eqnarray*}⑤ $\cfrac{11}{12}x+\cfrac{5}{6}y-\cfrac{13}{14}x-\cfrac{7}{8}y$
答え $-\cfrac{1}{84}x-\cfrac{1}{24}y$
\begin{eqnarray*} &&\cfrac{11}{12}x+\cfrac{5}{6}y-\cfrac{13}{14}x-\cfrac{7}{8}y\\ &=&\cfrac{11}{12}x-\cfrac{13}{14}x+\cfrac{5}{6}y-\cfrac{7}{8}y\\ &=&\cfrac{77}{84}x-\cfrac{78}{84}x+\cfrac{20}{24}y-\cfrac{21}{24}y\\ &=&-\cfrac{1}{84}x-\cfrac{1}{24}y \end{eqnarray*}⑥ $(-26a+27b)+(33a-35b)$
答え $7a-8b$
\begin{eqnarray*} &&(-26a+27b)+(33a-35b)\\ &=&-26a+27b+33a-35b\\ &=&-26a+33a+27b-35b\\ &=&7a-8b \end{eqnarray*}⑦ $-(7x^2+15x)+(-9x^2+6x)$
答え $-16x^2-9x$
\begin{eqnarray*} &&-(7x^2+15x)+(-9x^2+6x)\\ &=&-7x^2-15x-9x^2+6x\\ &=&-7x^2-9x^2-15x+6x\\ &=&-16x^2-9x \end{eqnarray*}⑧ $15(6x-5y)$
答え $90x-75y$
⑨ $20\left(\cfrac{3}{5}a-\cfrac{3}{4}b\right)$
答え $12a-15b$
\begin{eqnarray*} &&20\left(\cfrac{3}{5}a-\cfrac{3}{4}b\right)\\ &=&20\times\cfrac{3}{5}a+20\times\left(-\cfrac{3}{4}b\right)\\ &=&12a-15b \end{eqnarray*}⑩ $(36x^2-18x+72)\div(-18)$
答え $-2x^2+x-4$
⑪ $(45a-81b)\div\left(-\cfrac{9}{8}\right)$
答え $-40a+72b$
\begin{eqnarray*} &&(45a-81b)\div\left(-\cfrac{9}{8}\right)\\ &=&(45a-81b)\times\left(-\cfrac{8}{9}\right)\\ &=&45a\times\left(-\cfrac{8}{9}\right)-81b\times\left(-\cfrac{8}{9}\right)\\ &=&-40a+72b\end{eqnarray*}⑫ $5(8x+9y)+6(-6x-8y)$
答え $4x-3y$
\begin{eqnarray*} &&5(8x+9y)+6(-6x-8y)\\ &=&40x+45y-36x-48y\\ &=&40x-36x+45y-48y\\ &=&4x-3y \end{eqnarray*}⑬ $\cfrac{4}{5}(20a^2-15a)-\cfrac{5}{6}(18a^2-42a)$
答え $a^2+23a$
\begin{eqnarray*} &&\cfrac{4}{5}(20a^2-15a)-\cfrac{5}{6}(18a^2-42a)\\ &=&16a^2-12a-15a^2+35a\\ &=&16a^2-15a^2-12a+35a\\ &=&a^2+23a \end{eqnarray*}⑭ $\cfrac{x-2y}{4}-\cfrac{x+y}{2}$
答え $\cfrac{-x-4y}{4}\quad\left(-\cfrac{x+4y}{4},-\cfrac{1}{4}x-yも可\right)$
\begin{eqnarray*} &&\cfrac{x-2y}{4}-\cfrac{x+y}{2}\\ &=&\cfrac{(x-2y)-2(x+y)}{4}\\ &=&\cfrac{x-2y-2x-2y}{4}\\ &=&\cfrac{x-2x-2y-2y}{4}\\ &=&\cfrac{-x-4y}{4} \end{eqnarray*}⑮ $(-3x)^2\times(-2x)^3$
答え $-72x^5$
\begin{eqnarray*} &&(-3x)^2\times(-2x)^3\\ &=&9x^2\times(-8x^3)\\ &=&-72x^5 \end{eqnarray*}⑯ $-18ab\div(-27a^3b^3)\times(-3a^2b)$
答え $-\cfrac{2}{b}$
\begin{eqnarray*} &&-18ab\div(-27a^3b^3)\times(-3a^2b)\\ &=&-\cfrac{18ab\times3aab}{27aaabbb}\\ &=&-\cfrac{2}{b} \end{eqnarray*}⑰ $-64x^2y^2\div48x\div\left(-\cfrac{16}{3}xy\right)$
答え $\cfrac{1}{4}y$
\begin{eqnarray*} &&-64x^2y^2\div48x\div\left(-\cfrac{16}{3}xy\right)\\ &=&-\cfrac{64xxyy}{1}\times\cfrac{1}{48x}\times\left(-\cfrac{3}{16xy}\right)\\ &=&\cfrac{1}{4}y \end{eqnarray*}① $9(8x-2)=4(3x-6)$
答え $x=-\cfrac{1}{10}$
\begin{eqnarray*} 9(8x-2)&=&4(3x-6) \\ 72x-18&=&12x-24 \\ 72x-12x&=&-24+18\\ 60x&=&-6 \\ x&=&-\cfrac{6}{60}=-\cfrac{1}{10} \end{eqnarray*}② $-\cfrac{9x-16}{6}=\cfrac{-6x-4}{15}$
答え $x=\cfrac{8}{3}$
\begin{eqnarray*} -\cfrac{9x-16}{6}&=&\cfrac{-6x-4}{15}\quad(\times30)\\ -45x+80&=&-12x-8 \\ -45x+12x&=&-8-80\\ -33x&=&-88\\ x&=&\cfrac{88}{33}=\cfrac{8}{3} \end{eqnarray*}③ $\left\{\begin{array}{l} x=-y-1\\ -2x-3y=6 \end{array}\right.$
答え $x=3,y=-4$
\begin{eqnarray*} \left\{ \begin{array}{l} x=-y-1\qquad…①\\ -2x-3y=6\qquad…② \end{array} \right. \end{eqnarray*} $①を②に代入する$ \begin{eqnarray*} -2(-y-1)-3y&=&6\\ 2y+2-3y&=&6\\ 2y-3y&=&6-2\\ -y&=&4\\ y&=&-4\\ \end{eqnarray*} \begin{eqnarray*} y=-4を&①&に代入\\ x&=&-(-4)-1\\ x&=&4-1\\ x&=&3 \\ \left\{ \begin{array}{l} x=3\\ y=-4 \end{array} \right. \end{eqnarray*}④ $\left\{\begin{array}{l} 2x-y=10\\ 5x-4y=7 \end{array}\right.$
答え $x=11,y=12$
\begin{eqnarray*} \left\{ \begin{array}{l} 2x-y=10\qquad…①\\ 5x-4y=7\qquad…② \end{array} \right. \end{eqnarray*} $①\times4-②$ \begin{eqnarray*} 8x-4y=40\\ \underline{-) \quad 5x-4y=\phantom{1}7} \\ 3x\phantom{-14y}=33 \\ x\phantom{-14y}=11 \end{eqnarray*} \begin{eqnarray*} x=11を&①&に代入\\ 2\times11-y&=&10\\ 22-y&=&10\\ -y&=&10-22\\ -y&=&-12\\ y&=&12 \\ \left\{ \begin{array}{l} x=11\\ y=12 \end{array} \right. \end{eqnarray*}①$x=6,\ y=4$ のとき、次の式の値を求めなさい。
$\qquad \cfrac{2}{5}x^2y\div\left(-\cfrac{3}{10}xy^2\right)$
答え $-2$
いきなり代入しても同じ答えがでますが、ちょっと損なやり方です。文字のままやれるところまで計算して、それから代入したほうがラクです。
\begin{eqnarray*} &&\cfrac{2}{5}x^2y\div\left(-\cfrac{3}{10}xy^2\right) \\ &=&\cfrac{2xxy}{5}\times\left(-\cfrac{10}{3xyy}\right)\\ &=&-\cfrac{4x}{3y}\\ &&x=6,\ y=4 を代入\\ &=&-\cfrac{4\times6}{3\times4}\\ &=&-2 \end{eqnarray*}
② $y$ が $x$ に比例し、$x=16$ のとき、$y=-24$ である。 $x=22$ のときの $y$ の値を求めなさい。
答え $y=-33$
比例の式の形は $y=ax$ $$a=\cfrac{y}{x}=\cfrac{-24}{16}=-\cfrac{3}{2}\\ y=-\cfrac{3}{2}x\ に\ x=22\ を代入する\\ y=-\cfrac{3}{2}\times22=-33$$③ $y$ が $x$ に反比例し、$x=16$ のとき、$y=-5$ である。 $x=15$ のときの $y$ の値を求めなさい。
答え $y=-\cfrac{16}{3}$
反比例の式の形は $y=\cfrac{a}{x}$ $$a=x\times y=16\times(-5)=-80\\ y=-\cfrac{80}{x}\ に\ x=15\ を代入する\\ y=-\cfrac{80}{15}=-\cfrac{16}{3}$$④ 次の式の項を答えなさい。また、何次式かを答えなさい。
$\qquad ab-\cfrac{1}{2}ab^2$
答え $項…ab,\ -\cfrac{1}{2}ab^2 \\3次式$
式の途中に $+$ や $-$ がでてきたら、その直前にスラッシュ(斜め線)をいれて、項にわけます。 それぞれの項の次数をみて、いちばん高いところの次数を答えます。 $$ab/-\cfrac{1}{2}ab^2$$ $ab$ は $2$ 次、$-\cfrac{1}{2}ab^2$ は $3$ 次です。なので、$3$ 次式と答えます。次の式を$[\phantom{y}]$内の文字について解きなさい。
⑤
$c=ax+bx\quad[b]$
答え $b=\cfrac{-ax+c}{x}\left(-\cfrac{ax-c}{x},-a+\cfrac{c}{x}も可\right)$
\begin{eqnarray*} c&=&ax+bx\quad(左辺と右辺をとりかえる) \\ ax+bx&=&c \\ bx&=&-ax+c \\ b&=&\cfrac{-ax+c}{x} \end{eqnarray*}次の式を$[\phantom{h}]$内の文字について解きなさい。
⑥
$y=-\cfrac{3}{5}x+6\quad[x]$
答え $x=\cfrac{-5y+30}{3}\left(-\cfrac{5y-30}{3},-\cfrac{5}{3}y+10も可\right)$
\begin{eqnarray*} y&=&-\cfrac{3}{5}x+6\quad(両辺に\times5) \\ 5y&=&-3x+30 \\ 3x&=&-5y+30 \\ x&=&\cfrac{-5y+30}{3} \end{eqnarray*}⑦ 連続する $2$ つの奇数の和は $4$ の倍数となることを、 連続する $2$ つの奇数を $ 2n-1,\ 2n+1$ として説明しなさい。
説明
連続する $2$ つの奇数を $2n-1,\ 2n+1$ とする。ただし、$n$ は整数とする。
\begin{eqnarray*} &&2n-1+2n+1 \\ &=&4n \end{eqnarray*} $n$ は整数だから、$4n$ は $4$ の倍数である。
したがって、連続する $2$ つの奇数の和は $4$ の倍数となる。
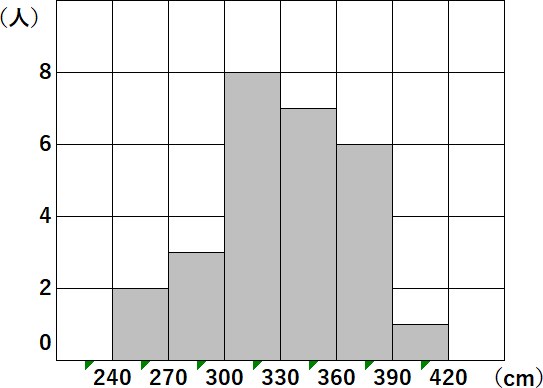
① あるクラスの女子の人数を答えなさい。
答え $27人$
② 最頻値(モード)を求めなさい。
答え $315$
人数がいちばん多い階級の階級値が最頻値(モード)です。グラフの、いちばん背が高いところの階級値だと思ってしまってもいいです。
このグラフで人数がいちばん多いのは、$300cm$ 以上 $330cm$ 未満の階級です。なので最頻値(モード)は、
\begin{eqnarray*}
(300+330)\div2=315
\end{eqnarray*}
$315$ です。ここで注意が必要なのは、「階級値を答える」ということです。最頻値(モード)をきかれたら、
階級値を答えてください。
階級値というのは、その階級のいちばん小さい数といちばん大きい数を足して $2$ で割った値のことです。
③ 中央値(メジアン)を求めなさい。
答え $345$
$27$ 人による記録ですから、その中央値(メジアン)は、$14$ 番目の記録です。
$27$ 人いるのだったら、まえから数えても $14$ 番目、うしろから数えても $14$ 番目がまんなかです。
その「まんなか」というのが中央値(メジアン)です。
$(1+27)\div2=14$ とやってしまうと話がはやいです。まんなかというのは、「足して $2$ で割る」とすぐに求まります。
んで、この問題の場合の中央値(メジアン)は、$14$ 番目の人がふくまれる階級の階級値になります。
$14$ 番目のひとがふくまれるのは $330cm$ 以上 $360cm$ 未満の階級です。なので中央値(メジアン)は、
\begin{eqnarray*}
(330+360)\div2=345
\end{eqnarray*}
$345$ です。ここで注意が必要なのは、「階級値を答える」ということです。こういう問題で中央値(メジアン)をきかれたら、
階級値を答えてください。
階級値というのは、その階級のいちばん小さい数といちばん大きい数を足して $2$ で割った値のことです。
④ 記録が $360cm$ 以上のひとの相対度数を、小数第 $3$ 位を四捨五入して求めなさい。
答え $0.26$
$360cm$ 以上の人数をあわせると、$7$ 人います。度数は $7$ です。
なのでその相対度数は $\cfrac{7}{27}$ です。
\begin{eqnarray*}
7\div27=0.259...
\end{eqnarray*}
小数第 $3$ 位を四捨五入して求めよというのだから、答えは $0.26$ です。
答え
$\boxed{\large{\ 1\ }}①-22②-\cfrac{11}{12}③1④-a-12b⑤-\cfrac{1}{84}x-\cfrac{1}{24}y\\ ⑥7a-8b⑦-16x^2-9x⑧90x-75y\\ ⑨12a-15b⑩-2x^2+x-4⑪-40a+72b\\ ⑫4x-3y⑬a^2+23a\\ ⑭\cfrac{-x-4y}{4}\quad\left(-\cfrac{x+4y}{4},-\cfrac{1}{4}x-yも可\right)\\ ⑮-72x^5 ⑯-\cfrac{2}{b}⑰\cfrac{1}{4}y\\ \boxed{\large{\ 2\ }}①x=-\cfrac{1}{10}②x=\cfrac{8}{3}③x=3, \ y=-4\\ ④x=11, \ y=12\\ \boxed{\large{\ 3\ }}①-2②y=-33③y=-\cfrac{16}{3}\\ ④項…ab, \ -\cfrac{1}{2}ab^2,3次式\\ ⑤b=\cfrac{-ax+c}{x}\quad\left(-\cfrac{ax-c}{x},-a+\cfrac{c}{x}も可\right)\\ ⑥x=\cfrac{-5y+30}{3}\quad\left(-\cfrac{5y-30}{3},-\cfrac{5}{3}y+10も可\right)\\ ⑥連続する\ 2 つの奇数を\ 2n-1,\ 2n+1\ とする。\\ ただし、n\ は整数とする。\\ \begin{eqnarray*} &&2n-1+2n+1 \\ &=&4n \end{eqnarray*}\\ n は整数だから、4n\ は\ 4\ の倍数である。\\ したがって、連続する\ 2\ つの奇数の和は\ 4\ の倍数である。\\ \boxed{\large{\ 4\ }}①27人②315③345④0.26 $