中2数学 3学期の計算 第8回 全30問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
① $-8-2\times(-6)$
答え $4$
\begin{eqnarray*} &&-8-2\times(-6)\\ &=&-8+12\\ &=&4 \end{eqnarray*}② $1-\cfrac{3}{4}-\cfrac{2}{3}$
答え $-\cfrac{5}{12}$
\begin{eqnarray*} &&1-\cfrac{3}{4}-\cfrac{2}{3}\\ &=&\cfrac{12}{12}-\cfrac{9}{12}-\cfrac{8}{12}\\ &=&-\cfrac{5}{12} \end{eqnarray*}③ $-3^2\times(-1)^2$
答え $-9$
\begin{eqnarray*} &&-3^2\times(-1)^2\\ &=&-9\times1\\ &=&-9 \end{eqnarray*}④ $-12x+6y-8x-18y$
答え $-20x-12y$
\begin{eqnarray*} &&-12x+6y-8x-18y\\ &=&-12x-8x+6y-18y\\ &=&-20x-12y \end{eqnarray*}⑤ $-\cfrac{5}{6}a-\cfrac{3}{4}b+2a+\cfrac{5}{3}b$
答え $\cfrac{7}{6}a+\cfrac{11}{12}b$
\begin{eqnarray*} &&-\cfrac{5}{6}a-\cfrac{3}{4}b+2a+\cfrac{5}{3}b\\ &=&-\cfrac{5}{6}a+2a-\cfrac{3}{4}b+\cfrac{5}{3}b\\ &=&-\cfrac{5}{6}a+\cfrac{12}{6}a-\cfrac{9}{12}b+\cfrac{20}{12}b\\ &=&\cfrac{7}{6}a+\cfrac{11}{12}b \end{eqnarray*}⑥ $(-3x-4y)-(-2x+2y)$
答え $-x-6y$
\begin{eqnarray*} &&(-3x-4y)-(-2x+2y)\\ &=&-3x-4y+2x-2y\\ &=&-3x+2x-4y-2y\\ &=&-x-6y \end{eqnarray*}⑦ $(4x^2-13x)-(5x^2-6x)$
答え $-x^2-7x$
\begin{eqnarray*} &&(4x^2-13x)-(5x^2-6x)\\ &=&4x^2-13x-5x^2+6x\\ &=&4x^2-5x^2-13x+6x\\ &=&-x^2-7x \end{eqnarray*}⑧ $-12(5a-4b)$
答え $-60a+48b$
⑨ $60\left(\cfrac{7}{12}x-\cfrac{8}{15}y\right)$
答え $35x-32y$
\begin{eqnarray*} &&60\left(\cfrac{7}{12}x-\cfrac{8}{15}y\right)\\ &=&60\times\cfrac{7}{12}x+60\times\left(-\cfrac{8}{15}y\right)\\ &=&35x-32y \end{eqnarray*}⑩ $(-60a^2+36a-48)\div(-12)$
答え $5a^2-3a+4$
⑪ $(60x-72y)\div\left(-\cfrac{12}{13}\right)$
答え $-65x+78y$
\begin{eqnarray*} &&(60x-72y)\div\left(-\cfrac{12}{13}\right)\\ &=&(60x-72y)\times\left(-\cfrac{13}{12}\right)\\ &=&60x\times\left(-\cfrac{13}{12}\right)-72y\times\left(-\cfrac{13}{12}\right)\\ &=&-65x+78y \end{eqnarray*}⑫ $12(5a+4b)-15(4a+3b)$
答え $3b$
\begin{eqnarray*} &&12(5a+4b)-15(4a+3b)\\ &=&60a+48b-60a-45b\\ &=&60a-60a+48b-45b\\ &=&3b \end{eqnarray*}⑬ $-\cfrac{5}{12}(60x-84y)+60\left(\cfrac{2}{15}x-\cfrac{7}{12}y\right)$
答え $-17x$
\begin{eqnarray*} &&-\cfrac{5}{12}(60x-84y)+60\left(\cfrac{2}{15}x-\cfrac{7}{12}y\right)\\ &=&-25x+35y+8x-35y\\ &=&-25x+8x+35y-35y\\ &=&-17x \end{eqnarray*}⑭ $\cfrac{7x-3y}{12}-\cfrac{3x-y}{5}$
答え $\cfrac{-x-3y}{60}\quad\left(-\cfrac{x+3y}{60},-\cfrac{1}{60}x-\cfrac{1}{20}yも可\right)$
\begin{eqnarray*} &&\cfrac{7x-3y}{12}-\cfrac{3x-y}{5}\\ &=&\cfrac{5(7x-3y)-12(3x-y)}{60}\\ &=&\cfrac{35x-15y-36x+12y}{60}\\ &=&\cfrac{35x-36x-15y+12y}{60}\\ &=&\cfrac{-x-3y}{60} \end{eqnarray*}⑮ $(-2a)^3\times(-12a^2)$
答え $96a^5$
\begin{eqnarray*} &&(-2a)^3\times(-12a^2)\\ &=&-8a^3\times (-12a^2)\\ &=&96a^5 \end{eqnarray*}⑯ $5ab\div(-60a^2b^2)\times(-12ab^2)$
答え $b$
\begin{eqnarray*} &&5ab\div(-60a^2b^2)\times(-12ab^2)\\ &=&\cfrac{5ab\times(-12abb)}{-60aabb}\\ &=&b \end{eqnarray*}⑰ $35xy\div\left(-\cfrac{60}{7}x^2y^2\right)\times\cfrac{12}{49}y$
答え $-\cfrac{1}{x}$
\begin{eqnarray*} &&35xy\div\left(-\cfrac{60}{7}x^2y^2\right)\times\cfrac{12}{49}y\\ &=&\cfrac{35xy}{1}\times\left(-\cfrac{7}{60xxyy}\right)\times\cfrac{12y}{49}\\ &=&-\cfrac{1}{x} \end{eqnarray*}① $13x-12=7(3x-2)$
答え $x=\cfrac{1}{4}$
\begin{eqnarray*} 13x-12&=&7(3x-2) \\ 13x-12&=&21x-14 \\ 13x-21x&=&-14+12\\ -8x&=&-2 \\ x&=&\cfrac{-2}{-8}=\cfrac{1}{4} \end{eqnarray*}② $\cfrac{1}{6}x+\cfrac{11}{12}=\cfrac{4}{15}x+1$
答え $x=-\cfrac{5}{6}$
\begin{eqnarray*} \cfrac{1}{6}x+\cfrac{11}{12}&=&\cfrac{4}{15}x+1\quad(\times60)\\ 10x+55&=&16x+60 \\ 10x-16x&=&60-55\\ -6x&=&5\\ x&=&-\cfrac{5}{6} \end{eqnarray*}③ $\left\{\begin{array}{l} 3x-2y=9\\ 4x-3y=7 \end{array}\right.$
答え $x=13,y=15$
\begin{eqnarray*} \left\{ \begin{array}{l} 3x-2y=9\qquad…①\\ 4x-3y=7\qquad…② \end{array} \right. \end{eqnarray*} $①\times3-②\times2$ \begin{eqnarray*} 9x-6y=27\\ \underline{-) \quad 8x-6y=14} \\ x\phantom{+16y}=13 \\ \end{eqnarray*} \begin{eqnarray*} x=13を①に代入\\ 3\times13-2y&=&9\\ 39-2y&=&9\\ -2y&=&9-39\\ -2y&=&-30\\ y&=&15 \\ \left\{ \begin{array}{l} x=13\\ y=15 \end{array} \right. \end{eqnarray*}④ $\left\{\begin{array}{l} x-y=3\\ 3x-\cfrac{1}{2}y=4 \end{array}\right.$
答え $x=1,y=-2$
\begin{eqnarray*} \left\{ \begin{array}{l} x-y=3\qquad…①\\ 3x-\cfrac{1}{2}y=4\qquad…② \end{array} \right. \end{eqnarray*} $②の分母をはらう$ \begin{eqnarray*} 3x-\cfrac{1}{2}y&=&4\quad(\times2)\\ 6x-y&=&8\qquad…③ \end{eqnarray*} $①-③$ \begin{eqnarray*} x-y=\phantom{-}3\\ \underline{-) \quad 6x-y=\phantom{-}8} \\ -5x\phantom{-6y}=-5 \\ x=\phantom{-}1 \\ \end{eqnarray*} \begin{eqnarray*} x=1を①に代入\\ 1-y&=&3\\ -y&=&3-1\\ -y&=&2\\ y&=&-2\\ \\ \left\{ \begin{array}{l} x=1\\ y=-2 \end{array} \right. \end{eqnarray*}次の式を$[\phantom{y}]$内の文字について解きなさい。
①
$4a-3b=c\quad[b]$
答え $b=\cfrac{4a-c}{3}\left(x=\cfrac{4}{3}a-\cfrac{1}{3}c\right)$
\begin{eqnarray*} 4a-3b&=&c \\ -3b&=&-4a+c \quad(-1を両辺にかける)\\ 3b&=&4a-c \\ b&=&\cfrac{4a-c}{3} \end{eqnarray*}次の式を$[\phantom{h}]$内の文字について解きなさい。
②
$y=\cfrac{2}{3}x-3\quad[x]$
答え $x=\cfrac{3y+9}{2}\left(\cfrac{3}{2}y+\cfrac{9}{2}も可\right)$
\begin{eqnarray*} y&=&\cfrac{2}{3}x-3\quad (右辺と左辺をとりかえる) \\ \cfrac{2}{3}x-3&=&y\quad(両辺に\times3) \\ 2x-9&=&3y \\ 2x&=&3y+9 \\ x&=&\cfrac{3y+9}{2} \\ \end{eqnarray*}③ $x=-2, \ y=-\cfrac{1}{3}$ のとき、次の式の値を求めなさい。
$\qquad 2(x+2y)-(x+y)$
答え $-3$
\begin{eqnarray*} &&2(x+2y)-(x+y)\\\\ &=&2x+4y-x-y\\\\ &=&2x-x+4y-y\\\\ &=&x+3y\\ &=&-2+3\times\left(-\cfrac{1}{3}\right)\\ &=&-2-1\\ &=&-3 \end{eqnarray*}④ $y$ が $x$ に比例し、$x=3$ のとき、$y=-4$ である。 $x=-9$ のときの $y$ の値を求めなさい。
答え $y=12$
比例の式の形は $y=ax$ $$a=\cfrac{y}{x}=\cfrac{-4}{3}=-\cfrac{4}{3}$$ $y=-\cfrac{4}{3}x$ に $x=-9$ を代入\begin{eqnarray*} y=-\cfrac{4}{3}\times(-9)=12 \end{eqnarray*}
⑤ $y$ が $x$ に反比例し、$x=3$ のとき、$y=-4$ である。 $x=-12$ のときの $y$ の値を求めなさい。
答え $y=1$
反比例の式の形は $y=\cfrac{a}{x}$ $$a=x \times y=3\times(-4)=-12$$ $y=-\cfrac{12}{x}$ に $x=-12$ を代入\begin{eqnarray*} y=-\cfrac{12}{-12}=1 \end{eqnarray*}
⑥ 変化の割合が $-1$ で、点 $\left(-2,\ \cfrac{1}{2}\right)$ を通る直線の式を求めなさい。
答え $y=-x-\cfrac{3}{2}$
直線の式の形は $y=ax+b$変化の割合が $-1$ なので$a=-1$
$y=-x+b$ に $x=-2,\ y=\cfrac{1}{2}$ を代入 \begin{eqnarray*} \cfrac{1}{2}&=&-1\times(-2)+b\\ \cfrac{1}{2}&=&2+b\\ \cfrac{1}{2}-2&=&b\\ \cfrac{1}{2}-\cfrac{4}{2}&=&b\\ -\cfrac{3}{2}&=&b \end{eqnarray*}
⑦ $2$ 点 $(-3,\ 6),\ (2,\ -4)$ を通る直線の式を求めなさい。
答え $y=-2x$
直線の式の形は $y=ax+b$ \begin{eqnarray*} a&=&\cfrac{y_2-y_1}{x_2-x_1}\\ &=&\cfrac{-4-6}{2-(-3)}=\cfrac{-10}{5}=-2\\ \end{eqnarray*} $y=-2x+b$ に $x=-3,\ y=6$ を代入 \begin{eqnarray*} 6&=&-3\times(-2)+b\\ 6&=&6+b\\ 0&=&b \end{eqnarray*}
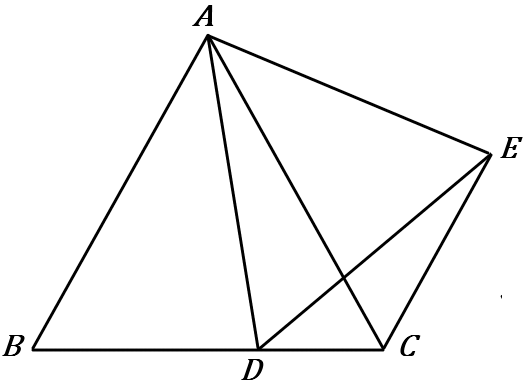
①右の図で、点$D$ は $BC$上にあり、$\triangle ABC$ と $\triangle ADE$ はどちらも正三角形である。$\triangle ABD \ \equiv \ \triangle ACE$ であることを証明しなさい。
答え
$\triangle ABD$ と $\triangle ACE$ で、
$\triangle ABC$ は正三角形だから、$AB=AC$ ……①
$\triangle ADE$ は正三角形だから、$AD=AE$ ……②
$\angle BAC=60^{ \circ }$ だから、$\angle BAD=60^{ \circ }-\angle DAC$ ……③
$\angle DAE=60^{ \circ }$ だから、$\angle CAE=60^{ \circ }-\angle DAC$ ……④
③④より、$\angle BAD=\angle CAE$ ……⑤
①②⑤より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle ABD \ \equiv \ \triangle ACE$
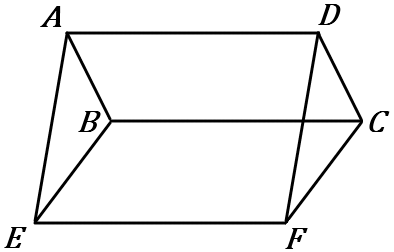
②右の図で、四角形$ABCD$ と四角形$BEFC$ はどちらも平行四辺形である。
四角形 $AEFD$ が平行四辺形であることを証明しなさい。
▱$ABCD$ で、平行四辺形の性質より、
$AD=BC, \ AD /\!/ BC$ ……①
▱$BEFC$ で、平行四辺形の性質より、
$BC=EF, \ BC /\!/ EF$ ……②
①②より、$AD=EF, \ \ AD /\!/ EF$
$1$組の対辺が平行で長さが等しいので、
四角形 $AEFD$ は平行四辺形である。
答え
$\boxed{\large{\ 1\ }}①4②-\cfrac{5}{12}③-9④-20x-12y⑤\cfrac{7}{6}a+\cfrac{11}{12}b\\
⑥-x-6y⑦-x^2-7x⑧-60a+48b\\
⑨35x-32y⑩5a^2-3a+4⑪-65x+78y\\
⑫3b⑬-17x⑭\cfrac{-x-3y}{60}⑮96a^5\\
⑯b⑰-\cfrac{1}{x}\\
\boxed{\large{\ 2\ }}①x=\cfrac{1}{4}②x=-\cfrac{5}{6}③x=13,y=15\\
④x=1,y=-2\\
\boxed{\large{\ 3\ }}①b=\cfrac{4a-c}{3}②x=\cfrac{3y+9}{2}③-3\\
④y=12⑤y=1⑥y=-x-\cfrac{3}{2}⑦y=-2x\\
\boxed{\large{\ 4\ }}$
① $\triangle ABD$ と $\triangle ACE$ で、
$\triangle ABC$ は正三角形だから、$AB=AC$ ……①
$\triangle ADE$ は正三角形だから、$AD=AE$ ……②
$\angle BAC=60^{ \circ }$ だから、$\angle BAD=60^{ \circ }-\angle DAC$ ……③
$\angle DAE=60^{ \circ }$ だから、$\angle CAE=60^{ \circ }-\angle DAC$ ……④
③④より、$\angle BAD=\angle CAE$ ……⑤
①②⑤より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle ABD \ \equiv \ \triangle ACE$
② ▱$ABCD$ で、平行四辺形の性質より、
$AD=BC, \ AD /\!/ BC$ ……①
▱$BEFC$ で、平行四辺形の性質より、
$BC=EF, \ BC /\!/ EF$ ……②
①②より、$AD=EF, \ \ AD /\!/ EF$
$1$組の対辺が平行で長さが等しいので、
四角形 $AEFD$ は平行四辺形である。