中3数学 3学期の計算 第3回 全33問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
① $-5-(-7)$
答え $2$
\begin{eqnarray*} &&-5-(-7)\\ &=&-5+7\\ &=&2 \end{eqnarray*}② $-3\times(-2^2)-(-3)^2\times2$
答え $-6$
\begin{eqnarray*} &&-3\times(-2^2)-(-3)^2\times2\\ &=&-3\times(-4)-9\times2\\ &=&12-18\\ &=&-6 \end{eqnarray*}③ $\cfrac{3}{5}-\cfrac{2}{3}\div\cfrac{4}{9}$
答え $-\cfrac{9}{10}$
\begin{eqnarray*} &&\cfrac{3}{5}-\cfrac{2}{3}\div\cfrac{4}{9}\\ &=&\cfrac{3}{5}-\cfrac{2}{3}\times\cfrac{9}{4}\\ &=&\cfrac{3}{5}-\cfrac{3}{2}\\ &=&\cfrac{6}{10}-\cfrac{15}{10}\\ &=&-\cfrac{9}{10} \end{eqnarray*}④ $4(3x-2)-(8x-7)$
答え $4x-1$
\begin{eqnarray*} &&4(3x-2)-(8x-7)\\ &=&12x-8-8x+7\\ &=&4x-1 \end{eqnarray*}⑤ $\cfrac{2x-3y}{6}-\cfrac{3x-y}{5}$
答え $\cfrac{-8x-9y}{30}\\\quad\left(-\cfrac{8x+9y}{30},-\cfrac{4}{15}x-\cfrac{3}{10}yも可\right)$
\begin{eqnarray*} &&\cfrac{2x-3y}{6}-\cfrac{3x-y}{5}\\ &=&\cfrac{5(2x-3y)-6(3x-y)}{30}\\ &=&\cfrac{10x-15y-18x+6y}{30}\\ &=&\cfrac{-8x-9y}{30} \end{eqnarray*}⑥ $-(2x+3)^2+2(x-4)(3x+1)$
答え $2x^2-34x-17$
\begin{eqnarray*} &&-(2x+3)^2+2(x-4)(3x+1)\\ &=&-(4x^2+12x+9)+2(3x^2+x-12x-4)\\ &=&-4x^2-12x-9+2(3x^2-11x-4)\\ &=&-4x^2-12x-9+6x^2-22x-8\\ &=&2x^2-34x-17 \end{eqnarray*}⑦ $-\cfrac{4}{\sqrt{5}}+\sqrt{10}\times\sqrt{2}$
答え $\cfrac{6\sqrt{5}}{5}$
\begin{eqnarray*} &&-\cfrac{4}{\sqrt{5}}+\sqrt{10}\times\sqrt{2}\\ &=&-\cfrac{4\sqrt{5}}{5}+\sqrt{20}\\ &=&-\cfrac{4\sqrt{5}}{5}+2\sqrt{5}\\ &=&-\cfrac{4\sqrt{5}}{5}+\cfrac{10\sqrt{5}}{5}\\ &=&\cfrac{6\sqrt{5}}{5} \end{eqnarray*}① $48x^2y-60xy^2+12xy$
答え $12xy(4x-5y+1)$
② $x^2-13x-30$
答え $(x+2)(x-15)$
③ $\cfrac{1}{4}x^2-xy+y^2$
答え $\left(\cfrac{1}{2}x-y\right)^2$
④ $121x^2-169y^2$
答え $(11x+13y)(11x-13y)$
⑤ $25x^2-100$
答え $25(x+2)(x-2)$
\begin{eqnarray*} &&25x^2-100\\ &=&25(x^2-4)\\ &=&25(x+2)(x-2) \end{eqnarray*}① $-\cfrac{1}{2}x+\cfrac{2}{3}=\cfrac{5}{6}x+1$
答え $x=-\cfrac{1}{4}$
\begin{eqnarray*} -\cfrac{1}{2}x+\cfrac{2}{3}&=&\cfrac{5}{6}x+1\quad(\times6) \\ -3x+4&=&5x+6 \\ -3x-5x&=&6-4\\ -8x&=&2 \\ x&=&-\cfrac{2}{8}=-\cfrac{1}{4} \end{eqnarray*}② $\left\{\begin{array}{l} 2x-3y=2\\ 6(x-y)=2y+5 \end{array}\right.$
答え $x=-\cfrac{1}{2},y=-1$
\begin{eqnarray*} \left\{ \begin{array}{l} 2x-3y=2\qquad…①\\ 6(x-y)=2y+5\qquad…② \end{array} \right. \end{eqnarray*} $②を整理$ \begin{eqnarray*} 6(x-y)&=&2y+5\\ 6x-6y&=&2y+5\\ 6x-6y-2y&=&5\\ 6x-8y&=&5\qquad…③ \end{eqnarray*} $①\times3-③$ \begin{eqnarray*} 6x-9y=6\\ \underline{-) \quad 6x-8y=5} \\ -y=1 \\ y=-1 \end{eqnarray*} \begin{eqnarray*} y=-1を①に代入\\ 2x-3\times(-1)&=&2\\ 2x+3&=&2\\ 2x&=&2-3\\ 2x&=&-1\\ x&=&-\cfrac{1}{2} \\ \left\{ \begin{array}{l} x=-\cfrac{1}{2}\\ y=-1 \end{array} \right. \end{eqnarray*}③ $ 3x-4y=5x+2y+6=17 $
答え $x=3,y=-2$
$3x-4y=5x+2y+6=17$ のまんなかを隠した式をつくり、①とする。左側を隠した式をつくり、②とする。
①と②を連立方程式として解く。 \begin{eqnarray*} \left\{ \begin{array}{l} 3x-4y=17\qquad…①\\ 5x+2y+6=17\qquad…② \end{array} \right. \end{eqnarray*} $②を整理$ \begin{eqnarray*} 5x+2y+6&=&17\\ 5x+2y&=&17-6\\ 5x+2y&=&11\qquad…③ \end{eqnarray*} $①+③\times2$ \begin{eqnarray*} \phantom{1}3x-4y=17\\ \underline{+) \quad 10x+4y=22} \\ 13x\phantom{-14y}=39\\ x=3\phantom{9}\\ \end{eqnarray*} \begin{eqnarray*} x=3を①に代入\\ 3\times3-4y&=&17\\ 9-4y&=&17\\ -4y&=&17-9\\ -4y&=&8\\ y&=&-2 \\ \left\{ \begin{array}{l} x=3\\ y=-2 \end{array} \right. \end{eqnarray*}
④ $x^2-13x-48=0$
答え $x=16 ,\ x=-3$
\begin{eqnarray*} x^2-13x-48&=&0 \\ (x-16)(x+3)&=&0\\ x&=&16,\ x=-3 \end{eqnarray*}⑤ $4x^2-2=0$
答え $x=\pm\cfrac{\sqrt{2}}{2}$
\begin{eqnarray*} 4x^2-2&=&0 \quad\left(両辺に\times\cfrac{1}{2}\right)\\ 2x^2-1&=&0\\ 2x^2&=&1\\ x^2&=&\cfrac{1}{2}\\ x&=&\pm\sqrt{\cfrac{1}{2}}=\pm\cfrac{\sqrt{1}}{\sqrt{2}}=\pm\cfrac{\sqrt{2}}{2} \end{eqnarray*}⑥ $\cfrac{1}{2}x^2+2x=-2$
答え $x=-2$
\begin{eqnarray*} \cfrac{1}{2}x^2+2x&=&-2 \quad\left(両辺に\times2\right)\\ x^2+4x&=&-4\\ x^2+4x+4&=&0\\ (x+2)^2&=&0\\ x&=&-2 \end{eqnarray*}⑦ $-4x^2=2x$
答え $x=0 ,\ x=-\cfrac{1}{2}$
\begin{eqnarray*} -4x^2&=&2x\quad(両辺を-2で割る)\\ 2x^2&=&-x\\ 2x^2+x&=&0\\ x(2x+1)&=&0\\ x&=&0 ,\ x=-\cfrac{1}{2} \end{eqnarray*}⑧ $(x+2)^2=8$
答え $x=-2\pm 2\sqrt{2}$
\begin{eqnarray*} (x+2)^2&=&8 \\ x+2&=&\pm\sqrt{8}\\ x&=&-2\pm 2\sqrt{2} \end{eqnarray*}⑨ $(x+1)(x+2)=x+4$
答え $x=-1\pm\sqrt{3}$
\begin{eqnarray*} (x+1)(x+2)&=&x+4\\ x^2+3x+2&=&x+4\\ x^2+3x+2-x-4&=&0\\ x^2+2x-2&=&0\\ \end{eqnarray*} $2$ 次方程式の解の公式により、 \begin{eqnarray*} x&=&\cfrac{-2\pm\sqrt{2^2-4\times1\times(-2)}}{2\times1}\\ &=&\cfrac{-2\pm\sqrt{4+8}}{2}\\ &=&\cfrac{-2\pm\sqrt{12}}{2}\\ &=&\cfrac{-2\pm2\sqrt{3}}{2}\\ &=&-1\pm\sqrt{3} \end{eqnarray*}① 水が $200L$ はいった水槽から、毎分 $xL$ の割合で水を抜く。$2$ 分後の水の量は、$yL$ より多い。この数量の関係を不等式で表しなさい。
②次の式を$[\phantom{x}]$内の文字について解きなさい。
$\qquad 3x=2y+\cfrac{1}{2}\quad[y]$
答え $y=\cfrac{6x-1}{4}\\\left(\cfrac{3}{2}x-\cfrac{1}{4}も可\right)$
\begin{eqnarray*} 3x&=&2y+\cfrac{1}{2}\quad(左辺と右辺をとりかえる) \\ 2y+\cfrac{1}{2}&=&3x\quad(\times2) \\ 4y+1&=&6x\\ 4y&=&6x-1\\ y&=&\cfrac{6x-1}{4} \end{eqnarray*}③ $x=\sqrt{2}+\sqrt{3}, \ y=\sqrt{3}$ のとき、次の式の値を求めなさい。
$\qquad 2x^2-4xy+2y^2$
答え $4$
\begin{eqnarray*} &&2x^2-4xy+2y^2\\ &=&2(x^2-2xy+y^2)\\ &=&2(x-y)^2\\ &=&2(\sqrt{2}+\sqrt{3}-\sqrt{3})^2\\ &=&2(\sqrt{2})^2\\ &=&2\times2\\ &=&4 \end{eqnarray*} やり方が思いつかないときや自信がないときは、単に代入して計算すれば答えがでます。 \begin{eqnarray*} &&2x^2-4xy+2y^2\\ &=&2(\sqrt{2}+\sqrt{3})^2-4\times(\sqrt{2}+\sqrt{3})\times(\sqrt{3})+2\times(\sqrt{3})^2\\ &=&2(2+2\sqrt{6}+3)-4\times(\sqrt{6}+3)+2\times3\\ &=&4+4\sqrt{6}+6-4\sqrt{6}-12+6\\ &=&4 \end{eqnarray*}④ $y$ が $x$ に比例し、$x=\cfrac{1}{2}$ のとき、$y=3$ である。$x=-4$ のときの $y$ の値を求めなさい。
答え $y=-24$
比例の式の形は $y=ax$この式に $x=\cfrac{1}{2}, \ y=3$ を代入して、 \begin{eqnarray*} 3&=&\cfrac{1}{2}a\quad両辺に\times2\\ 6&=&a \end{eqnarray*} $y=6x$ に $x=-4$ を代入する \begin{eqnarray*} y=6\times(-4)=-24 \end{eqnarray*}
⑤ $y$ が $x$ に反比例し、$x=\cfrac{1}{2}$ のとき、$y=6$ である。$x=-9$ のときの $y$ の値を求めなさい。
答え $y=-\cfrac{1}{3}$
反比例の式の形は $y=\cfrac{a}{x}$ $$a=x \times y=\cfrac{1}{2}\times6=3\\ y=\cfrac{3}{x}\ に\ x=-9\ を代入する\\ y=\cfrac{3}{-9}=-\cfrac{1}{3}$$⑥ $2$ 点 $(-8, \ -3), \ (4, \ 6)$ を通る直線の式を求めなさい。
答え $y=\cfrac{3}{4}x+3$
直線の式の形は $y=ax+b$ \begin{eqnarray*} a&=&\cfrac{y_2-y_1}{x_2-x_1}\\ &=&\cfrac{6-(-3)}{4-(-8)}=\cfrac{9}{12}=\cfrac{3}{4}\\ \end{eqnarray*} $y=\cfrac{3}{4}x+b$ に $x=4,\ y=6$ を代入 \begin{eqnarray*} 6&=&\cfrac{3}{4}\times4+b\\ 6&=&3+b\\ 3&=&b \end{eqnarray*}⑦ $y$ が $x$ の $2$ 乗に比例し、$x=2$ のとき、$y=2$ である。$x=-\cfrac{1}{2}$ のときの $y$ の値を求めなさい。
答え $y=\cfrac{1}{8}$
$2$ 乗に比例する関数の式の形は $y=ax^2$$y=ax^2$ に $x=2, \ y=2$ を代入 \begin{eqnarray*} 2&=&a\times(2)^2\\ 2&=&4a\\ \cfrac{1}{2}&=&a \end{eqnarray*} $y=\cfrac{1}{2}x^2$ に $ x=-\cfrac{1}{2}$ を代入する
$$y=\cfrac{1}{2}\times\left(-\cfrac{1}{2}\right)^2=\cfrac{1}{2}\times\cfrac{1}{4}=\cfrac{1}{8}$$
⑧ 大小 $2$ 個のサイコロを同時に投げるとき、大、小のサイコロの出た目をそれぞれ $a, \ b$ とする。 $\sqrt{ab}\lt3$ となる確率を求めなさい。
答え $\cfrac{4}{9}$
$2$ 乗しても数の大小関係は変わらないので、
\begin{eqnarray*}
\sqrt{ab}&\lt&3\\
(\sqrt{ab})^2&\lt&(3)^2\\
ab&\lt&9\\
\end{eqnarray*}
$ab$ を表にするとこうなる。
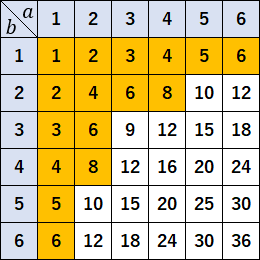
オレンジ色のところが問題にあうところ。
$$\cfrac{16}{36}=\cfrac{4}{9}$$
⑨ 袋の中に赤玉が $3$ 個と白玉が $2$ 個と青玉が $1$ 個はいっている。袋の中から玉を $1$ 個取り出してからそれを袋にもどし、また $1$ 個取り出す。このとき、取り出した玉の色のうち、少なくとも $1$ 個が白である確率を求めなさい。
答え $\cfrac{5}{9}$
①,②,③,④,⑤, ⑥と、$6$ 個の玉に番号をつけてしまいます。そして、①と②と③が赤玉、④と⑤が白玉、⑥が青玉ということにします。①②③④⑤⑥という感じ。
んで、樹形図をかいてもいけます。または、サイコロの問題のときのような表をかいてもいいです。ここでは表でやることにすると、
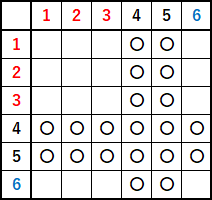
「玉を $1$ 個取り出してからそれを袋にもどし、また $1$ 個取り出す」ときは、同じ玉を取り出せるので、表にナナメ線は入れません。〇をつけたところが問題にあうところで、
$$\cfrac{20}{36}=\cfrac{5}{9}$$
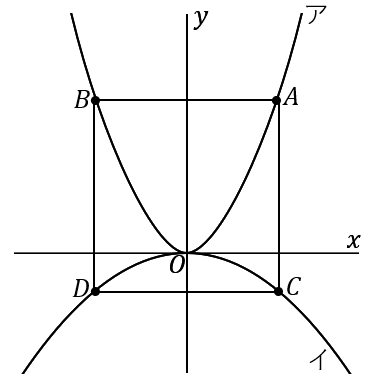
$①$ 点 $A$ の $x$ 座標が $3$ であるとき、点 $D$ の座標を求めなさい。
答え
$\left(-3, \ -\cfrac{9}{2}\right)$
 点 $A$ と点 $B$ は $y$ 軸について対称な点です。点 $A$ の $x$ 座標が $3$ ならば、点 $B$ の $x$ 座標は $-3$ になります。
点 $A$ と点 $B$ は $y$ 軸について対称な点です。点 $A$ の $x$ 座標が $3$ ならば、点 $B$ の $x$ 座標は $-3$ になります。
点 $B$ と点 $D$ の $x$ 座標は同じです。点 $B$ の $x$ 座標が $-3$ ならば、点 $D$ の $x$ 座標も $-3$ になります。
これで点 $D$ の $x$ 座標は $-3$ だとわかりました。あとは $y$ 座標を求めればよいです。
点 $D$ は曲線イ上の点で、曲線イの式は $y=-\cfrac{1}{2}x^2$ です。
$y=-\cfrac{1}{2}x^2$ に $x=-3$ を代入して、
\begin{eqnarray*}
y&=&-\cfrac{1}{2}\times(-3)^2=-\cfrac{9}{2}
\end{eqnarray*}
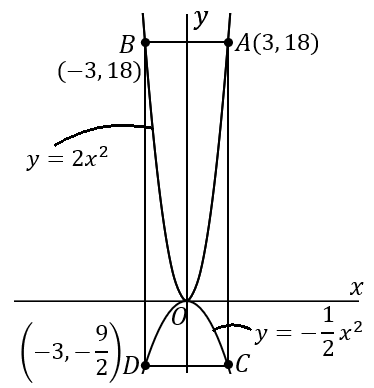
$②$ 四角形 $ABDC$ が正方形となるとき、点 $A$ の座標を求めなさい。
答え
$\left(\cfrac{4}{5}, \ \cfrac{32}{25}\right)$
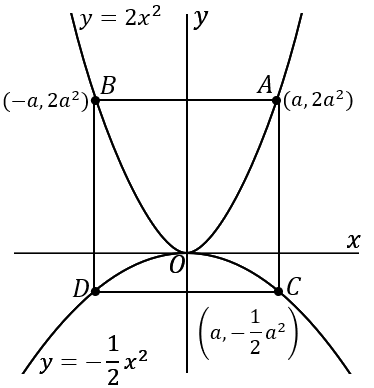 $AB$ の長さと $AC$ の長さを文字を使って表して、それが等しいということでやっていけばよいです。
$AB$ の長さと $AC$ の長さを文字を使って表して、それが等しいということでやっていけばよいです。
<点 $A$ の座標>
求めたい点です。点 $A$ の $x$ 座標を $a$ だということにします。文字はなんでもかまいません。ここでは $a$ ということにします。すると $y$ 座標は $2a^2$ ということになります。点 $A$ は関数 $y=2x^2$ 上の点だからです。点 $A$ の $x$ 座標を $a$ とすると、点 $A$ の座標は $\left(a, \ 2a^2\right)$ ということになります。
<点 $B$ の座標>
点 $B$ は、点 $A$ と $y$ 軸について対称です。点 $A$ の座標が $(a, \ 2a^2)$ ならば、点 $B$ の座標は $(-a, \ 2a^2)$ です。
<点 $C$ の座標>
点 $C$ は、$x$ 座標が点 $A$ の $x$ 座標と同じです。点 $A$ の $x$ 座標が $a$ ならば、点 $C$ の $x$ 座標も $a$ です。点 $C$ は関数 $y=-\cfrac{1}{2}x^2$ の上の点なのですから、$x$ 座標が $a$ ならば $y$ 座標は $-\cfrac{1}{2}a^2$ です。点 $A$ の座標が $(a, \ 2a^2)$ ならば、点 $C$ の座標は $\left(a, \ -\cfrac{1}{2}a^2\right)$ です。
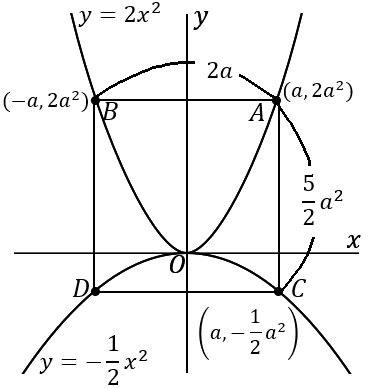 <$AB$ の長さ>
<$AB$ の長さ>
$AB$ の長さは、$2$ 点 $A, \ B$ の $x$ 座標の差をいえばよいです。
$$AB=a-(-a)=2a$$
<$AC$ の長さ>
$AC$ の長さは、$2$ 点 $A, \ C$ の $y$ 座標の差をいえばよいです。
$$AC=2a^2-\left(-\cfrac{1}{2}a^2\right)=\cfrac{5}{2}a^2$$
四角形 $ABDC$ が正方形であるということは、$AB=AC$ です。このことから式をたてて $a$ を求めていきます。
\begin{eqnarray*}
AB&=&AC\\
2a&=&\cfrac{5}{2}a^2\\
\cfrac{5}{2}a^2-2a&=&0\quad両辺に\times2\\
5a^2-4a&=&0\\
a(5a-4)&=&0\\
a&=&0, \ a=\cfrac{4}{5}
\end{eqnarray*}
$a\gt0$ ですから、$a=\cfrac{4}{5}$ です。
点 $A$ の座標を $(a, 2a^2)$ ということにしてやってきて $a$ の値が求まりました。なので答えは、
$$\left(\cfrac{4}{5}, \ \cfrac{32}{25}\right)$$
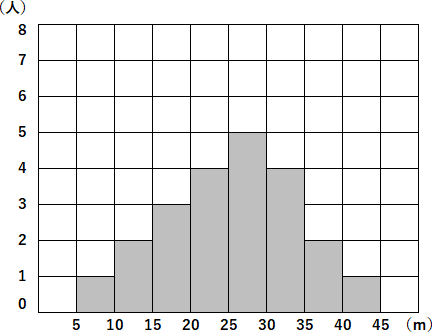
この記録の平均値を、小数第 $3$ 位を四捨五入して答えなさい。
答え
$25.45$
平均値は、記録ぜんぶを足して人数で割ればよいです。こういうとき、記録は、階級値を使います。
$(7.5\times1$+$12.5\times2$+$17.5\times3$+$22.5\times4$+$27.5\times5$+$32.5\times4$+$37.5\times2$+$42.5)\div22$
$=560\div22=25.454...$
<もうちょっとラクに>
さすがにこれだけの計算をやるとどこかでミスしそうで心配です。「仮平均」でやるとちょこっとラクにやれます。
度数のいちばん多い $25$~$30$ のところの階級値を仮平均にします。$27.5$ を $0$ だということにするわけです。そして計算をすると、
$\{(-20\times2)$+$(-15\times2)$+$(-10\times3)$+$(-5\times4)$+$(0\times5)$+$(5\times4)$+$(10\times2)$+$(15\times1)\}\div22$
$=-45\div22=-2.0454...$
んで$27.5$ との差をだして小数第 $3$ 位を四捨五入すれば答えです。
$27.5-2.0454...=25.454...$
このとき、小数第 $3$ 位の数が $4$ や $5$ になっているときは、答えをまちがえる可能性があるので、意味を考えてから答えましょう。平均を $-2.045$ として、
$27.5-2.045=25.455$ とすると、小数第 $3$ 位を四捨五入したら $25.46$ です。これはまちがいです。こういうことがあるので注意してください。
答え
$\boxed{\large{\ 1\ }}①2②-6③-\cfrac{9}{10}④4x-1\\ ⑤\cfrac{-8x-9y}{30}\quad\left(-\cfrac{8x+9y}{30},-\cfrac{4}{15}x-\cfrac{3}{10}yも可\right)\\ ⑥2x^2-34x-17⑦\cfrac{6\sqrt{5}}{5}\\ \boxed{\large{\ 2\ }}①12xy(4x-5y+1)②(x+2)(x-15)\\ ③\left(\cfrac{1}{2}x-y\right)^2④(11x+13y)(11x-13y)\\ ⑤25(x+2)(x-2)\\ \boxed{\large{\ 3\ }}①x=-\cfrac{1}{4}②x=-\cfrac{1}{2}, \ y=-1\\ ③x=3, \ y=-2④x=16, \ x=-3\\ ⑤x=\pm\cfrac{\sqrt{2}}{2}⑥x=-2⑦x=0 ,\ x=-\cfrac{1}{2}\\ ⑧x=-2\pm2\sqrt{2}⑨x=-1\pm\sqrt{3}\\ \boxed{\large{\ 4\ }}①200-2x\gt y ②y=\cfrac{6x-1}{4}\left(\cfrac{3}{2}x-\cfrac{1}{4}も可\right)\\ ③4 ④y=-24⑤y=-\cfrac{1}{3}⑥y=\cfrac{3}{4}x+3⑦y=\cfrac{1}{8}\\ ⑧\cfrac{4}{9}⑨\cfrac{5}{9}\\ \boxed{\large{\ 5\ }}①\left(-3, \ -\cfrac{9}{2}\right) ②\left(\cfrac{4}{5}, \ \cfrac{32}{25}\right)\\ \boxed{\large{\ 6\ }}25.45 $