中3数学 3学期の計算 第6回 全33問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
① $-3-4$
答え $-7$
② $-5\times(-3)^2-(-2^2)\times8$
答え $-13$
\begin{eqnarray*} &&-5\times(-3)^2-(-2^2)\times8\\ &=&-5\times9-(-4)\times8\\ &=&-5\times9+4\times8\\ &=&-45+32\\ &=&-13 \end{eqnarray*}③ $\cfrac{1}{2}+\cfrac{7}{12}\div\left(-\cfrac{3}{4}\right)$
答え $-\cfrac{5}{18}$
\begin{eqnarray*} &&\cfrac{1}{2}+\cfrac{7}{12}\div\left(-\cfrac{3}{4}\right)\\ &=&\cfrac{1}{2}+\cfrac{7}{12}\times\left(-\cfrac{4}{3}\right)\\ &=&\cfrac{1}{2}-\cfrac{7}{9}\\ &=&\cfrac{9}{18}-\cfrac{14}{18}\\ &=&-\cfrac{5}{18} \end{eqnarray*}④ $-5(x-3)+2(4x-8)$
答え $3x-1$
\begin{eqnarray*} &&-5(x-3)+2(4x-8)\\ &=&-5x+15+8x-16\\ &=&3x-1 \end{eqnarray*}⑤ $\cfrac{x-3y}{5}-\cfrac{2x-y}{2}$
答え $\cfrac{-8x-y}{10}\\\quad\left(-\cfrac{8x+y}{10},-\cfrac{4}{5}x-\cfrac{1}{10}yも可\right)$
\begin{eqnarray*} &&\cfrac{x-3y}{5}-\cfrac{2x-y}{2}\\ &=&\cfrac{2(x-3y)-5(2x-y)}{10}\\ &=&\cfrac{2x-6y-10x+5y}{10}\\ &=&\cfrac{-8x-y}{10} \end{eqnarray*}⑥ $2(3x-2)(x+4)-3(2x+3)^2$
答え $-6x^2-16x-43$
\begin{eqnarray*} &&2(3x-2)(x+4)-3(2x+3)^2\\ &=&2(3x^2+12x-2x-8)-3(4x^2+12x+9)\\ &=&2(3x^2+10x-8)-3(4x^2+12x+9)\\ &=&6x^2+20x-16-12x^2-36x-27\\ &=&-6x^2-16x-43 \end{eqnarray*}⑦ $-\cfrac{10}{\sqrt{3}}+\sqrt{6}\times\sqrt{8}$
答え $\cfrac{2\sqrt{3}}{3}$
\begin{eqnarray*} &&-\cfrac{10}{\sqrt{3}}+\sqrt{6}\times\sqrt{8}\\ &=&-\cfrac{10\sqrt{3}}{3}+\sqrt{48}\\ &=&-\cfrac{10\sqrt{3}}{3}+4\sqrt{3}\\ &=&-\cfrac{10\sqrt{3}}{3}+\cfrac{12\sqrt{3}}{3}\\ &=&\cfrac{2\sqrt{3}}{3} \end{eqnarray*}① $4a^2b-16ab^2-8ab$
答え $4ab(a-4b-2)$
② $x^2-25x+24$
答え $(x-1)(x-24)$
③ $\cfrac{1}{4}x^2-xy+y^2$
答え $\left(\cfrac{1}{2}x-y\right)^2$
④ $169x^2-196y^2$
答え $(13x+14y)(13x-14y)$
⑤ $ax+ay-x-y$
答え $(x+y)(a-1)$
\begin{eqnarray*} &&ax+ay-x-y\\ &=&a(x+y)-(x+y)\\ &=&aA-A\\ &=&A(a-1)\\ &=&(x+y)(a-1) \end{eqnarray*}① $-4x+1=\cfrac{x}{3}-12$
答え $x=3$
\begin{eqnarray*} -4x+1&=&\cfrac{x}{3}-12\quad(\times3) \\ -12x+3&=&x-36 \\ -12x-x&=&-36-3\\ -13x&=&-39 \\ x&=&3 \end{eqnarray*}② $\left\{\begin{array}{l} 0.3x+0.7y=4\\ 4x+21y=-5 \end{array}\right.$
答え $x=25,y=-5$
\begin{eqnarray*} \left\{ \begin{array}{l} 0.3x+0.7y=4\qquad…①\\ 4x+21y=-5\qquad…② \end{array} \right. \end{eqnarray*} $①を10倍する$ \begin{eqnarray*} 0.3x+0.7y&=&4\quad両辺に\times10\\ 3x+7y&=&40\qquad…③ \end{eqnarray*} $②-③\times3$ \begin{eqnarray*} 4x+21y=\phantom{2}-5\\ \underline{-) \quad 9x+21y=\phantom{-}120} \\ -5x\phantom{+21y}=-125\\ x=25\phantom{-1} \end{eqnarray*} \begin{eqnarray*} x=25を②に代入\\ 4\times25+21y&=&-5\\ 100+21y&=&-5\\ 21y&=&-5-100\\ 21y&=&-105\\ y&=&-5 \\ \left\{ \begin{array}{l} x=25\\ y=-5 \end{array} \right. \end{eqnarray*}③ $ x-2y=2x+y-12=2 $
答え $x=6,y=2$
$x-2y=2x+y-12=2$ のまんなかを隠した式をつくり、①とする。左側を隠した式をつくり、②とする。
①と②を連立方程式として解く。 \begin{eqnarray*} \left\{ \begin{array}{l} x-2y=2\qquad…①\\ 2x+y-12=2\qquad…② \end{array} \right. \end{eqnarray*} $②を整理$ \begin{eqnarray*} 2x+y-12&=&2\\ 2x+y&=&2+12\\ 2x+y&=&14\qquad…③ \end{eqnarray*} $①\times2-②\times2$ \begin{eqnarray*} 2x-4y=\phantom{-1}4\\ \underline{-) \quad 2x+\phantom{4}y=\phantom{-}14} \\ -5y=-10\\ y=2\phantom{-4} \end{eqnarray*} \begin{eqnarray*} y=2を①に代入\\ x-2\times2&=&2\\ x-4&=&2\\ x&=&2+4\\ x&=&6 \\ \left\{ \begin{array}{l} x=6\\ y=2 \end{array} \right. \end{eqnarray*}
④ $x^2-x-56=0$
答え $x=8 ,\ x=-7$
\begin{eqnarray*} x^2-x-56&=&0 \\ (x-8)(x+7)&=&0\\ x&=&8,\ x=-7 \end{eqnarray*}⑤ $\cfrac{5}{2}x^2-4=0$
答え $x=\pm\cfrac{2\sqrt{10}}{5}$
\begin{eqnarray*} \cfrac{5}{2}x^2-4&=&0 \quad(両辺に\times2)\\ 5x^2-8&=&0\\ 5x^2&=&8\\ x^2&=&\cfrac{8}{5}\\ x&=&\pm\sqrt{\cfrac{8}{5}}=\pm\cfrac{\sqrt{8}}{\sqrt{5}}=\pm\cfrac{2\sqrt{2}}{\sqrt{5}}=\pm\cfrac{2\sqrt{10}}{5} \end{eqnarray*}⑥ $0.04x^2+1=0.4x$
答え $x=5$
\begin{eqnarray*} 0.04x^2+1&=&0.4x \\ 0.04x^2-0.4x+1&=&0 \quad(両辺に\times100)\\ 4x^2-40x+100&=&0x \quad\left(両辺に\times\cfrac{1}{4}\right)\\ x^2-10x+25&=&0\\ (x-5)^2&=&0\\ x&=&5 \end{eqnarray*}⑦ $36x^2=49x$
答え $x=0 ,\ x=\cfrac{49}{36}$
\begin{eqnarray*} 36x^2&=&49x\\ 36x^2-49x&=&0\\ x(36x-49)&=&0\\ x&=&0 ,\ x=\cfrac{49}{36} \end{eqnarray*}⑧ $(x+2)^2=\cfrac{1}{4}$
答え $x=-\cfrac{3}{2}, \ x=-\cfrac{5}{2}$
\begin{eqnarray*} (x+2)^2&=&\cfrac{1}{4} \\ x+2&=&\pm\sqrt{\cfrac{1}{4}}=\pm\cfrac{\sqrt{1}}{\sqrt{4}}=\pm\cfrac{1}{2}\\ x&=&-2\pm \cfrac{1}{2}\\ x&=&-2+\cfrac{1}{2}, \ x=-2-\cfrac{1}{2}\\ x&=&-\cfrac{3}{2}, \ x=-\cfrac{5}{2} \end{eqnarray*}⑨ $3x^2+6x+2=0\\$
答え $x=\cfrac{-3\pm\sqrt{3}}{3}$
$2$ 次方程式の解の公式により、 \begin{eqnarray*} x&=&\cfrac{-6\pm\sqrt{6^2-4\times3\times2}}{2\times3}\\ &=&\cfrac{-6\pm\sqrt{36-24}}{6}\\ &=&\cfrac{-6\pm\sqrt{12}}{6}\\ &=&\cfrac{-6\pm2\sqrt{3}}{6}\\ &=&\cfrac{-3\pm\sqrt{3}}{3} \end{eqnarray*}① $1$ 個 $x$ 円のハンバーガーを $2$ 個と、$y$ 円の飲み物を $1$ つ買い、$1000$ 円を払ったらおつりがもらえた。この数量の関係を不等式で表しなさい。
②次の式を$[\phantom{x}]$内の文字について解きなさい。
$\qquad 5a-10b=2\quad[b]$
答え $b=\cfrac{5a-2}{10}\\\left(\cfrac{1}{2}a-\cfrac{1}{5}も可\right)$
\begin{eqnarray*} 5a-10b&=&2 \\ -10b&=&-5a+2 \quad両辺に\times(-1)\\ 10b&=&5a-2\\ b&=&\cfrac{5a-2}{10} \end{eqnarray*}③ $a=\sqrt{5}+\sqrt{3}, \ b=\sqrt{5}-\sqrt{3}$ のとき、次の式の値を求めなさい。
$\qquad a^2-2ab+b^2$
答え $12$
\begin{eqnarray*} &&a^2-2ab+b^2\\ &=&(a-b)^2\\ &=&\{(\sqrt{5}+\sqrt{3})-(\sqrt{5}-\sqrt{3})\}^2\\ &=&(\sqrt{5}+\sqrt{3}-\sqrt{5}+\sqrt{3})^2\\ &=&(2\sqrt{3})^2\\ &=&12 \end{eqnarray*} やり方が思いつかないときや自信がないときは、単に代入して計算すれば答えがでます。 \begin{eqnarray*} &&a^2-2ab+b^2\\ &=&(\sqrt{5}+\sqrt{3})^2-2(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})+(\sqrt{5}-\sqrt{3})^2\\ &=&5+2\sqrt{15}+3-2(5-3)+5-2\sqrt{15}+3\\ &=&5+2\sqrt{15}+3-4+5-2\sqrt{15}+3\\ &=&12 \end{eqnarray*}④ $y$ が $x$ に比例し、$x=-2$ のとき、$y=6$ である。$x=3$ のときの $y$ の値を求めなさい。
答え $y=-9$
比例の式の形は $y=ax$\begin{eqnarray*} a=\cfrac{y}{x}=\cfrac{6}{-2}=-3 \end{eqnarray*} $y=-3x$ に $x=3$ を代入する \begin{eqnarray*} y=-3\times3=-9 \end{eqnarray*}
⑤ $y$ が $x$ に反比例し、$x=-2$ のとき、$y=6$ である。$x=3$ のときの $y$ の値を求めなさい。
答え $y=-4$
反比例の式の形は $y=\cfrac{a}{x}$ $$a=x \times y=-2\times6=-12\\ y=-\cfrac{12}{x}\ に\ x=3\ を代入する\\ y=-\cfrac{12}{3}=-4$$⑥ 関数 $y=\cfrac{1}{2}x^2$ について、$x$ の変域が $-2 \leqq x \leqq 8$ のとき、$y$ の変域を求めなさい。
答え $0 \leqq y \leqq 32$
まず、答えの形はこうです。
$$小 \leqq y \leqq 大$$
んで、小と大にそれぞれ、小さい数と大きい数を書いておけばいいです。それを求めるためには、場合分けをしていきます。
①$x$ の変域が $0$ をまたいでいるか。
②$x$ の変域が $0$ をまたいでいるのなら、$a$ はプラスかマイナスか。
この問題は、$x$ の変域が $-2 \leqq x \leqq 8$ だから、$0$ をまたいでいます。この場合は、次に $y=ax^2$ の $a$ の符号がプラスかマイナスかをみます。この問題は、$\cfrac{1}{2}$ だからプラス。 $a$ がプラスのときは答えは
$$0 \leqq y \leqq 数$$
となります。 $a$ がプラスのときは、左側(最小値)が $0$ です。右側の数(最大値)は、$x$ の変域、 $-2 \leqq x \leqq 8$ の両はじの数のうち、$0$ から遠いほうを $y=\cfrac{1}{2}x^2$ に代入してでてくる数です。$-2$ と $8$ は、どちらのほうが $0$ から遠いかといえば、もちろん $8$ です。この $8$ を $y=\cfrac{1}{2}x^2$ に代入します。
$$y=\cfrac{1}{2}×8^2=\cfrac{1}{2}×64=32$$
この $32$ というのが、答えの右側の数(最大値)です。
⑦ 関数 $y=2x^2$ で、$x$ の値が $x=-3$ から $x=-1$ まで変化するときの、変化の割合を求めなさい。
答え $-8$
「関数 $y=ax^2$ について、$x$ の値が $x_1$ から $x_2$ まで変化するときの、変化の割合は?」ときかれたら、 $$変化の割合=(x_1+x_2)\times a$$ この問題は、どれとどれを足して、どれを掛けたら変化の割合になっているか、やってみると、 $$\{-3+(-1)\}×2=-8$$
⑧ $\sqrt{24n}$ の値ができるだけ小さい整数になるときの、正の整数 $n$ の値を求めなさい。
答え $n=6$
\begin{eqnarray*}
2) \underline{\quad 24} \\
2) \underline{\quad 12} \\
2) \underline{\quad \phantom{2}6} \\
\qquad 3
\end{eqnarray*}
やりかた
手順1 素因数分解してください。
手順2 同じ数が$2$つあったら、そこを〇で囲ってください。
手順3 〇がつかなかった数をかけてください。
その数が答えです。ルートを直すときとおなじような感じです。アレをやればいいです。
この問題の場合は、$6$ が答えだとすると、$\sqrt{24\times6}=\sqrt{144}=12$ となります。
⑨ 袋の中に赤玉が $2$ 個と青玉が $1$ 個と白玉が $1$ 個入っている。袋の中から玉を $2$ 個同時に取り出すとき、取り出した玉の色が同じである確率を求めなさい。
答え $\cfrac{1}{6}$
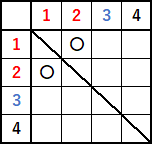 ①,②,③,④と、$4$ 個の玉に番号をつけてしまいます。そして、①と②が赤玉、③が青玉、④が白玉ということにします。①②③④という感じです。で、表をかくとこんな感じです。
①,②,③,④と、$4$ 個の玉に番号をつけてしまいます。そして、①と②が赤玉、③が青玉、④が白玉ということにします。①②③④という感じです。で、表をかくとこんな感じです。
「玉を $2$ 個同時に取り出す」のですから、同じ玉を $2$ 回取り出すことはできません。こういうとき、表にはナナメの線がはいります。〇印のついたところが、玉の色が同じところです。
$$\cfrac{2}{12}=\cfrac{1}{6}$$
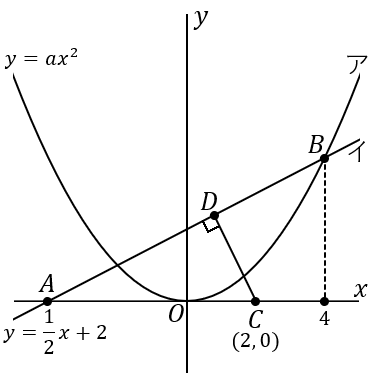
$①$ $a$ の値を求めなさい
答え
$a=\cfrac{1}{4}$
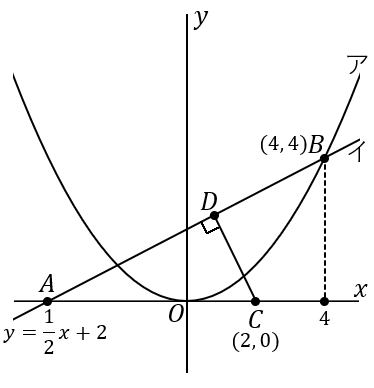 点 $B$ は直線イ上の点なのですから、その座標が求められます。点 $B$ が求められれば、曲線アの式が求まります。
点 $B$ は直線イ上の点なのですから、その座標が求められます。点 $B$ が求められれば、曲線アの式が求まります。
<点 $B$ の座標>
点 $B$ の $x$ 座標は $4$ です。また、点 $B$ は直線イ上の点なのですから、$y=\cfrac{1}{2}x+2$ に $x=4$ を代入して、
\begin{eqnarray*}
y&=&\cfrac{1}{2}\times4+2=4
\end{eqnarray*}
これで点 $B$ は $(4, \ 4)$ だとわかりました。
<$a$ の値>
曲線アは $y=ax^2$ です。これが点 $B$ を通るのですから、 $y=ax^2$ に $x=4, \ y=4$ を代入して、
\begin{eqnarray*}
4&=&a\times4^2\\
4&=&16a\\
16a&=&4\\
a&=&\cfrac{4}{16}=\cfrac{1}{4}\\
\end{eqnarray*}
$②$ 線分 $AD$ の長さを求めなさい。
答え
$\cfrac{12\sqrt{5}}{5}$
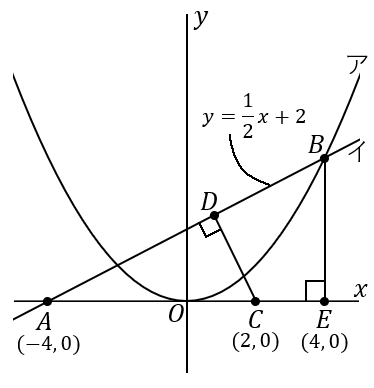 点 $B$ から $x$ 軸に垂線をおろし、$x$ 軸との交点を $E$ とします。すると、$\triangle ABE$ ∽$\triangle ACD$ となります。$A$ のところの角が共通で、あと直角は等しいので、$2$ 組の角がそれぞれ等しくなります。だから相似です。このように、この問題は三角形の相似を利用します。
点 $B$ から $x$ 軸に垂線をおろし、$x$ 軸との交点を $E$ とします。すると、$\triangle ABE$ ∽$\triangle ACD$ となります。$A$ のところの角が共通で、あと直角は等しいので、$2$ 組の角がそれぞれ等しくなります。だから相似です。このように、この問題は三角形の相似を利用します。
<点 $A$ の座標>
点 $A$ は $x$ 軸上の点ですから、$y=0$ です。また、関数 $y=\cfrac{1}{2}x+2$ 上の点なのですから、この式に $y=0$ を代入すると、
\begin{eqnarray*}
0&=&\cfrac{1}{2}x+2\\
-\cfrac{1}{2}x&=&2\quad両辺に\times2\\
-x&=&4\\
x&=&-4\\
\end{eqnarray*}
となります。点 $A$ の座標は $(-4, \ 0)$ です。
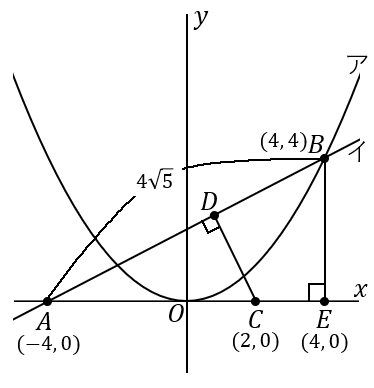 <点 $B$ の座標>
<点 $B$ の座標>
①の問題で求めたように、点 $B$ の座標は $(4, \ 4)$ です。
<線分 $AB$ の長さ>
$2$ 点 $A, \ B$ 間の距離をいえばよいです。点 $A(-4, \ 0)$ と点 $B(4, \ 4)$ の間の距離は、
\begin{eqnarray*}
AB&=&\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\
&=&\sqrt{\{(4-(-4)\}^2+(4-0)^2}\\
&=&\sqrt{64+16}\\
&=&\sqrt{80}\\
&=&4\sqrt{5}\\
\end{eqnarray*}
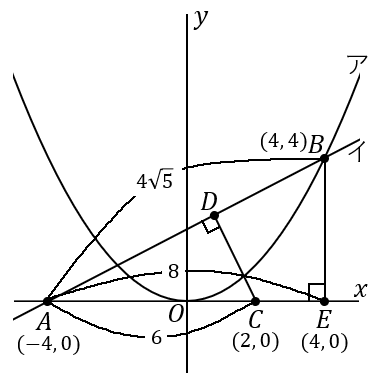 <線分 $AC$ の長さ>
<線分 $AC$ の長さ>
点 $A$ と点 $C$ の $x$ 座標の差をいえばよいです。
\begin{eqnarray*}
AC=2-(-4)=6
\end{eqnarray*}
<線分 $AE$ の長さ>
点 $A$ と点 $E$ の $x$ 座標の差をいえばよいです。
\begin{eqnarray*}
AE=4-(-4)=8
\end{eqnarray*}
 <$AD$ の長さ>
<$AD$ の長さ>
$\triangle ABE$ ∽$\triangle ACD$ より、
\begin{eqnarray*}
AB:AC&=&AE:AD\\
4\sqrt{5}:6&=&8:AD\\
4\sqrt{5}\times AD&=&48\\
AD&=&\cfrac{48}{4\sqrt{5}}=\cfrac{12}{\sqrt{5}}=\cfrac{12\sqrt{5}}{5}
\end{eqnarray*}
<別解>
座標平面上で、垂直な $2$ 直線は、傾きどうしをかけると $-1$ になります。そういうことになってます。なので、$y=\cfrac{1}{2}x+2$ と垂直な直線の傾きは、$-2$ です。
傾きが $-2$ で、点 $C(2, \ 0)$ を通る直線の切片 $b$ は、$y=-2x+b$ に $x=2, \ y=0$ を代入して、
\begin{eqnarray*}
0&=&-2\times2+b\\
0&=&-4+b\\
4&=&b
\end{eqnarray*}
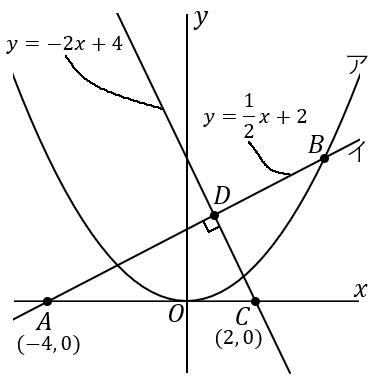 なので、$y=-2x+4$ というのが、点 $C$ を通って $y=\cfrac{1}{2}x+2$ に垂直な直線の方程式です。点 $D$ の座標は、この $2$ 直線の交点をいえばよいのだから、
\begin{eqnarray*}
\left\{
\begin{array}{l}
y=\cfrac{1}{2}x+2\\
y=-2x+4
\end{array}
\right.
\end{eqnarray*}
を解けばよいです。右辺=右辺の式をたてて、
\begin{eqnarray*}
\cfrac{1}{2}x+2&=&-2x+4\quad両辺に\times2\\
x+4&=&-4x+8\\
x+4x&=&8-4\\
5x&=&4\\
x&=&\cfrac{4}{5}
\end{eqnarray*}
$y=-2x+4$ に $x=\cfrac{4}{5}$ を代入して、
\begin{eqnarray*}
y&=&-2\times\cfrac{4}{5}+4\\
&=&-\cfrac{8}{5}+\cfrac{20}{5}\\
&=&\cfrac{12}{5}
\end{eqnarray*}
なので、$y=-2x+4$ というのが、点 $C$ を通って $y=\cfrac{1}{2}x+2$ に垂直な直線の方程式です。点 $D$ の座標は、この $2$ 直線の交点をいえばよいのだから、
\begin{eqnarray*}
\left\{
\begin{array}{l}
y=\cfrac{1}{2}x+2\\
y=-2x+4
\end{array}
\right.
\end{eqnarray*}
を解けばよいです。右辺=右辺の式をたてて、
\begin{eqnarray*}
\cfrac{1}{2}x+2&=&-2x+4\quad両辺に\times2\\
x+4&=&-4x+8\\
x+4x&=&8-4\\
5x&=&4\\
x&=&\cfrac{4}{5}
\end{eqnarray*}
$y=-2x+4$ に $x=\cfrac{4}{5}$ を代入して、
\begin{eqnarray*}
y&=&-2\times\cfrac{4}{5}+4\\
&=&-\cfrac{8}{5}+\cfrac{20}{5}\\
&=&\cfrac{12}{5}
\end{eqnarray*}
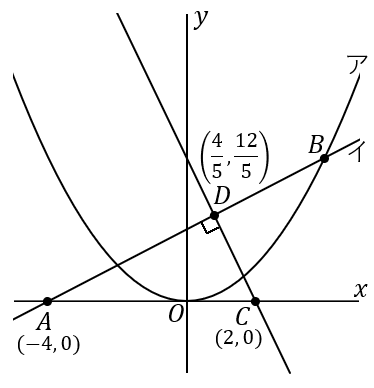 点 $D$ の座標は $\left(\cfrac{4}{5}, \ \cfrac{12}{5}\right)$ です。
線分 $AD$ の長さは、点 $A(-4, \ 0)$ と点 $D\left(\cfrac{4}{5}, \ \cfrac{12}{5}\right)$ の間の距離をいえばよいのだから、
\begin{eqnarray*}
AD&=&\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\
&=&\sqrt{\left( \cfrac{4}{5}-(-4) \right)^2+\left(\cfrac{12}{5}-0\right)^2}\\
&=&\sqrt{\left(\cfrac{24}{5}\right)^2+\left(\cfrac{12}{5}\right)^2}\\
&=&\sqrt{\cfrac{576}{25}+\cfrac{144}{25}}\\
&=&\sqrt{\cfrac{720}{25}}\\
&=&\cfrac{\sqrt{720}}{\sqrt{25}}\\
&=&\cfrac{12\sqrt{5}}{5}
\end{eqnarray*}
点 $D$ の座標は $\left(\cfrac{4}{5}, \ \cfrac{12}{5}\right)$ です。
線分 $AD$ の長さは、点 $A(-4, \ 0)$ と点 $D\left(\cfrac{4}{5}, \ \cfrac{12}{5}\right)$ の間の距離をいえばよいのだから、
\begin{eqnarray*}
AD&=&\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\
&=&\sqrt{\left( \cfrac{4}{5}-(-4) \right)^2+\left(\cfrac{12}{5}-0\right)^2}\\
&=&\sqrt{\left(\cfrac{24}{5}\right)^2+\left(\cfrac{12}{5}\right)^2}\\
&=&\sqrt{\cfrac{576}{25}+\cfrac{144}{25}}\\
&=&\sqrt{\cfrac{720}{25}}\\
&=&\cfrac{\sqrt{720}}{\sqrt{25}}\\
&=&\cfrac{12\sqrt{5}}{5}
\end{eqnarray*}
\begin{array}{c|cccccccccc} \hline 生徒 & A & B & C & D & E & F & G & H & I & J\\ \hline 得点 & 26 & 62 & 48 & 12 & 87 & 74 & 42 & 37 & 21 & 33\\ \hline \end{array}
中央値(メジアン)を求めなさい。
答え
$39.5$
得点を低い順にならべると、
$$12,\ 21,\ 26,\ 33,\ 37,\ 42,\ 48,\ 62,\ 74,\ 87$$
$10$ 人の中央値(メジアン)は $5$ 番目と $6$ 番目の平均ですから、
$$(37+42)\div2=39.5$$
答え
$\boxed{\large{\ 1\ }}①-7②-13③-\cfrac{5}{18}④3x-1\\ ⑤\cfrac{-8x-y}{10}\quad\left(-\cfrac{8x+y}{10},-\cfrac{4}{5}x-\cfrac{1}{10}yも可\right)\\ ⑥-6x^2-16x-43⑦\cfrac{2\sqrt{3}}{3}\\ \boxed{\large{\ 2\ }}①4ab(a-4b-2)②(x-1)(x-24)\\ ③\left(\cfrac{1}{2}x-y\right)^2④(13x+14y)(13x-14y)\\ ⑤(x+y)(a-1)\\ \boxed{\large{\ 3\ }}①x=3②x=25, \ y=-5\\ ③x=6, \ y=2④x=8, \ x=-7\\ ⑤x=\pm\cfrac{2\sqrt{10}}{5}⑥x=5⑦x=0 ,\ x=\cfrac{49}{36}\\ ⑧x=-\cfrac{3}{2}, \ x=-\cfrac{5}{2}⑨x=\cfrac{-3\pm\sqrt{3}}{3}\\ \boxed{\large{\ 4\ }}①2x+y\lt 1000 ②b=\cfrac{5a-2}{10}\left(\cfrac{1}{2}a-\cfrac{1}{5}も可\right)\\ ③12 ④y=-9⑤y=-4⑥0 \leqq y \leqq 32\\ ⑦-8 ⑧6⑨\cfrac{1}{6}\\ \boxed{\large{\ 5\ }}①a=\cfrac{1}{4} ②\cfrac{12\sqrt{5}}{5}\\ \boxed{\large{\ 6\ }}39.5 $