中3数学 3学期の計算 第7回 全33問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
① $-5+(-4)$
答え $-9$
\begin{eqnarray*} &&-5+(-4)\\ &=&-5-4\\ &=&-9 \end{eqnarray*}② $(-3)\times(-2)-3^2\times2$
答え $-12$
\begin{eqnarray*} &&(-3)\times(-2)-3^2\times2\\ &=&(-3)\times(-2)-9\times2\\ &=&6-18\\ &=&-12 \end{eqnarray*}③ $-\cfrac{1}{6}+\cfrac{3}{5}\div\left(-\cfrac{9}{10}\right)$
答え $-\cfrac{5}{6}$
\begin{eqnarray*} &&-\cfrac{1}{6}+\cfrac{3}{5}\div\left(-\cfrac{9}{10}\right)\\ &=&-\cfrac{1}{6}+\cfrac{3}{5}\times\left(-\cfrac{10}{9}\right)\\ &=&-\cfrac{1}{6}-\cfrac{2}{3}\\ &=&-\cfrac{1}{6}-\cfrac{4}{6}\\ &=&-\cfrac{5}{6} \end{eqnarray*}④ $2(2x-3)+2(-3x+7)$
答え $-2x+8$
\begin{eqnarray*} &&2(2x-3)+2(-3x+7)\\ &=&4x-6-6x+14\\ &=&-2x+8 \end{eqnarray*}⑤ $\cfrac{x-4y}{8}-\cfrac{x-2y}{7}$
答え $\cfrac{-x-12y}{56}\\\quad\left(-\cfrac{x+12y}{56}, \ -\cfrac{1}{56}x-\cfrac{3}{14}yも可\right)$
\begin{eqnarray*} &&\cfrac{x-4y}{8}-\cfrac{x-2y}{7}\\ &=&\cfrac{7(x-4y)-8(x-2y)}{56}\\ &=&\cfrac{7x-28y-8x+16y}{56}\\ &=&\cfrac{-x-12y}{56} \end{eqnarray*}⑥ $(x-2)(x+4)-2(x+3)^2$
答え $-x^2-10x-26$
\begin{eqnarray*} &&(x-2)(x+4)-2(x+3)^2\\ &=&x^2+2x-8-2(x^2+6x+9)\\ &=&x^2+2x-8-2x^2-12x-18\\ &=&-x^2-10x-26 \end{eqnarray*}⑦ $-\sqrt{18}+\sqrt{10}\times\sqrt{5}$
答え $2\sqrt{2}$
\begin{eqnarray*} &&-\sqrt{18}+\sqrt{10}\times\sqrt{5}\\ &=&-3\sqrt{2}+\sqrt{50}\\ &=&-3\sqrt{2}+5\sqrt{2}\\ &=&2\sqrt{2} \end{eqnarray*}① $6p^2q-12pq^2$
答え $6pq(p-2q)$
② $x^2-9x+18$
答え $(x-3)(x-6)$
③ $x^2-2xy+y^2$
答え $(x-y)^2$
④ $x^2-9y^2$
答え $(x+3y)(x-3y)$
⑤ $ax+ay+x+y$
答え $(x+y)(a+1)$
\begin{eqnarray*} &&ax+ay+x+y\\ &=&a(x+y)+(x+y)\\ &=&aA+A\\ &=&A(a+1)\\ &=&(x+y)(a+1) \end{eqnarray*}① $2x+1=-x-\cfrac{1}{2}$
答え $x=-\cfrac{1}{2}$
\begin{eqnarray*} 2x+1&=&-x-\cfrac{1}{2}\quad(\times2) \\ 4x+2&=&-2x-1 \\ 4x+2x&=&-1-2\\ 6x&=&-3\\ x&=&-\cfrac{3}{6}=-\cfrac{1}{2} \end{eqnarray*}② $\left\{\begin{array}{l} 2x+y=1\\ x-2y=13 \end{array}\right.$
答え $x=3,y=-5$
\begin{eqnarray*} \left\{ \begin{array}{l} 2x+y=1\qquad…①\\ x-2y=13\qquad…② \end{array} \right. \end{eqnarray*} $①+②\times2$ \begin{eqnarray*} 4x+2y=\phantom{2}2\\ \underline{+) \quad x-2y=13} \\ 5x\phantom{+11y}=15\\ x=3\phantom{1} \end{eqnarray*} \begin{eqnarray*} x=3を①に代入\\ 2\times3+y&=&1\\ 6+y&=&1\\ y&=&1-6\\ y&=&-5 \\ \left\{ \begin{array}{l} x=3\\ y=-5 \end{array} \right. \end{eqnarray*}③ $ 3x+4y=x+3y=5 $
答え $x=-1,y=2$
$3x+4y=x+3y=5$ のまんなかを隠した式をつくり、①とする。左側を隠した式をつくり、②とする。
①と②を連立方程式として解く。 \begin{eqnarray*} \left\{ \begin{array}{l} 3x+4y=5\qquad…①\\ x+3y=5\qquad…② \end{array} \right. \end{eqnarray*} $①-②\times3$ \begin{eqnarray*} 3x+4y=\phantom{-1}5\\ \underline{-) \quad 3x+9y=\phantom{-}15} \\ -5y=-10\\ y=2\phantom{-4} \end{eqnarray*} \begin{eqnarray*} y=2を②に代入\\ x+3\times2&=&5\\ x+6&=&5\\ x&=&5-6\\ x&=&-1 \\ \left\{ \begin{array}{l} x=-1\\ y=2 \end{array} \right. \end{eqnarray*}
④ $x^2+19x+90=0$
答え $x=-9 ,\ x=-10$
\begin{eqnarray*} x^2+19x+90&=&0 \\ (x+9)(x+10)&=&0\\ x&=&-9,\ x=-10 \end{eqnarray*}⑤ $x^2-12=0$
答え $x=\pm2\sqrt{3}$
\begin{eqnarray*} x^2-12&=&0\\ x^2&=&12\\ x&=&\pm\sqrt{12}=\pm2\sqrt{3} \end{eqnarray*}⑥ $9x^2+4=12x$
答え $x=\cfrac{2}{3}$
\begin{eqnarray*} 9x^2+4&=&12x \\ 9x^2-12x+4&=&0\\ (3x-2)^2&=&0\\ x&=&\cfrac{2}{3} \end{eqnarray*}⑦ $5x^2=x$
答え $x=0 ,\ x=\cfrac{1}{5}$
\begin{eqnarray*} 5x^2&=&x\\ 5x^2-x&=&0\\ x(5x-1)&=&0\\ x&=&0 ,\ x=\cfrac{1}{5} \end{eqnarray*}⑧ $(x+3)^2=20$
答え $x=-3\pm 2\sqrt{5}$
\begin{eqnarray*} (x+3)^2&=&20 \\ x+3&=&\pm\sqrt{20}\\ x&=&-3\pm 2\sqrt{5} \end{eqnarray*}⑨ $2x^2+4x-1=0\\$
答え $x=\cfrac{-2\pm\sqrt{6}}{2}$
$2$ 次方程式の解の公式により、 \begin{eqnarray*} x&=&\cfrac{-4\pm\sqrt{4^2-4\times2\times(-1)}}{2\times2}\\ &=&\cfrac{-4\pm\sqrt{16+8}}{4}\\ &=&\cfrac{-4\pm\sqrt{24}}{4}\\ &=&\cfrac{-4\pm2\sqrt{6}}{4}\\ &=&\cfrac{-2\pm\sqrt{6}}{2} \end{eqnarray*}① $x$ 冊のノートを $1$ 人 $2$ 冊ずつ $y$ 人に配ったところ、$13$ 冊以上あまった。この数量の関係を不等式で表しなさい。
②次の式を$[\phantom{x}]$内の文字について解きなさい。
$\qquad y=\cfrac{4x-1}{3}\quad[x]$
答え $x=\cfrac{3y+1}{4}\\\left(\cfrac{3}{4}y+\cfrac{1}{4}も可\right)$
\begin{eqnarray*} y&=&\cfrac{4x-1}{3}\quad 左辺と右辺をとりかえる \\ \cfrac{4x-1}{3}&=&y \quad両辺に\times3\\ 4x-1&=&3y\\ 4x&=&3y+1\\ x&=&\cfrac{3y+1}{4} \end{eqnarray*}③ $a=\sqrt{2}+1$ のとき、次の式の値を求めなさい。
$\qquad a^2-2a$
答え $1$
\begin{eqnarray*} &&a^2-2a\\ &=&(\sqrt{2}+1)^2-2(\sqrt{2}+1)\\ &=&2+2\sqrt{2}+1-2\sqrt{2}-2\\ &=&1 \end{eqnarray*}④ $y$ が $x$ に比例し、$x=6$ のとき、$y=2$ である。$x=15$ のときの $y$ の値を求めなさい。
答え $y=5$
比例の式の形は $y=ax$\begin{eqnarray*} a=\cfrac{y}{x}=\cfrac{2}{6}=\cfrac{1}{3} \end{eqnarray*} $y=\cfrac{1}{3}x$ に $x=15$ を代入する \begin{eqnarray*} y=\cfrac{1}{3}\times15=5 \end{eqnarray*}
⑤ $y$ が $x$ に反比例し、$x=6$ のとき、$y=2$ である。$x=15$ のときの $y$ の値を求めなさい。
答え $y=\cfrac{4}{5}$
反比例の式の形は $y=\cfrac{a}{x}$ $$a=x \times y=6\times2=12\\ y=\cfrac{12}{x}\ に\ x=15\ を代入する\\ y=\cfrac{12}{15}=\cfrac{4}{5}$$⑥ 関数 $y=-2x^2$ について、$x$ の変域が $-6 \leqq x \leqq -3$ のとき、$y$ の変域を求めなさい。
答え $-72 \leqq y \leqq -18$
まず、答えの形はこうです。
$$小 \leqq y \leqq 大$$
んで、小と大にそれぞれ、小さい数と大きい数を書いておけばいいです。それを求めるためには、場合分けをしていきます。
$x$ の変域が $0$ をまたいでいるか。
この問題は、$x$ の変域が $-6 \leqq x \leqq -3$ だから、$0$ をまたいでいません。この場合のやり方は、単純に $-6 \leqq x \leqq -3$ の両はじにかかれている $-6$ と $-3$ を $y=-2x^2$ に代入して、でてきた数を
$$小 \leqq y \leqq 大$$
の小と大にあてはめればOKです。じゃあ答えていきます。
まず $x=-6$ を $y=-2x^2$ に代入。
$$y=-2×(-6)^2=-2×36=-72$$
つぎに $x=-3$ を $y=-2x^2$ に代入。
$$y=-2×(-3)^2=-2×9=-18$$
これで、$-72$ と $-18$ というふたつの数がえられました。これを小と大にあてはめればOKです。
⑦ 関数 $y=ax^2$ で、$x$ の値が $x=-6$ から $x=2$ まで変化するときの、変化の割合が $-2$ であるとき、$a$ の値を求めなさい。
答え $a=\cfrac{1}{2}$
「関数 $y=ax^2$ について、$x$ の値が $x_1$ から $x_2$ まで変化するときの、変化の割合は?」ときかれたら、 $$変化の割合=(x_1+x_2)\times a$$ この問題は、どれとどれを足して、どれを掛けたら変化の割合になっているか、やってみると、 $$\{(-6)+2\}\times a=-2$$ あとは解くだけです。 \begin{eqnarray*} \{(-6)+2\}\times a&=&-2\\ -4 a&=&-2\\ a&=&\cfrac{2}{4}=\cfrac{1}{2}\\ \end{eqnarray*}
⑧ $\sqrt{108n}$ の値ができるだけ小さい整数になるときの、正の整数 $n$ の値を求めなさい。
答え $n=3$
\begin{eqnarray*}
2) \underline{\quad 108} \\
2) \underline{\quad \phantom{1}54} \\
3) \underline{\quad \phantom{1}27} \\
3) \underline{\quad \phantom{10}9} \\
\qquad 3
\end{eqnarray*}
やりかた
手順1 素因数分解してください。
手順2 同じ数が$2$つあったら、そこを〇で囲ってください。
手順3 〇がつかなかった数をかけてください。
その数が答えです。ルートを直すときとおなじような感じです。アレをやればいいです。
この問題の場合は、$3$ が答えだとすると、$\sqrt{108\times3}=\sqrt{324}=18$ となります。
⑨ $A$ と $B$ の $2$ つの箱がある。$A$ の箱には、$1, \ 2, \ 3, \ 4$ の数字が $1$ つずつ書かれた $4$ 個の玉がはいっている。$B$ の箱には、$3, \ 4, \ 5$ の数字が $1$ つずつ書かれた $3$ 個の玉がはいっている。玉をそれぞれの箱から $1$ 個ずつ取り出すとき、玉に書かれている数の積が奇数となる確率を求めなさい。ただし、どの玉の取り出し方も同様に確からしいとする。
答え $\cfrac{1}{3}$
 はじめから玉に番号をつけてくれてますので、自分でつける必要がありません。親切な問題です。
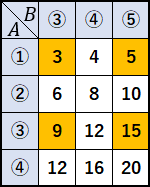
$2$ つの箱から取り出した玉の積の表をかくとこんな感じです。
はじめから玉に番号をつけてくれてますので、自分でつける必要がありません。親切な問題です。
$2$ つの箱から取り出した玉の積の表をかくとこんな感じです。
$2$ つの箱から取り出すのですから、表にはナナメの線はいれません。オレンジのところが、奇数です。
$$\cfrac{4}{12}=\cfrac{1}{3}$$
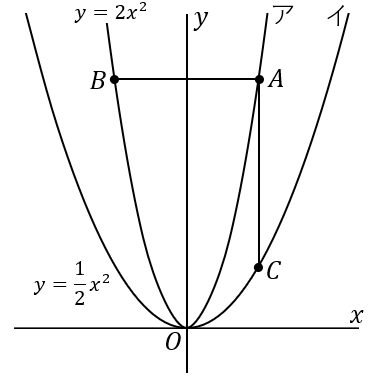
$①$ 点 $B$ の $x$ 座標が $-3$ のとき、点 $C$ の座標を求めなさい
答え
$\left(3, \ \cfrac{9}{2}\right)$
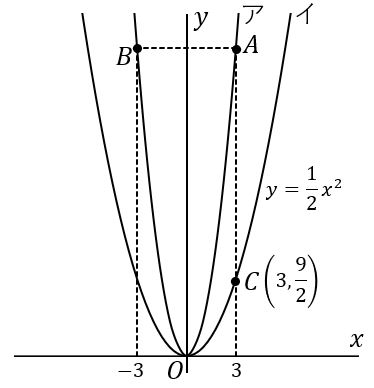 点 $B$ と 点 $A$ は $y$ 軸について対称です。点 $B$ の $x$ 座標が $-3$ ならば、点 $A$ の $x$ 座標は $3$ です。
点 $B$ と 点 $A$ は $y$ 軸について対称です。点 $B$ の $x$ 座標が $-3$ ならば、点 $A$ の $x$ 座標は $3$ です。
点 $A$ と点 $C$ の $x$ 座標はおなじです。点 $A$ の $x$ 座標が $3$ ならば、点 $C$ の $x$ 座標も $3$ です。というわけで、点 $C$ の $x$ 座標が求まりました。
あとは $y$ 座標を求めます。点 $C$ は曲線イ上の点なのですから、イの式が使えます。$y=\cfrac{1}{2}x^2$ に $x=3$ を代入して、
\begin{eqnarray*}
y&=&\cfrac{1}{2}\times3^2=\cfrac{9}{2}
\end{eqnarray*}
$②$ $AB:AC=4:5$ となるときの、点 $A$ の座標を求めなさい。
答え
$\left(\cfrac{5}{3}, \ \cfrac{50}{9}\right)$
$AB$ の長さと $AC$ の長さを文字を使って表して、その比が $4:5$ だということでやっていけばよいです。
 <点 $A$ の座標>
<点 $A$ の座標>
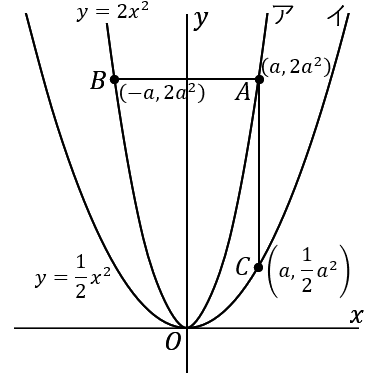
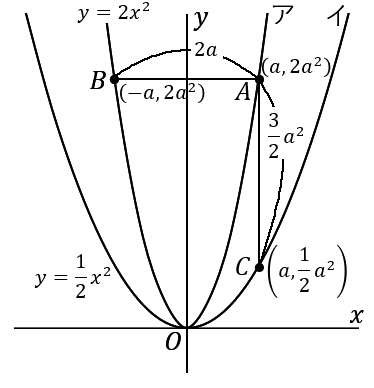
求めたい点です。点 $A$ の $x$ 座標を $a$ だということにします。文字はなんでもかまいません。ここでは $a$ ということにします。すると $y$ 座標は $2a^2$ ということになります。点 $A$ は関数 $y=2x^2$ 上の点だからです。点 $A$ の $x$ 座標を $a$ とすると、点 $A$ の座標は $\left(a, \ 2a^2\right)$ ということになります。
<点 $B$ の座標>
点 $B$ は、点 $A$ と $y$ 軸について対称です。点 $A$ の座標が $\left(a, \ 2a^2\right)$ ならば、点 $B$ の座標は $\left(-a, \ 2a^2\right)$ です。
<点 $C$ の座標>
点 $C$ の $x$ 座標は点 $A$ の $x$ 座標と同じです。点 $A$ の $x$ 座標が $a$ ならば、点 $C$ の $x$ 座標も $a$ です。点 $C$ は関数 $y=\cfrac{1}{2}x^2$ の上の点なのですから、$x$ 座標が $a$ ならば $y$ 座標は $\cfrac{1}{2}a^2$ です。点 $A$ の座標が $\left(a, \ 2a^2\right)$ ならば、点 $C$ の座標は $\left(a, \ \cfrac{1}{2}a^2\right)$ です。
 <$AB$ の長さ>
<$AB$ の長さ>
$AB$ の長さは、$2$ 点 $A, \ B$ の $x$ 座標の差をいえばよいです。
$$AB=a-(-a)=2a$$
<$AC$ の長さ>
$AC$ の長さは、$2$ 点 $A, \ C$ の $y$ 座標の差をいえばよいです。
\begin{eqnarray*}
AC&=&2a^2-\cfrac{1}{2}a^2\\
&=&\cfrac{4}{2}a^2-\cfrac{1}{2}a^2\\
&=&\cfrac{3}{2}a^2
\end{eqnarray*}
$AB:AC=4:5$ であるということで式をたてて $a$ を求めていきます。
\begin{eqnarray*}
AB:AC&=&4:5\\
2a:\cfrac{3}{2}a^2&=&4:5\\
\cfrac{3}{2}a^2\times4&=&2a\times5\\
6a^2&=&10a\quad両辺に\times\cfrac{1}{2}\\
3a^2&=&5a\\
3a^2-5a&=&0\\
a(3a-5)&=&0\\
a&=&0, \ a=\cfrac{5}{3}
\end{eqnarray*}
$a\gt0$ ですから、$a=\cfrac{5}{3}$ です。
点 $A$ の座標を $(a, 2a^2)$ ということにしてやってきて $a$ の値が求まりました。なので答えは、
$$\left(\cfrac{5}{3}, \ \cfrac{50}{9}\right)$$
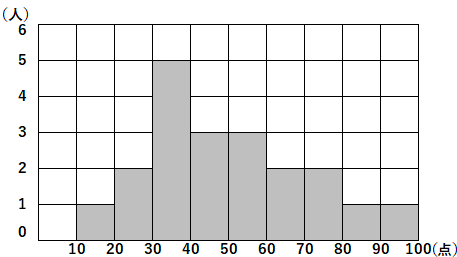
ア 階級の幅は $90$ 点である。
イ 最頻値(モード)のふくまれる階級の度数は $5$ である。
ウ 中央値(メジアン)は $40$~$50$ である。
エ 得点が $70$ 点以上の生徒の相対度数は $0.2$ である。
答え
$イ,エ$
ア…階級の幅は、$10$ です。
イ…最頻値(モード)のふくまれる階級は $30$~$40$ のところで、度数は $5$ です。
ウ…$20$ 人の中央値は、$10$ 番目の生徒と $11$ 番目の生徒の得点の平均です。$10$ 番目の生徒と $11$ 番目の生徒がふくまれるのは $40$~$50$ の階級です。その階級値は、
$$(40+50)\div2=45$$
こういうときの中央値(メジアン)は、階級値をいわなければいけません。なので、$45$ といわなければいけません。$40$~$50$ は誤りです。
エ…$70$ 点以上の生徒の度数は $4$ です。なのでその相対度数は、
$$4\div20=0.2$$
答え
$\boxed{\large{\ 1\ }}①-9②-12③-\cfrac{5}{6}④-2x+8\\ ⑤\cfrac{-x-12y}{56}\quad\left(-\cfrac{x+12y}{56},-\cfrac{1}{56}x-\cfrac{4}{13}yも可\right)\\ ⑥-x^2-10x-26⑦2\sqrt{2}\\ \boxed{\large{\ 2\ }}①6pq(p-2q)②(x-3)(x-6)\\ ③(x-y)^2④(x+3y)(x-3y)\\ ⑤(x+y)(a+1)\\ \boxed{\large{\ 3\ }}①x=-\cfrac{1}{2}②x=3, \ y=-5\\ ③x=-1, \ y=2④x=-9, \ x=-10\\ ⑤x=\pm2\sqrt{3}⑥x=\cfrac{2}{3}⑦x=0 ,\ x=\cfrac{1}{5}\\ ⑧x=-3\pm2\sqrt{5}⑨x=\cfrac{-2\pm\sqrt{6}}{2}\\ \boxed{\large{\ 4\ }}①x-2y\geqq 13 ②x=\cfrac{3y+1}{4}\left(\cfrac{3}{4}y+\cfrac{1}{4}も可\right)\\ ③1 ④y=5⑤y=\cfrac{4}{5}⑥-72 \leqq y \leqq -18\\ ⑦a=\cfrac{1}{2} ⑧3⑨\cfrac{1}{3}\\ \boxed{\large{\ 5\ }}①\left(3, \ \cfrac{9}{2}\right) ②\left(\cfrac{5}{3}, \ \cfrac{50}{9}\right)\\ \boxed{\large{\ 6\ }}イ,エ $