数学 中1 2学期期末模擬テスト 第1回
ページがちゃんと表示されるまで$10$秒くらいかかります。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
「印刷」をクリックすると同じ内容のpdfファイルが表示されます。また、解答用紙と答えも問題のあとに表示されます。1~6ページが問題、7~9ページが解答用紙、10~12ページが答えです。必要におうじて印刷してください。
問題をクリックすると答えがでます。
ふつうのテストより問題数は多いです。なのでふつうのテストをやるときより時間がかかると思います。がんばって！
$\huge{1}$ 次の①～⑩の計算をしなさい。⑪の問いに答えなさい。
$\qquad①$ $\quad -8+7+(-4) \qquad ② \quad \cfrac{7}{12}\div\left(-\cfrac{35}{24}\right)$
答え
$① \ -5$ $② \ -\cfrac{2}{5}$
\begin{eqnarray*} ①&& -8+7+(-4)\\ &=&-8+7-4\\ &=&-5 \end{eqnarray*} \begin{eqnarray*} \require{cancel} ②&& \cfrac{7}{12}\div\left(-\cfrac{35}{24}\right)\\ &=& \cfrac{7}{12}\times\left(-\cfrac{24}{35}\right)\\ &=& -\cfrac{2}{5} \end{eqnarray*}
$\qquad③$ $\quad -\cfrac{1}{3}+1-\cfrac{5}{6} \qquad ④ \quad (-2)^2+4\times(-8)$
答え
$③ \ -\cfrac{1}{6}$ $④ \ -28$
\begin{eqnarray*} ③&& -\cfrac{1}{3}+1-\cfrac{5}{6}\\ &=&-\cfrac{2}{6}+\cfrac{6}{6}-\cfrac{5}{6}\\ &=&-\cfrac{1}{6} \end{eqnarray*} \begin{eqnarray*} \require{cancel} ④&& (-2)^2+4\times(-8)\\ &=& 4+4\times(-8)\\ &=& 4-32\\ &=& -28 \end{eqnarray*}
$\qquad⑤$ $\quad -3x-11x \qquad ⑥ \quad (-18a)\div(-3)$
答え
$⑤ \ -14x$ $⑥ \ 6a$
$\qquad⑦$ $\quad -6x+3+7x-5 \qquad ⑧ \quad -3(4a-5)$
答え
$⑦ \ x-2$ $⑧ \ -12a+15$
\begin{eqnarray*} ⑦&& -6x+3+7x-5\\ &=&-6x+7x+3-5\\ &=&x-2 \end{eqnarray*} \begin{eqnarray*} \require{cancel} ⑧&& -3(4a-5)\\ &=& -12a+15 \end{eqnarray*}
$\qquad⑨$ $\quad (7a-5)-(3a-8) \qquad ⑩ \quad 16\times\cfrac{3x-5}{4}$
答え
$⑨ \ 4a+3$ $⑩ \ 12x-20$
\begin{eqnarray*} ⑨&& (7a-5)-(3a-8)\\ &=&7a-5-3a+8\\ &=&7a-3a-5+8\\ &=&4a+3 \end{eqnarray*} \begin{eqnarray*} \require{cancel} ⑩&& 16\times\cfrac{3x-5}{4}\\ &=& {}^4\bcancel{16}\times\cfrac{3x-5}{\bcancel{4}}\\ &=&12x-20 \end{eqnarray*}
$\qquad$⑪ $a=-3$ のとき、次の式の値を求めなさい。 $$\qquad -5a-8$$
答え
$7$
\begin{eqnarray*} &&-5a-8 \\ &=&-5\times(-3)-8 \\ &=&15-8 \\ &=&7 \end{eqnarray*}
$\huge{2}$ 次の$①～③$ の方程式を解きなさい。$④$ の比例式を解きなさい。
$①$ $-3(4x-5)=2x-20$
答え
$x=\cfrac{5}{2}$
\begin{eqnarray*} -3(4x-5)&=&2x-20\\ -12x+15&=&2x-20\\ -12x-2x&=&-20-15\\ -14x&=&-35\\ x&=&\cfrac{35}{14}\\ x&=&\cfrac{5}{2} \end{eqnarray*}
$②$ $-0.3x+1=0.5x+2.6$
答え
$x=-2$
\begin{eqnarray*} -0.3x+1&=&0.5x+2.6\quad両辺に\times10\\ -3x+10&=&5x+26\\ -3x-5x&=&26-10\\ -8x&=&16\\ x&=&-2 \end{eqnarray*}
$③$ $\cfrac{3}{4}x+\cfrac{2}{3}=\cfrac{1}{12}x+1$
答え
$x=\cfrac{1}{2}$
\begin{eqnarray*} \cfrac{3}{4}x+\cfrac{2}{3}&=&\cfrac{1}{12}x+1\quad両辺に\times12\\ 9x+8&=&x+12\\ 9x-x&=&12-8\\ 8x&=&4\\ x&=&\cfrac{4}{8}\\ x&=&\cfrac{1}{2} \end{eqnarray*}
$④$ $3:(x-4)=2:(2x-1)$
答え
$x=-\cfrac{5}{4}$
\begin{eqnarray*} 3:(x-4)&=&2:(2x-1)\\ 3(2x-1)&=&2(x-4)\\ 6x-3&=&2x-8\\ 6x-2x&=&-8+3\\ 4x&=&-5\\ x&=&-\cfrac{5}{4} \end{eqnarray*}
$\huge{3}$ 妹が駅をめざして、歩きで家を出た。妹が家を出てから $8$ 分後に兄が自転車で追いかけた。妹の速さを分速 $60m$，兄の速さを分速 $140m$ とすると、兄は家を出てから何分後に妹に追いつくか。
答え
$6分後$
兄が家を出てから $x$ 分後に妹に追いつくとすると、$140x$ というのは、兄が自転車で進んだ道のりをあらわします。「速さ×時間＝道のり」です。
妹が進んだ時間は、兄より $8$ 分多いのですから、$(x+8)$ 分です。なので、妹の進んだ道のりは $60(x+8)$ とあらわせます。
「兄が妹に追いつく」というのは、「兄の進んだ道のり＝妹の進んだ道のり」というふうに考えて、
$140x=60(x+8)$
これが式です。あとは解くだけです。
\begin{eqnarray*}
140x&=&60(x+8)\\
140x&=&60x+480\\
140x-60x&=&480\\
80x&=&480\\
x&=&6
\end{eqnarray*}
$\huge{4}$ $12$％ の食塩水が $300g$ ある。ここに $7$％ の食塩水をまぜて、$10$％の食塩水をつくりたい。$7$％ の食塩水を何$g$ まぜればよいか。
答え
$200g$
$7$％ の食塩水を$xg$ まぜることにします。すると、できあがる食塩水は $(300+x)g$ です。
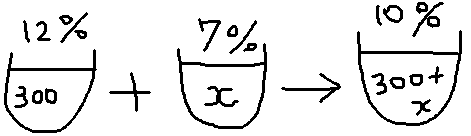
「濃度 $\times$ 食塩水 = 食塩」です。このことを使って、
「$12$％ の食塩水にふくまれる食塩」+「$7$％ の食塩水にふくまれる食塩」=「できあがった食塩水にふくまれる食塩」という式をたてて解いていきます。
$12$％ の食塩水にふくまれる食塩は、$\cfrac{12}{100}\times300$ グラムです。
$7$％ の食塩水にふくまれる食塩は、$\cfrac{7}{100}\times x$ グラムです。
できあがった食塩水にふくまれる食塩は、$\cfrac{10}{100}\times(300+x)$ グラムです。$300g$ の食塩水と $xg$ の食塩水をまぜるのだから、$(300+x)g$ の食塩水ができます。なので、「濃度 $\times$ 食塩水」をやるとこんな式になるわけです。
以上のことを使って「$12$％ の食塩水にふくまれる食塩」+「$7$％ の食塩水にふくまれる食塩」=「できあがった食塩水にふくまれる食塩」という式をたてると、
$\cfrac{12}{100}\times300+\cfrac{7}{100}\times x=\cfrac{10}{100}\times(300+x)$
これが式です。あとは解くだけです。
\begin{eqnarray*}
\cfrac{12}{100}\times300+\cfrac{7}{100}\times x&=&\cfrac{10}{100}\times(300+x)\quad両辺に\times100\\
12\times300+7x&=&10(300+x)\\
3600+7x&=&3000+10x\\
7x-10x&=&3000-3600\\
-3x&=&-600\\
x&=&200
\end{eqnarray*}
$\huge{5}$ 次の①～④の $x$ の変域を不等号を使った式で表しなさい。また、数直線上に変域を表しなさい。
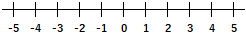
① $-1$ より大きい
答え
$$x \gt -1$$
以上、以下はその数をふくみます。記号はイコールがあるほうを使います。数直線上にあらわすときは、●を使います。
より大きい、より小さい、未満はその数をふくみません。記号はイコールがないやつを使います。数直線上にあらわすときは、〇を使います。
\begin{array}{c|c}
\hline
ふくむ & ふくまない \\
\hline
以上、以下 & より大きい、より小さい、未満 \\
\hline
\end{array}
② $-1$ 以上 $3$ 以下
答え
$$-1 \leqq x \leqq 3$$
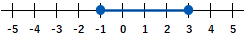
以上、以下はその数をふくみます。記号はイコールがあるほうを使います。数直線上にあらわすときは、●を使います。
より大きい、より小さい、未満はその数をふくみません。記号はイコールがないやつを使います。数直線上にあらわすときは、〇を使います。
\begin{array}{c|c}
\hline
ふくむ & ふくまない \\
\hline
以上、以下 & より大きい、より小さい、未満 \\
\hline
\end{array}
③ $-1$ より大きく $3$ 以下
答え
$$-1 \lt x \leqq 3$$
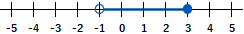
以上、以下はその数をふくみます。記号はイコールがあるほうを使います。数直線上にあらわすときは、●を使います。
より大きい、より小さい、未満はその数をふくみません。記号はイコールがないやつを使います。数直線上にあらわすときは、〇を使います。
\begin{array}{c|c}
\hline
ふくむ & ふくまない \\
\hline
以上、以下 & より大きい、より小さい、未満 \\
\hline
\end{array}
④ $-1$ 以上 $3$ 未満
答え
$$-1 \leqq x \lt 3$$
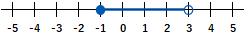
以上、以下はその数をふくみます。記号はイコールがあるほうを使います。数直線上にあらわすときは、●を使います。
より大きい、より小さい、未満はその数をふくみません。記号はイコールがないやつを使います。数直線上にあらわすときは、〇を使います。
\begin{array}{c|c}
\hline
ふくむ & ふくまない \\
\hline
以上、以下 & より大きい、より小さい、未満 \\
\hline
\end{array}
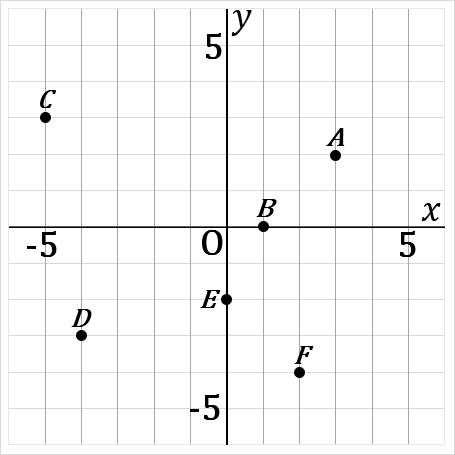
$\huge{6}$ 右の図について、点 $A \ ～ \ F$ の座標をいいなさい。
また、
点 $G(4, \ 5)$
点 $H(-4, \ 0)$
点 $I(-3, \ -5)$
点 $J(3, \ -2)$
をかきいれなさい。
答え
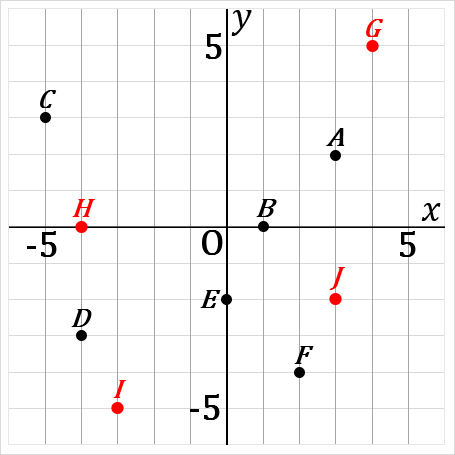
$A(3, \ 2)$
$B(1, \ 0)$
$C(-5, \ 3)$
$D(-4, \ -3)$
$E(0, \ -2)$
$F(2, \ -4)$
$x$ 軸上にある点は、かならず $y$ 座標が $0$ になっています。上の図でいうと、点 $B(1, \ 0)$ や点 $H(-4, \ 0)$ がそうです。
$y$ 軸上にある点は、かならず $x$ 座標が $0$ になっています。上の図でいうと、点 $E(0, \ -2)$ がそうです
$\huge{7}$ 次の①～⑩について、 $y$ を $x$ の式で表しなさい。
また、$y$ が $x$ に比例するときは、比例とかきなさい。
$y$ が $x$ に反比例するときは、反比例とかきなさい。
比例も反比例もしないときは、×とかきなさい。
① $1$ 個 $40$ 円のみかんを $x$ 個買うときの代金が $y$ 円
答え
① $y=40x$ 比例
② $1$ 個 $x$ 円のみかんを $y$ 個買うときの代金が $1200$ 円
答え
② $y=\cfrac{1200}{x}$ 反比例
$xy=1200$ だから $y=\cfrac{1200}{x}$
③ $1$ 個 $x$ 円のみかんを $5$ 個買って $1000$ 円はらったときのおつりが $y$ 円
答え
③ $y=1000-5x$ ×
$y=1000-5x$ というのは、比例でも反比例でもありません
④ 縦が $xcm$ で横が $15cm$ の長方形の面積が $ycm^2$
答え
④ $y=15x$ 比例
長方形の面積は、縦 $\times$ 横
⑤ 縦が $xcm$ で横が $ycm$ の長方形の面積が $30cm^2$
答え
⑤ $y=\cfrac{30}{x}$ 反比例
$xy=30$ だから $y=\cfrac{30}{x}$
⑥ 時速 $80km$ で走る自動車が $x$ 時間走ったときの進んだ距離が $ykm$
答え
⑥ $y=80x$ 比例
距離 $=$ 速さ $\times$ 時間
⑦ 時速 $xkm$ で走る自動車が $y$ 時間走ったときの進んだ距離が $300km$
答え
⑦ $y=\cfrac{300}{x}$ 反比例
$xy=300$ だから $y=\cfrac{300}{x}$
または、「時間 $=$ 距離 $\div$ 速さ」と考えてもよいです。
⑧ 水槽に $1$ 分で $15L$ ずつ水をいれる。$x$ 分水をいれたときの、いれた水の量が $yL$
答え
⑧ $y=15x$ 比例
⑨ 水槽に $1$ 分で $xL$ ずつ水をいれる。$y$ 分水をいれたときの、いれた水の量が $200L$
答え
⑨ $y=\cfrac{200}{x}$ 反比例
$xy=200$ だから $y=\cfrac{200}{x}$
⑩ 水槽に水が $500L$ はいっている。 $1$ 分で $10L$ ずつ水を抜くときの、 $x$ 分後の水の量が $yL$
答え
⑩ $y=500-10x$ ×
$y=500-10x$ というのは、比例でも反比例でもありません
$\huge{8}$
$y=2x$ について、次の①，②の問いに答えなさい。
① $x$ の値に対応する $y$ の値を求め、下の表を完成しなさい。
\begin{array}{c|ccccccccccc}
\hline
x & \cdots & -4 & -3 & -2 & -1 & \phantom{-}0 & \phantom{-}1 & \phantom{-}2 & \phantom{-}3 & \phantom{-}4 & \cdots\\
\hline
y & \cdots & & & & & & & & & & \cdots\\
\hline
\end{array}
答え
\begin{array}{c|ccccccccccc}
\hline
x & \cdots & -4 & -3 & -2 & -1 & \phantom{-}0 & \phantom{-}1 & \phantom{-}2 & \phantom{-}3 & \phantom{-}4 & \cdots\\
\hline
y & \cdots & -8 & -6 & -4 & -2 & \phantom{-}0 & \phantom{-}2 & \phantom{-}4 & \phantom{-}6 & \phantom{-}8 & \cdots\\
\hline
\end{array}
② 比例の式では、$x$ の値が $2$ 倍，$3$ 倍，…になると、対応する $y$ の値はどうなるか。
答え
$2$ 倍，$3$ 倍，…になる
$\huge{9}$ 下の表の $y$ は $x$ に比例している。ア～エにあてはまる数を答えなさい。
\begin{array}{c|cccc}
\hline
x & ア & -2 & -1 & \phantom{-}0 & \phantom{-}1 \\
\hline
y & -12 & イ & -4 & ウ & エ \\
\hline
\end{array}
答え
ア…$-3$ イ…$-8$ ウ…$0$ エ…$4$
$x$ になにを掛けたら $y$ になるかを考えましょう。この問題の場合は、$x=-1$ のとき $y=-4$ になっているから、$x$ に $4$ を掛けたら $y$ になります。つまり、$y=4x$ だということになります。
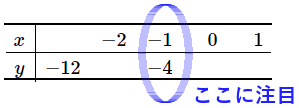
この手の問題は、かならずどこかに $x$ と $y$ の両方がわかっているところがあります。そこに注目して考えましょう。
$\huge{10}$ 次の①，②の問いに答えなさい。
① $y$ が $x$ に比例していて、$x=4$ のとき、$y=8$ である。$y$ を $x$ の式で表しなさい。
答え
$y=2x$
「比例」といわれたら、式の形は $y=ax$ で、 $a$ を求めるのが目標になります。$a$ の求め方は、$a=\cfrac{y}{x}$ です。
$a=\cfrac{y}{x}=\cfrac{8}{4}=2$
② $y$ が $x$ に比例していて、$x=5$ のとき、$y=15$ である。$x=-4$ のときの $y$ の値を求めなさい。
答え
$y=-12$
「比例」といわれたら、答えの形は $y=ax$ で、 $a$ を求めるのが目標になります。$a$ の求め方は、$a=\cfrac{y}{x}$ です。
$a=\cfrac{15}{5}=3$
$a$ が求められたら、$x=-4$ のときの $y$ の値を求めていきます。
$y=3x$ に $x=-4$ を代入する
$y=3\times(-4)=-12$
$\huge{11}$ 次の①～⑥のグラフをかきなさい。
\begin{eqnarray*}
&①& \quad y=x \quad&②& \quad y=2x
\end{eqnarray*}
答え
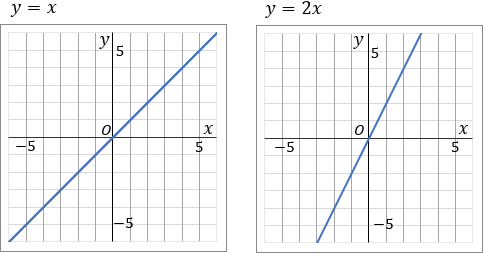
①てっとりばやいかき方として、$x=1$ のとき $y=1$ なのだから、原点と点$(1, \ 1)$ を通る直線を定規でむすんでしまう、というのがあります。ただ、原点とどこか $1$ 点をむすぶやり方だと、ちょっとズレちゃうことがあります。わりとよくあります。なのでそこに気をつけてください。
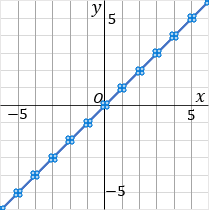もうひとつのかき方として、これがおすすめなんですが、このグラフは比例定数が $1$ です。$1$ は分数であらわすと $\cfrac{1}{1}$ です。というわけで、原点をスタート地点として、「右に $1$ マスいったら上に $1$ マスいく」というふうに点をとっていっちゃいます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に $1$ マスいったら下に $1$ マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。すべての点が定規の上にのっているはずです。点をいくつかとるので、ズレる心配がほぼないです。
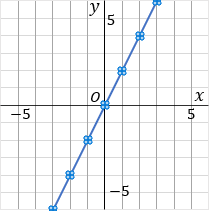②このグラフは比例定数が $2$ です。$2$ は分数であらわすと $\cfrac{2}{1}$ です。というわけで、原点をスタート地点として、「右に $1$ マスいったら上に $2$ マスいく」というふうに点をとっていきます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に $1$ マスいったら下に $2$ マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
\begin{eqnarray*} &③& \quad y=\cfrac{1}{2}x \quad&④& \quad y=-x \end{eqnarray*}
答え
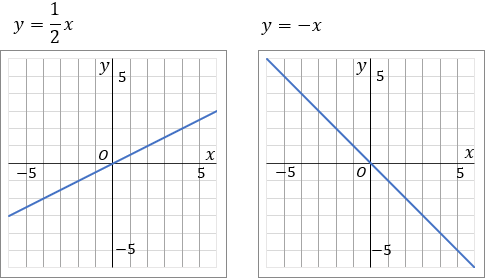
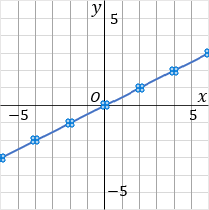③このグラフは比例定数が $\cfrac{1}{2}$ です。原点をスタート地点として、「右に $2$ マスいったら上に $1$ マスいく」というふうに点をとっていきます。比例定数の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に $2$ マスいったら下に $1$ マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
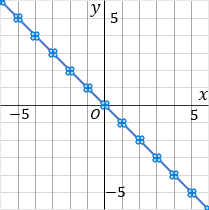④このグラフは比例定数が $-1$ です。比例定数が負の数なので、右下がりのグラフになるはずだ、ということを意識しておきましょう。$-1$ は分数であらわすと $\cfrac{-1}{1}$ です。グラフをかくときは、マイナスの符号は分子につけておきましょう。というわけで、原点をスタート地点として、「右に $1$ マスいったら下に $1$ マスいく」というふうに点をとっていきます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に $1$ マスいったら上に $1$ マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
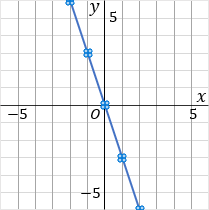
\begin{eqnarray*} &⑤& \quad y=-3x \quad&⑥& \quad y=-\cfrac{2}{3}x \end{eqnarray*}
答え
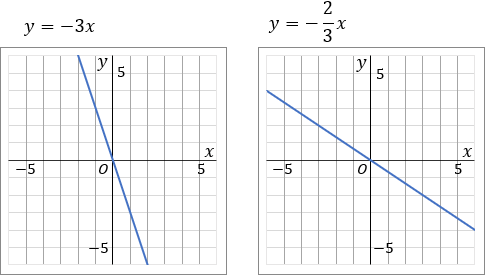
⑤このグラフは比例定数が $-3$ です。比例定数が負の数なので、右下がりのグラフになるはずだ、ということを意識しておきましょう。$-3$ は分数であらわすと $\cfrac{-3}{1}$ です。グラフをかくときは、マイナスの符号は分子につけておきましょう。というわけで、原点をスタート地点として、「右に $1$ マスいったら下に $3$ マスいく」というふうに点をとっていきます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に $1$ マスいったら上に $3$ マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
⑥このグラフは比例定数が $-\cfrac{2}{3}$ です。グラフをかくときは、マイナスの符号は分子につけておきましょう。つまり、$\cfrac{-2}{3}$ というふうに考えます。原点をスタート地点として、「右に $3$ マスいったら下に $2$ マスいく」というふうに点をとっていきます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に $3$ マスいったら上に $2$ マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
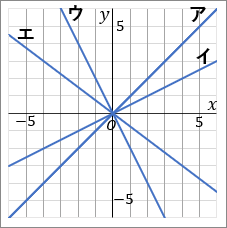
$\huge{12}$ 右の図のア～エの直線について、$y$ を $x$ の式で表しなさい。
答え
ア $y=x$
イ $y=\cfrac{1}{2}x$
ウ $y=-2x$
エ $y=-\cfrac{3}{4}x$
ア～エのグラフはすべて原点を通る直線です。比例のグラフです。比例のグラフについて、「$y$ を $x$ の式で表しなさい」といわれたら、式の形は $y=ax$ で、$a$ を求めるのが目標となります。$a$ の求め方は、$a=\cfrac{y}{x}$ です。グラフ上にある、どこかカドを通っているところをさがして、その座標を利用します。
＜アについて＞
アのグラフは、点$(1, \ 1)$ を通っています。なので、$x=1, \ y=1$ を $a=\cfrac{y}{x}$ に代入して $a$ を求めます。
$a=\cfrac{y}{x}=\cfrac{1}{1}=1$
これで $a=1$ だと求められました。なので答えは $y=x$ です。
ここでは点$(1, \ 1)$ を代入して $a$ を求めましたが、ほかの点でもだいじょうぶです。グラフ上にある点の座標を代入すれば、どこをいれても全部おなじ答えになります。ただ、原点だけはいれちゃダメです。
＜イについて＞
イのグラフは、点$(2, \ 1)$ を通っています。なので、$x=2, \ y=1$ を $a=\cfrac{y}{x}$ に代入して $a$ を求めます。
$a=\cfrac{y}{x}=\cfrac{1}{2}$
これで $a=\cfrac{1}{2}$ だと求められました。なので答えは $y=\cfrac{1}{2}x$ です。
ここでは点$(2, \ 1)$ を代入して $a$ を求めましたが、ほかの点でもだいじょうぶです。グラフ上にある点の座標を代入すれば、どこをいれても全部おなじ答えになります。ただ、原点だけはいれちゃダメです。
＜ウについて＞
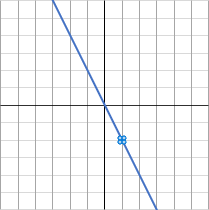
ウのグラフは、点$(1, \ -2)$ を通っています。なので、$x=1, \ y=-2$ を $a=\cfrac{y}{x}$ に代入して $a$ を求めます。
$a=\cfrac{y}{x}=\cfrac{-2}{1}=-2$
これで $a=-2$ だと求められました。なので答えは $y=-2x$ です。
ここでは点$(1, \ -2)$ を代入して $a$ を求めましたが、ほかの点でもだいじょうぶです。グラフ上にある点の座標を代入すれば、どこをいれても全部おなじ答えになります。ただ、原点だけはいれちゃダメです。
＜エについて＞
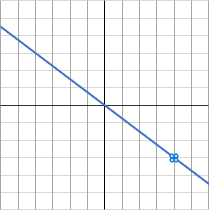
エのグラフは、点$(4, \ -3)$ を通っています。なので、$x=4, \ y=-3$ を $a=\cfrac{y}{x}$ に代入して $a$ を求めます。
$a=\cfrac{y}{x}=\cfrac{-3}{4}=-\cfrac{3}{4}$
これで $a=-\cfrac{3}{4}$ だと求められました。なので答えは $y=-\cfrac{3}{4}x$ です。
ここでは点$(4, \ -3)$ を代入して $a$ を求めましたが、ほかの点でもだいじょうぶです。グラフ上にある点の座標を代入すれば、どこをいれても全部おなじ答えになります。ただ、原点だけはいれちゃダメです。
$\huge{13}$
$y=\cfrac{12}{x}$ について、次の①，②の問いに答えなさい。
① $x$ の値に対応する $y$ の値を求め、下の表を完成しなさい。
\begin{array}{c|ccccccccccc}
\hline
x & \cdots & -4 & -3 & -2 & -1 & \phantom{-}0 & \phantom{-}1 & \phantom{-}2 & \phantom{-}3 & \phantom{-}4 & \cdots\\
\hline
y & \cdots & & & & & & & & & & \cdots\\
\hline
\end{array}
答え
\begin{array}{c|ccccccccccc}
\hline
x & \cdots & -4 & -3 & -2 & -1 & \phantom{-}0 & \phantom{-}1 & \phantom{-}2 & \phantom{-}3 & \phantom{-}4 & \cdots\\
\hline
y & \cdots & -3 & -4 & -6 & -12 & \phantom{-}× & \phantom{-}12 & \phantom{-}6 & \phantom{-}4 & \phantom{-}8 & \cdots\\
\hline
\end{array}
② 反比例の式では、$x$ の値が $2$ 倍，$3$ 倍，…になると、対応する $y$ の値はどうなるか。
答え
$\cfrac{1}{2}$ 倍，$\cfrac{1}{3}$ 倍，…になる
$\huge{14}$ 次の①，②の問いに答えなさい。
① $y$ が $x$ に反比例していて、$x=4$ のとき、$y=8$ である。$y$ を $x$ の式で表しなさい。
答え
$y=\cfrac{32}{x}$
「反比例」といわれたら、答えの形は $y=\cfrac{a}{x}$ で、 $a$ を求めるのが目標になります。$a$ の求め方は、$a=xy$ です。$x$ と $y$ をかけちゃえばいいんです。比例よりこっちのほうがもっとかんたん。
$a=xy=4\times8=32$
② $y$ が $x$ に反比例していて、$x=5$ のとき、$y=15$ である。$x=-25$ のときの $y$ の値を求めなさい。
答え
$y=-3$
「反比例」といわれたら、式の形は $y=\cfrac{a}{x}$ で、 $a$ を求めるのが目標になります。$a$ の求め方は、$a=xy$ です。
$a=5\times15=75$
$a$ が求められたら、$x=-4$ のときの $y$ の値を求めていきます。
$y=\cfrac{75}{x}$ に $x=-25$ を代入する
$y=\cfrac{75}{-25}=-3$
$\huge{15}$ 次の①，②のグラフをかきなさい。
\begin{eqnarray*}
&①& \quad y=\cfrac{4}{x} \qquad&②& \quad y=-\cfrac{12}{x}
\end{eqnarray*}
答え
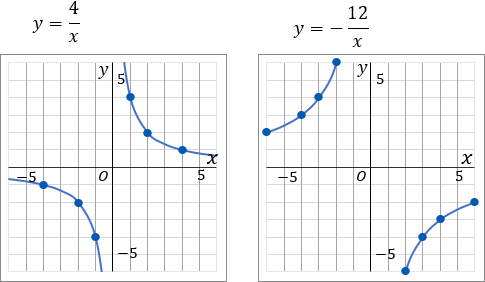
①反比例のグラフをかくときは、まず表をつくります。表をつくるところからはじめなきゃならんのです。めんどくさいのです。あきらめてください。グラフ用紙のマス目が $+6$ から $-6$ まであるので、$x$ が $+6$ から $-6$ までのあいだで、$x$ と $y$ がどちらも整数になるところをかんがえて、表をかきます。
$y=\cfrac{4}{x}$
\begin{array}{c|ccccccccc}
\hline
\small{x}&\cdots&\small{-4}&\small{-2}&\small{-1}&\small{\phantom{-}0}&\small{\phantom{-}1}&\small{\phantom{-}2}&\small{\phantom{-}4}&\cdots\\
\hline
\small{y}&\cdots&\small{-1}&\small{-2}&\small{-4}&\phantom{-}\times&\small{\phantom{-}4}&\small{\phantom{-}2}&\small{\phantom{-}1}&\cdots&\\
\hline
\end{array}
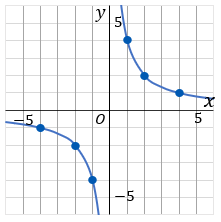表をかいたらグラフ用紙に点をとっていきます。とれる点をすべてとったら、双曲線になるように、点をむすびます。比例定数が正のとき($a\gt 0$)のときは、座標平面の右上と左下に双曲線をひくことになります。
②これもまず表をつくります。$x$ が $+6$ から $-6$ までのあいだで、$x$ と $y$ がどちらも整数になるところをかんがえて、表をかきます。
$y=-\cfrac{12}{x}$
\begin{array}{c|ccccccccccccc}
\hline
\small{x}&\cdots&\small{-6}&\small{-4}&\small{-3}&\small{-2}&\small{-1}&\small{\phantom{-}0}&\small{\phantom{-}1}&\small{\phantom{-}2}&\small{\phantom{-}3}&\small{\phantom{-}4}&\small{\phantom{-}6}&\cdots\\
\hline
\small{y}&\cdots&\small{\phantom{-}2}&\small{\phantom{-}3}&\small{\phantom{-}4}&\small{\phantom{-}6}&\small{\phantom{-}12}&\phantom{-}\times&\small{-12}&\small{-6}&\small{-4}&\small{-3}&\small{-2}&\cdots&\\
\hline
\end{array}
表をかいたらグラフ用紙に点をとっていきます。とれる点をすべてとったら、双曲線になるように、点をむすびます。比例定数が負のとき($a\lt 0$)のときは、座標平面の左上と右下に双曲線をひくことになります。
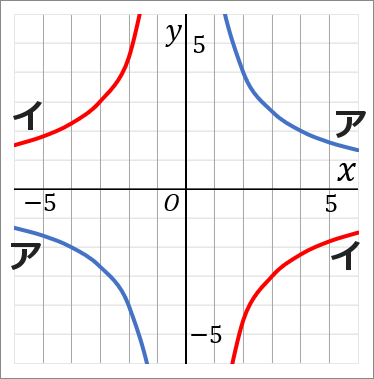
$\huge{16}$ 右の図のア，イはどちらも双曲線である。ア，イのそれぞれについて、$y$ を $x$ の式で表しなさい。
答え
ア $y=\cfrac{8}{x}$
イ $y=-\cfrac{9}{x}$
双曲線なのだから、反比例のグラフです。反比例のグラフについて、「$y$ を $x$ の式で表しなさい」といわれたら、式の形は $y=\cfrac{a}{x}$ で、$a$ を求めるのが目標となります。$a$ の求め方は、$a=xy$ です。$x$ と $y$ をかければよいです。グラフ上にある、どこかカドを通っているところをさがして、その座標を利用します。
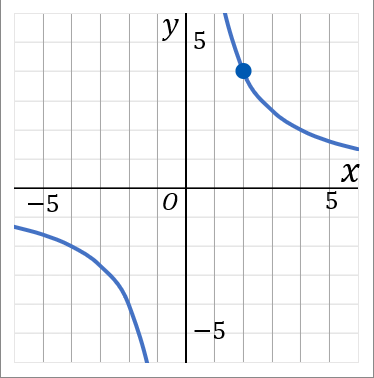＜アについて＞
アのグラフは、点$(2, \ 4)$ を通っています。なので、$x=2, \ y=4$ を $a=xy$ に代入して $a$ を求めます。
$a=xy=2\times4=8$
これで $a=8$ だと求められました。なので答えは $y=\cfrac{8}{x}$ です。
ここでは点$(2, \ 4)$ を代入して $a$ を求めましたが、ほかの点でもだいじょうぶです。グラフ上にある点の座標を代入すれば、どこをいれても全部おなじ答えになります。
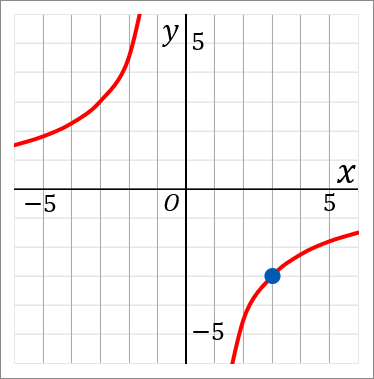＜イについて＞
イのグラフは、点$(3, \ -3)$ を通っています。なので、$x=3, \ y=-3$ を $a=xy$ に代入して $a$ を求めます。
$a=xy=3\times(-3)=-9$
これで $a=-9$ だと求められました。なので答えは $y=-\cfrac{9}{x}$ です。
ここでは点$(3, \ -3)$ を代入して $a$ を求めましたが、ほかの点でもだいじょうぶです。グラフ上にある点の座標を代入すれば、どこをいれても全部おなじ答えになります。というかこの問題の場合は、あとはいれるとしたら $(-3, \ 3)$ しかありませんけど。
$\huge{17}$ あるコピー用紙の $40$ 枚の重さが $100$ ｇである。次の①，②の問いに答えなさい。
① このコピー用紙 $x$ 枚のときの重さを $y$ ｇとして、$y$ を $x$ の式で表しなさい。
答え
$y=\cfrac{5}{2}x$
コピー用紙の枚数と重さは比例します。
比例のときの式の形は $y=ax$ で、$a$ を求めるのが目標になります。$a$ の求め方は $a=\cfrac{y}{x}$ です。
コピー用紙の枚数を $x$ 枚、重さを $y$ ｇとして、 $40$ 枚の重さが $100$ ｇなのですから、
$a=\cfrac{y}{x}=\cfrac{100}{40}=\cfrac{5}{2}$
なので、$y=\cfrac{5}{2}x$
②このコピー用紙 $290$ 枚の重さは何ｇか。
答え
$725$ ｇ
①の問題の答えを利用して、$x$ が $290$ のときの $y$ を求めればよいです。
$y=\cfrac{5}{2}x$ に $x=290$ を代入して、
$y=\cfrac{5}{2}\times290=725$
$\huge{18}$ 家から学校まで、分速 $70$ ｍで行くと $12$ 分かかる。次の①，②の問いに答えなさい。
① 速さが分速 $x$ ｍのときにかかる時間を $y$ 分として、$y$ を $x$ の式で表しなさい。
答え
$y=\cfrac{840}{x}$
速さと時間は反比例します。
反比例のときの式の形は $y=\cfrac{a}{x}$ で、$a$ を求めるのが目標になります。$a$ の求め方は $a=xy$ です。
速さを分速 $x$ ｍ、時間を $y$ 分として、分速 $70$ ｍときにかかる時間が $12$ 分なのですから、
$a=xy=70\times12=840$
なので、$y=\cfrac{840}{x}$
②家から学校まで、分速 $60$ ｍで行くと何分かかるか。
答え
$14$ 分
①の問題の答えを利用して、$x$ が $60$ のときの $y$ を求めればよいです。
$y=\cfrac{840}{x}$ に $x=60$ を代入して、
$y=\cfrac{840}{60}=14$
$\huge{19}$ 家から $1200$ ｍ 離れた駅にむかって、兄が家を出た。下のグラフはその進行のようすをしめしたものである。
兄と同時に弟が分速 $50$ ｍで、兄と同じ道を駅へむかって家をでた。これについて、以下の①～④の問いに答えなさい。
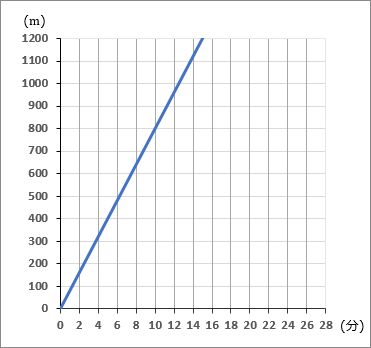
① 兄の速さは分速何ｍか。
答え
分速 $80$ ｍ
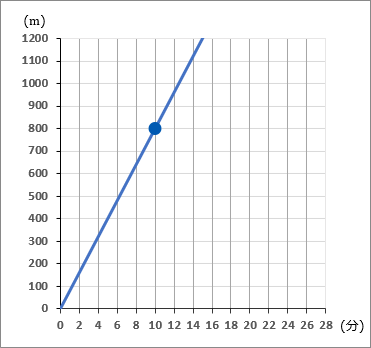$速さ=\cfrac{距離}{時間}$です。
グラフで、カドを通っているところをさがします。$(10, \ 800)$ のところを通っています。$10$ 分で $800$ ｍ進んだということですから、
$\cfrac{800}{10}=80$ ｍ/分。
②弟の進行のようすを、グラフにかきくわえなさい。
答え
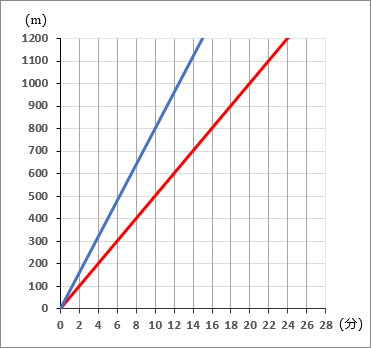
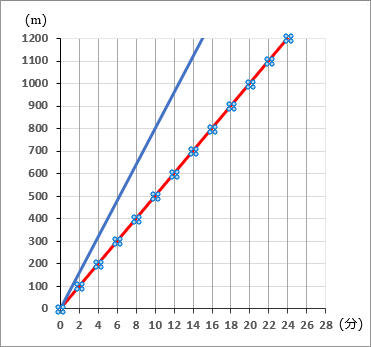分速 $50$ ｍならば、 $2$ 分で $100$ ｍ進むことになります。グラフ上で、原点をスタート地点として、右に $1$ マスいって縦に $1$ マスいくように点をとっていきます。このグラフ用紙だと、カドとカドをぜんぶ通っていくようになるわけですが。そしてそこをむすびます。
③兄と弟が $300$ ｍ離れるのは、二人が家を出てから何分後か。
答え
$10$ 分後
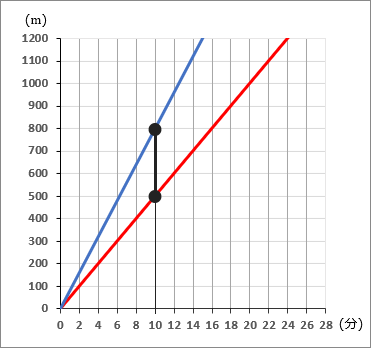$2$ 人のグラフ上で、縦に $300$ ｍ離れるところをさがします。縦に $3$ マスぶん離れるところです。もしちょうどいいところがない場合は、計算から求めていくことになりますが、この問題にはちょうどいいところがあります。$10$ 分後のところです。
④家から $800$ ｍ離れた地点を兄が通過したあと、何分後に弟はそこを通過するか。
答え
$6$ 分後
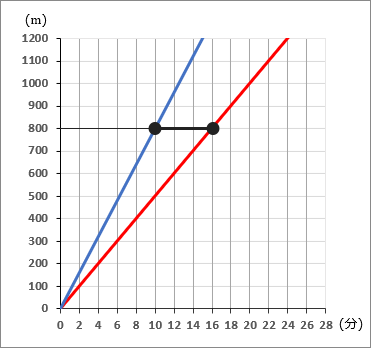$2$ 人のグラフ上で、 $800$ ｍのところを兄が通過したあと、何分後に弟が通過するを確認します。もし、ちょうどカドを通っていない場合は計算から求めていくことになりますが、この問題はちょうどカドとカドを通っています。 $3$ マスぶん離れています。なので $6$ 分後です。
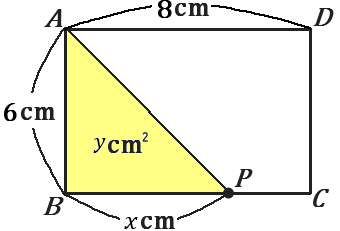
$\huge{20}$ $AB=6cm, \ AD=8cm$ の長方形 $ABCD$ がある。点 $P$ は 頂点 $B$ を出発して、辺 $BC$ 上を 頂点 $B$ から 頂点 $C$ まで動く。$BP=xcm$ のときの $\triangle ABP$ の面積を $ycm^2$ とするとき、以下の問いに答えなさい。
① $y$ を $x$ の式で表しなさい。
答え
$y=3x$
三角形の面積は、底辺 $\times$ 高さ $\times\cfrac{1}{2}$ です。 $\triangle ABP$ は、$BP$ を底辺、$AB$ を高さとみることができますので、その面積 $y$ は
$y=BP\times AB\times\cfrac{1}{2}=x\times6\times\cfrac{1}{2}=3x$
②$x$ と $y$ の変域をそれぞれ求めなさい。
答え
$0 \leqq x \leqq 8$
$0 \leqq y \leqq 24\quad$
$BP$ の長さは、$0cm$ 以上 $8cm$ 以下です。
なので $\triangle ABP$ の面積は、$BP=0$ のとき最小で、$0$ です。$BP=8$ のとき最大で、$6\times8\times\cfrac{1}{2}=24$ です。
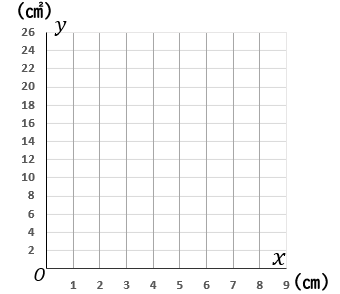
③$x$ と $y$ の関係を表すグラフをかきなさい。
答え
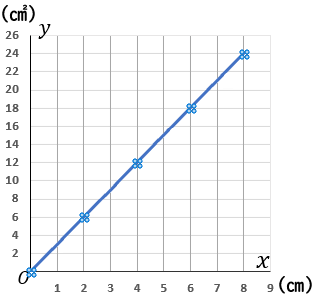①の答えから、比例のグラフをかくことになります。$x=1$ のとき $y=3$ です。$(1, \ 3)$ という座標はグラフのカドではありません。$x=2$ のとき $y=6$ です。これはグラフのカドになっています。というわけで、原点をスタート地点として、右に $2$ マスいって縦に $3$ マスいく点をグラフ上にとっていき、定規でむすびます。
注意点があります。グラフは点$ (8, \ 24)$ のところでとめてください。そこから先をかいてはいけません。かいてあるとバツになります。$x$ や $y$ の値に範囲があるときは、それを考えてグラフをかかなくちゃなりません。気をつけてください。
④$\triangle ABP$ の面積が $20cm^2$ となるのは、$BP$ の長さが何 $cm$ のときか。
答え
$\cfrac{20}{3}cm$
$y=20$ となるところの座標がグラフ上でちょうどカドになっていればいいのですが、なっていません。こういう場合は計算して求めていきます。
$y=3x$ の $y$ に $20$ を代入して、
\begin{eqnarray*}
20&=&3x\quad(左辺と右辺をとりかえる)\\
3x&=&20\\
x&=&\cfrac{20}{3}
\end{eqnarray*}
答え(中1 2学期期末模擬テスト 第1回)
1$①-5$ $②-\cfrac{2}{5}$ $③-\cfrac{1}{6}$ $④-28$ $⑤-14x$ $⑥6a$ $⑦x-2$ $⑧-12a+15$ $⑨4a+3$ $⑩12x-20$ $⑪7$
2$①x=\cfrac{5}{2}$ $②x=-2$ $③x=\cfrac{1}{2}$ $④x=-\cfrac{5}{4}$
3$\quad6 \ 分後$
4$\quad200 \ g$
5①$x \gt -1$
②$-1 \leqq x \leqq 3$
③$-1 \lt x \leqq 3$
④$-1 \leqq x \lt 3$
6$A(3, \ 2)$
$B(1, \ 0)$
$C(-5, \ 3)$
$D(-4, \ -3)$
$E(0, \ -2)$
$F(2, \ -4)$
7$①y=40x 比例$ $②y=\cfrac{1200}{x} 反比例$ $③y=1000-5x ×$ $④y=15x 比例$ $⑤y=\cfrac{30}{x} 反比例$ $⑥y=30x 比例$ $⑦y=\cfrac{300}{x} 反比例$ $⑧y=15x 比例$ $⑨y=\cfrac{200}{x} 反比例$ $⑩y=500-10x ×$
8①\begin{array}{c|ccccccccccc}
\hline
x & \cdots & -4 & -3 & -2 & -1 & \phantom{-}0 & \phantom{-}1 & \phantom{-}2 & \phantom{-}3 & \phantom{-}4 & \cdots\\
\hline
y & \cdots & -8 & -6 & -4 & -2 & \phantom{-}0 & \phantom{-}2 & \phantom{-}4 & \phantom{-}6 & \phantom{-}8 & \cdots\\
\hline
\end{array}
②$2$ 倍，$3$ 倍，…になる
9ア…$-3$ イ…$-8$ ウ…$0$ エ…$4$
10$①y=2x$ $②y=-12$
11
12ア…$y=x$ イ…$y=\cfrac{1}{2}x$ ウ…$y=-2x$ エ…$y=-\cfrac{3}{4}x$
13①\begin{array}{c|ccccccccccc}
\hline
x & \cdots & -4 & -3 & -2 & -1 & \phantom{-}0 & \phantom{-}1 & \phantom{-}2 & \phantom{-}3 & \phantom{-}4 & \cdots\\
\hline
y & \cdots & -3 & -4 & -6 & -12 & \phantom{-}× & \phantom{-}12 & \phantom{-}6 & \phantom{-}4 & \phantom{-}8 & \cdots\\
\hline
\end{array}
②$\cfrac{1}{2}$ 倍，$\cfrac{1}{3}$ 倍，…になる
14$①y=\cfrac{32}{x}$ $②y=-3$
15
16ア…$y=\cfrac{8}{x}$ イ…$y=-\cfrac{9}{x}$
17$①y=\cfrac{5}{2}x$ $②725g$
18$①y=\cfrac{840}{x}$ $②14分$
19$①分速80m$ $②右図$ $③10分後$ $④6分後$
20$①y=3x$ $②0 \leqq x \leqq 8\quad0 \leqq y \leqq 24\quad$ $③下図$ $④\cfrac{20}{3}cm$