数学 中2 4章 平行と合同 角と平行線 第1回(全18問)
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
以下の問いに答えなさい。
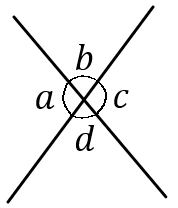
(1) 右の図で対頂角になっているのは、どの角とどの角か。2組あげなさい。
答え
$\angle a$と$\angle c$
$\angle b$と$\angle d$
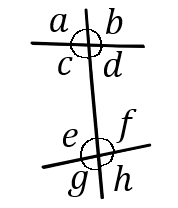
(2) 右の図で同位角になっているのは、どの角とどの角か。4組あげなさい。また、錯角になっているのは、どの角とどの角か。2組あげなさい。
答え
同位角…
$\angle a$と$\angle e$,
$\angle b$と$\angle f$,
$\angle c$と$\angle g$,
$\angle d$と$\angle h$
錯角…
$\angle c$と$\angle f$,
$\angle d$と$\angle e$,
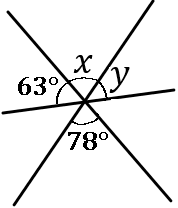
(3) 右の図で、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。
答え
$\angle x=78^{ \circ }$, $\angle y=39^{ \circ }$
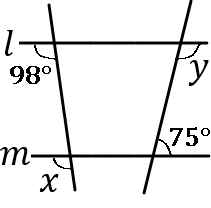
(4) 右の図で、$l /\!/ m$ のとき、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。
答え
$\angle x=98^{ \circ }$, $\angle y=105^{ \circ }$
(5) 下の図で、$\angle x$, $\angle y$, $\angle z$ の大きさをそれぞれ求めなさい。ただし、$l /\!/ m$ とする。
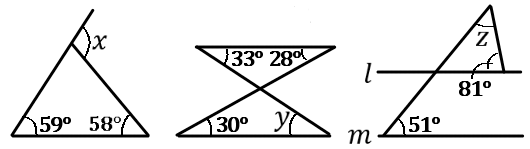
答え
$\angle x=117^{ \circ }$, $\angle y=31^{ \circ }$, $\angle z=48^{ \circ }$
$x=59+58\\30+y=28+33\\51+81+z=180$
(6) 下の図で、$\angle x$, $\angle y$, $\angle z$ の大きさをそれぞれ求めなさい。ただし、$l /\!/ m$ とする。
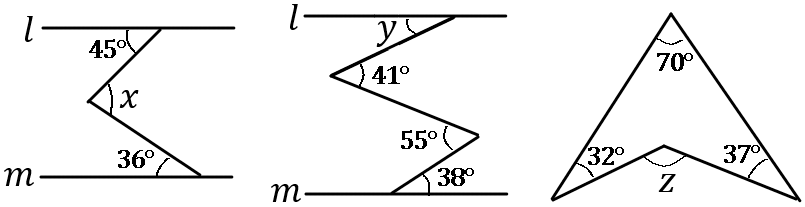
答え
$\angle x=81^{ \circ }$, $\angle y=24^{ \circ }$, $\angle z=139^{ \circ }$
※補助線をひいて考えます。色のついた部分の大きさがおなじです。
※最後の問題は、$A+B+C=D$になります。よく出てくる形なので、「この形は $A+B+C=D$」とおぼえてしまいましょう。また、なぜそうなるのか説明しなさいという問題もよくあるので、説明できるようにしておきましょう。
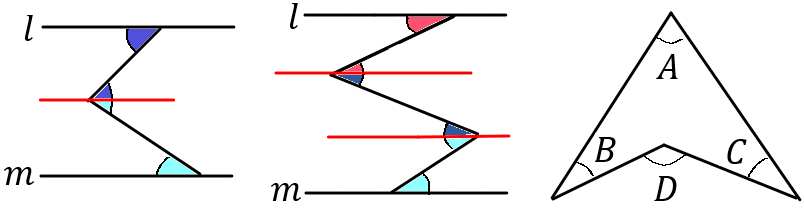
(7) 下の図で、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。ただし、〇のついている角同士、×のついている角同士等しいものとする。
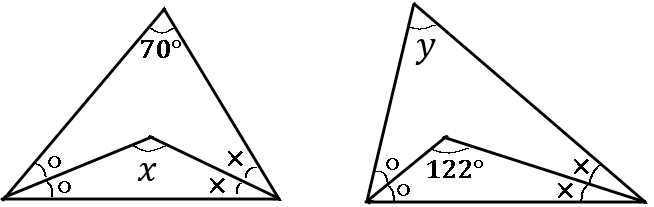
答え
$\angle x=125^{ \circ }$, $\angle y=64^{ \circ }$
※$x$ の求め方 \begin{eqnarray*} ○&=&a^{ \circ },×=b^{ \circ } とすると、\\ 2a+2b+70&=&180\\ 2a+2b&=&110 \quad \class{mathbg-r}{(両辺を\div2)} \\ a+b&=&55\\ x&=&180-(a+b)\\ &=&180-55=125 \end{eqnarray*} ※$y$ の求め方 \begin{eqnarray*} ○&=&a^{ \circ },×=b^{ \circ } とすると、\\ a+b+122&=&180\\ a+b&=&58 \quad \class{mathbg-r}{(両辺に\times2)} \\ 2a+2b&=&116\\ y&=&180-(2a+2b)\\ &=&180-116=64 \end{eqnarray*}
(8) $n$ 角形の内角の和は( )である。
(8) $n$ 角形の外角の和は( )である。
答え
内角の和…$180^{ \circ }\times(n-2)$
外角の和…$360^{ \circ }$
(9) 五角形の内角の和を求めなさい。
答え
$540^{ \circ }$
$180\times(5-2)=540$
(10) 内角の和が $900^{ \circ }$ になる多角形は何角形ですか。
答え
七角形
$900\div180+2=7$
(11) 正六角形の1つの内角の大きさは何度ですか。
答え
$120^{ \circ }$
$\{180\times(6-2)\}\div6=720\div6=120$
別解 (外角の和$=360^{ \circ }$を利用する)←おすすめ
$180-(360\div6)=180-60=120$
(12) 正五角形の1つの外角の大きさは何度ですか。
答え
$72^{ \circ }$
$360\div5=72$
(13) 1つの外角の大きさが $30^{ \circ }$になるのは正何角形ですか。
答え
正十二角形
$360\div30=12$
(14) 1つの内角の大きさが $160^{ \circ }$になるのは正何角形ですか。
答え
正十八角形
※内角が$160^{ \circ }$ということは、外角は$20^{ \circ }$だから、 $360\div20=18$
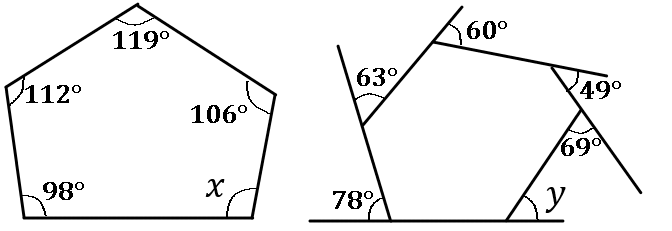
(15) 下の図で、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。
答え
$\angle x=105^{ \circ }$, $\angle y=41^{ \circ }$
$x=540-(98+112+119+106)\\ y=360-(78+63+60+49+69)$
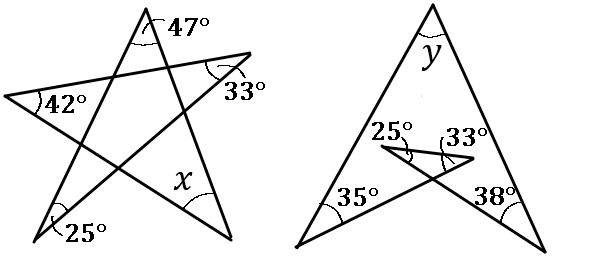
(16) 下の図で、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。
答え
$\angle x=33^{ \circ }$, $\angle y=49^{ \circ }$
$x=180-(25+42+47+33)$
五芒星(ごぼうせい)は色のついた $5$ つの角の和が $180^{ \circ }$ になるとおぼえてしまいましょう。また、なぜこの $5$ つを足すと $180^{ \circ }$ になるのかもよく問われるので、その理由の説明ができるようにしておきましょう。
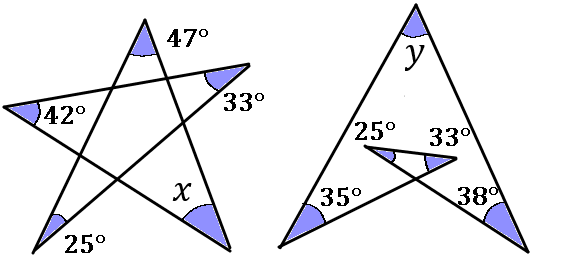 $y=180-(35+25+33+38)$
$y=180-(35+25+33+38)$
$y$ も $x$ とおなじように考えてしまえばよいです。
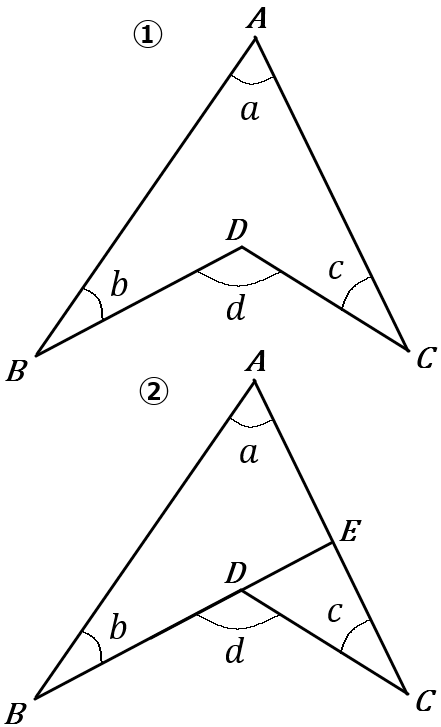 (17) 右の図①で、$\angle a+\angle b +\angle c =\angle d$ である。
(17) 右の図①で、$\angle a+\angle b +\angle c =\angle d$ である。
右の図②のように、$BD$ の延長と $AC$ との交点を $E$ とし、三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しい性質を利用して、この理由を説明しなさい。
答え
$\triangle ABE$ で、三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しいから、
$ \angle a +\angle b=\angle DEC$ …①
$\triangle CDE$ で、三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しいから、
$ \angle DEC +\angle c=\angle d$ …②
①②により、$\angle a+\angle b +\angle c =\angle d$
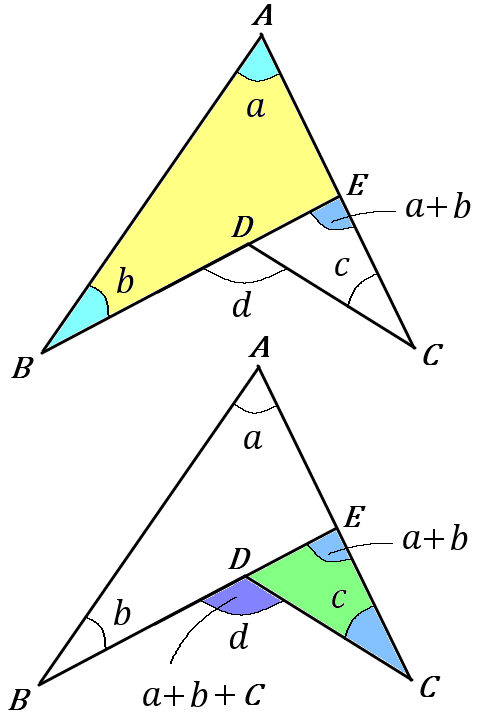 三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しいです。
三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しいです。
この性質を利用して、上の黄色の三角形で、$ \angle a +\angle b=\angle DEC$ です。
つぎに、下の緑の三角形で、$ \angle DEC +\angle c=\angle d$ です。
なので、$\angle a+\angle b +\angle c =\angle d$
(18) 下の図で、$\angle a+$ $\angle b+$ $\angle c+$ $\angle d+$ $\angle e$ $=180^{ \circ }$ である。この理由を説明しなさい。
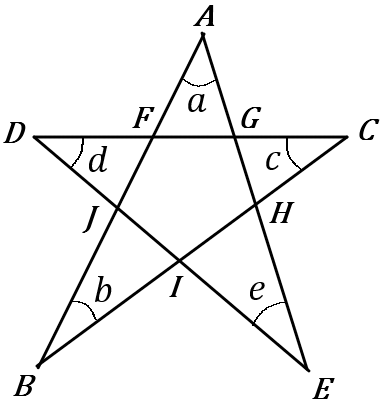
答え
$\triangle ABH$ で、三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しいから、
$ \angle a +\angle b=\angle EHI$ …①
$\triangle CDI$ で、三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しいから、
$ \angle c +\angle d=\angle EIH$ …②
$\triangle EHI$ で、三角形の内角の和は $180^{ \circ }$ だから、①②により、
$\angle a+$ $\angle b+$ $\angle c+$ $\angle d+$ $\angle e$ $=180^{ \circ }$
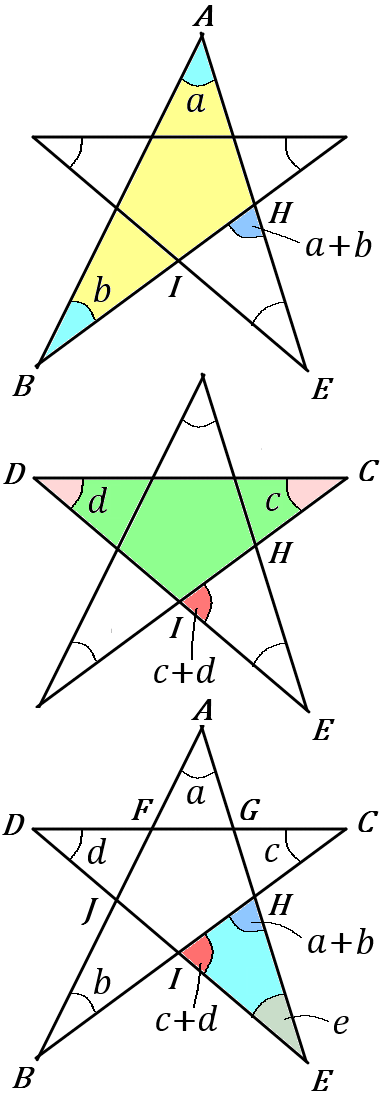 三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しいです。
三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しいです。
この性質を利用して、黄色の三角形で、$ \angle a +\angle b=\angle EHI$ です。
つぎに、その下の緑の三角形で、$ \angle c +\angle d=\angle EIH$ です。
三角形の内角の和は $180^{ \circ }$ ですから、いちばん下の水色の三角形で、
$\angle a+$ $\angle b+$ $\angle c+$ $\angle d+$ $\angle e$ $=180^{ \circ }$
答え(中2 4章 平行と合同 角と平行線 第1回)
(1)$\angle a$と$\angle c$, $\angle b$と$\angle d$
(2)同位角…
$\angle a$と$\angle e$,
$\angle b$と$\angle f$,
$\angle c$と$\angle g$,
$\angle d$と$\angle h$
錯角…
$\angle c$と$\angle f$,
$\angle d$と$\angle e$
(3)$\angle x=78^{ \circ }$, $\angle y=39^{ \circ }$
(4)$\angle x=98^{ \circ }$, $\angle y=105^{ \circ }$
(5)$\angle x=117^{ \circ }$, $\angle y=31^{ \circ }$, $\angle z=48^{ \circ }$
(6)$\angle x=81^{ \circ }$, $\angle y=24^{ \circ }$, $\angle z=139^{ \circ }$
(7)$\angle x=125^{ \circ }$, $\angle y=64^{ \circ }$
(8)内角の和…$180^{ \circ }\times(n-2)$,
外角の和…$360^{ \circ }$
(9)$540^{ \circ }$
(10)七角形
(11)$120^{ \circ }$
(12)$72^{ \circ }$
(13)正十二角形
(14)正十八角形
(15)$\angle x=105^{ \circ }$, $\angle y=41^{ \circ }$
(16)$\angle x=33^{ \circ }$, $\angle y=49^{ \circ }$
(17)$\triangle ABE$ で、三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しいから、
$ \angle a +\angle b=\angle DEC$ …①
$\triangle CDE$ で、三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しいから、
$ \angle DEC +\angle c=\angle d$ …②
①②により、$\angle a+\angle b +\angle c =\angle d$
(18)$\triangle ABH$ で、三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しいから、
$ \angle a +\angle b=\angle EHI$ …①
$\triangle CDI$ で、三角形の $1$つの外角は、それととなりあわない $2$つの内角の和に等しいから、
$ \angle c +\angle d=\angle EIH$ …②
$\triangle EHI$ で、三角形の内角の和は $180^{ \circ }$ だから、①②により、
$\angle a+$ $\angle b+$ $\angle c+$ $\angle d+$ $\angle e$ $=180^{ \circ }$