数学 中2 2学期期末模擬テスト 第1回
 ページがちゃんと表示されるまで$10$秒くらいかかります。
ページがちゃんと表示されるまで$10$秒くらいかかります。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
「印刷」をクリックすると同じ内容のpdfファイルが表示されます。また、解答用紙と答えも問題のあとに表示されます。1~6ページが問題、7~9ページが解答用紙、10~12ページが答えです。必要におうじて印刷してください。
問題をクリックすると答えがでます。
ふつうのテストより問題数は多いです。なのでふつうのテストをやるときより時間がかかると思います。がんばって!
$\huge{1}$ 次の①~⑧の計算をしなさい。
$\qquad①$ $\quad 8-6\times(-2)\qquad ② \quad \cfrac{2}{3}-1+\cfrac{1}{4}$
答え
$①20$ $②-\cfrac{1}{12}$
\begin{eqnarray*} &①& 8-6\times(-2)\\ &=& 8+12\\ &=&20 \end{eqnarray*} \begin{eqnarray*} \require{cancel} &②& \cfrac{2}{3}-1+\cfrac{1}{4}\\ &=& \cfrac{8}{12}-\cfrac{12}{12}+\cfrac{3}{12}\\ &=& -\cfrac{1}{12} \end{eqnarray*}
$\qquad③$ $\quad -8\times4+(-5)^2\qquad ④ \quad 2(3a-b)-(7a-2b)$
答え
$③-7$ $④-a$
\begin{eqnarray*} &③& -8\times4+(-5)^2\\ &=& -8\times4+25\\ &=&-32+25\\ &=&-7 \end{eqnarray*} \begin{eqnarray*} \require{cancel} &④& 2(3a-b)-(7a-2b)\\ &=& 6a-2b-7a+2b\\ &=& 6a-7a-2b+2b\\ &=& -a \end{eqnarray*}
$\qquad⑤$ $\quad \cfrac{2x-5y}{3}-\cfrac{x-4y}{2}\qquad ⑥ \quad 5ab^2\times(-3ab)$
答え
$⑤\cfrac{x+2y}{6}$ $⑥-15a^2b^3$
\begin{eqnarray*} &⑤& \cfrac{2x-5y}{3}-\cfrac{x-4y}{2}\\ &=& \cfrac{2(2x-5y)-3(x-4y)}{6}\\ &=& \cfrac{4x-10y-3x+12y}{6}\\ &=& \cfrac{4x-3x-10y+12y}{6}\\ &=& \cfrac{x+2y}{6} \end{eqnarray*} \begin{eqnarray*} \require{cancel} &⑥& 5ab^2\times(-3ab)\\ &=& -15a^2b^3 \end{eqnarray*}
$\qquad⑦$ $\quad 10x\div(-30xy)\times9y^2\qquad ⑧ \quad 2x^2\div\cfrac{6}{5}x^2y^2\times\cfrac{3}{10}y$
答え
$⑦-3y$ $⑧\cfrac{1}{2y}$
\begin{eqnarray*} \require{cancel} &⑦& 10x\div(-30xy)\times9y^2\\ &=& -\cfrac{10x\times9yy}{30xy}\\ &=& -\cfrac{\bcancel{10}\bcancel{x}\times{}^3\bcancel{9}\bcancel{y}y}{{}^{\bcancel{3}}\bcancel{30}\bcancel{x}\bcancel{y}}\\ &=& -3y \end{eqnarray*} \begin{eqnarray*} \require{cancel} &⑧& 2x^2\div\cfrac{6}{5}x^2y^2\times\cfrac{3}{10}y\\ &=& \cfrac{2xx}{1}\div\cfrac{6xxyy}{5}\times\cfrac{3y}{10}\\ &=& \cfrac{2xx}{1}\times\cfrac{5}{6xxyy}\times\cfrac{3y}{10}\\ &=& \cfrac{\bcancel{2}\bcancel{x}\bcancel{x}}{1}\times\cfrac{\bcancel{5}}{\bcancel{6}\bcancel{x}\bcancel{x}\bcancel{y}y}\times\cfrac{\bcancel{3}\bcancel{y}}{{}^2\bcancel{10}}\\ &=&\cfrac{1}{2y} \end{eqnarray*}
$\huge{2}$ 次の ①~③の連立方程式を解きなさい。また、④の方程式を解きなさい。
\begin{eqnarray*}
① \ \left\{
\begin{array}{l}
x=-2y-3\\
2x-3y=8
\end{array}
\right.
\qquad② \ \left\{
\begin{array}{l}
12(2x-1)+3y=-x-10\\
7x+2y=11
\end{array}
\right.\\
\end{eqnarray*}
答え
$①\phantom{ho}\begin{eqnarray*}
\left\{
\begin{array}{l}
x=1\\
y=-2
\end{array}
\right.
\quad②
\left\{
\begin{array}{l}
x=-1\\
y=9
\end{array}
\right.
\end{eqnarray*}$
①番 代入法で、①の式を②の式に代入して解きます。
\begin{eqnarray*}
2\times(-2y-3)-3y&=&8\\
-4y-6-3y&=&8\\
-7y&=&14\\
y&=&-2
\end{eqnarray*}
$y=-2を①に代入$
\begin{eqnarray*}
x&=&-2\times(-2)-3\\
&=&1\\
\\
\left\{
\begin{array}{l}
x=1\\
y=-2
\end{array}
\right.
\end{eqnarray*}
②番 ①の式のかっこをはずし、整理します。加減法で、$y$ の係数をそろえて解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
12(2x-1)+3y=-x-10\quad…①\\
7x+2y=11\quad…②
\end{array}
\right.
\end{eqnarray*}
$①を整理$
\begin{eqnarray*}
12(2x-1)+3y&=&-x-10\\
24x-12+3y&=&-x-10\\
24x+3y+x&=&-10+12\\
25x+3y&=&2\quad…③
\end{eqnarray*}
$②\times3 \ - \ ③\times2$
\begin{eqnarray*}
21x+6y=33\\
\underline{-) \quad 50x+6y=\phantom{3}4}\\
-29x\phantom{+6y}=29\\
x=-1
\end{eqnarray*}
$x=-1を②に代入$
\begin{eqnarray*}
7\times(-1)+2y&=&11\\
-7+2y&=&11\\
2y&=&18\\
y&=&9
\\
\left\{
\begin{array}{l}
x=-1\\
y=9
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*} ③ \ \left\{ \begin{array}{l} \cfrac{3}{4}x+\cfrac{5}{6}y=-4\\ 0.6x+0.7y=-3\\ \end{array} \right. \qquad④ \quad 3x-2y=x+2y=-4 \end{eqnarray*}
答え
$③\phantom{ho}\begin{eqnarray*}
\left\{
\begin{array}{l}
x=-12\\
y=6
\end{array}
\right.
\quad④
\left\{
\begin{array}{l}
x=-2\\
y=-1
\end{array}
\right.
\end{eqnarray*}$
③番 分数があるときは分母の公倍数をかけて分母をはらいます。小数があるときは $\times10$ や $\times100$ をして小数を消します。そのへんは $1$ 次方程式のときと同じです。そのあとは $x$ か $y$ の係数をそろえて足すか引くかして、$1$ 文字消去していけばいいです。
\begin{eqnarray*}
\left\{
\begin{array}{l}
\cfrac{3}{4}x+\cfrac{5}{6}y=-4\quad…①\\
0.6x+0.7y=-3\quad…②
\end{array}
\right.
\end{eqnarray*}
$①の式に12をかけて分母をはらう$
\begin{eqnarray*}
\cfrac{3}{4}x+\cfrac{5}{6}y&=&-4\\
9x+10y&=&-48\qquad…③
\end{eqnarray*}
$②の式に10をかけて小数をなくす$
\begin{eqnarray*}
0.6x+0.7y&=&-3\\
6x+7y&=&-30\qquad…④
\end{eqnarray*}
$③\times2\ - \ ④\times3$
\begin{eqnarray*}
18x+20y=-96\\
\underline{-) \quad 18x+21y=-90}\\
-y=-6\phantom{0}\\
y=6\phantom{0}
\end{eqnarray*}
\begin{eqnarray*}
y=6を④に代入\\
6x+7\times(6)&=&-30\\
6x+42&=&-30\\
6x&=&-72\\
x&=&-12\\
\\
\left\{
\begin{array}{l}
x=-12\\
y=6
\end{array}
\right.
\end{eqnarray*}
④番 まんなかをかくした式をつくり、①とします。左側をかくした式をつくって整理し、②とします。①の式と②の式を連立させ、$y$ の係数をそろえて加減法で解きます。
まず、まんなかをかくせば、
$3x-2y=-4$ という式ができます。
それから、左がわをかくせば、
$x+2y=-4$ という式ができます。
んで、この $2$ つの式を連立させて解いていくわけです。
\begin{eqnarray*}
\left\{
\begin{array}{l}
3x-2y=-4\qquad…①\\
x+2y=-4\qquad…②
\end{array}
\right.
\end{eqnarray*}
加減法で $y$ を消去して解くことにして、
$① \ + \ ②$
\begin{eqnarray*}
3x-2y=-4\\
\underline{-) \quad x+2y=-4}\\
4x\phantom{+21y}=-8\\
x=-2
\end{eqnarray*}
\begin{eqnarray*}
x=-2を②に代入\\
-2+2y&=&-4\\
2y&=&-2\\
y&=&-1\\
\\
\left\{
\begin{array}{l}
x=-2\\
y=-1
\end{array}
\right.
\end{eqnarray*}
$\huge{3}$ $1$ 次関数 $y=-\cfrac{1}{2}x+1$ について、次の $①~③$ の問いに答えなさい。
$①\quad x$ の値が $-4$ から$2$ まで増加するときの変化の割合を求めなさい。
答え
$-\cfrac{1}{2}$
$1$ 次関数 $y=ax+b$ で変化の割合をきかれたときは、$a$ を答えといてください。計算もなんもありません。$a$ を答えておけばいいんです。テストのときはそうやっちゃってください。
$②\quad x$ の値が $-4$ から$2$ まで増加するときの $y$ の増加量を求めなさい。
答え
$-3$
$yの増加量=xの増加量\times変化の割合$ です。
この問題の場合、$x$ の増加量は、$x$ の値が $-4$ から $2$ まで増加したのですから $6$ です。
変化の割合は $-\cfrac{1}{2}$ です。なので、
\begin{eqnarray*}
yの増加量&=&xの増加量\times変化の割合\\
&=&6\times\left(-\cfrac{1}{2}\right)\\
&=&-3
\end{eqnarray*}
$③\quad x$ の変域が $-6 \leqq x \leqq 2$ のとき、$y$ の変域を求めなさい。
答え
$0 \leqq y \leqq 4$
「$x$ の変域が $p \leqq x \leqq q$ のとき、$y$ の変域を求めなさい。」というお決まりの問題があって、こうきかれたときは、答えの形はこうです。 $$小 \leqq y \leqq 大$$ んで、小と大にそれぞれ、小さい数と大きい数を書いておけばいいです。小さい数と大きい数っていうのは、 $-6 \leqq x \leqq 2$ の $-6$ と $2$ をそれぞれ問題の $y=-\cfrac{1}{2}x+1$ の $x$ に代入してえられる数です。じゃあまず、 $x=-6$ を $y=-\cfrac{1}{2}x+1$ に代入します。 \begin{eqnarray*} y&=&-\cfrac{1}{2}\times(-6)+1\\ &=&3+1\\ &=&4\\ \end{eqnarray*} 次に、 $x=2$ を $y=-\cfrac{1}{2}x+1$ に代入します。 \begin{eqnarray*} y&=&-\cfrac{1}{2}\times2+1\\ &=&-1+1\\ &=&0\\ \end{eqnarray*} これで、$4$ と $0$ というふたつの数がえられました。これを小と大にあてはめればよいです。じゃあ答えを書きましょう。$$0 \leqq y \leqq 4$$ これでOKです。ただし、 $y$ の変域をきかれたときのこのやり方は、3年生で習う「2乗に比例する関数$y=ax^2$」では通用しないから気をつけてください。
$\huge{4}$ 次の $①~④$ の直線の式を求めなさい。
$①$ 傾きが $-2$ で点$(1,2)$を通る。
答え
$y=-2x+4$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
傾きというのは1次関数のときは $a$ のことです。だから $a=-2$ です。これを $y=ax+b$ に代入します。すると
$$y=-2x+b$$
となります。あと、「点$(1,2)$を通る」というのは、$x=1$ のとき $y=2$ という意味です。これをこの $y=-2x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
2&=&-2\times1+b\\
2&=&-2+b\\
2+2&=&b\\
4&=&b
\end{eqnarray*}
$b$ は右辺においたままにして解いていくのがおすすめです。どうしてもなじめなかったら由緒正しく $b$ を左辺にもってって解いてもいいです。ただその場合、符号でまちがえるのをとてもよく見るので、注意してください。
ともかく、これでめでたく $a=-2$ , $b=4$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-2x+4$$
$②$ $x$ の値が $3$ 増加すると $y$ の値が $2$ 減少し、$x=-9$ のとき $y=5$ となる。
答え
$y=-\cfrac{2}{3}x-1$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
1次関数のときは \(a=\cfrac{yの増加量\phantom{増加}}{xの増加量\phantom{増加}}\)だから、この問題の場合は $a=\cfrac{-2}{3}=-\cfrac{2}{3}$ となります。これを $y=ax+b$ に代入すると
$$y=-\cfrac{2}{3}x+b$$
となります。 $x=-9$ , $y=5$ をこの $y=-\cfrac{2}{3}x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
5&=&-\cfrac{2}{3}\times(-9)+b\\
5&=&6+b\\
5-6&=&b\\
-1&=&b
\end{eqnarray*}
これで $a=-\cfrac{2}{3}$ , $b=-1$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-\cfrac{2}{3}x-1$$
$③$ $y$ 切片が $-2$ で、点$(2,-1)$ を通る。
答え
$y=\cfrac{1}{2}x-2$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
$y$ 切片というのは $b$ のことです。だから $b=-2$ です。これを $y=ax+b$ に代入します。すると
$$y=ax-2$$
となります。 $x=2$ , $y=-1$ をこの $y=ax-2$ に代入して、 $a$ を求めます。
\begin{eqnarray*}
-1&=&2a-2\\
-2a&=&-2+1\\
-2a&=&-1\\
a&=&\cfrac{1}{2}
\end{eqnarray*}
これで $a=\cfrac{1}{2}$ , $b=-2$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=\cfrac{1}{2}x-2$$
$④$ $2$ 点$(-1,4),(3,0)$ を通る。
答え
$y=-x+3$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
$2$ 点を通る直線の式をきかれたときは、
$$a=\cfrac{y_2-y_1}{x_2-x_1}$$
という公式を使って $a$ を求めましょう。
$2$ 点の座標 $(-1,4),(3,0)$ を $(x_1,y_1),(x_2,y_2)$ だということにして、上の公式にあてはめると、
\begin{eqnarray*}
a&=&\cfrac{y_2-y_1}{x_2-x_1}\\
&=&\cfrac{0-4}{3-(-1)}\\
&=&\cfrac{-4}{4}\\
&=&-1\\
\end{eqnarray*}
これで $a=-1$ だということがわかりました。これを $y=ax+b$ に代入して、
$$y=-x+b$$
ここに、 $(-1,4),(3,0)$ のどちらかを代入して $b$ を求めます。代入するのはどっちでもよいです。今回は、 $(3,0)$ のほうをいれてみましょう。
\begin{eqnarray*}
0&=&-3+b\\
3&=&b
\end{eqnarray*}
これで $a=-1$ , $b=3$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-x+3$$
ところで、この問題に関してはもうひとつ、連立方程式をたてて $a$ と $b$ を求めていく、という定番のやり方があります。ここで紹介しているやり方と、連立方程式をたてるのと、両方ためして、好きなほうでやってください。連立方程式をたててやるやり方は、次の問題で説明します。
$\huge{5}$ $y$ が $x$ の1次関数であるとき、表のア~ウにあてはまる数をこたえなさい。また、$y$ を $x$ の式で表しなさい。
\begin{array}{c|ccccc}
\hline
x & -9 & -3 & イ & 6 & ウ \\
\hline
y & 32 & ア & 2 & -13 & -19 \\
\hline
\end{array}
答え
ア…$14$, イ…$1$, ウ…$8$, 式 $y=-3x+5$
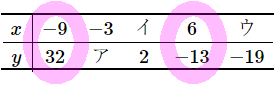 まず、$y$ を $x$ の式で表してしまいましょう。そのために、$x$ と $y$ がわかっている組を $2$ 組、見つけます。必ず $2$ 組はあるはずです。この問題の場合は、$x=-9$ のとき $y=32$, $x=6$ のとき $y=-13$ というのがありますね。これで $a$ を求めることができます。$(-9, 32), (6, -13)$ だと思ってもいいです。$a$ が求まりますよね?
まず、$y$ を $x$ の式で表してしまいましょう。そのために、$x$ と $y$ がわかっている組を $2$ 組、見つけます。必ず $2$ 組はあるはずです。この問題の場合は、$x=-9$ のとき $y=32$, $x=6$ のとき $y=-13$ というのがありますね。これで $a$ を求めることができます。$(-9, 32), (6, -13)$ だと思ってもいいです。$a$ が求まりますよね?
$a=\cfrac{y_2-y_1}{x_2-x_1}$ を使って、
$a=\cfrac{-13-32}{6-(-9)}=\cfrac{-45}{15}=-3$
$y=-3x+b$ に $(6,-13)$ を代入して、
\begin{eqnarray*}
-13&=&-3\times6+b\\
-13&=&-18+b\\
-13+18&=b\\
5&=&b
\end{eqnarray*}
これで、式は $y=-3x+5$ だと求められました。あとはアとイとウをだしていきましょう。
アは $x=-3$ のときの $y$ の値のことだから、
\begin{eqnarray*}
y&=&-3\times(-3)+5=9+5=14
\end{eqnarray*}
イは $y=2$ のときの $x$ の値のことだから、
\begin{eqnarray*}
2&=&-3x+5\\
3x&=&5-2\\
3x&=&3\\
x&=&1
\end{eqnarray*}
ウは $y=-19$ のときの $x$ の値のことだから、
\begin{eqnarray*}
-19&=&-3x+5\\
3x&=&5+19\\
3x&=&24\\
x&=&8
\end{eqnarray*}
これですべて求まりました。答えを書きましょう。
ア…$14$, イ…$1$, ウ…$8$, 式 $y=-3x+5$
$\huge{6}$
次の $①~③$ のグラフをかきなさい。
 \begin{eqnarray*}
&&① \quad y=-2x+3\\
&&② \quad 3x-2y=4\\
&&③ \quad x=2\\
\end{eqnarray*}
\begin{eqnarray*}
&&① \quad y=-2x+3\\
&&② \quad 3x-2y=4\\
&&③ \quad x=2\\
\end{eqnarray*}
答え
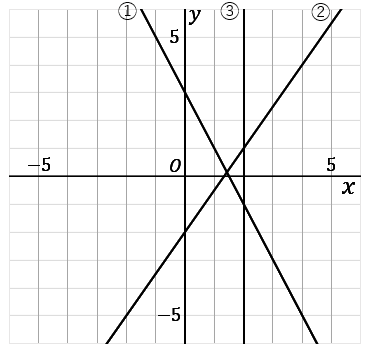
$①$ 切片が $3$ なので、$y$ 軸の $3$ をスタート地点にします。傾きが $-2$ なので、$\cfrac{-2}{1}$ なので、右に $1$ 歩行って下に $2$ 歩行く点をとっていきます。点を定規で結びます。
$②$ まず式を $y$ について解きます。
\begin{eqnarray*}
3x-2y&=&4\\
-2y&=&-3x+4\quad両辺に-1をかける\\
2y&=&3x-4\quad両辺に\cfrac{1}{2}をかける\\
y&=&\cfrac{3}{2}x-2\\
\end{eqnarray*}
これで $y=ax+b$ の形になったので、あとはこのグラフをかけばよいです。
$③$ $y$ 軸に平行な線です。たて線です。$x$ 軸の $2$ を通るようにします。
 $\huge{7}$
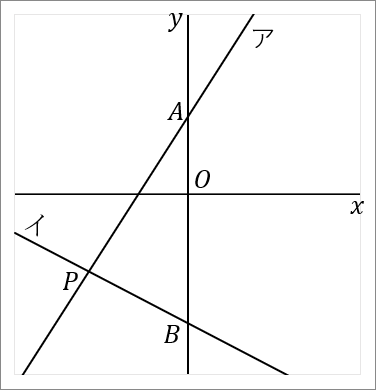
右の図で、直線アは関数 $y=\cfrac{3}{2}x+3$ のグラフであり、直線イは関数 $y=-\cfrac{1}{2}x-5$ のグラフである。直線アと $y$ 軸との交点を $A$ とし、直線イと $y$ 軸との交点を $B$ とする。直線アと直線イとの交点を $P$ とする。このとき、以下の問いに答えなさい。
$\huge{7}$
右の図で、直線アは関数 $y=\cfrac{3}{2}x+3$ のグラフであり、直線イは関数 $y=-\cfrac{1}{2}x-5$ のグラフである。直線アと $y$ 軸との交点を $A$ とし、直線イと $y$ 軸との交点を $B$ とする。直線アと直線イとの交点を $P$ とする。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(-4, \ -3)$
$2$ 直線の交点は連立方程式の解です。ア、イの式を連立方程式にして \begin{eqnarray*} && \ \left\{ \begin{array}{l} y=\cfrac{3}{2}x+3\quad…①\\ y=-\cfrac{1}{2}x-5\quad…② \end{array} \right. \end{eqnarray*} これを解けばいいです。解き方は、この手の連立方程式は代入法で、右辺 $=$ 右辺の式をたてて、$x$ を求めていきましょう。関数の問題でよく使うパターンです。 \begin{eqnarray*} 代入法で、右辺 &=& 右辺の式にする。\\\\ \cfrac{3}{2}x+3&=&-\cfrac{1}{2}x-5\quad(両辺に\times2)\\ 3x+6&=&-x-10\\ 3x+x&=&-10-6\\ 4x&=&-16\\ x&=&-4 \end{eqnarray*} $x=-4を①に代入$ \begin{eqnarray*} y&=&\cfrac{3}{2}\times(-4)+3\\ &=&-6+3\\ &=&-3 \\\\ 答え\\ (-4, \ -3) \end{eqnarray*} ※座標をきかれているのだから、かならず座標の答え方で答えましょう。
$(2)$ $\triangle PAB$ の面積を求めなさい。
答え
$16$
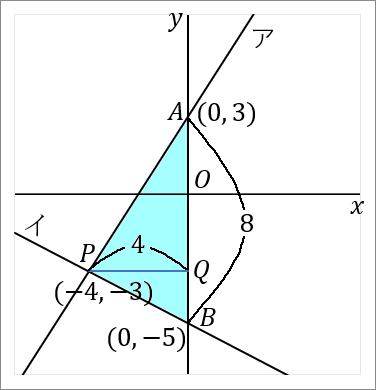 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
点 $A$ の座標は、直線ア $y=\cfrac{3}{2}x+3$ の切片ですから、$(0, \ 3)$ です。
点 $B$ の座標は、直線イ $y=-\cfrac{1}{2}x-5$ の切片ですから、$(0, \ -5)$ です。
なので、$AB$ の長さは $3+5=8$ です。点 $B$ の $y$ 座標は $-5$ ですが、長さの話なのですから絶対値をいうようにしましょう。
<$PQ$ について>
$PQ$ の長さは、点 $P$ の $x$ 座標をみればよいです。点 $P$ の $x$ 座標は $-4$ ですから、$PQ$ の長さは $4$ です。これも長さの話なのですから絶対値をいうようにしましょう。
これで底辺と高さがわかりました。では面積をだしましょう。
$$8\times4\times\cfrac{1}{2}=16$$
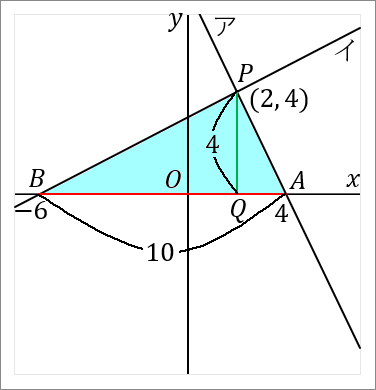
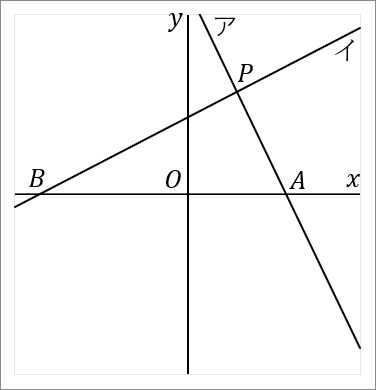 $\huge{8}$ 右の図で、直線アと直線イの交点を $P$ とする。直線ア,イと $x$ 軸との交点をそれぞれ $A, \ B$ とする。直線アは関数 $y=-2x+8$ のグラフである。点 $P$ の $x$ 座標が $2,$ 点 $B$ の座標が $(-6, \ 0)$ である。このとき、以下の問いに答えなさい。
$\huge{8}$ 右の図で、直線アと直線イの交点を $P$ とする。直線ア,イと $x$ 軸との交点をそれぞれ $A, \ B$ とする。直線アは関数 $y=-2x+8$ のグラフである。点 $P$ の $x$ 座標が $2,$ 点 $B$ の座標が $(-6, \ 0)$ である。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(2, \ 4)$
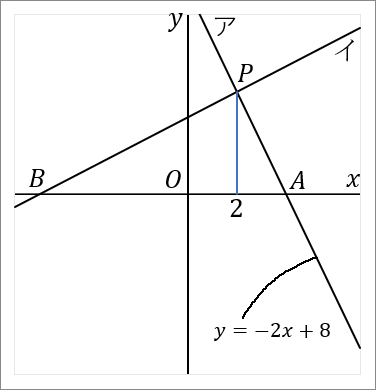 点 $P$ の $x$ 座標は $2$ だと問題にかかれています。あとは $y$ 座標がわかればよいです。また、点 $P$ は直線ア上の点です。アの式はわかっているので、この式を使えば $y$ 座標が求められます。
\begin{eqnarray*}
y&=&-2x+8 に、x=2を代入\\\\
y&=&-2\times2+8\\
&=&-4+8\\
&=&4
\end{eqnarray*}
これで $y=4$ だとわかりました。なので答えは $(2, \ 4)$ です。
点 $P$ の $x$ 座標は $2$ だと問題にかかれています。あとは $y$ 座標がわかればよいです。また、点 $P$ は直線ア上の点です。アの式はわかっているので、この式を使えば $y$ 座標が求められます。
\begin{eqnarray*}
y&=&-2x+8 に、x=2を代入\\\\
y&=&-2\times2+8\\
&=&-4+8\\
&=&4
\end{eqnarray*}
これで $y=4$ だとわかりました。なので答えは $(2, \ 4)$ です。
$(2)$ 直線イの式を求めなさい。
答え
$y=\cfrac{1}{2}x+3$
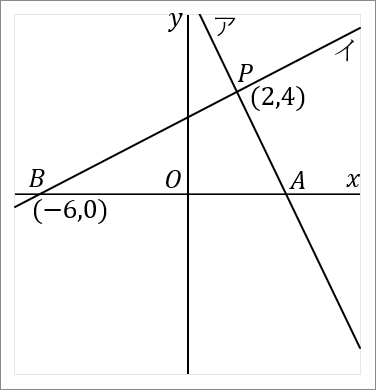 イの式は、点 $B(-6, \ 0)$ を通っています。また、点 $P$ も通っているのですが、その座標は $(1)$ の問題で $(2, \ 4)$ だと求めました。この $2$ 点を通る直線の式だということでやれば、イの式がでます。
イの式は、点 $B(-6, \ 0)$ を通っています。また、点 $P$ も通っているのですが、その座標は $(1)$ の問題で $(2, \ 4)$ だと求めました。この $2$ 点を通る直線の式だということでやれば、イの式がでます。
直線の式を求めなさいといわれたら、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$2$ 点 $(-6, \ 0), \ (2, \ 4)$ を通る直線の式を求めます。
\begin{eqnarray*}
a&=&\cfrac{y-y}{x-x}\\
&=&\cfrac{0-4}{-6-2}=\cfrac{-4}{-8}=\cfrac{1}{2}\\\\
y&=&\cfrac{1}{2}x+bにx=-6,y=0 を代入する\\
0&=&\cfrac{1}{2}\times(-6)+b\\
0&=&-3+b\\
3&=&b\\
\end{eqnarray*}
これで $a$ と $b$ がでました。答えは $y=\cfrac{1}{2}x+3$ です。
$(3)$ $\triangle PAB$ の面積を求めなさい。
答え
$20$
 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
点 $A$ の座標は、直線アと $x$ 軸との交点だということで求めます。
ここでポイントがあります。$x$ 軸上の点というのは、$y$ 座標がかならず $0$ です。あたりまえです。$y$ がかならず $0$ なんです。このことを利用して、アの式に $y=0$ を代入すれば、点 $A$ の $x$ 座標が求められます。
\begin{eqnarray*}
y&=&-2x+8にy=0 を代入\\
0&=&-2x+8\\
2x&=&8\\
x&=&4
\end{eqnarray*}
なので点 $A$ の座標は、$(4, \ 0)$ です。
点 $B$ の座標は、$(-6, \ 0)$ です。
というわけで、$AB$ の長さは $4+6=10$ です。点 $B$ の $x$ 座標は $-6$ ですが、長さの話なのですから絶対値をいうようにしましょう。
<$PQ$ について>
$PQ$ の長さは、点 $P$ の $y$ 座標をみればよいです。点 $P$ の $y$ 座標は $4$ ですから、$PQ$ の長さは $4$ です。
これで底辺と高さがわかりました。では面積をだしましょう。
$$10\times4\times\cfrac{1}{2}=20$$
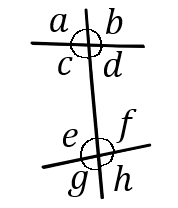
$\huge{9}$
右の図について、次の①~③の問いに答えなさい。
$①$ $\angle b$ の対頂角をいいなさい。
答え $\angle c$
$②$ $\angle h$ の同位角をいいなさい。
答え $\angle d$
$③$ $\angle e$ の錯角をいいなさい。
答え $\angle d$
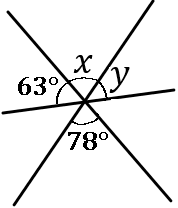
$\huge{10}$
右の図で、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。
答え
$\angle x=78^{ \circ }$, $\angle y=39^{ \circ }$
$\angle x$ の対頂角は $78^{ \circ }$ です。
$\angle y=180-(63+78)=39$
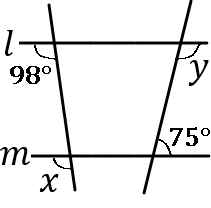
$\huge{11}$
右の図で、$l /\!/ m$ のとき、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。
答え
$\angle x=98^{ \circ }$, $\angle y=105^{ \circ }$
$\angle x$ の同位角は $98^{ \circ }$ です。
$\angle y$ の同位角や錯角の反対側が $75^{ \circ }$ なのを利用します。
$y=180-75=105$
$\huge{12}$
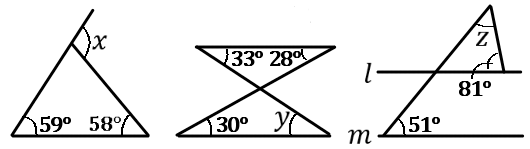
下の図で、$\angle x$, $\angle y$, $\angle z$ の大きさをそれぞれ求めなさい。ただし、$l /\!/ m$ とする。
答え
$\angle x=117^{ \circ }$, $\angle y=31^{ \circ }$, $\angle z=48^{ \circ }$
$x=59+58\\30+y=28+33\\51+81+z=180$
$\huge{13}$
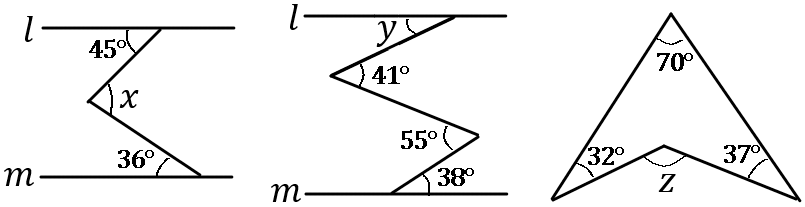
下の図で、$\angle x$, $\angle y$, $\angle z$ の大きさをそれぞれ求めなさい。ただし、$l /\!/ m$ とする。
答え
$\angle x=81^{ \circ }$, $\angle y=24^{ \circ }$, $\angle z=139^{ \circ }$
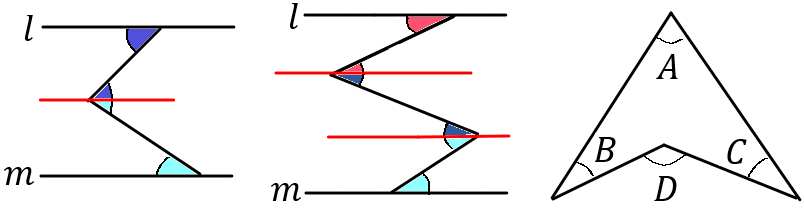
※補助線をひいて考えます。色のついた部分の大きさがおなじです。
※最後の問題は、$A+B+C=D$になります。よく出てくる形なので、「この形は $A+B+C=D$」とおぼえてしまいましょう。また、なぜそうなるのか説明しなさいという問題もよくあるので、説明できるようにしておきましょう。
$\huge{14}$
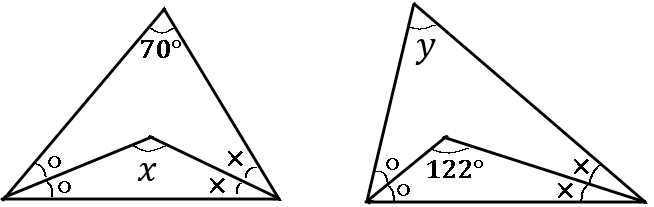
下の図で、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。ただし、〇のついている角同士、×のついている角同士等しいものとする。
答え
$\angle x=125^{ \circ }$, $\angle y=64^{ \circ }$
<$x$ の求め方> \begin{eqnarray*} ○&=&a^{ \circ },×=b^{ \circ } とすると、\\ 2a+2b+70&=&180\\ 2a+2b&=&110 \quad \class{mathbg-r}{(両辺を\div2)} \\ a+b&=&55\\ x&=&180-(a+b)\\ &=&180-55=125 \end{eqnarray*} <$y$ の求め方> \begin{eqnarray*} ○&=&a^{ \circ },×=b^{ \circ } とすると、\\ a+b+122&=&180\\ a+b&=&58 \quad \class{mathbg-r}{(両辺に\times2)} \\ 2a+2b&=&116\\ y&=&180-(2a+2b)\\ &=&180-116=64 \end{eqnarray*}
$\huge{15}$ 次の $①~⑥$ の問いに答えなさい。
$①$ 五角形の内角の和を求めなさい。
答え
$540^{ \circ }$
$180\times(5-2)=540$
$②$ 内角の和が $900^{ \circ }$ になる多角形は何角形ですか。
答え
七角形
$900\div180+2=7$
$③$ 正六角形の1つの内角の大きさは何度ですか。
答え
$120^{ \circ }$
$\{180\times(6-2)\}\div6=720\div6=120$
別解 (外角の和$=360^{ \circ }$を利用する)←おすすめ
$180-(360\div6)=180-60=120$
$④$ 正五角形の1つの外角の大きさは何度ですか。
答え
$72^{ \circ }$
$360\div5=72$
$⑤$ 1つの外角の大きさが $30^{ \circ }$になるのは正何角形ですか。
答え
正十二角形
$360\div30=12$
$⑥$ 1つの内角の大きさが $160^{ \circ }$になるのは正何角形ですか。
答え
正十八角形
内角が$160^{ \circ }$ということは、外角は$20^{ \circ }$だから、 $360\div20=18$
$\huge{16}$
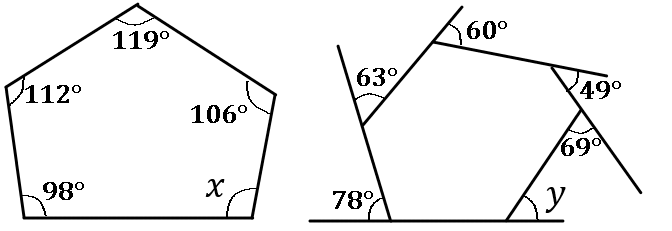
下の図で、下の図で、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。
答え
$\angle x=105^{ \circ }$, $\angle y=41^{ \circ }$
$x=540-(98+112+119+106)\\ y=360-(78+63+60+49+69)$
$\huge{17}$
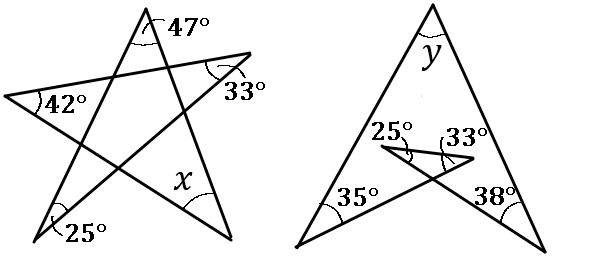
下の図で、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。
答え
$\angle x=33^{ \circ }$, $\angle y=49^{ \circ }$
$x=180-(25+42+47+33)$
五芒星(ごぼうせい)は色のついた $5$ つの角の和が $180^{ \circ }$ になるとおぼえてしまいましょう。また、なぜこの $5$ つを足すと $180^{ \circ }$ になるのかもよく問われるので、その理由の説明ができるようにしておきましょう。
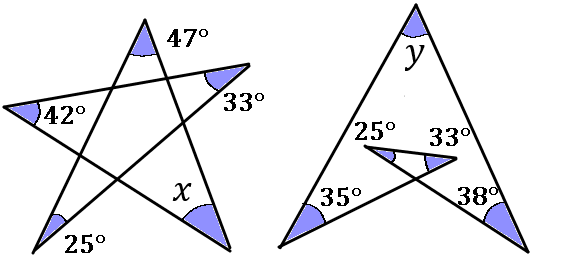 $y=180-(35+25+33+38)$
$y=180-(35+25+33+38)$
$y$ も $x$ とおなじように考えてしまえばよいです。
$\huge{18}$
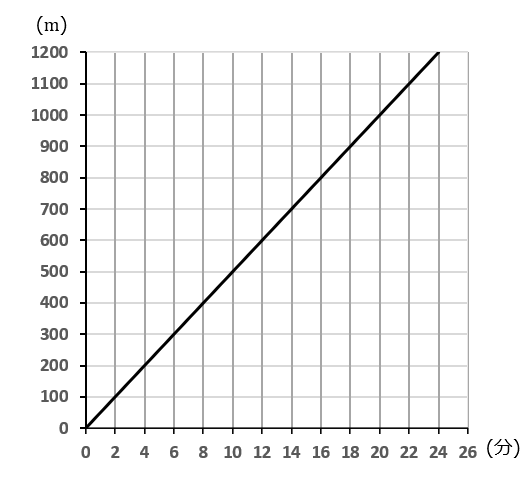
駅から $1200m$ 離れたところに学校がある。下の図は、Aさんが駅を出発して学校まで歩いたときの時間と道のりの関係を表したグラフである。以下の①,②の問いに答えなさい。
$①$ Aさんの歩く速さを求めなさい。
答え
$50m/分$
グラフから、Aさんは $2$ 分で $100m$ 進んでいます。
速さ $=$ 道のり $\div$ 時間ですから、答えは $100\div2=50(m/分)$ です。
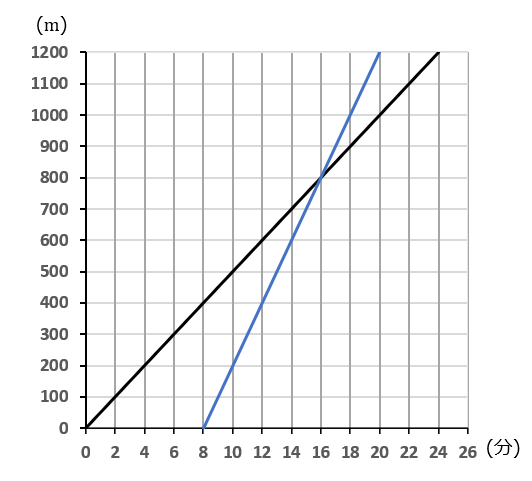
$②$ Aさんが出発してから $8$ 分後に、Bさんが分速 $100m$ の速さで駅から学校へ自転車で走った。このときのBさんが進んだようすをグラフにかきくわえなさい。また、BさんがAさんに追いついたのは、Aさんが出発してから何分後か。
答え
 $16$ 分後
$16$ 分後
〈グラフ〉
BさんはAさんが出発してから $8$ 分後に出発したわけですから、点 $(8, \ 0)$ からグラフをはじめます。
グラフをかくときは、目盛りに注意してください。$x$ 軸は $1$ 目盛りが $2$ 分です。$y$ 軸は $1$ 目盛りが $100m$ です。
Bさんの速さは分速 $100m$ なので、$2$ 分で $200m$ 進むことになります。なので、右に $1$ マスいって、上に $2$ マスいくように点をとっていきます。
〈時間〉
$2$ 直線の交点が、BさんがAさんに追いついた地点と時間を表します。なので、追いついたのは、Aさんが出発してから $16$ 分後です。
 $\huge{19}$
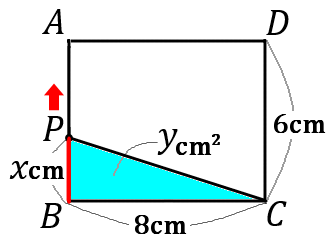
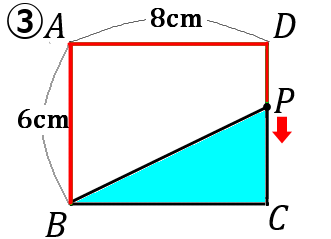
図のような長方形 $ABCD$ で、点 $P$ は辺上を点 $B$ から $A,D$ を通って $C$ まで動く。点 $P$ が辺上を点 $B$ から $xcm$ 動いたときの $\triangle PBC$ の面積を $ycm^2$ とする。以下の①~④の問いに答えなさい。
$\huge{19}$
図のような長方形 $ABCD$ で、点 $P$ は辺上を点 $B$ から $A,D$ を通って $C$ まで動く。点 $P$ が辺上を点 $B$ から $xcm$ 動いたときの $\triangle PBC$ の面積を $ycm^2$ とする。以下の①~④の問いに答えなさい。
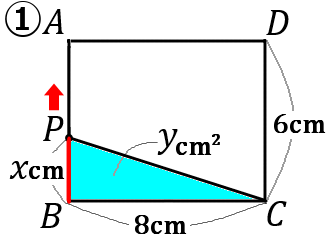
$①$ 点 $P$ が辺 $BA$ 上にあるとき、$y$ を $x$ の式で表しなさい。また、$x$ の変域をいいなさい。
答え
$y=4x\qquad (0 \leqq x \leqq 6)$
 〈式〉
〈式〉
三角形の面積は、底辺 $\times$ 高さ $\times\cfrac{1}{2}$ です。底辺を $BC$、高さを$PB$ ということにして、$y$ を $x$ で表します。
$BC$ の長さは $8$ です。
$P$ が動いた長さが $x$ なので、$PB$ の長さは $x$ です。
なので、三角形 $y$ の面積は、$y=8\times x \times \cfrac{1}{2}=4x$ となります。
〈変域〉
$P$ が $B$ 上にあるときは、$x=0$ です。最小値は $0$ です。$P$ が $A$ 上にきたときは、$x=6$ です。最大値は $6$ です。
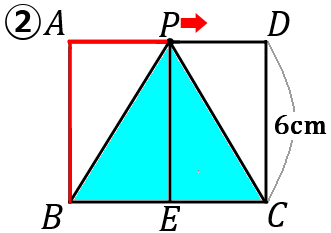
$②$ 点 $P$ が辺 $AD$ 上にあるとき、$y$ を $x$ の式で表しなさい。また、$x$ の変域をいいなさい。
答え
$y=24\qquad (6 \leqq x \leqq 14)$
 〈式〉
〈式〉
$P$ から $BC$ におろした垂線と、$BC$ との交点を $E$ とします。底辺を $BC$、高さを$PE$ ということにして、$y$ を $x$ で表します。
$BC$ の長さは $8$ です。
$PE$ の長さは、$P$ がどこにあっても $6$ です。
なので、三角形 $y$ の面積は、$y=8 \times 6 \times\cfrac{1}{2}=24$ となります。というわけでこの場合、式に $x$ はでてこなくなってしまいます。
〈変域〉
$x$ の変域は、$P$ が $A$ 上にきたときは、$x=6$ です。最小値は $6$ です。$P$ が $D$ 上にきたときは、$x=6+8=14$ です。最大値は $14$ です。
$③$ 点 $P$ が辺 $DC$ 上にあるとき、$y$ を $x$ の式で表しなさい。また、$x$ の変域をいいなさい。
答え
$y=-4x+80\qquad (14 \leqq x \leqq 20)$
 〈式〉
〈式〉
底辺を $BC$、高さを$PC$ ということにして、$y$ を $x$ で表します。
$BC$ の長さは $8$ です。
$PC$ の長さは、$20-x$ です。$x$ は $P$ が動いてきた長さです。③の図の赤い線が $x$ を表しています。$BA+AD+DC$ から $x$ をひけば、$PC$ になります。なので、$PC=6+8+6-x=20-x$ です。
なので、三角形 $y$ の面積は、
\begin{eqnarray*}
y&=&8 \times (20-x) \times\cfrac{1}{2} \quad(8\times\cfrac{1}{2}を先にやってしまう)\\
&=&4(20-x)\\
&=&80-4x\\
&=&-4x+80
\end{eqnarray*}
〈変域〉
$x$ の変域は、$P$ が $D$ 上にきたときは、$x=6+8=14$ です。最小値は $14$ です。$P$ が $C$ 上にきたときは、$x=6+8+6=20$ です。最大値は $20$ です。
$④$ $x$ の変域を $0 \leqq x \leqq 20$ とするときの $x$ と $y$ の関係をグラフに表しなさい。また、$\triangle PBC$ の面積が $8cm^2$ となるときの $x$ の値を求めなさい。
答え
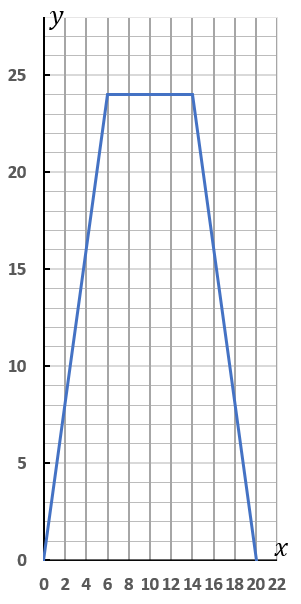
$\triangle PBC$ の面積が $8cm^2$ となるときの $x$ の値
$x=2, \ x=18$
〈グラフ〉
変域が $0 \leqq x \leqq 6$ のときの式は $y=4x$ です。原点を通る直線です。点$(0, \ 0),$ $(6, \ 24)$ をとって定規でむすんでしまいましょう。線は点 $(6, \ 24)$ で終わりにしてください。その先をかいちゃダメです。
変域が $6 \leqq x \leqq 14$ のときの式は $y=24$ です。$x$ 軸に平行な直線になります。$(6, \ 24)$ から$ (14, \ 24)$ までを定規でむすんでしまいましょう。
変域が $14 \leqq x \leqq 20$ のときの式は $y=-4x+80$ です。直線です。点$(14, \ 24)$ と $(20, \ 0)$ をとって定規でむすんでしまいましょう。$x=20$ のときに面積が $0$ になるはず、と考えて点 $(20, \ 0)$ をとるわけです。
〈面積〉
グラフから、面積 $y$ が $8$ になるのは、$2$ か所あります。$P$ が $y=4x$ 上にあるときと、$y=-4x+80$ 上にあるときです。それぞれの式の $y$ に $8$ を代入して $x$ を求めればOKです。
$P$ が $y=4x$ 上にあるとき
\begin{eqnarray*}
8&=&4x\\
x&=&2
\end{eqnarray*}
$P$ が $y=-4x+80$ 上にあるとき
\begin{eqnarray*}
8&=&-4x+80\\
4x&=&80-8\\
4x&=&72\\
x&=&18
\end{eqnarray*}
答え(中2 2学期期末模擬テスト 第1回)
1$①20$ $②-\cfrac{1}{12}$ $③-7$ $④-a$ $⑤\cfrac{x+2y}{6}$ $⑥-15a^2b^3$ $⑦-3y$ $⑧\cfrac{1}{2y}$
2$①x=1, \ y=-2$ $②x=-1, \ y=9$ $③x=-12, \ y=6$ $④x=-2, \ y=-1$
3$①-\cfrac{1}{2}$ $②-3$ $③0 \leqq y \leqq 4$
 4$①y=-2x+4$ $②y=-\cfrac{2}{3}x-1$ $③y=\cfrac{1}{2}x-1$ $④y=-x+3$
4$①y=-2x+4$ $②y=-\cfrac{2}{3}x-1$ $③y=\cfrac{1}{2}x-1$ $④y=-x+3$
5ア…$14$, イ…$1$, ウ…$8$, 式 $y=-3x+5$
6 右図
7(1)$(-2, \ 1)$ (2)$16$
8(1)$(2, \ 4)$ (2)$y=\cfrac{1}{2}x+3$ (3)$20$
9$①\angle c$ $②\angle d$ $③\angle d$
10 $\angle x=78^{ \circ }$, $\angle y=39^{ \circ }$
11 $\angle x=98^{ \circ }$, $\angle y=105^{ \circ }$
12 $\angle x=117^{ \circ }$, $\angle y=31^{ \circ }$, $\angle z=48^{ \circ }$
13 $\angle x=81^{ \circ }$, $\angle y=24^{ \circ }$, $\angle z=139^{ \circ }$
14 $\angle x=125^{ \circ }$, $\angle y=64^{ \circ }$
$B$ 地点から $C$ 地点までの道のり…$600m$
15 $①540^{ \circ }$ $②七角形$ $③120^{ \circ }$ $④72^{ \circ }$ $⑤正十二角形$ $⑥正十八角形$

16 $\angle x=105^{ \circ }$, $\angle y=41^{ \circ }$
17 $\angle x=33^{ \circ }$, $\angle y=49^{ \circ }$
18$①50m/分$ $②グラフ右図\quad 16分後$
19$①y=4x\qquad (0 \leqq x \leqq 6)$ $②y=24\qquad (6 \leqq x \leqq 14)$ $③y=-4x+80\qquad (14 \leqq x \leqq 20)$ $④グラフ下図\quad x=2, \ x=18$
