数学 中2 2学期期末模擬テスト 第2回
 ページがちゃんと表示されるまで$10$秒くらいかかります。
ページがちゃんと表示されるまで$10$秒くらいかかります。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
「印刷」をクリックすると同じ内容のpdfファイルが表示されます。また、解答用紙と答えも問題のあとに表示されます。1~6ページが問題、7~9ページが解答用紙、10~12ページが答えです。必要におうじて印刷してください。
問題をクリックすると答えがでます。
ふつうのテストより問題数は多いです。なのでふつうのテストをやるときより時間がかかると思います。がんばって!
$\huge{1}$ 次の①~⑧の計算をしなさい。
$\qquad①$ $\quad 5+7\times(-3)\qquad ② \quad \cfrac{2}{5}-1+\cfrac{1}{3}$
答え
$①-16$ $②-\cfrac{4}{15}$
\begin{eqnarray*} &①& 5+7\times(-3)\\ &=& 5-21\\ &=&-16 \end{eqnarray*} \begin{eqnarray*} \require{cancel} &②& \cfrac{2}{5}-1+\cfrac{1}{3}\\ &=& \cfrac{6}{15}-\cfrac{15}{15}+\cfrac{5}{15}\\ &=& -\cfrac{4}{15} \end{eqnarray*}
$\qquad③$ $\quad 6\times3-(-4)^2\qquad ④ \quad 4(5a-3b)-5(6a-2b)$
答え
$③2$ $④-10a-2b$
\begin{eqnarray*} &③& 6\times3-(-4)^2\\ &=& 6\times3-16\\ &=&18-16\\ &=&2 \end{eqnarray*} \begin{eqnarray*} \require{cancel} &④& 4(5a-3b)-5(6a-2b)\\ &=& 20a-12b-30a+10b\\ &=& 20a-30a-12b+10b\\ &=& -10a-2b \end{eqnarray*}
$\qquad⑤$ $\quad \cfrac{x-3y}{4}-\cfrac{3x-4y}{6}\qquad ⑥ \quad 25ab^2\div(-5ab)$
答え
$⑤\cfrac{-3x-y}{12} \ \left(-\cfrac{3x+y}{12},-\cfrac{1}{4}x-\cfrac{1}{12}y\right)$ $⑥-5b$
\begin{eqnarray*} &⑤& \cfrac{x-3y}{4}-\cfrac{3x-4y}{6}\\ &=& \cfrac{3(x-3y)-2(3x-4y)}{12}\\ &=& \cfrac{3x-9y-6x+8y}{12}\\ &=& \cfrac{3x-6x-9y+8y}{12}\\ &=& \cfrac{-3x-y}{12} \end{eqnarray*} \begin{eqnarray*} \require{cancel} &⑥& 25ab^2\div(-5ab)\\ &=& -\cfrac{{}^5\bcancel{25}\bcancel{a}\bcancel{b}b}{\bcancel{5}\bcancel{a}\bcancel{b}}\\ &=&-5b \end{eqnarray*}
$\qquad⑦$ $\quad -18x\div(-72xy)\times16y^2\qquad ⑧ \quad 15x\div\cfrac{30}{7}x^2y^2\times\cfrac{4}{21}y^2$
答え
$⑦4y$ $⑧\cfrac{2}{3x}$
\begin{eqnarray*} &⑦& -18x\div(-72xy)\times16y^2\\ &=& \cfrac{18x\times16yy}{72xy}\\ &=& \cfrac{\bcancel{18}\bcancel{x}\times{}^4\bcancel{16}\bcancel{y}y}{{}^{\bcancel{4}}\bcancel{72}\bcancel{x}\bcancel{y}}\\ &=& 4y \end{eqnarray*} \begin{eqnarray*} \require{cancel} &⑧& 15x\div\cfrac{30}{7}x^2y^2\times\cfrac{4}{21}y^2\\ &=& \cfrac{15x}{1}\div\cfrac{30xxyy}{7}\times\cfrac{4yy}{21}\\ &=& \cfrac{15x}{1}\times\cfrac{7}{30xxyy}\times\cfrac{4yy}{21}\\ &=& \cfrac{\bcancel{15}\bcancel{x}}{1}\times\cfrac{\bcancel{7}}{{}^{\bcancel{2}}\bcancel{30}\bcancel{x}x\bcancel{y}\bcancel{y}}\times\cfrac{{}^2\bcancel{4}\bcancel{y}\bcancel{y}}{{}^3\bcancel{21}}\\ &=&\cfrac{2}{3x} \end{eqnarray*}
$\huge{2}$ 次の ①~③の連立方程式を解きなさい。また、④の方程式を解きなさい。
\begin{eqnarray*}
① \ \left\{
\begin{array}{l}
y=2x-1\\
4x-y=7
\end{array}
\right.
\qquad② \ \left\{
\begin{array}{l}
2(x-2y)=-y+1\\
5x-7y=1
\end{array}
\right.\\
\end{eqnarray*}
答え
$①\phantom{ho}\begin{eqnarray*}
\left\{
\begin{array}{l}
x=16\\
y=-4
\end{array}
\right.
\quad②
\left\{
\begin{array}{l}
x=-4\\
y=-3
\end{array}
\right.
\end{eqnarray*}$
①番 代入法で、②の式を①の式に代入して解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
-x+8y+25=-23\quad…①\\
-\cfrac{1}{4}x=y\quad…②
\end{array}
\right.
\end{eqnarray*}
$②の-\cfrac{1}{4}xを①のyに代入$
\begin{eqnarray*}
-x+8\times\left(-\cfrac{1}{4}x\right)+25&=&-23\\
-x-2x+25&=&-23\\
-3x&=&-48\\
x&=&16
\end{eqnarray*}
$x=16を②に代入$
\begin{eqnarray*}
-\cfrac{1}{4}\times(16)&=&y\\
-4&=&y
\\
\left\{
\begin{array}{l}
x=16\\
y=-4
\end{array}
\right.
\end{eqnarray*}
②番 ①の式のかっこをはずし、整理します。加減法で、$x$ の係数をそろえて解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
2(x-2y)=-y+1\quad①\\
5x-7y=1\quad…②
\end{array}
\right.
\end{eqnarray*}
$①を整理$
\begin{eqnarray*}
2(x-2y)&=&-y+1\\
2x-4y&=&-y+1\\
2x-4y+y&=&1\\
2x-3y&=&1\quad…③
\end{eqnarray*}
$②\times2 \ - \ ③\times5$
\begin{eqnarray*}
10x-14y=\phantom{-}2\\
\underline{-) \quad 10x-15y=\phantom{-}5}\\
y=-3
\end{eqnarray*}
$y=-3を③に代入$
\begin{eqnarray*}
2x-3\times(-3)&=&1\\
2x+9&=&1\\
2x&=&-8\\
x&=&-4
\\
\left\{
\begin{array}{l}
x=-4\\
y=-3
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*} ③ \ \left\{ \begin{array}{l} \cfrac{1}{3}x+\cfrac{5}{2}y=12\\ 5x+6y=-9 \end{array} \right. \qquad④ \quad 3x+2y=9x+5y-3=3 \end{eqnarray*}
答え
$③\phantom{ho}\begin{eqnarray*}
\left\{
\begin{array}{l}
x=-9\\
y=6
\end{array}
\right.
\quad④
\left\{
\begin{array}{l}
x=-1\\
y=3
\end{array}
\right.
\end{eqnarray*}$
③番 ①の式を $6$ 倍して分母をはらいます。加減法で、$y$ を消去して解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
\cfrac{1}{3}x+\cfrac{5}{2}y=12\quad…①\\
5x+6y=-9…\quad②
\end{array}
\right.
\end{eqnarray*}
$①\times6$
\begin{eqnarray*}
2x+15y&=&72\quad…③
\end{eqnarray*}
$②\times5 \ - \ ③\times2$
\begin{eqnarray*}
25x+30y=-45\\
\underline{-) \quad 4x+30y=\phantom{1}144}\\
21x\phantom{+30y}=-189\\
x=-9\phantom{18}
\end{eqnarray*}
$x=-9を②に代入$
\begin{eqnarray*}
5\times(-9)+6y&=&-9\\
-45+6y&=&-9\\
6y&=&36\\
y&=&6
\\
\left\{
\begin{array}{l}
x=-9\\
y=6
\end{array}
\right.
\end{eqnarray*}
④番 まんなかをかくした式をつくり、①とします。左側をかくした式をつくって整理し、②とします。①の式と②の式を連立させ、$x$ の係数をそろえて加減法で解きます。
\begin{eqnarray*}
&& \ 3x+2y=9x+5y-3=3
\end{eqnarray*}
$まんなかをかくした式をたてる$
\begin{eqnarray*}
3x+2y&=&3\quad…①
\end{eqnarray*}
$左側をかくした式をたてて整理する$
\begin{eqnarray*}
9x+5y-3&=&3\\
9x+5y&=&6\quad…②
\end{eqnarray*}
$①と②を連立させる$
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
3x+2y=3\quad…①\\
9x+5y=6\quad…②
\end{array}
\right.
\end{eqnarray*}
$①\times3 \ - \ ②\times2$
\begin{eqnarray*}
9x+6y=9\\
\underline{-) \quad 9x+5y=6}\\
y=3
\end{eqnarray*}
$y=3を①に代入$
\begin{eqnarray*}
3x+2\times(3)&=&3\\
3x+6&=&3\\
3x&=&-3\\
x&=&-1
\\
\left\{
\begin{array}{l}
x=-1\\
y=3
\end{array}
\right.
\end{eqnarray*}
$\huge{3}$ $1$ 次関数 $y=\cfrac{2}{3}x-4$ について、次の $①~③$ の問いに答えなさい。
$①\quad x$ の値が $-4$ から$5$ まで増加するときの変化の割合を求めなさい。
答え
$\cfrac{2}{3}$
$1$ 次関数 $y=ax+b$ で変化の割合をきかれたときは、$a$ を答えといてください。計算もなんもありません。$a$ を答えておけばいいんです。テストのときはそうやっちゃってください。
$②\quad x$ の値が $-4$ から$5$ まで増加するときの $y$ の増加量を求めなさい。
答え
$6$
$yの増加量=xの増加量\times変化の割合$ です。
この問題の場合、$x$ の値が $-4$ から $5$ まで増加したのですから、$x$ の増加量は $9$ です。
変化の割合は $\cfrac{2}{3}$ です。なので、
\begin{eqnarray*}
yの増加量&=&xの増加量\times変化の割合\\
&=&9\times\cfrac{2}{3}\\
&=&6
\end{eqnarray*}
$③\quad x$ の変域が $-6 \leqq x \leqq 3$ のとき、$y$ の変域を求めなさい。
答え
$-8 \leqq y \leqq -2$
「$x$ の変域が $p \leqq x \leqq q$ のとき、$y$ の変域を求めなさい。」というお決まりの問題があって、こうきかれたときは、答えの形はこうです。 $$小 \leqq y \leqq 大$$ んで、小と大にそれぞれ、小さい数と大きい数を書いておけばいいです。小さい数と大きい数っていうのは、 $-6 \leqq x \leqq 3$ の $-6$ と $3$ をそれぞれ問題の $y=\cfrac{2}{3}x-4$ の $x$ に代入してえられる数です。じゃあまず、 $x=-6$ を $y=\cfrac{2}{3}x-4$ に代入します。 \begin{eqnarray*} y&=&\cfrac{2}{3}\times(-6)-4\\ &=&-4-4\\ &=&-8\\ \end{eqnarray*} 次に、 $x=3$ を $y=\cfrac{2}{3}x-4$ に代入します。 \begin{eqnarray*} y&=&\cfrac{2}{3}\times3-4\\ &=&2-4\\ &=&-2\\ \end{eqnarray*} これで、$-8$ と $-2$ というふたつの数がえられました。これを小と大にあてはめればよいです。じゃあ答えを書きましょう。$$-8 \leqq y \leqq -2$$ これでOKです。ただし、 $y$ の変域をきかれたときのこのやり方は、3年生で習う「2乗に比例する関数$y=ax^2$」では通用しないから気をつけてください。
$\huge{4}$ 次の $①~④$ の直線の式を求めなさい。
$①$ 傾きが $-3$ で点$(2,-5)$を通る。
答え
$y=-3x+1$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
傾きというのは1次関数のときは $a$ のことです。だから $a=-3$ です。これを $y=ax+b$ に代入します。すると
$$y=-3x+b$$
となります。あと、「点$(2,-5)$を通る」というのは、$x=2$ のとき $y=-5$ という意味です。これをこの $y=-3x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
-5&=&-3\times2+b\\
-5&=&-6+b\\
-5+6&=&b\\
1&=&b
\end{eqnarray*}
$b$ は右辺においたままにして解いていくのがおすすめです。どうしてもなじめなかったら由緒正しく $b$ を左辺にもってって解いてもいいです。ただその場合、符号でまちがえるのをとてもよく見るので、注意してください。
ともかく、これでめでたく $a=-3$ , $b=1$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-3x+1$$
$②$ $x$ の値が $2$ 増加すると $y$ の値が $3$ 減少し、$x=-2$ のとき $y=1$ となる。
答え
$y=-\cfrac{3}{2}x-2$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
1次関数のときは \(a=\cfrac{yの増加量\phantom{増加}}{xの増加量\phantom{増加}}\)だから、この問題の場合は $a=\cfrac{-3}{2}=-\cfrac{3}{2}$ となります。これを $y=ax+b$ に代入すると
$$y=-\cfrac{3}{2}x+b$$
となります。 $x=-2$ , $y=1$ をこの $y=-\cfrac{3}{2}x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
1&=&-\cfrac{3}{2}\times(-2)+b\\
1&=&3+b\\
1-3&=&b\\
-2&=&b
\end{eqnarray*}
これで $a=-\cfrac{3}{2}$ , $b=-2$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-\cfrac{3}{2}x-2$$
$③$ $y$ 切片が $3$ で、点$(-2,4)$ を通る。
答え
$y=-\cfrac{1}{2}x+3$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
$y$ 切片というのは $b$ のことです。だから $b=3$ です。これを $y=ax+b$ に代入します。すると
$$y=ax+3$$
となります。 $x=-2$ , $y=4$ をこの $y=ax+3$ に代入して、 $a$ を求めます。
\begin{eqnarray*}
4&=&-2a+3\\
2a&=&3-4\\
2a&=&-1\\
a&=&-\cfrac{1}{2}
\end{eqnarray*}
これで $a=-\cfrac{1}{2}$ , $b=3$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-\cfrac{1}{2}x+3$$
$④$ $2$ 点$(-10,-1),(15,4)$ を通る。
答え
$y=\cfrac{1}{5}x+1$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
$2$ 点を通る直線の式をきかれたときは、
$$a=\cfrac{y_2-y_1}{x_2-x_1}$$
という公式を使って $a$ を求めましょう。
$2$ 点の座標 $(-10,-1),(15,4)$ を $(x_1,y_1),(x_2,y_2)$ だということにして、上の公式にあてはめると、
\begin{eqnarray*}
a&=&\cfrac{y_2-y_1}{x_2-x_1}\\
&=&\cfrac{4-(-1)}{15-(-10)}\\
&=&\cfrac{5}{25}\\
&=&\cfrac{1}{5}\\
\end{eqnarray*}
これで $a=\cfrac{1}{5}$ だということがわかりました。これを $y=ax+b$ に代入して、
$$y=\cfrac{1}{5}x+b$$
ここに、 $(-10,-1),(15,4)$ のどちらかを代入して $b$ を求めます。代入するのはどっちでもよいです。今回は、 $(15,4)$ のほうをいれてみましょう。
\begin{eqnarray*}
4&=&\cfrac{1}{5}\times15+b\\
4&=&3+b\\
4-3&=&b\\
1&=&b
\end{eqnarray*}
これで $a=\cfrac{1}{5}$ , $b=1$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=\cfrac{1}{5}x+1$$
ところで、この問題に関してはもうひとつ、連立方程式をたてて $a$ と $b$ を求めていく、という定番のやり方があります。ここで紹介しているやり方と、連立方程式をたてるのと、両方ためして、好きなほうでやってください。連立方程式をたててやるやり方は、次の問題で説明します。
$\huge{5}$ $y$ が $x$ の1次関数であるとき、表のア~ウにあてはまる数をこたえなさい。また、$y$ を $x$ の式で表しなさい。
\begin{array}{c|ccccc}
\hline
x & -7 & -3 & イ & 1 & ウ \\
\hline
y & ア & 5 & -1 & -3 & -13 \\
\hline
\end{array}
答え
ア…$13$, イ…$0$, ウ…$6$, 式 $y=-2x-1$
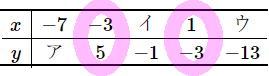 まず、$y$ を $x$ の式で表してしまいましょう。そのために、$x$ と $y$ がわかっている組を $2$ 組、見つけます。必ず $2$ 組はあるはずです。この問題の場合は、$x=-3$ のとき $y=5$, $x=1$ のとき $y=-3$ というのがありますね。これで $a$ を求めることができます。$(-3, 5), (1, -3)$ だと思ってもいいです。$a$ が求まりますよね?
まず、$y$ を $x$ の式で表してしまいましょう。そのために、$x$ と $y$ がわかっている組を $2$ 組、見つけます。必ず $2$ 組はあるはずです。この問題の場合は、$x=-3$ のとき $y=5$, $x=1$ のとき $y=-3$ というのがありますね。これで $a$ を求めることができます。$(-3, 5), (1, -3)$ だと思ってもいいです。$a$ が求まりますよね?
$a=\cfrac{y_2-y_1}{x_2-x_1}$ を使って、
$a=\cfrac{-3-5}{1-(-3)}=\cfrac{-8}{4}=-2$
$y=-2x+b$ に $(1,-3)$ を代入して、
\begin{eqnarray*}
-3&=&-2+b\\
-3+2&=b\\
-1&=&b
\end{eqnarray*}
これで、式は $y=-2x-1$ だと求められました。あとはアとイとウをだしていきましょう。
アは $x=-7$ のときの $y$ の値のことだから、
\begin{eqnarray*}
y&=&-2\times(-7)-1=14-1=13
\end{eqnarray*}
イは $y=-1$ のときの $x$ の値のことだから、
\begin{eqnarray*}
-1&=&-2x-1\\
2x&=&-1+1\\
2x&=&0\\
x&=&0
\end{eqnarray*}
ウは $y=-13$ のときの $x$ の値のことだから、
\begin{eqnarray*}
-13&=&-2x-1\\
2x&=&-1+13\\
2x&=&12\\
x&=&6
\end{eqnarray*}
これですべて求まりました。答えを書きましょう。
ア…$13$, イ…$0$, ウ…$6$, 式 $y=-2x-1$
$\huge{6}$
次の $①~③$ のグラフをかきなさい。
 \begin{eqnarray*}
&&① \quad y=\cfrac{2}{3}x-2\\
&&② \quad 6x-2y=-4\\
&&③ \quad x=-1\\
\end{eqnarray*}
\begin{eqnarray*}
&&① \quad y=\cfrac{2}{3}x-2\\
&&② \quad 6x-2y=-4\\
&&③ \quad x=-1\\
\end{eqnarray*}
答え
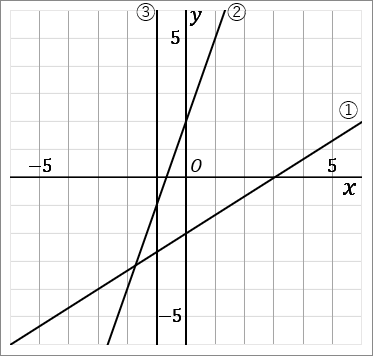
$①$ 切片が $-2$ なので、$y$ 軸の $-2$ をスタート地点にします。傾きが $\cfrac{2}{3}$ なので、右に $3$ 歩行って上に $2$ 歩行く点をとっていきます。点を定規で結びます。
$②$ まず式を $y$ について解きます。
\begin{eqnarray*}
6x-2y&=&-4\\
-2y&=&-6x-4\quad両辺に-1をかける\\
2y&=&6x+4\quad両辺に\cfrac{1}{2}をかける\\
y&=&\cfrac{6}{2}x+\cfrac{4}{2}\\
y&=&3x+2\\
\end{eqnarray*}
これで $y=ax+b$ の形になったので、あとはこのグラフをかけばよいです。
$③$ $y$ 軸に平行な線です。たて線です。$x$ 軸の $-1$ を通るようにします。
 $\huge{7}$
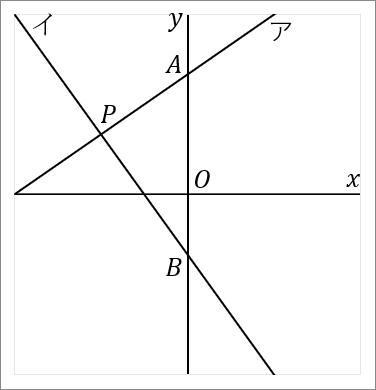
右の図で、直線アは関数 $y=\cfrac{2}{3}x+4$ のグラフであり、直線イは関数 $y=-\cfrac{4}{3}x-2$ のグラフである。直線アと $y$ 軸との交点を $A$ とし、直線イと $y$ 軸との交点を $B$ とする。直線アと直線イとの交点を $P$ とする。このとき、以下の問いに答えなさい。
$\huge{7}$
右の図で、直線アは関数 $y=\cfrac{2}{3}x+4$ のグラフであり、直線イは関数 $y=-\cfrac{4}{3}x-2$ のグラフである。直線アと $y$ 軸との交点を $A$ とし、直線イと $y$ 軸との交点を $B$ とする。直線アと直線イとの交点を $P$ とする。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(-3, \ 2)$
$2$ 直線の交点は連立方程式の解です。ア、イの式を連立方程式にして \begin{eqnarray*} && \ \left\{ \begin{array}{l} y=\cfrac{2}{3}x+4\quad…①\\ y=-\cfrac{4}{3}x-2\quad…② \end{array} \right. \end{eqnarray*} これを解けばいいです。解き方は、この手の連立方程式は代入法で、右辺 $=$ 右辺の式をたてて、$x$ を求めていきましょう。関数の問題でよく使うパターンです。 \begin{eqnarray*} 代入法で、右辺 &=& 右辺の式にする。\\\\ \cfrac{2}{3}x+4&=&-\cfrac{4}{3}x-2\quad(両辺に\times3)\\ 2x+12&=&-4x-6\\ 2x+4x&=&-6-12\\ 6x&=&-18\\ x&=&-3 \end{eqnarray*} $x=-3を①に代入$ \begin{eqnarray*} y&=&\cfrac{2}{3}\times(-3)+4\\ &=&-2+4\\ &=&2 \\\\ 答え\\ (-3, \ 2) \end{eqnarray*} ※座標をきかれているのだから、かならず座標の答え方で答えましょう。
$(2)$ $\triangle PAB$ の面積を求めなさい。
$9$
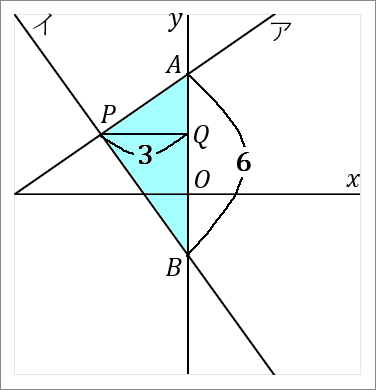 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
点 $A$ の座標は、直線ア $y=\cfrac{2}{3}x+4$ の切片ですから、$(0, \ 4)$ です。
点 $B$ の座標は、直線イ $y=-\cfrac{4}{3}x-2$ の切片ですから、$(0, \ -2)$ です。
なので、$AB$ の長さは $4+2=6$ です。点 $B$ の $y$ 座標は $-2$ ですが、長さの話なのですから絶対値をいうようにしましょう。
<$PQ$ について>
$PQ$ の長さは、点 $P$ の $x$ 座標をみればよいです。点 $P$ の $x$ 座標は $-3$ ですから、$PQ$ の長さは $3$ です。長さの話なのですから、絶対値でいうようにしましょう。
これで底辺と高さがわかりました。では面積をだしましょう。
$$6\times3\times\cfrac{1}{2}=9$$
※答えがでたあと、$9cm^2$ とかいうふうに、やみくもになんにでも単位をつけて答えてしまうひとがいますが、なんでもつけてはいけません。問題によります。この問題は単位をつけてはいけません。問題のどこにも $cm$ とはかかれていないからです。こういうときは答えに単位をつけてはいかんのです。気をつけて。
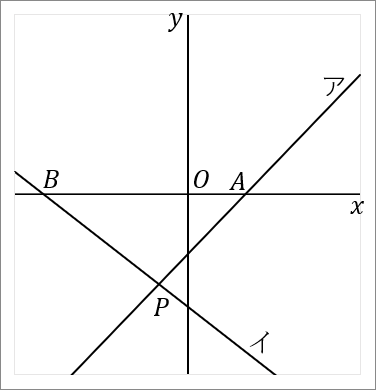 $\huge{8}$ 右の図で、直線アと直線イの交点を $P$ とする。直線ア,イと $x$ 軸との交点をそれぞれ $A, \ B$ とする。直線アは関数 $y=x-4$ のグラフである。点 $P$ の $x$ 座標が $-2,$ 点 $B$ の座標が $(-10, \ 0)$ である。このとき、以下の問いに答えなさい。
$\huge{8}$ 右の図で、直線アと直線イの交点を $P$ とする。直線ア,イと $x$ 軸との交点をそれぞれ $A, \ B$ とする。直線アは関数 $y=x-4$ のグラフである。点 $P$ の $x$ 座標が $-2,$ 点 $B$ の座標が $(-10, \ 0)$ である。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(-2, \ -6)$
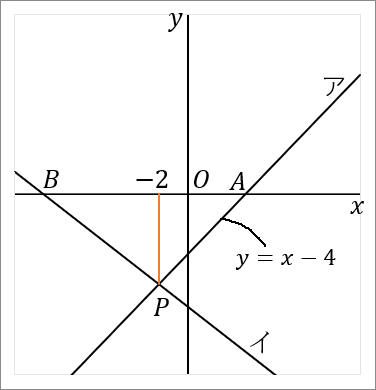 点 $P$ の $x$ 座標は $-2$ だと問題にかかれています。あとは $y$ 座標がわかればよいです。また、点 $P$ は直線ア上の点です。アの式はわかっているので、この式を使えば $y$ 座標が求められます。
\begin{eqnarray*}
y&=&x-4 に、x=-2を代入\\\\
y&=&-2-4\\
&=&-6
\end{eqnarray*}
これで $y=-6$ だとわかりました。なので答えは $(-2, \ -6)$ です。
点 $P$ の $x$ 座標は $-2$ だと問題にかかれています。あとは $y$ 座標がわかればよいです。また、点 $P$ は直線ア上の点です。アの式はわかっているので、この式を使えば $y$ 座標が求められます。
\begin{eqnarray*}
y&=&x-4 に、x=-2を代入\\\\
y&=&-2-4\\
&=&-6
\end{eqnarray*}
これで $y=-6$ だとわかりました。なので答えは $(-2, \ -6)$ です。
$(2)$ 直線イの式を求めなさい。
答え
$y=-\cfrac{3}{4}x-\cfrac{15}{2}$
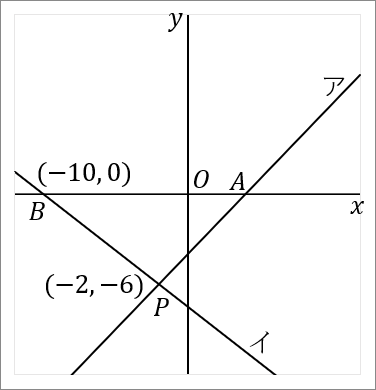 イの式は、点 $B(-10, \ 0)$ を通っています。また、点 $P$ も通っているのですが、その座標は $(1)$ の問題で $(-2, \ -6)$ だと求めました。この $2$ 点を通る直線の式だということでやれば、イの式がでます。
イの式は、点 $B(-10, \ 0)$ を通っています。また、点 $P$ も通っているのですが、その座標は $(1)$ の問題で $(-2, \ -6)$ だと求めました。この $2$ 点を通る直線の式だということでやれば、イの式がでます。
直線の式を求めなさいといわれたら、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$2$ 点 $(-10, \ 0), \ (-2, \ -6)$ を通る直線の式を求めます。
\begin{eqnarray*}
a&=&\cfrac{y-y}{x-x}\\
&=&\cfrac{0-(-6)}{-10-(-2)}=\cfrac{6}{-8}=-\cfrac{3}{4}\\\\
y&=&-\cfrac{3}{4}x+bにx=-10,y=0 を代入する\\
0&=&-\cfrac{3}{4}\times(-10)+b\\
0&=&\cfrac{15}{2}+b\\
-\cfrac{15}{2}&=&b\\
\end{eqnarray*}
これで $a$ と $b$ がでました。答えは $y=-\cfrac{3}{4}x-\cfrac{15}{2}$ です。
$(3)$ $\triangle PAB$ の面積を求めなさい。
答え
$42$
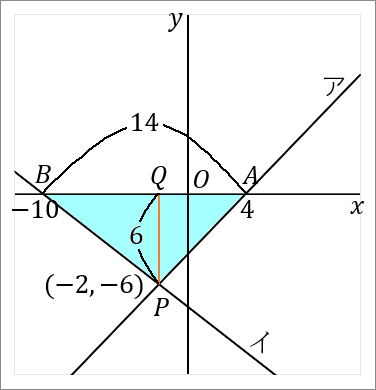 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $x$ 軸におろした垂線と $x$ 軸との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $x$ 軸におろした垂線と $x$ 軸との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
点 $A$ の座標は、直線アと $x$ 軸との交点だということで求めます。
ここでポイントがあります。$x$ 軸上の点というのは、$y$ 座標がかならず $0$ です。あたりまえです。$y$ がかならず $0$ なんです。このことを利用して、アの式に $y=0$ を代入すれば、点 $A$ の $x$ 座標が求められます。
\begin{eqnarray*}
y&=&x-4にy=0 を代入\\
0&=&x-4\\
4&=&x
\end{eqnarray*}
なので点 $A$ の座標は、$(4, \ 0)$ です。
点 $B$ の座標は、$(-10, \ 0)$ です。
というわけで、$AB$ の長さは $4+10=14$ です。点 $B$ の $x$ 座標は $-10$ ですが、長さの話なのですから絶対値をいうようにしましょう。
<$PQ$ について>
$PQ$ の長さは、点 $P$ の $y$ 座標をみればよいです。点 $P$ の $y$ 座標は $-6$ ですから、$PQ$ の長さは $6$ です。これも長さの話なのですから絶対値をいうようにしましょう。
これで底辺と高さがわかりました。では面積をだしましょう。
$$14\times6\times\cfrac{1}{2}=42$$
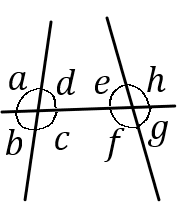
$\huge{9}$
右の図について、次の①~③の問いに答えなさい。
$①$ $\angle b$ の対頂角をいいなさい。
答え $\angle d$
$②$ $\angle h$ の同位角をいいなさい。
答え $\angle d$
$③$ $\angle e$ の錯角をいいなさい。
答え $\angle c$
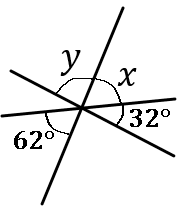
$\huge{10}$
右の図で、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。
答え
$\angle x=62^{ \circ }$, $\angle y=86^{ \circ }$
$\angle x$ の対頂角は $62^{ \circ }$ です。
$\angle y=180-(62+32)=86$
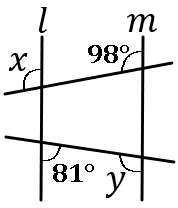
$\huge{11}$
右の図で、$l /\!/ m$ のとき、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。
答え
$\angle x=98^{ \circ }$, $\angle y=99^{ \circ }$
$\angle x$ の同位角は $98^{ \circ }$ です。
$\angle y$ の同位角や錯角の反対側が $81^{ \circ }$ なのを利用します。
$y=180-81=99$
$\huge{12}$
下の図で、$\angle x$, $\angle y$, $\angle z$ の大きさをそれぞれ求めなさい。ただし、$l /\!/ m$ とする。
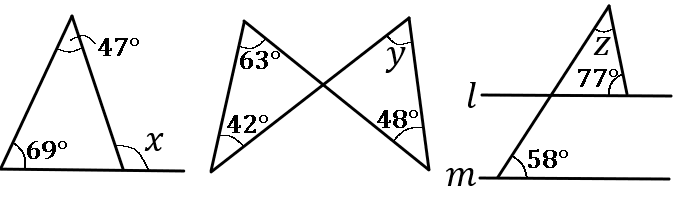
答え
$\angle x=116^{ \circ }$, $\angle y=57^{ \circ }$, $\angle z=45^{ \circ }$
$x=69+47\\y+48=63+42\\58+77+z=180$
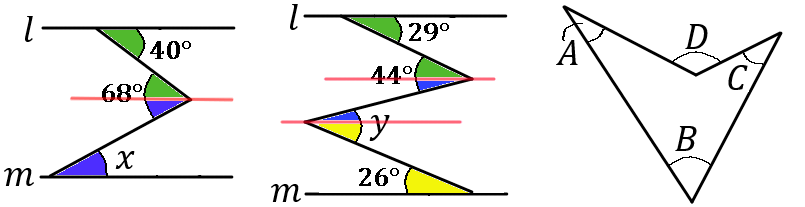
$\huge{13}$
下の図で、$\angle x$, $\angle y$, $\angle z$ の大きさをそれぞれ求めなさい。ただし、$l /\!/ m$ とする。

答え
$\angle x=28^{ \circ }$, $\angle y=41^{ \circ }$, $\angle z=31^{ \circ }$
※補助線をひいて考えます。色のついた部分の大きさがおなじです。
※最後の問題は、$A+B+C=D$になります。よく出てくる形なので、「この形は $A+B+C=D$」とおぼえてしまいましょう。また、なぜそうなるのか説明しなさいという問題もよくあるので、説明できるようにしておきましょう。
$\huge{14}$
下の図で、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。ただし、〇のついている角同士、×のついている角同士等しいものとする。
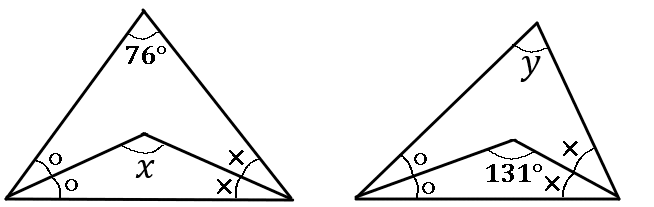
答え
$\angle x=128^{ \circ }$, $\angle y=82^{ \circ }$
※$x$ の求め方 \begin{eqnarray*} ○&=&a^{ \circ },×=b^{ \circ } とすると、\\ 2a+2b+76&=&180\\ 2a+2b&=&104 \quad \class{mathbg-r}{(両辺を\div2)} \\ a+b&=&52\\ x&=&180-(a+b)\\ &=&180-52=128 \end{eqnarray*} ※$y$ の求め方 \begin{eqnarray*} ○&=&a^{ \circ },×=b^{ \circ } とすると、\\ a+b+131&=&180\\ a+b&=&49 \quad \class{mathbg-r}{(両辺に\times2)} \\ 2a+2b&=&98\\ y&=&180-(2a+2b)\\ &=&180-98=82 \end{eqnarray*}
$\huge{15}$ 次の $①~⑥$ の問いに答えなさい。
$①$ 十五角形の内角の和を求めなさい。
答え
$2340^{ \circ }$
$180\times(15-2)=2340$
$②$ 内角の和が $1800^{ \circ }$ になる多角形は何角形ですか。。
答え
十二角形
$1800\div180+2=12$
$③$ 正二十角形の1つの内角の大きさは何度ですか。
答え
$162^{ \circ }$
$\{180\times(20-2)\}\div20=3240\div20=162$
別解 (外角の和$=360^{ \circ }$を利用する)←おすすめ
$180-(360\div20)=180-18=162$
$④$ 正十五角形の1つの外角の大きさは何度ですか。
答え
$24^{ \circ }$
$360\div15=24$
$⑤$ 1つの外角の大きさが $15^{ \circ }$になるのは正何角形ですか。
答え
正二十四角形
$360\div15=24$
$⑥$ 1つの内角の大きさが $135^{ \circ }$になるのは正何角形ですか。
答え
正八角形
内角が$135^{ \circ }$ということは、外角は$45^{ \circ }$だから、 $360\div45=8$
$\huge{16}$
下の図で、下の図で、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。

答え
$\angle x=111^{ \circ }$, $\angle y=118^{ \circ }$
$x=540-(90+111+147+81)\\ y=180-\{360-(69+47+58+53+71)\}$
$\huge{17}$
下の図で、$\angle x$, $\angle y$ の大きさをそれぞれ求めなさい。

答え
$\angle x=42^{ \circ }$, $\angle y=30^{ \circ }$
$x=180-(34+39+23+42)$
五芒星(ごぼうせい)は色のついた $5$ つの角の和が $180^{ \circ }$ になるとおぼえてしまいましょう。また、なぜこの $5$ つを足すと $180^{ \circ }$ になるのかもよく問われるので、その理由の説明ができるようにしておきましょう。
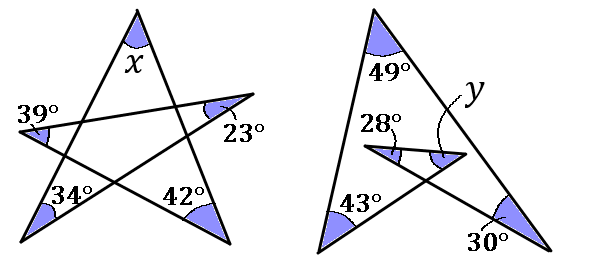 $y=180-(43+28+49+30)$
$y=180-(43+28+49+30)$
$y$ も $x$ とおなじように考えてしまえばよいです。
$\huge{18}$
駅から $1200m$ 離れたところに学校がある。Aさんが駅を出発して学校まで歩いた。途中でコンビニによって、そこで買い物をするのに $4$ 分かかり、あとはまた同じ速さで学校へ歩いた。下の図は、このときの時間と道のりの関係を表したグラフである。以下の①,②の問いに答えなさい。
$①$ Aさんの歩く速さを求めなさい。
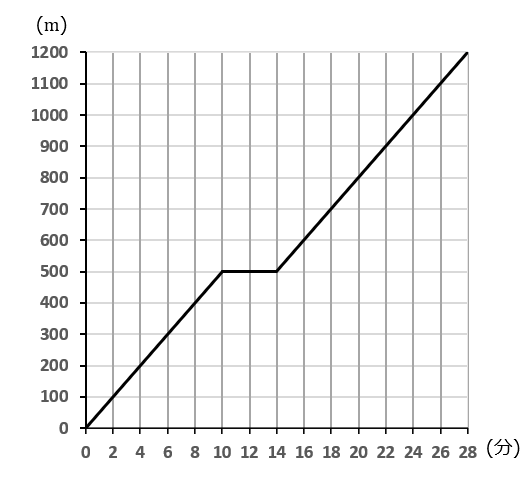
答え
$50m/秒$
グラフから、Aさんは $2$ 分で $100m$ 進んでいます。
速さ $=$ 道のり $\div$ 時間ですから、答えは $100\div2=50(m/秒)$ です。
$②$ Aさんが出発してから $10$ 分後に、Bさんが分速 $75m$ の速さで駅から学校へ自転車で走った。このときのBさんが進んだようすをグラフにかきくわえなさい。また、BさんがAさんに追いついたのは、Bさんが出発してから何分後か。
答え
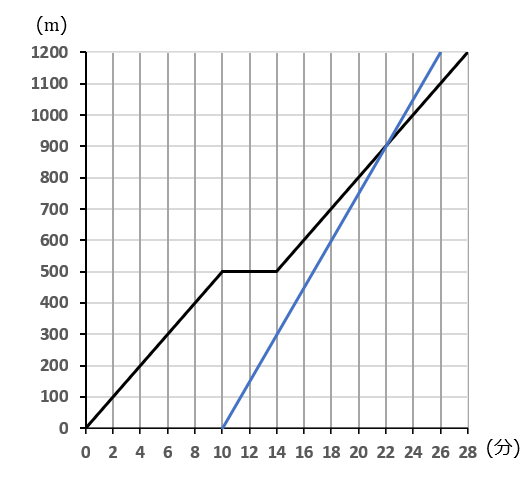 $12$ 分後
$12$ 分後
〈グラフ〉
BさんはAさんが出発してから $10$ 分後に学校を出発したわけですから、点 $(10, \ 0)$ からグラフをはじめます。
グラフをかくときは、目盛りに注意してください。$x$ 軸は $1$ 目盛りが $2$ 分です。$y$ 軸は $1$ 目盛りが $100m$ です。
Bさんの速さは分速 $75m$ なので、$2$ 分で $150m$、$4$ 分で $300m$ 進むことになります。なので、右に $2$ マスいって、上に $3$ マスいくように点をとっていきます。
〈時間〉
$2$ 直線の交点が、BさんがAさんに追いついた地点と時間を表します。なので、追いついたのは、Aさんが出発してから $22$ 分後です。Bさんが出発してからは、$22-10=12$ 分後です。
 $\huge{19}$
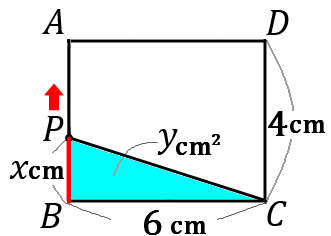
図のような長方形 $ABCD$ で、点 $P$ は辺上を点 $B$ から $A,D$ を通って $C$ まで動く。点 $P$ が辺上を点 $B$ から $xcm$ 動いたときの $\triangle PBC$ の面積を $ycm^2$ とする。以下の①~④の問いに答えなさい。
$\huge{19}$
図のような長方形 $ABCD$ で、点 $P$ は辺上を点 $B$ から $A,D$ を通って $C$ まで動く。点 $P$ が辺上を点 $B$ から $xcm$ 動いたときの $\triangle PBC$ の面積を $ycm^2$ とする。以下の①~④の問いに答えなさい。
$①$ 点 $P$ が辺 $BA$ 上にあるとき、$y$ を $x$ の式で表しなさい。また、$x$ の変域をいいなさい。
答え
① $y=3x\qquad (0 \leqq x \leqq 4)$
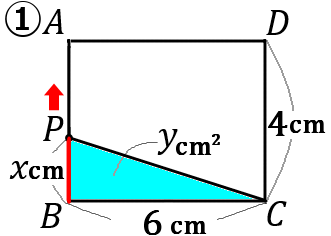 〈式〉
〈式〉
三角形の面積は、底辺 $\times$ 高さ $\times\cfrac{1}{2}$ です。底辺を $BC$、高さを$PB$ ということにして、$y$ を $x$ で表します。
$BC$ の長さは $6$ です。
$P$ が動いた長さが $x$ なので、$PB$ の長さは $x$ です。
なので、三角形 $y$ の面積は、$y=6\times x \times \cfrac{1}{2}=3x$ となります。
〈変域〉
$P$ が $B$ 上にあるときは、$x=0$ です。最小値は $0$ です。$P$ が $A$ 上にきたときは、$x=4$ です。最大値は $4$ です。
$②$ 点 $P$ が辺 $AD$ 上にあるとき、$y$ を $x$ の式で表しなさい。また、$x$ の変域をいいなさい。
答え
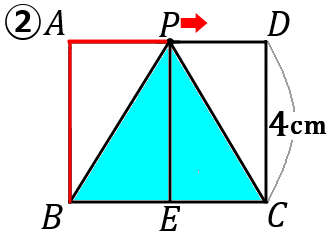
$y=12\qquad (4 \leqq x \leqq 10)$
 〈式〉
〈式〉
$P$ から $BC$ におろした垂線と、$BC$ との交点を $E$ とします。底辺を $BC$、高さを$PE$ ということにして、$y$ を $x$ で表します。
$BC$ の長さは $6$ です。
$PE$ の長さは、$P$ がどこにあっても $4$ です。
なので、三角形 $y$ の面積は、$y=6 \times 4 \times\cfrac{1}{2}=12$ となります。
〈変域〉
$x$ の変域は、$P$ が $A$ 上にきたときは、$x=4$ です。最小値は $4$ です。$P$ が $D$ 上にきたときは、$x=4+6=10$ です。最大値は $10$ です。
$③$ 点 $P$ が辺 $DC$ 上にあるとき、$y$ を $x$ の式で表しなさい。また、$x$ の変域をいいなさい。
答え
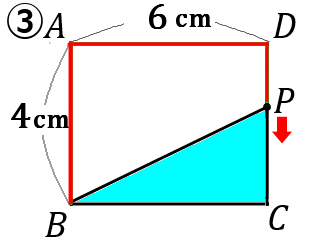
$y=-3x+42\qquad (10 \leqq x \leqq 14)$
 〈式〉
〈式〉
底辺を $BC$、高さを$PC$ ということにして、$y$ を $x$ で表します。
$BC$ の長さは $6$ です。
$PC$ の長さは、$14-x$ です。$x$ は $P$ が動いてきた長さです。③の図の赤い線が $x$ を表しています。$BA+AD+DC$ から $x$ をひけば、$PC$ になります。なので、$PC=4+6+4-x=14-x$ です。
なので、三角形 $y$ の面積は、
\begin{eqnarray*}
y&=&6 \times (14-x) \times\cfrac{1}{2} \quad(6\times\cfrac{1}{2}を先にやってしまう)\\
&=&3(14-x)\\
&=&42-3x\\
&=&-3x+42
\end{eqnarray*}
〈変域〉
$x$ の変域は、$P$ が $D$ 上にきたときは、$x=4+6=10$ です。最小値は $10$ です。$P$ が $C$ 上にきたときは、$x=4+6+4=14$ です。最大値は $14$ です。
$④$ $x$ の変域を $0 \leqq x \leqq 14$ とするときの $x$ と $y$ の関係をグラフに表しなさい。また、$\triangle PBC$ の面積が $8cm^2$ となるときの $x$ の値を求めなさい。
答え
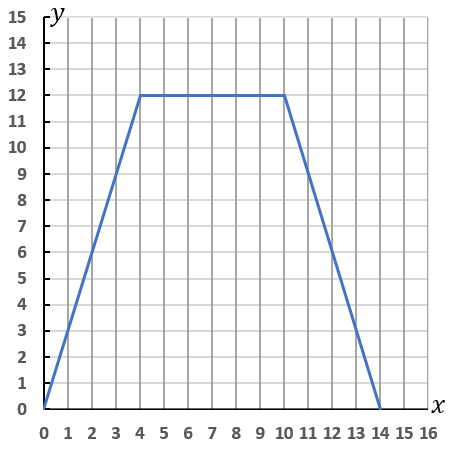
$\triangle PBC$ の面積が $8cm^2$ となるときの $x$ の値
$x=\cfrac{8}{3}, \ x=\cfrac{34}{3}$
〈グラフ〉
変域が $0 \leqq x \leqq 4$ のときの式は $y=3x$ です。原点を通る直線です。点$(0, \ 0),$ $(4, \ 12)$ をとって定規でむすんでしまいましょう。線は点 $(4, \ 12)$ で終わりにしてください。その先をかいちゃダメです。
変域が $4 \leqq x \leqq 10$ のときの式は $y=12$ です。$x$ 軸に平行な直線になります。$(4, \ 12)$ から$ (10, \ 12)$ までを定規でむすんでしまいましょう。
変域が $10 \leqq x \leqq 14$ のときの式は $y=-3x+42$ です。直線です。点$(10, \ 12)$ と $(14, \ 0)$ をとって定規でむすんでしまいましょう。$x=14$ のときに面積が $0$ になるはず、と考えて点 $(14, \ 0)$ をとるわけです。
〈面積〉
グラフから、面積 $y$ が $8$ になるのは、$2$ か所あります。$P$ が $y=3x$ 上にあるときと、$y=-3x+42$ 上にあるときです。それぞれの式の $y$ に $8$ を代入して $x$ を求めればOKです。
$P$ が $y=3x$ 上にあるとき
\begin{eqnarray*}
8&=&3x\\
x&=&\cfrac{8}{3}
\end{eqnarray*}
$P$ が $y=-3x+42$ 上にあるとき
\begin{eqnarray*}
8&=&-3x+42\\
3x&=&42-8\\
3x&=&34\\
x&=&\cfrac{34}{3}
\end{eqnarray*}
答え(中2 2学期期末模擬テスト 第2回)
1$①-16$ $②-\cfrac{4}{15}$ $③2$ $④-10a-2b$ $⑤\cfrac{-3x-y}{12} \ \left(-\cfrac{3x+y}{12},-\cfrac{1}{4}x-\cfrac{1}{12}y\right)$ $⑥-5b$ $⑦4y$ $⑧\cfrac{3}{3x}$
2$①x=16, \ y=-4$ $②x=-4, \ y=-3$ $③x=-9, \ y=6$ $④x=-1, \ y=3$
3$①\cfrac{2}{3}$ $②6$ $③-8 \leqq y \leqq -2$
 4$①y=-3x+1$ $②y=-\cfrac{3}{2}x-2$ $③y=-\cfrac{1}{2}x+3$ $④y=\cfrac{1}{5}x+1$
4$①y=-3x+1$ $②y=-\cfrac{3}{2}x-2$ $③y=-\cfrac{1}{2}x+3$ $④y=\cfrac{1}{5}x+1$
5ア…$13$, イ…$0$, ウ…$6$, 式 $y=-2x-1$
6 右図
7(1)$(-3, \ 2)$ (2)$9$
8(1)$(-2, \ -6)$ (2)$y=-\cfrac{3}{4}x-\cfrac{15}{2}$ (3)$42$
9$①\angle d$ $②\angle d$ $③\angle c$
10 $\angle x=62^{ \circ }$, $\angle y=86^{ \circ }$
11 $\angle x=98^{ \circ }$, $\angle y=99^{ \circ }$
12 $\angle x=116^{ \circ }$, $\angle y=57^{ \circ }$, $\angle z=45^{ \circ }$
13 $\angle x=28^{ \circ }$, $\angle y=41^{ \circ }$, $\angle z=31^{ \circ }$
14 $\angle x=128^{ \circ }$, $\angle y=82^{ \circ }$
$B$ 地点から $C$ 地点までの道のり…$600m$
15 $①2340^{ \circ }$ $②十二角形$ $③162^{ \circ }$ $④24^{ \circ }$ $⑤正二十四角形$ $⑥正八角形$

16 $\angle x=111^{ \circ }$, $\angle y=118^{ \circ }$
17 $\angle x=42^{ \circ }$, $\angle y=30^{ \circ }$
18$①50m/秒$ $②グラフ右図\quad 12分後$
19$①y=3x\qquad (0 \leqq x \leqq 4)$ $②y=12\qquad (4 \leqq x \leqq 10)$ $③y=-3x+42\qquad (10 \leqq x \leqq 14)$ $④グラフ下図\quad x=\cfrac{8}{3}, \ x=\cfrac{34}{3}$
