才塾　定期テスト対策

中2数学　3学期の計算　第1回　全32問

≡

■

ページがちゃんと表示されるまで $10$ 秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$\boxed{\phantom{ho}}$ ←ここに四角形が表示されていたら準備OKです。

問題をクリックすると答えがでます。

$\boxed{\large{\ 1\ }}$ 次の計算をしなさい。

$-8-3\times(-3)$

答え　 $1$

$\begin{eqnarray*} &&-8-3\times(-3)\\ &=&-8+9\\ &=&1 \end{eqnarray*}$

類題

$\cfrac{1}{2}-2+\cfrac{4}{3}$

答え　 $-\cfrac{1}{6}$

$\begin{eqnarray*} &&\cfrac{1}{2}-2+\cfrac{4}{3}\\ &=&\cfrac{3}{6}-\cfrac{12}{6}+\cfrac{8}{6}\\ &=&-\cfrac{1}{6} \end{eqnarray*}$

類題

$(-1)^3\times(-2)^2$

答え　 $-4$

$\begin{eqnarray*} &&(-1)^3\times(-2)^2\\ &=&-1\times4\\ &=&-4 \end{eqnarray*}$

類題

$-8x-7y+6x+5y$

答え　 $-2x-2y$

$\begin{eqnarray*} &&-8x-7y+6x+5y\\ &=&-8x+6x-7y+5y\\ &=&-2x-2y \end{eqnarray*}$

類題

$-x-\cfrac{1}{2}y+\cfrac{1}{3}x-\cfrac{1}{4}y$

答え　 $-\cfrac{2}{3}x-\cfrac{3}{4}y$

$\begin{eqnarray*} &&-x-\cfrac{1}{2}y+\cfrac{1}{3}x-\cfrac{1}{4}y\\ &=&-x+\cfrac{1}{3}x-\cfrac{1}{2}y-\cfrac{1}{4}y\\ &=&-\cfrac{3}{3}x+\cfrac{1}{3}x-\cfrac{2}{4}y-\cfrac{1}{4}y\\ &=&-\cfrac{2}{3}x-\cfrac{3}{4}y \end{eqnarray*}$

類題

$(3x-9y)+(-11x+15y)$

答え　 $-8x+6y$

$\begin{eqnarray*} &&(3x-9y)+(-11x+15y)\\ &=&3x-9y-11x+15y\\ &=&3x-11x-9y+15y\\ &=&-8x+6y \end{eqnarray*}$

類題

$(a^2-6a)-(3a^2-2a)$

答え　 $-2a^2-4a$

$\begin{eqnarray*} &&(a^2-6a)-(3a^2-2a)\\ &=&a^2-6a-3a^2+2a\\ &=&a^2-3a^2-6a+2a\\ &=&-2a^2-4a \end{eqnarray*}$

類題

$-8(7x-3y)$

答え　 $-56x+24y$

類題

$15\left(\cfrac{3}{5}x-\cfrac{1}{3}y\right)$

答え　 $9x-5y$

$\begin{eqnarray*} &&15\left(\cfrac{3}{5}x-\cfrac{1}{3}y\right)\\ &=&15\times\cfrac{3}{5}x+15\times\left(-\cfrac{1}{3}y\right)\\ &=&9x-5y \end{eqnarray*}$

類題

$(-72a^2+96a-144)\div6$

答え　 $-12a^2+16a-24$

類題

$(48x-64y)\div\left(-\cfrac{8}{3}\right)$

答え　 $-18x+24y$

$\begin{eqnarray*} &&(48x-64y)\div\left(-\cfrac{8}{3}\right)\\ &=&(48x-64y)\times\left(-\cfrac{3}{8}\right)\\ &=&48x\times\left(-\cfrac{3}{8}\right)-64y\times\left(-\cfrac{3}{8}\right)\\ &=&-18x+24y \end{eqnarray*}$

類題

$5(3x-2y)-4(5x-3y)$

答え　 $-5x+2y$

$\begin{eqnarray*} &&5(3x-2y)-4(5x-3y)\\ &=&15x-10y-20x+12y\\ &=&15x-20x-10y+12y\\ &=&-5x+2y \end{eqnarray*}$

類題

$\cfrac{1}{2}(2x+4y)-\cfrac{2}{3}(9x-3y)$

答え　 $-5x+4y$

$\begin{eqnarray*} &&\cfrac{1}{2}(2x+4y)-\cfrac{2}{3}(9x-3y)\\ &=&x+2y-6x+2y\\ &=&x-6x+2y+2y\\ &=&-5x+4y \end{eqnarray*}$

類題

$\cfrac{x-3y}{2}-\cfrac{2x-y}{3}$

答え　 $\cfrac{-x-7y}{6}\quad\left(-\cfrac{x+7y}{6},-\cfrac{1}{6}x-\cfrac{7}{6}yも可\right)$

$\begin{eqnarray*} &&\cfrac{x-3y}{2}-\cfrac{2x-y}{3}\\ &=&\cfrac{3(x-3y)-2(2x-y)}{6}\\ &=&\cfrac{3x-9y-4x+2y}{6}\\ &=&\cfrac{3x-4x-9y+2y}{6}\\ &=&\cfrac{-x-7y}{6} \end{eqnarray*}$

類題

$(-2x)^2\times2x^2$

答え　 $8x^4$

$\begin{eqnarray*} &&(-2x)^2\times2x^2\\ &=&4x^2\times2x^2\\ &=&8x^4 \end{eqnarray*}$

類題

$6xy\div(-48xy^2)\times(-16xy)$

答え　 $2x$

$\begin{eqnarray*} &&6xy\div(-48xy^2)\times(-16xy)\\ &=&\cfrac{6xy\times(-16xy)}{-48xyy}\\ &=&2x \end{eqnarray*}$

類題

$-12xy\div\cfrac{18}{7}x^2y\times(-9x)$

答え　 $42$

$\begin{eqnarray*} &&-12xy\div\cfrac{18}{7}x^2\times(-9x)\\ &=&-\cfrac{12xy}{1}\times\cfrac{7}{18xxy}\times\left(-\cfrac{9x}{1}\right)\\ &=&42 \end{eqnarray*}$

類題

$\boxed{\large{\ 2\ }}$ 次の①～④の方程式を解きなさい。

$-8x+5=-3(2x-1)-4$

答え　 $x=3$

$\begin{eqnarray*} -8x+5&=&-3(2x-1)-4 \\ -8x+5&=&-6x+3-4 \\ -8x+6x&=&3-4-5\\ -2x&=&-6 \\ x&=&3 \end{eqnarray*}$

類題

$\cfrac{3}{4}x-\cfrac{1}{2}=2x-1$

答え　 $x=\cfrac{2}{5}$

$\begin{eqnarray*} \cfrac{3}{4}x-\cfrac{1}{2}&=&2x-1\quad(\times4)\\ 3x-2&=&8x-4 \\ 3x-8x&=&-4+2\\ -5x&=&-2\\ x&=&\cfrac{2}{5} \end{eqnarray*}$

類題

$\left\{\begin{array}{l} 5x-2y=-7\\ -x-2y=-1 \end{array}\right.$

答え　 $x=-1,y=1$

$\begin{eqnarray*} \left\{ \begin{array}{l} 5x-2y=-7\qquad…①\\ -x-2y=-1\qquad…② \end{array} \right. \end{eqnarray*}$

$①-②$

$\begin{eqnarray*} 5x-2y=-7\\ \underline{-) \quad -x-2y=-1} \\ 6x\phantom{-22y}=-6 \\ x=-1 \\ \end{eqnarray*}$

$\begin{eqnarray*} x=-1を②に代入\\ -(-1)-2y&=&-1\\ 1-2y&=&-1\\ -2y&=&-1-1\\ -2y&=&-2\\ y&=&1 \\ \left\{ \begin{array}{l} x=-1\\ y=1 \end{array} \right. \end{eqnarray*}$

類題

$\left\{\begin{array}{l} 2x+3y=1\\ 2(x-y)=3x-2 \end{array}\right.$

答え　 $x=-4,y=3$

$\begin{eqnarray*} \left\{ \begin{array}{l} 2x+3y=1\qquad…①\\ 2(x-y)=3x-2\qquad…② \end{array} \right. \end{eqnarray*}$

$②を整理$

$\begin{eqnarray*} 2x-2y&=&3x-2\\ 2x-3x-2y&=&-2\\ -x-2y&=&-2\qquad…③ \end{eqnarray*}$

$①+③\times2$

$\begin{eqnarray*} 2x+3y=\phantom{-}1\\ \underline{+) \quad -2x-4y=-4} \\ -y=-3 \\ y=\phantom{-}3 \\ \end{eqnarray*}$

$\begin{eqnarray*} y=3を③に代入\\ -x-2\times3&=&-2\\ -x-6&=&-2\\ -x&=&-2+6\\ -x&=&\phantom{-}4\\ x&=&-4 \\ \left\{ \begin{array}{l} x=-4\\ y=3 \end{array} \right. \end{eqnarray*}$

類題

$\boxed{\large{\ 3\ }}$ 以下の問いに答えなさい。

次の式を $[\phantom{y}]$ 内の文字について解きなさい。
$2x=3y+6\quad[y]$

答え　 $y=\cfrac{2x-6}{3}\left(\cfrac{2}{3}x-2も可\right)$

$\begin{eqnarray*} 2x&=&3y+6\quad(左辺と右辺をとりかえる） \\ 3y+6&=&2x \\ 3y&=&2x-6 \\ y&=&\cfrac{2x-6}{3} \end{eqnarray*}$

類題

次の式を $[\phantom{h}]$ 内の文字について解きなさい。
$S=\cfrac{ah}{2}\quad[h]$

答え　 $h=\cfrac{2S}{a}$

$\begin{eqnarray*} S&=&\cfrac{ah}{2}\quad(左辺と右辺をとりかえる） \\ \cfrac{ah}{2}&=&S\quad(両辺に\times2) \\ ah&=&2S \\ h&=&\cfrac{2S}{a} \end{eqnarray*}$

類題

$x=-\cfrac{2}{3},\ y=5$ のとき、次の式の値を求めなさい。
$36x^2y\div12x$

答え　 $-10$

$\begin{eqnarray*} &&36x^2y\div12x \\ &=&\cfrac{36xxy}{12x}\\ &=&3xy \end{eqnarray*}$

$x=-\cfrac{2}{3},\ y=5$ を代入

$3xy=3\times\left(-\cfrac{2}{3}\right)\times5=-10$

類題

$y$ が $x$ に比例し、 $x=6$ のとき、 $y=-8$ である。 $y$ を $x$ の式で表しなさい。

答え　 $y=-\cfrac{4}{3}x$

比例の式の形は

$y=ax$

$a=\cfrac{y}{x}=\cfrac{-8}{6}=-\cfrac{4}{3}$

類題

$y$ が $x$ に反比例し、 $x=15$ のとき、 $y=-\cfrac{2}{5}$ である。 $y$ を $x$ の式で表しなさい。

答え　 $y=-\cfrac{6}{x}$

反比例の式の形は

$y=\cfrac{a}{x}$

$a=x \times y=15\times\left(-\cfrac{2}{5}\right)=-6$

類題

傾きが $-2$ で、点 $(6,\ -10)$ を通る直線の式を求めなさい。

答え　 $y=-2x+2$

直線の式の形は

$y=ax+b$
傾きが

$-2$ なので

$a=-2$

$y=-2x+b$ に

$x=6,\ y=-10$ を代入

$\begin{eqnarray*} -10&=&-2\times6+b\\ -10&=&-12+b\\ -10+12&=&b\\ 2&=&b \end{eqnarray*}$

類題

$2$ 点 $(-2,\ -5),\ (4,\ 7)$ を通る直線の式を求めなさい。

答え　 $y=2x-1$

直線の式の形は

$y=ax+b$

$\begin{eqnarray*} a&=&\cfrac{y_2-y_1}{x_2-x_1}\\ &=&\cfrac{7-(-5)}{4-(-2)}=\cfrac{12}{6}=2\\ \end{eqnarray*}$

$y=2x+b$ に

$x=4,\ y=7$ を代入

$\begin{eqnarray*} 7&=&2\times4+b\\ 7&=&8+b\\ -1&=&b \end{eqnarray*}$

類題

$\boxed{\large{\ 4\ }}$ 以下の問いに答えなさい。

三角形
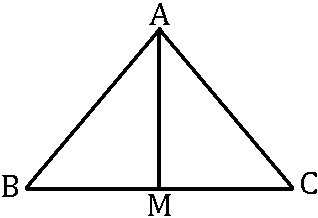
右の図において、 $AB=AC,$ 点 $M$ が $BC$ の中点ならば、 $\triangle ABM \ \equiv \ \triangle ACM$ となる。これについて、以下の①,②の問いに答えなさい。
①　仮定と結論をいいなさい。

②　 $\triangle ABM \ \equiv \ \triangle ACM$ を証明しなさい。

①　〈仮定〉　 $AB=AC, \ BM=CM$
　　〈結論〉　 $\triangle ABM \ \equiv \ \triangle ACM$
②　〈証明〉
$\triangle ABM$ と $\triangle ACM$ で、
仮定から、
$AB=AC$ 　……①
$BM=CM$ 　……②
共通な辺だから、 $AM = AM$ 　……③
①②③より、 $3$ 組の辺がそれぞれ等しいので
$\triangle ABM \ \equiv \ \triangle ACM$

類題

三角形
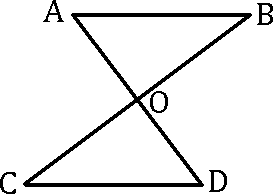
右の図において、 $OA=OD, \ AB /\!/ CD$ であるならば、 $AB=DC$ となる。これについて、以下の①,②の問いに答えなさい。
③　仮定と結論をいいなさい。

④　 $AB=DC$ を証明しなさい。

③　〈仮定〉　 $OA=OD, \ AB /\!/ CD$
　　〈結論〉　 $AB=DC$
④　〈証明〉
$\triangle OAB$ と $\triangle ODC$ で、
仮定から、
$OA=OD$ 　……①
対頂角だから、 $\angle AOB= \angle DOC$ 　……②
平行線の錯角だから、 $\angle OAB= \angle ODC$ 　……③
①②③より、 $1$ 組の辺とその両端の角がそれぞれ等しいので
$\triangle OAB \ \equiv \ \triangle ODC$
合同な図形の対応する辺だから、
$AB=DC$

類題

答え

$\boxed{\large{\ 1\ }}①1②-\cfrac{1}{6}③-4④-2x-2y⑤-\cfrac{2}{3}x-\cfrac{3}{4}y\\ ⑥-8x+6y⑦-2a^2-4a⑧-56x+24y\\ ⑨9x-5y⑩-12a^2+16a-24⑪-18x+24y\\ ⑫-5x+2y⑬-5x+4y⑭\cfrac{-x-7y}{6}⑮8x^4\\ ⑯2x⑰42\\ \boxed{\large{\ 2\ }}①x=3②x=\cfrac{2}{5}③x=-1,y=1\\ ④x=-4,y=3\\ \boxed{\large{\ 3\ }}①y=\cfrac{2x-6}{3}②h=\cfrac{2S}{a}③-10\\ ④y=-\cfrac{4}{3}x⑤y=-\cfrac{6}{x}⑥y=-2x+2⑦y=2x-1\\ \boxed{\large{\ 4\ }}$
①　〈仮定〉　　 $AB=AC, \ BM=CM$
　　〈結論〉　 $\triangle ABM \ \equiv \ \triangle ACM$
②　〈証明〉
$\triangle ABM$ と $\triangle ACM$ で、
仮定から、
$AB=AC$ 　……①
$BM=CM$ 　……②
共通な辺だから、 $AM = AM$ 　……③
①②③より、 $3$ 組の辺がそれぞれ等しいので
$\triangle ABM \ \equiv \ \triangle ACM$
③　〈仮定〉　 $OA=OD, \ AB /\!/ CD$
　　〈結論〉　 $AB=DC$
④　〈証明〉
$\triangle OAB$ と $\triangle ODC$ で、
仮定から、
$OA=OD$ 　……①
対頂角だから、 $\angle AOB= \angle DOC$ 　……②
平行線の錯角だから、 $\angle OAB= \angle ODC$ 　……③
①②③より、 $1$ 組の辺とその両端の角がそれぞれ等しいので
$\triangle OAB \ \equiv \ \triangle ODC$
合同な図形の対応する辺だから、
$AB=DC$

■

▶