数学 入試過去問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
【2006年の大問8】
1辺が$\sqrt{2}cm$の立方体$ABCDEFGH$と、$OA=OB=OC=OD=\sqrt{3}cm$の四角すい$OABCD$を
あわせた立体$OABCDEFGH$
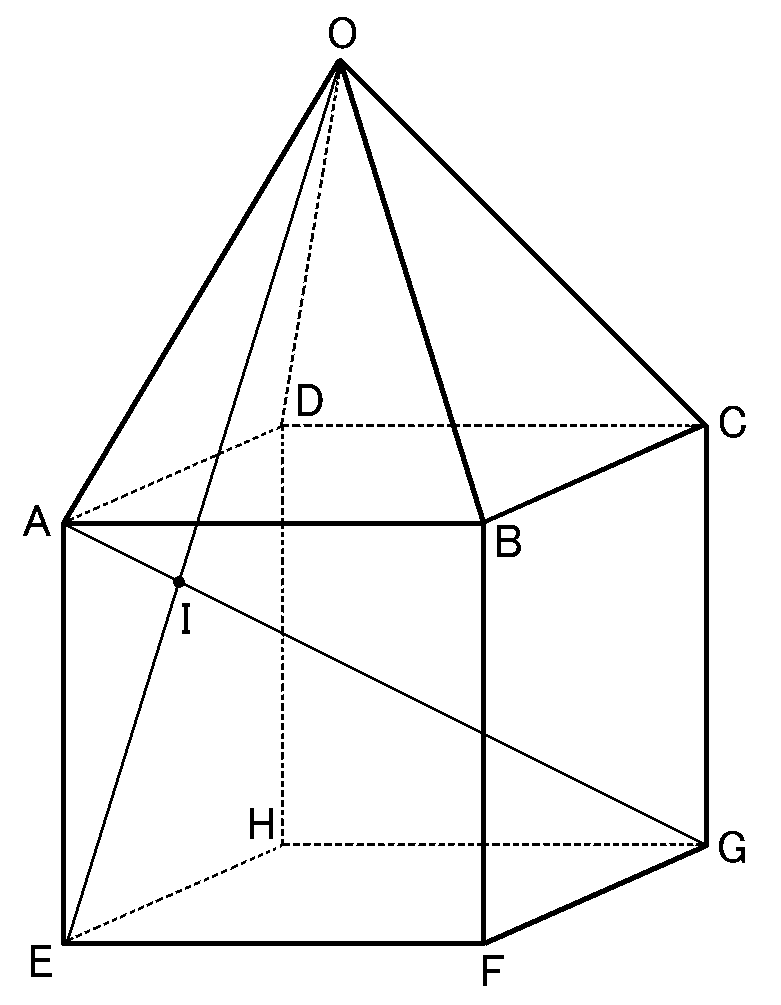
(1) 立体$OABCDEFGH$の表面積
答え
$10+2\sqrt{5}(cm^2)$
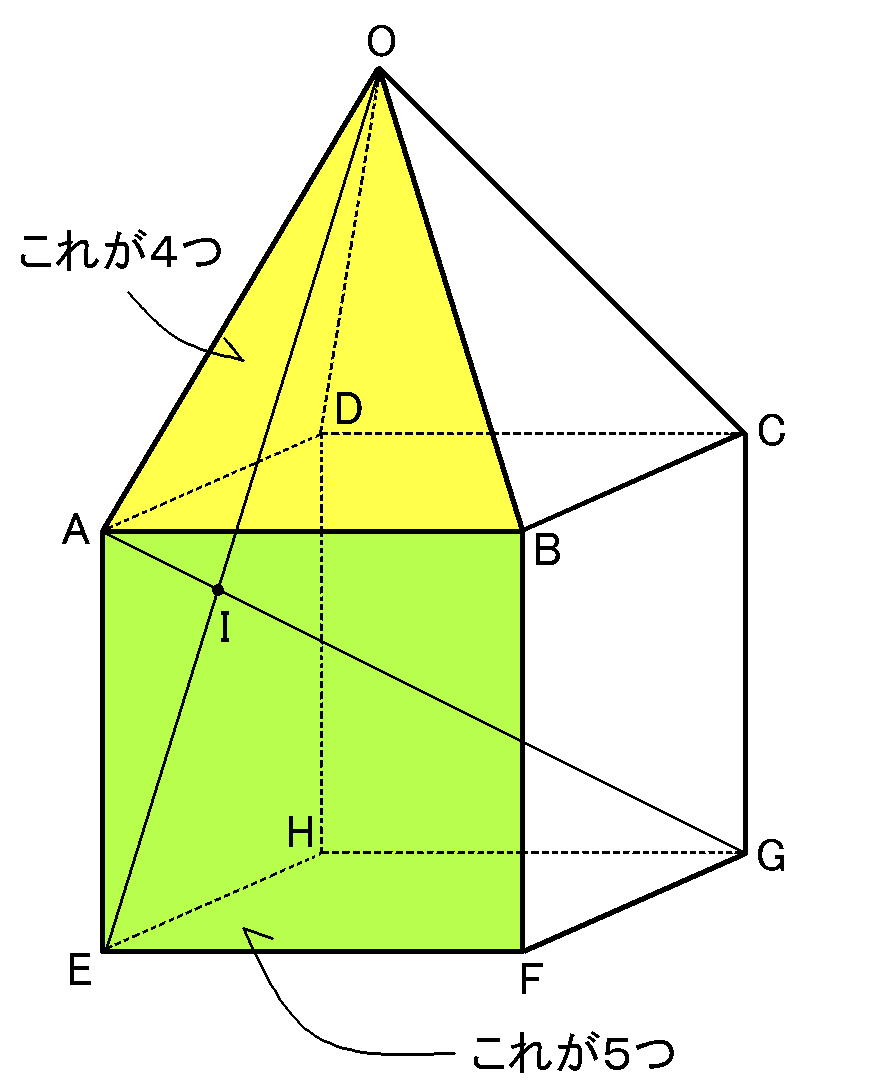
まわりの面の面積を全部足したのが表面積です。
この立体は、面が9つあります。合同な正方形が全部で5つ、
合同な二等辺三角形が全部で4つ、あわせて9つです。それぞれの面積を全部足したのが答えです。
まず正方形の面積をもとめます。正方形の面積は、1辺$\times$1辺です。仮定から、正方形の1辺は$\sqrt{2}cm$なので、$\sqrt{2}\times\sqrt{2}=2cm^2$がひとつの正方形の面積になります。
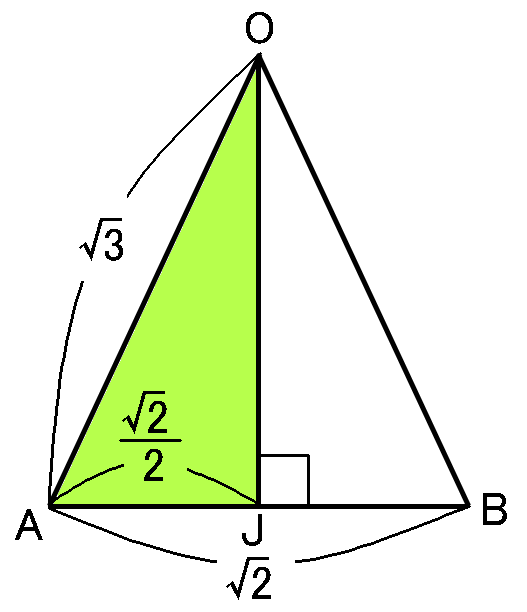
つぎに二等辺三角形の面積をもとめます。三角形の面積は底辺$\times$高さ$\times\cfrac{1}{2}$です。
$\triangle OAB$の頂点$O$から底辺$AB$におろした垂線と$AB$との交点を$J$とします。二等辺三角形の頂角から垂線をおろしているので、この線は底辺を二等分します。
なので$AJ=\cfrac{\sqrt{2}}{2}cm$です。
$\triangle OAJ$は、$OA=\sqrt{3}cm,$$AJ=\cfrac{\sqrt{2}}{2}cm,$$\angle OJA=90^{ \circ }$の直角三角形になるので、三平方の定理より、
\begin{eqnarray*}
(OJ)^2&=&(OA)^2-(AJ)^2\\
&=&\sqrt{3}^2-\left(\cfrac{\sqrt{2}}{2}\right)^2\\
&=&3-\cfrac{1}{2}\\
&=&\cfrac{5}{2}\\
OJ>0なので\\
OJ&=&\sqrt{\cfrac{5}{2}}=\cfrac{\sqrt{10}}{2}cm
\end{eqnarray*}
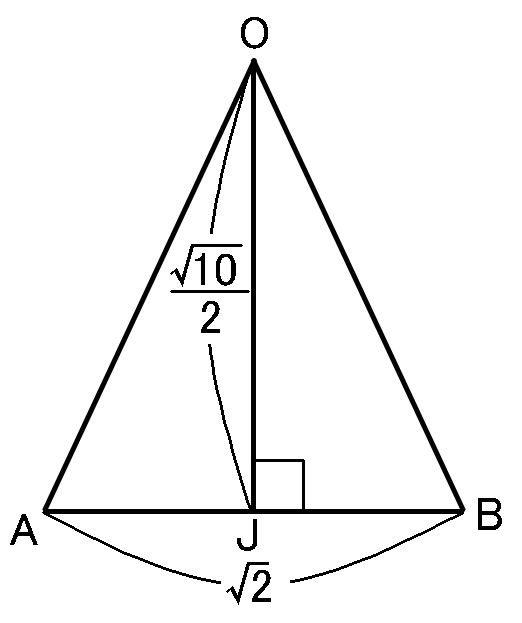
なので$\triangle OAB$の面積は、
\begin{eqnarray*}
&&底辺\times高さ\times\cfrac{1}{2}\\
&=&\sqrt{2}\times\cfrac{\sqrt{10}}{2}\times\cfrac{1}{2}\\
&=&\cfrac{\sqrt{20}}{4}=\cfrac{2\sqrt{5}}{4}=\cfrac{\sqrt{5}}{2}cm^2
\end{eqnarray*}
なのでこの立体の表面積は、
\begin{eqnarray*}
&&正方形\times5+二等辺三角形\times4\\
&=&2\times5+\cfrac{\sqrt{5}}{2}\times4\\
&=&10+2\sqrt{5}(cm^2)
\end{eqnarray*}
(2) 線分$OE$と線分$AG$との交点を$I$とするとき、$AI$の長さ
答え
$\cfrac{\sqrt{6}}{5}cm$

5点$O,A,E,G,C$のある平面でこの立体を切断します。切断した面にできた五角形$OAEGC$で考えます。線分$OE$も線分$AG$もどちらもこの五角形のうえにあります。なので$I$もこのうえにあることになります。
$AI$の長さはこの五角形で考えます。
まず、わかっている辺の長さです。仮定から、$OA=OC=\sqrt{3}cm,$$AE=CG=\sqrt{2}cm$です。
あと、$EG$の長さですが、これは正方形$EFGH$の対角線になっています。1辺の長さがわかっている正方形の対角線の長さを求めたいときは、
$1:1:\sqrt{2}$の直角二等辺三角形の辺の比を使います。
$\triangle EFG$は直角二等辺三角形ですから、
$EG=EF\times\sqrt{2}=\sqrt{2}\times\sqrt{2}=2cm$です。
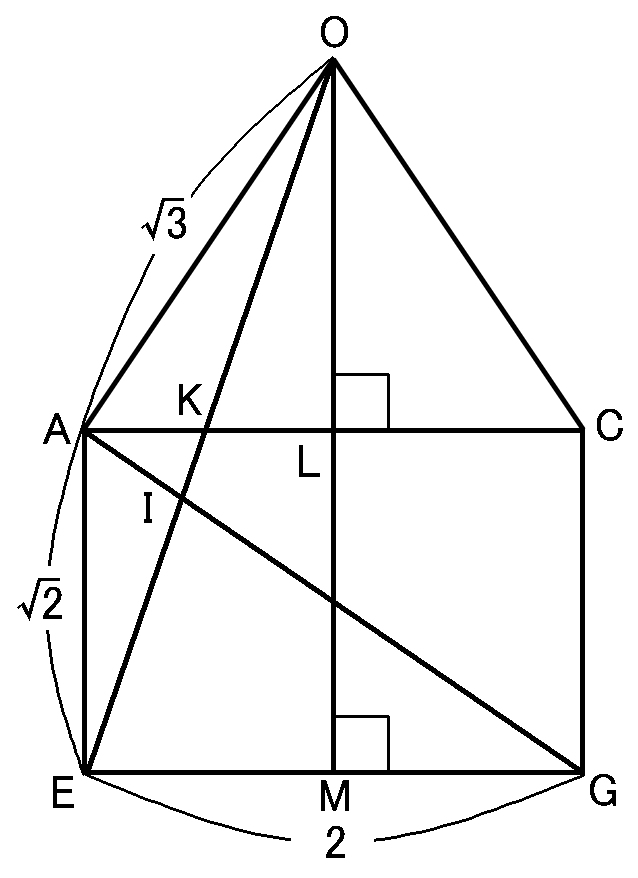
ここで、$A$と$C$をむすびます。$OE$と$AC$の交点を$K$とします。また、$O$から$EG$に垂線をおろして、$AC,EG$との交点をそれぞれ$L,M$とします。
この問題の目標は$AI$の長さです。これを求めるために、$\triangle IKA$と$\triangle IEG$の相似を利用します。その相似比を知るためには、$AK$の長さが必要になります。
そのために、$\triangle AEK$と$\triangle LOK$の相似を利用します。その相似比を知るために、$OL$の長さが必要となります。というわけでまず、$OL$の長さを求めます。
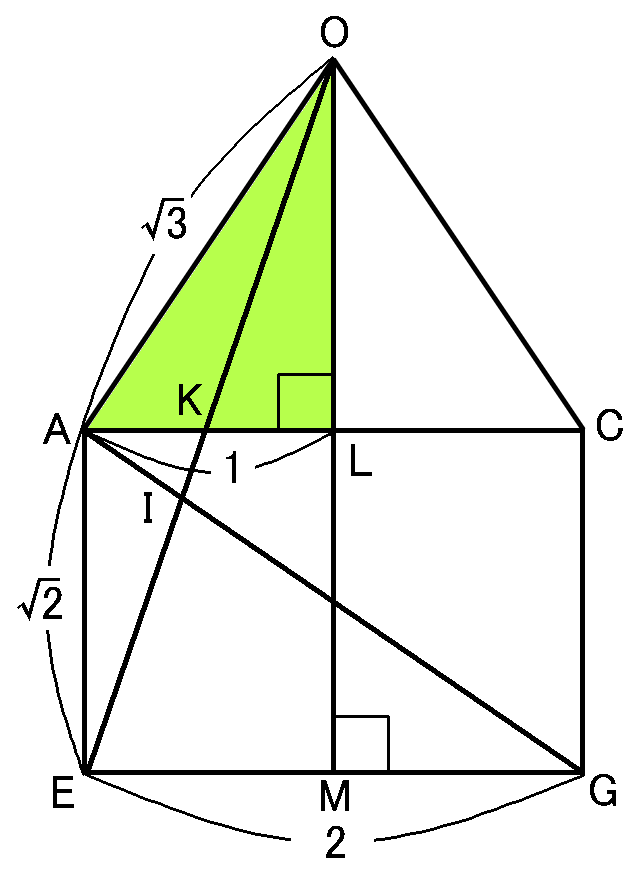
【$OL$の長さ】
四角形$AEGC$は長方形になるので$AC=EG=2cm$です。$L,M$はそれぞれ、$AC,EG$の中点になります。なので$AL=LC$$=EM$$=MG$$=1cm$です。
$\triangle OAL$は、$OA=\sqrt{3}cm,$$AL=1cm,$$\angle OLA=90^{ \circ }$の直角三角形になるので、三平方の定理より、
\begin{eqnarray*}
(OL)^2&=&(OA)^2-(AL)^2\\
&=&\sqrt{3}^2-1^2\\
&=&2\\
OL>0なので\\
OL&=&\sqrt{2}cm
\end{eqnarray*}
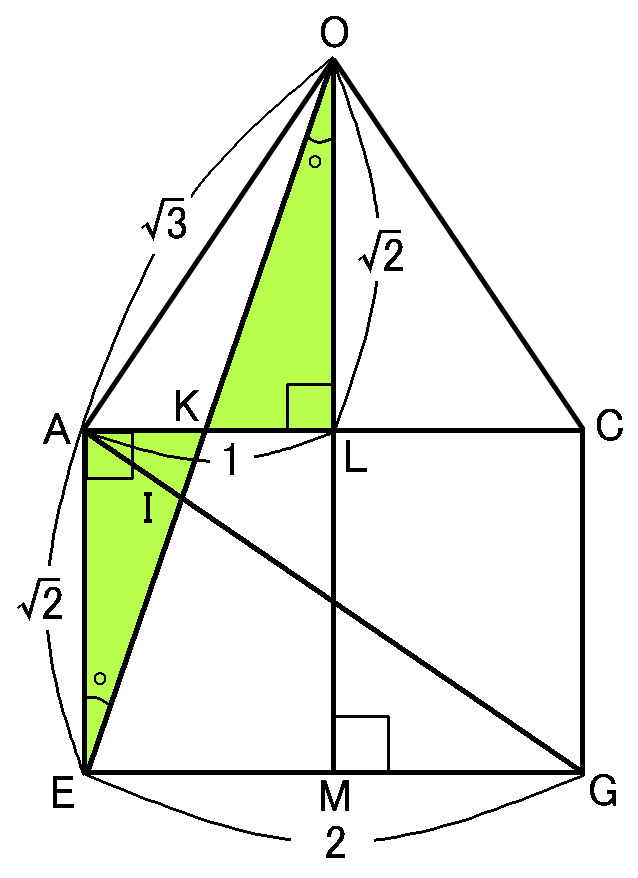
【$AK$の長さ】
$\triangle AEK$と$\triangle LOK$で、$AE=OL=\sqrt{2}cm,$$\angle KAE=\angle KLO=90^{ \circ },$$\angle AEK=\angle LOK$(平行線の錯角)となって、
1組の辺とその両端の角が等しいので$\triangle AEK \equiv \triangle LOK$です。合同な三角形の対応する辺なので、$AK=LK$となります。$K$は$AK$の中点ということです。
なので$AK=\cfrac{1}{2}AL=\cfrac{1}{2}cm$となります。
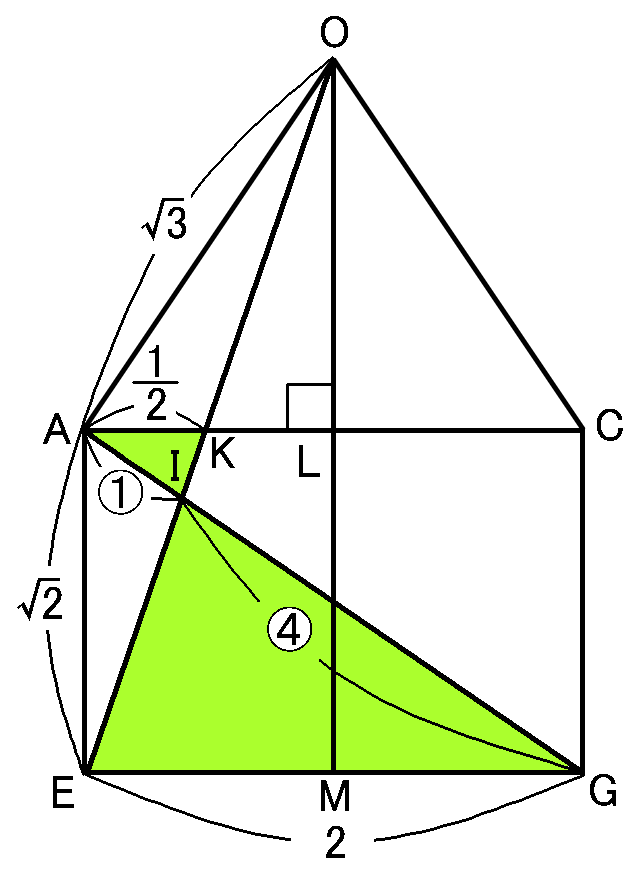
さて、$AC /\!/ EG$です。なので$\triangle IKA$ ∽$\triangle IEG$です。
$AK=\cfrac{1}{2}cm,$$EG=2cm$なので、$\triangle IKA$と$\triangle IEG$の相似比は、$AK:EG=\cfrac{1}{2}:2=1:4$です。
なので、$AI:IG=1:4$です。$AI$の長さは$AG$の長さの$\cfrac{1}{5}$ということです。なので、$AG$の長さをもとめて、それを$\cfrac{1}{5}$倍すればそれが答えです。
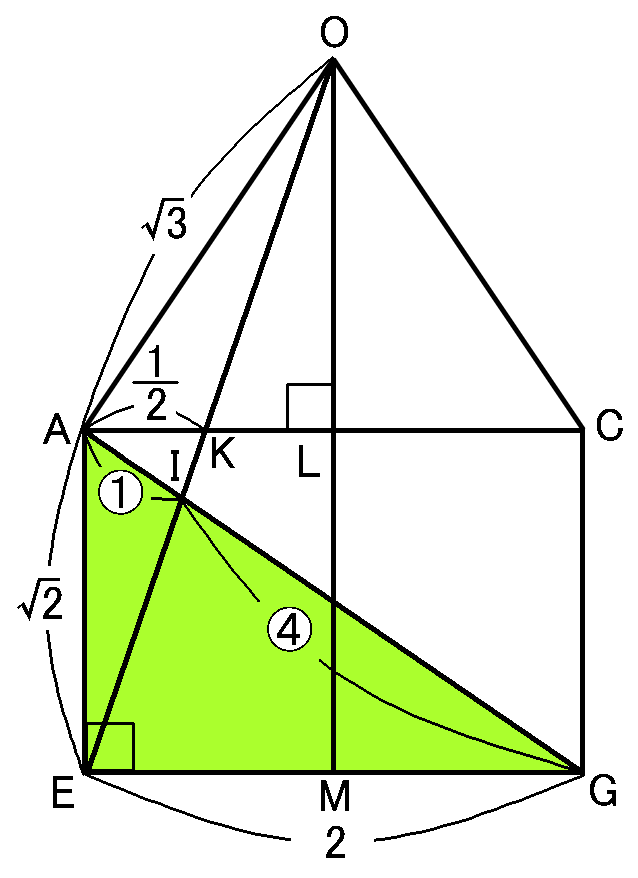
【$AG$の長さ】
$\triangle AEG$は、$AE=\sqrt{2}cm,$$EG=2cm,$$\angle AEG=90^{ \circ }$の直角三角形になので、三平方の定理より、
\begin{eqnarray*}
(AG)^2&=&(AE)^2+(EG)^2\\
&=&\sqrt{2}^2+2^2\\
&=&6\\
AG>0なので\\
AG&=&\sqrt{6}cm
\end{eqnarray*}
なので、$AI=\sqrt{6}\times\cfrac{1}{5}=\cfrac{\sqrt{6}}{5}cm$