数学 入試過去問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
【2007年の大問8】
$AB=6cm,BC=8cm$の長方形$ABCD$を底面とし、$OA=OB=OC=OD=6cm$の四角すい$OABCD$
2辺$OC,OD$の中点をそれぞれ$E,F$
線分$AE$と線分$BF$との交点を$G$とする
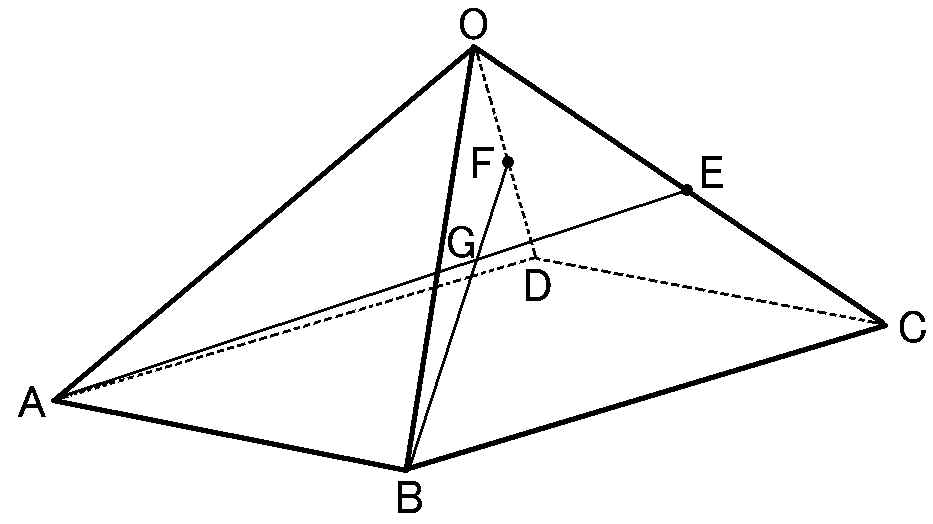
(1) $\triangle OEF$の面積
答え
$\cfrac{9\sqrt{3}}{4}(cm^2)$
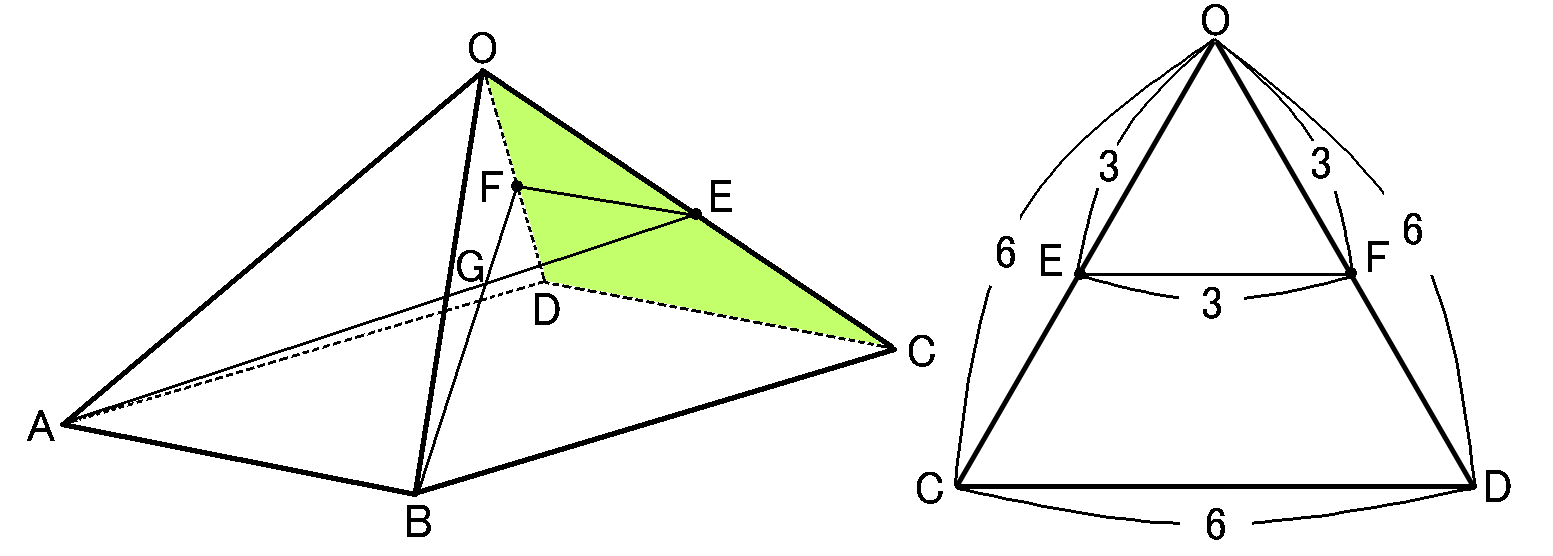
$OCD$で、仮定から点$E,F$は$OC,OD$の中点ですから、中点連結定理より、$EF=\cfrac{1}{2}CD=3cm$です。
また、$OE=\cfrac{1}{2}OC=3cm,$$OF=\cfrac{1}{2}OD=3cm$なので、$\triangle OEF$は1辺が$3cm$の正三角形となります。
1辺が$3cm$の正三角形の面積をこたえればよいわです。
もし、「1辺が$a$の正三角形の面積は$\cfrac{\sqrt{3}}{4}a^2$」というのをおぼえてしまっているのなら、$\cfrac{\sqrt{3}}{4}\times3^2=\cfrac{9\sqrt{3}}{4}(cm^2)$
とこたえておしまいです。
おぼえていないのなら、地道に計算しましょう。たいした手間じゃありません。
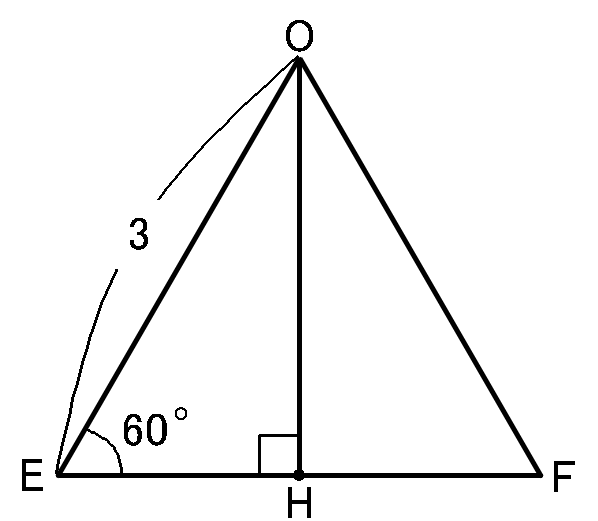 三角形の面積はもちろん、底辺$\times$高さ$\times\cfrac{1}{2}$です。
三角形の面積はもちろん、底辺$\times$高さ$\times\cfrac{1}{2}$です。
$\triangle OEF$で、頂点$O$から$EF$に垂線をおろして、$EF$との交点を$H$とします。
正三角形の1つの内角は$60^{ \circ }$ですから、$\angle OEH=60^{ \circ }$です。
すると$\triangle OEH$は、$\angle OHE=90^{ \circ },$$\angle OEH=60^{ \circ },$$\angle EOH=30^{ \circ }$の直角三角形となって、$1:2:\sqrt{3}$の辺の比が使えることになります。
$\triangle OEH$で、
\begin{eqnarray*}
OE:OH&=&2:\sqrt3 \\
3:OH&=&2:\sqrt3 \\
OH\times2&=&3\times\sqrt{3}\\
OH&=&\cfrac{3\sqrt{3}}{2}\\
\end{eqnarray*}
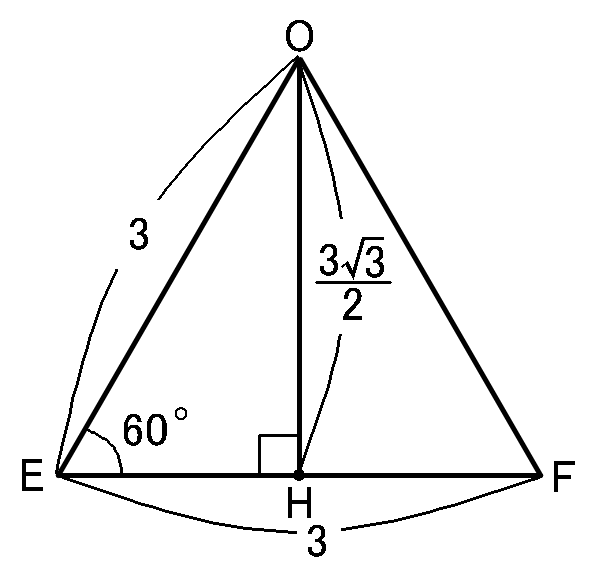 というわけで$OH$の長さがでました。
というわけで$OH$の長さがでました。
$\triangle OEF$は、$EF$を底辺とすれば高さは$OH$です。
なので$\triangle OEF$の面積は、
$$3\times\cfrac{3\sqrt{3}}{2}\times\cfrac{1}{2}=\cfrac{9\sqrt{3}}{4}(cm^2)$$
(2) 線分$EG$の長さ
答え
$\cfrac{\sqrt{59}}{3}cm$
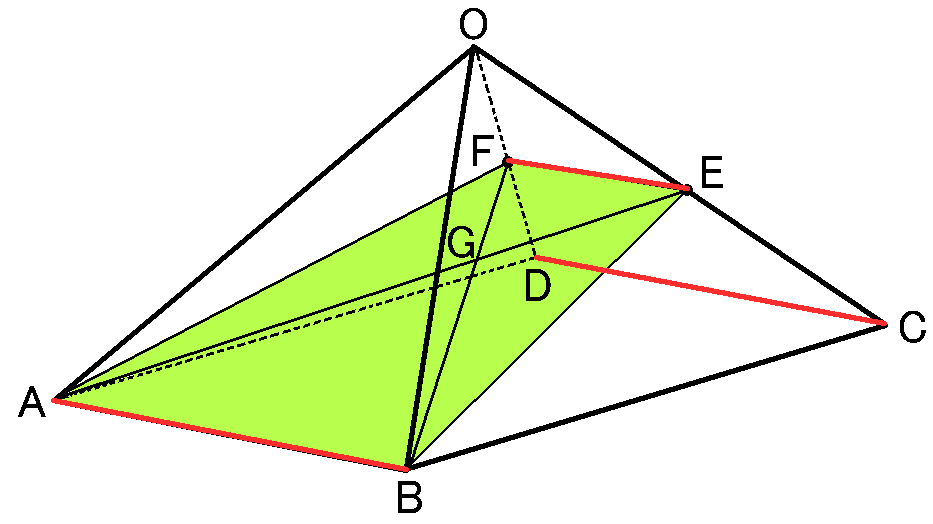
$F$と$E$、$F$と$A$、$E$と$B$をむすんで、四角形$FABE$で考えます。
まず、$\triangle OCD$で、中点連結定理より、$FE /\!/ DC$です。また、仮定より$AB /\!/ DC$ですから、$AB /\!/ FE$となって、四角形
$FABE$は台形ということになります。
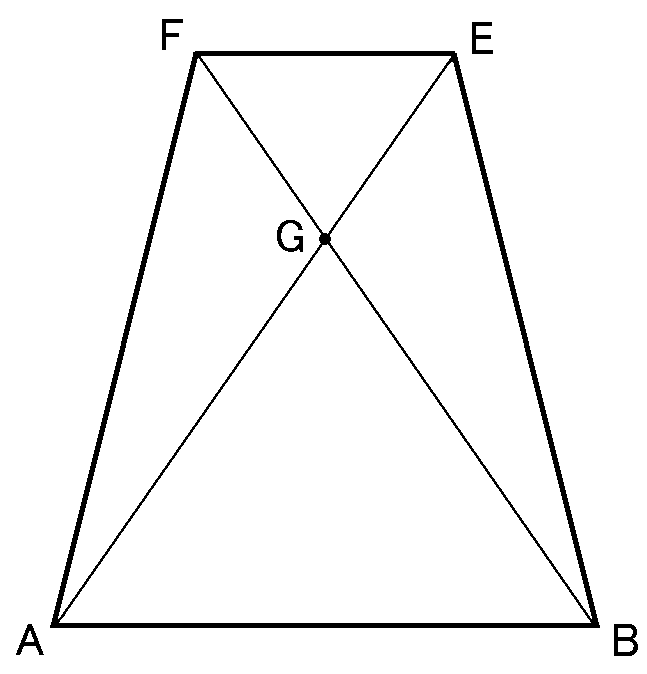
また、$\triangle OAD$における$FA$と、$\triangle OBC$における$EB$は、合同な二等辺三角形の1つの底角からむかいあう辺の中点にひいた線なので、
長さがおなじになります。なのでけっきょく四角形$FABE$は等脚台形ということになります。
この問題は$EG$の長さをもとめるのが目標です。そのためには$EA$の長さが必要になります。$EA$を求めるためには$E$から$AB$におろした垂線の長さが必要になります。
この垂線の長さを求めるためには、$EB$の長さが必要です。というわけで、まず$EB$の長さを求めていきます。
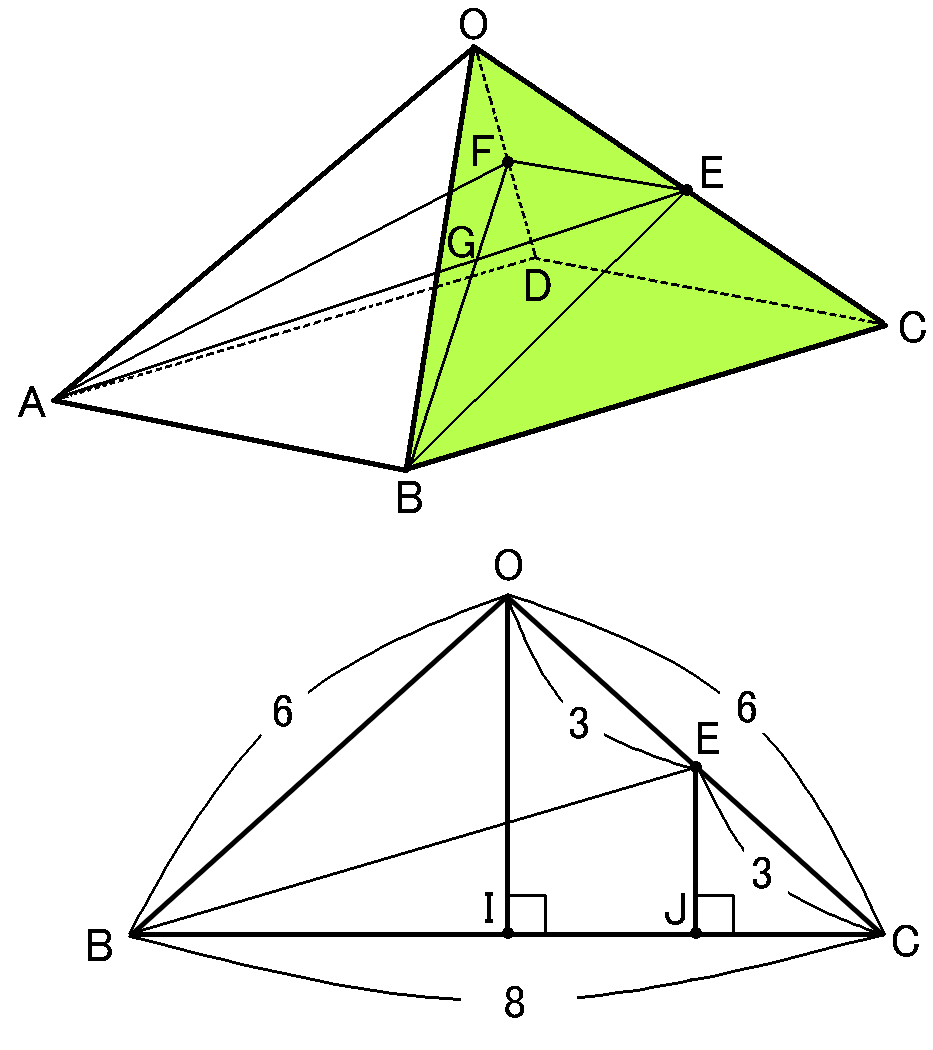
$EB$の長さをもとめるために、$\triangle OBC$に着目します。これは$OB=OC=6cm,$$BC=8cm$の二等辺三角形で、点$E$は$OC$の中点です。
まず、$E$と$B$をむすびます。あと、頂点$O$、点$E$から$BC$に垂線をおろして、その交点をそれぞれ$I,J$ということにします。
【$IC$の長さ】
$OI$というのは二等辺三角形$OBC$の頂角から底辺にひいた垂線なので、底辺を二等分します。なので$IC=\cfrac{1}{2}BC=4cm$です。
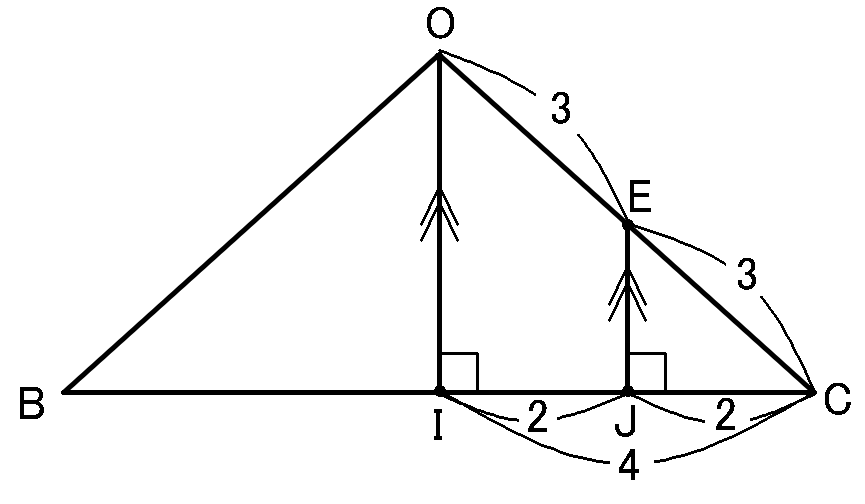
【$JC$の長さ】
また、同位角が等しいので$OI /\!/ EJ$です。仮定から$OE:EC=1:1$なので、平行線と線分の比の定理から、$IJ:JC=1:1$になります。$J$は$IC$の中点になっている、ということです。
なので$JC=2cm$です。
【$EC$の長さ】
仮定から、$EC=\cfrac{1}{2}OC=3cm$です。
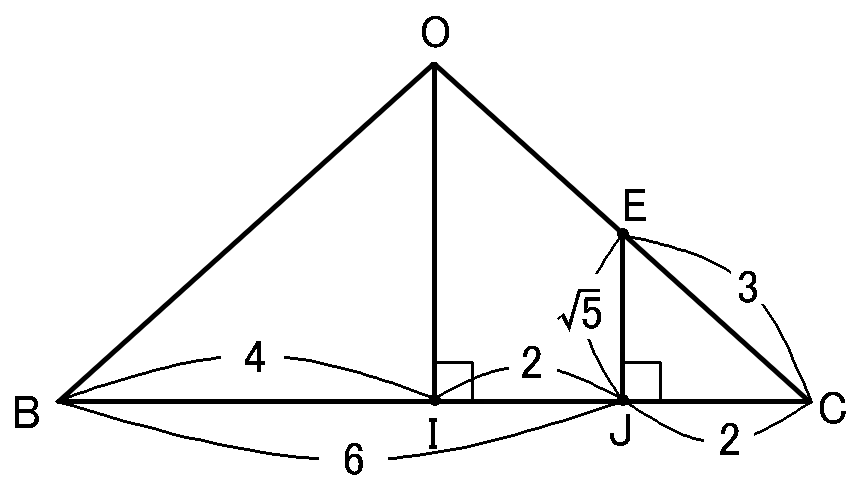
【$EJ$の長さ】
$\triangle EJC$は、$EC=3cm,$$JC=2cm,$$\angle EJC=90^{ \circ }$の直角三角形になるので、三平方の定理より、
\begin{eqnarray*}
(EJ)^2&=&(EC)^2-(JC)^2\\
&=&3^2-2^2\\
&=&5\\
EJ>0なので\\
EJ&=&\sqrt{5}cm
\end{eqnarray*}
【$BJ$の長さ】
$BJ$の長さは、$BC-JC=8-2=6cm$です。$BI+IJ=4+2=6cm$と考えてもいいです。どちらにしても$6cm$です。
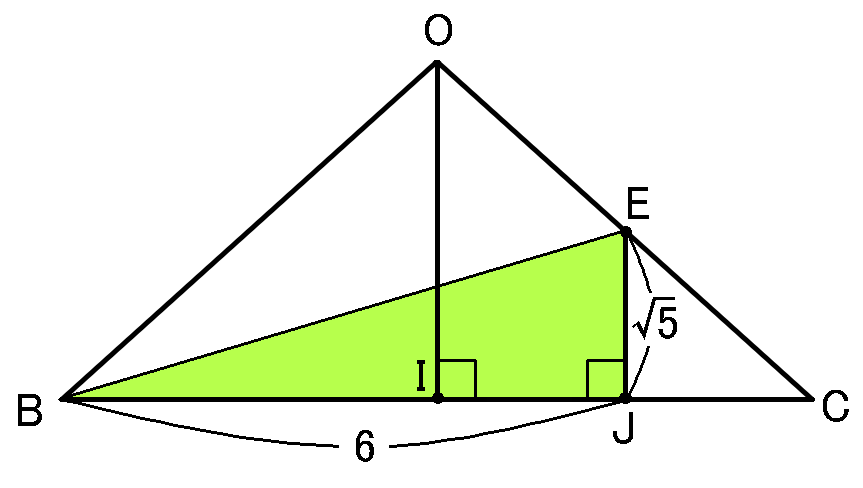
【$EB$の長さ】
すると$\triangle EJB$は、$EJ=\sqrt{5}cm,$$BJ=6cm,$$\angle EJB=90^{ \circ }$の直角三角形となって、三平方の定理より、
\begin{eqnarray*}
(EB)^2&=&(EA)^2+(BJ)^2\\
&=&\sqrt{5}^2+6^2\\
&=&41\\
EB>0なので\\
EB&=&\sqrt{41}cm
\end{eqnarray*}
これで$EB=\sqrt{41}cm$ともとめられました。
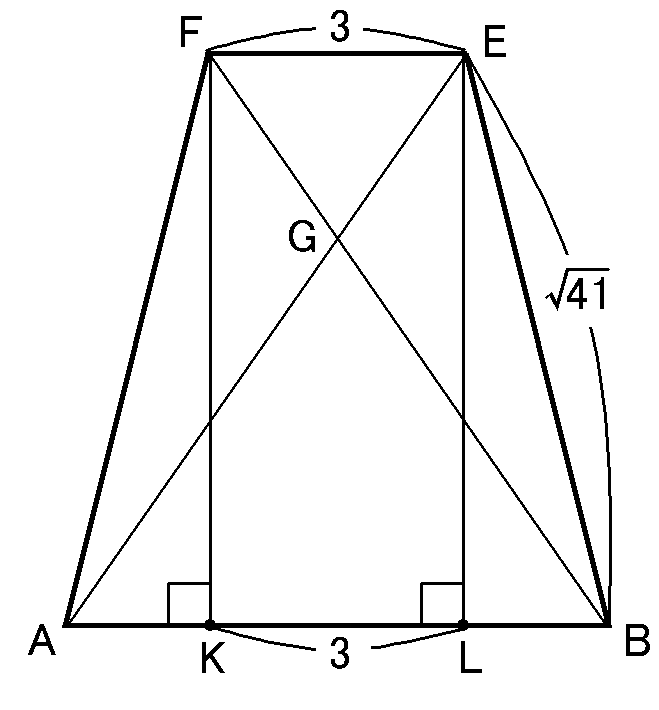
ここで等脚台形$FABE$にもどります。頂点$F,E$から辺$AB$に垂線をおろし、$AB$との交点をそれぞれ$K,L$とします。
【$LB$の長さ】
(1)の問題で、$EF=\cfrac{1}{2}CD=3cm$ともとめました。$EF=KL$なので、$KL=3cm$です。
$FABE$は等脚台形なので、$\triangle FAK \equiv \triangle EBL$となります。合同な図形の対応する辺なので、$KA=LB$です。$KA+LB=AB-KL=6-3=3cm$なので、
$KA=LB=\cfrac{3}{2}cm$となります。

【$(EL)^2$の値】
$\triangle ELB$は、$EB=\sqrt{41}cm,$$LB=\cfrac{3}{2}cm,$$\angle ELB=90^{ \circ }$の直角三角形となるので、三平方の定理より、
\begin{eqnarray*}
(EL)^2&=&(EB)^2-(LB)^2\\
&=&\sqrt{41}^2-\left(=\cfrac{3}{2}\right)^2\\
&=&41-\cfrac{9}{4}\\
&=&\cfrac{155}{4}
\end{eqnarray*}
ほしいのは$(EL)^2$の値なので、ここはこのままでだいじょうぶです。
【$AL$の長さ】
$AL=AK+KL=\cfrac{3}{2}+3=\cfrac{9}{2}cm$です。
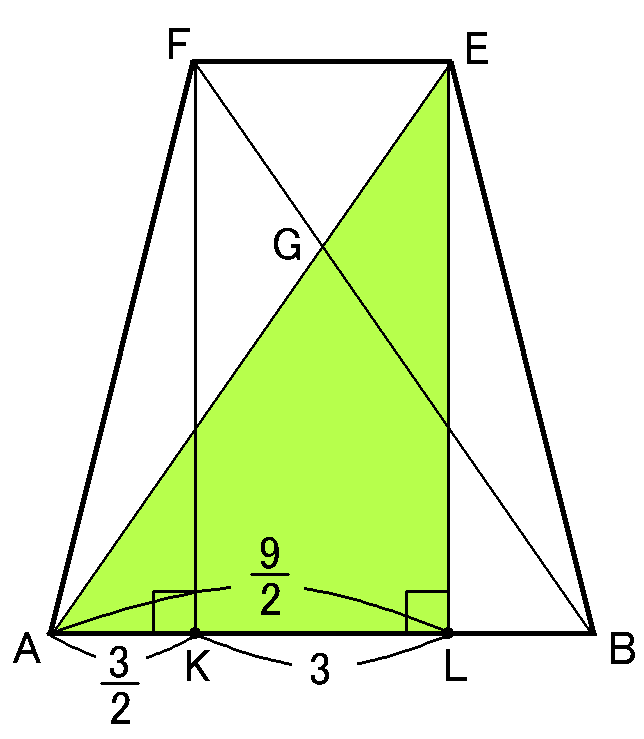
【$EA$の長さ】
$\triangle EAL$は、$(EL)^2=\cfrac{155}{4},$$AL=\cfrac{9}{2}cm,$$\angle ELA=90^{ \circ }$の直角三角形となって、三平方の定理より、
\begin{eqnarray*}
(EA)^2&=&(EL)^2+(AL)^2\\
&=&\cfrac{155}{4}+\left(\cfrac{9}{2}\right)^2\\
&=&\cfrac{155}{4}+\cfrac{81}{4}\\
&=&\cfrac{236}{4}\\
&=&59\\
EA>0なので\\
EA&=&\sqrt{59}cm
\end{eqnarray*}
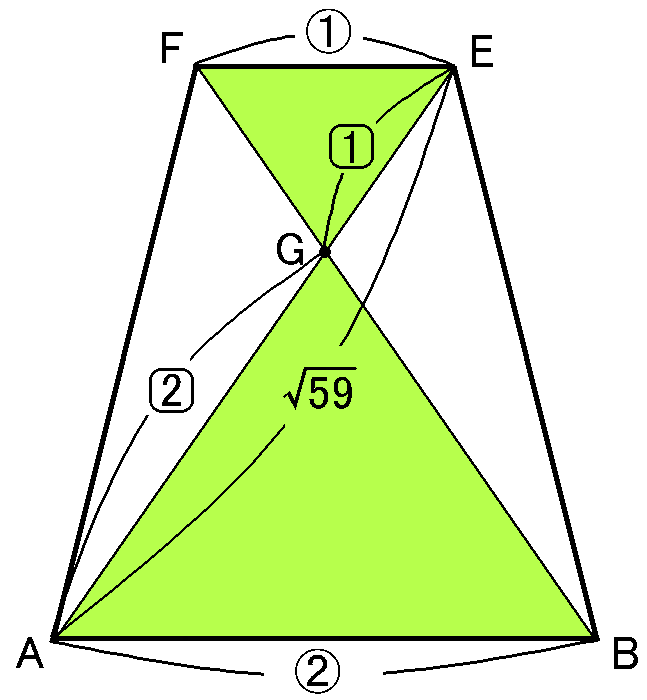
$EA=\sqrt{59}cm$ともとめられました。
ここで、$\triangle EFG$と$\triangle ABG$の相似を利用します。$AB /\!/ FE$なのですから、
2組の角がそれぞれ等しいので、$\triangle EFG$ ∽$\triangle ABG$です。
$EF=3cm,$$AB=6cm$なので、$\triangle EFG$と$\triangle ABC$の相似比は$3:6=1:2$となります。
なので$EG:GA=1:2$となります。ということは、$EG$の長さは$EA$の長さの$\cfrac{1}{3}$ということになります。なので、
【$EG$の長さ】
$$EG=EA\times\cfrac{1}{3}=\cfrac{\sqrt{59}}{3}cm$$