数学 入試過去問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
【2008年の大問8】
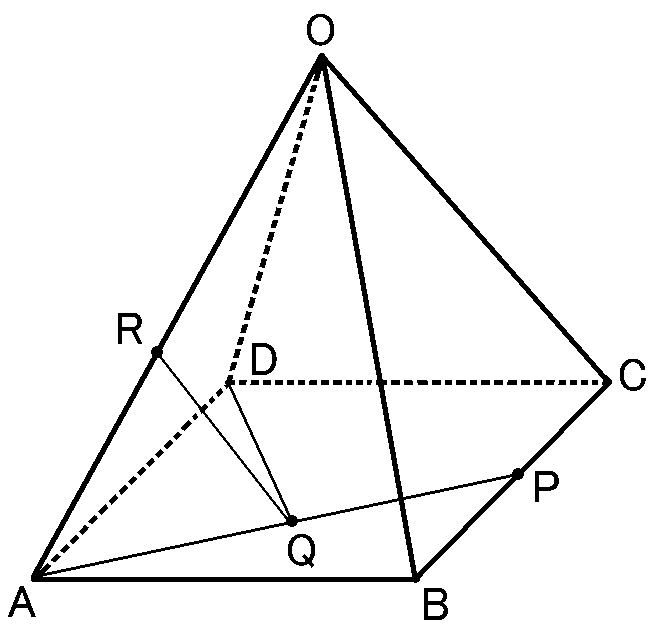
1辺が$4cm$の正方形$ABCD$を底面とし、$OA=OB=OC=OD=4\sqrt{2}cm$の正四角すい$OABCD$
辺$BC$の中点を$P$とし、線分$AP$の中点を$Q$とする
また、辺$OA$上に$QA=QR$となる点$R$をとる
(1) $\triangle ADQ$の面積
答え
$4cm^2$
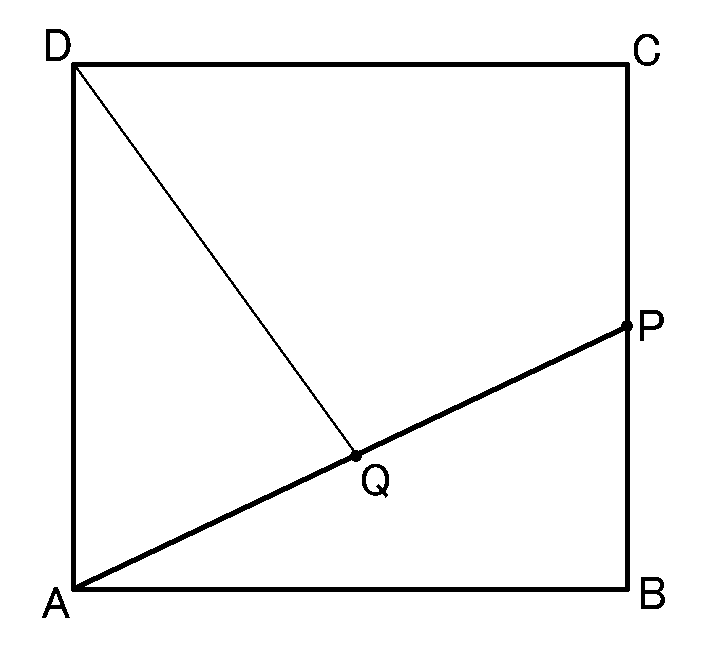
底面の正方形$ABCD$で考えます。
$\triangle ADQ$の面積は、底面の正方形$ABCD$の$\cfrac{1}{4}$になっているなあ、と考えるのがてっとりばやいです。
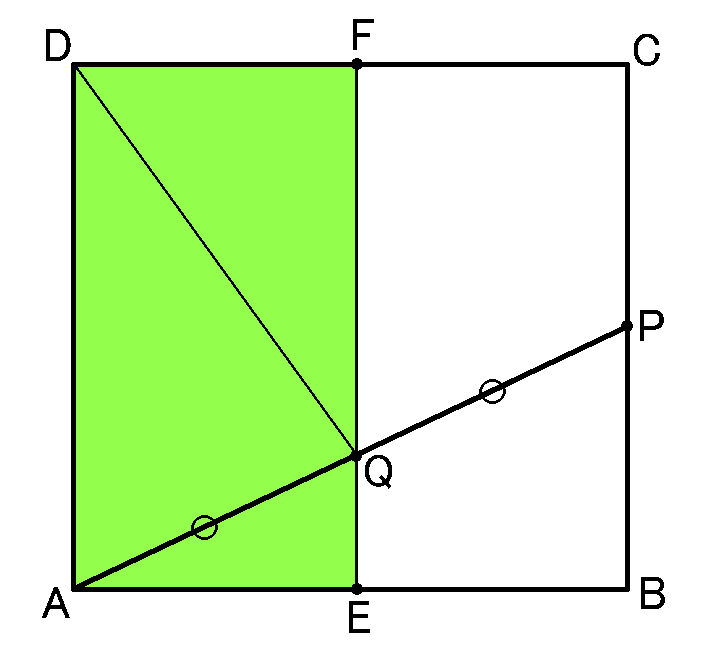
底面の正方形$ABCD$で、$Q$を通って$AD$と平行な線をひいて、$AB,DC$との交点をそれぞれ$E,F$とします。$AD /\!/ EF /\!/ BC$で、仮定から$AQ=QP$ですから、
平行線と線分の比の定理から、$AE=EB,DF=FC$です。なので長方形$AEFD$の面積は底面の正方形$ABCD$の面積の半分です。
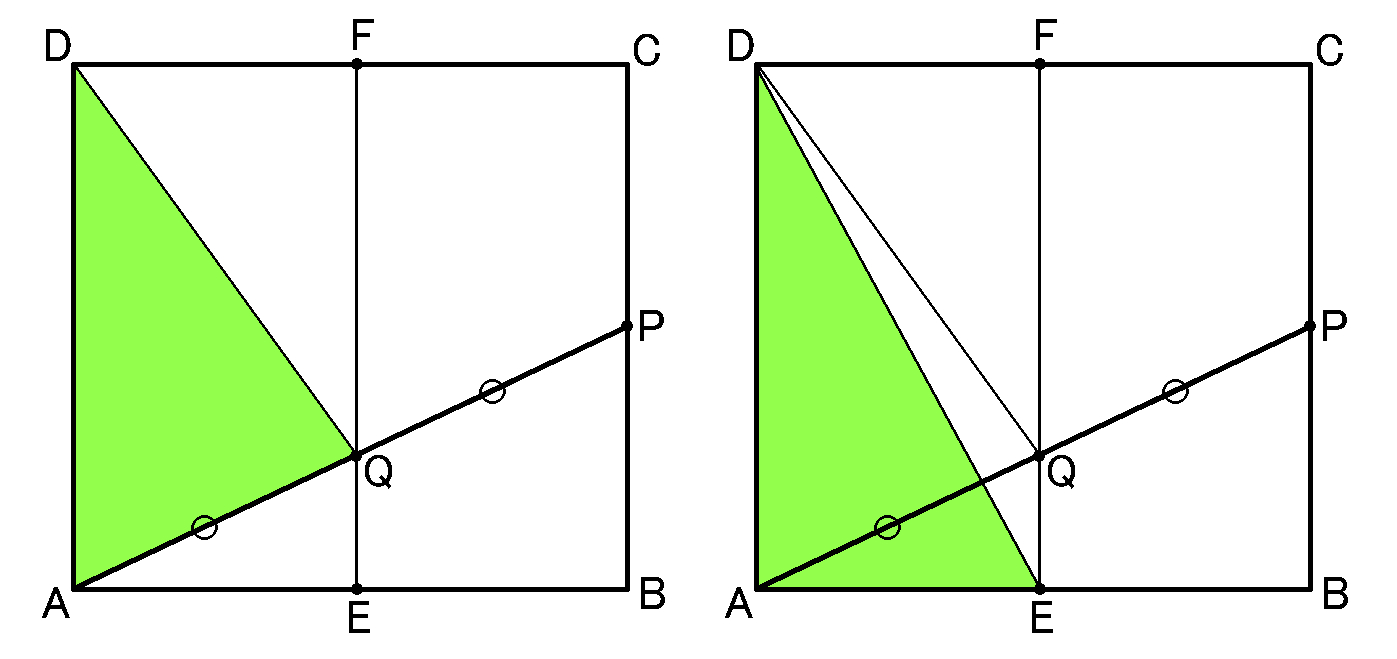
また、$\triangle ADQ$の面積は、等積変形をすれば$\triangle ADF$や$\triangle ADE$の面積と等しくなって、これは長方形$AEFD$の半分です。
ということは、$\triangle ADQ$の面積は、底面の正方形$ABCD$の面積の半分の半分、すなわち4分の1になっています。
底面の正方形$ABCD$の面積は$4\times4=16cm^2$ですから、$\triangle ADQ$の面積は、$16\times\cfrac{1}{4}=4cm^2$(答え)
あともちろん、由緒正しく、底辺$\times$高さ$\times\cfrac{1}{2}$とやってもOKです。
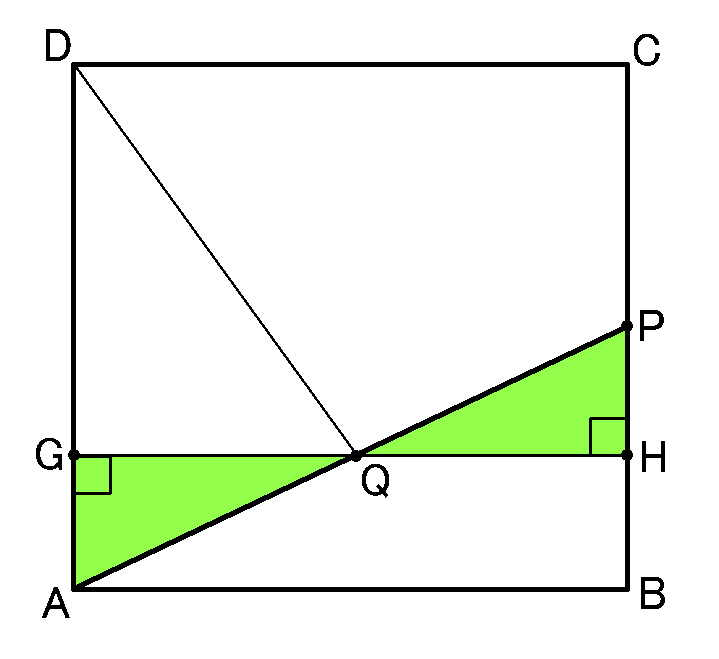
$\triangle ADQ$の底辺を$AD$とします。$Q$から$AD$におろした垂線と$AD$との交点を$G$とします。ついでに$BC$との交点を$H$としておきます。
$\triangle ADQ$の底辺を$AD$とすると、高さは$QG$ということになります。
$\triangle QGA$と$\triangle QHP$は、斜辺と1鋭角が等しい直角三角形なので合同です。なので$QG=QH$となって、$QG$の長さは$GH$の半分ということになって、
$2cm$です。$AD$の長さはもちろん$4cm$です。なので、$\triangle ADQ$の面積は、
$$4\times2\times\cfrac{1}{2}=4cm^2$$
(2) 線分$AR$の長さ
答え
$\cfrac{3\sqrt{2}}{2}(cm)$
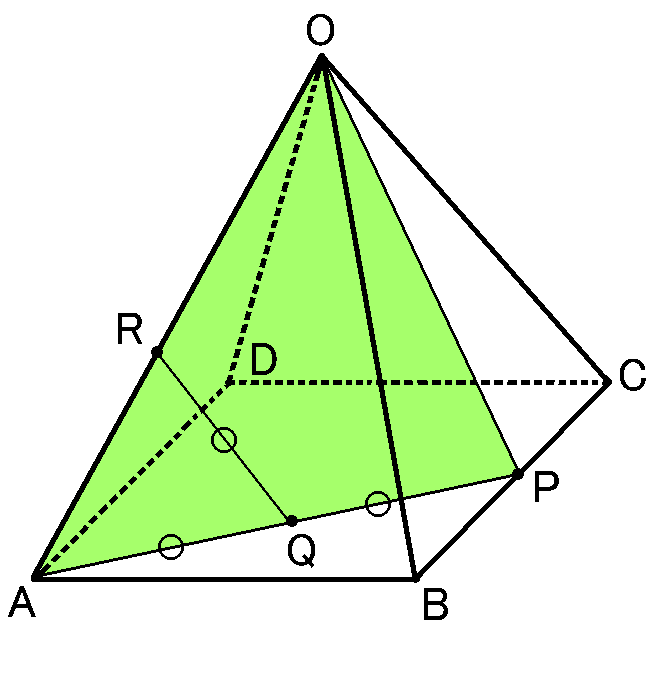
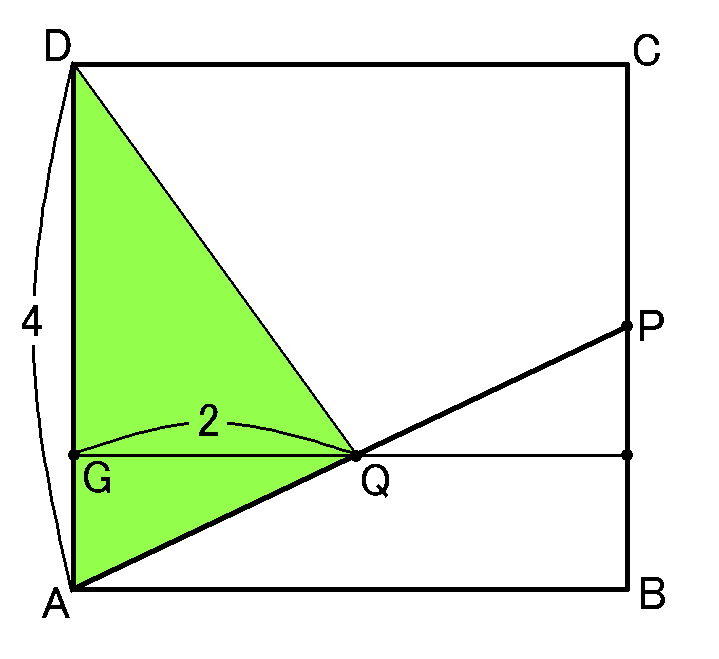
$O$と$P$をむすんで、$\triangle OAP$で考えます。ポイントは、仮定から、$QA=QR=QP$であることです。
1年生のときに、定規とコンパスを使って作図の練習をしたとおもいます。垂直二等分線とか、角の二等分線とかを作図したとおもいます。そのときに、
3点から等しい距離にある点を作図によってもとめる、という練習をしたはずです。そして、3点から等しい距離にある点は、その3点を通る円の中心になっている、
というのを教わったはずです。そのことをおもいだしてください。忘れていたならここでもういちどおぼえなおしてください。3点から等しい距離にある点は、
その3点を通る円の中心になっています。下の図でいうと、3点$A,B,C$から等しい距離にある点$O$は、3点$A,B,C$を通る円の中心になっている、ということです。あるいは、
点$O$を中心として、半径$OA$の円をかくと、その円は点$B,C$を通るはずだよね、といったほうがわかりやすいかも。そりゃそうですよね。$OA=OB=OC$なんだから。
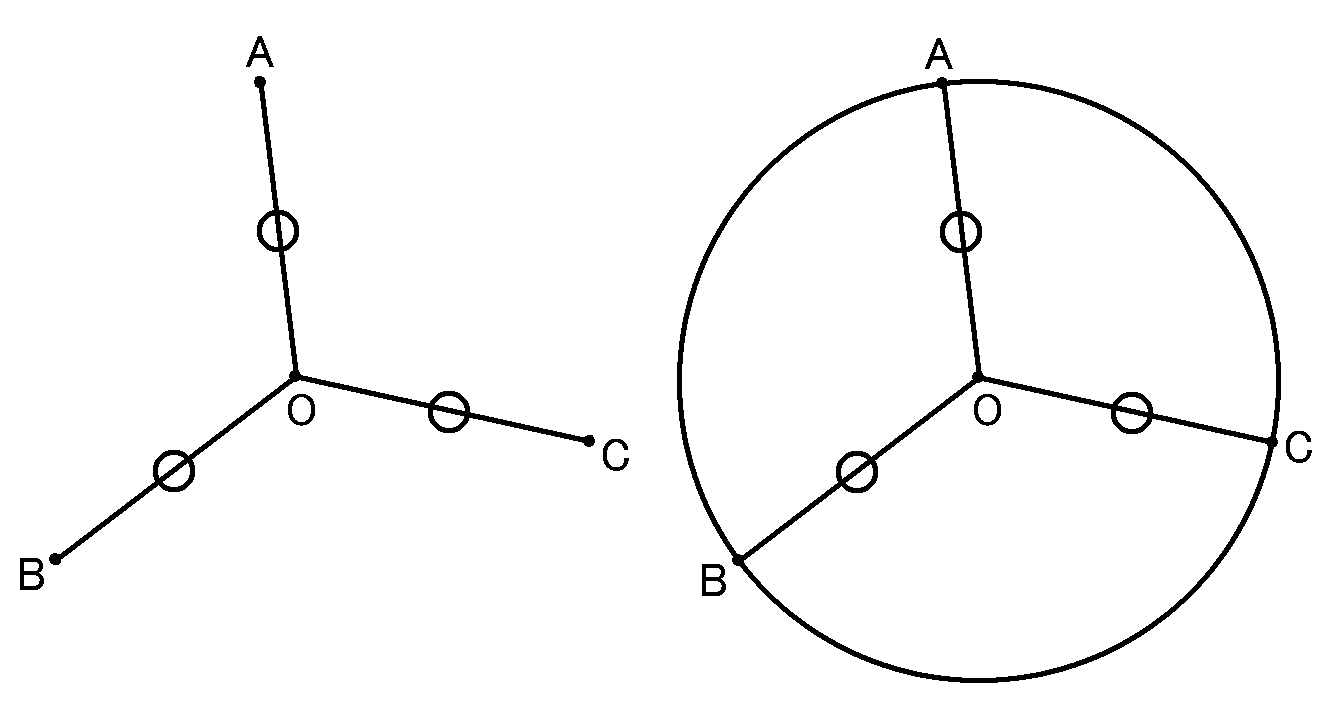
というわけで図をみなおしてみましょう。
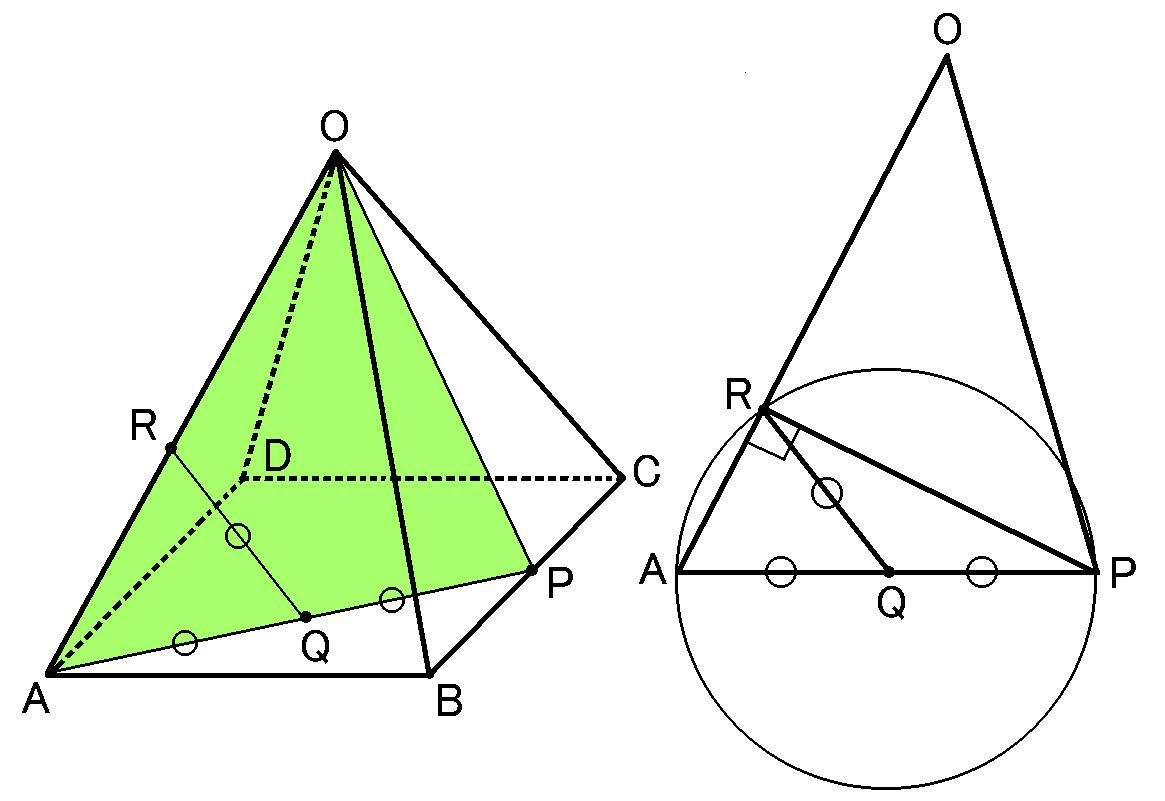
仮定から、$QA=QR=QP$です。ということは、$Q$は3点$A,R,P$を通る円の中心になっています。なので、
$AP$は3点$A,R,P$を通る円の直径になっています。直径の円周角は$90^{ \circ }$です。ということは、$\angle ARP=90^{ \circ }$です。
$\angle ARP$が直角なんだ、ということに気づけば、$AR$の長さは、三平方の定理で$(PR)^2$を2通りの方法であらわしていくというおなじみのやりかたでもとめられます。
まず、$\triangle OAP$の3辺の長さをもとめましょう。

【$AP$の長さ】
$AP$の長さは$\triangle PAB$でもとめます。$\triangle PAB$は、$AB=4cm,$$PB=2cm,$$\angle PBA=90^{ \circ }$の直角三角形なので、三平方の定理より、
\begin{eqnarray*}
(AP)^2&=&(AB)^2+(PB)^2\\
&=&4^2+2^2\\
&=&20\\
AP>0なので\\
AP&=&\sqrt{20}=2\sqrt{5}cm
\end{eqnarray*}
ということは、$QA=QR=QP=\cfrac{1}{2}AP=\sqrt{5}cm$です。
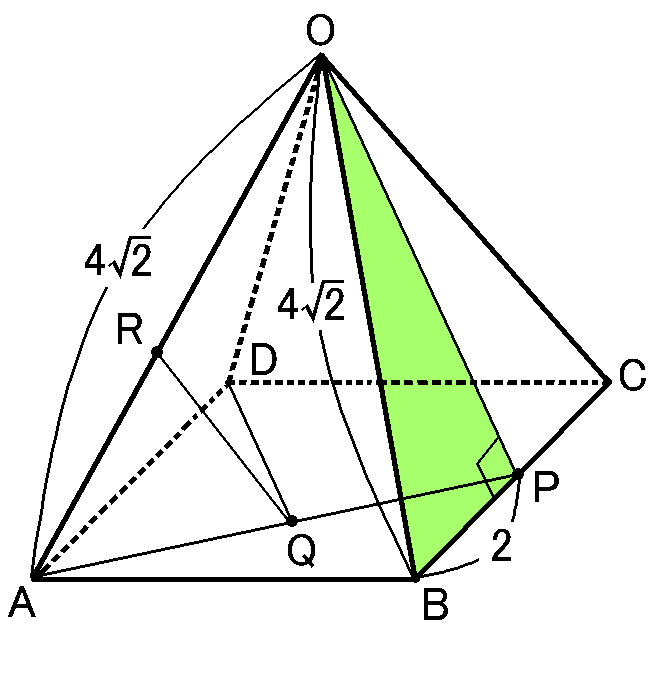
【$OA$の長さ】
$OA$の長さは仮定から$4\sqrt{2}cm$です。
【$OP$の長さ】
$OP$の長さは$\triangle OBP$でもとめます。$\triangle OBP$は、$OB=4\sqrt{2}cm,$$PB=2cm,$$\angle OPB=90^{ \circ }$の直角三角形なので、三平方の定理より、
\begin{eqnarray*}
(OP)^2&=&(OB)^2-(PB)^2\\
&=&(4\sqrt{2})^2-2^2\\
&=&28\\
OP>0なので\\
OP&=&\sqrt{28}=2\sqrt{7}cm
\end{eqnarray*}
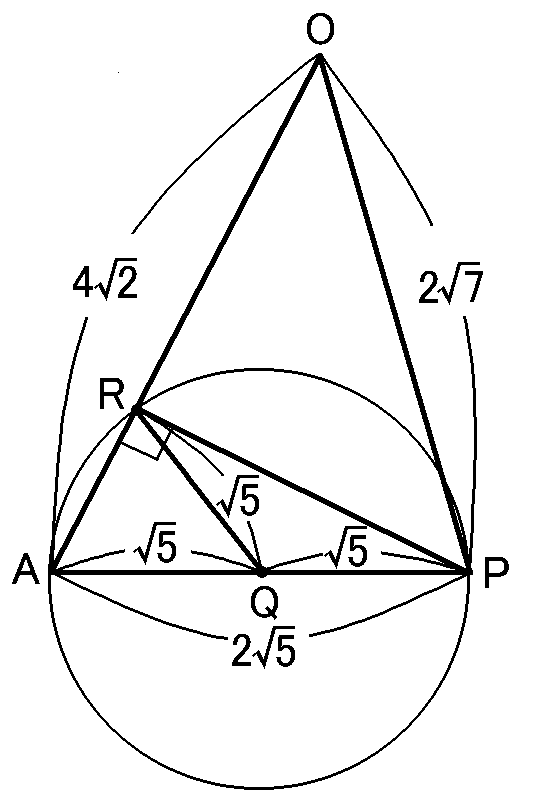
これで$\triangle OAP$の3辺の長さがでました。$AP=2\sqrt{5}cm,$$OA=4\sqrt{2}cm,$$OP=2\sqrt{7}cm$です。
そして、ここでポイントとなるのが、さいしょに説明したとおり、$QA=QR=QP$であることです。
$Q$は3点$A,R,P$を通る円の中心になって、
$AP$は3点$A,R,P$を通る円の直径になります。直径の円周角は$90^{ \circ }$ですから、$\angle ARP=90^{ \circ }$です。
というわけで$\triangle ARP$は、$\angle ARP=90^{ \circ }$の直角三角形になります。
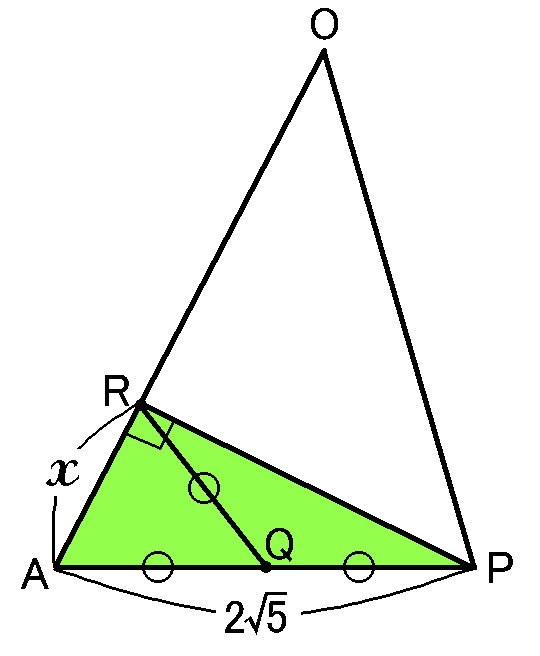
$AR=x$とすると、$\triangle ARP$で、三平方の定理より、
\begin{eqnarray*}
(PR)^2&=&(AP)^2-(AR)^2\\
&=&(2\sqrt{5})^2-x^2\\
&=&20-x^2
\end{eqnarray*}
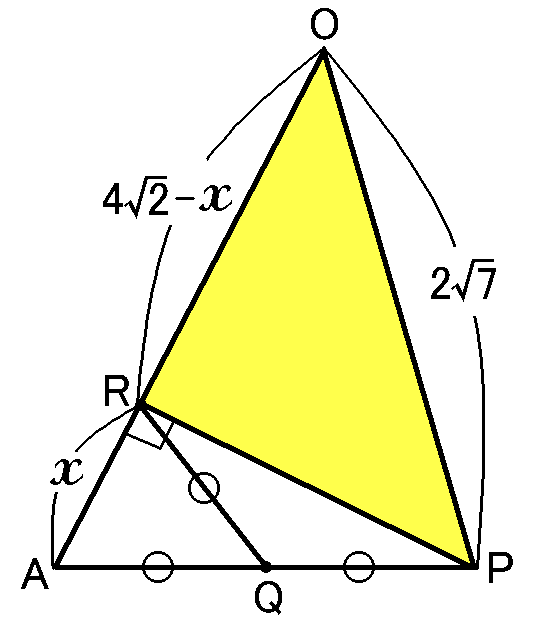
また、$AR=x$とすると、$OR=OA-x$となります。
$\triangle ORP$は$\angle ORP=90^{ \circ }$の直角三角形なので、三平方の定理より、
\begin{eqnarray*}
(PR)^2&=&(OP)^2-(OR)^2\\
&=&(OP)^2-(OA-x)^2\\
&=&(2\sqrt{7})^2-(4\sqrt{2}-x)^2\\
&=&28-(32-8\sqrt{2}x+x^2)\\
&=&28-32+8\sqrt{2}x-x^2\\
&=&-4+8\sqrt{2}x-x^2
\end{eqnarray*}
これで$(PR)^2$を$x$をもちいた2通りの式であらわすことができました。ならべてかくとこうなります。
$(PR)^2=20-x^2$
$(PR)^2=-4+8\sqrt{2}x-x^2$
どちらの式も左辺が$(PR)^2$なので、じゃあ右辺も等しいだろうということで、
$$20-x^2=-4+8\sqrt{2}x-x^2$$
こういう式ができます。これを解きます。
\begin{eqnarray*}
20-x^2&=&-4+8\sqrt{2}x-x^2\\
-x^2+x^2-8\sqrt{2}x&=&-4-20\\
-8\sqrt{2}x&=&-24\\
x&=&\cfrac{24}{8\sqrt{2}}=\cfrac{3}{\sqrt{2}}=\cfrac{3\sqrt{2}}{2}
\end{eqnarray*}
これで$x$がもとめられました。$x$というのは、$AR$のことです。
なので$AR=\cfrac{3\sqrt{2}}{2}(cm)$