数学 入試過去問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
【2009年の大問8】
1辺が$4cm$の正三角形$ABC$を底面とし、側面がすべて正方形の三角柱$ABCDEF$
辺$AC$の中点を$G$とし、線分$EG$の中点を$H$とする
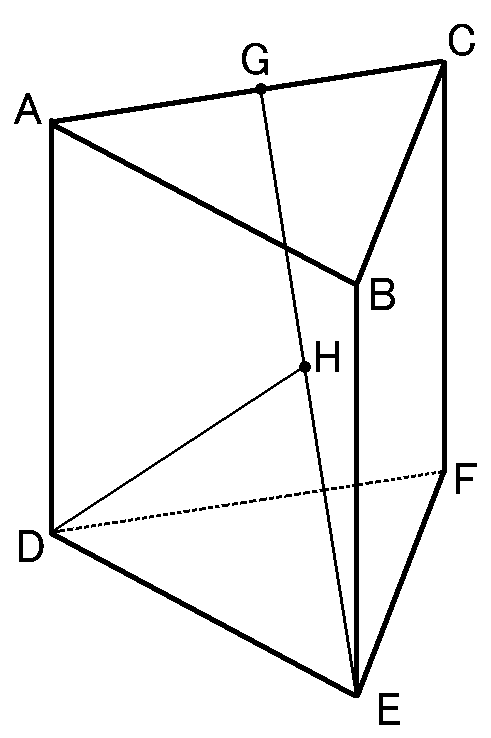
(1) 三角柱$ABCDEF$の体積
答え
$16\sqrt{3}cm^3$
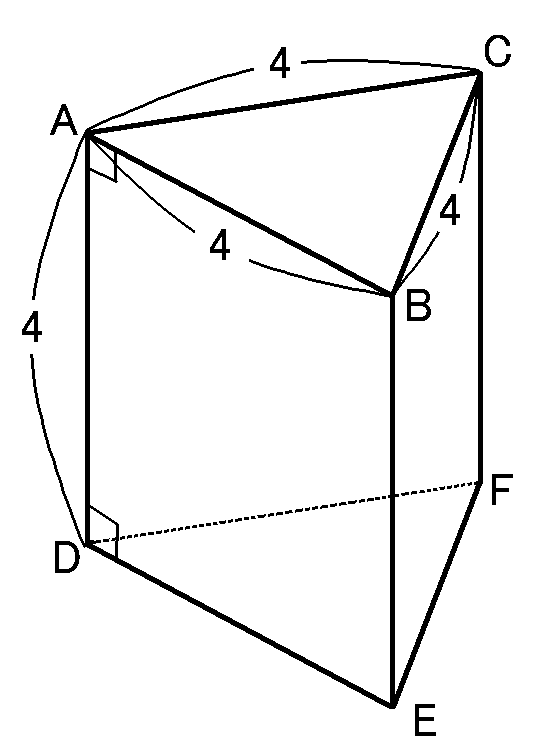 三角柱の体積は底面積$\times$高さです。
三角柱の体積は底面積$\times$高さです。
仮定から、高さは$4cm$です。
底面の$\triangle ABC$は1辺$4cm$の正三角形です。
三角形の面積は、底辺$\times$高さ$\times\cfrac{1}{2}$です。
$\triangle ABC$の、$C$から$AB$におろした垂線と$AB$との交点を$M$とします。
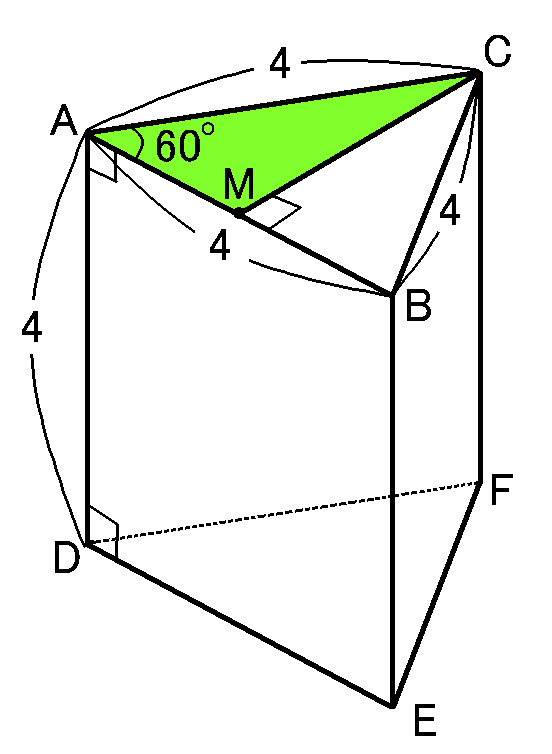 すると$\triangle AMC$は、正三角形の1つの内角は$60^{ \circ }$だから$\angle CAM=60^{ \circ },$$\angle CMA=90^{ \circ }$の直角三角形となって、$1:2:\sqrt{3}$の辺の比が使えることになります。
すると$\triangle AMC$は、正三角形の1つの内角は$60^{ \circ }$だから$\angle CAM=60^{ \circ },$$\angle CMA=90^{ \circ }$の直角三角形となって、$1:2:\sqrt{3}$の辺の比が使えることになります。
$\triangle AMC$で、
\begin{eqnarray*}
CA:CM&=&2:\sqrt3 \\
4:CM&=&2:\sqrt3 \\
CM\times2&=&4\times\sqrt{3}\\
CM&=&2\sqrt{3}\\
\end{eqnarray*}
 なので$\triangle ABC$の面積は、
\begin{eqnarray*}
&&底辺\times高さ\times\cfrac{1}{2}\\
&=&4\times2\sqrt{3}\times\cfrac{1}{2}\\
&=&4\sqrt{3}cm^2
\end{eqnarray*}
なので三角柱$ABCDEF$の体積は、
\begin{eqnarray*}
&&底面積\times高さ\\
&=&4\sqrt{3}\times4\\
&=&16\sqrt{3}cm^3
\end{eqnarray*}
なので$\triangle ABC$の面積は、
\begin{eqnarray*}
&&底辺\times高さ\times\cfrac{1}{2}\\
&=&4\times2\sqrt{3}\times\cfrac{1}{2}\\
&=&4\sqrt{3}cm^2
\end{eqnarray*}
なので三角柱$ABCDEF$の体積は、
\begin{eqnarray*}
&&底面積\times高さ\\
&=&4\sqrt{3}\times4\\
&=&16\sqrt{3}cm^3
\end{eqnarray*}
(2) 線分$DH$の長さ
答え
$\sqrt{11}cm$
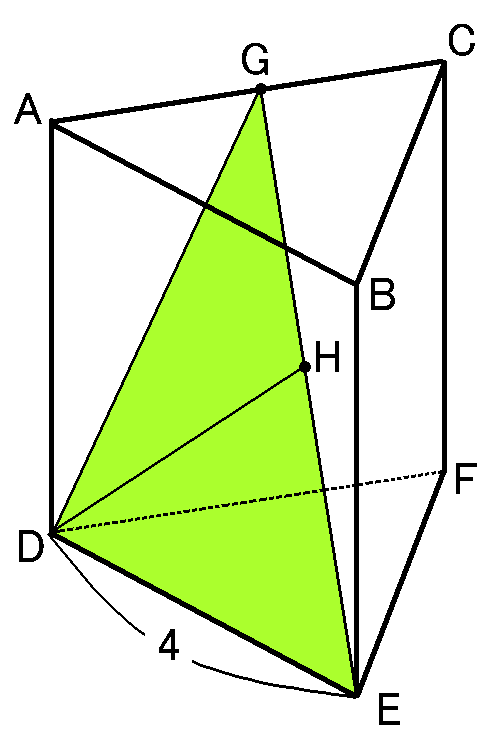
$G$と$D$をむすんで、$\triangle GDE$で考えます。まず、この三角形の3辺の長さをもとめましょう。
仮定から、$DE=4cm$です。
$GD$は、$\triangle GAD$で求められます。
$\triangle GAD$は、$AD=4cm,$$AG=2cm,$$\angle GAD=90^{ \circ }$の直角三角形ですから、三平方の定理より、

\begin{eqnarray*}
(GD)^2&=&(AD)^2+(AG)^2\\
&=&4^2+2^2\\
&=&20\\
GD>0なので\\
GD&=&\sqrt{20}=2\sqrt{5}cm
\end{eqnarray*}
$GE$は、$\triangle GBE$で求められます。$G$と$B$をむすびます。面$ABC \perp BE$ですから、$\triangle GBE$は$\angle GBE=90^{ \circ }$の直角三角形です。また、
仮定から、$BE=4cm$です。
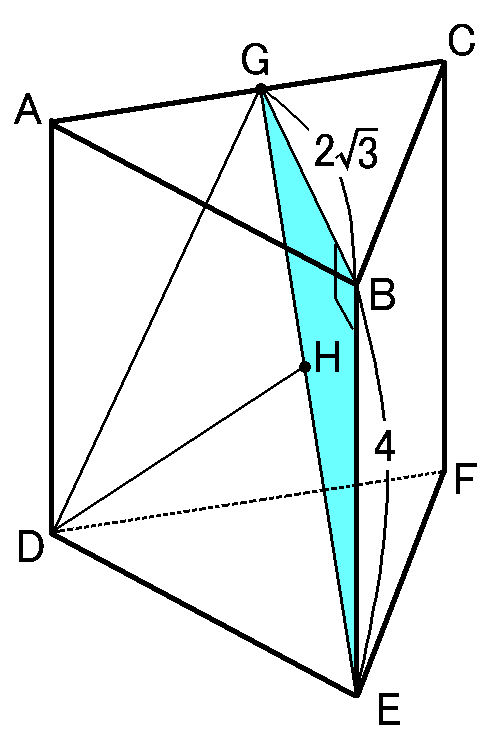
あと、$BG$は、$\triangle ABC$で$AC$を底辺としたときの高さになっているので、これは(1)の問題で求めた$CM$の長さとおなじことです。
なので$BG=2\sqrt{3}cm$です。というわけで$\triangle GBE$において三平方の定理より、
\begin{eqnarray*}
(GE)^2&=&(BE)^2+(BG)^2\\
&=&4^2+(2\sqrt{3})^2\\
&=&28\\
GE>0なので\\
GE&=&\sqrt{28}=2\sqrt{7}cm
\end{eqnarray*}
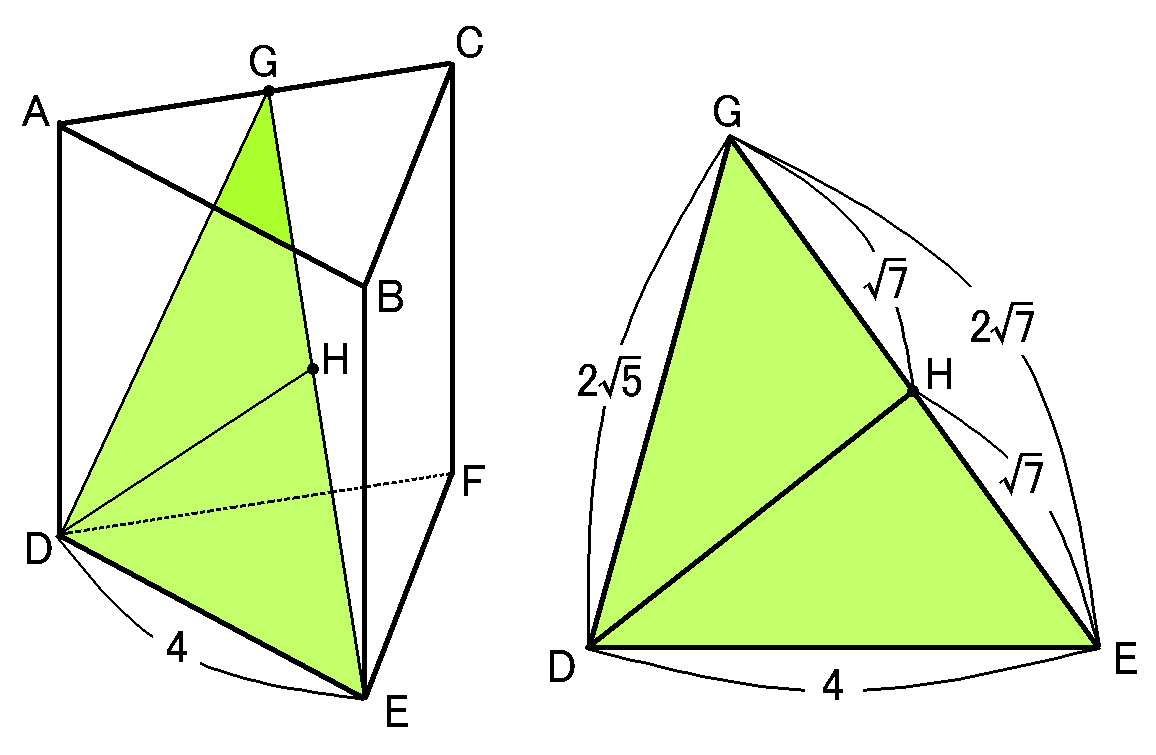
これで$\triangle GDE$の3辺の長さがわかりました。$GD=2\sqrt{5}cm,$$DE=4cm,$$GE=2\sqrt{7}cm$です。それと、$H$は$GE$の中点です。なので$GH=HE=\sqrt{7}cm$です。
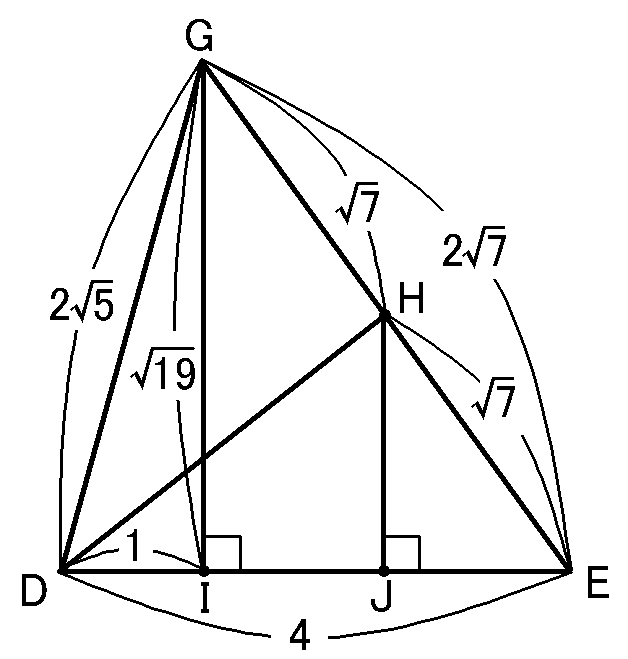
図をかくと、こんなかんじです。
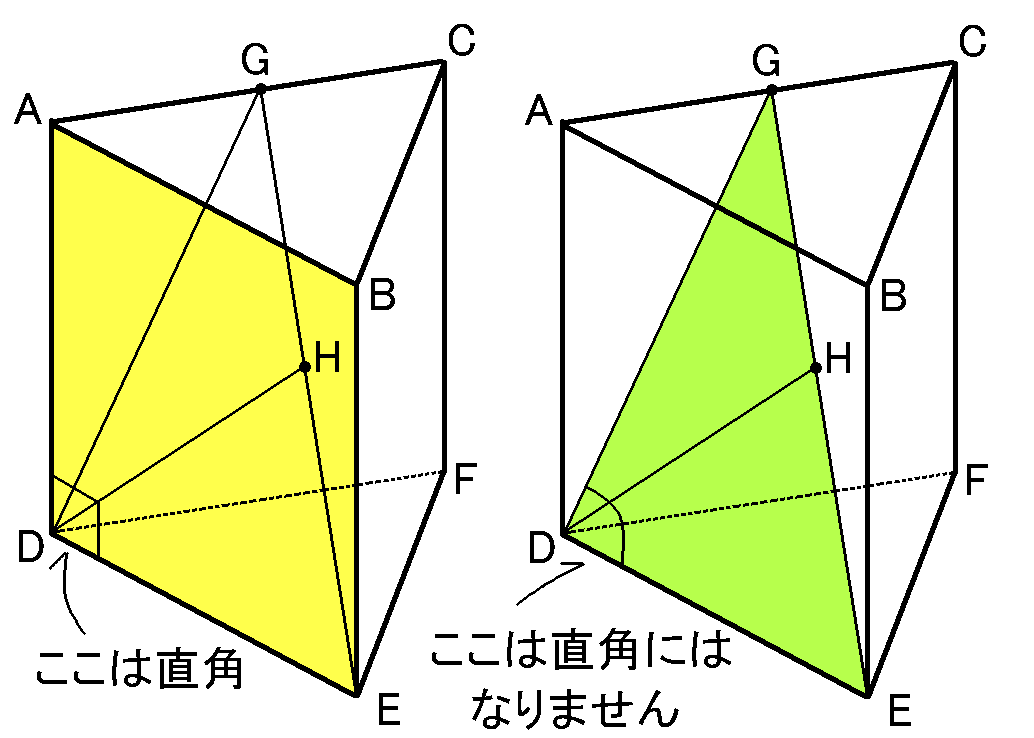
あと、ちょっと錯覚してしまうかもしれないのですが、
$\angle GDE$は直角ではありません。$\angle ADE$はたしかに直角なんですけど、$\angle GDE$は直角にはなりません。
三平方の定理の逆をやってみれば確認できます。$(2\sqrt{5})^2+4^2=36$です。$(2\sqrt{7})^2=28$です。なので$\angle GDE$は直角ではありません。
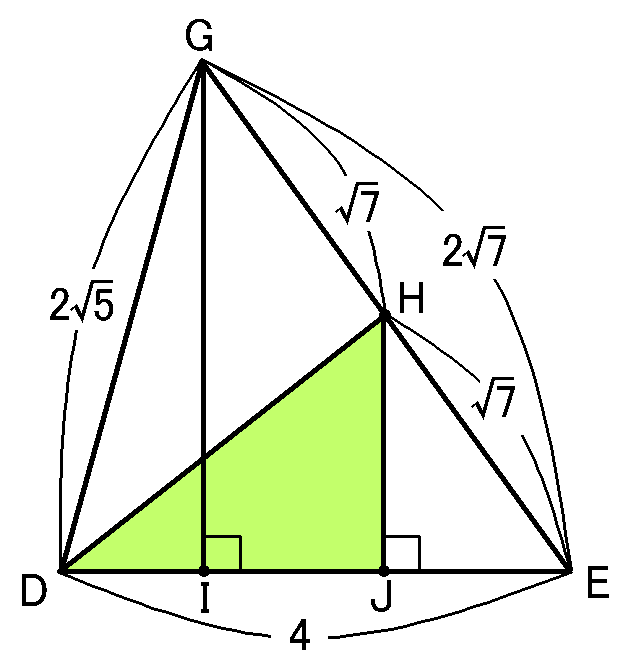
というわけで、$\triangle GDE$を使って$HD$の長さをもとめましょう。
ではどうやってもとめるか、という話なんですが、まず、頂点$G$と点$H$から辺$DE$に垂線をおろします。$DE$との交点をそれぞれ$I,J$ということにしましょう。
んで、$\triangle HDJ$という直角三角形の三平方の定理を利用して$HD$をもとめる、というだんどりです。
そのためには$HJ$と$DJ$の長さが必要です。
そのためには$GI$や$DI$や$IJ$の長さが必要になってきます。
まず、$DI$の長さをもとめていきます。
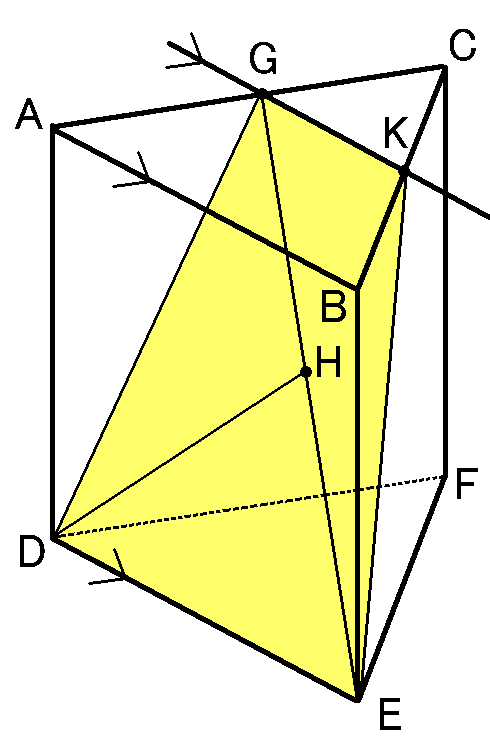
【$DI$の長さ】
いちばんさいしょの図にもどります。$\triangle ABC$の辺$BC$の中点を$K$として、$G$と$K$をむすびます。すると、$\triangle ABC$で中点連結定理により、
$GK /\!/ AB$となります。仮定から、$AB /\!/ DE$ですから、$GK /\!/ DE$になります。なので四角形$GDEK$は台形ということになります。
あと、$GD$と$EK$の長さについてかんがえます。
正方形$ADFC$上の$GD$の長さと、正方形$BEFC$上の$KE$の長さはおなじです。合同な正方形の1辺の中点から、むかいあう辺上の頂点にひいた線なので、長さはおなじです。$GD=2\sqrt{5}cm$だったので、$KE$の長さも$2\sqrt{5}cm$です。
四角形$GDEK$は等脚台形です。
また、$\triangle ABC$で中点連結定理により、$GK=\cfrac{1}{2}AB=2cm$です。
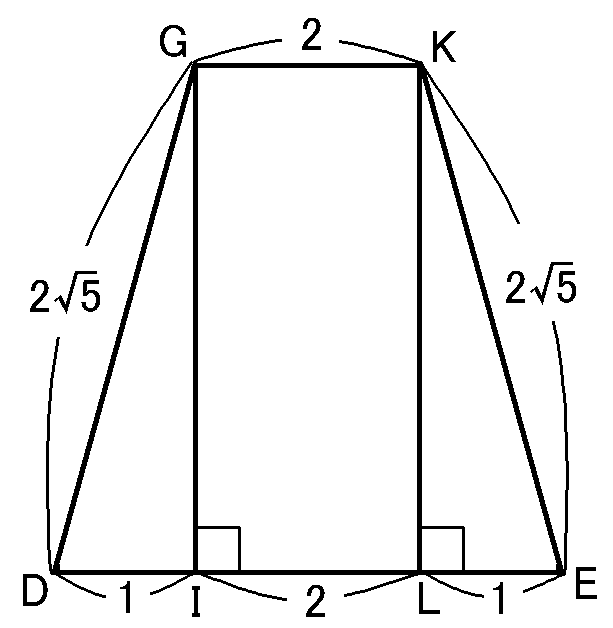
等脚台形$GDEK$で、$G,K$から$DE$におろした垂線と$DE$との交点をそれぞれ$I,L$とすると、$GK=IL=2cm$です。仮定から$DE=4cm$だったので、$DI=LE=1cm$ということになります。
こんなふうに考えれば、$DI$の長さがもとめられます。
もし、等脚台形$GDEK$を利用するのがおもいつかなかれば、$\triangle GDE$で、三平方の定理で$(GI)^2$の大きさを2通りの方法であらわしていくという、おなじみのやりかたでもいけます。
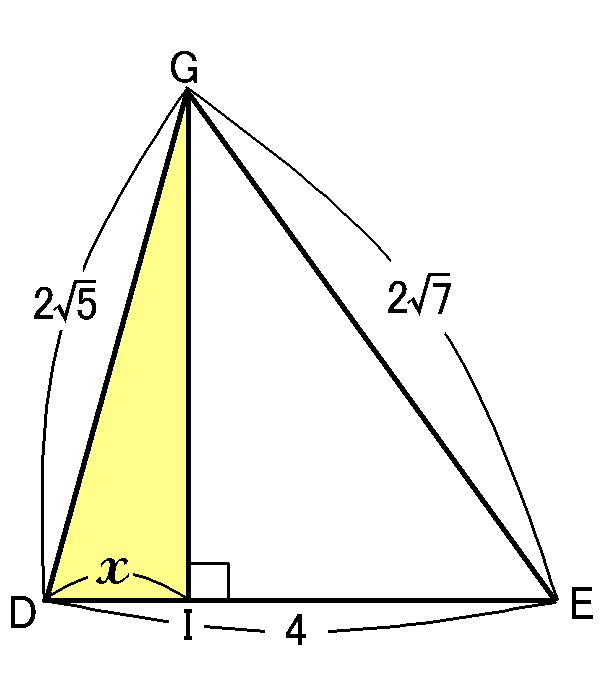
$\triangle GDE$で、$DI=xcm$とします。すると、$\triangle GDI$は$\angle GID=90^{ \circ }$の直角三角形ですから、三平方の定理より、
\begin{eqnarray*}
(GI)^2&=&(GD)^2-(DI)^2\\
&=&(2\sqrt{5})^2-x^2\\
\end{eqnarray*}
また、$\triangle GIE$は$\angle GIE=90^{ \circ }$の直角三角形ですから、三平方の定理より、
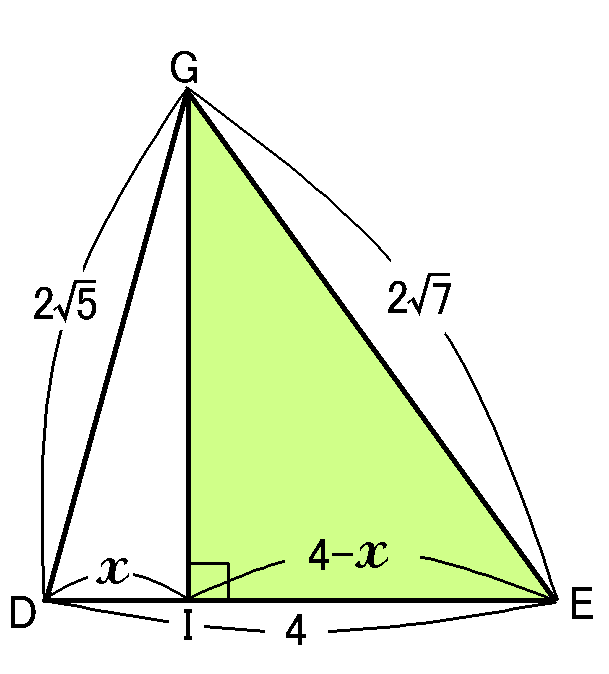
\begin{eqnarray*}
(GI)^2&=&(GE)^2-(IE)^2\\
&=&(2\sqrt{7})^2-(4-x)^2\\
\end{eqnarray*}
と、こんなふうに$(GI)^2$を2通りの$x$の式であらわして、
$(2\sqrt{5})^2-x^2=(2\sqrt{7})^2-(4-x)^2$
という方程式をたててこれを
解けば、$x=1cm$ともとめられます。ただ、このやりかたは計算が面倒です。
この問題の場合は、$DI$の長さをもとめるには、はじめに説明した等脚台形$GDEK$を利用するのがおすすめです。

【$GI$の長さ】
$DI=1cm$とわかったので、$\triangle GDI$で三平方の定理を使えば$GI$の長さがもとめられます。
$\triangle GDI$は$GD=2\sqrt{5},$$DI=1,$$\angle GID=90^{ \circ }$の直角三角形ですから、三平方の定理より、
\begin{eqnarray*}
(GI)^2&=&(GD)^2-(DI)^2\\
&=&(2\sqrt{5})^2-1^2\\
&=&19\\
GI>0なので\\
GI&=&\sqrt{19}cm
\end{eqnarray*}
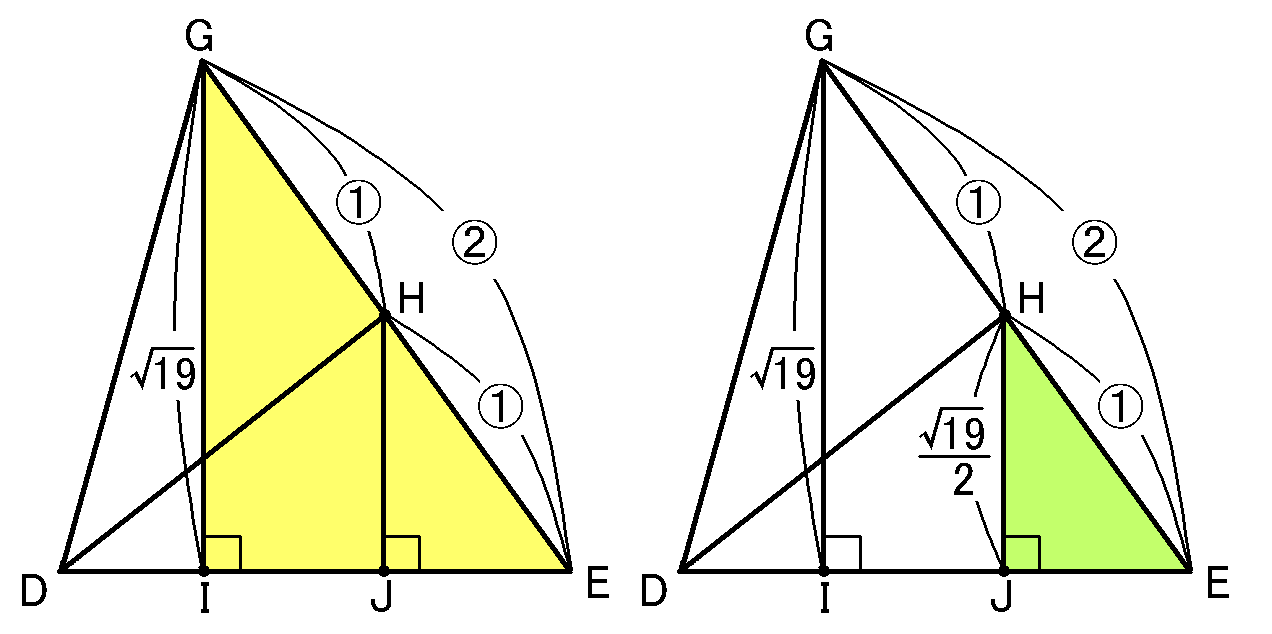
【$HJ$の長さ】
$H$というのは$GE$の中点で、$H$から$DE$におろした垂線と$DE$との交点を$J$ということにしています。
$GI$の長さがわかったので、相似な三角形を利用して$HJ$の長さをもとめていきます。
$\triangle GIE$ と$\triangle HJE$において、$\angle GIE=\angle HJE=90^{ \circ }$で、$\angle E$が共通ですから、2組の角が等しいので$\triangle GIE$ ∽$\triangle HJE$です。
また、仮定から、$GH=HE$ですから、$GE:HE=2:1$となるので、$\triangle GIE$と$\triangle HJE$の相似比は$2:1$です。
なので、$HJ=\cfrac{1}{2}GI=\cfrac{\sqrt{19}}{2}cm$です。
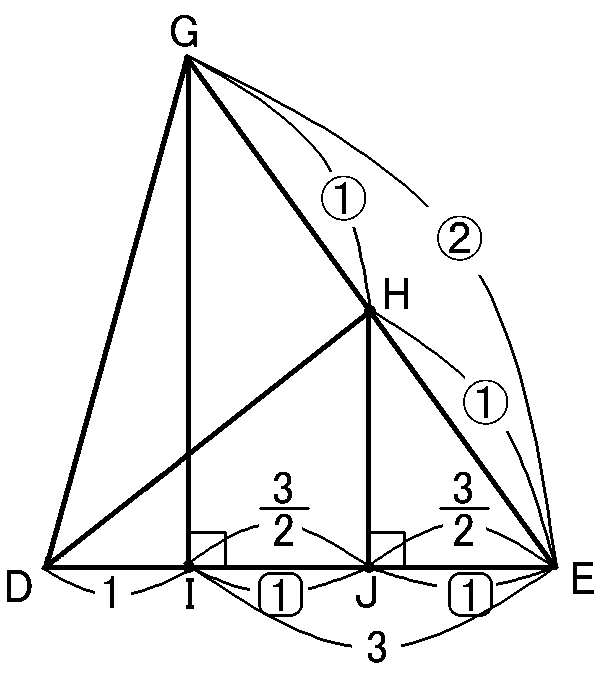
【$DJ$の長さ】
$\angle GIE=\angle HJE=90^{ \circ }$ですから、同位角が等しいので$GI /\!/ HJ$です。平行線と線分の比の定理から、
$GH:HE=IJ:JE=1:1$です。
$J$は$IE$の中点ということです。
また、$DE=4cm,$$DI=1cm$なので、$IE=4-1=3cm$です。
なので、$IJ=\cfrac{1}{2}IE=\cfrac{3}{2}cm$となります。
なので、$DJ=DI+IJ=1+\cfrac{3}{2}=\cfrac{5}{2}cm$です。
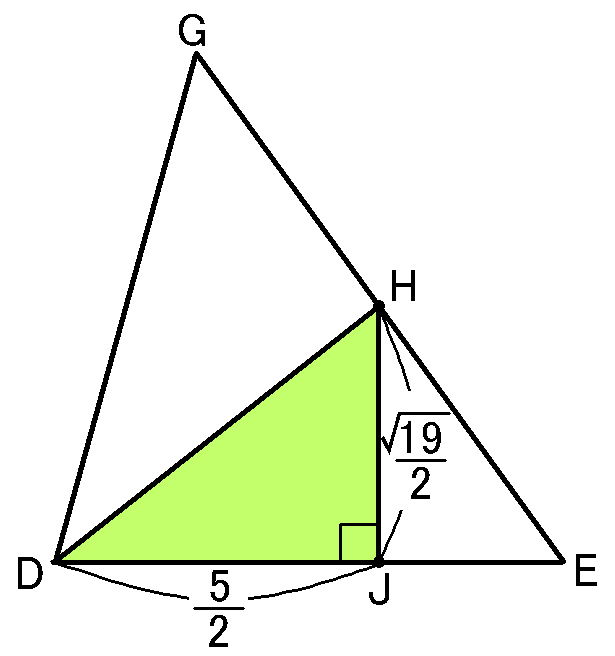
【$DH$の長さ】
$\triangle HDJ$は$DJ=\cfrac{5}{2},$$HJ=\cfrac{\sqrt{19}}{2},$$\angle HJD=90^{ \circ }$の直角三角形ですから、三平方の定理より、
\begin{eqnarray*}
(DH)^2&=&(DJ)^2+(HJ)^2\\
&=&\left(\cfrac{5}{2}\right)^2+\left(\cfrac{\sqrt{19}}{2}\right)^2\\
&=&\cfrac{25}{4}+\cfrac{19}{4}=11\\
DH>0なので\\
DH&=&\sqrt{11}cm
\end{eqnarray*}