数学 入試過去問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
【2010年の大問8】
1辺が$4cm$の正三角形$ABC$を底面とし、$OA=OB=OC=8cm$の正三角すい$OABC$
辺$OB$上に点$P$をとる
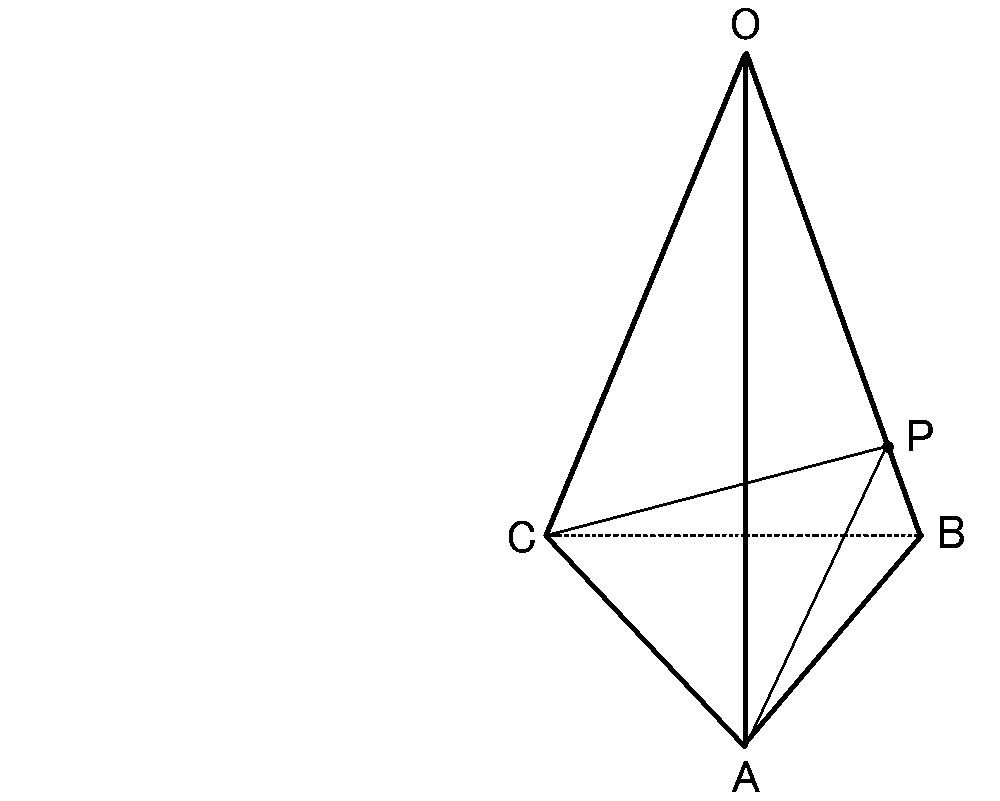
(1) $\triangle OAC$の面積
答え
$4\sqrt{15}cm^2$
 三角形の面積は底辺$\times$高さ$\times \cfrac{1}{2}$です。
三角形の面積は底辺$\times$高さ$\times \cfrac{1}{2}$です。
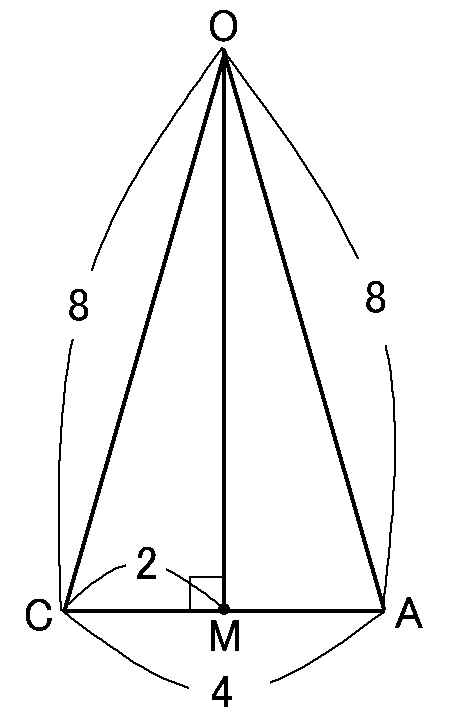
$\triangle OAC$は$CA=4cm,$$OA=OC=8cm$の二等辺三角形です。
$O$から$CA$におろした垂線と$CA$との交点を$M$とすると、$\triangle OCM \equiv \triangle OAM$です。理由は、「直角三角形の斜辺と他の1辺」でも
「直角三角形の斜辺と1鋭角」でも、どっちでもいけます。合同です。
なので、$M$は$CA$の中点になります。
なので$CM=2cm$です。
$\triangle OCM$は、$OC=8cm,$$CM=2cm,$$\triangle OMC=90^{ \circ }$の直角三角形ですから、三平方の定理より、
\begin{eqnarray*}
(OM)^2&=&(OC)^2-(CM)^2\\
&=&8^2-2^2\\
&=&60\\
OM>0なので\\
OM&=&\sqrt{60}=2\sqrt{15}cm
\end{eqnarray*}
なので、$\triangle OAC$の面積は、
\begin{eqnarray*}
&&底辺\times高さ\times\cfrac{1}{2}\\
&=&CA\times OM\times\cfrac{1}{2}\\
&=&4\times2\sqrt{15}\times\cfrac{1}{2}\\
&=&4\sqrt{15}cm^2\\
\end{eqnarray*}
(2) $AP+PC$の長さをもっとも短くしたとき、4点$P,A,B,C$を頂点とする立体の体積
答え
$\cfrac{2\sqrt{11}}{3}(cm^3)$
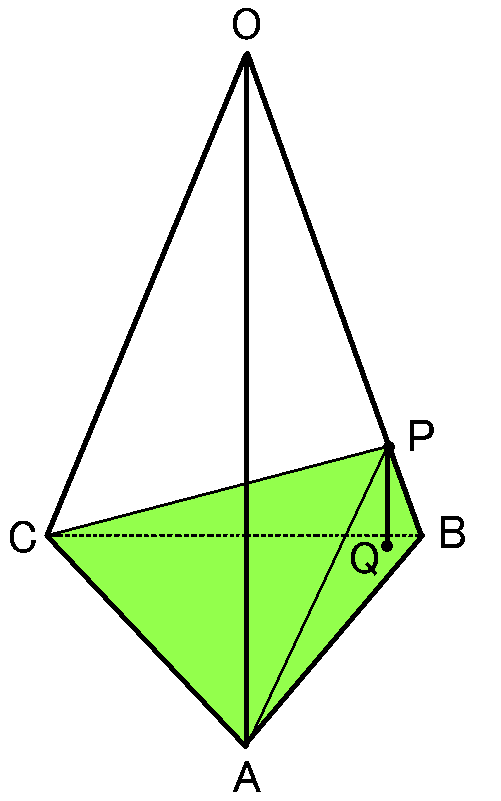
4点$P,A,B,C$を頂点とする立体というのは三角すいになります。三角すいの体積は、底面積$\times$高さ$\times\cfrac{1}{3}$です。
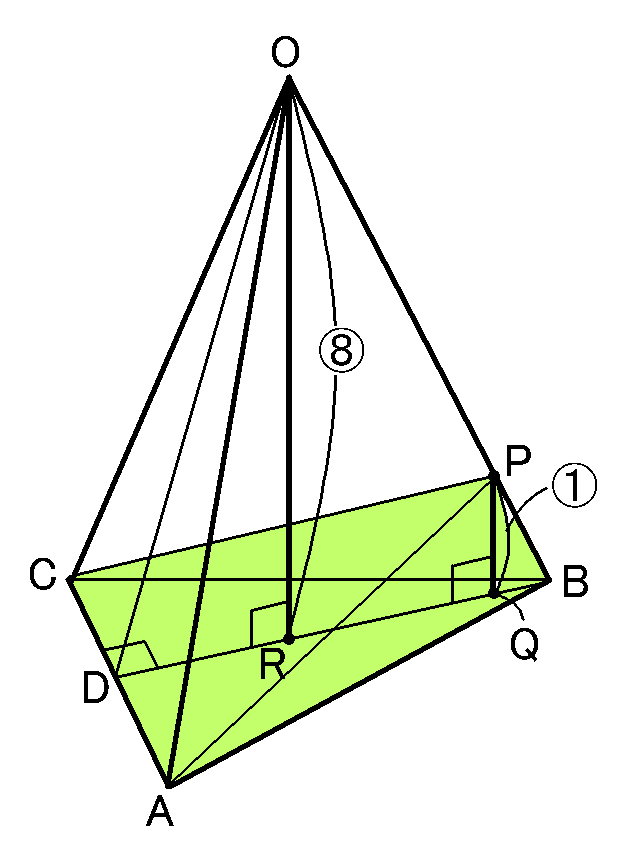
底面を$\triangle ABC$とします。$P$からこの面にまっすぐにおろした線とこの面との交点を$Q$とします。$PQ$がこの三角すいの高さになります。
底面の$\triangle ABC$は、1辺の長さがわかっている正三角形なので、面積はすぐにでます。あと、高さ$PQ$の長さがわかればこの問題はOKです。
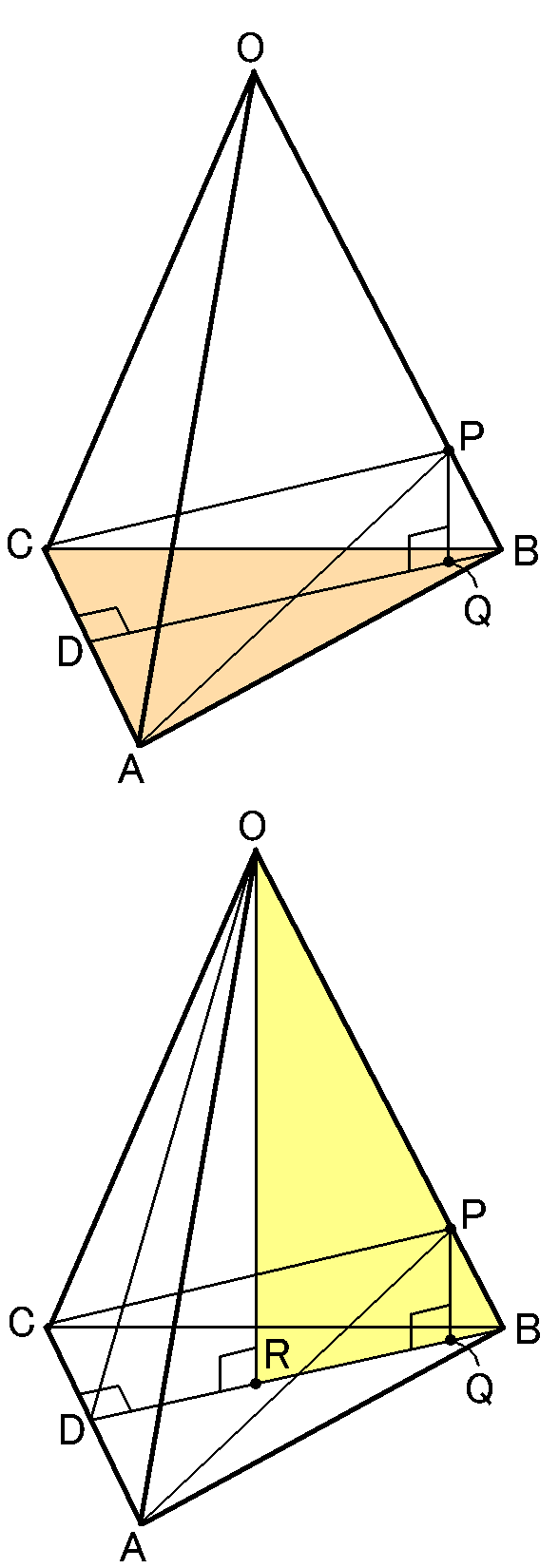
では$PQ$の長さはどう考えればよいのでしょうか。
底面の$\triangle ABC$で、$B$から$AC$におろした垂線と$AC$との交点を$D$とします。すると、$Q$は$BD$上にあるはすです。
3点$O,B,D$を通る平面でこの三角すいを切って、その断面図を考えます。$PQ \perp DB$です。また、$O$から$BD$に垂線をおろして、$BD$との交点を
$R$とすると、2組の角がそれぞれ等しいので、$\triangle ORB$ ∽$\triangle PQB$です。この相似をつかえば、$PQ$の長さは求められそうです。
相似比はどうやって求めるか、ですが、$OB$がもうわかっているので、あと$PB$の長さを求めることができれば、ここで相似比がだせそうです。
$PB$の長さを求めるためにはまず、$P$が$OB$上のどこを通るかがわかっていなくてはなりません。
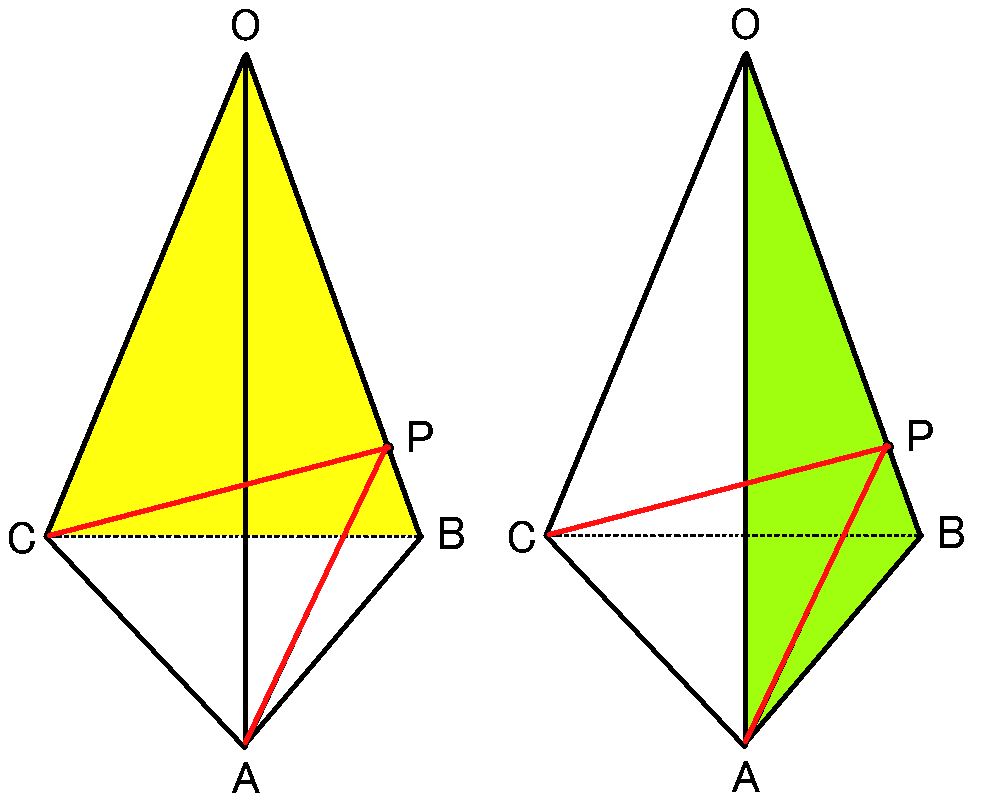
【$PB$の長さ】
$AP+PC$の長さがもっとも短くなるときというのは、展開図で考えます。
$AP+PC$に関係がある面は、$\triangle OCB$と$\triangle OAB$です。
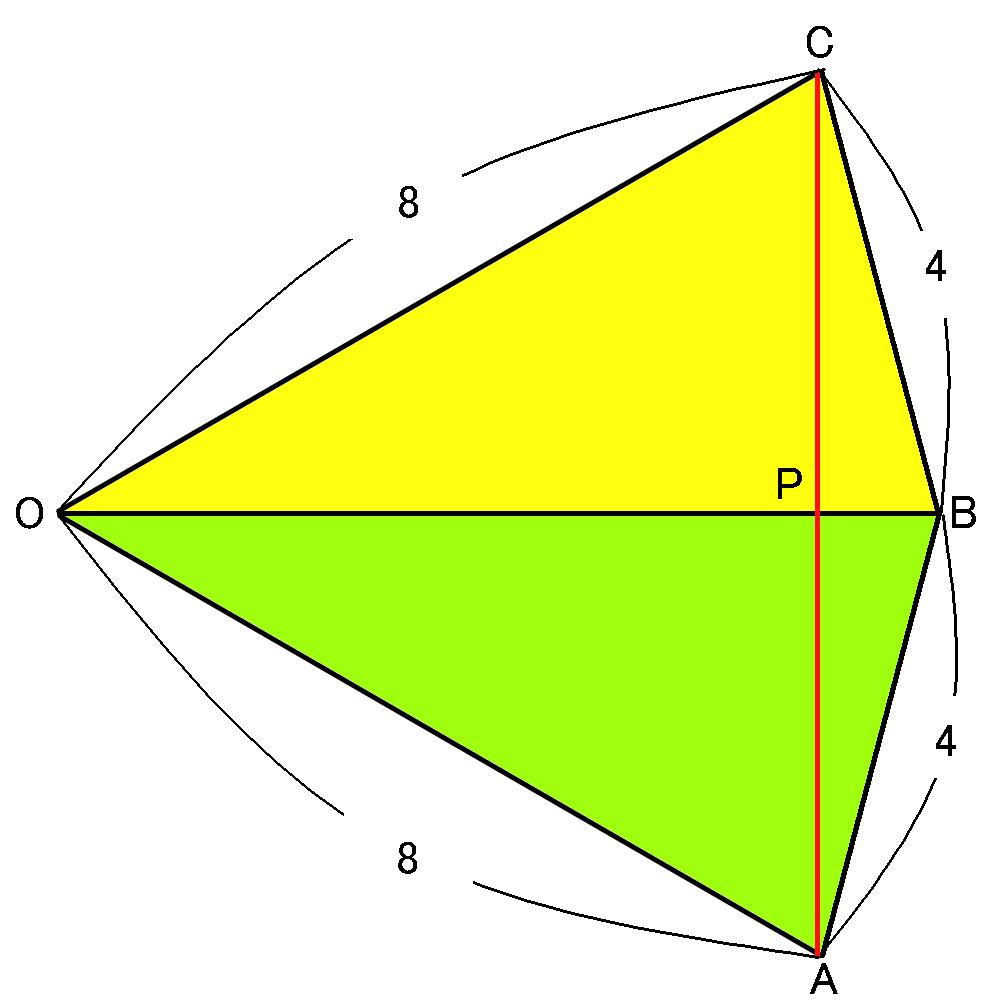
この部分を展開すると、図のようになります。
$AP+PC$の長さがもっとも短くなるときというのはもちろん、$A$と$C$をまっすぐにむすんだときです。
立体$OABC$は正三角すいだったので、$\triangle OCB$と$\triangle OAB$は合同です。なので、$\angle AOB= \angle COB$です。
$\triangle OAC$は、$OA=OC$の二等辺三角形です。二等辺三角形の頂角の二等分線は底辺を垂直に二等分するので、$OB \perp AC$となります。
…とまあ、いろいろ説明しましたが、四角形$OABC$のようなのをタコ型といって、タコ型の対角線は垂直に交わるというのをしっていると、話がはやいです。
タコ型というのは、四角形$OABC$でいうと、$OC=OA,$$BC=BA$みたいになってるカタチです。対角線垂直です。
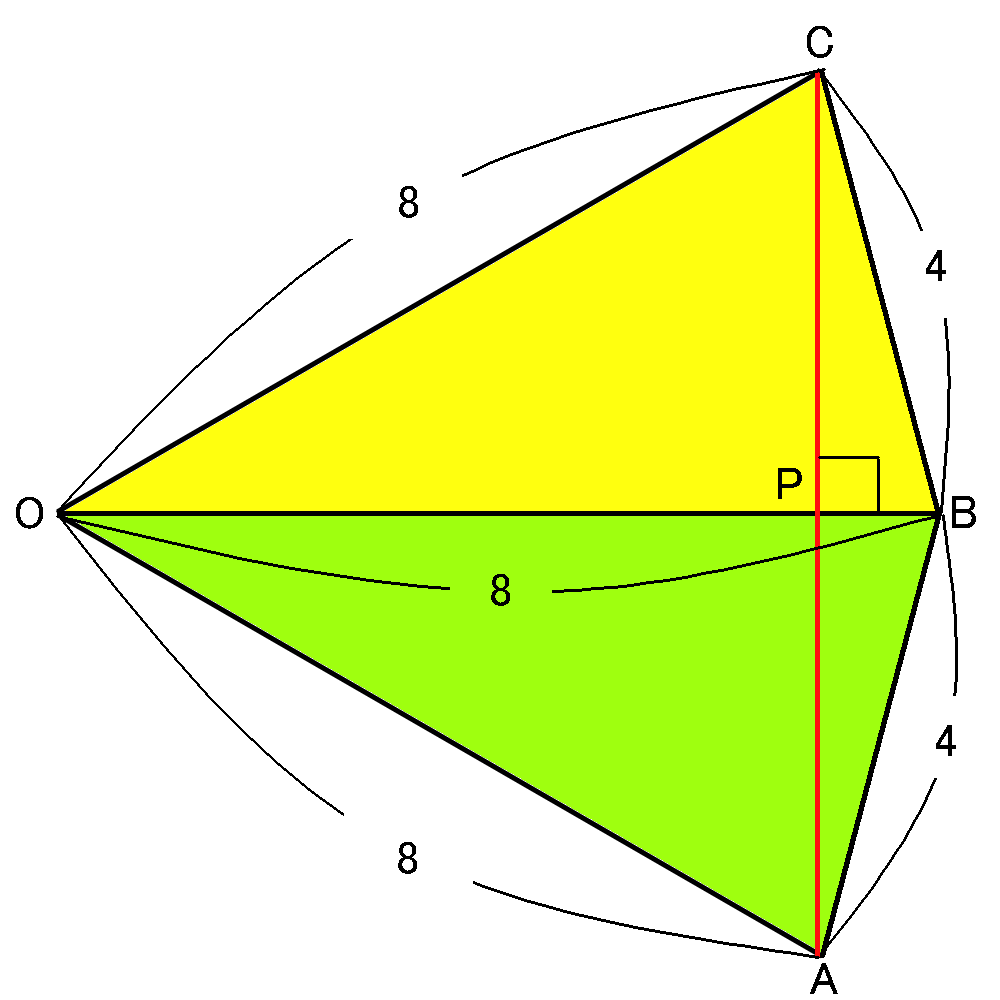
ところで、(1)の問題で、この三角すいの側面の面積を求めています。$4\sqrt{15}cm^2$です。なので、展開図の$\triangle COB$の面積も$4\sqrt{15}cm^2$です。
これを利用して、$CP$を求めることができます。三角形の面積は底辺$\times$高さ$\times\cfrac{1}{2}$ですから、$\triangle COB$で、$OB$を底辺とすると、
\begin{eqnarray*}
OB\times CP\times\cfrac{1}{2}&=&4\sqrt{15}\\
8\times CP\times\cfrac{1}{2}&=&4\sqrt{15}\\
4\times CP&=&4\sqrt{15}\\
CP&=&\sqrt{15}cm
\end{eqnarray*}
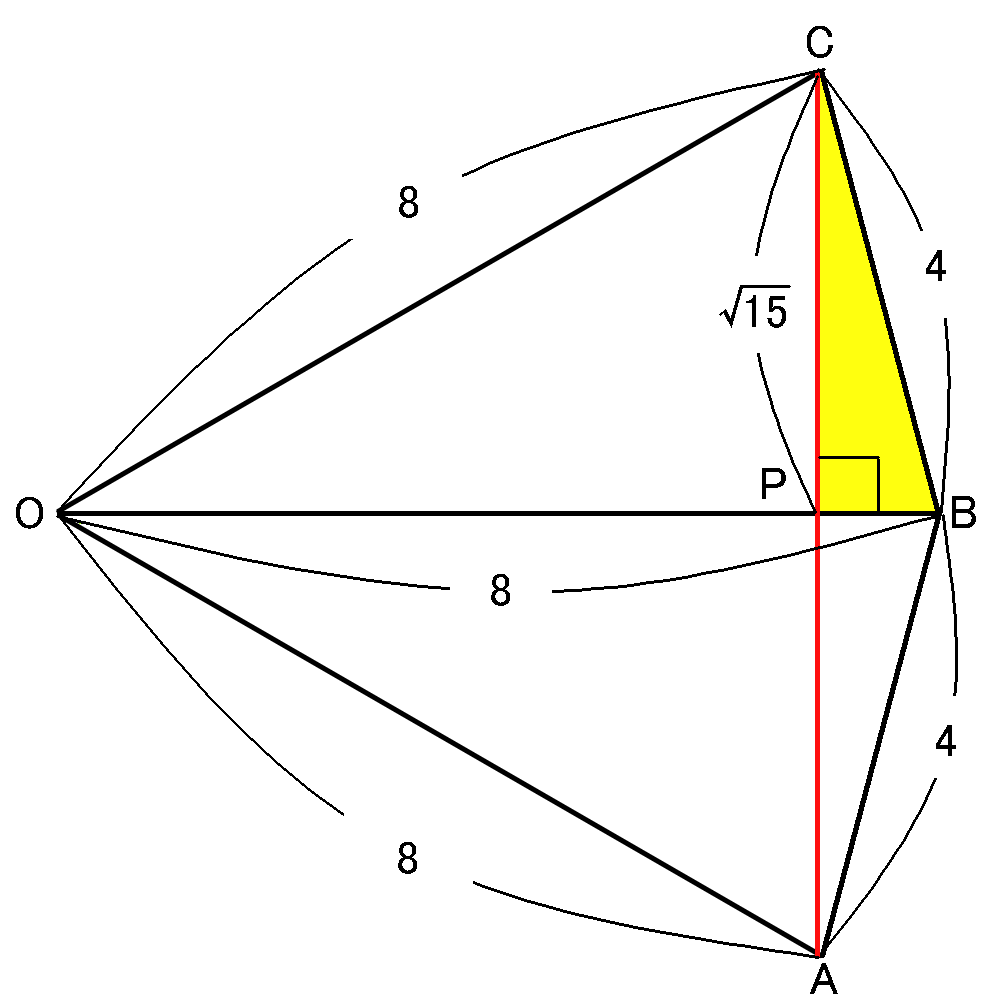
すると$\triangle CPB$は、$CB=4cm,$$CP=\sqrt{15}cm,$$\angle CPB=90^{ \circ }$の直角三角形ということになって、三平方の定理より、
\begin{eqnarray*}
(PB)^2&=&(CB)^2-(CP)^2\\
&=&4^2-(\sqrt{15})^2\\
&=&1\\
PB>0なので\\
PB&=&\sqrt{1}=1cm
\end{eqnarray*}
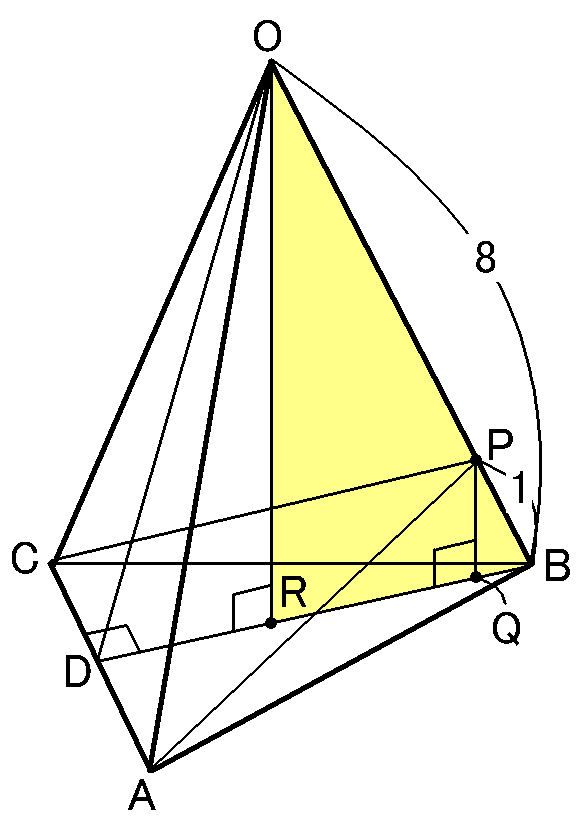
これで$PB=1cm$だとわかりました。この長さを、$\triangle ORB$ ∽$\triangle PQB$にもってきます。
仮定から、$OB=8cm$ですから、$\triangle ORB$と$\triangle PQB$の相似比は、$OB:PB=8:1$となります。
つぎに$OR$の長さを求めていきます。これは$\triangle ORB$で三平方の定理を使います。そのために、$RB$の長さが必要です。

【$RB$の長さ】
$R$というのは、頂点$O$から底面の$\triangle ABC$にまっすぐおろした垂線です。では、この$R$は、$\triangle ABC$で、どういう点になっているのでしょうか。
$R$というのは、$\triangle ABC$の$BD$上にあるはずです。さらにいうと、$\triangle ABC$の、$A$から$BC$におろした垂線の上にもあるはずです。さらに、$C$から$AB$におろした垂線の上にもあるはずです。
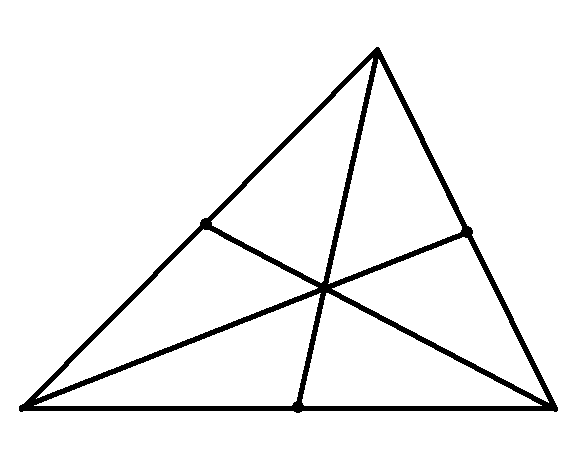
この状態を、つまり、底面の三角形に3本の中線をひいた状態を、三角すいの真上から見ると、こんなふうに見えるはずです。中線というのは、三角形のひとつの頂点から、むかいあう辺の中点にひいた線です。それを3本ひいて、真上からみると、こんなふうになるはずです。
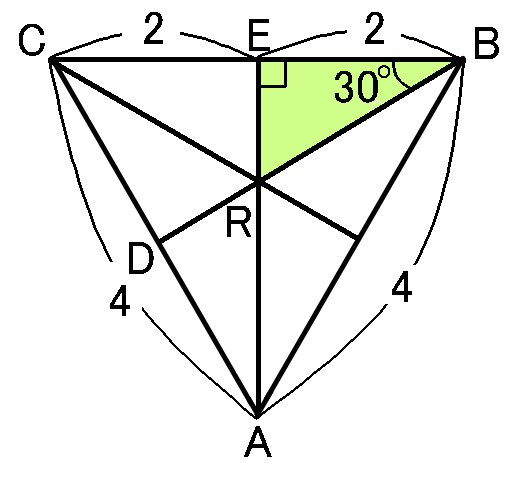
$A$から$BC$におろした垂線と$BC$との交点を$E$とします。んで、$\triangle BER$に着目します。
$BD$は$\angle ABC$の二等分線ですから、$\angle EBR=30^{ \circ }$です。正三角形のひとつの内角は$60^{ \circ }$で、$\angle EBR$はその半分だからです。
あと、$\triangle BER=90^{ \circ }$です。
すると$\triangle BER$は、$30^{ \circ },$$60^{ \circ },$$90^{ \circ }$の直角三角形となって、$1:2:\sqrt{3}$の辺の比が使えることになります。
$\triangle BER$で、
\begin{eqnarray*}
RB:EB&=&2:\sqrt3 \\
RB:2&=&2:\sqrt3 \\
\sqrt3 \times RB&=&2\times2\\
RB&=&\cfrac{4}{\sqrt{3}}=\cfrac{4\sqrt{3}}{3}\\
\end{eqnarray*}
ちなみに$\triangle ABC$の$R$みたいな点を「三角形の重心」といいます。三角形の3本の中線は、1点で交わります。たとえ正三角形でなくても、3本の中線は、一点で交わるんです。そこを三角形の重心といって、中線を$2:1$の比にわけます。このことを知っていて、$R$は$\triangle ABC$の重心になってるなあ、と気がつくと話がはやかったです。
1辺が$4cm$の正三角形$\triangle ABC$の高さをだして、それに$\cfrac{2}{3}$をかければOKでした。
ともかくこれで$RB$の長さがわかったので、$\triangle ORB$で三平方の定理から、$OR$の長さを求めていきます。
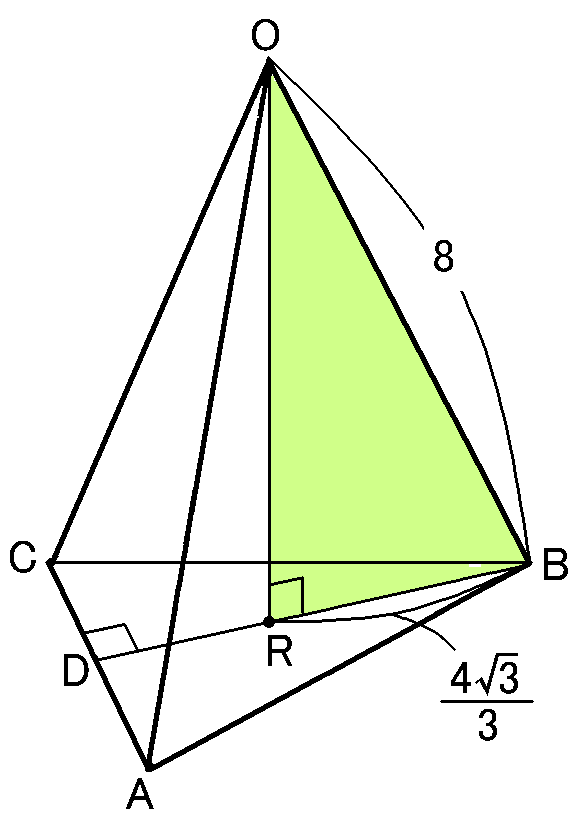
【$OR$の長さ】
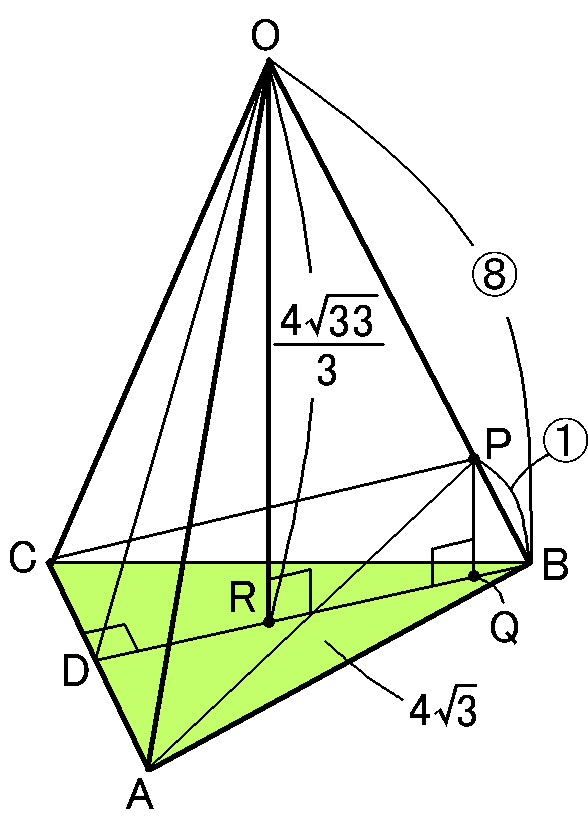
$\triangle ORB$は、$OB=8cm,$$RB=\cfrac{4\sqrt{3}}{3}cm,$$\angle ORB=90^{ \circ }$の直角三角形ですから、三平方の定理より、
\begin{eqnarray*}
(OR)^2&=&(OB)^2-(RB)^2\\
&=&8^2-\left(\cfrac{4\sqrt{3}}{3}\right)^2\\
&=&64-\cfrac{16}{3}=\cfrac{176}{3}\\
OR>0なので\\
OR&=&\sqrt{\cfrac{176}{3}}=\cfrac{4\sqrt{11}}{\sqrt{3}}=\cfrac{4\sqrt{33}}{3}cm
\end{eqnarray*}
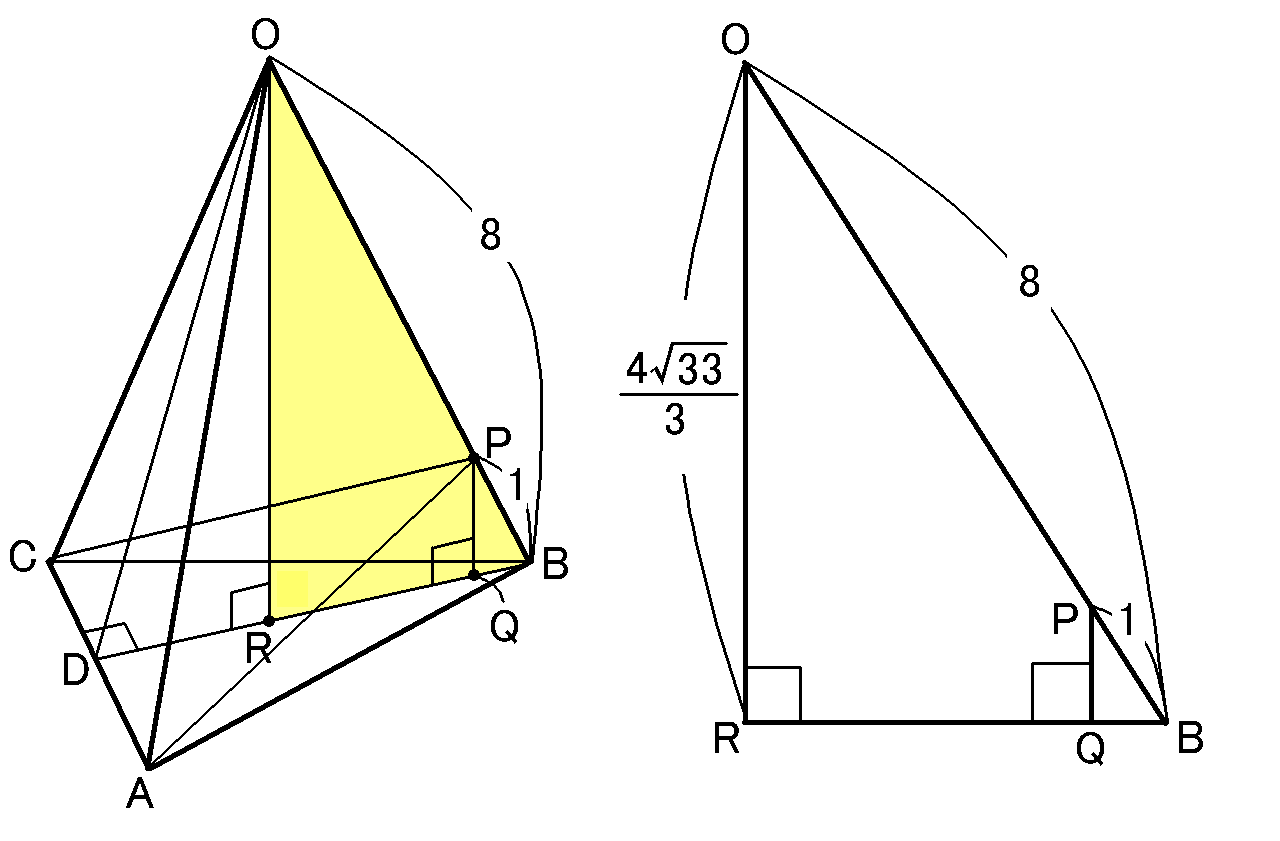
これで$OR$の長さがわかったので、$\triangle ORB$ ∽$\triangle PQB$で、相似比が$8:1$なことを使えば$PQ$の長さが求まります。
……。
いやちょっと待てよ。これ、三角すい$OABC$と三角すい$PABC$というのは、底面が共通で、高さの比が$8:1$なのだから、
体積の比も$8:1$になるはず。じゃあ$PQ$の長さを求めなくても、このまま三角すい$OABC$の体積をだして、それを$\cfrac{1}{8}$倍すればよいわけですよね。
三角すいの体積は、底面積$\times$高さ$\times\cfrac{1}{3}$です。三角すい$OABC$の高さ$OR$の長さはもうわかっています。
じゃあ、底面の$\triangle ABC$の面積を求めましょう。

【$\triangle ABC$の面積】
$\triangle ABC$は1辺が$4cm$の正三角形です。んで、$BD \perp AC$です。すると$\triangle BAD$は、$30^{ \circ },$$60^{ \circ },$$90^{ \circ }$の直角三角形となって、$1:2:\sqrt{3}$の辺の比が使えることになります。
$\triangle BAD$で、
\begin{eqnarray*}
AD:BD&=&1:\sqrt3 \\
2:BD&=&1:\sqrt3 \\
BD&=2\sqrt{3}\\
\end{eqnarray*}
なので$\triangle ABC$の面積は、
\begin{eqnarray*}
&&底辺\times高さ\times\cfrac{1}{2}\\
&=&4\times2\sqrt{3}\times\cfrac{1}{2}\\
&=&4\sqrt{3}cm^2
\end{eqnarray*}
【三角すい$PABC$の体積】
というわけで、
\begin{eqnarray*}
&&三角すいPABCの体積\\
&=&三角すいOABCの体積\times\cfrac{1}{8}\\
&=&\triangle ABCの面積\times OR\times\cfrac{1}{3}\times\cfrac{1}{8}\\
&=&4\sqrt{3}\times\cfrac{4\sqrt{33}}{3}\times\cfrac{1}{3}\times\cfrac{1}{8}\\
&=&\cfrac{2\times\sqrt{3}\times\sqrt{33}}{9}\\
&=&\cfrac{2\sqrt{11}}{3}(cm^3)\\
\end{eqnarray*}
もちろん相似を使って$PQ$の長さをだして、底面積$\times$高さ($PQ$)$\times\cfrac{1}{3}$とやってもぜんぜんOKです。手間もたいしてかわりません。
ただ、三角すい$OABC$の体積$\times\cfrac{PB}{OB}$とやると、三角すい$PABC$の体積になっている、みたいなパターンは、さらに応用された問題が出たりします。
なのでこの考え方はおぼえておきたいところです。
この問題の解説は以上です。あと、とちゅうででてきた重心についてちょっと。
【三角形の重心のこと】
三角形の3本の中線は1点で交わります。その交わった点を「三角形の重心」といって、それぞれの中線を$2:1$にわけます。なぜそういえるのかの説明です。
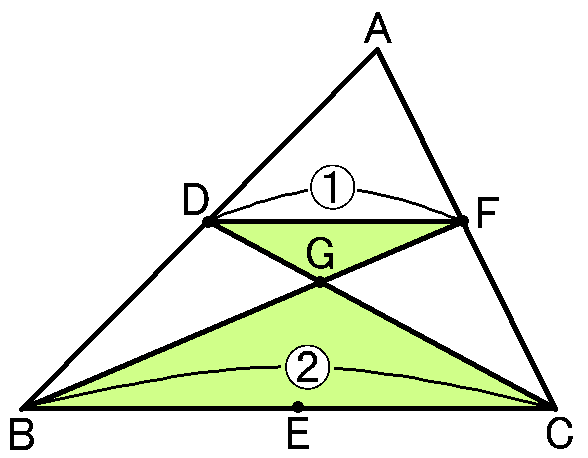
$\triangle ABC$の辺$AB,BC,CA$の中点をそれぞれ$D,E,F$とします。
まず、$B$と$F,C$と$D$をむすんで、$BF$と$CD$の交点を$G$とします。中点連結定理により、$DF /\!/ BC$,$DF=\cfrac{1}{2}BC$です。
$DF /\!/ BC$なのだから、$\triangle GBC$ ∽$\triangle GFD$で、相似比は$BC:FD=2:1$です。
なので$BG:GF=CG:GD=2:1$です。…①
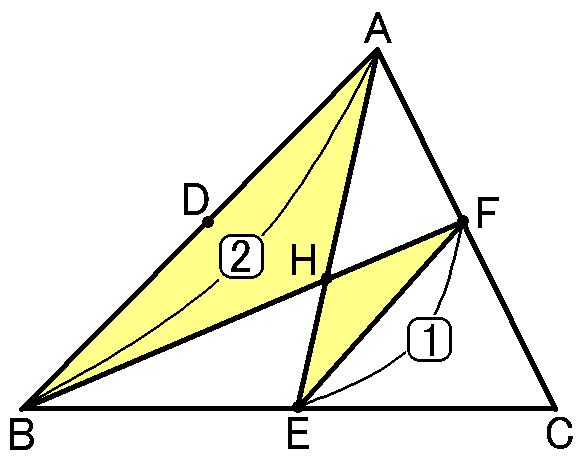
つぎに、$B$と$F,A$と$E$をむすんで、$BF$と$AE$の交点を$H$とします。中点連結定理により、$FE /\!/ AB$,$FE=\cfrac{1}{2}AB$です。
$FE /\!/ AB$なのだから、$\triangle ABH$ ∽$\triangle EFH$で、相似比は$AB:FE=2:1$です。
なので$BH:HF=AH:HE=2:1$です。…②
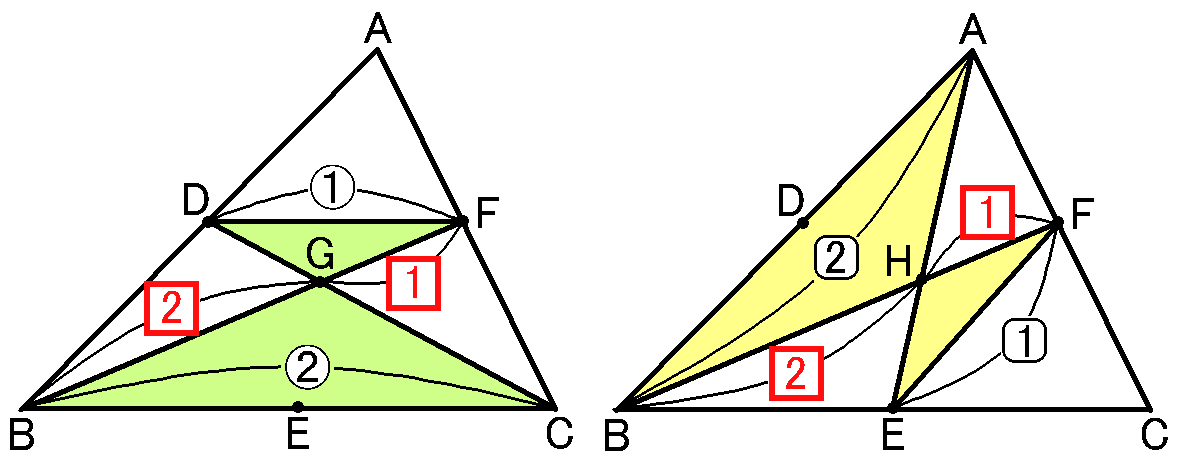
ここでよくみてほしいのですが、①から、$BG:GF=2:1$です。また、②から、$BH:HF=2:1$です。じゃあ、$G$と$H$はおなじところにある点です。
どちらも$BF$を$2:1$にわける点だからです。おなじじゃないとツジツマあいません。
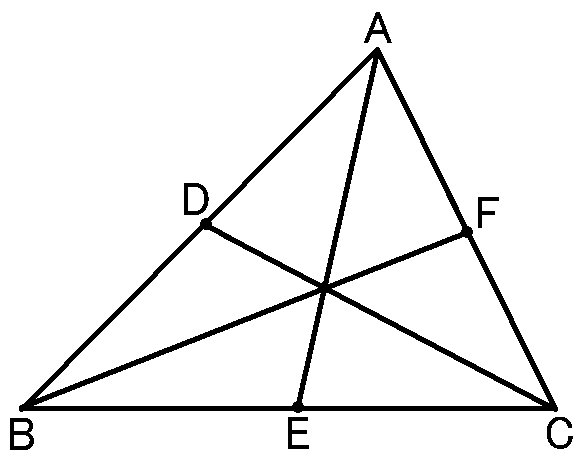
というわけで、三角形の3本の中線は1点で交わります。その交わった点を「三角形の重心」といって、それぞれの中線を$2:1$にわけます。