数学 入試過去問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
【2013年の大問8】
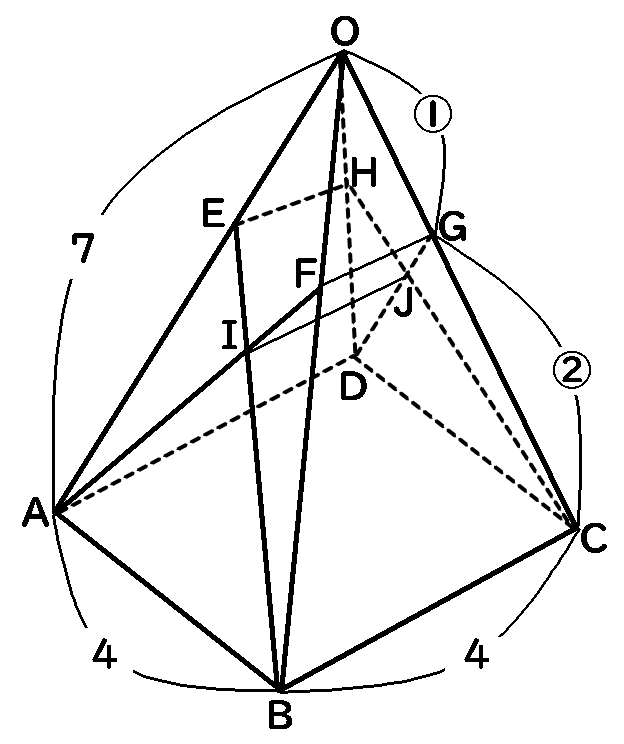
正四角すい$O-ABCD$
$AB=BC=CD=DA=4$
$OA=OB=OC=OD=7$
$OE:EA=OF:FB=OG:GC=OH:HD=1:2$
$AF$と$BE$の交点を$I,DG$と$CH$の交点を$J$とする。
(1) $\triangle OAB$の面積
答え
$6\sqrt{5} $
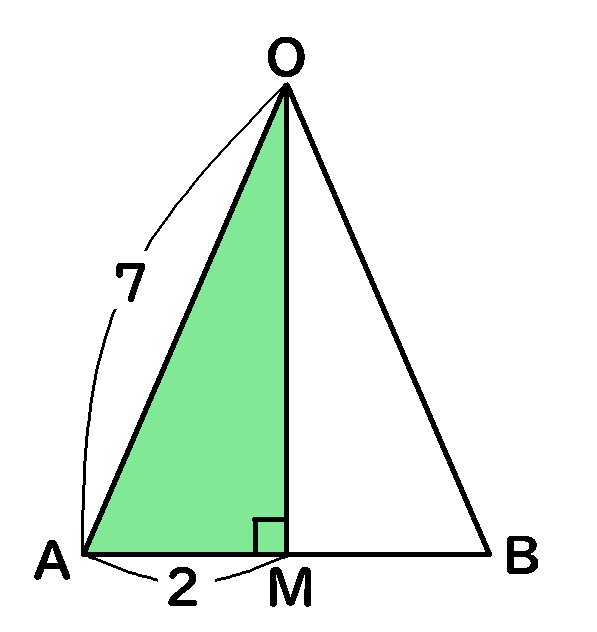 三角形の面積を求めなさいというのだから、底辺$\times$高さ$\times\cfrac{1}{2}$をすればよいです。
三角形の面積を求めなさいというのだから、底辺$\times$高さ$\times\cfrac{1}{2}$をすればよいです。
三辺がわかっている二等辺三角形は、三平方の定理を使えば高さがでます。
二等辺三角形の頂角の二等分線は底辺を垂直に二等分します。
$AB$の中点を$M$とすれば、$AM=BM=2$です。
仮定から、$OA=7$です。
$\triangle OAM$は$\angle OMA=90^{ \circ }$の
直角三角形だから、三平方の定理から、
\begin{eqnarray*}
OM&=&\sqrt{OA^2-AM^2} \\
&=&\sqrt{49-4} \\
&=&\sqrt{45} \\
&=&3\sqrt{5}
\end{eqnarray*}
なので、$\triangle OAB$の面積は、
\begin{eqnarray*}
&&4 \times 3\sqrt{5} \times \cfrac{1}{2} \\
&=&6\sqrt{5}
\end{eqnarray*}
(2) $\triangle OIJ$の面積
答え
$\cfrac{\sqrt{41}}{2}$
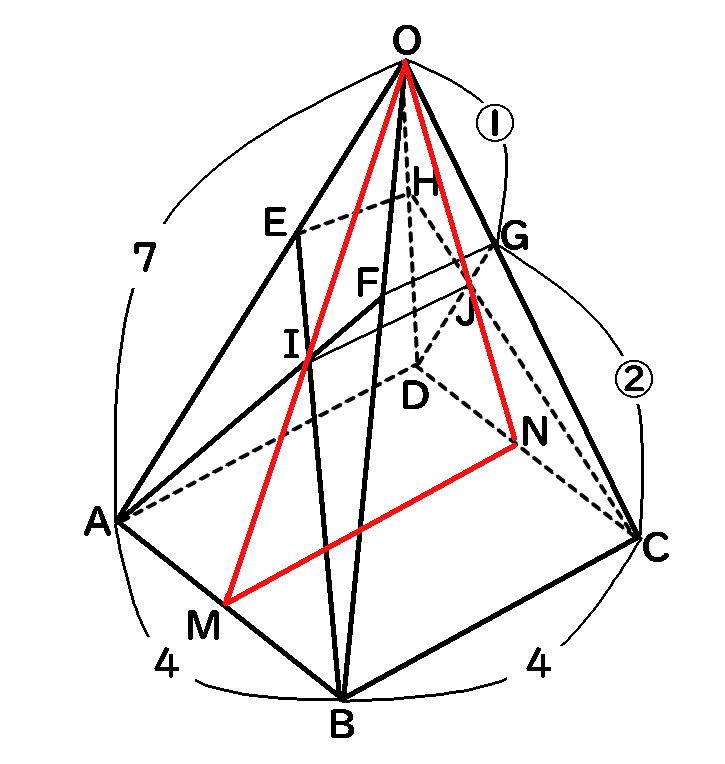 まず、$O$と$I$と$J$をふくむ平面で四角すいを切ってみましょう。
まず、$O$と$I$と$J$をふくむ平面で四角すいを切ってみましょう。
べつないいかたをすると、$I$と$J$を通るように、真上のとがっているところから包丁をいれて四角すいを切る、ということです。
そして、その切り口を考えます。$AB$の中点を$M$、$CD$の中点を$N$とすれば、$I$と$J$は、$\triangle OMN$の$OM$と$ON$の上にあるはずです。$M$と$N$を通るように$O$からまっすぐ下に切れば、$I$と$J$を通っているはず、というふうに考えてもいいです。
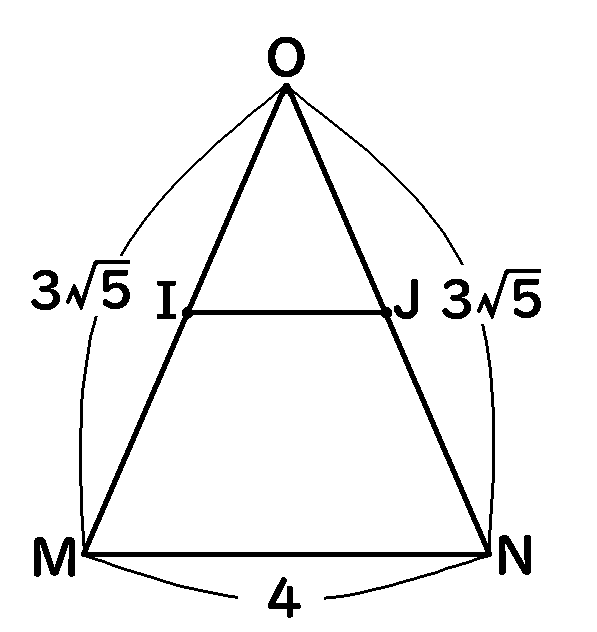 こんなふうに、「立体を切って、その切り口の平面で考える」というのが、定番のやりかたです。
こんなふうに、「立体を切って、その切り口の平面で考える」というのが、定番のやりかたです。
んで、今回はこの、切り口にできた$\triangle OMN$で、考えていきます。これは、$OM=ON$の二等辺三角形です。$MN$の長さは$4$です。$OM$の長さは、⑴の
問題ですでに求めています。$3\sqrt5$です。$ON$も$3\sqrt5$ということになります。
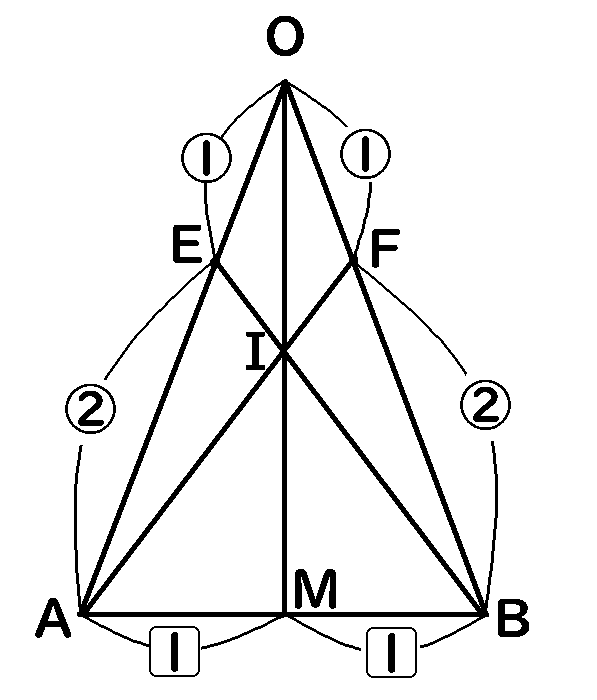 三角形の面積を求めなさいというのだから、底辺$\times$高さ$\times\cfrac{1}{2}$をすればよいわけです。
三角形の面積を求めなさいというのだから、底辺$\times$高さ$\times\cfrac{1}{2}$をすればよいわけです。
底辺や高さをだすには、まず、$I$や$J$がどこにあるのか、を考える必要があります。そこで、さきほどの
$\triangle OAB$についてふたたび考えます。
$AB$の中点が$M$で、$I$は$OM$の上にあります。
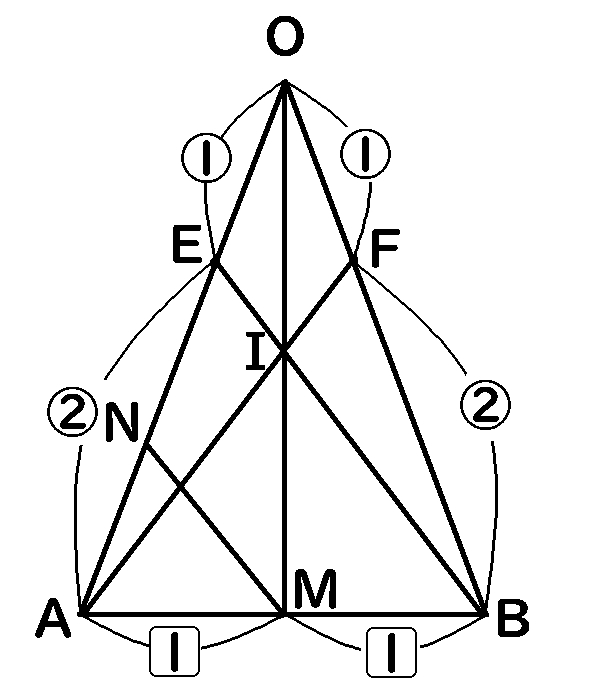 それでは、$OI:IM$はどうなっているのでしょうか。
それでは、$OI:IM$はどうなっているのでしょうか。
これについて、今回は、補助線をひいて考えることにします。$M$を通って$EB$に平行な線をひきます。そして、この線と$OA$の交点を$N$とします。
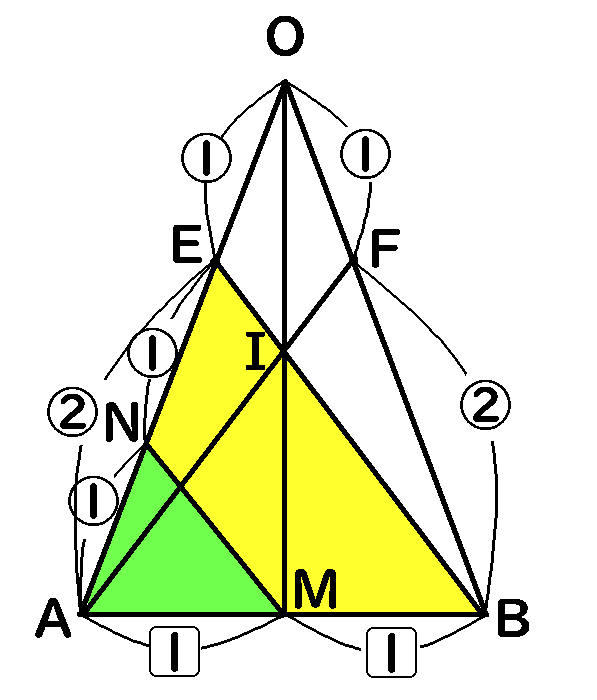 すると、$EB /\!/ NM$なのだから、$AM:MB=AN:NE$です。$AM:MB=1:1$ですから、$AN:NE=1:1$になります。
すると、$EB /\!/ NM$なのだから、$AM:MB=AN:NE$です。$AM:MB=1:1$ですから、$AN:NE=1:1$になります。
ところで、そもそも$OE:EA=1:2$でした。ということは、$OE:EN:NA=1:1:1$となります。
つまり、$OE:EN=1:1$です。
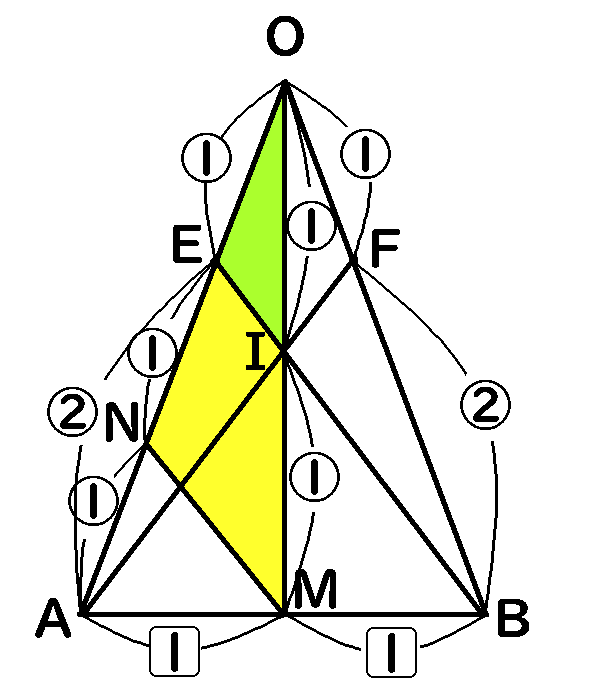 この比を、$OI:IM$にもってきます。$EB /\!/ NM$なのだから、$OE:EN=OI:IM$になります。
この比を、$OI:IM$にもってきます。$EB /\!/ NM$なのだから、$OE:EN=OI:IM$になります。
$OE:EN=1:1$であるのなら、$OI:IM=1:1$です。
べつないいかたをすると、$I$は$OM$の中点ということになります。
ここまできてしまえば、あとはたいしたことはありません。
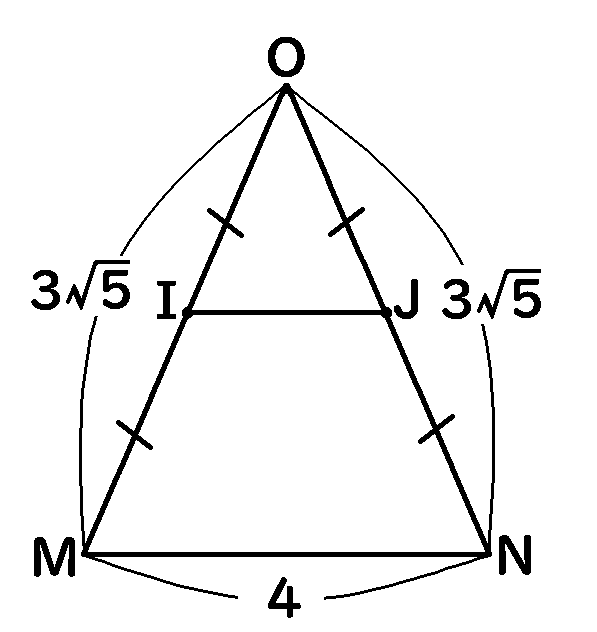 この問題の最初に考えた、切り口にできた$\triangle OMN$にもどります。
この問題の最初に考えた、切り口にできた$\triangle OMN$にもどります。
$\triangle OMN$について、$I$は$OM$の中点です。ならば$J$は$ON$の中点です。
$\triangle OIJ$の面積を求めなさいというのなら、$\triangle OIJ$ ∽$\triangle OMN$で、相似比が$1:2$だから、
面積比は$1:4$です。$\triangle OIJ$の面積は$\triangle OMN$の$\cfrac{1}{4}$だということで、$\triangle OMN$の面積をだしていけば、いけます。
または、おとなしく$\triangle OIJ$の底辺と高さをだしてもいいです。こっちのほうがちょっとめんどくさい気はしますが、まあたいしたちがいはないです。
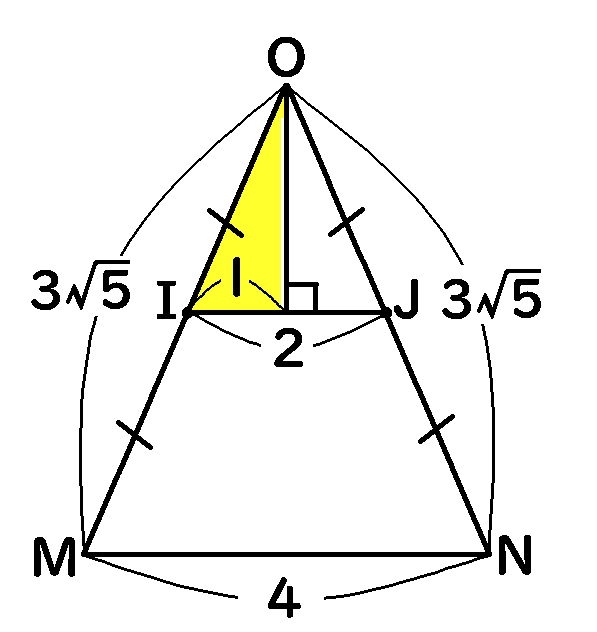 今回は、ちょっとめんどくさいほうでやってみましょう。中点連結定理から、$IJ$の長さは$MN$の$\cfrac{1}{2}$だから、$2$です。
今回は、ちょっとめんどくさいほうでやってみましょう。中点連結定理から、$IJ$の長さは$MN$の$\cfrac{1}{2}$だから、$2$です。
$OI$は$OM$の$\cfrac{1}{2}$だから、$\cfrac{3\sqrt{5}}{2}$です。
$\triangle OIJ$で、$IJ$を底辺としたとき、高さは、三平方の定理から、
$$\sqrt{\left(\cfrac{3\sqrt{5}}{2}\right)^2-1^2}=\sqrt{\cfrac{41}{4}}=\cfrac{\sqrt{41}}{2}$$
なので$\triangle OIJ$の面積は、
$$2\times\cfrac{\sqrt{41}}{2}\times\cfrac{1}{2}=\cfrac{\sqrt{41}}{2}$$