数学 入試過去問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
【2016年の大問8】
正三角すい$OABC$
$AB=BC=CA=2\sqrt3cm$
$OA=OB=OC=10cm$
$BM=MC$
$OD\perp 面ABC$
$D$は$AM$上にあって、$OD=4\sqrt6cm$
$\triangle OAM$において、$\angle OAM$の二等分線と$OM$の交点を$E$,
$OD$と$AE$の交点を$F$とする
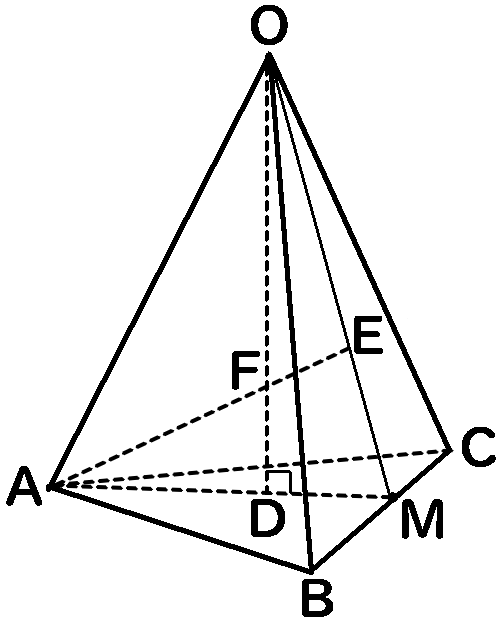
(1) 正三角すい$OABC$の体積
答え
$12\sqrt2 cm^2$

三角すいの体積ですから、底面積$\times$高さ$\times\cfrac{1}{3}$をやればOKです。
【底面積】
底面の$\triangle ABC$は$1$辺が$2\sqrt3$の正三角形です。
$BC$の中点が$M$なので、$AM\perp BC$です。
正三角形は$3$つの角がそれぞれ$60^{ \circ }$ですから、
$\triangle ABM$は
$1:2:\sqrt3$の比が使えて、
\begin{eqnarray*}
AB:AM&=&2:\sqrt3 \\
2\sqrt3:AM&=&2:\sqrt3 \\
2\times AM&=&2\sqrt3\times\sqrt3\\
2\times AM&=&6\\
AM&=&3
\end{eqnarray*}
$AM$というのは$BC$を底辺としたときの高さになります。
なので底面$\triangle ABC$の面積は、
$$2\sqrt3\times3\times\cfrac{1}{2}=3\sqrt3$$
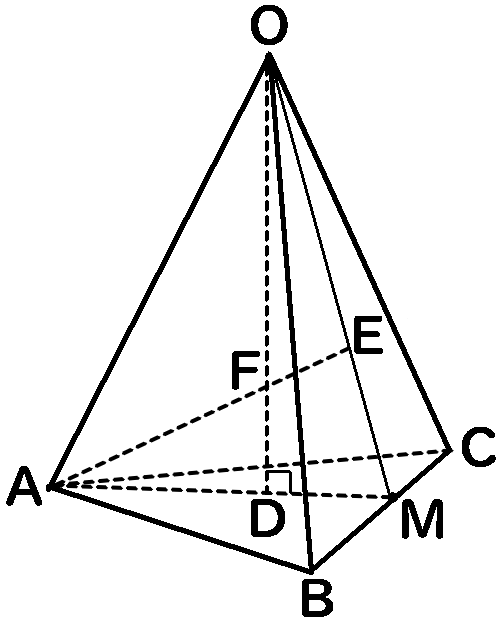
【体積】
三角すいの体積は、底面積$\times$高さ$\times\cfrac{1}{3}$です。
高さというのはこの場合、$OD$のことで、長さは問題に書いてあるとおり、$OD=4\sqrt6$です。
なので体積は、
$$3\sqrt3\times4\sqrt6\times\cfrac{1}{3}=12\sqrt2$$
(2) $\triangle ADF$と$\triangle OFE$の面積の比
答え
$13:25$
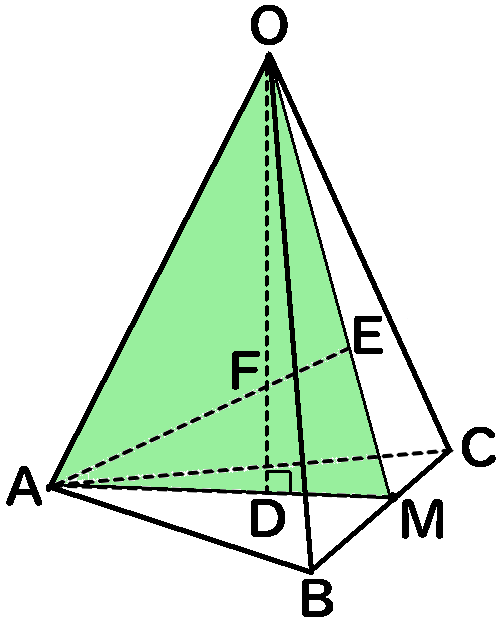 $\triangle OAM$について考えます。
$\triangle OAM$について考えます。
仮定から、$OA=10,OD=2\sqrt6$です。
(1)の問題で求めたように、$AM=3$です。
あと$AE$は$\angle OAM$の二等分線です。べつないいかたをすると、$\angle OAE=\angle MAE$です。
すると三角形の角の二等分線と辺の比の定理が使えることになって、$OF:FD$や、$OE:EM$が求められそうです。そのために、$AD$と$DM$の長さを求めましょう。
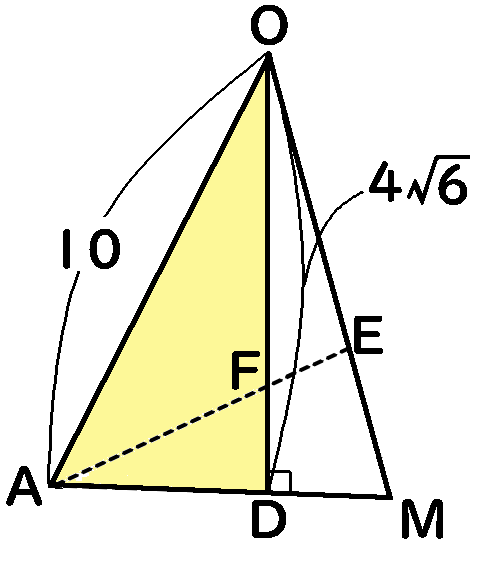 $\triangle OAD$は$\angle ODA=90^{ \circ }$の直角三角形だから、三平方の定理を使えば$AD$がでます。
\begin{eqnarray*}
AD&=&\sqrt{(OA)^2-(OD)^2}\\
&=&\sqrt {(10)^2-(4\sqrt6)^2}\\
&=&\sqrt{100-96}=2
\end{eqnarray*}
また、(1)の問題で$AM=3$と求めていますから、
$$DM=AM-AD=3-2=1$$
$\triangle OAD$は$\angle ODA=90^{ \circ }$の直角三角形だから、三平方の定理を使えば$AD$がでます。
\begin{eqnarray*}
AD&=&\sqrt{(OA)^2-(OD)^2}\\
&=&\sqrt {(10)^2-(4\sqrt6)^2}\\
&=&\sqrt{100-96}=2
\end{eqnarray*}
また、(1)の問題で$AM=3$と求めていますから、
$$DM=AM-AD=3-2=1$$
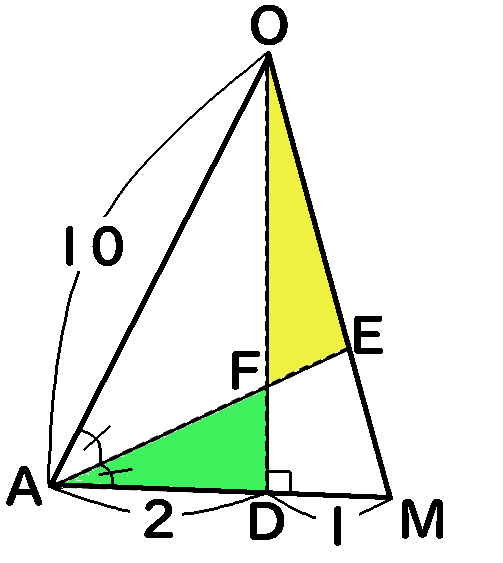 これでもう、$\triangle ADF$と$\triangle OFE$の面積の比がでます。材料が足りないのではないかと感じる人もいると思いますが、そんなことはありません。これでもういけます。やっていきましょう。
これでもう、$\triangle ADF$と$\triangle OFE$の面積の比がでます。材料が足りないのではないかと感じる人もいると思いますが、そんなことはありません。これでもういけます。やっていきましょう。
$\triangle OAM$をもとにして、$\triangle OAM:\triangle ADF$という面積の比と、
$\triangle OAM:\triangle OFE$という面積の比について考えます。
【$\triangle OAM:\triangle ADF$】
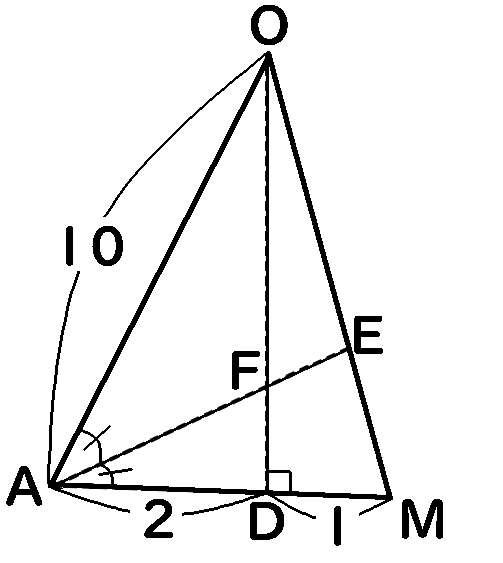 まず、$\triangle OAD$と、$\triangle OAM$(全体)の比を考えます。
まず、$\triangle OAD$と、$\triangle OAM$(全体)の比を考えます。
$AM:AD=3:2$ですから、$\triangle OAM$と$\triangle OAD$の面積の比も$3:2$になります。つまり、$\triangle OAD$は$\triangle OAM$の$\cfrac{2}{3}$ということです。
次に、$\triangle OAD$に着目して、$\triangle ADF$との比を考えます。
 $\angle OAE=\angle MAE$ですから、三角形の角の二等分線と辺の比の定理により、
\begin{eqnarray*}
OF:FD&=&AO:AD\\
&=&10:2\\
&=&5:1
\end{eqnarray*}
$OF:FD=5:1$ならば、$OD:FD=6:1$ですから、$\triangle OAD$と$\triangle ADF$の面積の比も$6:1$になります。
つまり、$\triangle ADF$は$\triangle OAD$の$\cfrac{1}{6}$ということです。
$\angle OAE=\angle MAE$ですから、三角形の角の二等分線と辺の比の定理により、
\begin{eqnarray*}
OF:FD&=&AO:AD\\
&=&10:2\\
&=&5:1
\end{eqnarray*}
$OF:FD=5:1$ならば、$OD:FD=6:1$ですから、$\triangle OAD$と$\triangle ADF$の面積の比も$6:1$になります。
つまり、$\triangle ADF$は$\triangle OAD$の$\cfrac{1}{6}$ということです。
というわけで、$\triangle ADF$は$\triangle OAM$の$\cfrac{2}{3}$の$\cfrac{1}{6}$ということになりますから、
\begin{eqnarray*}
\triangle ADF&=&\triangle OAM \times\cfrac{2}{3} \times\cfrac{1}{6} \\
&=&\triangle OAM \times\cfrac{1}{9}
\end{eqnarray*}
$\triangle ADF$は$\triangle OAM$の$\cfrac{1}{9}$です。
【$\triangle OAM:\triangle OFE$】
 これもまず、$\triangle OMD$と$\triangle OAM$(全体)との比を考えます。
これもまず、$\triangle OMD$と$\triangle OAM$(全体)との比を考えます。
$AM:DM=3:1$ですから、$\triangle OAM$と$\triangle OMD$の面積の比も$3:1$になります。つまり、$\triangle OMD$は$\triangle OAM$の$\cfrac{1}{3}$ということです。
次に、$F$と$M$をむすんで、$\triangle ODM$と$\triangle OFM$の比を考えます。
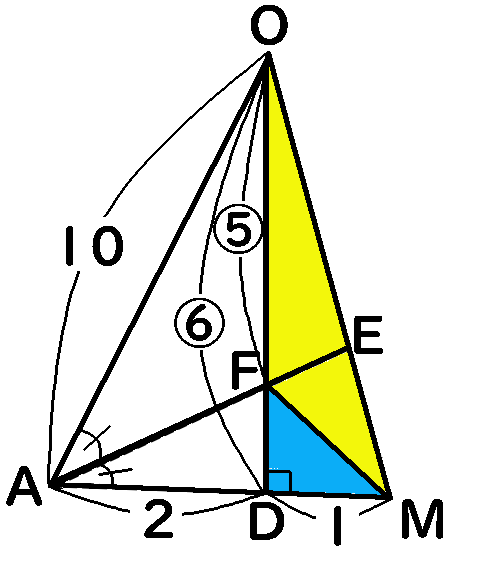 さきほど求めたように、$OF:FD=5:1$です。
ならば、$OD:OF=6:5$ですから、$\triangle ODM$と$\triangle OFM$の面積の比も$6:5$になります。
つまり、$\triangle OFM$は$\triangle ODM$の$\cfrac{5}{6}$ということです。
さきほど求めたように、$OF:FD=5:1$です。
ならば、$OD:OF=6:5$ですから、$\triangle ODM$と$\triangle OFM$の面積の比も$6:5$になります。
つまり、$\triangle OFM$は$\triangle ODM$の$\cfrac{5}{6}$ということです。
さらに、$\triangle OFM$と$\triangle OFE$の比について考えます。
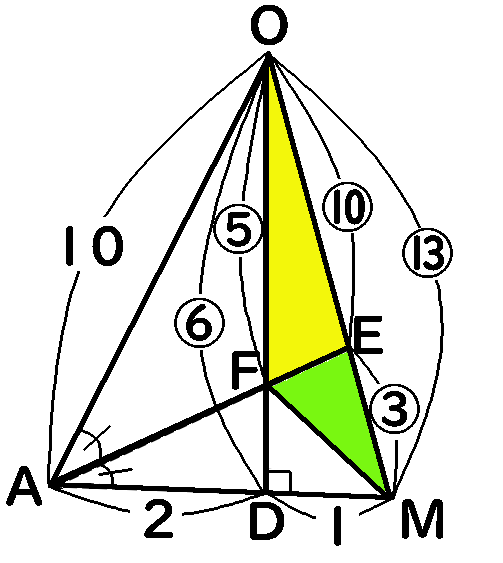 $\angle OAE=\angle MAE$ですから、三角形の角の二等分線と辺の比の定理により、
\begin{eqnarray*}
OE:EM&=&AO:AM\\
&=&10:3
\end{eqnarray*}
$OE:EM=10:3$ならば、$OM:OE=13:10$ですから、$\triangle OFM$と$\triangle OFE$の面積の比も$13:10$になります。
つまり、$\triangle OFE$は$\triangle OFM$の$\cfrac{10}{13}$ということです。
$\angle OAE=\angle MAE$ですから、三角形の角の二等分線と辺の比の定理により、
\begin{eqnarray*}
OE:EM&=&AO:AM\\
&=&10:3
\end{eqnarray*}
$OE:EM=10:3$ならば、$OM:OE=13:10$ですから、$\triangle OFM$と$\triangle OFE$の面積の比も$13:10$になります。
つまり、$\triangle OFE$は$\triangle OFM$の$\cfrac{10}{13}$ということです。
というわけで、$\triangle OFE$は$\triangle OAM$の$\cfrac{1}{3}$の$\cfrac{5}{6}$の$\cfrac{10}{13}$ということになりますから、
\begin{eqnarray*}
\triangle OFE&=&\triangle OAM \times\cfrac{1}{3} \times\cfrac{5}{6}\times\cfrac{10}{13} \\
&=&\triangle OAM \times\cfrac{25}{117}
\end{eqnarray*}
$\triangle OFE$は$\triangle OAM$の$\cfrac{25}{117}$です。
これで$\triangle ADF$と$\triangle OFE$の面積の比がいえます。
$\triangle ADF$は$\triangle OAM$の$\cfrac{1}{9}$です。
$\triangle OFE$は$\triangle OAM$の$\cfrac{25}{117}$です。
$\triangle OAM$をもとにすれば、
\begin{eqnarray*}
\triangle ADF:\triangle OFE&=&\cfrac{1}{9}:\cfrac{25}{117}\\
&=&\cfrac{1}{9}\times117:\cfrac{25}{117}\times117\\
&=&13:25
\end{eqnarray*}