数学 入試過去問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
【2017年の大問8】
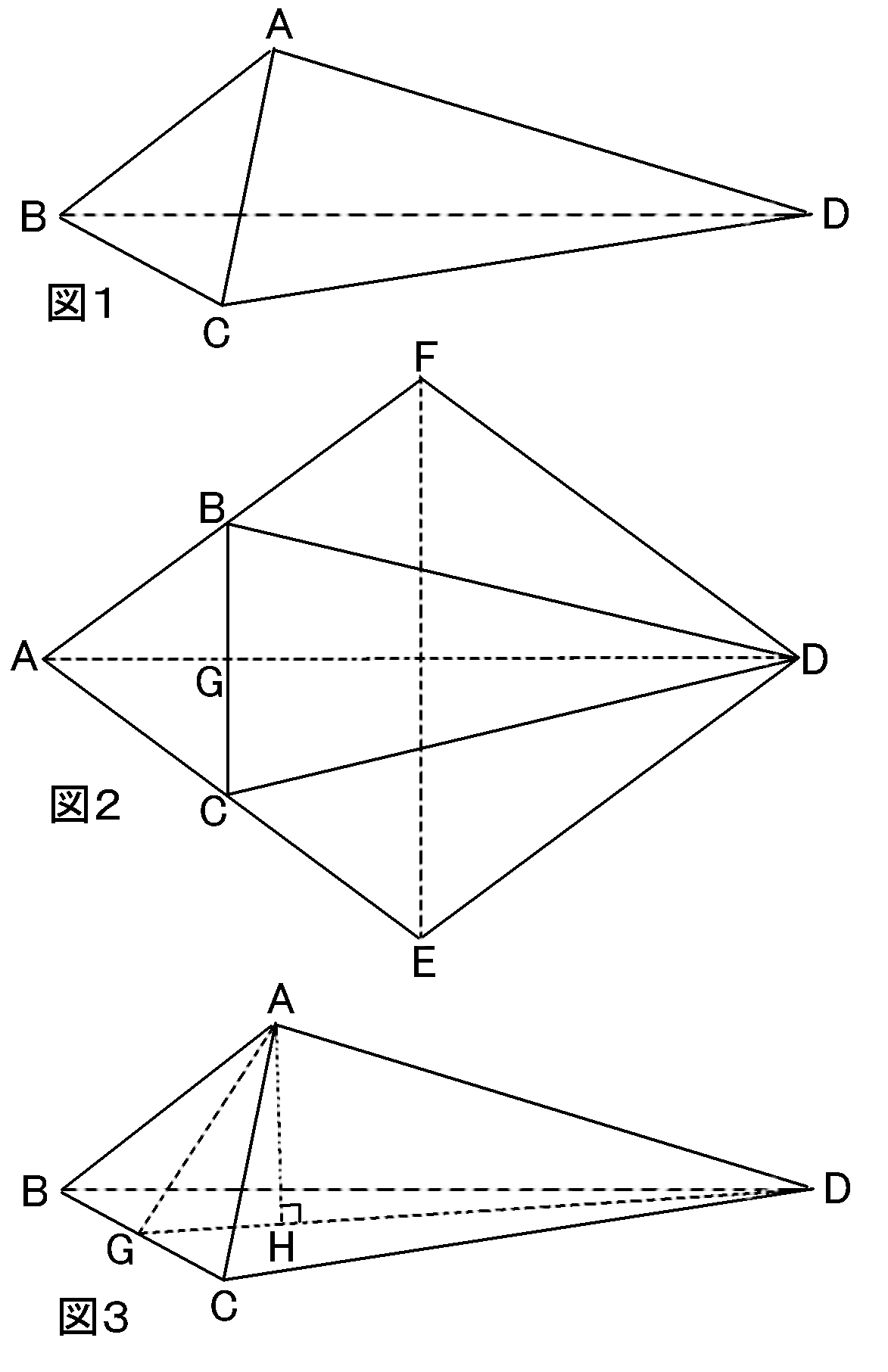
図1は三角すい$ABCD$
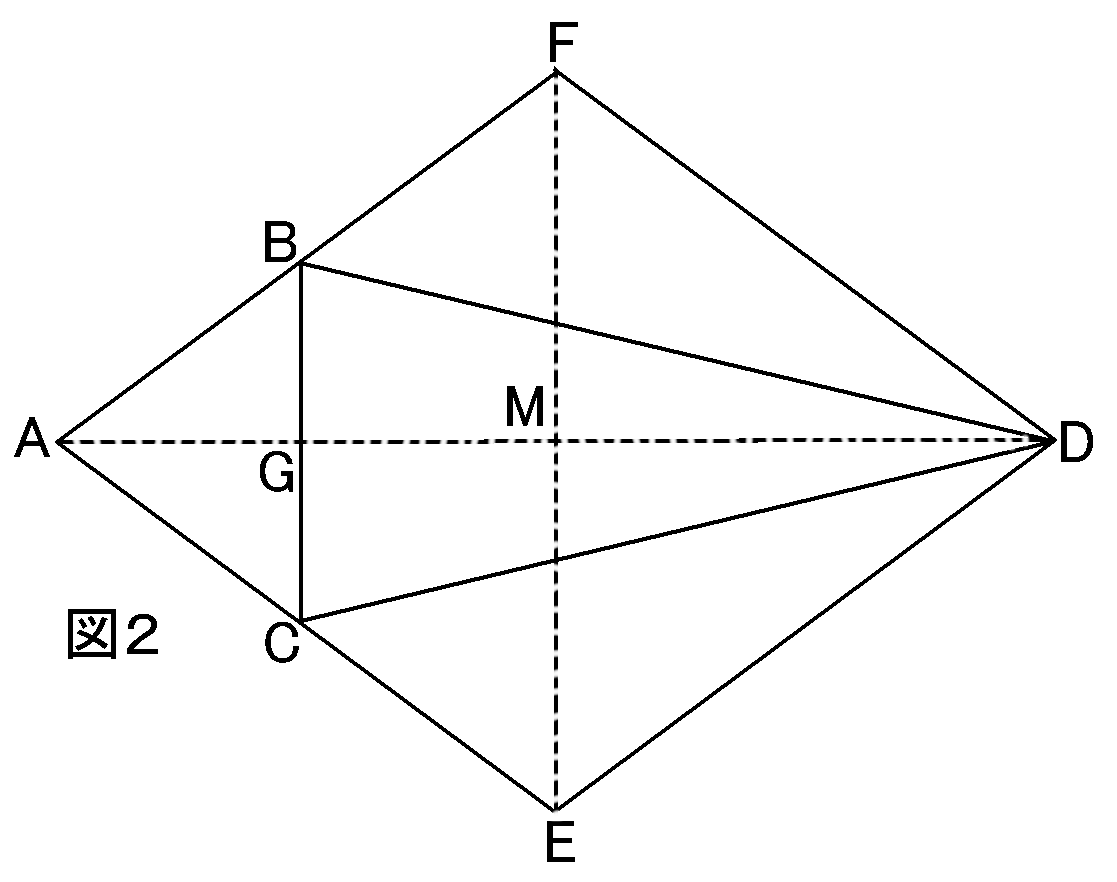
図2はその展開図で、四角形$AEDF$は、
$AD=8cm$,
$EF=6cm$のひし形、
線分$AD$と線分$BC$の交点を$G$とする
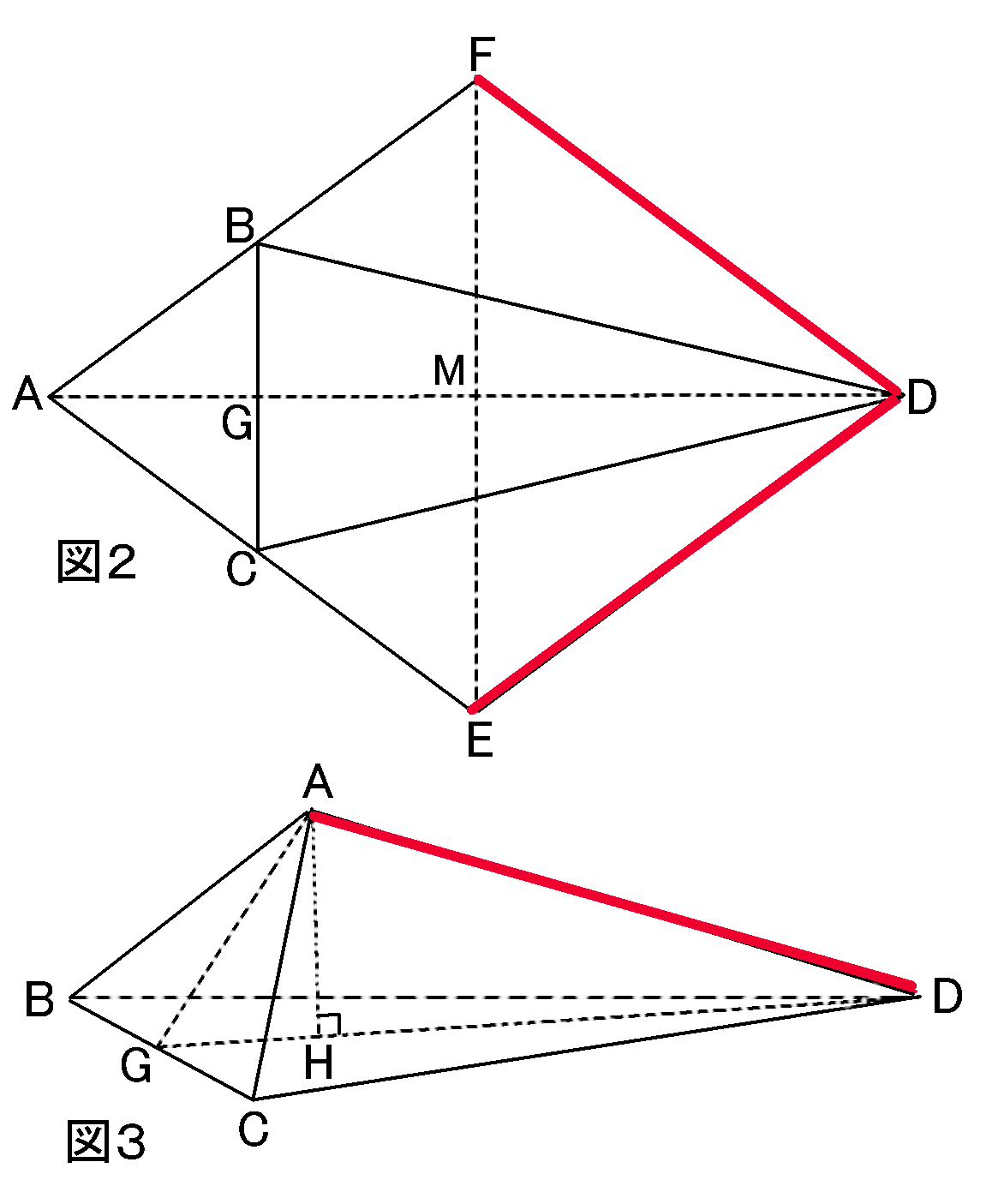
図3は図1の頂点$A$から線分$DG$に垂線をひき、その交点を$H$としたもの
(1) 図2において、$\triangle ABC$の面積は、四角形$AEDF$の何倍か。
答え
$\cfrac{1}{8}$倍
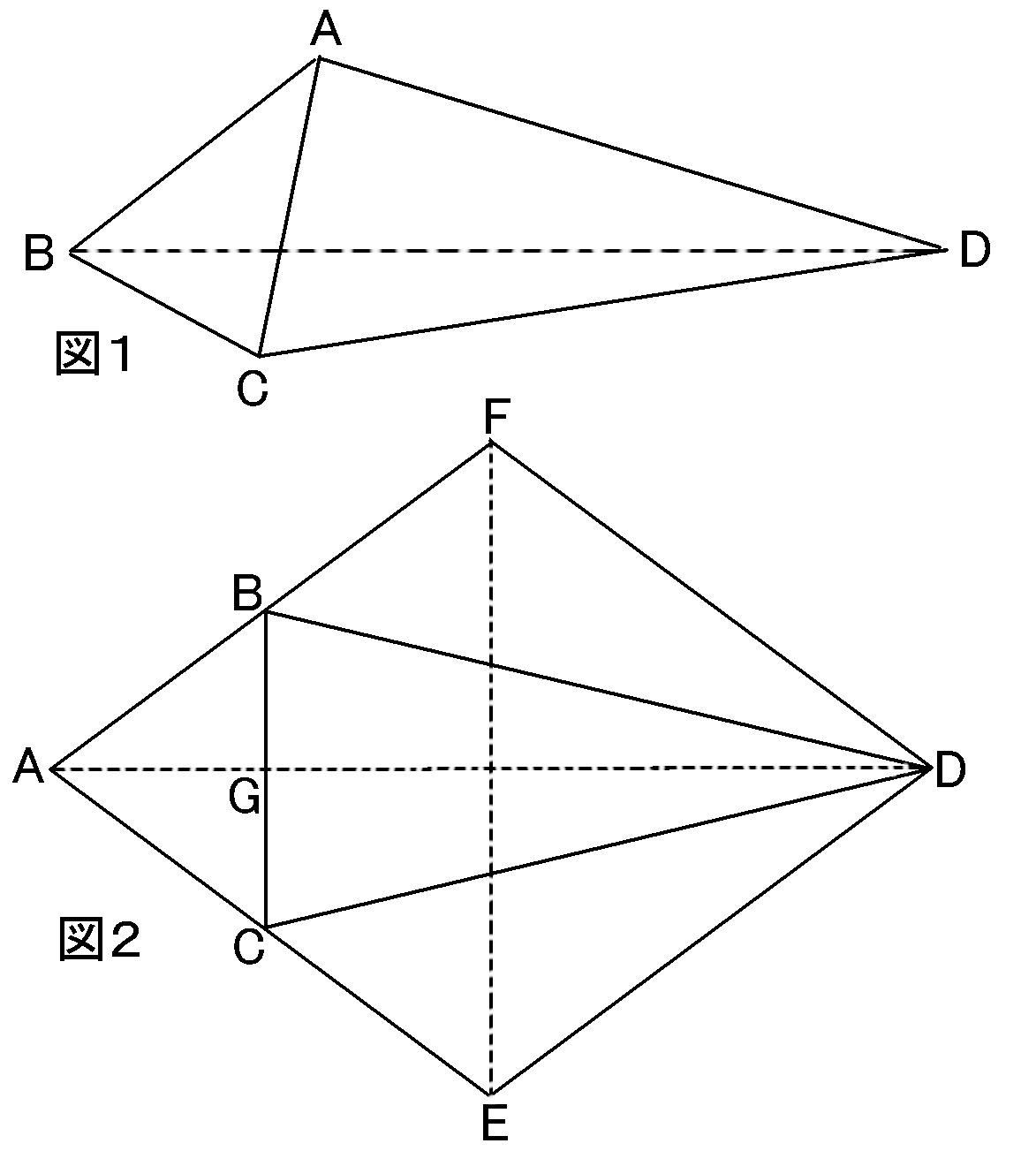
図2は図1の展開図です。図2を$BC$と$BD$と$CD$のところで折り曲げて組み立てると図1になるのだから、$AB=BF,AC=CE$です。
$\triangle ABC$と$\triangle AFE$で、
$\angle A$は共通
$AB:AF=AC:AE=1:2$
$2$組の辺の比とその間の角が等しいので、
$\triangle ABC$ ∽$\triangle AFE$です。
そしてその相似比は$1:2$です。
相似比が$1:2$なら、面積比は$1:4$です。
なので$\triangle ABC$の面積は$\triangle AFE$の$\cfrac{1}{4}$です。
なので$\triangle ABC$の面積は、四角形$AEDF$の$\cfrac{1}{8}$です。
【別解】
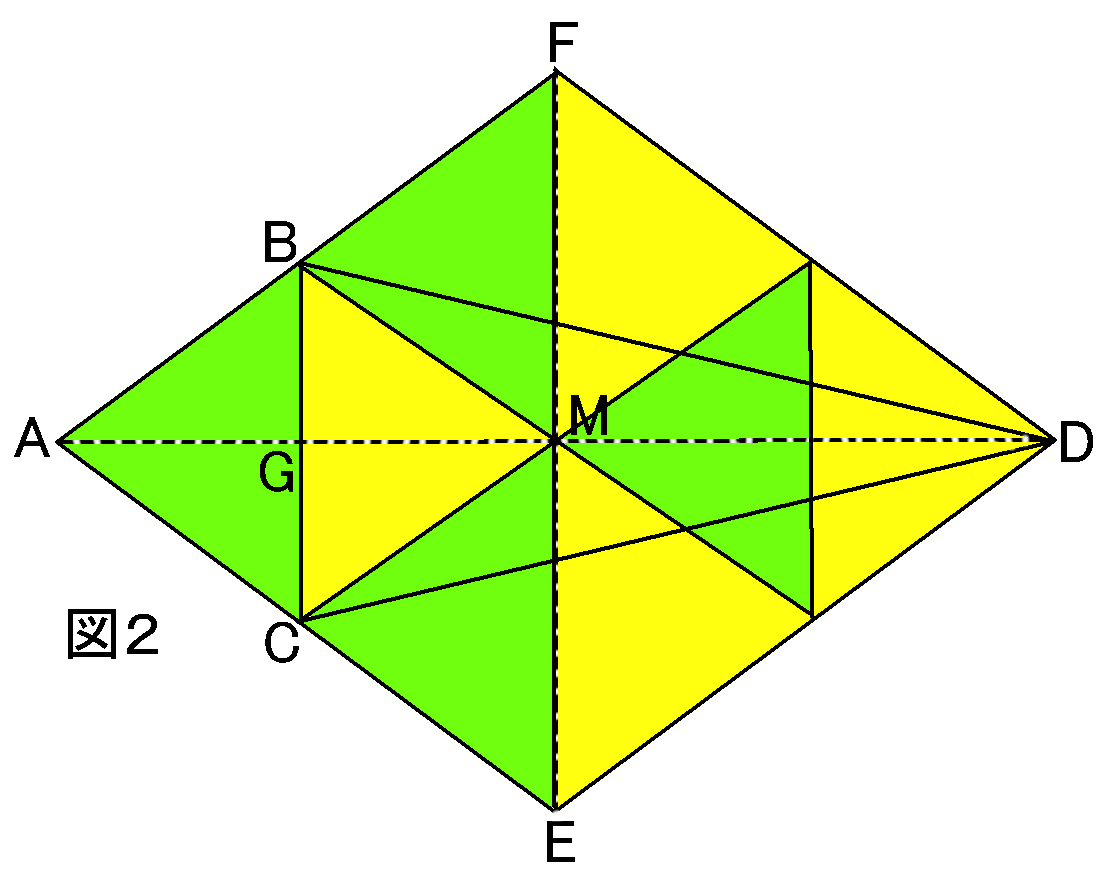
図を見てください。こんなふうに考えれば、8つの合同な三角形にわけることができますから、$\triangle ABC$の面積は、四角形$AEDF$の$\cfrac{1}{8}$ですよね。
なぜ8つの合同な三角形になるのかを簡単に説明すると、ひし形は平行四辺形にふくまれます。平行四辺形の対角線はそれぞれの中点で交わるので、ひし形$AEDF$対角線の交点を$M$とすると、
$FM=EM$です。あと、$AB=BF,AC=CE$です。$\triangle AEF$で、中点連結定理より、$BC /\!/ FE,BM /\!/ AE,CM /\!/ AF$となって、四角形$ACMB$,四角形$BCMF$,四角形$BCEM$は、
ぜんぶ平行四辺形になります。平行四辺形を対角線で切れば、合同な2つの三角形になりますよね。3組の辺がそれぞれ等しい2つの三角形になるのだから。なので、▱$ACMB$において、
$\triangle ACB \ \equiv \ \triangle MCB$です。さらに、▱$BCMF$において、…という感じでぜんぶ合同になっていきます。
(2) 図3において$AH$の長さ
答え
$\cfrac{\sqrt{39}}{4}cm$
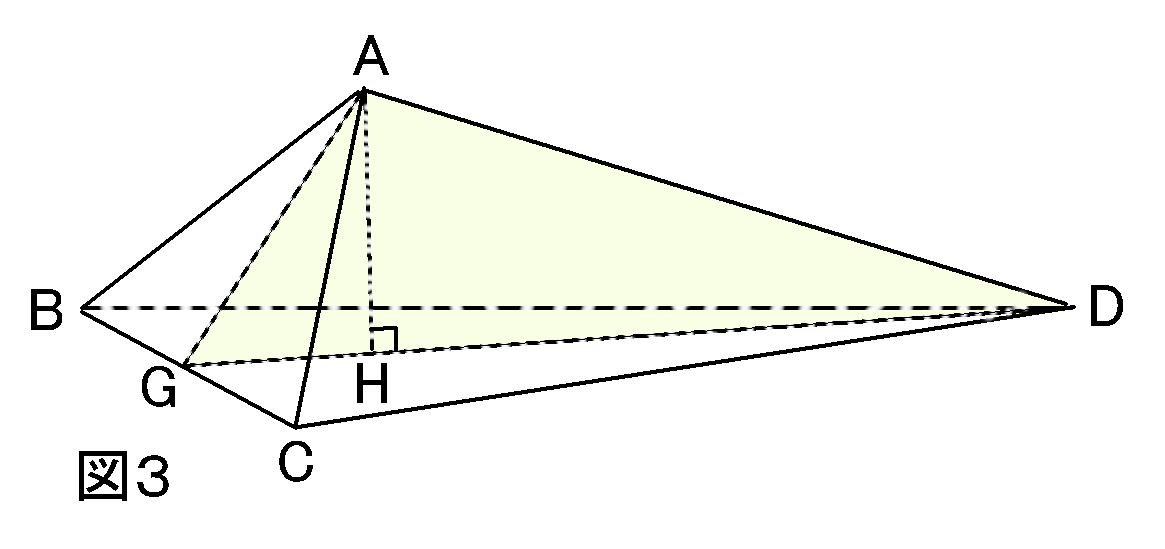
$AH$の長さを求めるために、図3の$\triangle AGD$について考えます。
その3辺の$AG,GD,AD$の長さについて考えます。
【$AG$の長さ】
まず$AG$について。図2の展開図で、$AD$と$FE$の交点を$M$とします。
図2は図3の展開図なのだから、$BC$と$BD$と$CD$のところで折り曲げて組み立てたときに、点$A$と点$F$と点$E$は重なります。なので、$AB=BF,AC=CE$です。
比でいうと、$AB:BF=AC:CE=1:1$です。
ということは、$\triangle AEF$で、中点連結定理により、$BC /\!/ FE$ということになります。
なので$AG:GM$も$AB:BF$や$AC:CE$と等しくなって、その比は$1:1$です。
$AG$は$AM$の半分になる、ということです。
$AM$は$AD$の半分なのだから$4cm$,$AG$はその半分なのだから$2cm$となります。
【$GD$の長さ】
$AD=8cm,AG=2cm$なのだから$GD$は$6cm$です。
【$AD$の長さ】
図2と図3見比べてください。$BC$と$BD$と$CD$のところで折り曲げて図2を組み立てると図3になるのだから、$ED$と$FD$と$AD$は重なります。長さでいうと、$AD=FD=ED$です。
それから、図2の四角形$AEDF$はひし形です。ひし形の対角線は垂直に交わるので、$\triangle FMD$は直角三角形です。
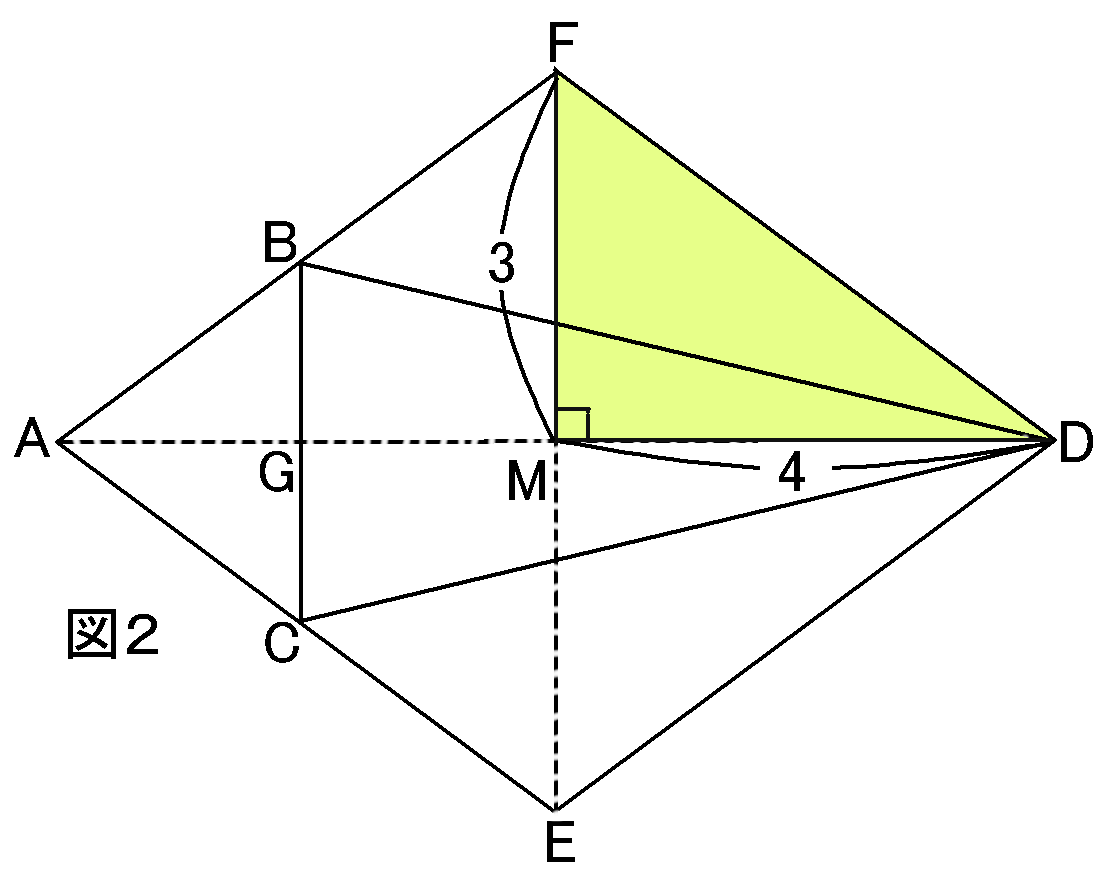
また、ひし形は平行四辺形にふくまれているので、対角線がそれぞれの中点で交わります。
なので$FM=3cm,MD=4cm$です。
というわけで$\triangle FMD$において三平方の定理から、
\begin{eqnarray*}
(FD)^2&=&(FM)^2+(MD)^2\\
&=&3^2+4^2=25\\
FD>0なので\\
FD&=&\sqrt{25}=5
\end{eqnarray*}
$FD$は$AD$と同じですから、$AD=5cm$です。
これで図3の$\triangle AGD$の3辺、$AG,GD,AD$の長さがわかりました。
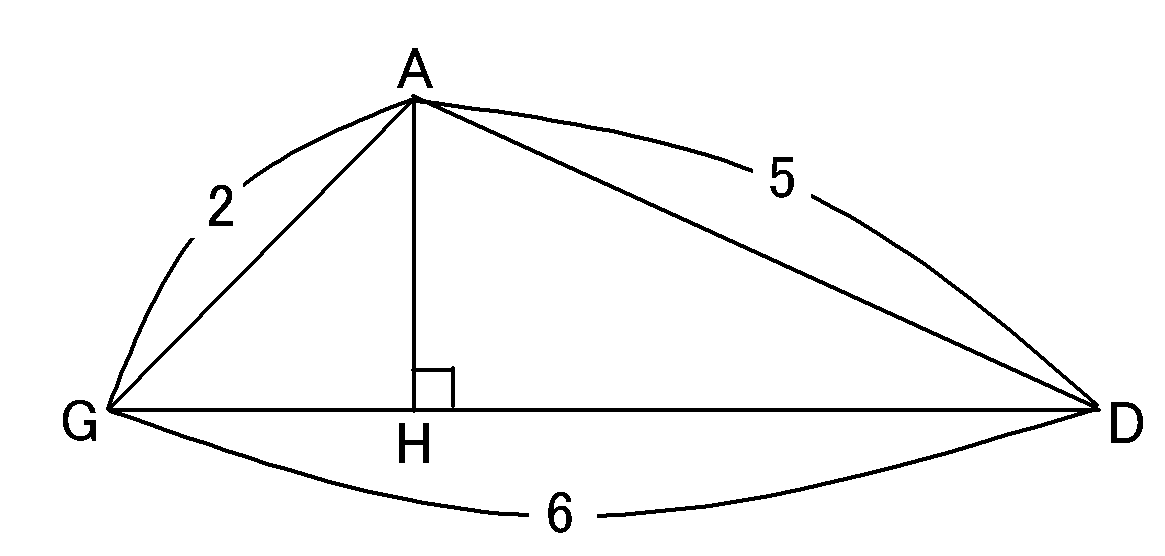
3辺の長さがわかっている三角形なので、三平方の定理を使って、点$A$から$GD$におろした垂線$AH$の長さを求めていきましょう。
そのためにまず、$GH$の長さを求めていきます。

【$GH$の長さ】
$\triangle AGH$は$\angle AHG=90^{ \circ }$の直角三角形だから、$GH$の長さを$x$とすると、三平方の定理より、
\begin{eqnarray*}
(AH)^2&=&(AG)^2-x^2\\
&=&2^2-x^2\\
&=&-x^2+4
\end{eqnarray*}
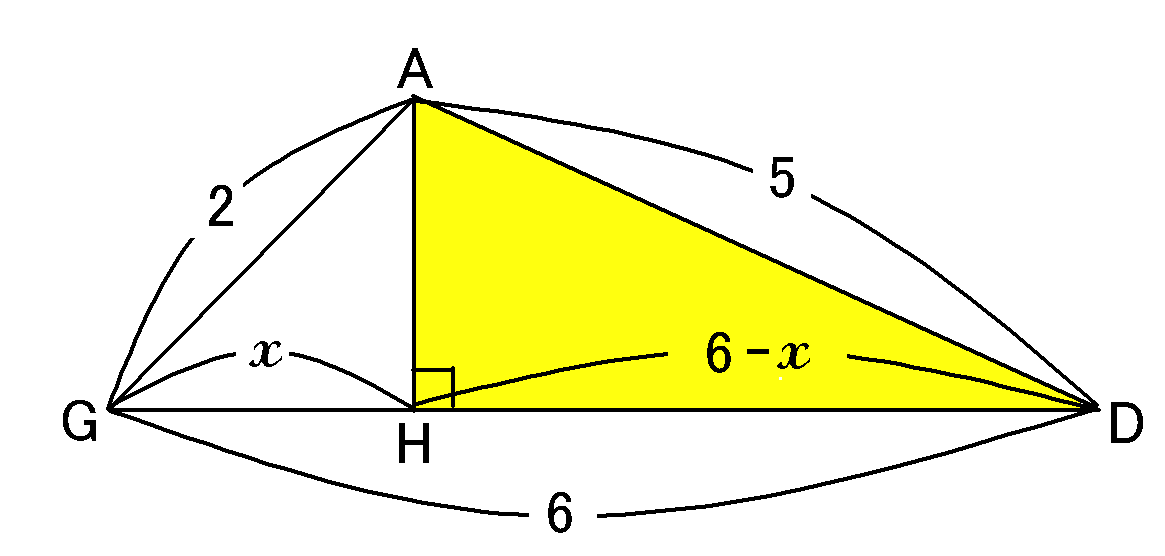
$\triangle AHD$は$\angle AHD=90^{ \circ }$の直角三角形だから、三平方の定理より、
\begin{eqnarray*}
(AH)^2&=&(AD)^2-(HD)^2\\
&=&(AD)^2-(GD-x)^2\\
&=&5^2-(6-x)^2\\
&=&25-(36-12x+x^2)\\
&=&25-36+12x-x^2\\
&=&-x^2+12x-11
\end{eqnarray*}
これで$AH^2$を2通りの表し方で表せました。並べて書くと、
\begin{eqnarray*}
\left\{
\begin{array}{l}
(AH)^2=-x^2+4\qquad…①\\
(AH)^2=-x^2+12x-11\qquad…②
\end{array}
\right.\\
\end{eqnarray*}
こんなふうになります。①と②の式について、代入法で、右辺$=$右辺の式をたてて$x$を求めていきます。
\begin{eqnarray*}
-x^2+4&=&-x^2+12x-11\\
-x^2+x^2-12x&=&-11-4\\
-12x&=&-15\\
x&=&\cfrac{15}{12}=\cfrac{5}{4}\\
\end{eqnarray*}

これで$x$が求まりました。
【$AH$の長さ】
いま求めた$x$を利用して、$\triangle AGH$で、三平方の定理より、
\begin{eqnarray*}
(AH)^2&=&(AG)^2-x^2\\
&=&2^2-\left(\cfrac{5}{4}\right)^2\\
&=&4-\cfrac{25}{16}\\
&=&\cfrac{64}{16}-\cfrac{25}{16}\\
&=&\cfrac{39}{16}
\end{eqnarray*}
$AH>0$なので
\begin{eqnarray*}
AH&=&\sqrt{\cfrac{39}{16}}\\
&=&\cfrac{\sqrt{39}}{4}
\end{eqnarray*}