数学 入試過去問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
【2020年の大問6】
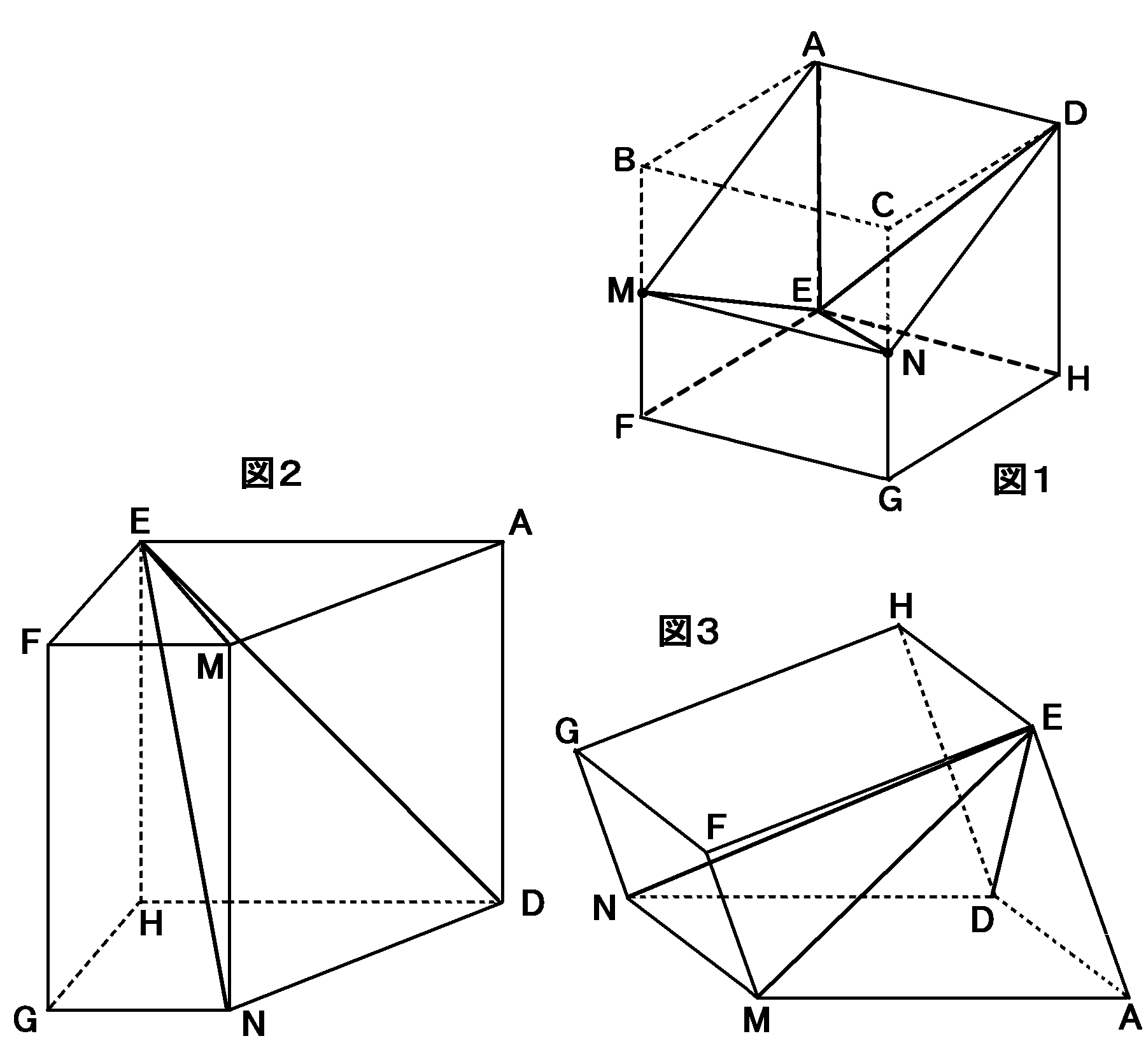
1辺$2cm$の立方体$ABCDEFGH$(図1)
辺$BF,CG$の中点をそれぞれ$M,N$とする。
4点$A,D,M,N$を通る平面でこの立方体を切ったとき、
点$E$をふくむ立体を立体$P$とする。
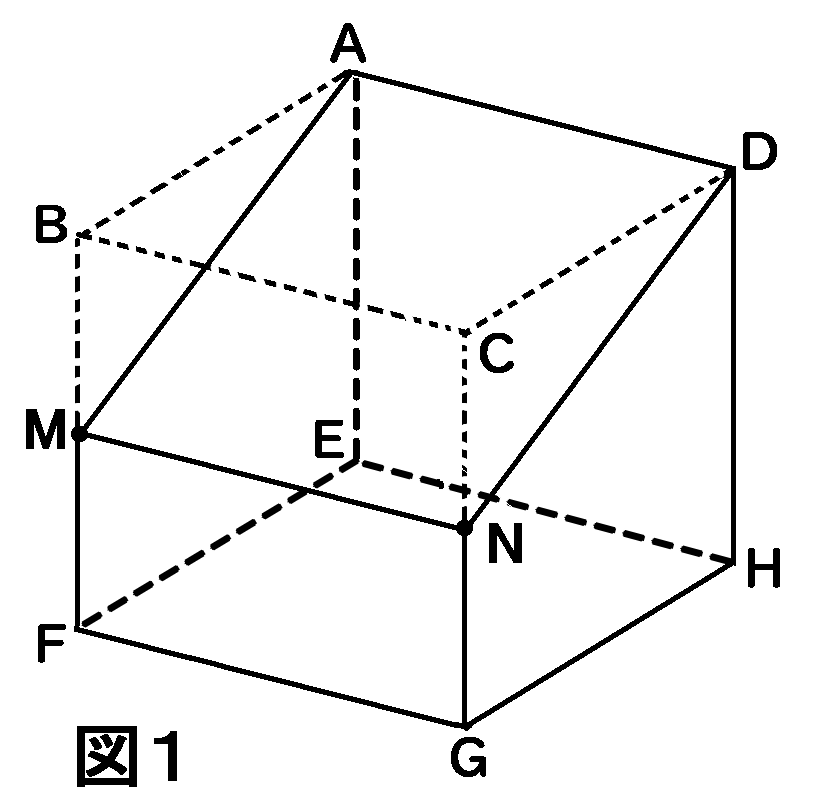
(1) 立体$P$の投影図として正しいものを、次のア~エのうちから2つ選んでその記号を答えよ。
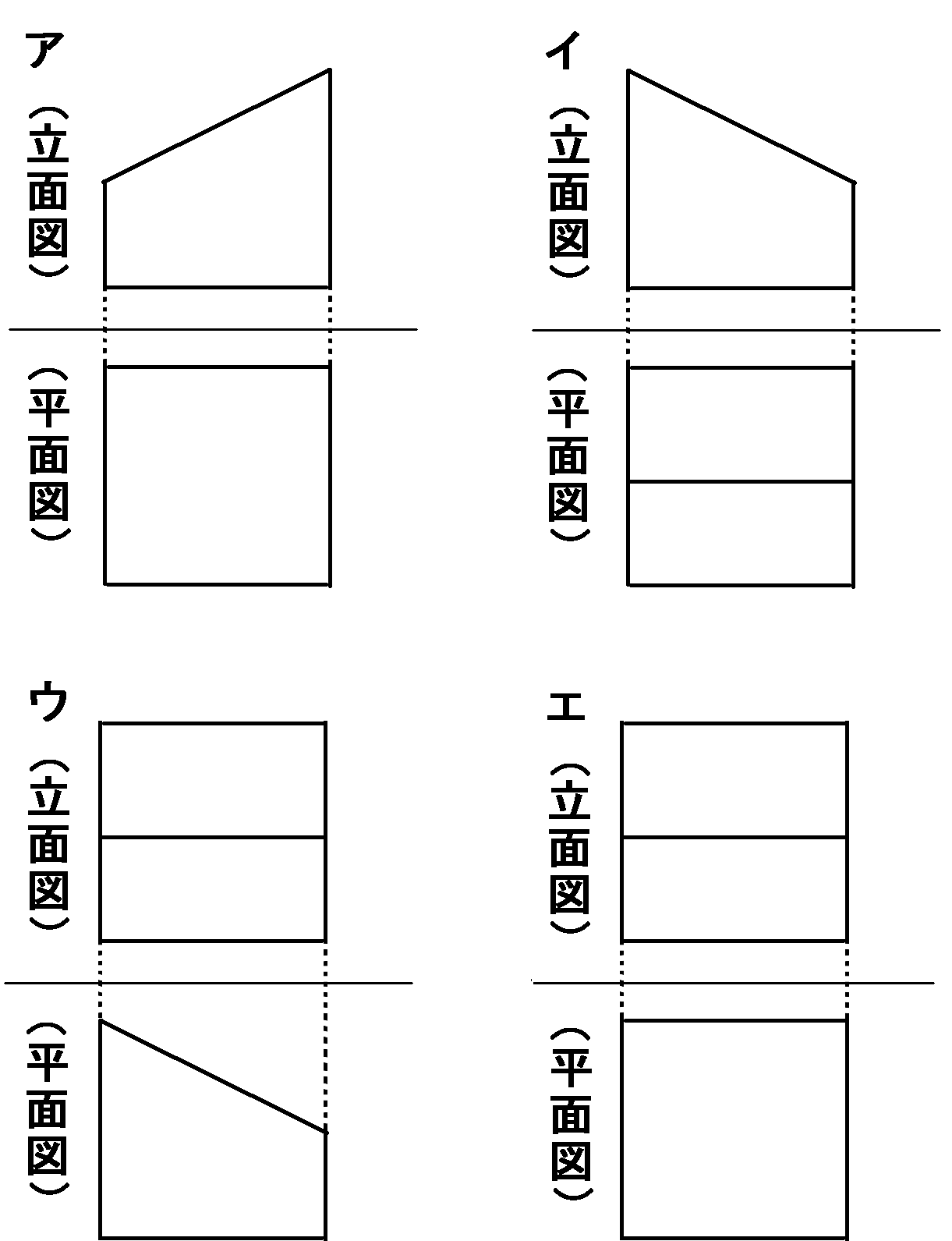
答え
ア,エ
立面図というのは、真横から見たときの図です。平面図というのは、真上から見たときの図です。投影図というのは、立面図と平面図をいっぺんに考えます。
真横からこんなふうに見えるように見たときに、真上から見たらどう見えるか、というのをいっぺんに表した図です。
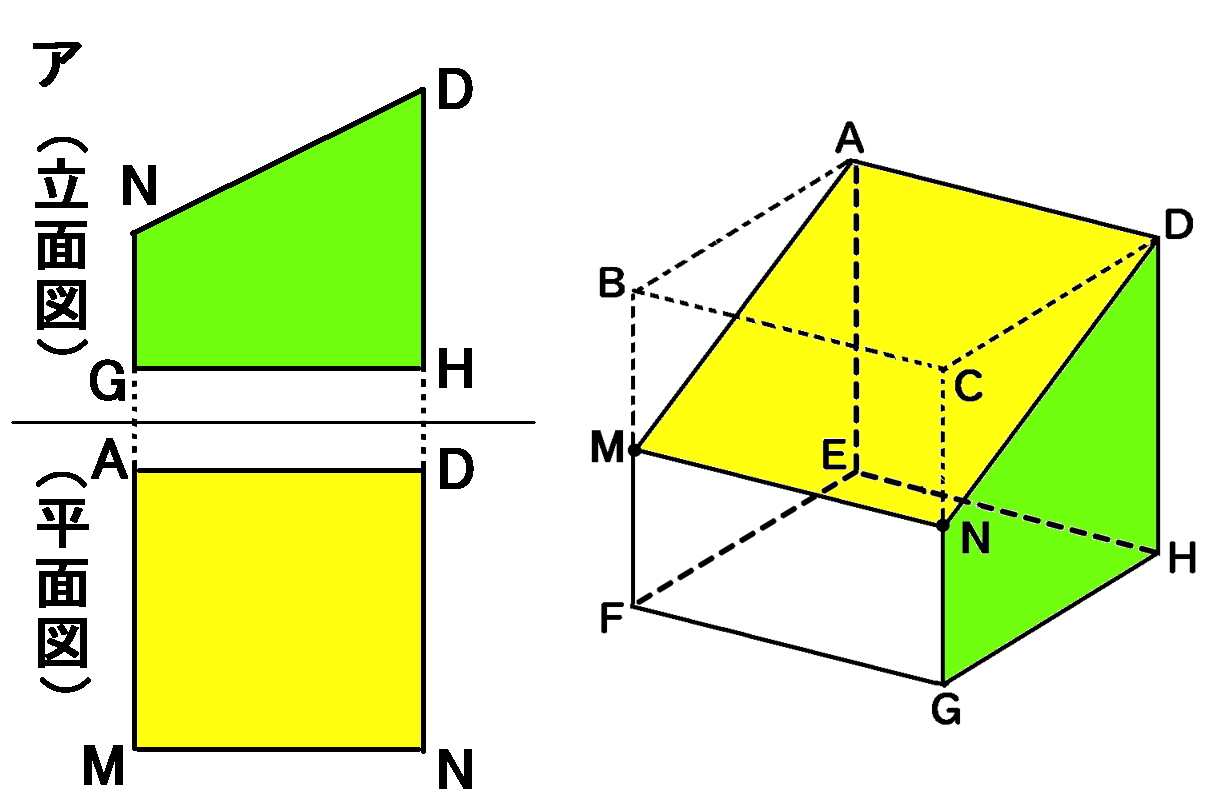
アは、こんなふうに見ることは可能です。投影図として、正しいといえます。参考になるように、色分けしましたので、これで考えてください。
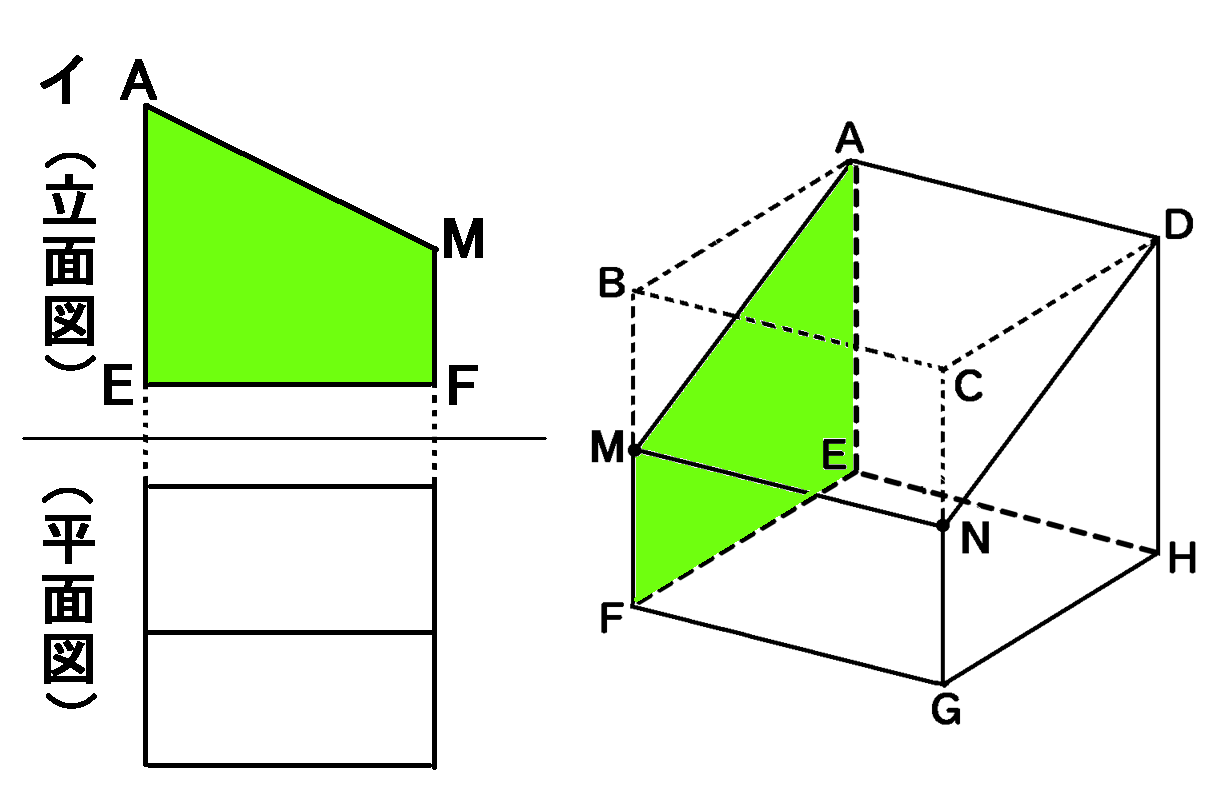
イは、こんなふうに見ることはできません。立面図(真横から見た図)がイのようになるように見たとき、平面図(真上から見た図)は、イのようにはなりません。
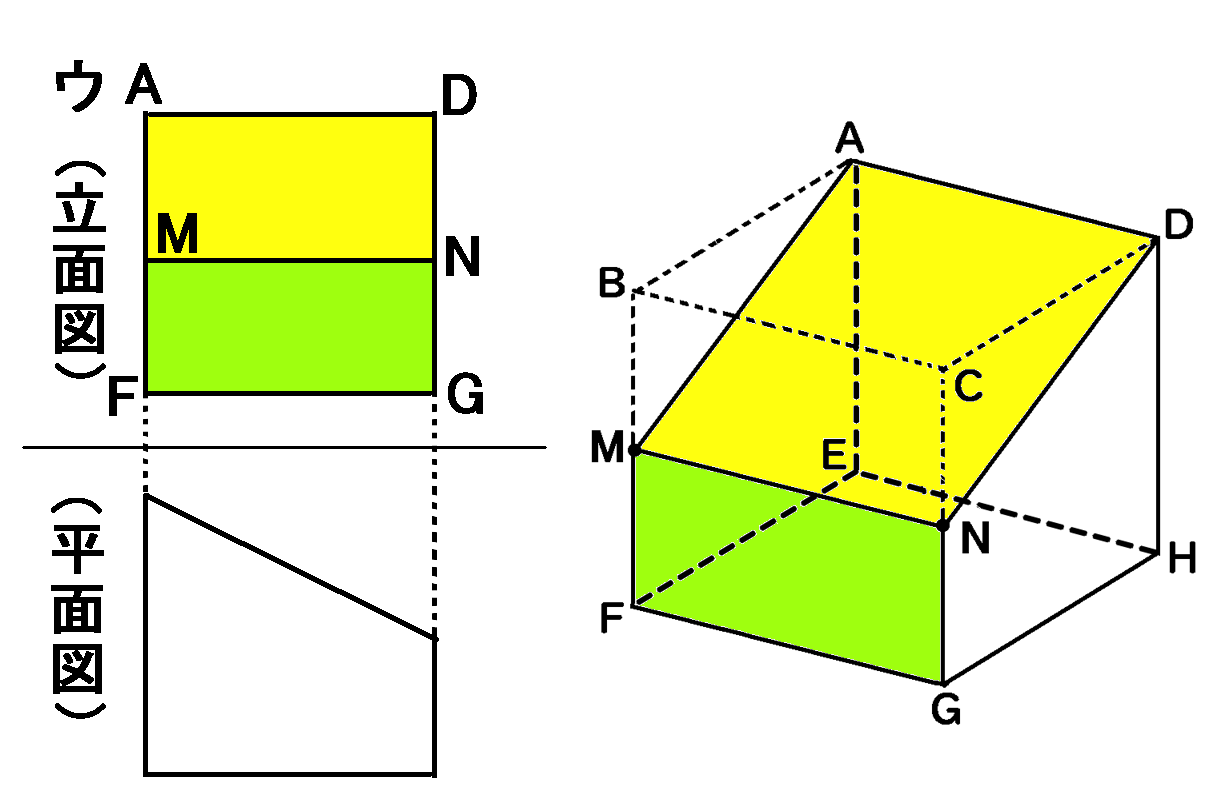
ウも、こんなふうに見ることはできません。立面図(真横から見た図)がウのようになるように見たとき、平面図(真上から見た図)は、ウのようにはなりません。
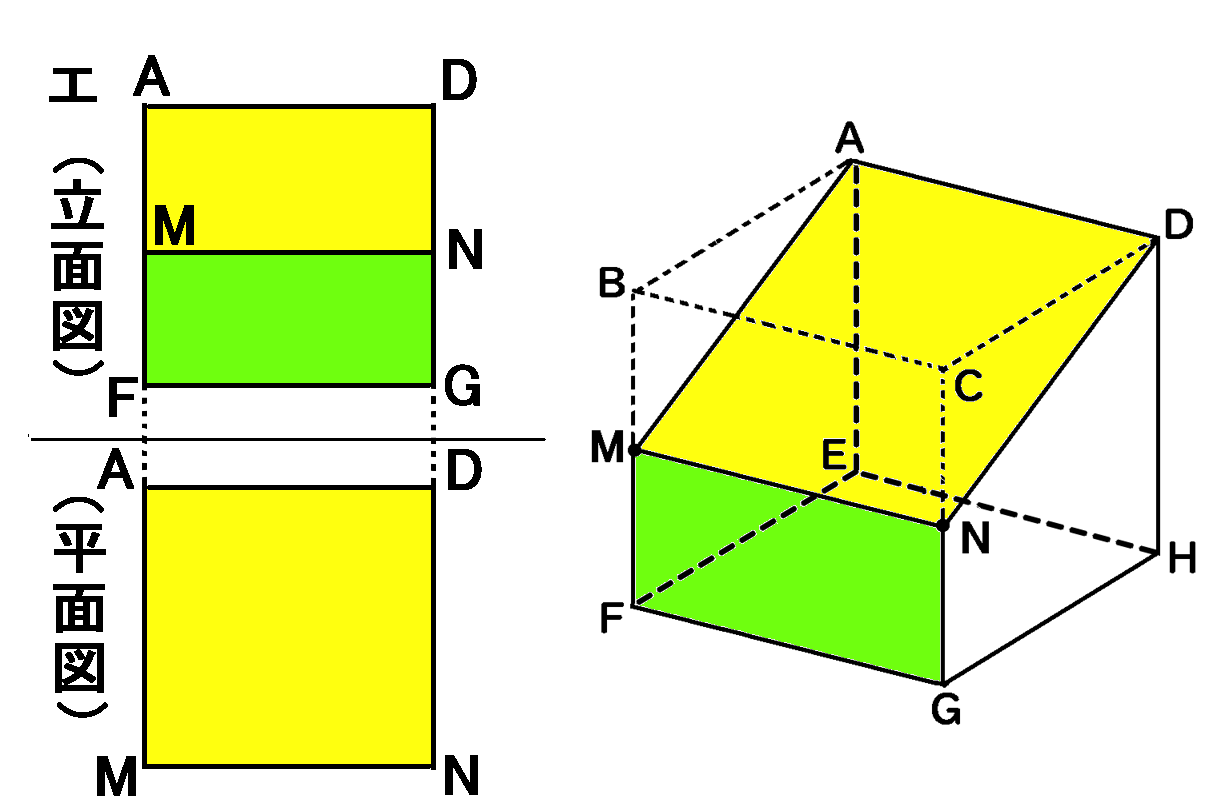
エは、こんなふうに見ることは可能です。投影図として、正しいといえます。
(2) 四角形$AMND$の面積
答え
$2\sqrt{5}cm^2$
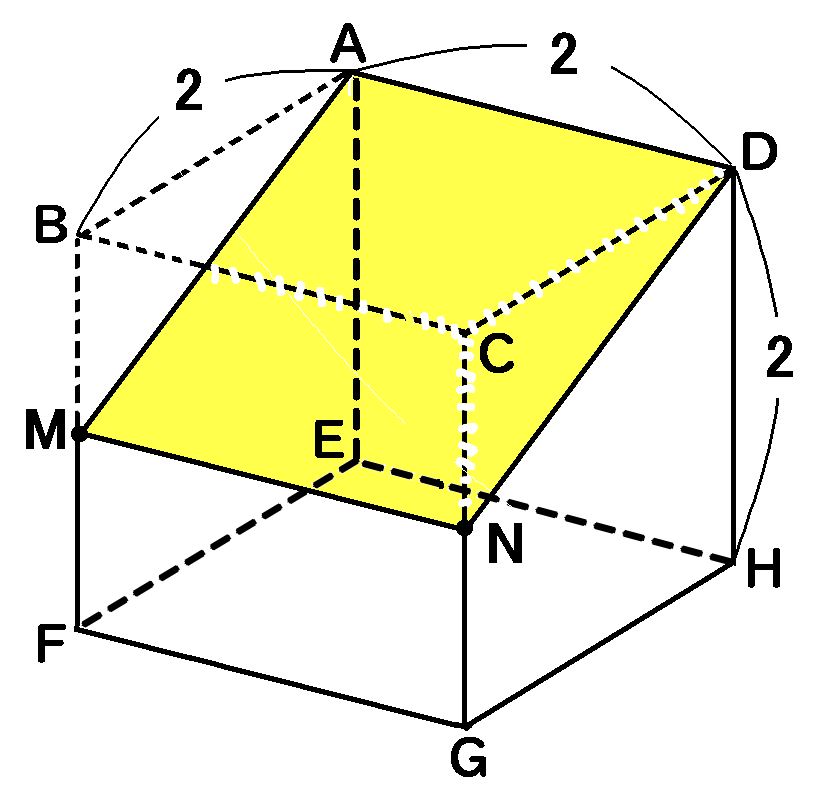
四角形$AMND$は長方形になります。長方形の面積は、縦$\times$横です。
横を$AD$とすれば縦は$AM$です。
【$AD$の長さ】
仮定から$AD=2cm$です。
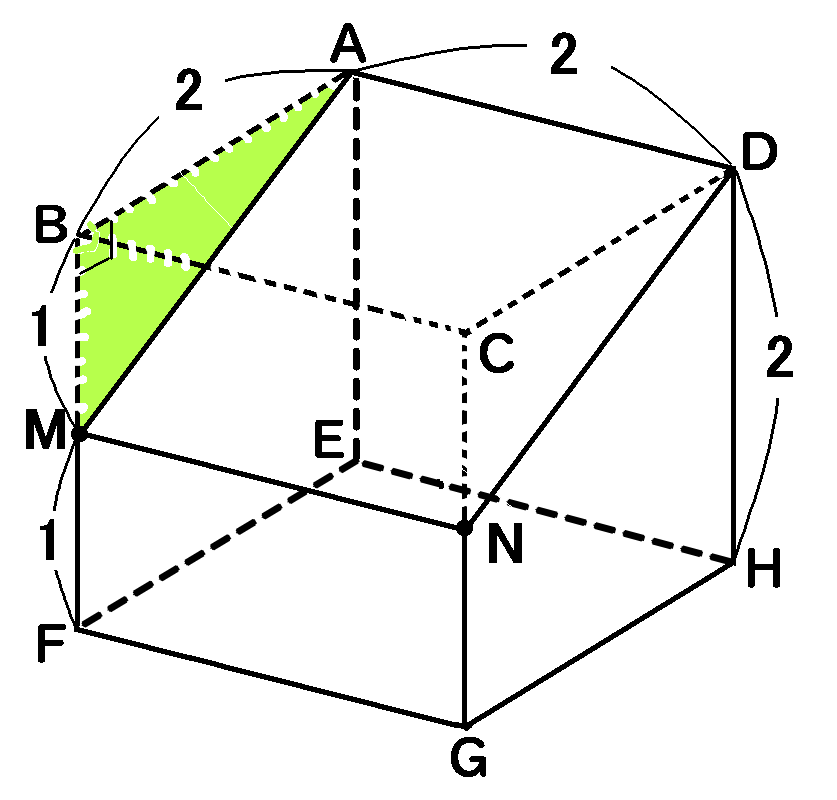
【$AM$の長さ】
$AM$は、 $\triangle ABM$で考えます。
$\triangle ABM$は$\angle ABM=90^{ \circ }$の直角三角形だから、三平方の定理により、
\begin{eqnarray*}
(AM)^2&=&(AB)^2+(BM)^2\\
&=&2^2+1^2\\
&=&5\\
AM>0なので\\
AM&=&\sqrt{5}cm
\end{eqnarray*}
なので、四角形$AMND$の面積は、
$$AD\times AM=\sqrt{5}\times2=2\sqrt{5}cm^2$$
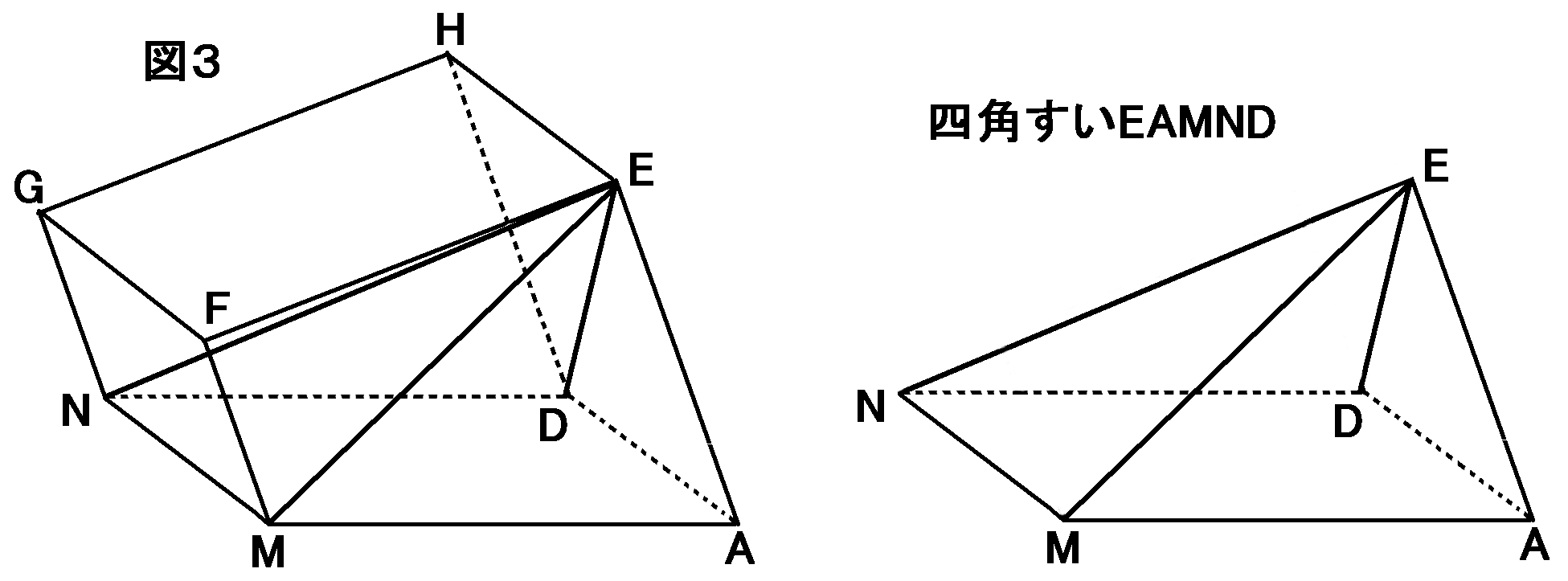
(3) 立体$P$で、点$E,A,M,N,D$を頂点とする四角すい$EAMND$の体積を求めよ。
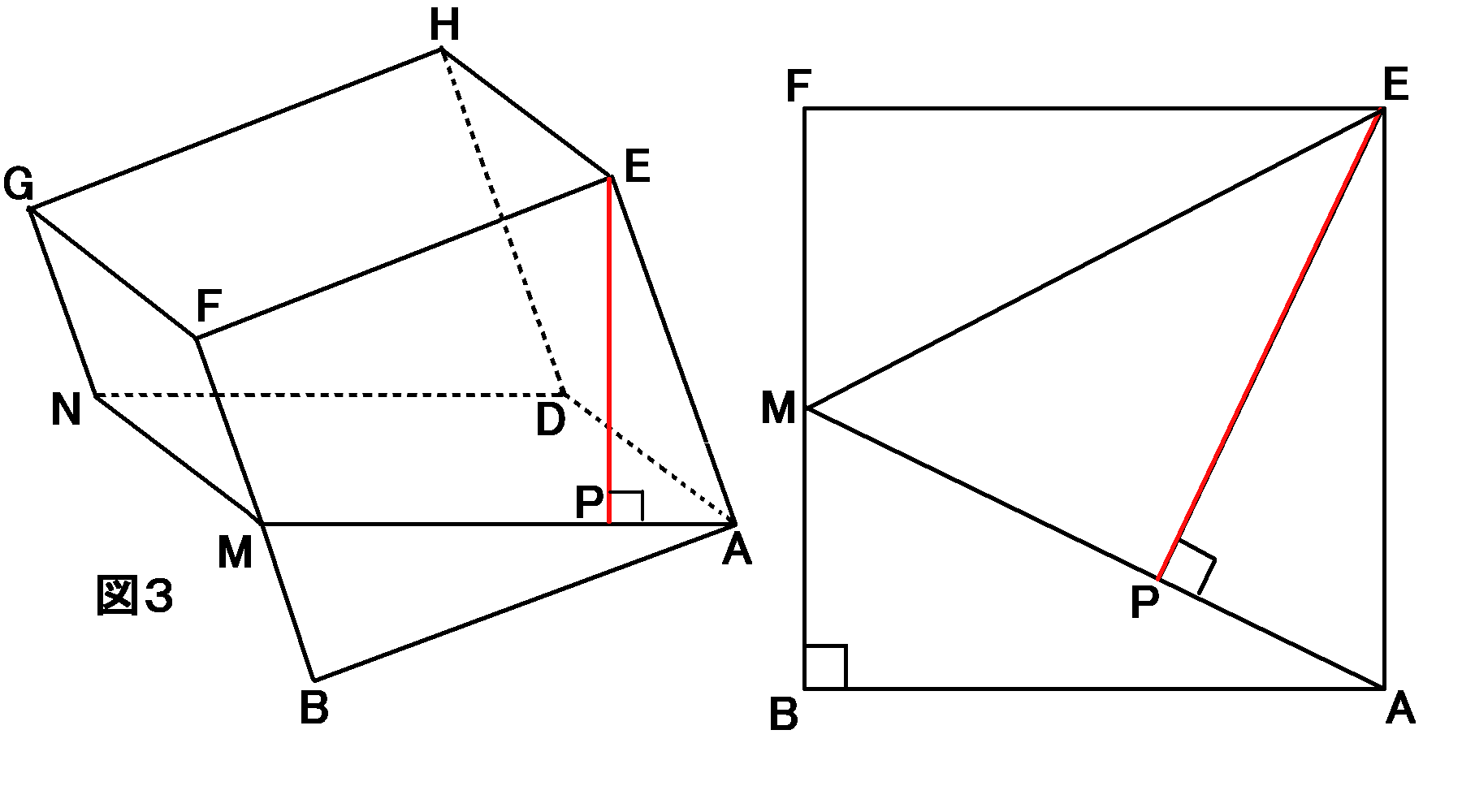
なお、下の図2,図3は四角すい$EAMND$の辺や位置関係を考えるために、立体$P$をそれぞれ
面$DNGH$、面$AMND$が下になるように置いたものである。

答え
$\cfrac{8}{3}cm^3$
四角すい$EAMND$の体積を求めよとのことですので、それはどんな四角すいなのか、図1図2図3に線をかきくわえてみましょう。
点$E,A,M,N,D$をむすんだ線です。するとこんな感じになります。
四角すいというからには、底面が四角形で、三角形の側面が4つあって、体積は底面積$\times$高さ$\times\cfrac{1}{3}$をやればOKです。
じゃあどこを底面だとおもえばよいのでしょうか。四角形になっている面はどこでしょうか。面$AMND$ですよね。なので図3があるわけです。親切な問題です。図3があるので、考えやすいです。図3をもとにして考えていきましょう。
【底面積】
四角形$AMND$の面積は、(2)の問題でもう求めています。 $2\sqrt{5}cm^2$です。
【高さ】
面$AMND$を底面としてみたとき、高さは頂点$E$から面$AMND$にまっすぐおろした線になります。それはどこを通るのでしょうか。面$AMND$と
面$EFMA$は垂直ですから、この線は面$EFMA$上にあることになります。なので垂線は辺$MA$と交わることになります。点$E$を通る$MA$の垂線と
$MA$との交点を$P$とすると、$EP$が、面$AMND$を底面としてみたときの四角すいの高さになります。赤い線がこの場合の高さです。
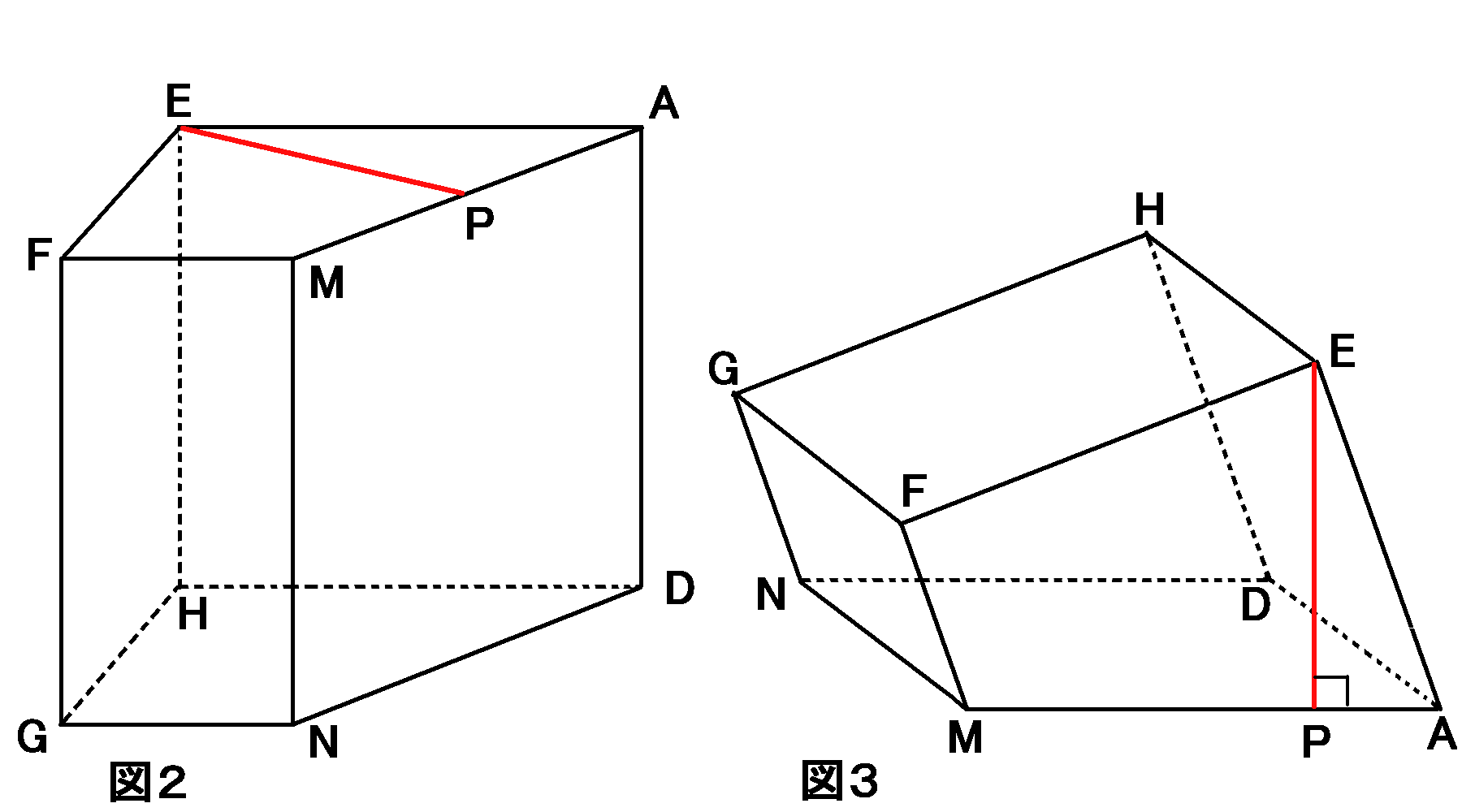
それでは$EP$の長さを求めていきましょう。2通りのやり方で説明します。相似を利用するやり方と、面積を利用するやり方です。まず、
相似を利用するやり方で説明します。図3で省略されてしまった点$B$を復活させます。すると、下の左側の図のようになります。この図の、
面$FBAE$という正方形をとりだして、$BA$を水平にして描いたのが右側の図です。
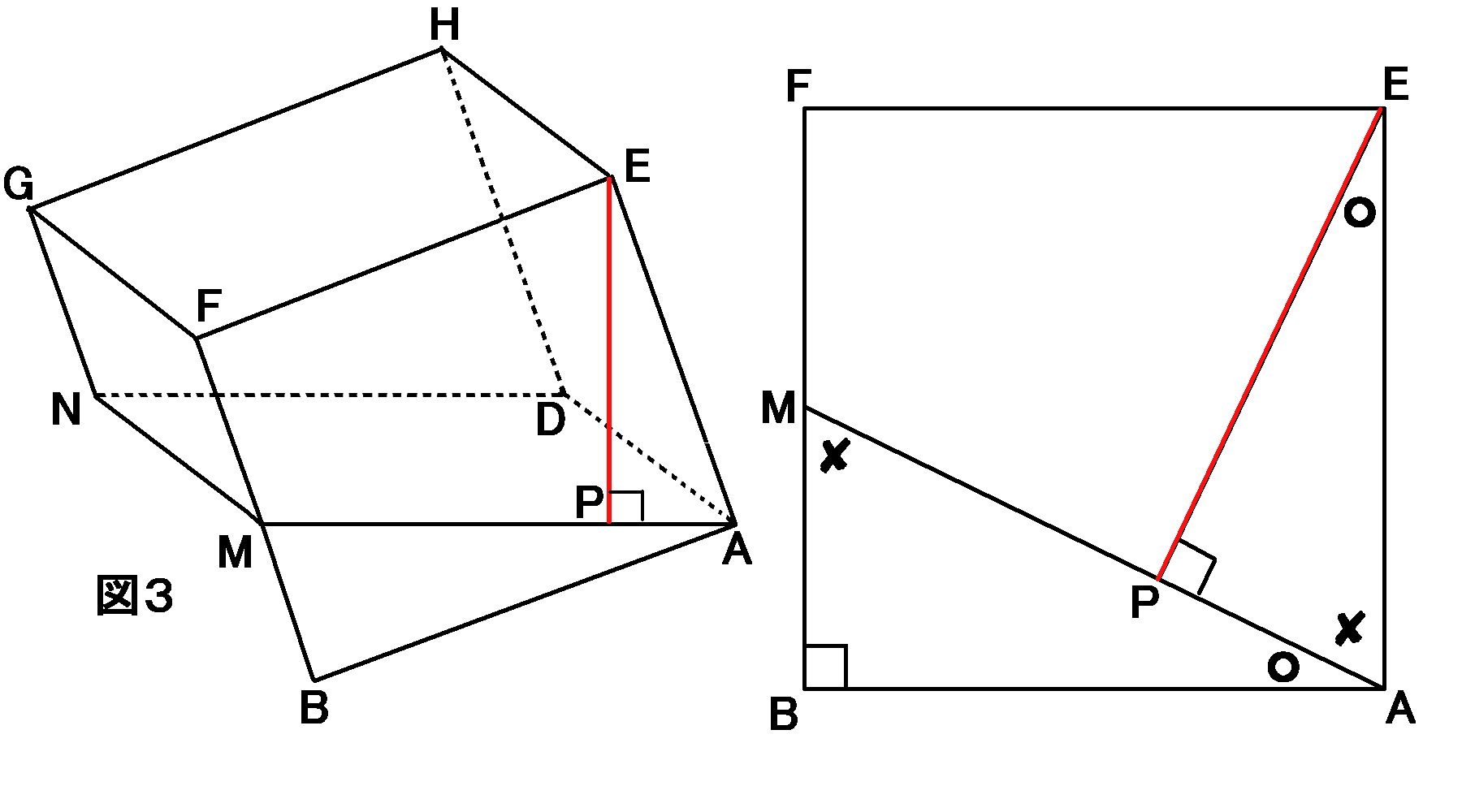
右側の図で、○と☓を足すと$90^{ \circ }$になるので、2か所ある○と☓の角度はどちらも同じ大きさです。
なので$\triangle MBA$ ∽$\triangle APE$
です。この相似を使えば$EP$が求まります。
まず、$\triangle MBA$で、三平方の定理から$MA$を求めます。
$\triangle MBA$で、仮定より、$MB=1,BA=2,\angle MBA=90^{ \circ }$
三平方の定理により、
\begin{eqnarray*}
(MA)^2&=&(MB)^2+(BA)^2\\
&=&1^2+2^2\\
&=&5\\
MA>0なので\\
MA&=&\sqrt{5}cm
\end{eqnarray*}

$\triangle MBA$ ∽$\triangle APE$なのだから、
\begin{eqnarray*}
MA:AE&=&AB:EP\\
\sqrt{5}:2&=&2:EP\\
\sqrt{5}\times EP&=&2\times2\\
EP&=&\cfrac{4}{\sqrt{5}}cm
\end{eqnarray*}
あとで約分できることがよくあるので、ここでは分母の有理化はしません。
というわけで四角すい$EAMND$の高さがでました。底面積もだしてあります。なのでその体積は、
\begin{eqnarray*}
&&底面積\times高さ\times\cfrac{1}{3}\\
&=&2\sqrt{5}\times\cfrac{4}{\sqrt{5}}\times\cfrac{1}{3}\\
&=&\cfrac{8}{3}cm^3(答え)
\end{eqnarray*}
【$EP$のべつな求め方】
$EP$のべつな求め方で、面積を利用するやりかたを紹介します。
図3で省略されてしまった点$B$を復活させるところは同じです。下の左側の図です。この図の、
面$FBAE$という正方形をとりだして、$BA$を水平にして描いたのが右側の図です。
さきほどはここで、$EP$を求めるために$\triangle MBA$ ∽$\triangle APE$を利用したのですが、今回はそうではなく
$E$と$M$をむすんで、$\triangle MEA$の面積について考えます。
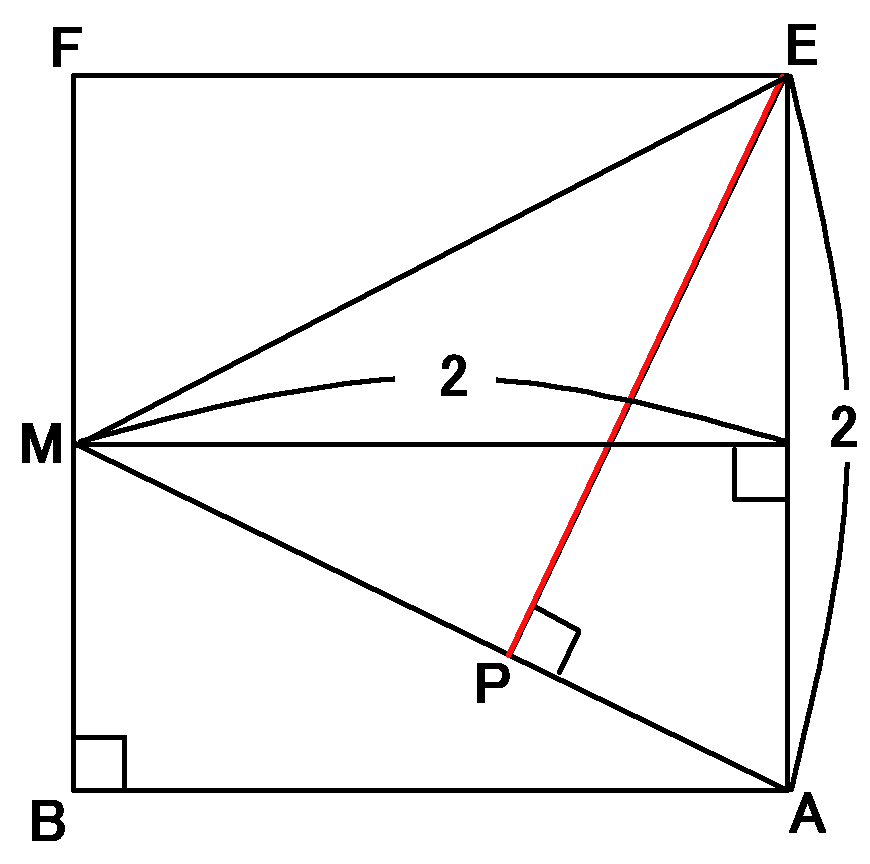
底辺を$EA$とすれば、その長さはもちろん$2cm$です。
高さは$M$から$EA$におろした垂線を考えればよいわけで、やっぱり$2cm$です。
なので$\triangle MEA$の面積の面積は
$$2\times2\times\cfrac{1}{2}=2cm^2$$
さて、$\triangle MEA$の面積の面積について、こんどは$MA$を底辺ということにして考えます。
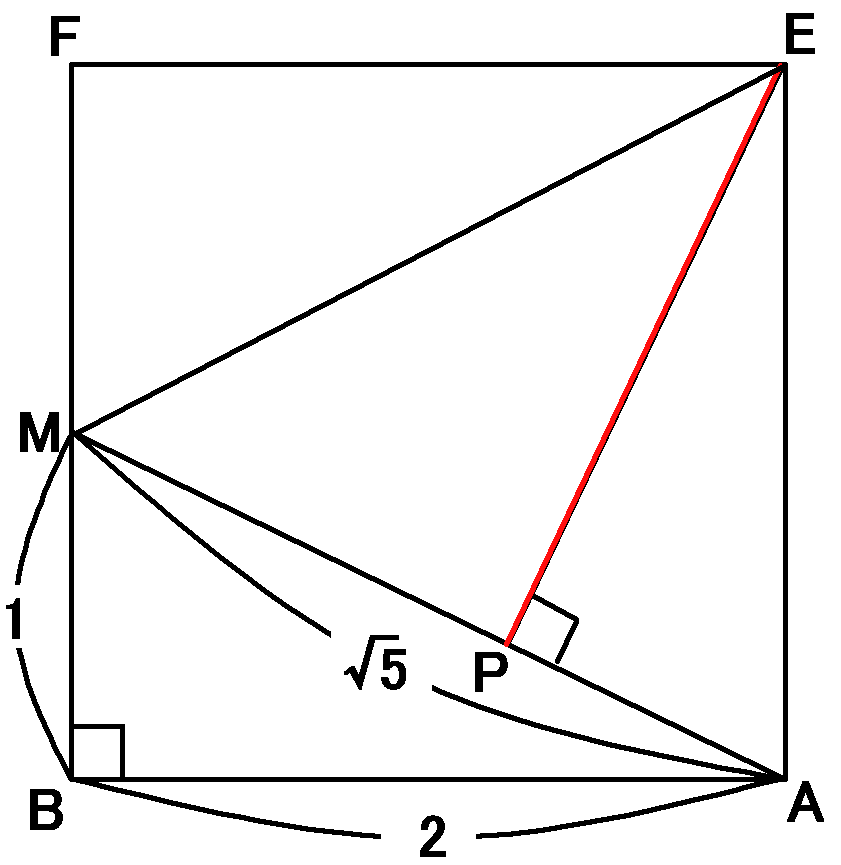
$MA$の長さは、$\triangle MBA$で、三平方の定理より、$\sqrt{5}cm$です。さきほども求めたので、くわしい計算は省略です。
んで、$MA$を底辺としたら、高さはもちろん、$EP$です。$\triangle MEA$の面積は$2cm^2$なので、じゃあ、
底辺$\times$高さ$\times\cfrac{1}{2}=$面積なのだから、
こんな式ができるはずです。
$$MA\times EP\times\cfrac{1}{2}=2$$
ということは、
$$\sqrt{5}\times EP\times\cfrac{1}{2}=2$$
これを解いて、
\begin{eqnarray*}
\sqrt{5}\times EP\times\cfrac{1}{2}&=&2(両辺に\times2)\\
\sqrt{5}\times EP&=&4\\
EP&=&\cfrac{4}{\sqrt{5}}cm
\end{eqnarray*}
ここからさきは、さきほどとおなじです。