数学 入試過去問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
【2021年の大問6】
図1は三角すいの展開図で、$AB=12cm,AC=9cm,ED=5cm$
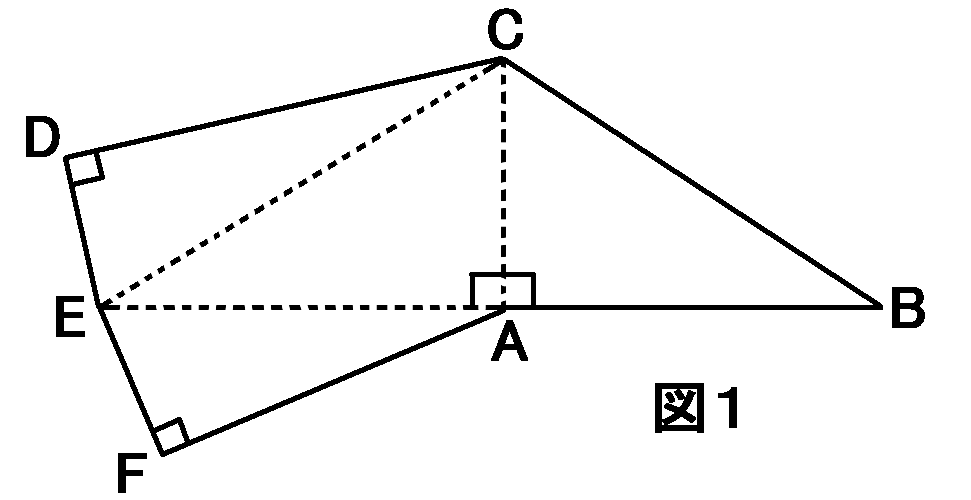
(1) $\triangle CDE$の面積を求めよ。
答え
$$\cfrac{75}{2}cm^2$$
三角すいの展開図です。組んだら三角すいになります。どことどこが重なるかを確認しましょう。同じ色のところが、組んだときに重なります。
破線は折り目です。こういうときの破線は、折り目ということになっとります。
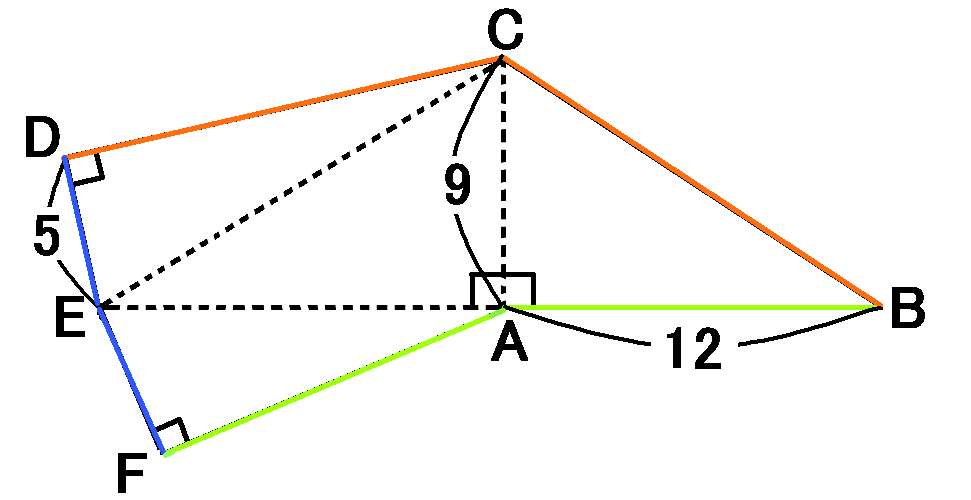
んで、$\triangle CDE$の面積をきかれています。三角形の面積はもちろん、底辺$\times$高さ$\times\cfrac{1}{2}$です。
$DE\times CD\times\cfrac{1}{2}$をやればよく、$DE$の長さは与えられているので、あとは$CD$の長さがわかればOKです。
$CD$はの長さは$CB$の長さと同じです。$CB$は、$\triangle ABC$で、三平方の定理を使えば求められますね。
$\triangle ABC$で、仮定より、$CA=9,AB=12,\angle CAB=90^{ \circ }$
三平方の定理により、
\begin{eqnarray*}
(CB)^2&=&(CA)^2+(AB)^2\\
&=&9^2+12^2\\
&=&225\\
CB>0なので\\
CB&=&\sqrt{225}=15cm
\end{eqnarray*}
ちなみにこれ、$\triangle ABC$は辺の比が$3:4:5$の三角形であることに気づけば、もっと計算はラクです。
というわけで、$\triangle CDE$は、直角をはさむ2辺(底辺と高さ)が$5cm$と$15cm$の三角形なので、その面積は、
$$5\times15\times\cfrac{1}{2}=\cfrac{75}{2}cm^2$$
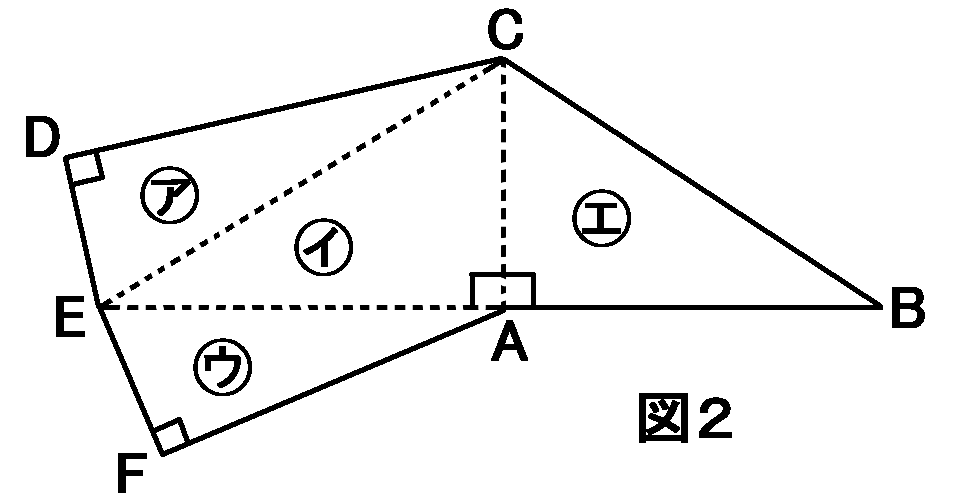
(2) 図2のように展開図に面㋐、面㋑、面㋒、面㋓と名前をつける。面㋓と垂直になるのは、どの面か。面㋐~㋒のの中からすべて選んでその記号を答えよ。
また、三角すいの体積を求めよ。
答え
㋓と垂直になる面…面㋐、面㋒
体積…$90cm^3$
三角すいというのは、四面体です。4つの三角形があって、どれも底面になりえます。この展開図の三角すいの体積を求めようとしたときに、
三角すいの体積はもちろん、底面積$\times$高さ$\times\cfrac{1}{3}$をやればよいのですが、どこを底面にして考えたらラクかを伝えようとしてくれています。
そして、それは㋒か㋓がいいんだよ、と伝えようとしてくれています。そういう問題なんじゃないかなあ、とおもいます。
まあともかく、㋓と垂直になるのはどの面か、ということなので、㋓を底面としてこの展開図を組んだときの、できあがった三角すいの見取り図をなんとなくかいてみましょう。
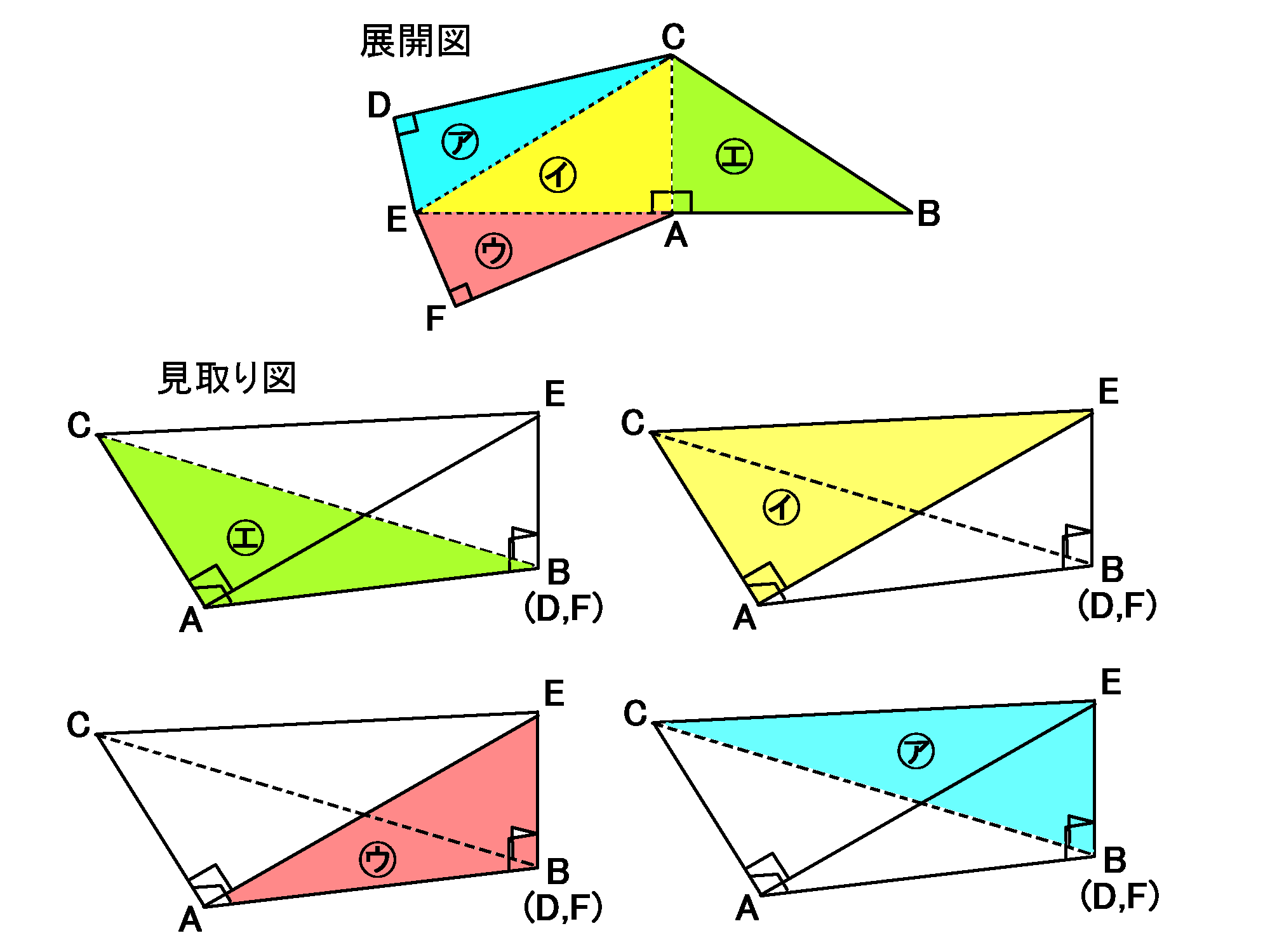
いちばんうえが展開図で、下のの4つが㋓を底面としたときの見取り図です。
色分けをしてみたので、しばらく眺めて考えてみてください。どこがどうなっているのか、わかるまで見てください。見えてきたら、じゃあ、㋓と垂直になる面は
どこかを考えてみましょう。㋑ではないのは明らかです。見るからにこれはむりです。答えは、㋐か、㋒か、㋐と㋒の両方か、です。
ところで、平面$P$と直線$l$が垂直になる条件は、平面$P$上の交わる2直線の両方に$l$が垂直であること、です。
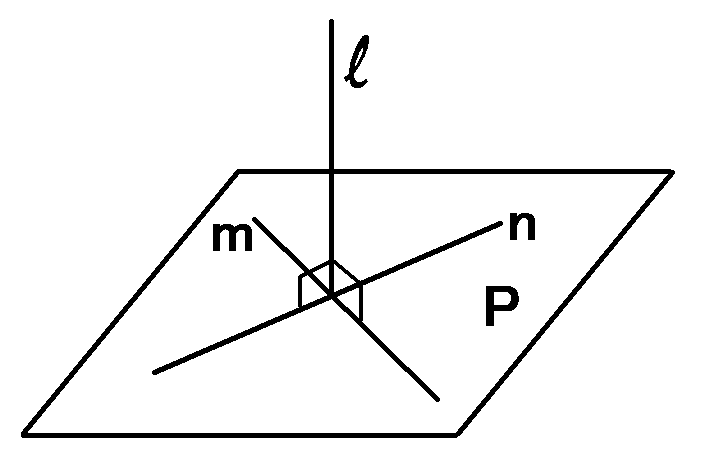
右の図で、直線$l$と直線$m$が垂直、直線$l$と直線$n$が垂直なら、$m$と$n$の両方をふくんだ面$P$と、$l$は垂直になります。
なぜそういえるのか、その証明は中学ではでてこないような気がするのですが(高校ではでてきます)、知識として、知っておきましょう。
また、ある面$P$に対して垂直な直線をふくんでいる面は、面$P$に垂直になります。
ということをふまえて。
仮定から、$EB \perp AB,EB \perp CB$です。
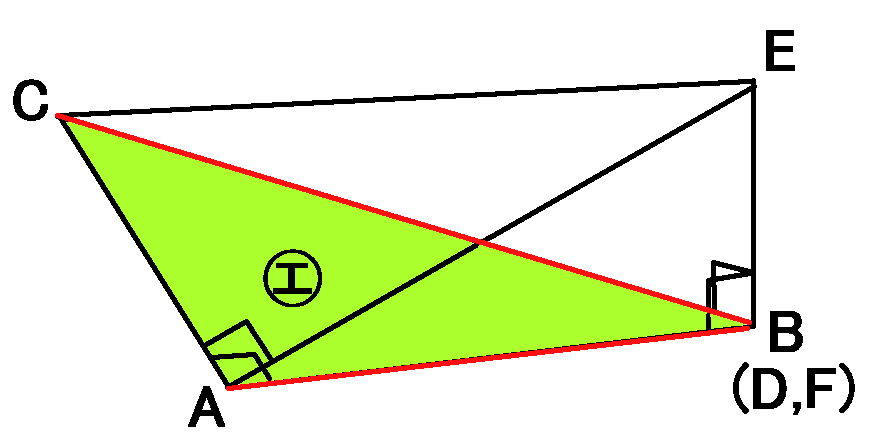
直線$AB,CB$は、ともに面㋓にふくまれます。$EB$はその2つの直線に垂直です。なので、面㋓と$EB$は垂直ということになります。
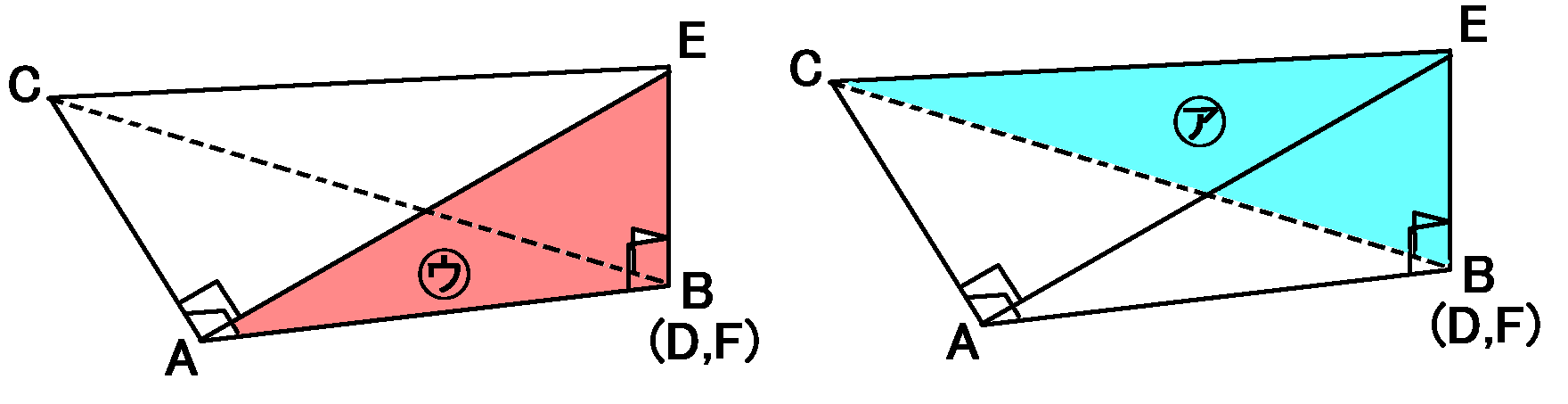
$EB$は面㋐にふくまれるので、面㋐と面㋓は垂直です。
$EB$は面㋒にもふくまれるので、面㋒と面㋓も垂直です。
なので、面㋓と垂直になる面は、㋐と㋒です。
【三角すいの体積】
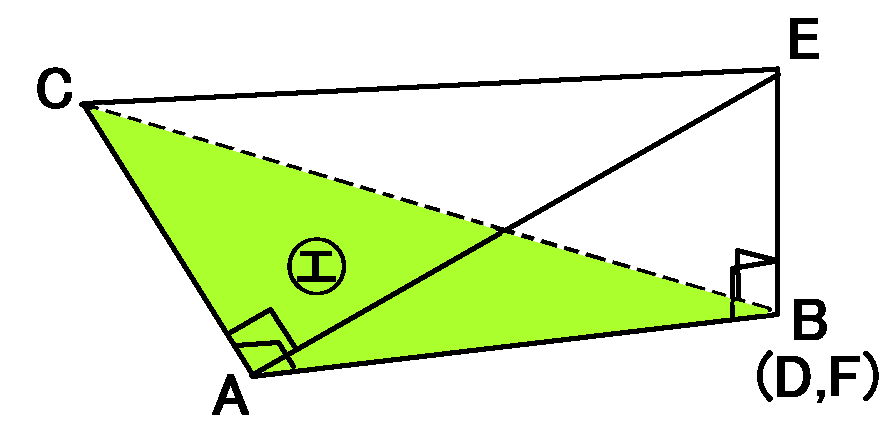
この三角すいは、面㋓を底面とすれば、高さは$EB$になります。面㋓と$EB$は垂直だからです。
なので、この三角すいの体積は、面㋓の面積$\times EB$の長さ$\times \cfrac{1}{3}$をやればOKです。
【面㋓の面積】
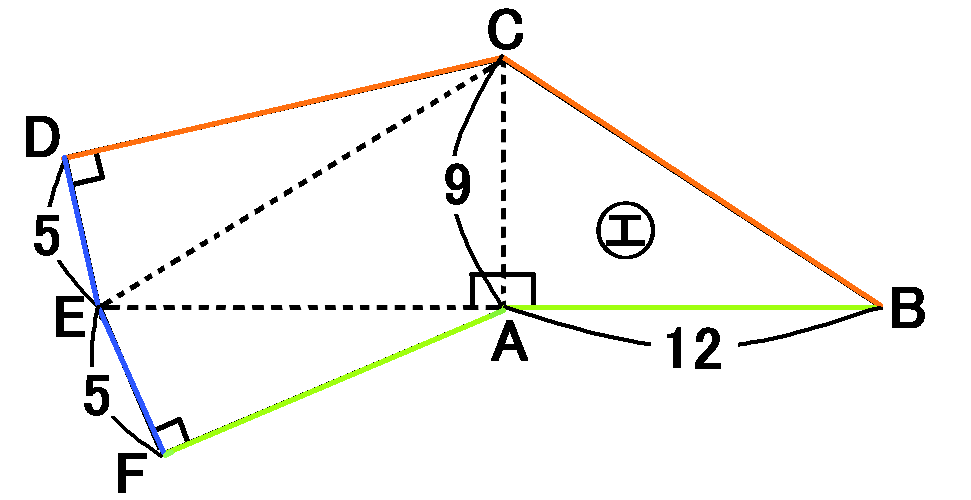
面㋓というのは$\triangle ABC$のことです。仮定から、$AB=12cm,AC=9cm,\angle CAB=90^{ \circ }$ですから、その面積は、
$$12\times9\times\cfrac{1}{2}=54cm^2$$
あと、$EB$の長さですが、$EB=ED=EF=5cm$です。
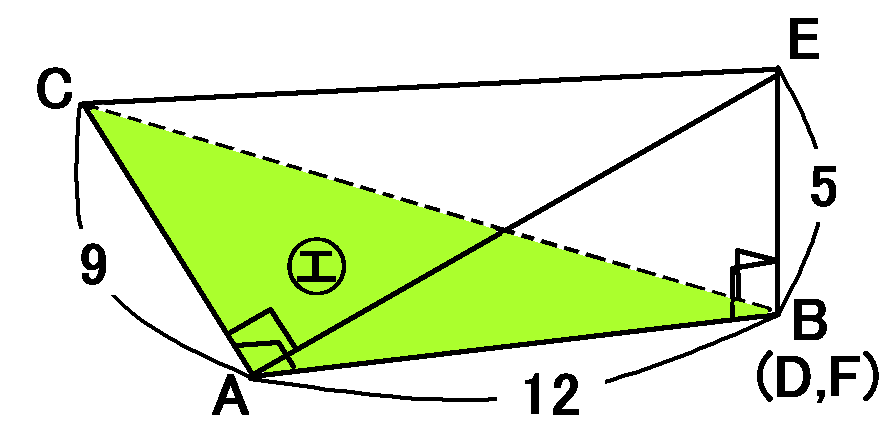
なので、この三角すいの体積は、
\begin{eqnarray*}
&&底面積\times 高さ\times\cfrac{1}{3}\\
&=&54\times5\times\cfrac{1}{3}\\
&=&90cm^3\\
\end{eqnarray*}
(3) 三角すいの高さが一番高くなるのはどの面を下にしたときか。図2の面㋐~㋓の中から一つ選んでその記号を答えよ。
また、三角すいの高さが一番低くなるのはどの面を下にしたときか。図2の面㋐~㋓の中から一つ選んでその記号を答えよ。
答え
高さが一番高くなるときに下にする面…㋒
高さが一番低くなるときに下にする面…㋑
三角すいというのは、四面体です。4つの三角形があって、どれも底面になりえます。では、展開図がこのような三角すいの場合は、どこを底面にしたときに、
高さが一番高くなりますか。また、一番低くなりますか、という問題です。
すい体の体積というは、底面積$\times$高さ$\times\cfrac{1}{3}$です。
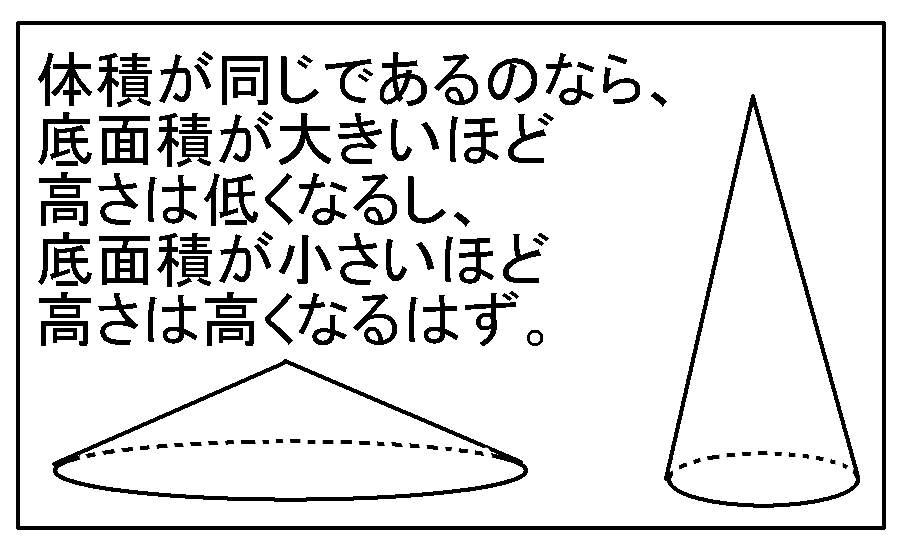
もし体積がおなじであるのなら、底面積が大きければ大きいほど、高さは低くなります。また、底面積が小さければ小さいほど、高さは高くなります。
そりゃそうですよね。体積がおなじであるのなら、底面積と高さは反比例の関係になっている、といういいかたもできます。
というわけで、もう、なにがいいたいか、わかってもらえているでしょうか。
面㋐~㋓まで、どこを底面にしようとも、三角すいの体積はおなじなのだから、底面積が一番小さいとき、高さが一番高くなります。
また、底面積が一番大きいとき、高さが一番低くなります。
なので、この問題は、面㋐~㋓まで、4つの面の面積をだせば、それでほぼおしまいです。正直に高さをだして比べる必要はありません。
面積をだせばいけます。じゃあ、それぞれの面積を求めていきましょう。
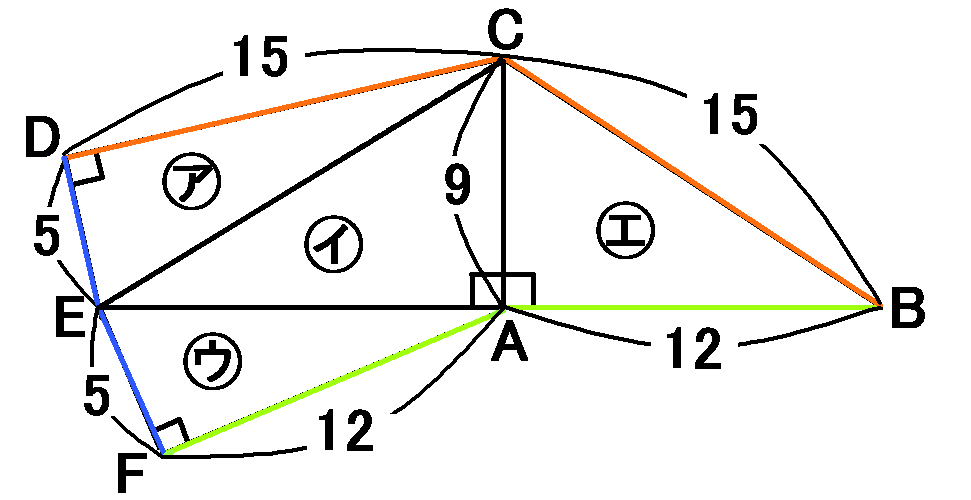
手始めに、展開図に、わかる辺の長さをかきくわえていきましょう。
仮定から、$AB=12cm,AC=9cm,ED=5cm$です。あと、$AB=AF,ED=EF$です。あと、(1)の問題で、$CB=15$を求めています。さらに、$CB=CD$です。
ここまではすんなりかきこめるはずです。あと、$AE$の長さですが、これは、
$\triangle EFA$で、$AF=12,EF=5,\angle EFA=90^{ \circ }$
三平方の定理により、
\begin{eqnarray*}
(AE)^2&=&(AF)^2+(EF)^2\\
&=&12^2+5^2\\
&=&169\\
AE>0なので\\
AE&=&\sqrt{169}=13cm
\end{eqnarray*}
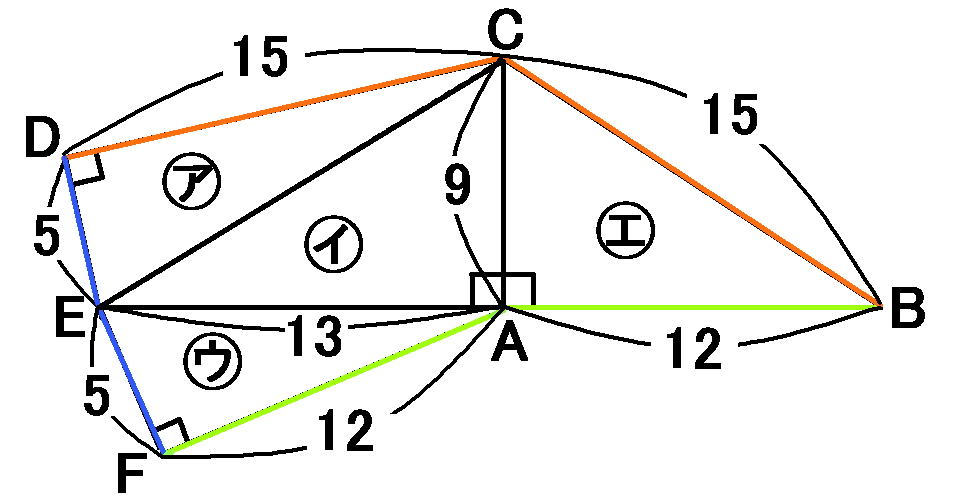
これでもう、面㋐~面㋓まで、ぜんぶの面積がだせます。
【面㋐の面積】
これは(1)の問題で求めています。$\cfrac{75}{2}cm^2$です。
【面㋑の面積】
$$13\times9\times\cfrac{1}{2}=\cfrac{117}{2}cm^2$$
【面㋒の面積】
$$5\times12\times\cfrac{1}{2}=30cm^2$$
【面㋓の面積】
これは(2)の問題で求めています。$54cm^2$です。
というわけで、面積がいちばん小さいのは、㋒です。この面を底面としたとき、高さが一番高くなります。
また、面積がいちばん大きいのは、㋑です。この面を底面としたとき、高さが一番低くなります。