数学 入試過去問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
【2022年の大問6】
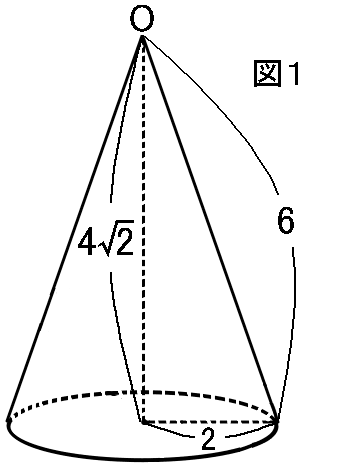
図1は底面の半径が$2cm$、母線の長さが$6cm$、高さが$4\sqrt{2}cm$、頂点がOの円すい
円周率を$\pi$とする
(1) 円すいの体積
答え
$$\cfrac{16\sqrt{2}}{3}\pi cm^3\left(\quad \cfrac{16}{3}\sqrt{2}\pi , \quad \cfrac{16\sqrt{2}\pi}{3} なども可\right)$$
円すいの体積はもちろん、底面積$\times$高さ$\times\cfrac{1}{3}$です。
底面は、半径が$2cm$の円なので、その面積は$4\pi cm^2$、高さは$4\sqrt{2}cm$です。なのでこの円すいの体積は、
$$4\pi\times4\sqrt{2}\times\cfrac{1}{3}=\cfrac{16\sqrt{2}}{3}\pi cm^3$$
(2) 円すいの表面積
答え
$$16\pi cm^2$$
円すいの表面積は、底面積と側面積の和です。それぞれを求めて、足せばOKです。
【底面積】
底面は、半径が$2cm$の円なので、その面積は$4\pi cm^2$です。
【側面積】
円すいの側面積は、母線$\times$底面の半径$\times \pi$です。なので、
$$6\times2\times\pi=12\pi cm^2$$
【表面積】
表面積は、
$$4\pi+12\pi=16\pi cm^2$$
これが答えです。
【円すいの側面積が母線$\times$底面の半径$\times \pi$になることの説明】
円すいの母線を$l$、底面の半径を$r$とすると、側面積は$\pi lr$になります。その理由を説明します。
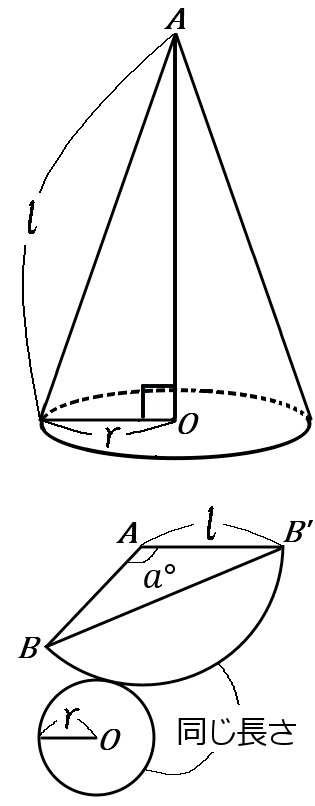
まず、展開図で考えます。
円すいを展開図にすると、側面はおうぎ形になります。おうぎ形の半径は、母線とおなじです。$l$です。
おうぎ形の面積は、もともとの円の面積$\times\cfrac{中心角}{360}$です。
中心角を$a$ということにすると、もともとの円の面積$\times\cfrac{a}{360}$です。
おうぎ形の中心角は、$\cfrac{弧}{もともとの円の円周}\times360$です。
弧は底面の円周と等しいっす。
というわけで、ひとつひとつやっていくと、
<底面の円周>
$2\pi r$
<おうぎ形の弧>
おうぎ形の弧は底面の円周とおなじなので、$2\pi r$
<おうぎ形の、もともとの円の円周>
おうぎ形の半径は$l$なので、円周は$2\pi l$
<おうぎ形の中心角>
$\cfrac{2\pi r}{2\pi l}\times360=\cfrac{360r}{l}$
<おうぎ形の面積>
\begin{eqnarray*}
&&もともとの円の面積\times\cfrac{中心角}{360}\\
&=&\pi l^2\times\cfrac{\left(\cfrac{360r}{l}\right)}{360}\\
&=&\pi l^2\times\cfrac{360r}{l}\div 360\\
&=&\pi l^2\times\cfrac{360r}{l}\times\cfrac{1}{360}\\
&=&\pi lr\\
\end{eqnarray*}
展開図のおうぎ形の面積というのは、円すいの側面積のことです。
なので、円すいの側面積は$\pi lr$です。母線$\times$底面の半径$\times \pi$です。
【おうぎ形の面積】
ところで、おうぎ形の面積は、半径$\times$弧$\times\cfrac{1}{2}$でOK、というのもあります。
これを知っていると、この場合のおうぎ形(半径が$l$で弧が$2\pi r$)の場合は、
\begin{eqnarray*}
&&半径\times弧\times\cfrac{1}{2}\\
&=&l\times2\pi r\times\cfrac{1}{2}\\
&=&\pi lr\\
\end{eqnarray*}
こんなふうにだすこともできます。
もし、【円すいの側面積は母線$\times$底面の半径$\times \pi$になる】ことも、【おうぎ形の面積$=$半径$\times$弧$\times\cfrac{1}{2}$】であることも
知らない(忘れている)のであれば、おうぎ形の中心角をもとめて、地道にやっていってください。まあ、
そいういうひとも多いのではないかと思います。地道にやっていってください。やってみせます。こんな感じです。
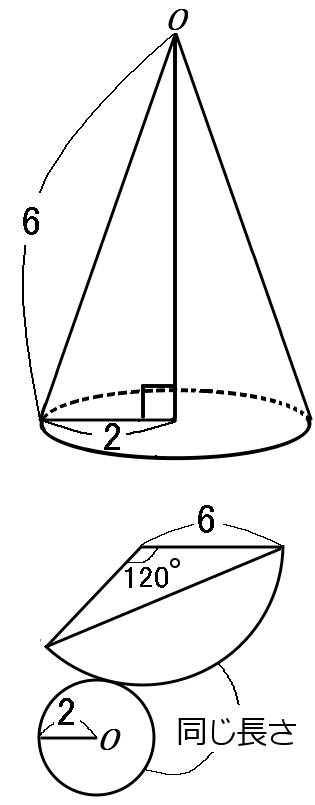
まずは展開図をかいて、わかっているところの長さもかきくわえておきましょう。ほしいのは、底面積と、側面積です。底面積は$4\pi cm^2$です。
側面積というのは、展開図のおうぎ形の面積になります。
おうぎ形の面積ですが、まず孤の長さをだしましょう。これは底面の円の円周とおなじです。なので、$4\pi cm$です。
つぎに、おうぎ形のもとの円の円周をだしましょう。おうぎ形のもとの円の半径は、母線とおなじです。$6cm$です。なので、
もとの円の円周は、$12\pi cm$です。
これらをもとにして、おうぎ形の中心角の大きさをだします。おうぎ形の中心角は、
\begin{eqnarray*}
&&\cfrac{孤}{円周}\times360\\
&=&\cfrac{4\pi}{12\pi}\times360\\
&=&120\\
\end{eqnarray*}
おうぎ形の面積は、もともとの円の面積$\times\cfrac{中心角}{360}$なので、
$$36\pi\times\cfrac{120}{360}=12\pi cm^2$$
なので表面積は、
$$4\pi+12\pi=16\pi cm^2$$
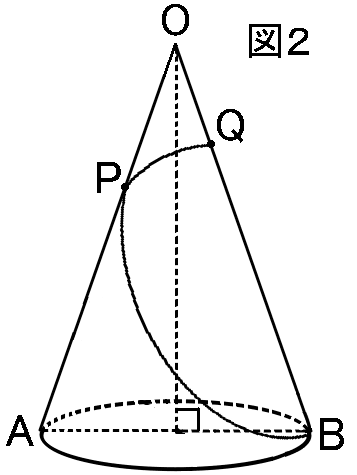
(3) 図2のように、底面の直径の1つを$AB$とする。点$P$は$OA$上の点で、$OP=2cm$であり、点$Q$は$OB$上を動く点である。
点$B$から点$P$を通るようにして点$Q$までひもをかける。ひもの長さが最短となるように点$Q$をとるとき、そのひもの長さを求めよ。
ただし、ひもの太さや伸び縮みは考えないものとする。
答え
$$2\sqrt{7}+\sqrt{3}(cm)$$
立体にひもをかける問題は、展開図で考えます。まず、展開図を考えましょう。円すいの展開図は、底面が円で側面がおうぎ形です。
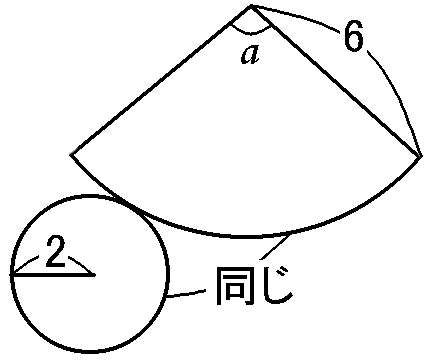
まだ中心角がわかっていません。だから最初の図のおうぎ形はテキトーです。まずは中心角を求めましょう。
おうぎ形の中心角は、$\cfrac{弧}{もともとの円の円周}\times360$です。
弧は底面の円周とおなじです。底面の半径は$2cm$だから円周は$4\pi cm$、おうぎ形の半径は$6cm$だからもともとの円の円周$12\pi cm$、なので、中心角$a$は、
$$a=\cfrac{4\pi}{12\pi}\times360=120^{ \circ }$$
これで中心角は$120^{ \circ }$だと求まりました。ちなみにですが、これ、求めるときに$\cfrac{弧}{もともとの円の円周}\times360$とやっていますが、
じつは$\cfrac{底面の半径}{おうぎ形の半径}\times360$とやればOKなんですよね。おうぎ形の半径というのは母線のことなので、
$\cfrac{底面の半径}{母線}\times360$とあらわすこともできます。こっちのほうがちょっと計算がラクです。
まあともかく中心角が求まりましたので、こんどはちゃんと、中心角を意識して展開図をかいてみましょう。
中心角が$120^{ \circ }$になる感じでおうぎ形をかいて、あとは点$A,B,P,Q$もかきくわえていきましょう。
ひもは$B$から$P$を通って$Q$にかかります。
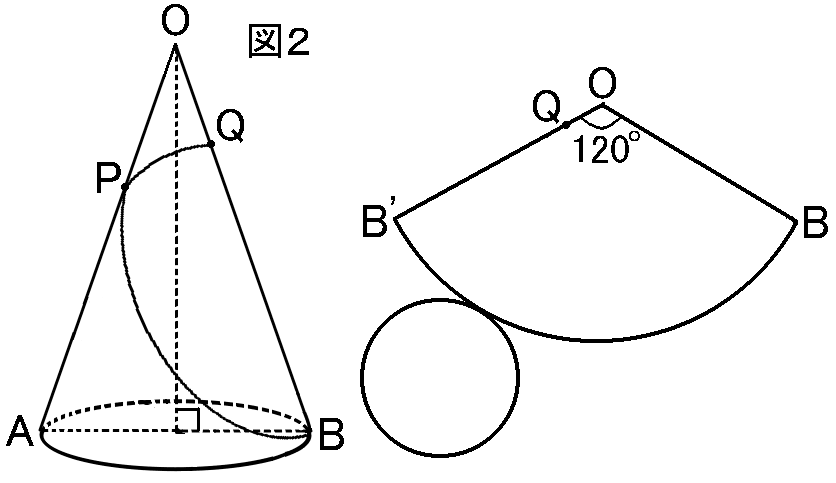
おうぎ形の右はじを$B$としたら、左はじも$B$になります。それだとわかりづらいので、ここは$B'$ということにしましょう。図のような感じです。
ひもを$B$からかけるなら、$Q$は$OB'$上にあるわけです。
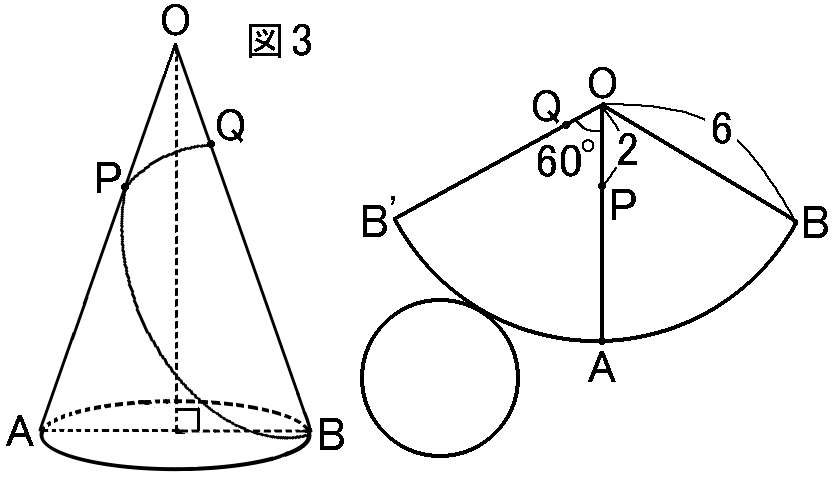
つぎに$A$がどこにあるかです。$AB$は底面の半径なのだから、展開図で、$A$は弧$\stackrel{\huge\frown}{BB'}$の真ん中になるはずです。そういう感じに点$A$とり、$O$と$A$をむすびます。
このとき、$\angle BOA=\angle B'OA=60^{ \circ }$になっています。そして、$OA$上に$OP=2cm$となる点$P$をとります。ここまでが図3です。
では、$B$から$Q$までかかっているひもを、展開図にかけていきます。$B$から$Q$にまっすぐにひもをかけてはいけません。$B$から$P$にひもをかけ、
さらに$P$から$Q$にかけていきます。
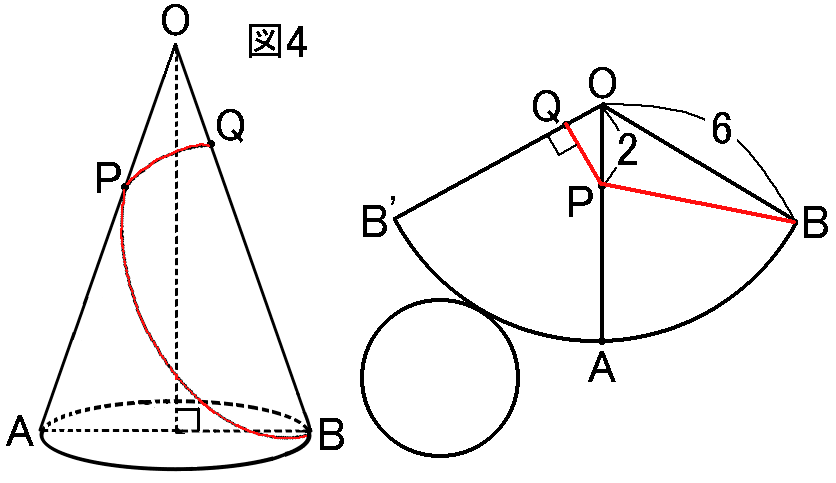
まず、$B$と$P$をまっすぐにむすびます。これが$BP$です。
つぎに、$Q$はどこにあるか、ですが、これは$P$から$OB'$までの最短距離です。$PQ \perp OB'$になるように線をひけば、そこが$Q$です。(図4)
これでひもがかかりました。$BP+PQ$の長さがこの問題の答えです。では$BP$と$PQ$の長さをそれぞれ求めていきましょう。
【$BP$の長さ】
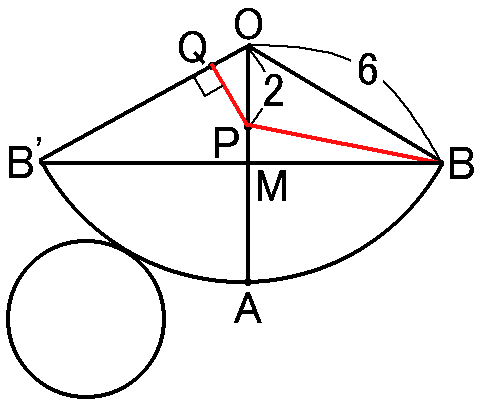
$B$と$B'$をむすんで、$BB'$と$OA$との交点を$M$とします。すると、$\triangle OMB \equiv \triangle OMB'$です。
$\triangle OBB'$という二等辺三角形で、$OA$というの頂角の二等分線をひいているのだから、$OM \perp BB'$になって、直角三角形で斜辺と1鋭角でも、
斜辺と他の1辺でも、どちらでもいけます。$\triangle OMB \equiv \triangle OMB'$です。
また、$\triangle OMB$の$\angle BOM$は$60^{ \circ }$です。$\angle BOB'$が$120^{ \circ }$で、$\angle BOM$はその半分
だからです。すると、$\triangle OMB$は$60^{ \circ },30^{ \circ },90^{ \circ }$の三角形ということになって、$1:2:\sqrt{3}$の辺の比が使えることに
なります。
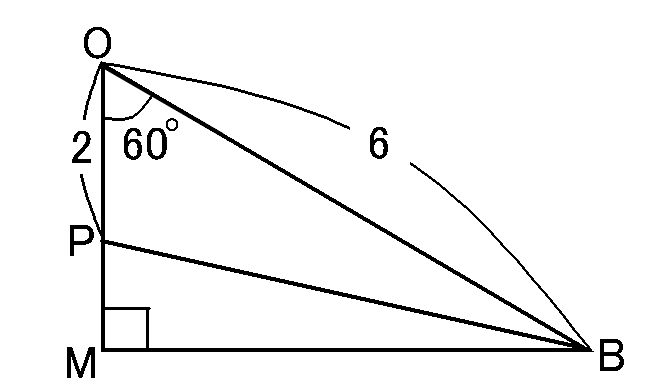
ちょっとごちゃごちゃしてわかりづらいので、$\triangle OMB$だけとりだして、大きくかいてみますと、こうです。
$OB:OM=2:1$です。$OM$は$OB$の半分です。なので$OM=3cm$です。なので$PM=1cm$です。
また、$OM:MB=1:\sqrt{3}$ですから、$MB$は$OM$の$\sqrt{3}$倍です。なので$MB=3\sqrt{3}cm$です。
これで、$\triangle PMB$で三平方の定理を使えば、$BP$の長さがだせます。
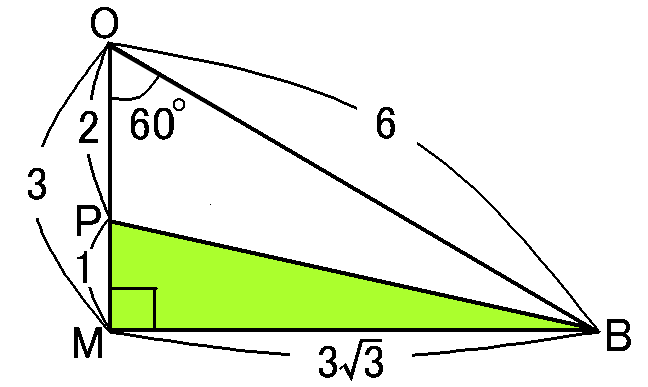
$\triangle PMB$で、$PM=1,$$MB=3\sqrt{3},$$\angle PMB=90^{ \circ }$
三平方の定理により、
\begin{eqnarray*}
(BP)^2&=&(PM)^2+(MB)^2\\
&=&1^2+(3\sqrt{3})^2\\
&=&28\\
BP>0なので\\
BP&=&\sqrt{28}=2\sqrt{7}cm
\end{eqnarray*}
これで$BP$の長さはでました。こんどは$PQ$の長さをだしていきましょう。
【$PQ$の長さ】

$\angle B'OM$の大きさは$60^{ \circ }$なので、$\triangle OQP$は$60^{ \circ },30^{ \circ },90^{ \circ }$の三角形ということになって、
これもやはり$1:2:\sqrt{3}$の辺の比が使えることになります。
 $\triangle OQP$で、
\begin{eqnarray*}
OP:PQ&=&2:\sqrt{3}\\
2:PQ&=&2:\sqrt{3}\\
PQ&=&\sqrt{3}cm
\end{eqnarray*}
$\triangle OQP$で、
\begin{eqnarray*}
OP:PQ&=&2:\sqrt{3}\\
2:PQ&=&2:\sqrt{3}\\
PQ&=&\sqrt{3}cm
\end{eqnarray*}
【最短のひもの長さ】

最短のひもの長さは、$BP+PQ$なので、
$$2\sqrt{7}+\sqrt{3}(cm)$$