数学 入試過去問
ページがちゃんと表示されるまで10秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
ho←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
【2023年の大問6】
図は1辺が6cmの正四面体
BP:PC=2:1
CQ:QD=2:1
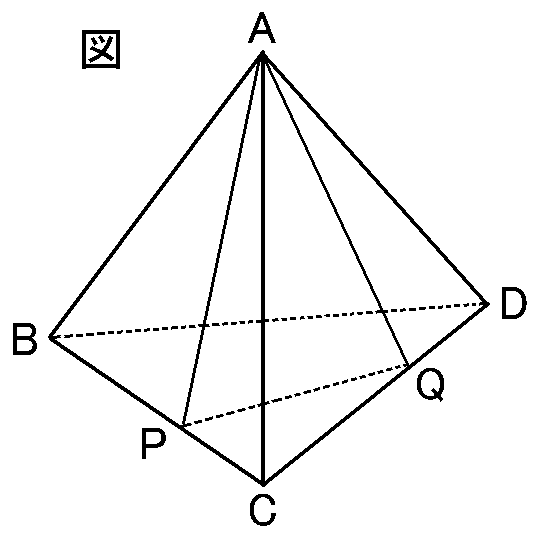
(1) △CPQはどんな三角形か。次のア~エから1つ選んで、その記号を答えよ。
ア 正三角形 イ 二等辺三角形
ウ 直角三角形 エ 直角二等辺三角形
答え
ウ
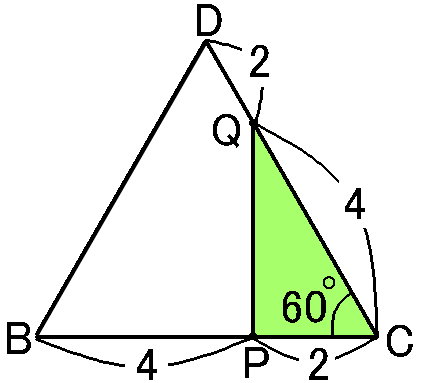 底面の△DBCは正三角形です。3つの角はそれぞれ60∘です。
底面の△DBCは正三角形です。3つの角はそれぞれ60∘です。
仮定から、BP:PC=2:1,CQ:QD=2:1で、1辺が6cmなのだから、PC=2cm,QC=4cmとなって、
PC:QC=2:4=1:2です。
60∘の角をはさむ辺の比が1:2になる三角形なのですから、
これは辺の比が1:2:√3、角度の比は60∘,30∘,90∘のの直角三角形です。
なので答えはウです。
なぜ直角三角形といってよいのかを再確認しておきましょう。
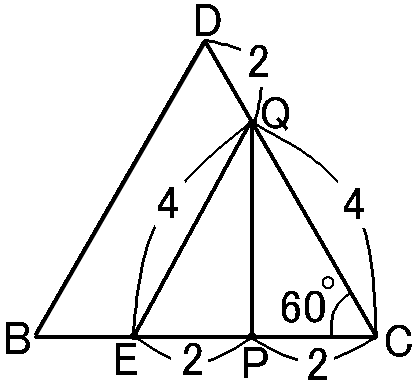 まず、BP上に、PE=2cmとなるように、点Eをとります。するとEC=4cmになります。
まず、BP上に、PE=2cmとなるように、点Eをとります。するとEC=4cmになります。
CQ=4cmなのだから、△QECは、CE=CQで、∠ECQ=60∘の二等辺三角形になります。
頂角が60∘の二等辺三角形なのだから、これは正三角形です。なので、QE=4cmです。
この正三角形の底辺をECとします。
すると、QPは頂点Qから底辺の中点におろした線ということになります。
△QEPと△QCPは、3辺が等しいので
合同となって、対応する角だから∠QPE=∠QPC、というわけで∠QPE=∠QPC=90∘です。
(2) AQの長さ
答え
2√7cm
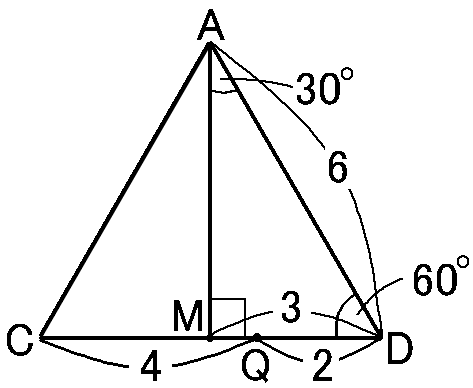 QはCD上にあるので、AQの長さは△ACDで考えます。
QはCD上にあるので、AQの長さは△ACDで考えます。
これは1辺が6cmの正三角形で、仮定からCQ:QD=2:1なので、CQ=4cm,QD=2cmです。
また、∠Aの二等分線をひいてCDとの交点をMとすると、「二等辺三角形の頂角の二等分線は底辺を垂直に二等分する」という定理をもちいて、
MD=3cm,∠AMD=90∘です。
また、∠ADM=60∘,∠MAD=30∘なので、
△AMDの辺の比は1:2:√3になります。なので、
AD:AM=2:√36:AM=2:√3AM=3√3cm
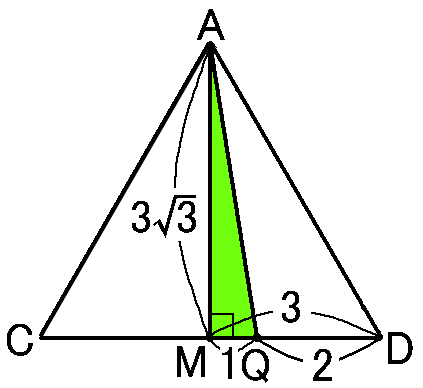 これで、△AMQで三平方の定理を使えば、AQが求められます。
これで、△AMQで三平方の定理を使えば、AQが求められます。△AMQで、AM=3√3,MQ=1,∠AMQ=90∘
三平方の定理により、 (AQ)2=(AM)2+(MQ)2=(3√3)2+12=28AQ>0なのでAQ=√28=2√7cm
(3) 直線APを軸として△APQを一回転させてできる立体の体積
ただし円周率をπとする
答え
50√77π(cm3)
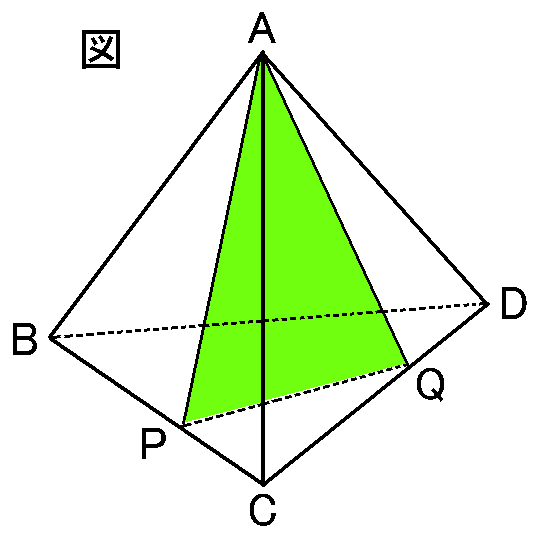 まず、△APQはどんな三角形なのか、その3辺の長さを考えましょう。
まず、△APQはどんな三角形なのか、その3辺の長さを考えましょう。
AQの長さは(2)で求めています。2√7cmです。
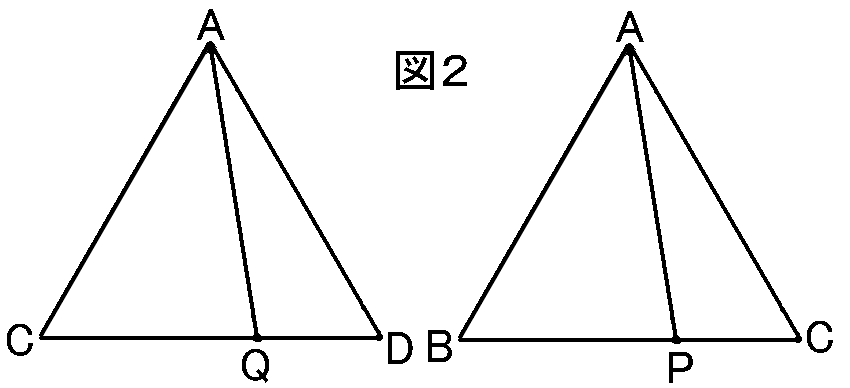 APの長さはどうかというと、△ACDのAQと、
△ABCのAPはおなじことなので、APもやっぱり2√7cmです。(図2)
APの長さはどうかというと、△ACDのAQと、
△ABCのAPはおなじことなので、APもやっぱり2√7cmです。(図2)
あとPQなのですが、これは(1)の問題で考えた、△DBCの中の△QPCをおもいだして(図3)、
これは辺の比が1:2:√3になる三角形だったので、
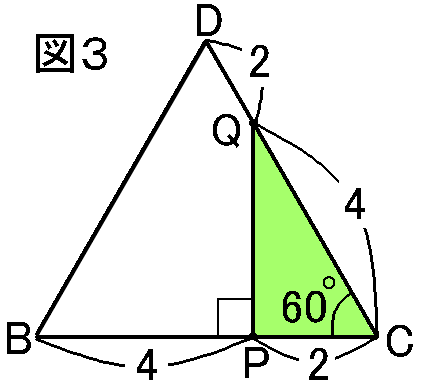 PC:PQ=1:√32:PQ=1:√3PQ=2√3cm
PC:PQ=1:√32:PQ=1:√3PQ=2√3cm
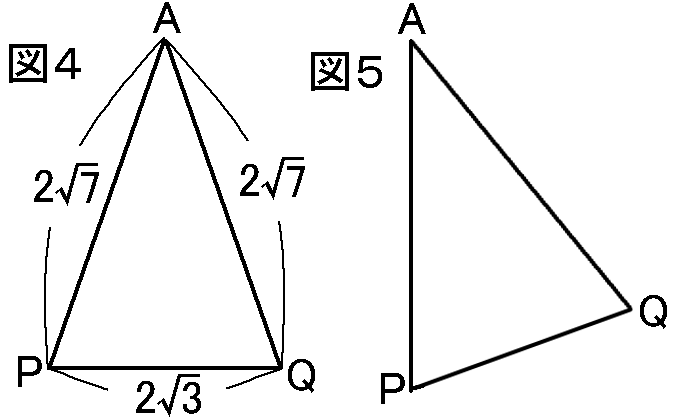 これのAPを軸として一回転せよということなので、APをまっすぐにたてて図をかくとこうなって(図5)、
これをAPを軸にして一回転させると、こんなふうになります。(図6)
これのAPを軸として一回転せよということなので、APをまっすぐにたてて図をかくとこうなって(図5)、
これをAPを軸にして一回転させると、こんなふうになります。(図6)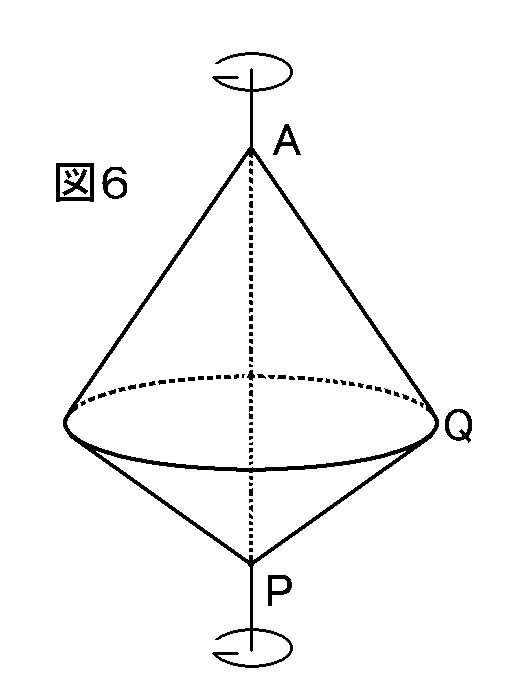 図6はふたつの円すいを、底面をあわせて上下に重ねたものです。これの体積を求めなさいという問題なので、上の円すいと下の円すいの
体積をそれぞれ求めて、足せばよさそうです。そういうことでやっていきましょう。
図6はふたつの円すいを、底面をあわせて上下に重ねたものです。これの体積を求めなさいという問題なので、上の円すいと下の円すいの
体積をそれぞれ求めて、足せばよさそうです。そういうことでやっていきましょう。【上の円すいの体積】
円すいの体積は、底面積×高さ×13です。
底面は円なので、その面積は半径の2乗×πです。
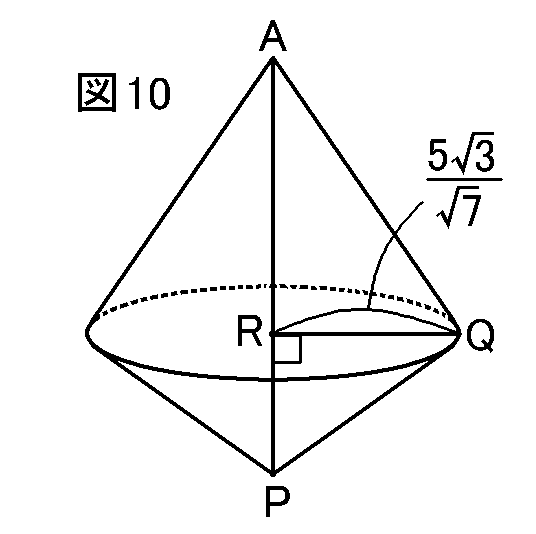
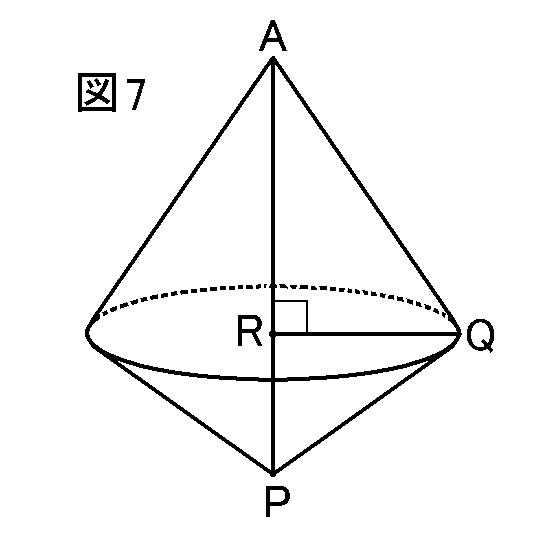 QからAPに垂線をおろして、APとの交点をRということにします。(図7)
QからAPに垂線をおろして、APとの交点をRということにします。(図7)すると、QRが、この円すいの底面の円の半径ということになります。また、ARが上の円すいの高さということになります。 そしてPRが下の円すいの高さということになります。
【底面の半径】
QR(底面の半径)は、△APQの面積を利用して求めることができます。△APQは、3辺がわかっている二等辺三角形なので、 三平方の定理を使えば高さがだせて、面積がでます。
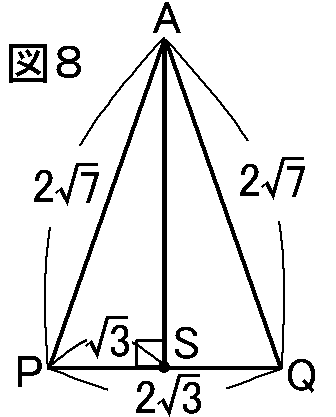 △APQの∠Aの二等分線とPQの交点をSとします。(図8)
△APQの∠Aの二等分線とPQの交点をSとします。(図8)二等辺三角形の頂角の二等分線は底辺を垂直に二等分するので、PS=√3cm,∠ASP=90∘になります。あと、AP=2√7cmなので、△APSにおいて、三平方の定理より、 (AS)2=(AP)2−(PS)2=(2√7)2−√32=28−3=25AS>0なのでAS=√25=5cm
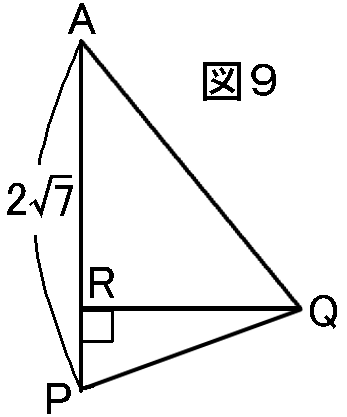 そしてこんどは、△APQで、APを底辺とした式をたてます。APを底辺ということにすれば、高さはQRです。(図9)
そしてこんどは、△APQで、APを底辺とした式をたてます。APを底辺ということにすれば、高さはQRです。(図9)この三角形で面積をあらわす式をたてると、 底辺×高さ×12=面積AP×QR×12=面積2√7×QR×12=5√3(両辺に×2)2√7×QR=10√3QR=10√32√7=5√3√7cm
 あとで2乗するので、分母の有理化はしません。
あとで2乗するので、分母の有理化はしません。【底面の面積】
というわけで、これで上の円すいの底面の半径がでました。なので上の円すいの底面積は、
π×(QR)2=757πとなります。とうぜん下の円すいの底面積もおなじです。
【立体の体積】
ところで、この問題できかれている立体の体積は、上の円すいと下の円すいの体積を求めて足せばOKなのですが、 上下にわけてそれぞれを求めていくより、もうすこしラクにやることができます。
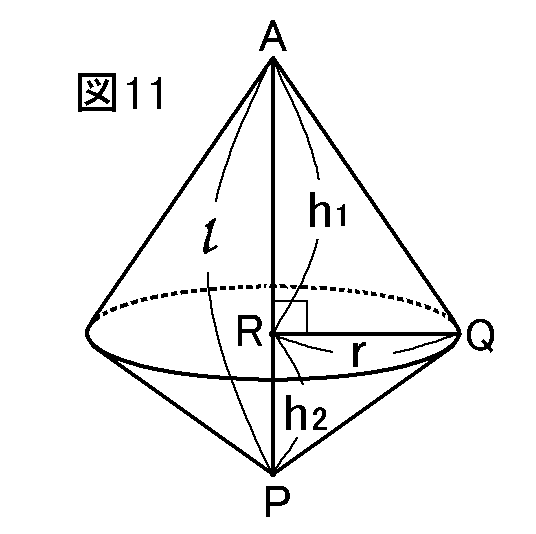 図11のように、AP=l,AR=h1,RP=h2,QR=rということにします。
図11のように、AP=l,AR=h1,RP=h2,QR=rということにします。すると、h1+h2=lです。
上の円すいの体積は、 13πr2h1です。
下の円すいの体積は、 13πr2h2です。
上の円すいの体積と下の円すいの体積を足したものは、 13πr2h1+13πr2h2=13πr2(h1+h2)=13πr2l
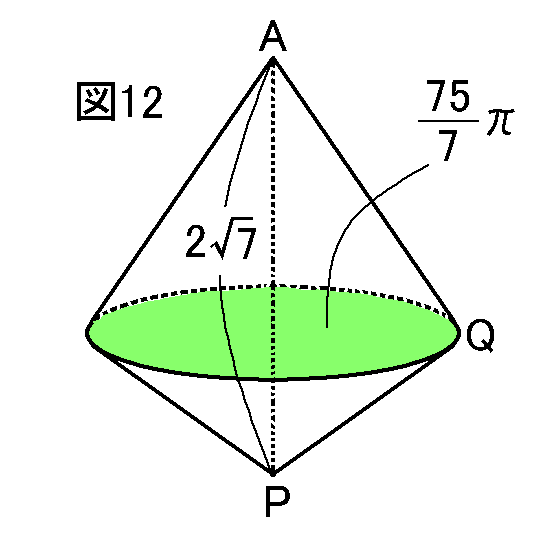 したがって、この問題できかれている立体の体積は、13×底面積×APをやればOKということになって(図12)、
したがって、この問題できかれている立体の体積は、13×底面積×APをやればOKということになって(図12)、13×底面積×AP=13×757π×2√7=50√77π(cm3)(答え)
【QRのべつな求め方】
この問題の解説は以上なのですが、QRのべつな求め方もすこし説明します。ちょっと計算が面倒なので、上で説明したやりかたのほうがとくだとは思うのですが、まあいちおう。
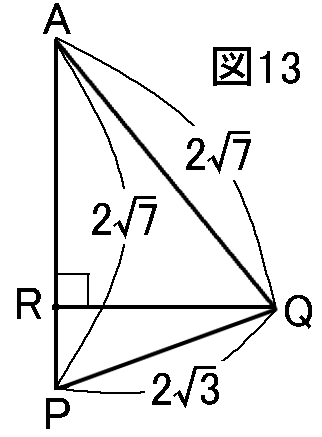 △APQで、AP=AQ=2√7,PQ=2√3です。(図13)
△APQで、AP=AQ=2√7,PQ=2√3です。(図13)3辺の長さがわかっている三角形なので、三平方の定理を使って、点QからAPにおろした垂線QRの長さを求めていきましょう。
そのためにまず、ARの長さを求めていきます。
AR=xとして、xを使った三平方の定理の式を2つたてて、連立させて解いていきます。
【ARの長さ】
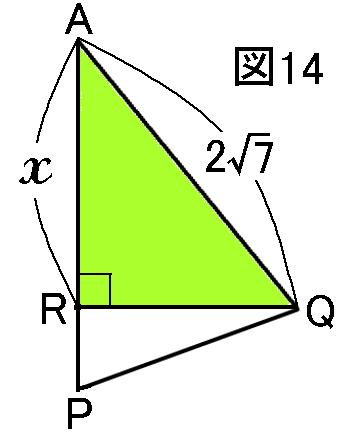
△ARQは∠ARQ=90∘の直角三角形だから(図14)、ARの長さをxとすると、三平方の定理より、 (QR)2=(AQ)2−(AR)2=(2√7)2−x2=28−x2
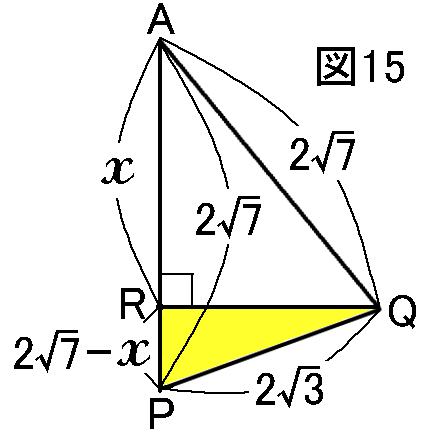
△PRQは∠PRQ=90∘の直角三角形だから(図15)、三平方の定理より、 (QR)2=(QP)2−(RP)2=(2√3)2−(2√7−x)2=12−(28−4√7x+x2)=12−28+4√7x−x2=−16+4√7x−x2
これでxが求まりました。xというのは、ARのことです。
【QRの長さ】
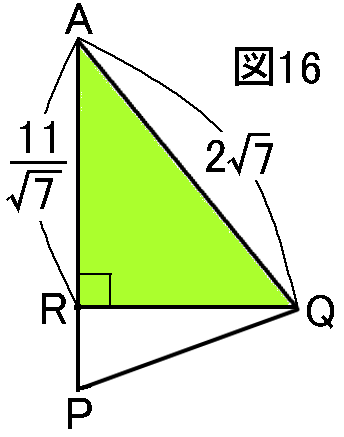
いま求めたxを利用して、△ARQで、三平方の定理より(図16)、 (QR)2=(AQ)2−(AR)2=(2√7)2−(11√7)2=28−1217=1967−1217=757
 これに平方根をつければQRになるのですが、考えてみるとほしいのは(QR)2の値なので、じゃあこのままでだいじょうぶです。
これに平方根をつければQRになるのですが、考えてみるとほしいのは(QR)2の値なので、じゃあこのままでだいじょうぶです。図7の(QR)2=757ということです。
なので上の円すいの底面積は、
π×(QR)2=757πとなります。とうぜん下の円すいの底面積もおなじです。
……というわけで、こんなふうにやってもQRは求められて、円すいの底面積がでます。でますが、ちょっとめんどくさいかも。
youtube 解説動画