数学 中1 4章 比例,反比例 第2回(全28問)
ページがちゃんと表示されるまで10秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
ho←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
ともなって変わる 2 つの量
(1) 次の hoge の中にあてはまる言葉をいれましょう。
ともなって変わる 2 つの量 x, y があって、x の値がさだまると、それに対応する y の値がただ 1 つだけ決まるとき、y は x の hoge であるという。
答え
関数
あるひとの身長を xcm,体重を ykg とします。この場合、y は x の関数ではありません。身長が決まっても、体重は決まりません。たとえば、x=150 であったとして、y は 1 つだけ決まりますか? 決まらないですよね。身長が 150cm だったとして、体重は 40kg なのかもしれないし、 45kg なのかもしれないし、 50kg なのかもしれない。こういうのは関数ではありません。
時速 100km で x 時間すすむときの、すすんだ距離を ykm とします。この場合、y は x の関数です。たとえば、x=1 のとき、y=100 です。x=2 のとき、y=200 です。「x の値がさだまると、それに対応する y の値がただ 1 つだけ決まる」というのは、こういうときです。こういうのを y は x の関数であるといいます。
(2) 次の①~⑧について、 y は x の関数であるといえるか。
① 1 個 120 円のりんごを x 個買うときの代金が y 円
② 1 辺が xcm の正三角形の周の長さが ycm
③ 身長が xcm であるひとの髪の毛の長さが ycm
④ 時速 60km で走る自動車が x 時間走ったときの進んだ距離が ykm
⑤ あるクラスの x 人が 50m 走をしたときの、平均が y 秒
⑥ 1000mL のペットボトルの水を、xmL 飲んだときの、残りの水の量が ymL
⑦ 水槽に 1 分で 20L ずつ水をいれる。x 分水をいれたときの、いれた水の量が yL
⑧ 15cm のろうそくを xcm 燃やしたときの、残りの長さが ycm
答え
① いえる
② いえる
③ いえない
④ いえる
⑤ いえない
⑥ いえる
⑦ いえる
⑧ いえる
① y=120x
② y=3x
③ 式にならない
④ y=60x
⑤ x が決まっても y の値はさだまらない
⑥ y=1000−x
⑦ y=20x
① y=15−x
(3) 次の hoge の中にあてはまる言葉をいれましょう。
いろいろな値をとる文字を変数という。
変数のとりうる値の範囲を、その変数の hoge という。
答え
変域
(4) 次の①~④の x の変域を不等号を使った式で表しなさい。また、数直線上に変域を表しなさい。

① 3 より大きい
② −2 以上 5 以下
③ 0 より大きく 2 以下
④ −4 以上 −2 未満
 答え
答え
①x>3
②−2≦x≦5
③0<x≦2
④−4≦x<−2
以上、以下はその数をふくみます。記号はイコールがあるほうを使います。数直線上にあらわすときは、●を使います。
より大きい、より小さい、未満はその数をふくみません。記号はイコールがないやつを使います。数直線上にあらわすときは、〇を使います。
ふくむふくまない以上、以下より大きい、より小さい、未満
比例
(5) 次の hoge の中にあてはまる式や言葉をいれましょう。
比例の式の形は hogehoge
a の呼び方は hogehoge
a の求め方は a=ho
答え
y=ax
比例定数
yx
y が x の関数で、その関係が y=ax で表されるとき、
y は x に比例するといいます。
たとえば、時速 60km で x 時間すすむときの、すすんだ距離を ykm とします。この場合、x と y の関係は、距離=速さ×時間ですから、
y=60x
と表せます。なので、y は x に比例するといえます。この場合の比例定数は 60 です。
(6) 次の①~⑥について、 y を x の式で表しなさい。また、比例定数をいいなさい。
① 1 個 120 円のりんごを x 個買うときの代金が y 円
② 1 辺が xcm の正三角形の周の長さが ycm
③ 底辺が xcm で高さが 5m の三角形の面積が ycm2
④ 時速 60km で走る自動車が x 時間走ったときの進んだ距離が ykm
⑤ 水槽に 1 分で 20L ずつ水をいれる。x 分水をいれたときの、いれた水の量が yL
⑥ 縦が30cm で横が xcm の長方形の面積が ycm2
答え
① y=120x 比例定数… 120
② y=3x 比例定数… 3
③ y=52x 比例定数… 52
④ y=60x 比例定数… 60
⑤ y=20x 比例定数… 20
⑥ y=30x 比例定数… 30
② 正三角形の周は 1 辺 ×3
③ 三角形の面積は、底辺 × 高さ ×12
④ 距離 = 速さ × 時間
⑥ 長方形の面積は、縦 × 横
(7) ① y=3x について、x の値に対応する y の値を求め、下の表を完成しなさい。 x⋯−4−3−2−1−0−1−2−3−4⋯y⋯⋯ ② y=−14x について、x の値に対応する y の値を求め、下の表を完成しなさい。 x⋯−4−3−2−1−0−1−2−3−4⋯y⋯12⋯ ③ 比例の式では、x の値が 2 倍,3 倍,…になると、対応する y の値はどうなるか。
答え
①y=3x
x⋯−4−3−2−1−0−1−2−3−4⋯y⋯−12−9−6−3−0−3−6−9−12⋯
②y=−14x
x⋯−4−3−2−1−0−1−2−3−4⋯y⋯−1−34−12−14−0−14−12−34−1⋯
③ 2 倍,3 倍,…になる
(8) 下の表の y は x に比例している。表を完成させなさい。
x−2−1−0−1y−15−10
答え x−3−2−1−0−1y−15−10−5−0−5
x になにを掛けたら y になるかを考えましょう。この問題の場合は、x=−2 のとき y=−10 になっているから、x に 5 を掛けたら y になります。つまり、y=5x だということになります。
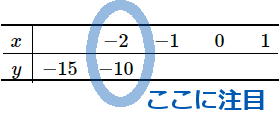
この手の問題は、かならずどこかに x と y の両方がわかっているところがあります。そこに注目して考えましょう。
(9)
① y が x に比例していて、x=5 のとき、y=15 である。y を x の式で表しなさい。
② y が x に比例していて、x=−9 のとき、y=6 である。y を x の式で表しなさい。
③ y が x に比例していて、x=13 のとき、y=4 である。y を x の式で表しなさい。
答え
①y=3x
②y=−23x
③y=12x
「比例」といわれたら、答えの形は y=ax で、 a を求めるのが目標になります。a の求め方は、a=yx です。
①a=yx=155=3
②a=yx=6−9=−23
③問題に分数があるときは、a=yxにそのまま代入するとややこしいです。そうではなく、a=y÷x ということにして a を求めていきましょう。
a=yx=y÷x=4÷13=4×31=12
(10)
① y が x に比例していて、x=8 のとき、y=16 である。x=−3 のときの y の値を求めなさい。
② y が x に比例していて、x=15 のとき、y=−5 である。x=−12 のときの y の値を求めなさい
③ y が x に比例していて、x=−10 のとき、y=−6 である。x=−23 のときの y の値を求めなさい
答え
①y=−6
②y=4
③y=−25
「比例」といわれたら、式の形は y=ax で、 a を求めるのが目標になります。a の求め方は、a=yx です。
①a=168=2
y=2x に x=−3 を代入する
y=2×(−3)=−6
②a=−515=−13
y=−13x に x=−12 を代入する
y=−13×(−12)=4
③a=−6−10=35
y=35x に x=−23 を代入する
y=35×(−23)=−25
座標
(11) 次の hoge の中にあてはまる言葉をいれましょう。
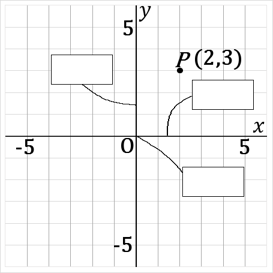 点 O で垂直に交わる 2 つの数直線について、横の数直線を hoge 、縦の数直線を hoge という。両方あわせて hogeho という。その平面を hogehoge という。
点 O で垂直に交わる 2 つの数直線について、横の数直線を hoge 、縦の数直線を hoge という。両方あわせて hogeho という。その平面を hogehoge という。
2 つの数直線の交点 O を hoge という。
点P(2 , 3) について、(2 , 3) を点P の hoge という。2 を点P の hogeho という。3 を点P の hogeho という。
答え
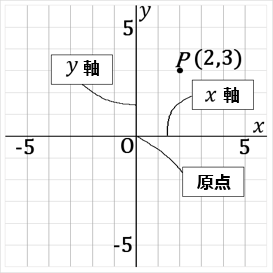 点 O で垂直に交わる 2 つの数直線について、横の数直線を x軸ho 、縦の数直線を y軸ho という。両方あわせて 座標軸h という。その平面を 座標平面h という。
点 O で垂直に交わる 2 つの数直線について、横の数直線を x軸ho 、縦の数直線を y軸ho という。両方あわせて 座標軸h という。その平面を 座標平面h という。
2 つの数直線の交点 O を 原点h という。
点P(2 , 3) について、(2 , 3) を点P の 座標h という。2 を点P の x座標ho という。3 を点P の y座標ho という。
座標というのは (x, y) になっています。x がいくつで、y がいくつか。たとえば x=−1, y=5 なら、(−1, 5) というふうに表します。
(横, 縦) だと思っちゃってもいいです。たとえば点P は原点から横に 2 歩いって、縦に 3 歩いっています。なので点P の座標は (2, 3) です。原点をスタート地点ということにして、横に何歩いって縦に何歩いっているか、ということです。
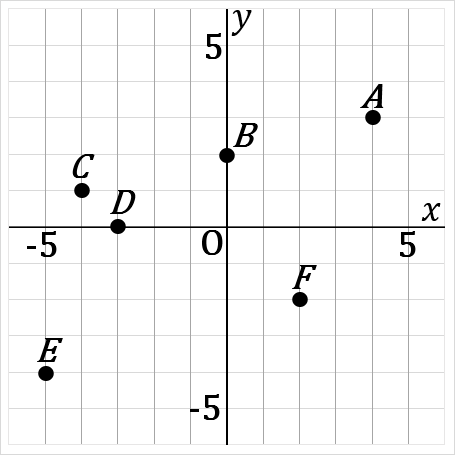
(12) 右の図について、点 A, B, C, D, E, F の座標をいいなさい。
また、
点 G(2, 1)
点 H(−2, 4)
点 I(0, −4)
点 J(4, −3)
をかきいれなさい。
答え
A(4, 3)
B(0, 2)
C(−4, 1)
D(−3, 0)
E(−5, −4)
F(2, −2)
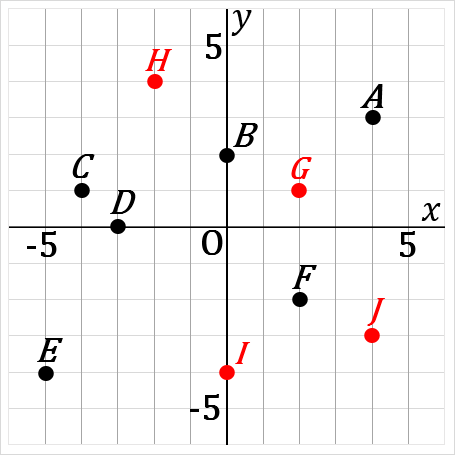
x 軸上にある点は、かならず y 座標が 0 になっています。上の図でいうと、点 D(−3, 0) がそうです。
y 軸上にある点は、かならず x 座標が 0 になっています。上の図でいうと、点 B(0, 2) や点 I(0, −4) がそうです。
比例のグラフ
(13) 次の hoge の中にあてはまる言葉をいれましょう。
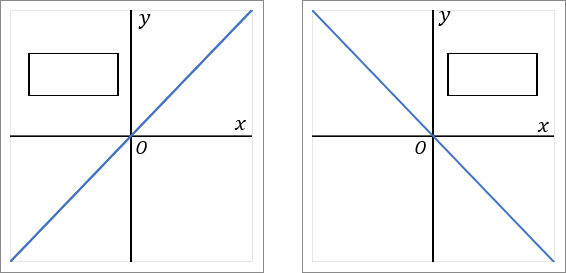
y=ax のグラフは hoge を通る hoge である。
比例定数が正のとき(a>0 のとき)、グラフは hogehoge の直線となる。
比例定数が負のとき(a<0 のとき)、グラフは hogehoge の直線となる。
答え
y=ax のグラフは 原点h を通る 直線h である。
比例定数が正のとき(a>0 のとき)、グラフは 右上がりh の直線となる。
比例定数が負のとき(a<0 のとき)、グラフは 右下がりh の直線となる。
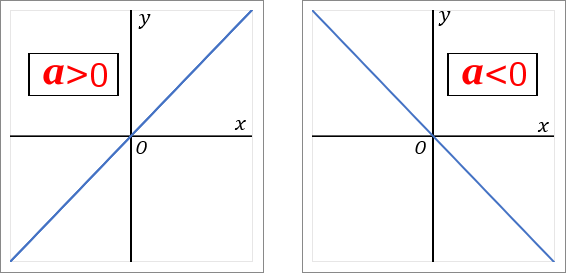
比例のグラフ(y=ax のグラフ)は原点を通る直線です。
「a は正の数である」というのを数学では a>0 と表します。「a は 0 より大きい」ということです。0 より大きいのなら、そりゃ正ですよね。
「a は負の数である」というのなら a<0 です。
比例定数 a が正の数のとき(a>0 のとき)、グラフは右上がりとなります。x の値が増加すると、それに対応する y の値も増加します。
比例定数 a が負の数のとき(a<0 のとき)、グラフは右下がりとなります。x の値が増加すると、それに対応する y の値は減少します。
(14) 次の①~⑥のグラフをかきなさい。
①y=x②y=3x
答え
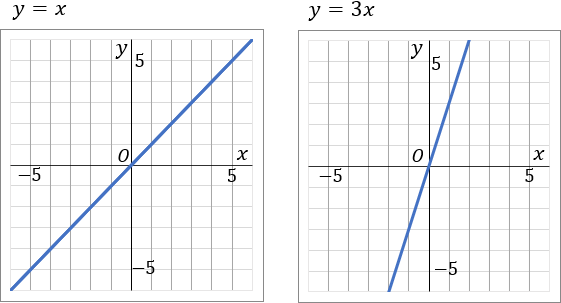
①てっとりばやいかき方として、x=1 のとき y=1 なのだから、原点と点(1, 1) を通る直線を定規でむすんでしまう、というのがあります。ただ、原点とどこか 1 点をむすぶやり方だと、ちょっとズレちゃうことがあります。わりとよくあります。なのでそこに気をつけてください。
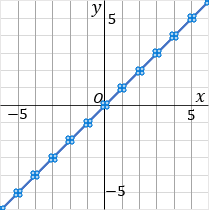 もうひとつのかき方として、これがおすすめなんですが、このグラフは比例定数が 1 です。1 は分数であらわすと 11 です。というわけで、原点をスタート地点として、「右に 1 マスいったら上に 1 マスいく」というふうに点をとっていっちゃいます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に 1 マスいったら下に 1 マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。すべての点が定規の上にのっているはずです。点をいくつかとるので、ズレる心配がほぼないです。
もうひとつのかき方として、これがおすすめなんですが、このグラフは比例定数が 1 です。1 は分数であらわすと 11 です。というわけで、原点をスタート地点として、「右に 1 マスいったら上に 1 マスいく」というふうに点をとっていっちゃいます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に 1 マスいったら下に 1 マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。すべての点が定規の上にのっているはずです。点をいくつかとるので、ズレる心配がほぼないです。
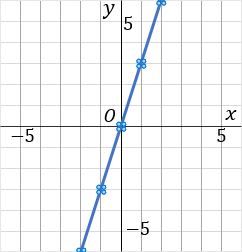 ②このグラフは比例定数が 3 です。3 は分数であらわすと 31 です。というわけで、原点をスタート地点として、「右に 1 マスいったら上に 3 マスいく」というふうに点をとっていきます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に 1 マスいったら下に 3 マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
②このグラフは比例定数が 3 です。3 は分数であらわすと 31 です。というわけで、原点をスタート地点として、「右に 1 マスいったら上に 3 マスいく」というふうに点をとっていきます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に 1 マスいったら下に 3 マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
③y=23x④y=−x
答え
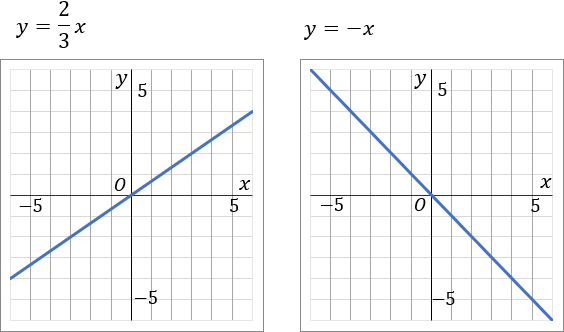
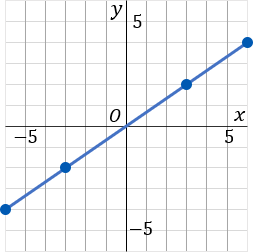 ③このグラフは比例定数が 23 です。原点をスタート地点として、「右に 3 マスいったら上に 2 マスいく」というふうに点をとっていきます。比例定数の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に 3 マスいったら下に 2 マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
③このグラフは比例定数が 23 です。原点をスタート地点として、「右に 3 マスいったら上に 2 マスいく」というふうに点をとっていきます。比例定数の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に 3 マスいったら下に 2 マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
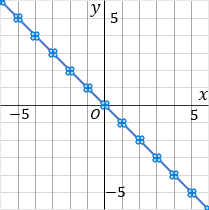 ④このグラフは比例定数が −1 です。比例定数が負の数なので、右下がりのグラフになるはずだ、ということを意識しておきましょう。−1 は分数であらわすと −11 です。グラフをかくときは、マイナスの符号は分子につけておきましょう。というわけで、原点をスタート地点として、「右に 1 マスいったら下に 1 マスいく」というふうに点をとっていきます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に 1 マスいったら上に 1 マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
④このグラフは比例定数が −1 です。比例定数が負の数なので、右下がりのグラフになるはずだ、ということを意識しておきましょう。−1 は分数であらわすと −11 です。グラフをかくときは、マイナスの符号は分子につけておきましょう。というわけで、原点をスタート地点として、「右に 1 マスいったら下に 1 マスいく」というふうに点をとっていきます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に 1 マスいったら上に 1 マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
⑤y=−2x⑥y=−34x
答え
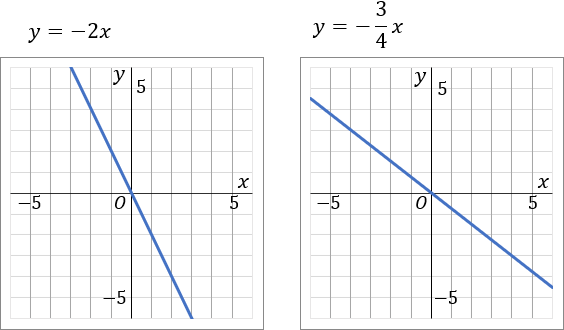
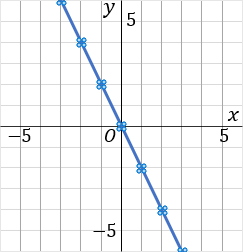 ⑤このグラフは比例定数が −2 です。比例定数が負の数なので、右下がりのグラフになるはずだ、ということを意識しておきましょう。−2 は分数であらわすと −21 です。グラフをかくときは、マイナスの符号は分子につけておきましょう。というわけで、原点をスタート地点として、「右に 1 マスいったら下に 2 マスいく」というふうに点をとっていきます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に 1 マスいったら上に 2 マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
⑤このグラフは比例定数が −2 です。比例定数が負の数なので、右下がりのグラフになるはずだ、ということを意識しておきましょう。−2 は分数であらわすと −21 です。グラフをかくときは、マイナスの符号は分子につけておきましょう。というわけで、原点をスタート地点として、「右に 1 マスいったら下に 2 マスいく」というふうに点をとっていきます。比例定数を分数で表した時の、分母が右で、分子が縦です。んで、一通り点をとったら、こんどは原点から左側に、さっきと逆のことをします。「左に 1 マスいったら上に 2 マスいく」というふうにして点をとっていきます。んで、とった点を定規でむすびます。
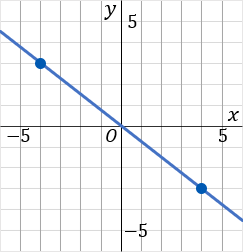 ⑥このグラフは比例定数が −34 です。グラフをかくときは、マイナスの符号は分子につけておきましょう。つまり、−34 というふうに考えます。原点をスタート地点として、「右に 4 マスいったら下に 3 マスいく」というふうに点をとります。比例定数を分数で表した時の、分母が右で、分子が縦です。つぎに、原点から左側に、さっきと逆のことをします。「左に 4 マスいったら上に 3 マスいく」というふうにして点をとります。んで、とった点を定規でむすびます。原点をふくめて 3 つの点を通すように線をひくので、ずれる心配がすくなくなります。
⑥このグラフは比例定数が −34 です。グラフをかくときは、マイナスの符号は分子につけておきましょう。つまり、−34 というふうに考えます。原点をスタート地点として、「右に 4 マスいったら下に 3 マスいく」というふうに点をとります。比例定数を分数で表した時の、分母が右で、分子が縦です。つぎに、原点から左側に、さっきと逆のことをします。「左に 4 マスいったら上に 3 マスいく」というふうにして点をとります。んで、とった点を定規でむすびます。原点をふくめて 3 つの点を通すように線をひくので、ずれる心配がすくなくなります。
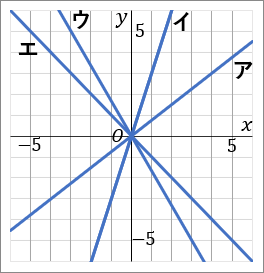
(15) 右の図のア~エの直線について、y を x の式で表しなさい。
答え
ア y=34x
イ y=3x
ウ y=−53x
エ y=−x
ア~エのグラフはすべて原点を通る直線です。比例のグラフです。比例のグラフについて、「y を x の式で表しなさい」といわれたら、式の形は y=ax で、a を求めるのが目標となります。a の求め方は、a=yx です。グラフ上にある、どこかカドを通っているところをさがして、その座標を利用します。
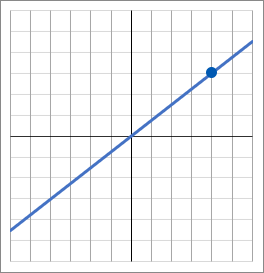 <アについて>
<アについて>
アのグラフは、点(4, 3) を通っています。なので、x=4, y=3 を a=yx に代入して a を求めます。
a=yx=34
これで a=34 だと求められました。なので答えは y=34x です。
ここでは点(4, 3) を代入して a を求めましたが、ほかの点でもだいじょうぶです。グラフ上にある点の座標を代入すれば、どこをいれても全部おなじ答えになります。ただ、原点だけはいれちゃダメです。
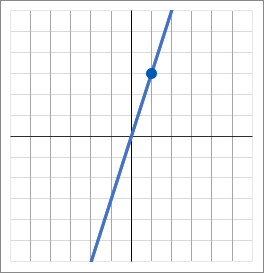 <イについて>
<イについて>
イのグラフは、点(1, 3) を通っています。なので、x=1, y=3 を a=yx に代入して a を求めます。
a=yx=31=3
これで a=3 だと求められました。なので答えは y=3x です。
ここでは点(1, 3) を代入して a を求めましたが、ほかの点でもだいじょうぶです。グラフ上にある点の座標を代入すれば、どこをいれても全部おなじ答えになります。ただ、原点だけはいれちゃダメです。
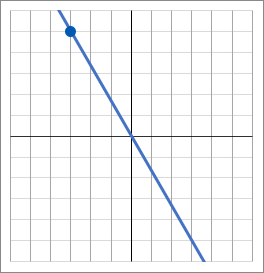 <ウについて>
<ウについて>
ウのグラフは、点(−3, 5) を通っています。なので、x=−3, y=5 を a=yx に代入して a を求めます。
a=yx=5−3=−53
これで a=−53 だと求められました。なので答えは y=−53x です。
ここでは点(−3, 5) を代入して a を求めましたが、ほかの点でもだいじょうぶです。グラフ上にある点の座標を代入すれば、どこをいれても全部おなじ答えになります。ただ、原点だけはいれちゃダメです。
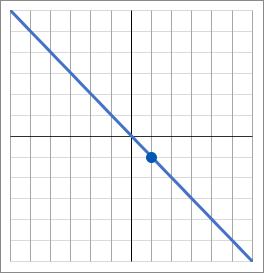 <エについて>
<エについて>
エのグラフは、点(1, −1) を通っています。なので、x=1, y=−1 を a=yx に代入して a を求めます。
a=yx=−11=−1
これで a=−1 だと求められました。なので答えは y=−x です。
ここでは点(1, −1) を代入して a を求めましたが、ほかの点でもだいじょうぶです。グラフ上にある点の座標を代入すれば、どこをいれても全部おなじ答えになります。ただ、原点だけはいれちゃダメです。
反比例
(16) 次の hoge の中にあてはまる式や言葉をいれましょう。
反比例の式の形は hogeho
a の呼び方は hogehoge
a の求め方は a=hoge
答え
y=ax
比例定数
xy
y が x の関数で、その関係が y=ax で表されるとき、
y は x に反比例するといいます。
たとえば、面積が 12cm2 の長方形の、縦の長さを xcm, 横の長さを ycm とします。この場合、x と y の関係は、縦×横=長方形の面積ですから、xy=12 となります。この式を変形すると、
y=12x
となります。横=面積÷縦という意味の式です。こういう形の式になるので、y は x に反比例するといえます。この場合の比例定数は 12 です。
(17) 次の①~⑩について、 y を x の式で表しなさい。
また、y が x に比例するときは、比例とかきなさい。
y が x に反比例するときは、反比例とかきなさい。
比例も反比例もしないときは、×とかきなさい。
① 1 個 60 円のりんごを x 個買うときの代金が y 円
② 1 個 x 円のりんごを y 個買うときの代金が 2400 円
③ 1 個 x 円のりんごを 6 個買って 1000 円はらったときのおつりが y 円
④ 縦が xcm で横が 12cm の長方形の面積が ycm2
⑤ 縦が xcm で横が ycm の長方形の面積が 20cm2
⑥ 時速 50km で走る自動車が x 時間走ったときの進んだ距離が ykm
⑦ 時速 xkm で走る自動車が y 時間走ったときの進んだ距離が 250km
⑧ 水槽に 1 分で 20L ずつ水をいれる。x 分水をいれたときの、いれた水の量が yL
⑨ 水槽に 1 分で xL ずつ水をいれる。y 分水をいれたときの、いれた水の量が 300L
⑩ 水槽に水が 300L はいっている。 1 分で 20L ずつ水を抜くときの、 x 分後の水の量が yL
答え
① y=60x 比例
② y=2400x 反比例
③ y=1000−6x ×
④ y=12x 比例
⑤ y=20x 反比例
⑥ y=50x 比例
⑦ y=250x 反比例
⑧ y=20x 比例
⑨ y=300x 反比例
⑩ y=300−20x ×
② xy=2400 だから y=2400x
③ y=1000−6x というのは、比例でも反比例でもありません
④ 長方形の面積は、縦 × 横
⑤ xy=20 だから y=20x
⑥ 距離 = 速さ × 時間
⑦ xy=250 だから y=250x
⑨ xy=300 だから y=300x
⑩ y=300−20x というのは、比例でも反比例でもありません
(18) ① y=6x について、x の値に対応する y の値を求め、下の表を完成しなさい。 x⋯−4−3−2−1−0−1−2−3−4⋯y⋯12⋯ ② y=−4x について、x の値に対応する y の値を求め、下の表を完成しなさい。 x⋯−4−3−2−1−0−1−2−3−4⋯y⋯12⋯ ③ 反比例の式では、x の値が 2 倍,3 倍,…になると、対応する y の値はどうなるか。
答え
①y=6x
x⋯−4−3−2−1−0−1−2−3−4⋯y⋯−32−2−3−6−×−6−3−2−32⋯
②y=−4x
x⋯−4−3−2−1−0−1−2−3−4⋯y⋯−1−43−2−4−×−4−2−43−4⋯
③ 12 倍,13 倍,…になる
x=0 のときの y の値はありません。数を 0 で割ったり、分数の分母を 0 にしたりはしません。
(19)
① y が x に反比例していて、x=5 のとき、y=4 である。y を x の式で表しなさい。
② y が x に反比例していて、x=−8 のとき、y=3 である。y を x の式で表しなさい。
③ y が x に反比例していて、x=−5 のとき、y=−25 である。y を x の式で表しなさい。
答え
①y=20x
②y=−24x
③y=125x
「反比例」といわれたら、答えの形は y=ax で、 a を求めるのが目標になります。a の求め方は、a=xy です。x と y をかけちゃえばいいんです。比例よりこっちのほうがもっとかんたん。
①a=xy=5×4=20
②a=xy=−8×3=−24
③a=xy=−5×(−25)=125
(20)
① y が x に反比例していて、x=6 のとき、y=8 である。x=−16 のときの y の値を求めなさい。
② y が x に反比例していて、x=4 のとき、y=−6 である。x=−10 のときの y の値を求めなさい
③ y が x に反比例していて、x=−4 のとき、y=−50 である。x=−100 のときの y の値を求めなさい
答え
①y=−3
②y=125
③y=−2
「反比例」といわれたら、式の形は y=ax で、 a を求めるのが目標になります。a の求め方は、a=xy です。
①a=6×8=48
y=48x に x=−16 を代入する
y=48−16=−3
②a=4×(−6)=−24
y=−24x に x=−10 を代入する
y=−24−10=125
③a=−4×(−50)=200
y=200x に x=−100 を代入する
y=200−100=−2
反比例のグラフ
(21) 次の hoge の中にあてはまる言葉をいれましょう。
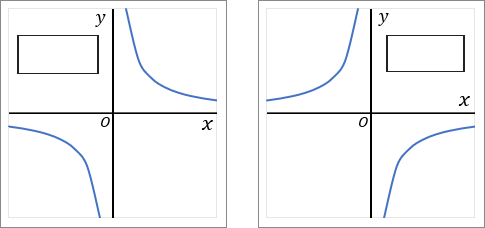
y=ax のグラフのことを hogeho という。
答え
双曲線
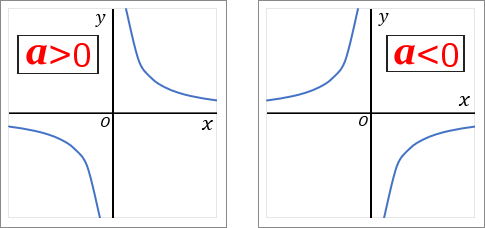
反比例のグラフ(y=ax のグラフ)は双曲線です。
座標軸(x 軸や y 軸)にそってのびていく、1 組のなめらかな線です。どこまでのばしても、座標軸と交わることはありません。
というわけで、上のふたつのグラフの形をおぼえましょう。そして、それを「双曲線」というんだ、というのをおぼえましょう。
比例定数 a が正の数のとき(a>0 のとき)、x>0 の範囲で、x の値が増加すると、対応する y の値は減少します。x<0 の範囲でも、x の値が増加すると、対応する y の値は減少します。どちらも右下がりになっている、ということです。
比例定数 a が負の数のとき(a<0 のとき)、x>0 の範囲で、x の値が増加すると、対応する y の値も増加します。x<0 の範囲でも、x の値が増加すると、対応する y の値も増加します。どちらも右上がりになっている、ということです。
(22) 次の①②の式について、x の値に対応する y の値を求め、表を完成しなさい。また、グラフをかきなさい。
① y=12x
x⋯−6−4−3−2−1−0−1−2−3−4−6⋯y⋯⋯
② y=−12x
x⋯−6−4−3−2−1−0−1−2−3−4−6⋯y⋯⋯

答え
① y=12x
x⋯−6−4−3−2−1−0−1−2−3−4−6⋯y⋯−2−3−4−6−12−×−12−6−4−3−2⋯
② y=−12x
x⋯−6−4−3−2−1−0−1−2−3−4−6⋯y⋯−2−3−4−6−12−×−12−6−4−3−2⋯
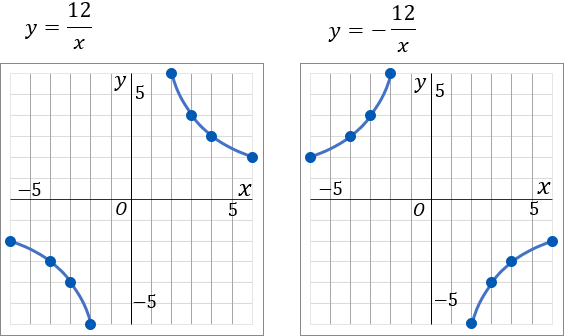
 ①反比例のグラフは双曲線になります。比例定数が正のとき(a>0)のときは、座標平面の右上と左下、比例定数が負のとき(a<0)のときは、座標平面の左上と右下に双曲線をかく、ということをまずおぼえておきましょう。y=12x のグラフは、比例定数が正なので、右上と左下に双曲線をかいていきます。
①反比例のグラフは双曲線になります。比例定数が正のとき(a>0)のときは、座標平面の右上と左下、比例定数が負のとき(a<0)のときは、座標平面の左上と右下に双曲線をかく、ということをまずおぼえておきましょう。y=12x のグラフは、比例定数が正なので、右上と左下に双曲線をかいていきます。
そのかき方なんですが、めんどくさいです。x と y がどちらも整数になってるところの表をつくって、その点をグラフ上にとっていきます。んで、これをなんとなく結びます。定規は使いません。ていうか使えません。なんとなくの線でいいです。だいたいでいいです。それでテストはマルにしてくれます。ただ、通るべき点を通していないとダメなので、そこは気をつけてください。
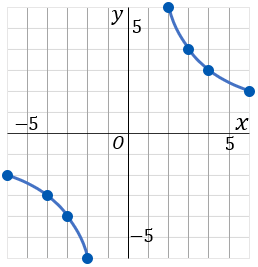
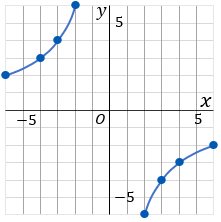 ②y=−12x のグラフは比例定数が負なので、座標平面の左上と右下に双曲線をかくことになります。x と y がどちらも整数になるところの表をつくって、その点をグラフ上にとって、なんとなくむすびましょう。
②y=−12x のグラフは比例定数が負なので、座標平面の左上と右下に双曲線をかくことになります。x と y がどちらも整数になるところの表をつくって、その点をグラフ上にとって、なんとなくむすびましょう。
いちいち表をつくらなくちゃならないので、めんどくさいです。慣れると表をつくらずにいきなり点をとっていけるようになると思いますが、まあはじめはおとなしく表をかいてやっていきましょう。
(23) 次の①~④のグラフをかきなさい。
①y=6x②y=−4x

答え
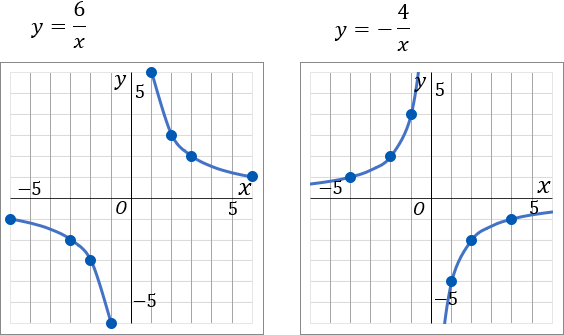
①反比例のグラフをかくときは、まず表をつくります。表をつくるところからはじめなきゃならんのです。めんどくさいのです。あきらめてください。グラフ用紙のマス目が +6 から −6 まであるので、x が +6 から −6 までのあいだで、x と y がどちらも整数になるところをかんがえて、表をかきます。
y=6x
x⋯−6−3−2−1−0−1−2−3−6⋯y⋯−1−2−3−6−×−6−3−2−1⋯
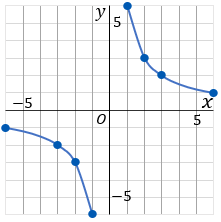 表をかいたらグラフ用紙に点をとっていきます。とれる点をすべてとったら、双曲線になるように、点をむすびます。比例定数が正のとき(a>0)のときは、座標平面の右上と左下に双曲線をひくことになります。
表をかいたらグラフ用紙に点をとっていきます。とれる点をすべてとったら、双曲線になるように、点をむすびます。比例定数が正のとき(a>0)のときは、座標平面の右上と左下に双曲線をひくことになります。
②これもまず表をつくります。x が +6 から −6 までのあいだで、x と y がどちらも整数になるところをかんがえて、表をかきます。
y=−4x
x⋯−4−2−1−0−1−2−4⋯y⋯−1−2−4−×−4−2−1⋯
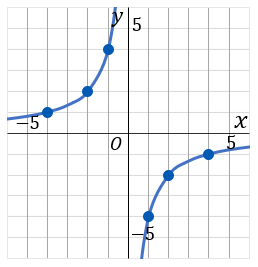 表をかいたらグラフ用紙に点をとっていきます。とれる点をすべてとったら、双曲線になるように、点をむすびます。比例定数が負のとき(a<0)のときは、座標平面の左上と右下に双曲線をひくことになります。
表をかいたらグラフ用紙に点をとっていきます。とれる点をすべてとったら、双曲線になるように、点をむすびます。比例定数が負のとき(a<0)のときは、座標平面の左上と右下に双曲線をひくことになります。
③y=5x④y=−8x

答え
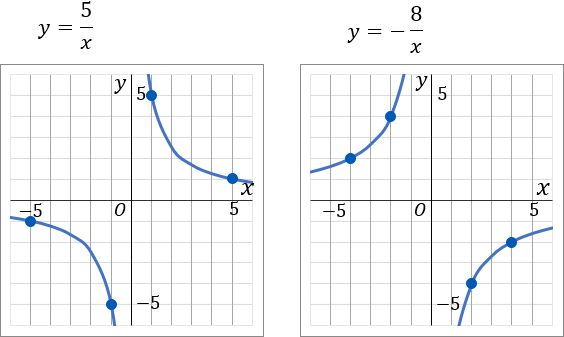
③まず表をつくります。グラフ用紙のマス目が 6 まであるので、x が +6 から −6 までのあいだで、x と y がどちらも整数になるところをかんがえて、表をかきます。
y=5x
x⋯−5−1−0−1−5⋯y⋯−1−5−×−5−1⋯
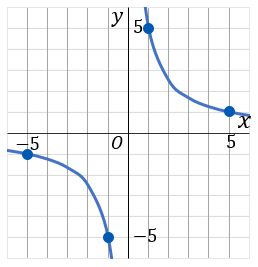 表をかいたらグラフ用紙に点をとっていきます。
表をかいたらグラフ用紙に点をとっていきます。
すべての点をとったら、双曲線になるように、点をむすぶわけですが、これだけだとちょっと足りないかもしれません。ねんのため、x=−4, −3, −2, +2, +3, +4 のときも確認しておいたほうがいいです。x=2 のとき y=52 だから 2.5 ぐらいのところを通るな、x=3 のとき y=53 だからだいたい 1.7 ぐらいのところを通るな、x=4 のとき y=54 だから 1.25 ぐらいのところだな、というふうに確認してから線をかいたほうがいいです。
いちおう、そのへんのこともかきくわえ、また、グラフをかくときに必要ないところは省略した表を、したにつくっておきます。
y=5x
x⋯−5−4−3−2−1−1−2−3−4−5⋯y⋯−1−54−53−52−5−5−52−53−54−1⋯
④まず表をつくります。グラフ用紙のマス目が 6 まであるので、x が +6 から −6 までのあいだで、x と y がどちらも整数になるところをかんがえて、表をかきます。
y=8x
x⋯−4−2−1−0−1−2−4⋯y⋯−2−4−8−×−8−4−2⋯
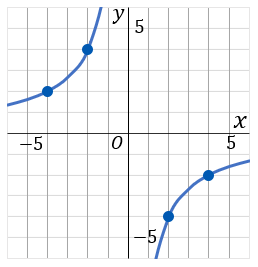 表をかいたらグラフ用紙に点をとっていきます。
表をかいたらグラフ用紙に点をとっていきます。
すべての点をとったら、双曲線になるように、点をむすぶわけですが、これのグラフもまた、これだけだとちょっと足りないです。x=−3, +3 のときと、x=−6, +6 のときも確認しておいたほうがいいです。x=3 のとき y=−83 だからだいたい −2.7 ぐらいのところだな、x=6 のとき y=−43 だからだいたい −1.3 ぐらいのところだな、というふうに確認してから線をかいたほうがいいです。
いちおう、そのへんのこともかきくわえ、また、グラフをかくときに必要ないところは省略した表を、したにつくっておきます。
y=8x
x⋯−6−4−3−2−2−3−4−6⋯y⋯−43−2−83−4−4−83−2−43⋯
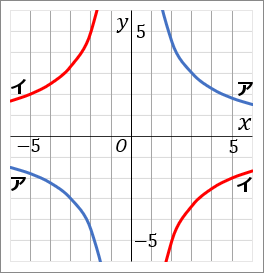
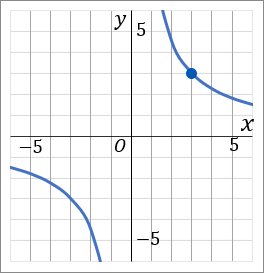
(24) 右の図のア,イはどちらも双曲線である。ア,イのそれぞれについて、y を x の式で表しなさい。
答え
ア y=9x
イ y=−10x
双曲線なのだから、反比例のグラフです。反比例のグラフについて、「y を x の式で表しなさい」といわれたら、式の形は y=ax で、a を求めるのが目標となります。a の求め方は、a=xy です。x と y をかければよいです。グラフ上にある、どこかカドを通っているところをさがして、その座標を利用します。
 <アについて>
<アについて>
アのグラフは、点(3, 3) を通っています。なので、x=3, y=3 を a=xy に代入して a を求めます。
a=xy=3×3=9
これで a=9 だと求められました。なので答えは y=9x です。
ここでは点(3, 3) を代入して a を求めましたが、ほかの点でもだいじょうぶです。グラフ上にある点の座標を代入すれば、どこをいれても全部おなじ答えになります。というかこの問題の場合は、あとはいれるとしたら (−3, −3) しかありませんけど。
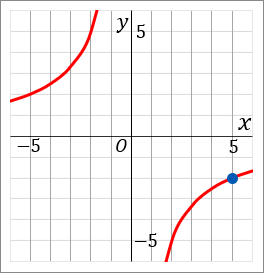 <イについて>
<イについて>
イのグラフは、点(5, −2) を通っています。なので、x=5, y=−2 を a=xy に代入して a を求めます。
a=xy=5×(−2)=−10
これで a=−10 だと求められました。なので答えは y=−10x です。
ここでは点(5, −2) を代入して a を求めましたが、ほかの点でもだいじょうぶです。グラフ上にある点の座標を代入すれば、どこをいれても全部おなじ答えになります。
比例,反比例の利用
(25) あるコピー用紙の 45 枚の重さが 110 gである。
①このコピー用紙 x 枚のときの重さを y gとして、y を x の式で表しなさい。
②このコピー用紙 315 枚の重さは何gか。
答え
① y=229x
② 770 g
①コピー用紙の枚数と重さは比例します。
比例のときの式の形は y=ax で、a を求めるのが目標になります。a の求め方は a=yx です。
コピー用紙の枚数を x 枚、重さを y gとして、 45 枚の重さが 110 gなのですから、
a=yx=11045=229
なので、y=229x
②x が 315 のときの y を求めればよいです。
y=229x に x=315 を代入して、
y=229×315=770
(26) 家から学校まで、分速 75 mで行くと 8 分かかる。
①速さが分速 x mのときにかかる時間を y 分として、y を x の式で表しなさい。
②分速 120 mで行くと何分かかるか。
答え
① y=600x
② 5 分
①速さと時間は反比例します。
反比例のときの式の形は y=ax で、a を求めるのが目標になります。a の求め方は a=xy です。
速さを分速 x m、時間を y 分として、分速 75 mときにかかる時間が 8 分なのですから、
a=xy=75×8=600
なので、y=600x
②x が 120 のときの y を求めればよいです。
y=600x に x=120 を代入して、
y=600120=5
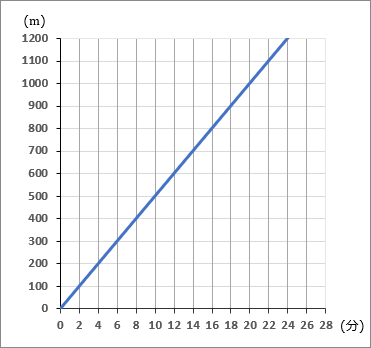
(27) 家から 1200 m 離れた駅にむかって、兄が家を出た。右のグラフはその進行のようすをしめしたものである。
兄と同時に弟が分速 150 mで、兄と同じ道を駅へむかって家をでた。
これについて、以下の問いに答えなさい。
①兄の速さは分速何mか。
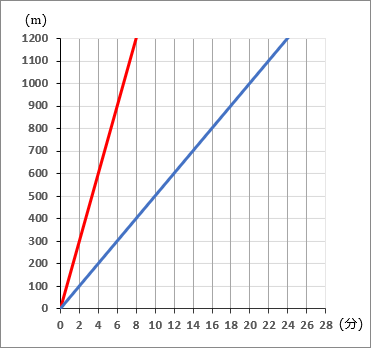
②弟の進行のようすを、グラフにかきくわえなさい。
③兄と弟が 600 m離れるのは、二人が家を出てから何分後か。
④家から 600 m離れた地点を弟が通過したあと、何分後に兄はそこを通過するか。
答え
① 分速 50 m
②
③ 6 分後
④ 8 分後
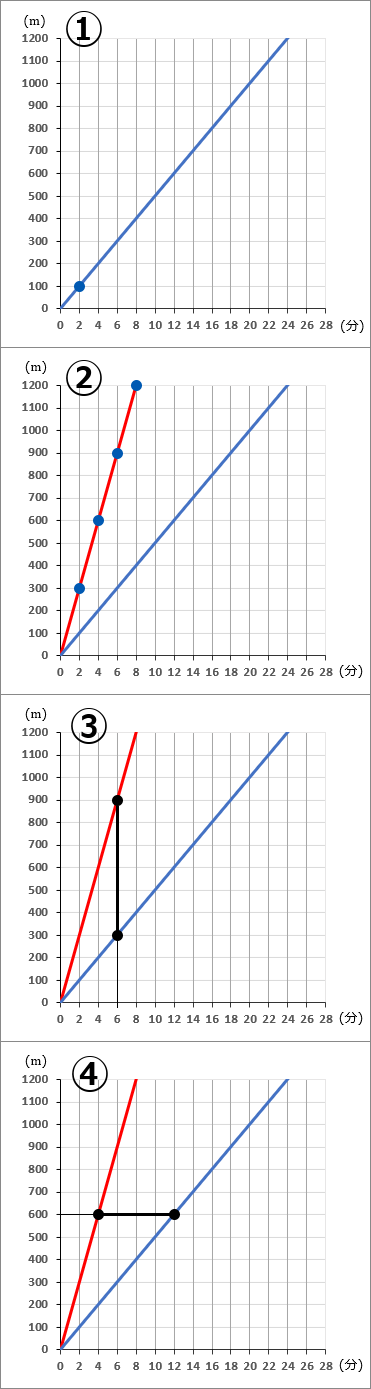 ①速さ=距離時間です。
①速さ=距離時間です。
グラフで、カドを通っているところをさがします。(2, 100) のところを通っています。2 分で 100 m進んだということですから、
1002=50 m/分。
②分速 150 mならば、 2 分で 300 m進むことになります。グラフ上で、原点をスタート地点として、右に 1 マスいって縦に 3 マスいくように点をとっていきます。そしてそこをむすびます。
③2 人のグラフ上で、縦に 600 m離れるところをさがします。縦に 6 マスぶん離れるところです。もしちょうどいいところがない場合は、計算から求めていくことになりますが、この問題にはちょうどいいところがあります。6 分後のところです。
④2 人のグラフ上で、 600 mのところを弟が通過したあと、何分後に兄が通過するを確認します。もし、ちょうどカドを通っていない場合は計算から求めていくことになりますが、この問題はちょうどカドとカドを通っています。 4 マスぶん離れています。なので 8 分後です。
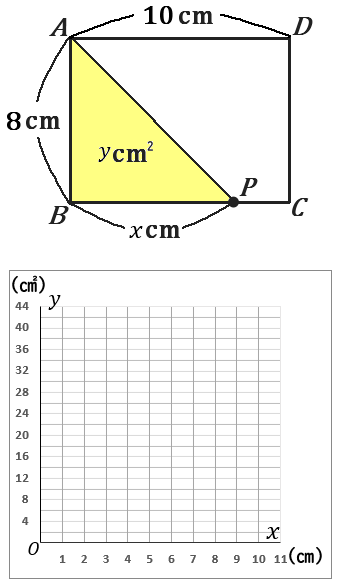
(28) AB=8cm, AD=10cm の長方形 ABCD がある。点 P は 頂点 B を出発して、辺 BC 上を 頂点 B から 頂点 C まで動く。BP=xcm のときの △ABP の面積を ycm2 とするとき、以下の問いに答えなさい。
①y を x の式で表しなさい。
②x と y の変域をそれぞれ求めなさい。
③x と y の関係を表すグラフをかきなさい。
④△ABP の面積が 30cm2 となるのは、BP の長さが何 cm のときか。
答え
 ① y=4x
① y=4x
② 0≦x≦10
0≦y≦40
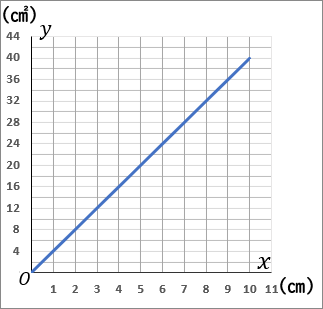
③ 右図
④ 152cm
①三角形の面積は、底辺 × 高さ ×12 です。 △ABP は、BP を底辺、AB を高さとみることができますので、その面積 y は
y=BP×AB×12=x×8×12=4x
②BP の長さは、0cm 以上 10cm 以下です。
なので △ABP の面積は、BP=0 のとき最小で、0 です。BP=10 のとき最大で、10×8×12=40 です。
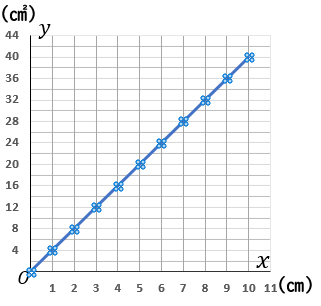 ③①の答えから、比例のグラフをかくことになります。x=1 のとき y=4 です。(1, 4) という座標はグラフのカドになっています。というわけで、原点をスタート地点として、右に 1 マスいって縦に 2 マスいく点をグラフ上にとっていき、定規でむすびます。
③①の答えから、比例のグラフをかくことになります。x=1 のとき y=4 です。(1, 4) という座標はグラフのカドになっています。というわけで、原点をスタート地点として、右に 1 マスいって縦に 2 マスいく点をグラフ上にとっていき、定規でむすびます。
注意点があります。グラフは点(10, 40) のところでとめてください。そこから先をかいてはいけません。かいてあるとバツになります。x や y の値に範囲があるときは、それを考えてグラフをかかなくちゃなりません。気をつけてください。
④y=30 となるところの座標がグラフ上でちょうどカドになっていればいいのですが、なっていません。こういう場合は計算して求めていきます。
y=4x の y に 30 を代入して、
30=4x(左辺と右辺をとりかえる)4x=30x=304=152
答え(中1 4章 比例,反比例 第2回)
(1) 関数
(2) ① いえる
② いえる
③ いえない
④ いえる
⑤ いえない
⑥ いえる
⑦ いえる
⑧ いえる
(3) 変域
 (4) ①x>3
②−2≦x≦5
③0<x≦2
④−4≦x<−2
(5) y=ax 比例定数 y=ax
(6) ① y=120x 比例定数… 120
② y=3x 比例定数… 3
③ y=52x 比例定数… 52
④ y=60x 比例定数… 60
⑤ y=20x 比例定数… 20
⑥ y=30x 比例定数… 30
(4) ①x>3
②−2≦x≦5
③0<x≦2
④−4≦x<−2
(5) y=ax 比例定数 y=ax
(6) ① y=120x 比例定数… 120
② y=3x 比例定数… 3
③ y=52x 比例定数… 52
④ y=60x 比例定数… 60
⑤ y=20x 比例定数… 20
⑥ y=30x 比例定数… 30
(7) ①y=3x
x⋯−4−3−2−1−0−1−2−3−4⋯y⋯−12−9−6−3−0−3−6−9−12⋯
②y=−14x
x⋯−4−3−2−1−0−1−2−3−4⋯y⋯−1−34−12−14−0−14−12−34−1⋯
③ 2 倍,3 倍,…になる
(8)
\begin{array}{c|cccc}
\hline
x & -3 & -2 & -1 & \phantom{-}0 & \phantom{-}1 \\
\hline
y & -15 & -10 & -5 & \phantom{-}0 & \phantom{-}5 \\
\hline
\end{array}

(9) ①y=3x
②y=-\cfrac{2}{3}x
③y=12x
(10) ①y=-6
②y=4
③y=-\cfrac{2}{5}
(11)
点 O で垂直に交わる 2 つの数直線について、横の数直線を \boxed{x軸\phantom{ho}} 、縦の数直線を \boxed{y軸\phantom{ho}} という。両方あわせて \boxed{座標軸\phantom{h}} という。その平面を \boxed{座標平面\phantom{h}} という。
2 つの数直線の交点 O を \boxed{原点\phantom{h}} という。
点P(2 \ , \ 3) について、(2 \ , \ 3) を点P の \boxed{座標\phantom{h}} という。2 を点P の \boxed{x座標\phantom{ho}} という。3 を点P の \boxed{y座標\phantom{ho}} という。
(12)
A(4, \ 3)
B(0, \ 2)
C(-4, \ 1)
D(-3, \ 0)
E(-5, \ -4)
F(2, \ -2)
 (13) y=ax のグラフは \boxed{原点\phantom{h}} を通る \boxed{直線\phantom{h}} である。
(13) y=ax のグラフは \boxed{原点\phantom{h}} を通る \boxed{直線\phantom{h}} である。
比例定数が正のとき(a\gt 0 のとき)、グラフは \boxed{右上がり\phantom{h}} の直線となる。
比例定数が負のとき(a\lt 0 のとき)、グラフは \boxed{右下がり\phantom{h}} の直線となる。

(14)
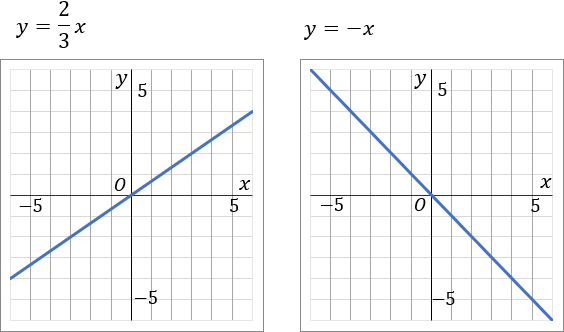

(15) ア y=\cfrac{3}{4}x
イ y=3x
ウ y=-\cfrac{5}{3}x
エ y=-x
(16) y=\cfrac{a}{x}, \ 比例定数, \ xy
(17) ① y=60x 比例
② y=\cfrac{2400}{x} 反比例
③ y=1000-6x ×
④ y=12x 比例
⑤ y=\cfrac{20}{x} 反比例
⑥ y=50x 比例
⑦ y=\cfrac{250}{x} 反比例
⑧ y=20x 比例
⑨ y=\cfrac{300}{x} 反比例
⑩ y=300-20x ×
(18) ①y=\cfrac{6}{x}
\begin{array}{c|ccccccccccc}
\hline
x & \cdots & -4 & -3 & -2 & -1 & \phantom{-}0 & \phantom{-}1 & \phantom{-}2 & \phantom{-}3 & \phantom{-}4 & \cdots\\
\hline
y & \cdots & -\cfrac{3}{2} & -2 & -3 & -6 & \phantom{-}× & \phantom{-}6 & \phantom{-}3 & \phantom{-}2 & \phantom{-}\cfrac{3}{2} & \cdots\\
\hline
\end{array}
②y=-\cfrac{4}{x}
\begin{array}{c|ccccccccccc}
\hline
x & \cdots & -4 & -3 & -2 & -1 & \phantom{-}0 & \phantom{-}1 & \phantom{-}2 & \phantom{-}3 & \phantom{-}4 & \cdots\\
\hline
y & \cdots & \phantom{-}1 & \phantom{-}\cfrac{4}{3} & \phantom{-}2 & \phantom{-}4 & \phantom{-}× & -4 & -2 & -\cfrac{4}{3} & -4 & \cdots\\
\hline
\end{array}
③ \cfrac{1}{2} 倍,\cfrac{1}{3} 倍,…になる
(19) ①y=\cfrac{20}{x}
②y=-\cfrac{24}{x}
③y=\cfrac{125}{x}
(20) ①y=-3
②y=\cfrac{12}{5}
③y=-2
(21)双曲線
(22) ① y=\cfrac{12}{x}
\begin{array}{c|ccccccccccccc}
\hline
\small{x}&\cdots&\small{-6}&\small{-4}&\small{-3}&\small{-2}&\small{-1}&\small{\phantom{-}0}&\small{\phantom{-}1}&\small{\phantom{-}2}&\small{\phantom{-}3}&\small{\phantom{-}4}&\small{\phantom{-}6}&\cdots\\
\hline
\small{y}&\cdots&\small-2&\small-3&\small-4&\small-6&\small-12&\phantom{-}\times&\small\phantom{-}12&\small\phantom{-}6&\small\phantom{-}4&\small\phantom{-}3&\small\phantom{-}2&\cdots&\\
\hline
\end{array}
② y=-\cfrac{12}{x}
\begin{array}{c|ccccccccccccc}
\hline
\small{x}&\cdots&\small{-6}&\small{-4}&\small{-3}&\small{-2}&\small{-1}&\small{\phantom{-}0}&\small{\phantom{-}1}&\small{\phantom{-}2}&\small{\phantom{-}3}&\small{\phantom{-}4}&\small{\phantom{-}6}&\cdots\\
\hline
\small{y}&\cdots&\small{\phantom{-}2}&\small{\phantom{-}3}&\small{\phantom{-}4}&\small{\phantom{-}6}&\small{\phantom{-}12}&\phantom{-}\times&\small{-12}&\small{-6}&\small{-4}&\small{-3}&\small{-2}&\cdots&\\
\hline
\end{array}

(23)


 (24) ア y=\cfrac{9}{x}
イ y=-\cfrac{10}{x}
(24) ア y=\cfrac{9}{x}
イ y=-\cfrac{10}{x}
(25)① y=\cfrac{22}{9}x
② 770 g
(26)① y=\cfrac{600}{x}
② 5 分
(27)① 分速 50 m
②右図
③ 6 分後
④ 8 分後
(28) ① y=4x
① y=4x
② 0 \leqq x \leqq 10
0 \leqq y \leqq 40\quad
③ 右図
④ \cfrac{15}{2}cm