数学 中2 1章 単項式と多項式 第1回
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
単項式と多項式
(1) 次の $ \boxed{\LARGE\phantom{hoge}}$ の中にあてはまる言葉をいれましょう。
①項が $1$ つだけの式を $ \boxed{\LARGE\phantom{hogeho}}$ という。
項が $2$ つ以上ある式を $ \boxed{\LARGE\phantom{hogeho}}$ という。
多項式で、文字をふくんでいない項を $ \boxed{\LARGE\phantom{hogeho}}$ という。
②単項式で、かけあわされている文字の個数を、その単項式の $ \boxed{\LARGE\phantom{hogeh}}$ という。多項式では、それがもっとも高い項の次数がその多項式の次数となる。
次数が $1$ の式を $ \boxed{\LARGE\phantom{hogeho}}$ という。次数が $2$ の式を $ \boxed{\LARGE\phantom{hogeho}}$ という。
③多項式で、文字と次数がおなじ項を $ \boxed{\LARGE\phantom{hogeho}}$ という。
答え
①項が $1$ つだけの式を $ \boxed{単項式}$ という。
項が $2$ つ以上ある式を $ \boxed{多項式}$ という。
多項式で、文字をふくんでいない項を $ \boxed{定数項}$ という。
②単項式で、かけあわされている文字の個数を、その単項式の $ \boxed{次数}$ という。多項式では、それがもっとも高い項の次数がその多項式の次数となる。
次数が $1$ の式を $ \boxed{1次式\phantom{ho}}$ という。次数が $2$ の式を $ \boxed{2次式\phantom{ho}}$ という。
③多項式で、文字と次数がおなじ項を $ \boxed{同類項}$ という。
①単項式…$3x, \ -\cfrac{2}{3}x^2y^3z$ など
多項式…$2x+1, \ 3a^2+5a+4$ など
また、$3a^2+5a+4$ の $4$ を定数項といいます。
②たとえば、$x$ は $1$ 次です。$x^2$ は $xx$ と考えて、$2$ 次です。$x^2y^3z$ は $xxyyyz$ と考えて、$6$ 次です。
多項式の次数についてですが、たとえば $3a^2+5a+4$ は、$3a^2$ が $2$ 次、$5a$ が $1$ 次なので、この式は $2$ 次式となります。
③たとえば $3x^2-4x+5x$ という式では、$-4x$ と $5x$ が同類項です。$3x^2$ と $-4x$ や、$3x^2$ と $5x$ は同類項ではありません。
(2) 次の①,②の多項式の項をいいなさい。また、何次式かをいいなさい。
$
\qquad① \ -3x+\cfrac{1}{2}y-4\qquad\quad② \ 2a^2-3ab^3+4c-5
$
答え
$①-3x, \ \cfrac{1}{2}y, \ -4\qquad1次式$
$②2a^2, \ -3ab^3, \ 4c,-5\qquad4次式$
①ひとつひとつ項にわけるときは、いちばんでだしはよしとして、そこから先は、$+$ や $-$ があったらスラッシュをいれるとわかりやすくなります。スラッシュというのは、$/$ のことです。ナナメの線です。これをいれます。こんな感じです。
$$\large{-3x/+\cfrac{1}{2}y/-4}$$
んで、ひとつひとつの次数をみていけばいいです。$-3x$ は $1$ 次、$\cfrac{1}{2}y$ は $1$ 次、$-4$ のような定数項は気にしません。なので、これは $1$ 次式と答えます。
②$-3ab^3$ というのは $-3abbb$ と考えて、$4$ 次です。ここがいちばん次数の高い項なので、②は $4$ 次式と答えます。
多項式の加法・減法
(3) 次の①~④の式の同類項をまとめなさい。
\begin{eqnarray*}
&①& \quad 8a-b+7a-10b&②& \quad \cfrac{1}{2}x-3y+\cfrac{3}{4}x+\cfrac{2}{3}y\\
\\
&③& \quad (2x-3y)+(-3x-5y)\quad&④& \quad (-a^2+10a)-(9a^2-15a)
\end{eqnarray*}
答え
$①15a-11b$ $②\cfrac{5}{4}x-\cfrac{7}{3}y$ $③-x-8y$ $④-10a^2+25a$
「同類項をまとめなさい」というのは、「計算をしなさい」とおなじ意味です。多項式の足し算や引き算は、文字のところが同じならできます。ちがっていたらできません。$3x+2y$ とか、$2x^2-5x$ とかは、もうこれ以上できません。そこでやめてください。それ以上やっちゃダメです。 \begin{eqnarray*} &①& 8a-b+7a-10b\\ &=& 8a+7a-b-10b\\ &=& 15a-11b \end{eqnarray*} 分数の足し算・引き算はもちろん分母をそろえます。通分します。こういう問題のときは、$x$ は $x$ で、$y$ は $y$ で、べつべつに通分します。 \begin{eqnarray*} &②& \cfrac{1}{2}x-3y+\cfrac{3}{4}x+\cfrac{2}{3}y\\ &=& \cfrac{1}{2}x+\cfrac{3}{4}x-3y+\cfrac{2}{3}y\\ &=& \cfrac{2}{4}x+\cfrac{3}{4}x-\cfrac{9}{3}y+\cfrac{2}{3}y\\ &=& \cfrac{5}{4}x-\cfrac{7}{3}y \end{eqnarray*} かっこがあったらまずかっこをはずしましょう。 \begin{eqnarray*} &③& (2x-3y)+(-3x-5y)\\ &=& 2x-3y-3x-5y\\ &=& 2x-3x-3y-5y\\ &=& -x-8y \end{eqnarray*} かっこの前に $-$ があったら、かっこをはずしたときに、かっこの中の符号が逆になります。 \begin{eqnarray*} &④& (-a^2+10a)-(9a^2-15a)\\ &=& -a^2+10a-9a^2+15a\\ &=& -a^2-9a^2+10a+15a\\ &=& -10a^2+25a \end{eqnarray*}
(4) 次の①~④の計算をしなさい。
\begin{eqnarray*}
①&& \phantom{+)} \quad 5x+\phantom{6}y\qquad&②& \phantom{+} \quad -2x-4y+2\\
&&\underline{+) \quad \phantom{5}x-6y} &\phantom{②}& \underline{+) \quad \phantom{-}3x+2y-2}\\\\
③&& \phantom{+)} \quad -2a+3b\qquad&④& \phantom{+} \quad \phantom{hoge}x-2y+3\\
&&\underline{-) \quad \phantom{5}-a+4b} &\phantom{②}& \underline{-) \quad -2x+4y+5}
\end{eqnarray*}
答え
$①6x-5y$ $②x-2y$ $③-a-b$ $④3x-6y-2$
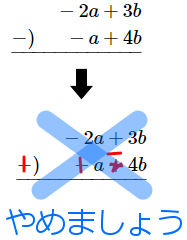 足し算は上から下に足せばよいです。引き算は、頭の中で下の式の符号を逆だと思って上から下に足せばよいです。
足し算は上から下に足せばよいです。引き算は、頭の中で下の式の符号を逆だと思って上から下に足せばよいです。
引き算についてですが、下の式の符号を実際に逆にかきかえて足していくひとがいます。逆の符号を実際に問題にかきくわえるのは、なるべくやめましょう。
これからしばらくしたら連立方程式を教わります。そこでこの手の計算をたくさんやることになります。初めのうちはミスします。自分がどこでまちがえたのかを確認するために、自分の計算の過程を見直すとき、符号を逆にしてあると、苦労します。わけがわからなくなったりします。
なので、符号を逆にしたのを書きくわえるのはやめましょう。すべて頭の中でやる練習をしましょう。慣れの問題だと思います。慣れたら自然にできるようになります。私が勉強を教えている生徒には、問題を書きかえているひとがいたら、やめてもらっています。みんな、だんだん慣れてきて、そのうちふつうに、書きかえなくてもできるようになってます。
(5) 次の①,②のそれぞれの $2$ つの式について、左の式に右の式を足しなさい。また、左の式から右の式を引きなさい。
$
\qquad① \quad 3x-4y+6,\qquad6x-3y+7\\
\qquad② \quad -5x+3y-1,\qquad-2x+3y-5
$
答え
$①和 9x-7y+13$ $差 -3x-y-1$
$①和 -7x+6y-6$ $差 -3x+4$
どちらもかっこをつけて足したり引いたりします。足すときはまあ、どうでもいいっちゃいいのですが、引き算のときは、かならずかっこをつけてください。そしてかっこをはずすと、符号が逆になります。
\begin{eqnarray*}
① 和 &&(3x-4y+6)+(6x-3y+7)\\
&=& 3x-4y+6+6x-3y+7\\
&=& 3x+6x-4y-3y+6+7\\
&=& 9x-7y+13
\end{eqnarray*}
\begin{eqnarray*}
① 差 &&(3x-4y+6)-(6x-3y+7)\\
&=& 3x-4y+6-6x+3y-7\\
&=& 3x-6x-4y+3y+6-7\\
&=& -3x-y-1
\end{eqnarray*}
\begin{eqnarray*}
② 和 &&(-5x+3y-1)+(-2x+3y-5)\\
&=& -5x+3y-1-2x+3y-5\\
&=& -5x-2x+3y+3y-1-5\\
&=& -7x+6y-6
\end{eqnarray*}
\begin{eqnarray*}
② 差 &&(-5x+3y-1)-(-2x+3y-5)\\
&=& -5x+3y-1+2x-3y+5\\
&=& -5x+2x-3y+3y-1+5\\
&=& -3x+4
\end{eqnarray*}
単項式と単項式の乗法
(6) 次の ①~⑥の計算をしなさい。
\begin{eqnarray*}
&①& \quad x \times x \times x \quad&②& \quad 2x^3\times3x^4 \quad&③& \quad 3a \times 5b\\
\\
&④& \quad (-2x)^2 &⑤& \quad \left(-\cfrac{2}{3}x\right)^3 &⑥& \quad -2a\times(-3a)^2
\end{eqnarray*}
答え
$①x^3$ $②6x^7$ $③15ab$ $④4x^2$ $⑤-\cfrac{8}{27}x^3$ $⑥-18a^3$
\begin{eqnarray*}
&①&x \times x \times x=x^3\\
&②&2x^3\times3x^4=2\times xxx \times 3\times xxxx=6x^7
\end{eqnarray*}
かけ算のときは指数は足すんだ、と思っちゃったほうがいいです。$x^3\times x^4=x^{3+4}=x^7$ というふうに。これがおすすめ。
かっこの $2$ 乗やかっこの $3$ 乗は、マイナスのときは符号に注意しましょう。指数が偶数のときはプラスになります。奇数のときはマイナスになります。なので
$$④(-2x)^2=4x^2,\quad⑤\left(-\cfrac{2}{3}x\right)^3=-\cfrac{8}{27}x^3$$
です。
⑥は、$(2x)^2$ とか $(-2a)^3$ といった、指数のついたかっこがあったら、それは、計算の順番として、優先順位がいちばん高いと思っちゃうといいです。なによりもそこが先です。まず指数のかっこをはずしましょう。
$$⑥-2a\times(-3a)^2=-2a\times9a^2=-18a^3$$
単項式と単項式の除法
(7) 次の ①~③の計算をしなさい。
$
\quad① \quad 20xy \div 5x \quad② \ -8x^5\div4x^3 \quad③ \quad 6ab \div \cfrac{2}{3}b
$
答え
$①4y$ $②-2x^2$ $③9a$
割り算は分数にして、約分できるところは約分しましょう。そのさい、$x^3$ を $xxx$ というふうにかいてしまうとわかりやすくなります。ミスが心配なひとは、そうかきましょう。
\begin{eqnarray*}
\require{cancel}
&①&20xy \div 5x=\cfrac{20xy}{5x}=\cfrac{{}^4\bcancel{20}\bcancel{x}y}{\bcancel{5}\bcancel{x}}=4y\\
&②&-8x^5 \div 4x^3=-\cfrac{8x^5}{4x^3}=-\cfrac{{}^2\bcancel{8}\bcancel{xxx}xx}{\bcancel{4}\bcancel{xxx}}=-2x^2
\end{eqnarray*}
③分数の割り算は逆数をかけます。いわゆる「ひっくり返して掛ける」というやつです。そのさい、注意点があります。$b$ は分母のほうにいきます。
$\qquad \cfrac{2}{3}b=\cfrac{2b}{3}$ なので、逆数にすると$\cfrac{3}{2b}$
なので、
\begin{eqnarray*}
③&& 6ab\div \cfrac{2}{3}b\\
&=& 6ab\times \cfrac{3}{2b}\\
&=& {}^3\bcancel{6}a\bcancel{b} \times \cfrac{3}{\bcancel{2}\bcancel{b}}
= 9a
\end{eqnarray*}
まちがえやすい注意点なので、もういちど整理しておきますね。
$\qquad \cfrac{2}{3}b$ を逆数にすると $\cfrac{3}{2}b$ ←まちがい
$\qquad \cfrac{2}{3}b$ を逆数にすると $\cfrac{3}{2b}$ ←正しい
多項式と数の計算
(8) 次の ①~④の計算をしなさい。
\begin{eqnarray*}
&①& \quad 2(3x+4y) &②& \quad \cfrac{2}{3}(6x-9y)\\
\\
&③& \quad (12a-8b)\div4 \qquad &④& \quad (15x+20y)\div\cfrac{5}{3}
\end{eqnarray*}
$$ \large{a(b+c)=ab+ac \qquad (a+b)c=ac+bc}$$
$$ \large{(b+c)\div a=\cfrac{b+c}{a}=\cfrac{b}{a}+\cfrac{c}{a}}$$
答え
$①6x+8y$ $②4x-6y$ $③3a-2b$ $④9x+12y$
分配法則でまんべんなくかけていきましょう。または、まんべんなく割っていきましょう。③の割り算は、分数にしなくてもわかるときは、いちいち分数にする必要はありません。でも慣れてないうちはひとつひとつ分数にしたほうがよいかもしれません。めんどくさいけど。④の分数の割り算は、逆数をかける形にします。「ひっくり返してかける」です。そのあとは分配法則。 \begin{eqnarray*} &①& 2(3x+4y)\\ &=&2\times3x+2\times4y\\ &=&6x+8y\\ \\ &②& \cfrac{2}{3}(6x-9y)\\ &=&=\cfrac{2}{3}\times6x-\cfrac{2}{3}\times9y\\ &=&4x-6y\\ \\ &③& (12a-8b)\div4\\ &=&\cfrac{12a}{4}-\cfrac{8b}{4}\\ &=&\cfrac{{}^3\bcancel{12}a}{\bcancel{4}}-\cfrac{{}^2\bcancel{8}b}{\bcancel{4}}\\ &=&3a-2b\\ \\ &④& (15x+20y)\div\cfrac{5}{3}\\ &=&(15x+20y)\times\cfrac{3}{5}\\ &=&15x\times\cfrac{3}{5}+20y\times\cfrac{3}{5}\\ &=&{}^3\bcancel{15}x\times\cfrac{3}{\bcancel{5}}+{}^4\bcancel{20}y\times\cfrac{3}{\bcancel{5}}\\ &=&9x+12y \end{eqnarray*}
やや複雑な計算
(9) 次の ①~⑥の計算をしなさい。
\begin{eqnarray*}
&①& \quad -3xy\div2x^2y\times(-4xy) \quad &②& \quad \cfrac{1}{4}x^2\times3x\div\cfrac{3}{2}x^2y\\
\\
&③& \quad 2(x+2y)+3(2x-y) \quad &④& \quad -(4a+6b)-2(2a-b)\\
\\
&⑤& \quad \cfrac{a+2b}{3}+\cfrac{2a-3b}{4}&⑥& \quad \cfrac{x+2y}{5}-\cfrac{3x-4y}{2}
\end{eqnarray*}
$$ \large{a(b+c)=ab+ac \qquad (a+b)c=ac+bc}$$
答え
$①6y$ $②\cfrac{x}{2y}$ $③8x+y$ $④-8a-4b$ $⑤\cfrac{10a-b}{12}$ $\left(\cfrac{5}{6}a-\cfrac{1}{12}b\right)$ $⑥\cfrac{-13x+24y}{10}$ $\left(-\cfrac{13x-24y}{10}, \ -\cfrac{13}{10}x+\cfrac{12}{5}y\right)$
①$\times$ と $\div$ だけの式のときは、まず最初に答えの符号がプラスなのかマイナスなのかをみきわめたあと、ひとつの分数にして、上と下にハッキリとわけて、約分すればよいです。そのさい、$\div$ の直後にかかれているものは分母にかきます。また、たとえば $x^2$ を $xx$ のようにかくと、約分がしやすいです。
\begin{eqnarray*}
&①& -3xy\div2x^2y\times(-4xy)\\
&=& \cfrac{3xy\times4xy}{2x^2y}\\
&=& \cfrac{3xy\times4xy}{2xxy}\\
&=& \cfrac{3\bcancel{x}\bcancel{y}\times{}^2\bcancel{4}\bcancel{x}y}{\bcancel{2}\bcancel{x}\bcancel{x}\bcancel{y}}\\
&=& 6y
\end{eqnarray*}
②$\times$ と $\div$ だけの式に分数があるときは、まず最初に答えの符号がプラスなのかマイナスなのかをみきわめたあと、すべてをかけ算になおします。そのさい、上と下にハッキリとわけるとミスがすくなくなります。それから約分すればよいです。
\begin{eqnarray*}
&②& \cfrac{1}{4}x^2\times3x\div\cfrac{3}{2}x^2y\\
&=& \cfrac{x^2}{4}\times\cfrac{3x}{1}\times\cfrac{2}{3x^2y}\\
&=& \cfrac{xx}{4}\times\cfrac{3x}{1}\times\cfrac{2}{3xxy}\\
&=& \cfrac{\bcancel{x}\bcancel{x}}{{}^2\bcancel{4}}\times\cfrac{\bcancel{3}x}{1}\times\cfrac{\bcancel{2}}{\bcancel{3}\bcancel{x}\bcancel{x}y}\\
&=& \cfrac{x}{2y}
\end{eqnarray*}
③④の問題は、分配法則でかっこをはずしたあと、文字の同じ項どうしを足したり引いたりすればOKです。
\begin{eqnarray*}
&③& 2(x+2y)+3(2x-y)\\
&=&2x+4y+6x-3y\\
&=&2x+6x+4y-3y\\
&=&8x+y\\
\\
&④& -(4a+6b)-2(2a-b)\\
&=&-4a-6b-4a+2b\\
&=&-4a-4a-6b+2b\\
&=&-8a-4b\\
\end{eqnarray*}
⑤⑥の問題は、こういうのは分母をひとつにして、なが~い分数の線をひいて、そこに分子をぜんぶ乗せてしまうといいです。とくに⑥は符号のことでまちがえやすいので、いったんかっこをつけて分子をかくといいです。それからかっこをはずしてください。そうやると符号のまちがいがなくなります。
\begin{eqnarray*}
&⑤& \cfrac{a+2b}{3}+\cfrac{2a-3b}{4}\\
&=& \cfrac{4(a+2b)+3(2a-3b)}{12}\\
&=& \cfrac{4a+8b+6a-9b}{12}\\
&=& \cfrac{4a+6a+8b-9b}{12}\\
&=& \cfrac{10a-b}{12}
\end{eqnarray*}
\begin{eqnarray*}
&⑥& \cfrac{x+2y}{5}-\cfrac{3x-4y}{2}\\
&=& \cfrac{2(x+2y)-5(3x-4y)}{10}\\
&=& \cfrac{2x+4y-15x+20y}{10}\\
&=& \cfrac{2x-15x+4y+20y}{10}\\
&=& \cfrac{-13x+24y}{10}
\end{eqnarray*}
約分についてですが、たとえば、
$$\cfrac{9x+5y}{6}$$
こういうのは約分できません。$9$ と $5$ と $6$ はいっぺんに割れないからです。なのでここでやめてください。それから、
$$\cfrac{9x+y}{6}$$
こういうのも約分しちゃダメです。これでやめてください。そんで、
$$\cfrac{9x+3y}{6}=\cfrac{{}^3\bcancel{9}x+\bcancel{3}y}{{}^2\bcancel{6}}=\cfrac{3x+y}{2}$$
こういうときが約分できます。$9$ と $3$ と $6$ は $3$ で割れます。約分してください。約分できるのにしてないと、それはそれでバツになります。
あと答えの書き方ですが、
$\cfrac{-13x+24y}{10}$ となったときに、これを $-\cfrac{13x+24y}{10}$ とかくとバツになります。式の意味がちがってしまうので、ダメです。やらないでください。マイナスを前にだしたいのであれば、
$$-\cfrac{13x-24y}{10}$$
こうかくことになります。気をつけてね。だからおすすめは、余計なことは考えずにそのまま $\cfrac{-13x+24y}{10}$ と答えておくことです。マイナスを前にださなきゃいいんです。そうすりゃバツにならんです。
いろいろな計算(まとめ)
(10) 次の①~の計算をしなさい。
\begin{eqnarray*}
&①& \quad 3x^2+5x^2 &②& \quad \cfrac{1}{3}ab+2ab\\
\\
&③& \quad \cfrac{3}{4}x^2+\cfrac{1}{2}x-2x^2-\cfrac{2}{3}x \quad&④& \quad (2m-3n+4)-(4m-3n+7)\\
\\
&⑤& \quad -\cfrac{1}{6}x^2 \times (-2x)^2 &⑥& \quad 12x^5\div(-9x^3)\\
\\
&⑦& \quad \cfrac{1}{12}a^2b\div \cfrac{2}{9}ab &⑧& \quad -3(4p-3q)\\
\\
&⑨& \quad (25x+100y)\div(-25) &⑩& \quad (3a+15b)\div\cfrac{3}{4}\\
\\
&⑪& \quad x^2\div5xy\times3y &⑫& \quad 4x^2y^2\div(-4y)\div\cfrac{2}{3}xy\\
\\
&⑬& \quad 2(5x+4y)-3(3x-y) \qquad &⑭& \quad \cfrac{3x-2y}{3}-\cfrac{x+3y}{2}
\end{eqnarray*}
答え
$①8x^2$ $②\cfrac{7}{3}ab$ $③-\cfrac{5}{4}x^2-\cfrac{1}{6}x$ $④-2m-3$ $⑤-\cfrac{2}{3}x^4$ $⑥-\cfrac{4}{3}x^2$ $⑦\cfrac{3}{8}a$ $⑧-12p+9q$ $⑨-x-4y$ $⑩4a+20b$ $⑪\cfrac{3}{5}x$ $⑫-\cfrac{3}{2}x$ $⑬x+11y$ $⑭\cfrac{3x-13y}{6}$ $\left(\cfrac{1}{2}x-\cfrac{13}{6}y\right)$
\begin{eqnarray*} &①& 3x^2+5x^2\\ &=& 8x^2 \end{eqnarray*} \begin{eqnarray*} &②& \cfrac{1}{3}ab+2ab\\ &=& \cfrac{1}{3}ab+\cfrac{6}{3}ab\\ &=& \cfrac{7}{3}ab \end{eqnarray*} \begin{eqnarray*} &③& \cfrac{3}{4}x^2+\cfrac{1}{2}x-2x^2-\cfrac{2}{3}x\\ &=& \cfrac{3}{4}x^2-2x^2+\cfrac{1}{2}x-\cfrac{2}{3}x\\ &=& \cfrac{3}{4}x^2-\cfrac{8}{4}x^2+\cfrac{3}{6}x-\cfrac{4}{6}x\\ &=& -\cfrac{5}{4}x^2-\cfrac{1}{6}x \end{eqnarray*} \begin{eqnarray*} &④& (2m-3n+4)-(4m-3n+7)\\ &=& 2m-3n+4-4m+3n-7\\ &=& 2m-4m-3n+3n+4-7\\ &=& -2m-3 \end{eqnarray*} \begin{eqnarray*} &⑤& -\cfrac{1}{6}x^2 \times (-2x)^2\\ &=& -\cfrac{1}{6}x^2 \times 4x^2\\ &=& -\cfrac{1}{{}^3\bcancel{6}}\times xx\times{}^2\bcancel{4}\times xx\\ &=& -\cfrac{2}{3}x^4 \end{eqnarray*} \begin{eqnarray*} &⑥& 12x^5\div(-9x^3)\\ &=& -\cfrac{12x^5}{9x^3}\\ &=& -\cfrac{{}^4\bcancel{12}\bcancel{x}\bcancel{x}\bcancel{x}xx}{{}^3\bcancel{9}\bcancel{x}\bcancel{x}\bcancel{x}}\\ &=& -\cfrac{4}{3}x^2 \end{eqnarray*} \begin{eqnarray*} &⑦& \cfrac{1}{12}a^2b\div \cfrac{2}{9}ab\\ &=& \cfrac{a^2b}{12}\times \cfrac{9}{2ab}\\ &=& \cfrac{\bcancel{a}a\bcancel{b}}{{}^4\bcancel{12}}\times \cfrac{{}^3\bcancel{9}}{2\bcancel{a}\bcancel{b}}\\ &=& \cfrac{3}{8}a \end{eqnarray*} \begin{eqnarray*} &⑧& -3(4p-3q)\\ &=& -12p+9q \end{eqnarray*} \begin{eqnarray*} &⑨& (25x+100y)\div(-25)\\ &=& -\cfrac{25x}{25}-\cfrac{100y}{25}\\ &=& -\cfrac{\bcancel{25}x}{\bcancel{25}}-\cfrac{{}^4\bcancel{100}y}{\bcancel{25}}\\ &=& -x-4y \end{eqnarray*} \begin{eqnarray*} &⑩& (3a+15b)\div\cfrac{3}{4}\\ &=& (3a+15b)\times\cfrac{4}{3}\\ &=& 3a\times\cfrac{4}{3}+15b\times\cfrac{4}{3}\\ &=& \bcancel{3}a\times\cfrac{4}{\bcancel{3}}+{}^5\bcancel{15}b\times\cfrac{4}{\bcancel{3}}\\ &=& 4a+20b \end{eqnarray*} \begin{eqnarray*} &⑪& x^2\div5xy\times3y\\ &=& \cfrac{x^2\times3y}{5xy}\\ &=& \cfrac{\bcancel{x}x\times3\bcancel{y}}{5\bcancel{x}\bcancel{y}}\\ &=& \cfrac{3}{5}x \end{eqnarray*} \begin{eqnarray*} &⑫& 4x^2y^2\div(-4y)\div\cfrac{2}{3}xy\\ &=& \cfrac{4x^2y^2}{1}\times\left(-\cfrac{1}{4y}\right)\times\cfrac{3}{2xy}\\ &=& -\cfrac{\bcancel{4}\bcancel{x}x\bcancel{y}\bcancel{y}}{1}\times\cfrac{1}{\bcancel{4}\bcancel{y}}\times\cfrac{3}{2\bcancel{x}\bcancel{y}}\\ &=& -\cfrac{3}{2}x \end{eqnarray*} \begin{eqnarray*} &⑬& 2(5x+4y)-3(3x-y)\\ &=& 10x+8y-9x+3y\\ &=& 10x-9x+8y+3y\\ &=& x+11y \end{eqnarray*} \begin{eqnarray*} &⑭& \cfrac{3x-2y}{3}-\cfrac{x+3y}{2}\\ &=& \cfrac{2(3x-2y)-3(x+3y)}{6}\\ &=& \cfrac{6x-4y-3x-9y}{6}\\ &=& \cfrac{6x-3x-4y-9y}{6}\\ &=& \cfrac{3x-13y}{6} \end{eqnarray*}
「~のとき、~の値」の問題
(11) 次の①,②の問いに答えなさい。
① $x=1.7, \ y=8.3$ のとき、次の式の値を求めなさい。
$$\quad \ 2(3x-2y)-5(x-y)$$
② $a=6, \ b=-5$ のとき、次の式の値を求めなさい。
$$\qquad \ (-a)^3\div (2ab)^2$$
答え
$①10$ $②-\cfrac{3}{50}$
問題の式に $x$ や $y$,$a$ や $b$ の値を代入しても答えは求められますが、めんどうくさいことになります。整理できるところまで整理してから代入するとラクになります。 \begin{eqnarray*} &①& 2(3x-2y)-5(x-y)\\ &=& 6x-4y-5x+5y\\ &=& 6x-5x-4y+5y\\ &=& x+y \quad \class{mathbg-r}{(ここまでやってから代入する)} \\ &=& (1.7)+(8.3)\\ &=& 10 \end{eqnarray*} \begin{eqnarray*} &②& (-a)^3\div (2ab)^2\\ &=& -a^3\div 4a^2b^2\\ &=& -\cfrac{aaa}{4aabb}\\ &=& -\cfrac{\bcancel{aa}a}{4\bcancel{aa}bb}\\ &=& -\cfrac{a}{4b^2} \quad \class{mathbg-r}{(ここまでやってから代入する)} \\ &=& -\cfrac{6}{4\times(-5)^2}\\ &=& -\cfrac{{}^3\bcancel{6}}{{}^2\bcancel{4}\times25}\\ &=& -\cfrac{3}{50} \end{eqnarray*}
数学のおやくそく
(12) 文字 $n$ を使って、次の①~⑤の数を表しなさい。ただし、$n$ は整数とします。
また、文字 $x, \ y$ を使って⑥の数を表しなさい。ただし、$x, \ y$ は $1$~$9$ までの整数とします。
\begin{eqnarray*}
&①&\ 偶数 \qquad\qquad &②& \ 奇数\qquad\qquad &③& \ 連続する 2 つの数 \\
\\
&④&\ 連続する 3 つの数 \qquad\qquad &⑤& \ 3 の倍数 \qquad\qquad &⑥&\ 2けたの数
\end{eqnarray*}
答え
$①2n$ $②2n+1(2n-1でもよい)$ $③n,n+1(n-1,nでもよい)$ $④n-1,n,n+1(n,n+1,n+2などでもよい)$ $⑤3n$ $⑥10x+y$
式の利用
(13) 連続する $2$ つの整数の和は 奇数であることを説明したい。これについて、次の①,②の問いに答えなさい。
① 連続する $2$ つの整数を、文字 $n$ を使って表しなさい。ただし、$n$ は整数とします。
② ①で表した連続する $2$ つの整数を使って、連続する $2$ つの整数の和は奇数であることを説明しなさい。
答え
① $n, \ n+1 \ (n-1, \ n \ でもよい)$
② 連続する $2$つの整数を $n, \ n+1$ と表す。ただし、$n$ は整数である。
\begin{eqnarray*}
&& (n)+(n+1)\\
&=& 2n+1
\end{eqnarray*}
$n$ は整数だから、$2n+1$ は奇数である。したがって、連続する $2$ つの整数の和は奇数である。
<おぼえておきたい数学のおやくそく>
偶数…$2n$
奇数…$2n+1 \quad (2n-1)$
$3$の倍数…$3n$
$5$の倍数…$5n$
連続する $2$つの数…$n, \ n+1$
連続する $3$つの数…$n-1, \ n, \ n+1 \quad (n, \ n+1, \ n+2)$
連続する $2$つの偶数…$2n, \ 2n+2$
連続する $2$つの奇数…$2n-1, \ 2n+1$
※ただし、$n$ は整数とする。
(14) $1$ の位が $0$ でない $2$ けたの自然数を $A$ とする。$A$ の十の位と一の位をいれかえてできる数を $B$ とする。このとき、次の①,②の問いに答えなさい。
① $A$ の十の位を $x, \ $一の位を $y$ として、$A$ を $x, \ y$ を使って表しなさい。また、$B$ を $x, \ y$ を使って表しなさい。ただし、$x, \ y$ は $1$ から $9$ までの整数とします。
② ①で表した $A, \ B$ を使って、$A+B$ は $11$ の倍数になることを説明しなさい。
答え
① $A=10x+y, \ B=10y+x$
② $A$ を $10x+y$ と表すと、$B$ は $10y+x$ と表せる。ただし、$x, \ y$ は $1$ から $9$ までの整数である。
\begin{eqnarray*}
&&A+B\\
&=& (10x+y)+(10y+x)\\
&=& 10x+y+10y+x\\
&=& 10x+x+y+10y\\
&=& 11x+11y\\
&=& 11(x+y)\\
\end{eqnarray*}
$x+y$ は整数だから、$11(x+y)$ は $11$ の倍数である。したがって、$A+B$ は $11$ の倍数になる。
<おぼえておきたい数学のおやくそく>
$2$ けたの数
$\large{10x+y}$
十の位と一の位をいれかえた数
$\large{10y+x}$
※ただし、$x, \ y$ は $1$ から $9$ までの整数とする。
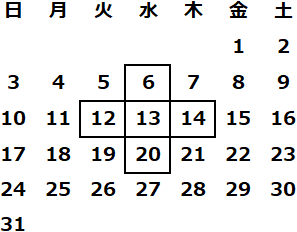 (15) 右の図は、ある年のある月のカレンダーである。これを、図のような$\large{+}$の形の線で囲むと、その中の数にある $5$ つの数の和は $5$ の倍数になる。このことについて、次の①,②の問いに答えなさい。
(15) 右の図は、ある年のある月のカレンダーである。これを、図のような$\large{+}$の形の線で囲むと、その中の数にある $5$ つの数の和は $5$ の倍数になる。このことについて、次の①,②の問いに答えなさい。
① 線で囲まれた $5$ つの数を、真ん中の数を $n$ として表しなさい。ただし、$n$ は整数とします。
② ①で表した数を使って、線で囲まれた $5$ つの数の和は $5$ の倍数になることを説明しなさい。
答え
① $n-7,n-1,n,n+1,n+7$
② 線で囲まれた $5$ つの数は、$n-7,n-1,n,n+1,n+7$ と表せる。ただし、$n$ は 整数である。
\begin{eqnarray*}
&&(n-7)+(n-1)+n+(n+1)+(n+7)\\
&=& n-7+n-1+n+n+1+n+7\\
&=& 5n
\end{eqnarray*}
$n$ は整数だから、$5n$ は $5$ の倍数である。したがって、線で囲まれた $5$ つの数の和は $5$ の倍数になる。
~について解く
(16) 次の①,②の式を、$[\phantom{ho}]$ 内の文字について解きなさい。
$$①\quad y=4x+16\quad[x]\qquad\quad②\quad S=\cfrac{1}{2}ah\quad[a]$$
答え
$①x=\cfrac{y-16}{4}\left(x=\cfrac{y}{4}-4\right)$ $②a=\cfrac{2S}{h}$
\begin{eqnarray*} ①\\ y&=&4x+16\quad \class{mathbg-r}{(左辺と右辺をとりかえる)}\\ 4x+16&=&y\\ 4x&=&y-16\\ x&=&\cfrac{y-16}{4} \end{eqnarray*} \begin{eqnarray*} ②\\ S&=&\cfrac{1}{2}ah\quad \class{mathbg-r}{(左辺と右辺をとりかえる)}\\ \cfrac{1}{2}ah&=&S\quad \class{mathbg-r}{(両辺に\times2)}\\ ah&=&2S\\ a&=&\cfrac{2S}{h} \end{eqnarray*}
答え(中2 1章 単項式と多項式 第1回)
(1) ①項が $1$ つだけの式を $ \boxed{単項式}$ という。
項が $2$ つ以上ある式を $ \boxed{多項式}$ という。
多項式で、文字をふくんでいない項を $ \boxed{定数項}$ という。
②単項式で、かけあわされている文字の個数を、その単項式の $ \boxed{次数}$ という。多項式では、それがもっとも高い項の次数がその多項式の次数となる。
次数が $1$ の式を $ \boxed{1次式\phantom{ho}}$ という。次数が $2$ の式を $ \boxed{2次式\phantom{ho}}$ という。
③多項式で、文字と次数がおなじ項を $ \boxed{同類項}$ という。
(2)$①-3x, \ \cfrac{1}{2}y, \ -4\qquad1次式$
$②2a^2, \ -3ab^3, \ 4c,-5\qquad4次式$
(3)$①15a-11b$ $②\cfrac{5}{4}x-\cfrac{7}{3}y$ $③-x-8y$ $④-10a^2+25a$
(4)$①6x-5y$ $②x-2y$ $③-a-b$ $④3x-6y-2$
(5)$①和 9x-7y+13$ $差 -3x-y-1$
$①和 -7x+6y-6$ $差 -3x+4$
(6)$①x^3$ $②6x^7$ $③15ab$ $④4x^2$ $⑤-\cfrac{8}{27}x^3$ $⑥-18a^3$
(7)$①4y$ $②-2x^2$ $③9a$
(8)$①6x+8y$ $②4x-6y$ $③3a-2b$ $④9x+12y$
(9)$①6y$ $②\cfrac{x}{2y}$ $③8x+y$ $④-8a-4b$ $⑤\cfrac{10a-b}{12}$ $\left(\cfrac{5}{6}a-\cfrac{1}{12}b\right)$ $⑥\cfrac{-13x+24y}{10}$ $\left(-\cfrac{13x-24y}{10}, \ -\cfrac{13}{10}x+\cfrac{12}{5}y\right)$
(10)$①8x^2$ $②\cfrac{7}{3}ab$ $③-\cfrac{5}{4}x^2-\cfrac{1}{6}x$ $④-2m-3$ $⑤-\cfrac{2}{3}x^4$ $⑥-\cfrac{4}{3}x^2$ $⑦\cfrac{3}{8}a$ $⑧-12p+9q$ $⑨-x-4y$ $⑩4a+20b$ $⑪\cfrac{3}{5}x$ $⑫-\cfrac{3}{2}x$ $⑬x+11y$ $⑭\cfrac{3x-13y}{6}$ $\left(\cfrac{1}{2}x-\cfrac{13}{6}y\right)$
(11)$①10$ $②-\cfrac{3}{50}$
(12)$①2n$ $②2n+1(2n-1でもよい)$ $③n,n+1(n-1,nでもよい)$ $④n-1,n,n+1(n,n+1,n+2などでもよい)$ $⑤3n$ $⑥10x+y$
(13)① $n, \ n+1 \ (n-1, \ n \ でもよい)$
② 連続する $2$つの整数を $n, \ n+1$ と表す。ただし、$n$ は整数である。
\begin{eqnarray*}
&& (n)+(n+1)\\
&=& 2n+1
\end{eqnarray*}
$n$ は整数だから、$2n+1$ は奇数である。したがって、連続する $2$ つの整数の和は奇数である。
(14)① $A=10x+y, \ B=10y+x$
② $A$ を $10x+y$ と表すと、$B$ は $10y+x$ と表せる。ただし、$x, \ y$ は $1$ から $9$ までの整数である。
\begin{eqnarray*}
&&A+B\\
&=& (10x+y)+(10y+x)\\
&=& 10x+y+10y+x\\
&=& 10x+x+y+10y\\
&=& 11x+11y\\
&=& 11(x+y)\\
\end{eqnarray*}
$x+y$ は整数だから、$11(x+y)$ は $11$ の倍数である。したがって、$A+B$ は $11$ の倍数になる。
(15)① $n-7,n-1,n,n+1,n+7$
② 線で囲まれた $5$ つの数は、$n-7,n-1,n,n+1,n+7$ と表せる。ただし、$n$ は 整数である。
\begin{eqnarray*}
&&(n-7)+(n-1)+n+(n+1)+(n+7)\\
&=& n-7+n-1+n+n+1+n+7\\
&=& 5n
\end{eqnarray*}
$n$ は整数だから、$5n$ は $5$ の倍数である。したがって、線で囲まれた $5$ つの数の和は $5$ の倍数になる。
(16)$①x=\cfrac{y-16}{4}\left(x=\cfrac{y}{4}-4\right)$ $②a=\cfrac{2S}{h}$