数学 中2 4章 平行と合同 図形の合同 第3回(全15問)
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
(1)
合同な図形の性質
① 合同な図形では、 $ \boxed{\LARGE\phantom{hogehogehoge}}$ の長さはそれぞれ等しい。
② 合同な図形では、 $ \boxed{\LARGE\phantom{hogehogehoge}}$ の大きさはそれぞれ等しい。
答え
対応する辺, 対応する角
(2) 「三角形$ABC$と三角形$DEF$は合同である」というのを記号でかくと、
$\qquad \qquad \boxed{\LARGE\phantom{hogehogehogehoge}}$
答え
$\triangle ABC \ \equiv \ \triangle DEF$
(3) 三角形の合同条件
① $ \boxed{\LARGE\phantom{hogehogehogehogehoge}}$ がそれぞれ等しい。
② $ \boxed{\LARGE\phantom{hogehogehogehogehoge}}$ がそれぞれ等しい。
③ $ \boxed{\LARGE\phantom{hogehogehogehogehoge}}$ がそれぞれ等しい。
答え
$3$ 組の辺
$2$ 組の辺とその間の角
$1$ 組の辺とその両端の角
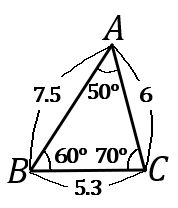
(4) 右の図の $\triangle ABC$ と合同な三角形を、下のア～オからすべて選んでその記号を答えなさい。また、そのときに使った合同条件をいいなさい。
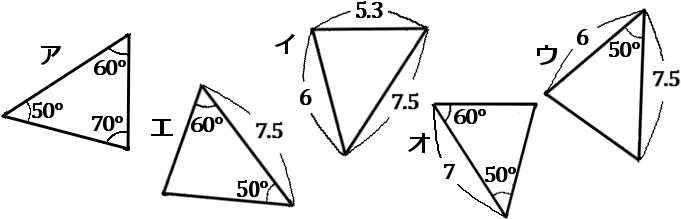
答え
イ…$3$ 組の辺がそれぞれ等しい
ウ…$2$ 組の辺とその間の角がそれぞれ等しい
エ…$1$ 組の辺とその両端の角がそれぞれ等しい
(5) 下の図のなかから、合同な三角形の組を見つけ、記号 $\equiv$ を使って表しなさい。また、そのときに使った合同条件をいいなさい。
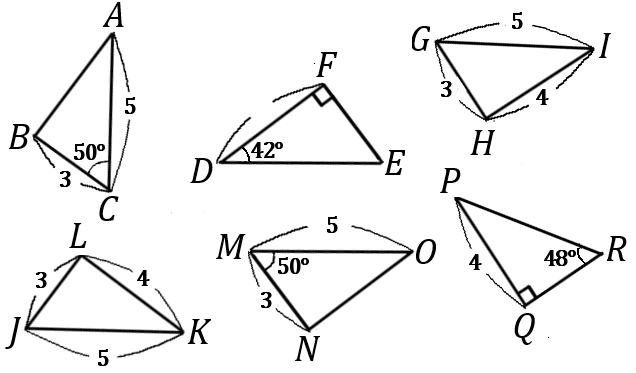
答え
$\triangle ABC \ \equiv \ \triangle ONM$…$2$ 組の辺とその間の角がそれぞれ等しい。
$\triangle DEF \ \equiv \ \triangle PRQ$…$1$ 組の辺とその両端の角がそれぞれ等しい。
$\triangle GHI \ \equiv \ \triangle JLK$…$3$ 組の辺がそれぞれ等しい。
対応する辺や角に注意する。
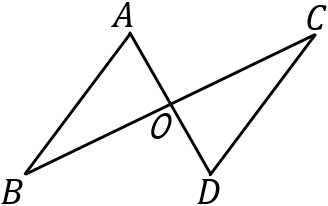
(6) 右の図で、合同な三角形を見つけ、記号 $\equiv$ を使って表しなさい。また、そのときに使った合同条件をいいなさい。ただし、$OA=OD, \ OB=OC$ とする。
答え
$\triangle OAB \ \equiv \ \triangle ODC$
$2$ 組の辺とその間の角がそれぞれ等しい。
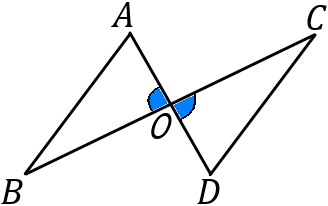問題にかいてあることだから、$OA=OD, \ OB=OC$。
また、対頂角は等しいから、$\angle AOB=\angle DOC$。
これで、「$2$ 組の辺とその間の角がそれぞれ等しい」ということになります。
それと、$\triangle ABO \ \equiv \ \triangle DCO$ とかでもOKです。どこからいいはじめてもバツにはなりません。ただ、対応する辺や角がちがっているとダメなので、そこは注意しましょう。
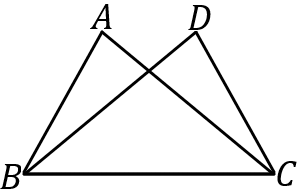
(7) 右の図で、合同な三角形を見つけ、記号 $\equiv$ を使って表しなさい。また、そのときに使った合同条件をいいなさい。ただし、$AB=DC, \ AC=DB$ とする。
答え
$\triangle ABC \ \equiv \ \triangle DCB$
$3$ 組の辺がそれぞれ等しい。
問題にかいてあることだから、$AB=DC, \ AC=DB$。
また、共通な辺だから、$BC=CB$。
これで、「$3$ 組の辺がそれぞれ等しい」ということになります。
(8) 以下の①～③について、仮定と結論をいいなさい。
① $\angle A +\angle B =90^{ \circ }$ ならば、$\angle C =90^{ \circ }$ である。
② $\cfrac{1}{3}x=6$ ならば、$x=18$ である。
③ 平行四辺形$ABCD$ において、$AC \perp BD$ ならば、ひし形である。
答え
① 仮定…$\angle A +\angle B =90^{ \circ }$ 結論…$\angle C =90^{ \circ }$
② 仮定…$\cfrac{1}{3}x=6$ 結論…$x=18$
③ 仮定…平行四辺形$ABCD$ において、$AC \perp BD$ 結論…平行四辺形$ABCD$ はひし形
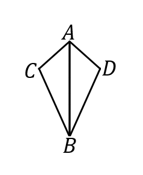
(9) 右の図において、$AC=AD, \ BC=BD$ であるならば、$\triangle ABC \ \equiv \ \triangle ABD$ となる。これについて、以下の①,②の問いに答えなさい。
① 仮定と結論をいいなさい。
② $\triangle ABC \ \equiv \ \triangle ABD$ を証明しなさい。
答え
① 〈仮定〉 $AC=AD, \ BC=BD$
〈結論〉 $\triangle ABC \ \equiv \ \triangle ABD$
② 〈証明〉
$\triangle ABC$ と $\triangle ABD$ で、
仮定から、
$AC=AD$ ……①
$BC=BD$ ……②
共通な辺だから、$AB=AB$ ……③
①②③より、$3$ 組の辺がそれぞれ等しいので
$\triangle ABC \ \equiv \ \triangle ABD$
(10) 右の図において、$AC=AD, \ \angle CAB=\angle DAB$ であるならば、$BC=BD$ となる。これについて、以下の①,②の問いに答えなさい。
① 仮定と結論をいいなさい。
② $BC=BD$ を証明しなさい。
答え
① 〈仮定〉 $AC=AD, \ \angle CAB=\angle DAB$
〈結論〉 $BC=BD$
② 〈証明〉
$\triangle ABC$ と $\triangle ABD$ で、
仮定から、
$AC=AD$ ……①
$\angle CAB=\angle DAB$ ……②
共通な辺だから、$AB=AB$ ……③
①②③より、$2$ 組の辺とその間の角がそれぞれ等しいので
$\triangle ABC \ \equiv \ \triangle ABD$
合同な三角形の対応する辺なので
$BC=BD$
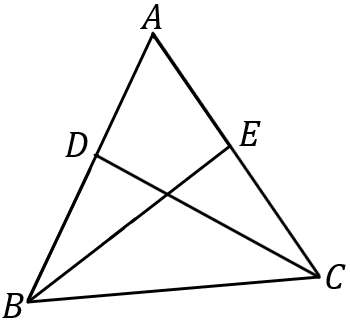
(11) 右の図において、$AB=AC, \ AD=AE$ であるならば、$\angle ABE=\angle ACD$ となる。これについて、以下の①,②の問いに答えなさい。
① 仮定と結論をいいなさい。
② $\angle ABE=\angle ACD$ を証明しなさい。
答え
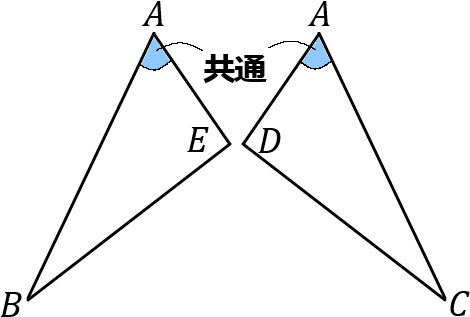
① 〈仮定〉 $AB=AC, \ AD=AE$
〈結論〉 $\angle ABE=\angle ACD$
② 〈証明〉
$\triangle ABE$ と $\triangle ACD$ で、
仮定から、
$AB=AC$ ……①
$AD=AE$ ……②
共通な角だから、$\triangle BAE = \triangle CAD$ ……③
①②③より、$2$ 組の辺とその間の角がそれぞれ等しいので
$\triangle ABE \ \equiv \ \triangle ACD$
合同な三角形の対応する角なので
$\angle ABE=\angle ACD$
(12) 右の図において、$AB=AC, \ \angle ABE=\angle ACD$ であるならば、$AD=AE$ となる。これについて、以下の①,②の問いに答えなさい。
① 仮定と結論をいいなさい。
② $\angle ABE=\angle ACD$ を証明しなさい。
答え
① 〈仮定〉 $AB=AC, \ \angle ABE=\angle ACD$
〈結論〉 $AD=AE$
② 〈証明〉
$\triangle ABE$ と $\triangle ACD$ で、
仮定から、
$AB=AC$ ……①
$\angle ABE=\angle ACD$ ……②
共通な角だから、$\triangle BAE = \triangle CAD$ ……③
①②③より、$1$ 組の辺とその両端の角がそれぞれ等しいので
$\triangle ABE \ \equiv \ \triangle ACD$
合同な三角形の対応する辺なので
$AD=AE$
(13) 右の図において、$OA=OD, \ AB /\!/ CD$ であるならば、$AB=DC$ となる。これについて、以下の①,②の問いに答えなさい。
① 仮定と結論をいいなさい。
② $AB=DC$ を証明しなさい。
答え
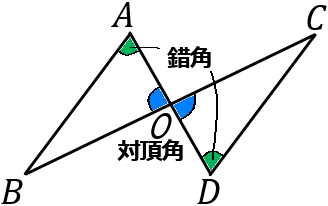
① 〈仮定〉 $OA=OD, \ AB /\!/ CD$
〈結論〉 $AB=DC$
② 〈証明〉
$\triangle OAB$ と $\triangle ODC$ で、
仮定から、$OA=OD$ ……①
対頂角だから、$\triangle AOB = \triangle DOC$ ……②
平行線の錯角だから、$\triangle OAB = \triangle ODC$ ……③
①②③より、$1$ 組の辺とその両端の角がそれぞれ等しいので
$\triangle OAB \ \equiv \ \triangle ODC$
合同な三角形の対応する辺なので
$AB=DC$
(14) 右の図において、$AB=DC, \ AB /\!/ CD$ であるならば、$OB=OC$ となる。これについて、以下の①,②の問いに答えなさい。
① 仮定と結論をいいなさい。
② $OB=OC$ を証明しなさい。
答え
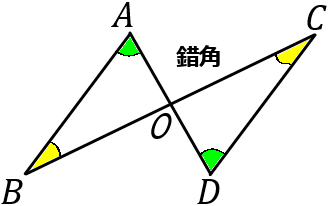
① 〈仮定〉 $AB=DC, \ AB /\!/ CD$
〈結論〉 $OB=OC$
② 〈証明〉
$\triangle OAB$ と $\triangle ODC$ で、
仮定から、$AB=DC$ ……①
平行線の錯角だから、
$\triangle OAB = \triangle ODC$ ……②
$\triangle OBA = \triangle OCD$ ……③
①②③より、$1$ 組の辺とその両端の角がそれぞれ等しいので
$\triangle OAB \ \equiv \ \triangle ODC$
合同な三角形の対応する辺なので
$OB=OC$
(15) おさらい
① $ \boxed{\LARGE\phantom{hogehoge}}$は等しい。
平行な $2$ 直線に $1$ つの直線が交わるとき、
② $ \boxed{\LARGE\phantom{hogehoge}}$は等しい。
③ $ \boxed{\LARGE\phantom{hogehoge}}$は等しい。
合同な図形の性質
合同な図形では、
④ $ \boxed{\LARGE\phantom{hogehogehoge}}$ の長さはそれぞれ等しい。
⑤ $ \boxed{\LARGE\phantom{hogehogehoge}}$ の大きさはそれぞれ等しい。
三角形の合同条件
⑥ $ \boxed{\LARGE\phantom{hogehogehogehogehoge}}$ がそれぞれ等しい。
⑦ $ \boxed{\LARGE\phantom{hogehogehogehogehoge}}$ がそれぞれ等しい。
⑧ $ \boxed{\LARGE\phantom{hogehogehogehogehoge}}$ がそれぞれ等しい。
答え
①対頂角 ②同位角 ③錯角 ④対応する辺 ⑤対応する角 ⑥$3$ 組の辺 ⑦$2$ 組の辺とその間の角 ⑧$1$ 組の辺とその両端の角
答え(中2 4章 平行と合同 図形の合同 第3回)
(1)①対応する辺 ②対応する角
(2)$\triangle ABC \ \equiv \ \triangle DEF$
(3)①$3$ 組の辺 ②$2$ 組の辺とその間の角 ③$1$ 組の辺とその両端の角
(4)ア…イ…$3$ 組の辺がそれぞれ等しい
ウ…$2$ 組の辺とその間の角がそれぞれ等しい
エ…$1$ 組の辺とその両端の角がそれぞれ等しい
(5)$\triangle ABC \ \equiv \ \triangle ONM$…$2$ 組の辺とその間の角がそれぞれ等しい。
$\triangle DEF \ \equiv \ \triangle PRQ$…$1$ 組の辺とその両端の角がそれぞれ等しい。
$\triangle GHI \ \equiv \ \triangle JLK$…$3$ 組の辺がそれぞれ等しい。
(6)$\triangle OAB \ \equiv \ \triangle ODC$
$2$ 組の辺とその間の角がそれぞれ等しい
(7)$\triangle ABC \ \equiv \ \triangle DCB$
$3$ 組の辺がそれぞれ等しい。
(8)
① 仮定…$\angle A +\angle B =90^{ \circ }$ 結論…$\angle C =90^{ \circ }$
② 仮定…$\cfrac{1}{3}x=6$ 結論…$x=18$
③ 仮定…平行四辺形$ABCD$ において、$AC \perp BD$ 結論…平行四辺形$ABCD$ はひし形
(9)
① 〈仮定〉 $AC=AD, \ BC=BD$
〈結論〉 $\triangle ABC \ \equiv \ \triangle ABD$
② 〈証明〉
$\triangle ABC$ と $\triangle ABD$ で、
仮定から、
$AC=AD$ ……①
$BC=BD$ ……②
共通な辺だから、$AB=AB$ ……③
①②③より、$3$ 組の辺がそれぞれ等しいので
$\triangle ABC \ \equiv \ \triangle ABD$
(10)
① 〈仮定〉 $AC=AD, \ \angle CAB=\angle DAB$
〈結論〉 $BC=BD$
② 〈証明〉
$\triangle ABC$ と $\triangle ABD$ で、
仮定から、
$AC=AD$ ……①
$\angle CAB=\angle DAB$ ……②
共通な辺だから、$AB=AB$ ……③
①②③より、$2$ 組の辺とその間の角がそれぞれ等しいので
$\triangle ABC \ \equiv \ \triangle ABD$
合同な三角形の対応する辺なので
$BC=BD$
(11)
① 〈仮定〉 $AB=AC, \ AD=AE$
〈結論〉 $\angle ABE=\angle ACD$
② 〈証明〉
$\triangle ABE$ と $\triangle ACD$ で、
仮定から、
$AB=AC$ ……①
$AD=AE$ ……②
共通な角だから、$\triangle BAE = \triangle CAD$ ……③
①②③より、$2$ 組の辺とその間の角がそれぞれ等しいので
$\triangle ABE \ \equiv \ \triangle ACD$
合同な三角形の対応する角なので
$\angle ABE=\angle ACD$
(12)
① 〈仮定〉 $AB=AC, \ \angle ABE=\angle ACD$
〈結論〉 $AD=AE$
② 〈証明〉
$\triangle ABE$ と $\triangle ACD$ で、
仮定から、
$AB=AC$ ……①
$\angle ABE=\angle ACD$ ……②
共通な角だから、$\triangle BAE = \triangle CAD$ ……③
①②③より、$1$ 組の辺とその両端の角がそれぞれ等しいので
$\triangle ABE \ \equiv \ \triangle ACD$
合同な三角形の対応する辺なので
$AD=AE$
(13)
① 〈仮定〉 $OA=OD, \ AB /\!/ CD$
〈結論〉 $AB=DC$
② 〈証明〉
$\triangle OAB$ と $\triangle ODC$ で、
仮定から、$OA=OD$ ……①
対頂角だから、$\triangle AOB = \triangle DOC$ ……②
平行線の錯角だから、$\triangle OAB = \triangle ODC$ ……③
①②③より、$1$ 組の辺とその両端の角がそれぞれ等しいので
$\triangle OAB \ \equiv \ \triangle ODC$
合同な三角形の対応する辺なので
$AB=DC$
(14)
① 〈仮定〉 $AB=DC, \ AB /\!/ CD$
〈結論〉 $OB=OC$
② 〈証明〉
$\triangle OAB$ と $\triangle ODC$ で、
仮定から、$AB=DC$ ……①
平行線の錯角だから、
$\triangle OAB = \triangle ODC$ ……②
$\triangle OBA = \triangle OCD$ ……③
①②③より、$1$ 組の辺とその両端の角がそれぞれ等しいので
$\triangle OAB \ \equiv \ \triangle ODC$
合同な三角形の対応する辺なので
$OB=OC$
(15)①対頂角 ②同位角 ③錯角 ④対応する辺 ⑤対応する角 ⑥$3$ 組の辺 ⑦$2$ 組の辺とその間の角 ⑧$1$ 組の辺とその両端の角