数学 中2 5章 三角形と四角形 第1回(全26問)
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
二等辺三角形
(1) 次の $ \boxed{\LARGE\phantom{hoge}}$ の中にあてはまる言葉をいれましょう。
① 用語や記号の意味をはっきりとのべたものを $ \boxed{\LARGE\phantom{hoge}}$ という。
② $2$つの $ \boxed{\LARGE\phantom{hogehoge}}$ が等しい三角形を二等辺三角形という。
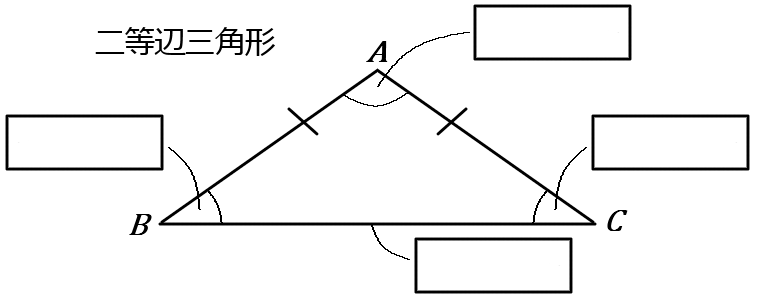 ③ $3$つの辺の長さが等しい三角形を $ \boxed{\LARGE\phantom{hogehoge}}$ という。
③ $3$つの辺の長さが等しい三角形を $ \boxed{\LARGE\phantom{hogehoge}}$ という。
④ すでに証明されたことのうちで、いろいろな証明をするときによく使われるものを $ \boxed{\LARGE\phantom{hoge}}$ という。
⑤ 二等辺三角形の $2$つの $ \boxed{\LARGE\phantom{hoge}}$ は等しい。
⑥ 二等辺三角形の頂角の二等分線は、底辺を $ \boxed{\LARGE\phantom{hogehogehogeho}}$ する。
答え
① 定義 ② 辺の長さ ③ 正三角形 ④ 定理
⑤ 底角 ⑥ 垂直に二等分
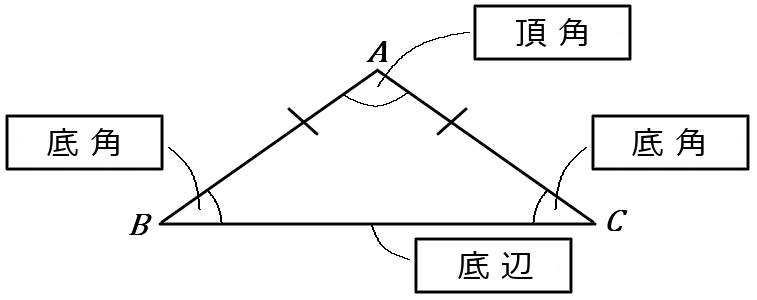
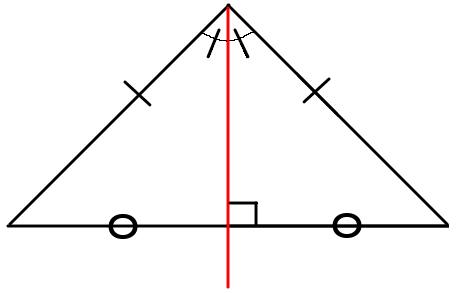 ※二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する。
※二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する。
(2) 下の①②の図で、$\angle x, \ \angle y$ の大きさをそれぞれ求めなさい。ただし①は $AB=AC$,②は$AE=ED=DC=CB$, $\angle ACB=120^{ \circ }$ とする。

答え
①$\angle x=70^{ \circ }, \ \angle y=110^{ \circ }$ ②$\angle x=15^{ \circ }, \ \angle y=45^{ \circ }$
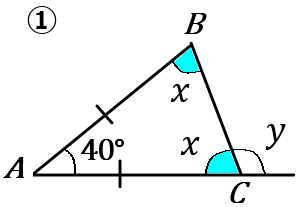 ①$\triangle ABC$ は二等辺三角形で、水色の角の大きさは等しいです。なので、$\triangle ABC$ で考えて、
①$\triangle ABC$ は二等辺三角形で、水色の角の大きさは等しいです。なので、$\triangle ABC$ で考えて、
$\angle x=(180^{ \circ }-40^{ \circ })\times \cfrac{1}{2}$
また、$\angle y=180^{ \circ }-70^{ \circ }$
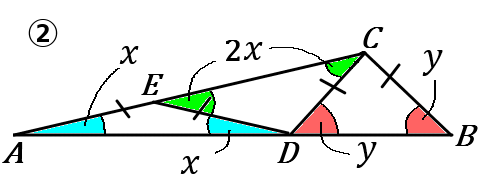
②区切ってできた $3$つの三角形はどれも二等辺三角形で、同じ色のついた部分の角の大きさがそれぞれ等しくなります。なので、$\angle EAD=\angle EDA=x,$ $\angle DEC=DCE=2x,$ $\angle CBD=\angle CDB=y$ となります。$\angle DEC=2x$ なのは、$\triangle EAD$ の外角だからです。
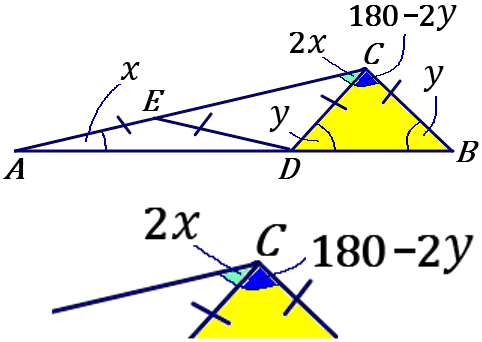
黄色の三角形で考えて、
$\angle BCD=180^{ \circ }-2y$ です。
また、$\angle ECD=2x$ なので、
$\angle ACB=\angle ACD+\angle BCD$
$=2x+180^{ \circ }-2y=120^{ \circ }$
したがって、$2x-2y=-60^{ \circ }$
この式を$y$ について解くと、
$y=x+30^{ \circ }$
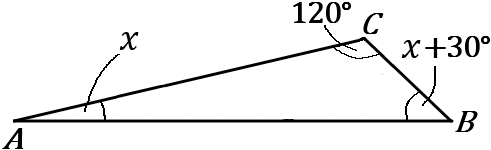
なので、$\triangle ABC$で考えて、
$120^{ \circ }+x+x+30^{ \circ }=180^{ \circ }$
あとは解くだけです。
 二等辺三角形であるための条件
二等辺三角形であるための条件
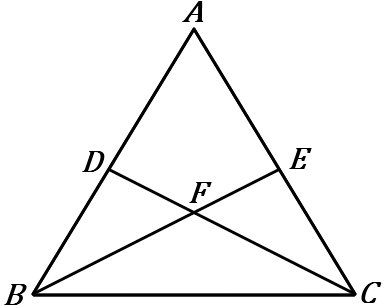
(3) 右の図で、$\triangle ABC$ は $AB=AC$ の二等辺三角形である。$DB=EC$ ならば、$\triangle FBC$ は二等辺三角形であることを証明しなさい。
 答え
答え
〈証明〉
$\triangle DBC$ と $\triangle ECB$ で、
仮定から、$DB=EC$ ……①
二等辺三角形の底角だから、$\angle DBC=\angle ECB$ ……②
共通な辺だから、$BC=CB$ ……③
①②③より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle DBC \ \equiv \ \triangle ECB$
合同な図形の対応する角だから、$\angle DCB=\angle EBC$
$2$つの角が等しい三角形だから、$\triangle FBC$ は二等辺三角形である
定理 $2$つの角が等しい三角形は二等辺三角形である。
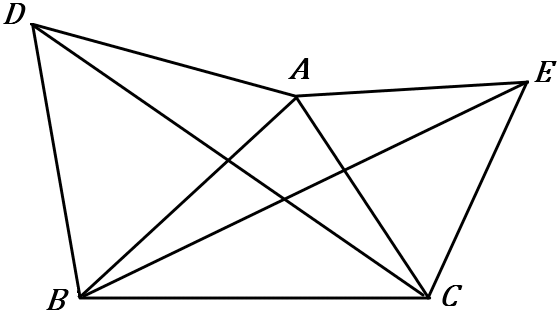 (4) 右の図で、$\triangle ADB$ と $\triangle ACE$ はどちらも正三角形である。$DC=BE$ であることを証明しなさい。
(4) 右の図で、$\triangle ADB$ と $\triangle ACE$ はどちらも正三角形である。$DC=BE$ であることを証明しなさい。
 答え
答え
〈証明〉
$\triangle ADC$ と $\triangle ABE$ で、
$\triangle ADB$ は正三角形だから、$AD=AB$ ……①
$\triangle ACE$ は正三角形だから、$AC=AE$ ……②
$\angle DAB=60^{ \circ }$ だから、$\angle DAC=60^{ \circ }+\angle BAC$ ……③
$\angle CAE=60^{ \circ }$ だから、$\angle BAE=60^{ \circ }+\angle BAC$ ……④
③④より、$\angle DAC=\angle BAE$ ……⑤
①②⑤より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle ADC \ \equiv \ \triangle ABE$
合同な図形の対応する辺だから、$DC=BE$
正三角形の $3$つの辺の長さは等しいです。(定義)
正三角形の $3$つの角の大きさは等しくて、すべて $60^{ \circ }$ です。
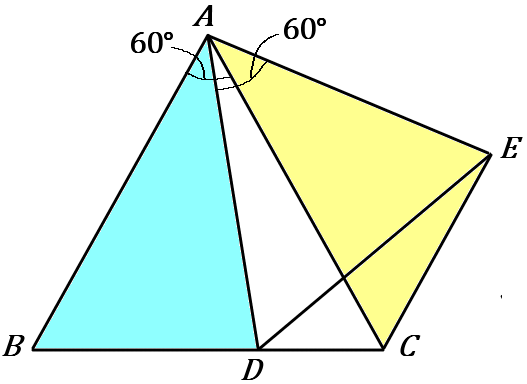
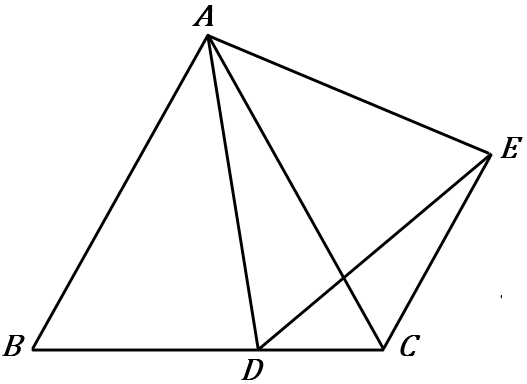 (5) 右の図で、点$D$ は $BC$上にあり、$\triangle ABC$ と $\triangle ADE$ はどちらも正三角形である。$BD=CE$ であることを証明しなさい。
(5) 右の図で、点$D$ は $BC$上にあり、$\triangle ABC$ と $\triangle ADE$ はどちらも正三角形である。$BD=CE$ であることを証明しなさい。
 答え
答え
〈証明〉
$\triangle ABD$ と $\triangle ACE$ で、
$\triangle ABC$ は正三角形だから、$AB=AC$ ……①
$\triangle ADE$ は正三角形だから、$AD=AE$ ……②
$\angle BAC=60^{ \circ }$ だから、$\angle BAD=60^{ \circ }-\angle DAC$ ……③
$\angle DAE=60^{ \circ }$ だから、$\angle CAE=60^{ \circ }-\angle DAC$ ……④
③④より、$\angle BAD=\angle CAE$ ……⑤
①②⑤より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle ABD \ \equiv \ \triangle ACE$
合同な図形の対応する辺だから、$BD=CE$
正三角形の $3$つの辺の長さは等しいです。(定義)
正三角形の $3$つの角は等しくて、すべて $60^{ \circ }$ です。
(6) 次の $ \boxed{\LARGE\phantom{hoge}}$ の中にあてはまる言葉をいれましょう。
あることがらの仮定と結論をいれかえたものを $ \boxed{\LARGE\phantom{hoge}}$ という。
答え
逆
(7) 次の①~③のことがらの逆をいいなさい。また、それは成り立つか。
① $2$直線が平行ならば、同位角は等しい。
② $x=3, \ y=4$ ならば、$x+y=7$
③ $\triangle ABC$で、$AB=AC$ ならば、$\angle B=\angle C$
答え
① 同位角が等しいならば、$2$直線は平行である。 …成り立つ
② $x+y=7$ ならば、$x=3, \ y=4$ …成り立たない
③ $\triangle ABC$で、$\angle B=\angle C$ならば、$AB=AC$ …成り立つ
仮定と結論をいれかえたものを逆といいます。
逆はつねに成り立つとは限りません。成り立つこともあれば、成り立たないこともあります。
直角三角形
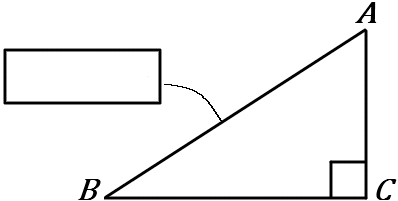
(8) ① $1$つの角が直角である三角形を直角三角形といい、直角に対する辺を $ \boxed{\LARGE\phantom{hoge}}$ という。
② $1$つの角が直角である二等辺三角形を $ \boxed{\LARGE\phantom{hogehogehogehoge}}$ という。
③ $90^{ \circ }$より小さい角を $ \boxed{\LARGE\phantom{hoge}}$ という。
④ $90^{ \circ }$より大きい角を $ \boxed{\LARGE\phantom{hoge}}$ という。
⑤ $3$つの角がすべて $90^{ \circ }$より小さい三角形を $ \boxed{\LARGE\phantom{hoge}}$ 三角形という。
⑥ $1$つの角が $90^{ \circ }$より大きい三角形を $ \boxed{\LARGE\phantom{hoge}}$ 三角形という。
直角三角形の合同条件
⑦$ \boxed{\LARGE\phantom{hogehogehogehogehogeho}}$ がそれぞれ等しい。
⑧$ \boxed{\LARGE\phantom{hogehogehogehogehogeho}}$ がそれぞれ等しい。
答え
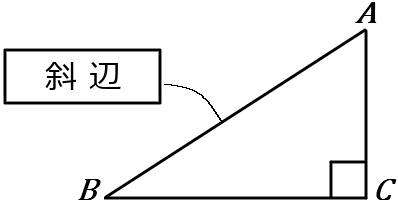
① 斜辺 ② 直角二等辺三角形 ③ 鋭角 ④ 鈍角
⑤ 鋭角 ⑥ 鈍角
⑦ 斜辺と他の$1$辺
⑧ 斜辺と$1$鋭角
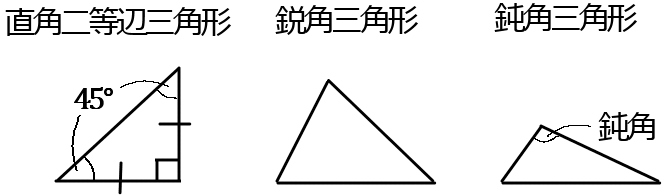 ※直角二等辺三角形の直角でない角はどちらも $45^{ \circ }$ になります。
※直角二等辺三角形の直角でない角はどちらも $45^{ \circ }$ になります。
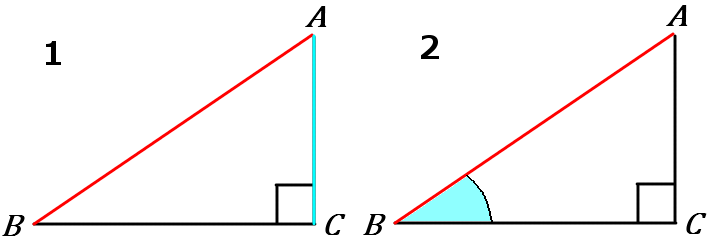 直角三角形の合同条件
直角三角形の合同条件
1 斜辺と他の$1$辺がそれぞれ等しい。
2 斜辺と$1$鋭角がそれぞれ等しい。
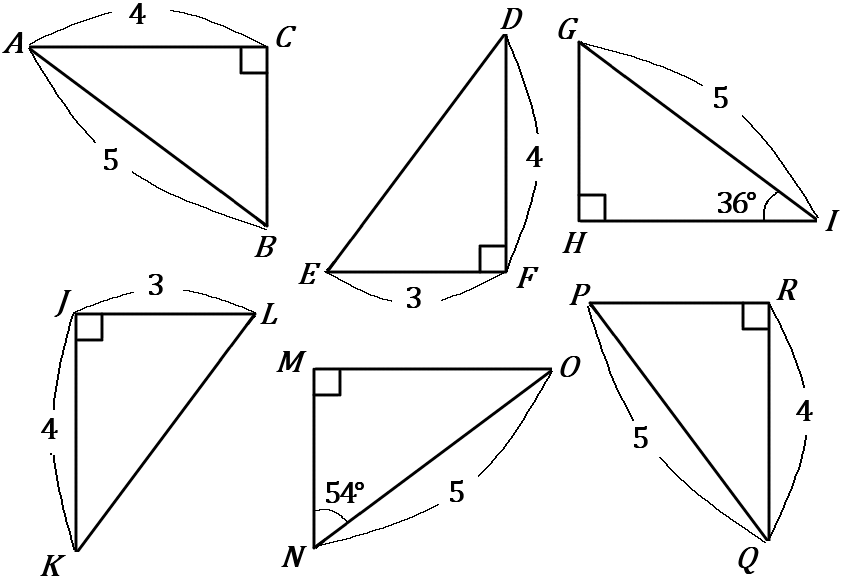
(9) 下の図のなかから、合同な三角形の組を見つけ、記号 $\equiv$ を使って表しなさい。また、そのときに使った合同条件をいいなさい。
答え
$\triangle ABC \ \equiv \ \triangle QPR$…直角三角形で、斜辺と他の$1$辺がそれぞれ等しい。
$\triangle DEF \ \equiv \ \triangle KLJ$…$2$ 組の辺とその間の角がそれぞれ等しい。
$\triangle GHI \ \equiv \ \triangle NMO$…直角三角形で、斜辺と$1$鋭角がそれぞれ等しい。
※対応する辺や角に注意しましょう。
※直角三角形の合同条件をいうときは、「直角三角形で」と最初にいうのを忘れないようにしましょう。
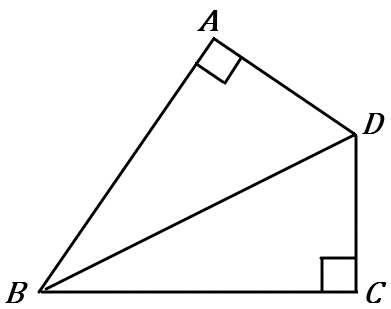 (10) 右の図で、$\angle A =\angle C =90^{ \circ },$ $AD=CD$である。
(10) 右の図で、$\angle A =\angle C =90^{ \circ },$ $AD=CD$である。
$\angle ABD=\angle CBD$ を証明しなさい。
答え
〈証明〉
$\triangle ABD$ と $\triangle CBD$ で、
仮定から、$\angle A =\angle C =90^{ \circ }$ ……①
$AD=CD$ ……②
共通な辺だから、$BD=BD$ ……③
①②③より、直角三角形で、斜辺と他の$1$辺がそれぞれ等しいので
$\triangle ABD \ \equiv \ \triangle CBD$
合同な図形の対応する角だから、
$\angle ABD=\angle CBD$
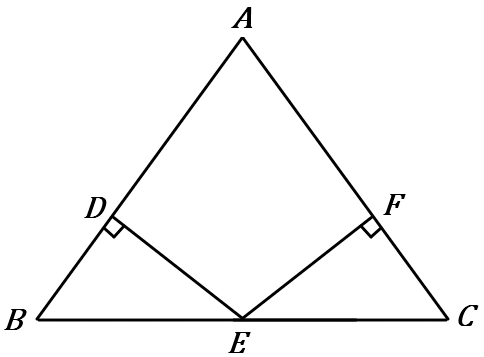 (11) 右の図の $\triangle ABC$ で、$AB=AC$, $BE=CE$, $AB \perp ED$, $AC \perp EF$である。
(11) 右の図の $\triangle ABC$ で、$AB=AC$, $BE=CE$, $AB \perp ED$, $AC \perp EF$である。
$DB=FC$ を証明しなさい。
答え
〈証明〉
$\triangle DBE$ と $\triangle FCE$ で、
仮定から、$\angle BDE =\angle CFE =90^{ \circ }$ ……①
$BE=CE$ ……②
二等辺三角形の底角だから、$\angle B=\angle C$ ……③
①②③から、直角三角形で、斜辺と$1$鋭角がそれぞれ等しいので
$\triangle DBE \ \equiv \ \triangle FCE$
合同な図形の対応する辺だから、
$DB=FC$
平行四辺形
(12) ① 四角形の向かい合う辺を $ \boxed{\LARGE\phantom{hoge}}$、向かい合う角を $ \boxed{\LARGE\phantom{hoge}}$ という。
② $2$組の対辺がそれぞれ $ \boxed{\LARGE\phantom{hogehoge}}$ 四角形を平行四辺形という。(定義)
平行四辺形の性質
③ $2$組の $ \boxed{\LARGE\phantom{hoge}}$ はそれぞれ等しい。
④ $2$組の $ \boxed{\LARGE\phantom{hoge}}$ はそれぞれ等しい。
⑤ $2$つの対角線はそれぞれの $ \boxed{\LARGE\phantom{hoge}}$ で交わる。
答え
① 対辺 対角 ② 平行な ③ 対辺 ④ 対角
⑤ 中点
 定義 $2$組の対辺がそれぞれ平行な四角形を平行四辺形という。
定義 $2$組の対辺がそれぞれ平行な四角形を平行四辺形という。
性質1 平行四辺形の$2$組の対辺はそれぞれ等しい。
性質2 平行四辺形の$2$組の対角はそれぞれ等しい。
性質3 平行四辺形の$2$つの対角線はぞれぞれの中点で交わる。
(13) 下の図の四角形 $ABCD$ と四角形 $EFGH$ はどちらも平行四辺形である。$x, \ y, \ z$ の値をそれぞれ求めなさい。また、そのときに利用した平行四辺形の性質をいいなさい。

答え
$x=10$ 平行四辺形の$2$組の対辺はそれぞれ等しい。
$y=70$ 平行四辺形の$2$組の対角はそれぞれ等しい。
$z=8$ 平行四辺形の$2$つの対角線はぞれぞれの中点で交わる。
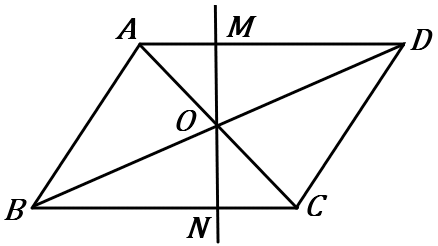 (14) 右の ▱$ABCD$ で、対角線の交点を $O$ とする。$O$ を通る直線と辺 $AD, \ BC$ との交点をそれぞれ $M, \ N$ とする。
(14) 右の ▱$ABCD$ で、対角線の交点を $O$ とする。$O$ を通る直線と辺 $AD, \ BC$ との交点をそれぞれ $M, \ N$ とする。
$AM=CN$ であることを証明しなさい。
答え
 〈証明〉
〈証明〉
$\triangle OAM$ と $\triangle OCN$ で、
対頂角だから、$\angle AOM =\angle CON $ ……①
平行四辺形の対角線はそれぞれの中点で交わるから、$OA=OC$ ……②
平行線の錯角だから、$\angle OAM =\angle OCN $ ……③
①②③より、$1$組の辺とその両端の角がそれぞれ等しいので、
$\triangle OAM \ \equiv \ \triangle OCN$
合同な図形の対応する辺だから、
$ AM= CN$
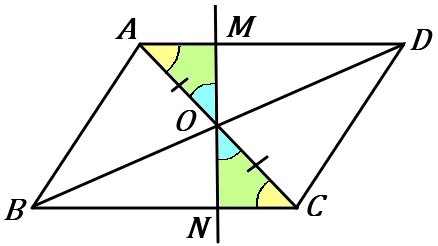
$\triangle OAM \ \equiv \ \triangle OCN$ を証明すればいいです。合同条件は $1$辺両端角です。
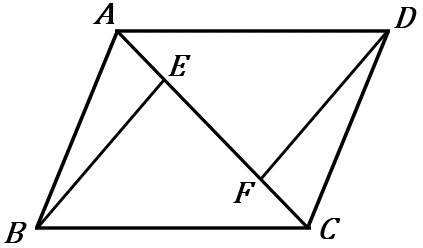 (15) 右の ▱$ABCD$ で、$E, \ F$ は対角線上の点である。また、$AE=CF$ である。
(15) 右の ▱$ABCD$ で、$E, \ F$ は対角線上の点である。また、$AE=CF$ である。
$\angle ABE =\angle CDF$ であることを証明しなさい。
答え
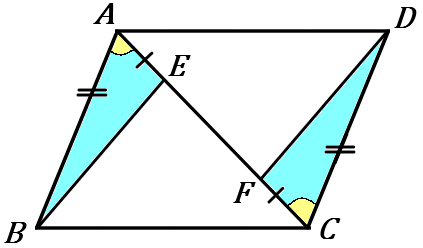 〈証明〉
〈証明〉
$\triangle ABE$ と $\triangle CDF$ で、
仮定から、$AE=CF$……①
平行線の錯角だから、$\angle BAE =\angle DCF $ ……②
平行四辺形の対辺だから、$AB=CD$ ……③
①②③より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle ABE \ \equiv \ \triangle CDF$
合同な図形の対応する角だから、
$\angle ABE =\angle CDF$
$\triangle ABE \ \equiv \ \triangle CDF$ を証明すればいいです。合同条件は $2$辺挟角です。
平行四辺形であるための条件
(16) 次の $ \boxed{\LARGE\phantom{hoge}}$ の中にあてはまる言葉をいれましょう。
定理 四角形は次のどれかが成り立つとき、平行四辺形である。
① $2$組の $ \boxed{\LARGE\phantom{hoge}}$ がそれぞれ等しい。
② $2$組の $ \boxed{\LARGE\phantom{hoge}}$ がそれぞれ等しい。
③ $2$つの対角線がそれぞれの $ \boxed{\LARGE\phantom{hoge}}$ で交わる。
④ $1$組の $ \boxed{\LARGE\phantom{hoge}}$ が $ \boxed{\LARGE\phantom{hogehogehoge}}$ が等しい。
答え
① 対辺 ② 対角 ③ 中点
④ 対辺 平行で長さ
 定義 $2$組の対辺がそれぞれ平行な四角形を平行四辺形という。
定義 $2$組の対辺がそれぞれ平行な四角形を平行四辺形という。
平行四辺形であるための条件
条件1 $2$組の対辺がそれぞれ等しい。
条件2 $2$組の対角がそれぞれ等しい。
条件3 $2$つの対角線がぞれぞれの中点で交わる。
条件4 $1$組の対辺が平行で長さが等しい。
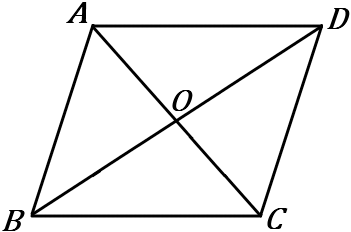 (17) 右の四角形 $ABCD$ が①~③の条件をみたすとき、平行四辺形であるといえるか。また、いえるときは、平行四辺形であるための条件をいいなさい。
(17) 右の四角形 $ABCD$ が①~③の条件をみたすとき、平行四辺形であるといえるか。また、いえるときは、平行四辺形であるための条件をいいなさい。
① $AB /\!/ DC, \ AD /\!/ BC$
② $OA=OB, \ OC=OD$
③ $AB /\!/ DC, AB=DC$
答え
①…いえる $2$組の対辺がそれぞれ平行(定義)
②…いえない
③…いえる $1$組の対辺が平行で長さが等しい(条件4)
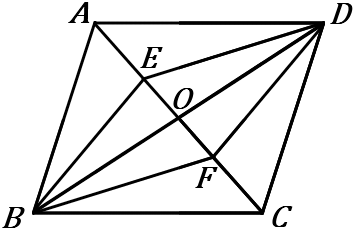
(18) 右の ▱$ABCD$ で、$O$ は対角線の交点である。また、$E, \ F$ は対角線上の点であり、$AE=CF$ である。
四角形 $BEDF$ が平行四辺形であることを証明しなさい。
答え
〈証明〉
▱$ABCD$の対角線だから、
$BO=DO$ ……①
$AO=CO$ ……②
仮定から、$AE=CF$ ……③
②③より、$AO-AE=CO-CF$
したがって、$EO=FO$ ……④
①④より、$2$つの対角線がそれぞれの中点で交わるので、
四角形 $BEDF$ は平行四辺形である。
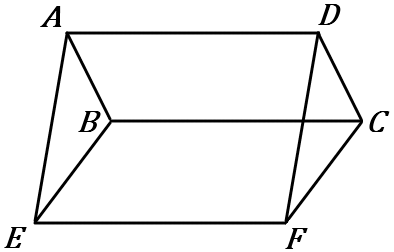 (19) 右の図で、四角形$ABCD$ と四角形$BEFC$ はどちらも平行四辺形である。
(19) 右の図で、四角形$ABCD$ と四角形$BEFC$ はどちらも平行四辺形である。
四角形 $AEFD$ が平行四辺形であることを証明しなさい。
答え
〈証明〉
▱$ABCD$ で、
$AD=BC, \ AD /\!/ BC$ ……①
▱$BEFC$ で、
$BC=EF, \ BC /\!/ EF$ ……②
①②より、$AD=EF, \ \ AD /\!/ EF$
$1$組の対辺が平行で長さが等しいので、
四角形 $AEFD$ は平行四辺形である。
特別な平行四辺形
(20) ①$4$つの辺が等しい四角形を $ \boxed{\LARGE\phantom{hogeho}}$ という。(定義)
②$4$つの角が等しい四角形を $ \boxed{\LARGE\phantom{hogeho}}$ という。(定義)
③$4$つの辺が等しく、$4$つの角が等しい四角形を $ \boxed{\LARGE\phantom{hogeho}}$ という。(定義)
また、それぞれの $2$つの対角線は次のような性質がある。
④ ひし形の対角線は、$ \boxed{\LARGE\phantom{hogeho}}$ 交わる。
⑤ 長方形の対角線は、$ \boxed{\LARGE\phantom{hogeho}}$ 等しい。
⑥ 正方形の対角線は、$ \boxed{\LARGE\phantom{hoge}}$ で $ \boxed{\LARGE\phantom{hogeho}}$ 等しい。
答え
① ひし形 ② 長方形 ③ 正方形 ④垂直に
⑤ 長さが ⑥ 垂直 長さが
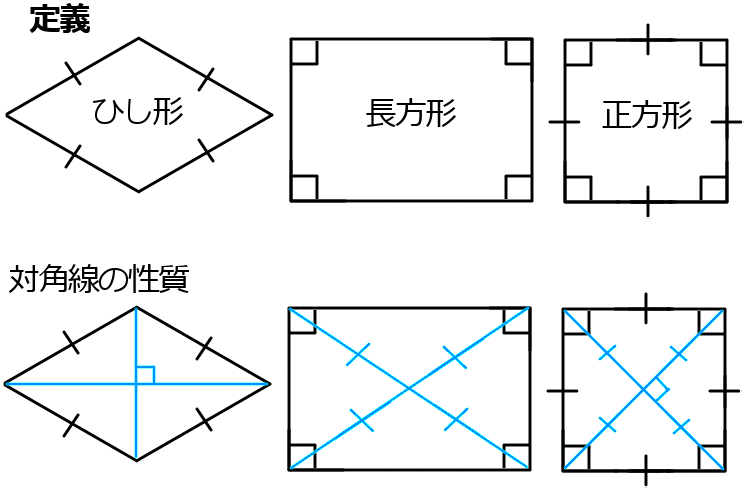 定義
定義
ひし形 …$4$つの辺が等しい。
長方形 …$4$つの角が等しい。
正方形 …$4$つの辺が等しく、$4$つの角が等しい。
※長方形や正方形の $4$つの角はすべて直角になります。
また、それぞれの $2$つの対角線には次のような性質があります。
ひし形 …垂直に交わる。
長方形 …長さが等しい。
正方形 …垂直で、長さが等しい。
ひし形や長方形は、平行四辺形にふくまれます。
正方形は、ひし形にも長方形にもふくまれます。
(21) 特別な平行四辺形の $2$つの対角線について、次の表に〇か×をいれましょう。
\begin{array}{c|c|c|c}
\hline
& ひし形 & 長方形 & 正方形 \\
\hline
垂直に交わる & & & \\
\hline
長さが等しい & & & \\
\hline
\end{array}
答え
\begin{array}{c|c|c|c}
\hline
& ひし形 & 長方形 & 正方形 \\
\hline
垂直に交わる & 〇 & × & 〇 \\
\hline
長さが等しい & × & 〇 & 〇 \\
\hline
\end{array}
 平行線と面積
平行線と面積
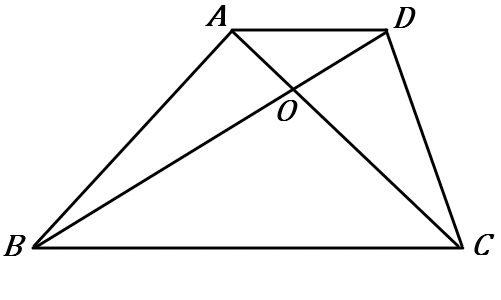
(22) 右の四角形$ABCD$ は、$AD /\!/ BC$ の台形であり、$O$ は対角線の交点である。
$\triangle ABO$ と $\triangle DCO$ の面積が等しくなる理由を説明しなさい。
答え
$\triangle ABC$ と $\triangle DBC$ について、
$BC$ を底辺とすると、どちらも底辺と高さの長さが等しいので、
$\triangle ABC =\triangle DBC$
また、$\triangle ABO=\triangle ABC -\triangle OBC$
また、$\triangle DCO=\triangle DBC -\triangle OBC$
したがって、
$\triangle ABO$ と $\triangle DCO$ の面積は等しい。
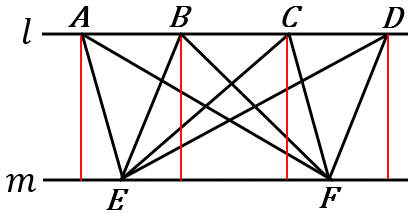 右の図で、$l /\!/ m$ とすると、$\triangle AEF$ と $\triangle BEF$ と $\triangle CEF$ と $\triangle DEF$ の面積はどれも同じす。$EF$ を底辺とすると、どれも底辺が共通で高さの長さが同じだからです。このことをふまえて、
右の図で、$l /\!/ m$ とすると、$\triangle AEF$ と $\triangle BEF$ と $\triangle CEF$ と $\triangle DEF$ の面積はどれも同じす。$EF$ を底辺とすると、どれも底辺が共通で高さの長さが同じだからです。このことをふまえて、
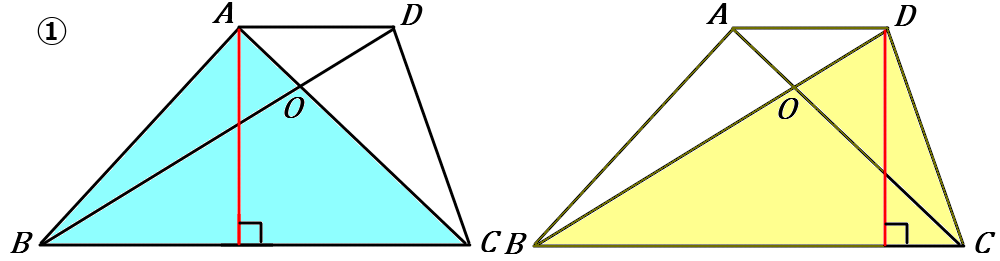 ①$\triangle ABC$ と $\triangle DBC$ は、$BC$ を底辺とすると、底辺は共通で、高さの長さも同じです。なので、面積は等しいです。
①$\triangle ABC$ と $\triangle DBC$ は、$BC$ を底辺とすると、底辺は共通で、高さの長さも同じです。なので、面積は等しいです。
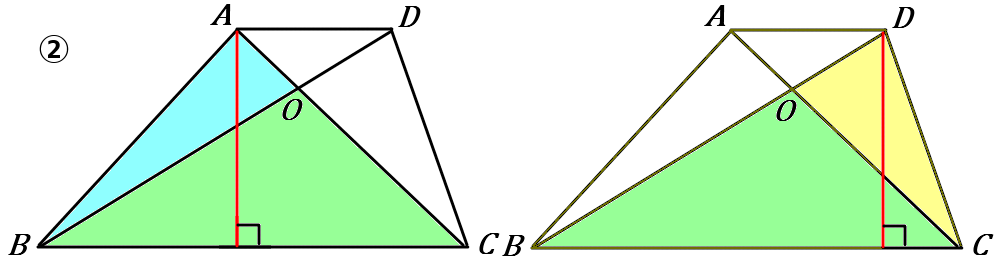 ②$\triangle ABO=\triangle ABC -\triangle OBC$ です。
②$\triangle ABO=\triangle ABC -\triangle OBC$ です。
$\triangle DCO=\triangle DBC -\triangle OBC$ です。
同じものから同じものを引いたのだから、
$\triangle ABO$ と $\triangle DCO$ の面積は等しいです。
等積変形
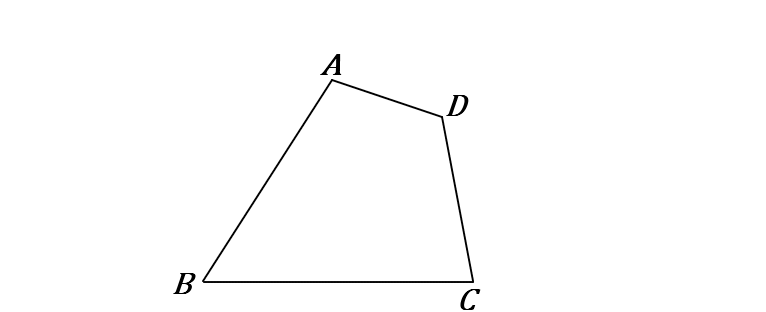
(23) 下の四角形$ABCD$ に線をかきくわえて、面積が等しい三角形をかきなさい。また、そのときの手順を説明しなさい。
答え
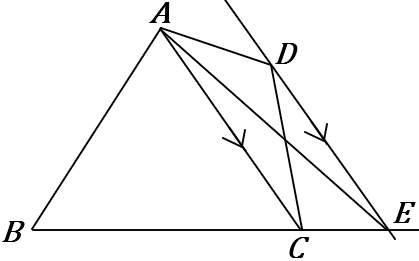
①辺$BC$ を $C$側に延長する。
②$A$ と $C$ をむすぶ。
③$D$ を通り、$AC$ と平行な線をひき、半直線$BC$ との交点を $E$ とする。
④$A$ と $E$ をむすぶ。
$\triangle ABE$ は四角形$ABCD$ と面積が等しい。
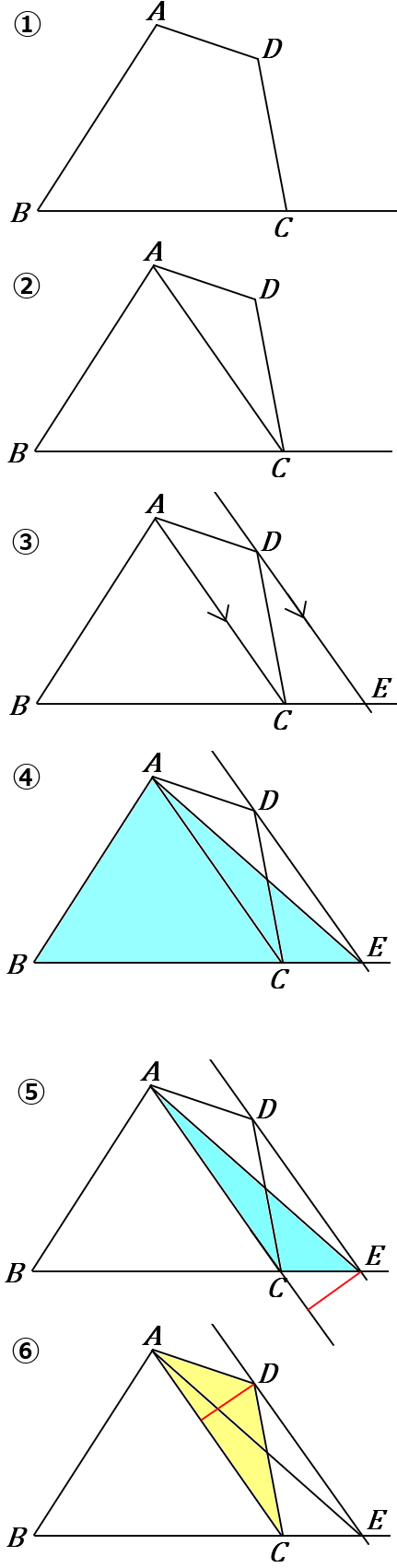 ①辺$BC$ を $C$側に延長します。
①辺$BC$ を $C$側に延長します。
②$A$ と $C$ をむすびます。
③$D$ を通り、$AC$ と平行な線をひき、半直線$BC$ との交点を $E$ とします。平行な線は、だいたい見た感じで平行になってればOKです。コンパスとか使ってなくていいです。そういうことになってます。
④$A$ と $E$ をむすびます。
$\triangle ABE$ と 四角形$ABCD$ の面積は等しいです。理由は、$\triangle ACE =\triangle ACD$ だからです。どちらの三角形も、$AC$ を底辺とすれば、高さの長さ(赤線のところ)が同じになります。(⑤⑥)
この答えでは、辺$BC$ を $C$側に延長して三角形をつくりましたが、このほかにもいくつか、面積の等しい三角形がかけます。同じやり方をしていれば、どれをかいてもOKです。
このようにして、面積の等しい図形をつくることを、数学では等積変形といいます。
(22)の問題の考え方や、この問題の手順を利用するととてもラクになる問題が、関数でよく出題されます。また、この等積変形の考え方を利用しないと、たぶん解けない問題が、特に私立高校の入試問題でよく出題されます。なので、ぜひおぼえておきたい手順です。
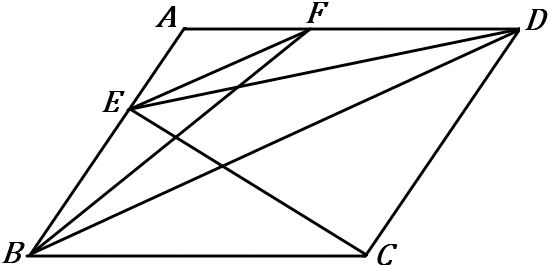 (24) 右の ▱$ABCD$ で、$EF /\!/ BD$ である。
(24) 右の ▱$ABCD$ で、$EF /\!/ BD$ である。
$\triangle EBC$ と面積が等しい三角形を $2$ついいなさい。
答え $\triangle EBD$ $\triangle FBD$
 $EB$ を底辺とすれば、$\triangle EBC$ と $\triangle EBD$ は面積が等しいことがいえます。
$EB$ を底辺とすれば、$\triangle EBC$ と $\triangle EBD$ は面積が等しいことがいえます。
$BD$ を底辺とすれば、$\triangle EBD$ と $\triangle FBD$ は面積が等しいことがいえます。
(25) 定義・定理のおさらい その1
二等辺三角形
① 用語や記号の意味をはっきりとのべたものを $ \boxed{\LARGE\phantom{hoge}}$ という。
② $2$つの $ \boxed{\LARGE\phantom{hogehoge}}$ が等しい三角形を二等辺三角形という。
③ $3$つの辺の長さが等しい三角形を $ \boxed{\LARGE\phantom{hogehoge}}$ という。
④ すでに証明されたことのうちで、いろいろな証明をするときによく使われるものを $ \boxed{\LARGE\phantom{hoge}}$ という。
⑤ 二等辺三角形の $2$つの $ \boxed{\LARGE\phantom{hoge}}$ は等しい。
⑥ 二等辺三角形の頂角の二等分線は、底辺を $ \boxed{\LARGE\phantom{hogehogehogeho}}$ する。
直角三角形
⑦ あることがらの仮定と結論をいれかえたものを $ \boxed{\LARGE\phantom{hoge}}$ という。
⑧ $1$つの角が直角である三角形を直角三角形といい、直角に対する辺を $ \boxed{\LARGE\phantom{hoge}}$ という。
⑨ $1$つの角が直角である二等辺三角形を $ \boxed{\LARGE\phantom{hogehogehogehoge}}$ という。
⑩ $90^{ \circ }$より小さい角を $ \boxed{\LARGE\phantom{hoge}}$ という。
⑪ $90^{ \circ }$より大きい角を $ \boxed{\LARGE\phantom{hoge}}$ という。
⑫ $3$つの角がすべて $90^{ \circ }$より小さい三角形を $ \boxed{\LARGE\phantom{hoge}}$ 三角形という。
⑬ $1$つの角が $90^{ \circ }$より大きい三角形を $ \boxed{\LARGE\phantom{hoge}}$ 三角形という。
直角三角形の合同条件
⑭ $ \boxed{\LARGE\phantom{hogehogehogehogehoge}}$ がそれぞれ等しい。
⑮ $ \boxed{\LARGE\phantom{hogehogehogehogehoge}}$ がそれぞれ等しい。
答え ① 定義 ② 辺の長さ ③ 正三角形 ④ 定理 ⑤ 底角 ⑥ 垂直に二等分 ⑦ 逆 ⑧ 斜辺 ⑨ 直角二等辺三角形 ⑩ 鋭角 ⑪ 鈍角 ⑫ 鋭角 ⑬ 鈍角 ⑭ 斜辺と他の$1$辺 ⑮ 斜辺と$1$鋭角
(26) 定義・定理のおさらい その2
平行四辺形
① 四角形の向かい合う辺を $ \boxed{\LARGE\phantom{hoge}}$、向かい合う角を $ \boxed{\LARGE\phantom{hoge}}$ という。
② $2$組の対辺がそれぞれ $ \boxed{\LARGE\phantom{hogehoge}}$ 四角形を平行四辺形という。(定義)
平行四辺形の性質
③ $2$組の $ \boxed{\LARGE\phantom{hoge}}$ はそれぞれ等しい。
④ $2$組の $ \boxed{\LARGE\phantom{hoge}}$ はそれぞれ等しい。
⑤ $2$つの対角線はそれぞれの $ \boxed{\LARGE\phantom{hoge}}$ で交わる。
平行四辺形であるための条件
四角形は次のどれかが成り立つとき、平行四辺形である。
⑥ $2$組の $ \boxed{\LARGE\phantom{hoge}}$ がそれぞれ等しい。
⑦ $2$組の $ \boxed{\LARGE\phantom{hoge}}$ がそれぞれ等しい。
⑧ $2$つの対角線がそれぞれの $ \boxed{\LARGE\phantom{hoge}}$ で交わる。
⑨ $1$組の $ \boxed{\LARGE\phantom{hoge}}$ が $ \boxed{\LARGE\phantom{hogehogehoge}}$ が等しい。
特別な平行四辺形
⑩$4$つの辺が等しい四角形を $ \boxed{\LARGE\phantom{hogeho}}$ という。(定義)
⑪$4$つの角が等しい四角形を $ \boxed{\LARGE\phantom{hogeho}}$ という。(定義)
⑫$4$つの辺が等しく、$4$つの角が等しい四角形を $ \boxed{\LARGE\phantom{hogeho}}$ という。(定義)
また、それぞれの $2$つの対角線は次のような性質がある。
⑬ ひし形の対角線は、$ \boxed{\LARGE\phantom{hogeho}}$ 交わる。
⑭ 長方形の対角線は、$ \boxed{\LARGE\phantom{hogeho}}$ 等しい。
⑮ 正方形の対角線は、$ \boxed{\LARGE\phantom{hoge}}$ で $ \boxed{\LARGE\phantom{hogeho}}$ 等しい。
答え ① 対辺 対角 ② 平行な ③ 対辺 ④ 対角 ⑤ 中点 ⑥ 対辺 ⑦ 対角 ⑧ 中点 ⑨ 対辺 平行で長さ ⑩ ひし形 ⑪ 長方形 ⑫ 正方形 ⑬ 垂直に ⑭ 長さが ⑮ 垂直 長さが
答え(中2 5章 三角形と四角形 第1回(全26問))
(1)① 定義 ② 辺の長さ ③ 正三角形 ④ 定理
⑤ 底角 ⑥ 垂直に二等分

(2)①$\angle x=70^{ \circ }, \ \angle y=110^{ \circ }$
②$\angle x=15^{ \circ }, \ \angle y=45^{ \circ }$
(3)〈証明〉
$\triangle DBC$ と $\triangle ECB$ で、
仮定から、$DB=EC$ ……①
二等辺三角形の底角だから、$\angle DBC=\angle ECB$ ……②
共通な辺だから、$BC=CB$ ……③
①②③より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle DBC \ \equiv \ \triangle ECB$
合同な図形の対応する角だから、$\angle DCB=\angle EBC$
$2$つの角が等しい三角形だから、$\triangle FBC$ は二等辺三角形である
(4)〈証明〉
$\triangle ADC$ と $\triangle ABE$ で、
$\triangle ADB$ は正三角形だから、$AD=AB$ ……①
$\triangle ACE$ は正三角形だから、$AC=AE$ ……②
$\angle DAB=60^{ \circ }$ だから、$\angle DAC=60^{ \circ }+\angle BAC$ ……③
$\angle CAE=60^{ \circ }$ だから、$\angle BAE=60^{ \circ }+\angle BAC$ ……④
③④より、$\angle DAC=\angle BAE$ ……⑤
①②⑤より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle ADC \ \equiv \ \triangle ABE$
合同な図形の対応する辺だから、$DC=BE$
(5)〈証明〉
$\triangle ABD$ と $\triangle ACE$ で、
$\triangle ABC$ は正三角形だから、$AB=AC$ ……①
$\triangle ADE$ は正三角形だから、$AD=AE$ ……②
$\angle BAC=60^{ \circ }$ だから、$\angle BAD=60^{ \circ }-\angle DAC$ ……③
$\angle DAE=60^{ \circ }$ だから、$\angle CAE=60^{ \circ }-\angle DAC$ ……④
③④より、$\angle BAD=\angle CAE$ ……⑤
①②⑤より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle ABD \ \equiv \ \triangle ACE$
合同な図形の対応する辺だから、$BD=CE$
(6)逆
(7)① 同位角が等しいならば、$2$直線は平行である。 …成り立つ
② $x+y=7$ ならば、$x=3, \ y=4$ …成り立たない
③ $\triangle ABC$で、$\angle B=\angle C$ならば、$AB=AC$ …成り立つ
 (8)① 斜辺 ② 直角二等辺三角形 ③ 鋭角 ④ 鈍角
(8)① 斜辺 ② 直角二等辺三角形 ③ 鋭角 ④ 鈍角
⑤ 鋭角 ⑥ 鈍角
⑦ 斜辺と他の$1$辺
⑧ 斜辺と$1$鋭角
(9)$\triangle ABC \ \equiv \ \triangle QPR$…直角三角形で、斜辺と他の$1$辺がそれぞれ等しい。
$\triangle DEF \ \equiv \ \triangle KLJ$…$2$ 組の辺とその間の角がそれぞれ等しい。
$\triangle GHI \ \equiv \ \triangle NMO$…直角三角形で、斜辺と$1$鋭角がそれぞれ等しい。
(10)〈証明〉
$\triangle ABD$ と $\triangle CBD$ で、
仮定から、$\angle A =\angle C =90^{ \circ }$ ……①
$AD=CD$ ……②
共通な辺だから、$BD=BD$ ……③
①②③より、直角三角形で、斜辺と他の$1$辺がそれぞれ等しいので
$\triangle ABD \ \equiv \ \triangle CBD$
合同な図形の対応する角だから、
$\angle ABD=\angle CBD$
(11)〈証明〉
$\triangle DBE$ と $\triangle FCE$ で、
仮定から、$\angle BDE =\angle CFE =90^{ \circ }$ ……①
$BE=CE$ ……②
二等辺三角形の底角だから、$\angle B=\angle C$ ……③
①②③から、直角三角形で、斜辺と$1$鋭角がそれぞれ等しいので
$\triangle DBE \ \equiv \ \triangle FCE$
合同な図形の対応する辺だから、
$DB=FC$
(12)① 対辺 対角 ② 平行な ③ 対辺 ④ 対角
⑤ 中点
(13)$x=10$ 平行四辺形の$2$組の対辺はそれぞれ等しい。
$y=70$ 平行四辺形の$2$組の対角はそれぞれ等しい。
$z=8$ 平行四辺形の$2$つの対角線はぞれぞれの中点で交わる。
(14)〈証明〉
$\triangle OAM$ と $\triangle OCN$ で、
対頂角だから、$\angle AOM =\angle CON $ ……①
平行四辺形の対角線はそれぞれの中点で交わるから、$OA=OC$ ……②
平行線の錯角だから、$\angle OAM =\angle OCN $ ……③
①②③より、$1$組の辺とその両端の角がそれぞれ等しいので、
$\triangle OAM \ \equiv \ \triangle OCN$
合同な図形の対応する辺だから、
$ AM= CN$
(15)〈証明〉
$\triangle ABE$ と $\triangle CDF$ で、
仮定から、$AE=CF$……①
平行線の錯角だから、$\angle BAE =\angle DCF $ ……②
平行四辺形の対辺だから、$AB=CD$ ……③
①②③より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle ABE \ \equiv \ \triangle CDF$
合同な図形の対応する角だから、
$\angle ABE =\angle CDF$
(16)① 対辺 ② 対角 ③ 中点
④ 対辺 平行で長さ
(17)①…いえる $2$組の対辺がそれぞれ平行(定義)
②…いえない
③…いえる $1$組の対辺が平行で長さが等しい(条件4)
(18)〈証明〉
▱$ABCD$の対角線だから、
$BO=DO$ ……①
$AO=CO$ ……②
仮定から、$AE=CF$ ……③
②③より、$AO-AE=CO-CF$
したがって、$EO=FO$ ……④
①④より、$2$つの対角線がそれぞれの中点で交わるので、
四角形 $BEDF$ は平行四辺形である。
(19)〈証明〉
▱$ABCD$ で、
$AD=BC, \ AD /\!/ BC$ ……①
▱$BEFC$ で、
$BC=EF, \ BC /\!/ EF$ ……②
①②より、$AD=EF, \ \ AD /\!/ EF$
$1$組の対辺が平行で長さが等しいので、
四角形 $AEFD$ は平行四辺形である。
(20)① ひし形 ② 長方形 ③ 正方形 ④垂直に
⑤ 長さが ⑥ 垂直 長さが
(21)\begin{array}{c|c|c|c}
\hline
& ひし形 & 長方形 & 正方形 \\
\hline
垂直に交わる & 〇 & × & 〇 \\
\hline
長さが等しい & × & 〇 & 〇 \\
\hline
\end{array}
(22)$\triangle ABC$ と $\triangle DBC$ について、
$BC$ を底辺とすると、どちらも底辺と高さの長さが等しいので、
$\triangle ABC =\triangle DBC$
また、$\triangle ABO=\triangle ABC -\triangle OBC$
また、$\triangle DCO=\triangle DBC -\triangle OBC$
したがって、
$\triangle ABO$ と $\triangle DCO$ の面積は等しい。

(23)①辺$BC$ を $C$側に延長する。
②$A$ と $C$ をむすぶ。
③$D$ を通り、$AC$ と平行な線をひき、半直線$BC$ との交点を $E$ とする。
④$A$ と $E$ をむすぶ。
$\triangle ABE$ は四角形$ABCD$ と面積が等しい。
(24)$\triangle EBD$ $\triangle FBD$
(25) ① 定義 ② 辺の長さ ③ 正三角形 ④ 定理 ⑤ 底角 ⑥ 垂直に二等分 ⑦ 逆 ⑧ 斜辺 ⑨ 直角二等辺三角形 ⑩ 鋭角 ⑪ 鈍角 ⑫ 鋭角 ⑬ 鈍角 ⑭ 斜辺と他の$1$辺 ⑮ 斜辺と$1$鋭角
(26)① 対辺 対角 ② 平行な ③ 対辺 ④ 対角 ⑤ 中点 ⑥ 対辺 ⑦ 対角 ⑧ 中点 ⑨ 対辺 平行で長さ ⑩ ひし形 ⑪ 長方形 ⑫ 正方形 ⑬ 垂直に ⑭ 長さが ⑮ 垂直 長さが