数学 中2 6章 確率 第3回
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
(1) 次の $ \boxed{\LARGE\phantom{hoge}}$ の中にあてはまる言葉や式や数をいれましょう。④は「入る」か「入らない」をいれましょう。
① あることがらの起こりやすさの程度を表す数を確率という。
あることがらで、起こりやすさの程度が同じであるとき、$ \boxed{\LARGE\phantom{hogehogehogehogeho}}$ という。正しくつくられたさいころでは、$1$ から $6$ までのどの目が出ることも $ \boxed{\LARGE\phantom{hogehogehogehogeho}}$。
② 起こりうる場合が全部で $n$ 通りあり、そのどれが起こることも同様に確からしい。そのうち、ことがら $A$ の起こる場合が $a$ 通りあるとき、$A$ の起こる確率 $p$ は $p= \boxed{\huge\phantom{hoge}}$
③ 確率で、もっとも大きい数は $ \boxed{\LARGE\phantom{ho}}$ である。もっとも小さい数は $ \boxed{\LARGE\phantom{ho}}$ である。
④ 「$n$ 以上」「$n$ 以下」というとき、$n$ は $ \boxed{\LARGE\phantom{hogehogehoge}}$。
「$n$ より大きい」「$n$ より小さい」というとき、$n$ は $ \boxed{\LARGE\phantom{hogehogehoge}}$。
「$n$ 未満」というとき、$n$ は $ \boxed{\LARGE\phantom{hogehogehoge}}$。
答え
① 同様に確からしい, 同様に確からしい ② $\cfrac{a}{n}$ ③ $1$, $0$ ④ 入る, 入らない, 入らない
※たとえばさいころの目の出方は $6$ 通りあります。でも、「$1$ の目が出る確率」とか「偶数の目が出る確率」など、「確率」は $1$ より大きくなることはありません。また、$0$ より小さくなることもありません。
(2) 次の①~⑧の確率を求めなさい。
①さいころを投げて、$3$ の目が出る確率
②さいころを投げて、$3$ 以上の目が出る確率
③さいころを投げて、$3$ より大きい目が出る確率
④さいころを投げて、$3$ 以下の目が出る確率
⑤さいころを投げて、$3$ より小さい目が出る確率
⑥さいころを投げて、$2$ か $6$ の目が出る確率
⑦さいころを投げて、奇数の目が出る確率
⑧さいころを投げて、素数の目が出る確率
答え
①$\cfrac{1}{6}$ ②$\cfrac{2}{3}$ ③$\cfrac{1}{2}$ ④$\cfrac{1}{2}$ ⑤$\cfrac{1}{3}$ ⑥$\cfrac{1}{3}$ ⑦$\cfrac{1}{2}$ ⑧$\cfrac{1}{2}$
②「$3$ 以上」なので $3$ が入ります。$3,4,5,6$ の $4$ つです。
③「$3$ より大きい」なので $3$ は入りません。$4, \ 5, \ 6$ の $3$ つです。
④「$3$ 以下」なので $3$ が入ります。$1, \ 2, \ 3$ の $3$ つです。
⑤「$3$ より小さい」なので $3$ は入りません。。$1, \ 2$ の $2$ つです。
⑦奇数は $1, \ 3, \ 5$ の $3$ つです。
⑧素数に $1$ ははいりません。さいころの目だと、$2, \ 3, \ 5$ の $3$ つです。
(3) 次の①~⑨の確率を求めなさい。
①ジョーカーを除いた $52$ 枚のトランプから $1$ 枚引くとき、絵札である確率
②ジョーカーを除いた $52$ 枚のトランプから $1$ 枚引くとき、絵札でない確率
③ジョーカーを除いた $52$ 枚のトランプから $1$ 枚引くとき、ダイヤである確率
④ジョーカーを除いた $52$ 枚のトランプから $1$ 枚引くとき、ダイヤでない確率
⑤硬貨を投げて、表が出る確率
⑥硬貨を投げて、裏が出る確率
⑦袋の中に赤玉$8$個と白玉$12$個が入っている。ここから玉を$1$個取り出すとき、赤玉である確率
⑧袋の中に赤玉$8$個と白玉$12$個が入っている。ここから玉を$1$個取り出すとき、赤玉でない確率
⑨箱の中にくじが $20$ 本入っていて、そのうちの $8$ 本が当たりである。ここからくじを $1$ 本引くとき、当たりである確率
答え
①$\cfrac{3}{13}$ ②$\cfrac{10}{13}$ ③$\cfrac{1}{4}$ ④$\cfrac{3}{4}$ ⑤$\cfrac{1}{2}$ ⑥$\cfrac{1}{2}$ ⑦$\cfrac{2}{5}$ ⑧$\cfrac{3}{5}$ ⑨$\cfrac{2}{5}$
①絵札は$12$枚です。$\cfrac{12}{52}=\cfrac{3}{13}$
②絵札でないのは$40$枚です。$\cfrac{40}{52}=\cfrac{10}{13}$
③ハートは$13$枚です。$\cfrac{13}{52}=\cfrac{1}{4}$
④ハートでないのは$39$枚です。$\cfrac{39}{52}=\cfrac{3}{4}$
⑦$\cfrac{8}{20}=\cfrac{2}{5}$
⑧$\cfrac{12}{20}=\cfrac{3}{5}$
⑨$\cfrac{8}{20}=\cfrac{2}{5}$
樹形図
(4) $1$ 枚の硬貨を $3$ 回投げるとき、
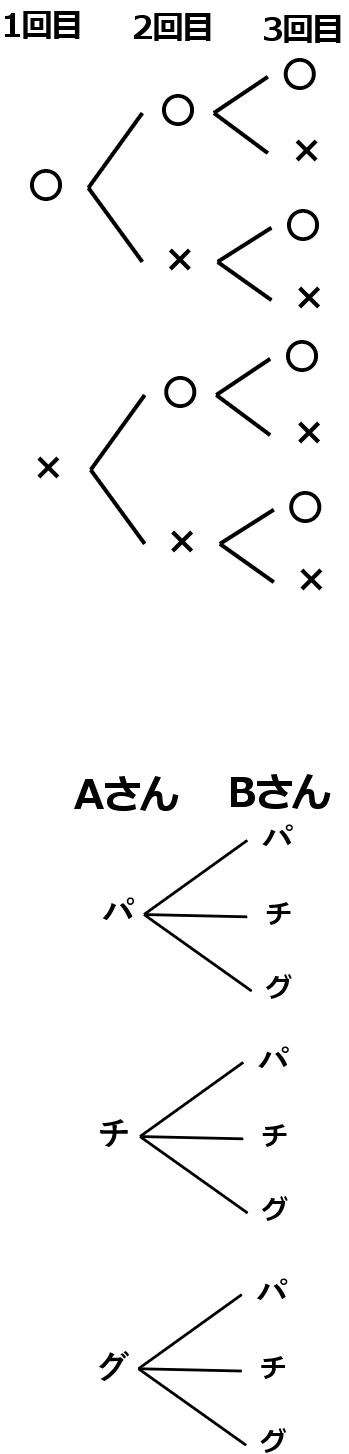
① 表を〇,裏を×として樹形図をかきなさい。
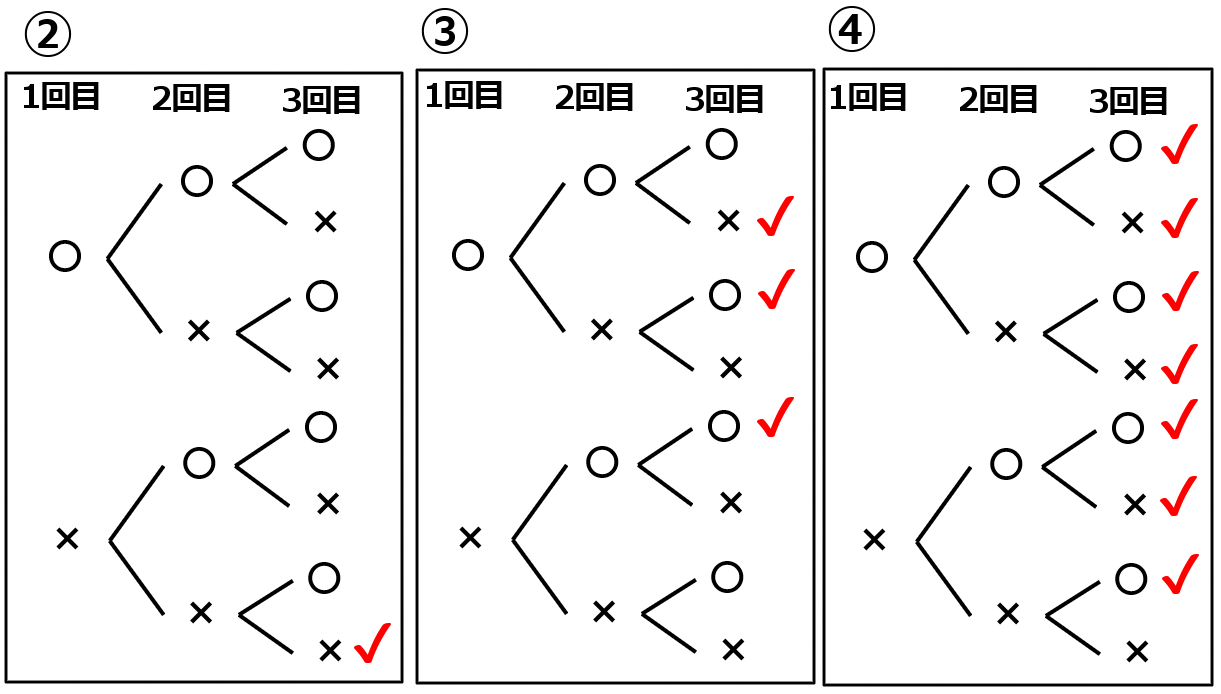
② $3$ 枚とも裏である確率を求めなさい。
③ $2$ 枚が表、$1$ 枚が裏である確率を求めなさい。
④ 少なくとも $1$ 枚が表である確率を求めなさい。
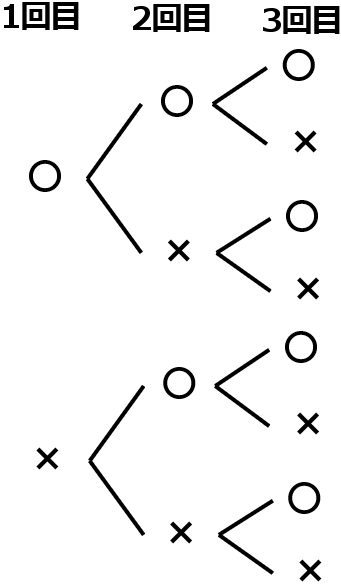 答え
答え
① 右図
② $\cfrac{1}{8}$
③ $\cfrac{3}{8}$
④ $\cfrac{7}{8}$
答えのような図を樹形図といいます。しらみつぶしに全パターンを調べるのに便利です。
右側の足の数を数えてください。それの本数が、全部で何パターンあるか、というのを表すことになります。全部で $8$ 通りのパターンがあります。なので分母は $8$ です。
下の図で、赤でチェックしてあるところが、問題に該当するところです。
(5) AさんとBさんがじゃんけんをするとき、
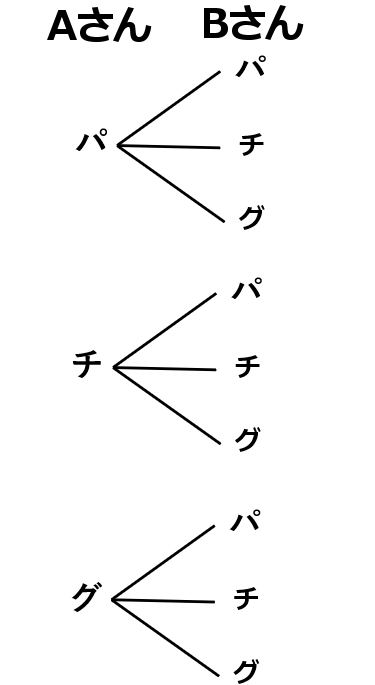
① パーを「パ」、チョキを「チ」、グーを「グ」として樹形図をかきなさい。
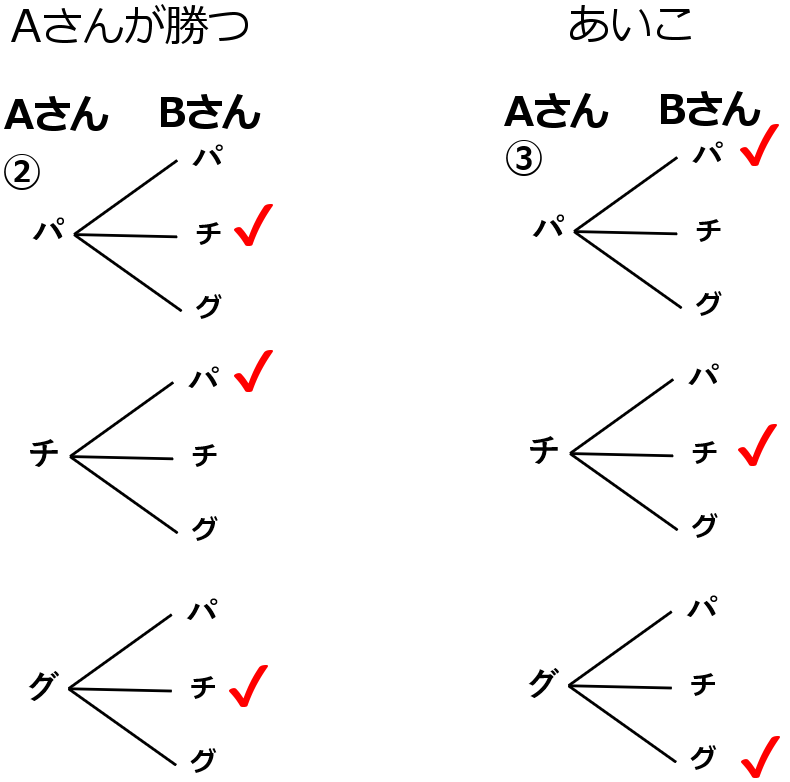
② Aさんが勝つ確率を求めなさい。
③ あいこになる確率を求めなさい。
 答え
答え
① 右図
② $\cfrac{1}{3}$
③ $\cfrac{1}{3}$
答えのような図を樹形図といいます。しらみつぶしに全パターンを調べるのに便利です。
右側の足の数を数えてください。それの本数が、全部で何パターンあるか、というのを表すことになります。全部で $9$ 通りのパターンがあります。なので分母は $9$ です。
下の図で、赤でチェックしてあるところが、問題に該当するところです。
(6) $\boxed{\large{\ 0\ }}$$\boxed{\large{\ 5\ }}$$\boxed{\large{\ 6\ }}$$\boxed{\large{\ 8\ }}$ と数字のかかれたカードが全部で $4$ 枚ある。この中から $2$ 枚のカードを抜き取ってならべ、$2$ けたの整数をつくるとき、偶数となる確率を求めなさい。
答え
$\cfrac{7}{9}$
「$2$ 枚のカードを抜き取ってならべ、$2$ けたの整数をつくる」というのは、たとえば、$\boxed{\large{\ 5\ }}$$\boxed{\large{\ 6\ }}$ というのは、$56$ だということになります。左が $10$ の位で、右が $1$ の位です。
気をつけなければならないのは、左側に $\boxed{\large{\ 0\ }}$ のカードは置けない、ということです。
$\boxed{\large{\ 0\ }}$$\boxed{\large{\ 5\ }}$ とか $\boxed{\large{\ 0\ }}$$\boxed{\large{\ 6\ }}$ とかは、$2$ けたの整数とはいえません。
そのようなことをふまえて、樹形図をかきます。
 足の本数が、全部で何パターンあるか、というのを表すことになります。全部で $9$ 通りのパターンがあります。なので分母は $9$ です。
足の本数が、全部で何パターンあるか、というのを表すことになります。全部で $9$ 通りのパターンがあります。なので分母は $9$ です。
赤でチェックしてあるところが、問題に該当するところです。なので、
$$\cfrac{7}{9}$$
(7) Aさんと、Bさんと、Cさんと、Dさんの $4$ 人の生徒について、
① $4$ 人の中から班長と副班長を $1$ 人ずつ選ぶ。Dさんが班長でAさんが副班長に選ばれる確率を求めなさい。
② $4$ 人の中から委員を $2$ 人選ぶ。AさんとDさんが選ばれる確率を求めなさい。
答え
① $\cfrac{1}{12}$
② $\cfrac{1}{6}$
①下の図で、足の数を数えてください。その本数が、全部で何パターンあるか、というのを表すことになります。全部で $12$ 通りのパターンがあります。なので分母は $12$ です。赤でチェックしてあるところが、問題に該当するところです。

②下の図で、赤でチェックしてあるところが、問題に該当するところです。なので、
$\cfrac{2}{12}=\cfrac{1}{6}$ が答えです。これでOKです。なのですが。

①と②の問題の違いについて、少し説明します。
<①の問題>
$4$ 人の中から班長と副班長を選ぶとき、「$A$ さんが班長で、$B$ さんが副班長」というのと、「$B$ さんが班長で、$A$ さんが副班長」というのとでは、意味がちがいます。だからこれは区別しなくてはいけません。
<②の問題>
$4$ 人の中から $2$ 人の委員を選ぶとき、「AさんとBさんを選ぶ」というのと、「BさんとAさんを選ぶ」というのとでは、意味がおなじです。区別する必要はありません。こういうとき、樹形図の足の本数を減らすことができます。こんな感じです。

BさんからAさんへの足はかきません。A━BとB━Aは同じ意味だからです。同様に、CさんからAさんやBさんへの足はかきません。Dさんについては、もう全部かいてしまっているので、かく必要がありません。こんなふうに、足を$1$ 本ずつ減らすことができます。そして赤くチェックしてあるところが答えなので、答えは$\cfrac{1}{6}$ となります。さきほどの答えと同じになっています。
この問題については、こうやってしまったほうがぜんぜんラクです。
①と②のちがいをしっかり把握しましょう。「班長と副班長を選ぶ」というときと、「$2$ 人の委員を選ぶ」というのとでは、このようなちがいがあります。樹形図の足を$1$ 本ずつ減らせるときがあります。減らせるときは、減らしてしまったほうがいいです。
なんのことだかよくわからないな、というひとは、毎回全部足をかいて数えておけば大丈夫です。ちょっとめんどうくさくなっちゃうことがありますが、答えはちゃんとでてきます。
でも、どのみち高校へいったら、減らせるときと減らせないときの区別をつけないといけなくなるので、だったらいまがんばって、区別がつけられるようにしておくのがおすすめです。そして、区別がつけられるようになったら、足が減らせるときは減らしましょう。そんなにややこしい話ではないと思います。たとえばこの問題で、AさんとBさんを選ぶとき、A━BというのとB━Aというのとでは、①「意味がちがうからわけなければならない」のか、②「意味がおなじだからわける必要がない」のか、という話です。
ただし、$1$つ気をつけてもらいたいのは、足を減らすことにしたのなら、減らせるやつは全部減らさないとダメです。
全部かくことにしたのなら全部かくし、減らすことにしたのなら減らせるところは全部減らす。
中間はありません。どっちでやるにしても、まぜちゃダメです。
(8) 大小 $2$つのさいころを投げるとき、
① 同じ目が出る確率を求めなさい。
② 出る目の積が$8$ 以上になる確率を求めなさい。
③ 出る目の差の絶対値が$1$ より大きくなる確率を求めなさい。
答え
① $\cfrac{1}{6}$ ② $\cfrac{11}{18}$ ③ $\cfrac{5}{9}$
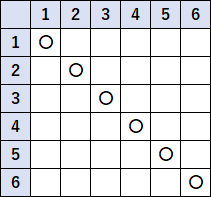 ①樹形図をかいてもいけます。関数の座標のかき方みたいなのをかいてもいいです。右の図のような表をかいてもいいです。すきなやり方でやってください。ここでは表でやっておきます。
①樹形図をかいてもいけます。関数の座標のかき方みたいなのをかいてもいいです。右の図のような表をかいてもいいです。すきなやり方でやってください。ここでは表でやっておきます。
目の出方は、表のマス目の数だけパターンがあります。なので $36$ パターンあります。分母は $36$ です。
表で、出た目がおなじところに〇印をつけます。ここが問題に該当するところです。
なので、
$$\cfrac{6}{36}=\cfrac{1}{6}$$
 ②出る目の積を表にかきこんでしまいます。「$8$ 以上」というのは、$8$ がふくまれます。なので、色のついているところが問題に該当するところです。なので、
②出る目の積を表にかきこんでしまいます。「$8$ 以上」というのは、$8$ がふくまれます。なので、色のついているところが問題に該当するところです。なので、
$$\cfrac{22}{36}=\cfrac{11}{18}$$
 ③出る目の差を表にかきこんでしまいます。「$1$より大きい」というのは、$1$ はふくまれません。なので、色のついているところが問題に該当するところです。なので、
③出る目の差を表にかきこんでしまいます。「$1$より大きい」というのは、$1$ はふくまれません。なので、色のついているところが問題に該当するところです。なので、
$$\cfrac{20}{36}=\cfrac{5}{9}$$
 (9) 袋の中に赤玉が $4$ 個と白玉が $3$ 個入っている。次の①,②の問いに答えなさい。
(9) 袋の中に赤玉が $4$ 個と白玉が $3$ 個入っている。次の①,②の問いに答えなさい。
①袋の中から玉を $1$ 個取り出してからそれを袋にもどし、また玉を $1$ 個取り出す。このとき、取り出した玉の色が同じである確率を求めなさい。
②袋の中から玉を $2$ 個同時に取り出すとき、取り出した玉の色が同じである確率を求めなさい。
答え
① $\cfrac{25}{49}$ ② $\cfrac{3}{7}$
<①の問題>
①,②,③,④,⑤,⑥,⑦と、$7$ 個の玉に番号をつけてしまいます。そして、①と②と③と④が赤玉、⑤と⑥と⑦が白玉ということにします。①②③④⑤⑥⑦という感じです。
んで、樹形図をかいてもいけます。または、関数の座標のかき方みたいなのをかいてもいいです。図のような表をかいてもいいです。すきなやり方でやってください。ここでは表でやっていきます。
 玉の出方は、表のマス目の数だけパターンがあります。なので $49$ パターンあります。分母は $49$ です。
玉の出方は、表のマス目の数だけパターンがあります。なので $49$ パターンあります。分母は $49$ です。
表で、玉の色がおなじところに〇印をつけます。ここが問題に該当するところです。
なので、
$$\cfrac{25}{49}$$
<②の問題>
玉に番号をつけるところは同じです。今回も表でやりますが、はじめの問題とちがうのは、今回は同じ玉を取り出すことはできません。はじめの問題では、たとえば①①というふうに、同じ玉を$2$ 回取り出せますが、今回はそれができません。こういうときは、表に斜めの線がはいります。こんな感じです。
 線をいれたのはもちろん、「同じ番号の玉はとり出せない」という意味です。
線をいれたのはもちろん、「同じ番号の玉はとり出せない」という意味です。
玉の出方は、表のマス目の数だけパターンがあります。なので $42$ パターンあります。分母は $42$ です。
表で、玉の色がおなじところに〇印をつけます。ここが問題に該当するところです。
なので、
$$\cfrac{18}{42}=\cfrac{3}{7}$$
Aの起こらない確率
(10) 大小 $2$つのさいころを投げるとき、次の①,②の問いに答えなさい。
① 出る目の和が $4$ の倍数である確率を求めなさい。
② 出る目の和が $4$ の倍数でない確率を求めなさい。
答え
① $\cfrac{1}{4}$ ② $\cfrac{3}{4}$
 ①樹形図をかいてもいけます。関数の座標のかき方みたいなのをかいてもいいです。右の図のような表をかいてもいいです。すきなやり方でやってください。ここでは出る目の和の表をかいて、この表でやっていきます。
①樹形図をかいてもいけます。関数の座標のかき方みたいなのをかいてもいいです。右の図のような表をかいてもいいです。すきなやり方でやってください。ここでは出る目の和の表をかいて、この表でやっていきます。
目の出方は、表のマス目の数だけパターンがあります。なので $36$ パターンあります。分母は $36$ です。
出る目の和が $4$ の倍数なのは、$4$ のときと $8$ のときと $12$ のときです。そこに色をつけます。ここが問題に該当するところです。
なので、
$$\cfrac{9}{36}=\cfrac{1}{4}$$
②表の、色のついてないところが答えですので、そこを数えればいいのですが、「$4$ の倍数ではない」ということから、①の問題の答え以外、と考えて、
$$ 1-\cfrac{1}{4}=\cfrac{3}{4}$$
これでいけます。「起こらない確率」という考え方があります。この考え方を使うとラクにできる問題がよく出題されます。
一般に、ことがらAの起こる確率を $p$ とすると、
Aの起こらない確率$\large{=1-p}$
(11) 袋の中に赤玉が $3$ 個と白玉が $4$ 個入っている。袋の中から玉を $2$ 個同時に取り出すとき、次の①,②の問いに答えなさい。
① 取り出した玉の色がどちらも赤である確率を求めなさい。
② 取り出した玉の色が少なくとも$1$ 個は白である確率を求めなさい。
答え
① $\cfrac{1}{7}$ ② $\cfrac{6}{7}$
<①の問題>
①,②,③,④,⑤,⑥,⑦と、$7$ 個の玉に番号をつけてしまいます。そして、①と②と③が赤玉、④と⑤と⑥と⑦が白玉ということにします。①②③④⑤⑥⑦という感じです。
今回も表でやりますが、同じ玉を取り出すことができない問題です。なので、表には斜めの線がはいります。
玉の出方は、表のマス目の数だけパターンがあります。なので $42$ パターンあります。分母は $42$ です。
 表で、玉の色がどちらも赤のところに〇印をつけます。ここが問題に該当するところです。なので、
表で、玉の色がどちらも赤のところに〇印をつけます。ここが問題に該当するところです。なので、
$$\cfrac{6}{42}=\cfrac{1}{7}$$
<②の問題>
「少なくとも $1$ 個 が白玉」というのは、「両方とも赤玉だったとき以外」というふうに考えることができます。なので、「起こらない確率」の考え方を使って、
$$1-\cfrac{1}{7}=\cfrac{6}{7}$$
(12) 箱の中にくじが $5$ 本入っている。このうち、当たりくじは $3$ 本である。
箱の中からまずAさんがくじを $1$ 本引く。Aさんがひいたくじは箱には戻さず、次にBさんがくじを $1$ 本引く。このとき、次の①~④の問いに答えなさい。
① Aさんが当たる確率を求めなさい。
② Bさんが当たる確率を求めなさい。
③ AさんBさんの $2$ 人ともはずれる確率を求めなさい。
④ AさんBさんのうち、少なくとも $1$ 人が当たる確率を求めなさい。
答え
①$\cfrac{3}{5}$ ② $\cfrac{3}{5}$ ③ $\cfrac{1}{10}$ ④ $\cfrac{9}{10}$
<①の問題>
$5$ 本のくじの中に $3$ 本の当たりくじが入っているわけですから、Aさんが当たる確率は $\cfrac{3}{5}$ です。
<②の問題>
①,②,③,④,⑤と、$5$ 本のくじに番号をつけてしまいます。そして、①と②と③が当たり、④と⑤がはずれということにします。①②③④⑤という感じです。
表でもいけますが、今回は樹形図をかいていきます。①━④と引く場合と、④━①と引く場合とでは意味がちがいますので、足は減らせません。

足の数だけパターンがあります。なので $20$ パターンあります。分母は $20$ です。そのうち、赤でチェックしたところがBさんが当たったところです。なので、
$$\cfrac{12}{20}=\cfrac{3}{5}$$
先に引いても後に引いても、何番目に引いてもくじに当たる確率は変わりません。それがくじです。
<③の問題>
さきほどの樹形図をまた利用して、赤でチェックをしたところが、$2$ 人ともはずれているところです。

$$\cfrac{2}{20}=\cfrac{1}{10}$$
<④の問題>
「少なくとも $1$ 人が当たる」というのは、「$2$ 人ともはずれてしまったとき以外」ということですから、「起こらない確率」の考え方で、
$$1-\cfrac{1}{10}=\cfrac{9}{10}$$
(13) AさんとBさんとCさんとDさんとEさんの $5$ 人の生徒のうちから、$3$ 人の代表を選ぶとき、次の①,②の確率を求めなさい。
①選ばれた $3$ 人のうちにEさんがはいっている確率。
②Aさん、Eさんのうち、少なくとも $1$ 人が選ばれる確率。
答え
① $\cfrac{3}{5}$ ② $\cfrac{9}{10}$
<①の問題>
樹形図で全パターンをかきます。ちょっと嫌だけど。でもがんばってかきます。するとこうなります。
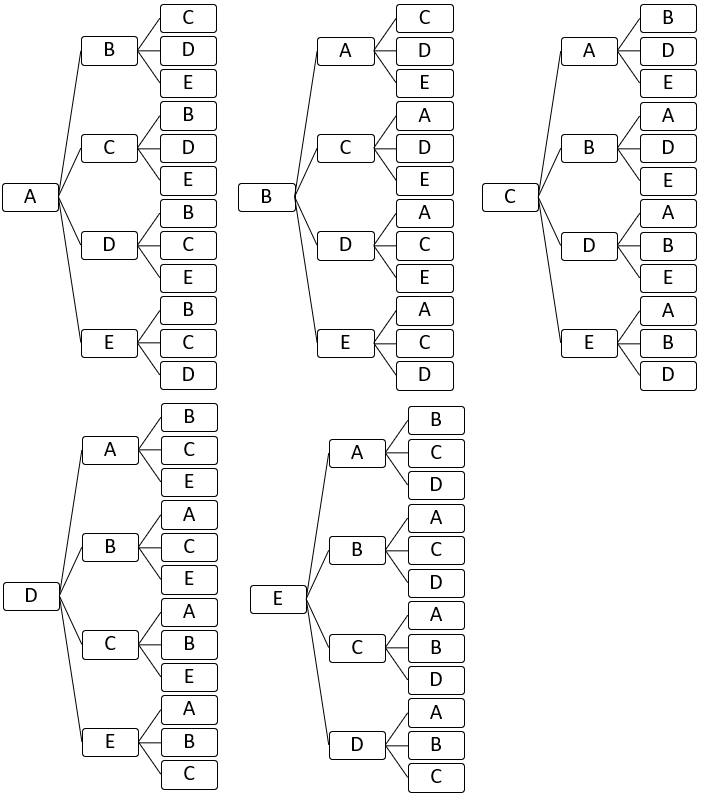
何も考えずに、やみくもにやると、こうなります。この中から、Eさんが選ばれているのを数えていくことになります。制限時間を考えずにやるのならそれでもいいですが、テストのときはこんなのかいてられません。なのでぜひ、足を減らせる、ということを考えましょう。
(6)②の問題の解説で説明したように、この問題では、たとえば、A━B━CとA━C━Bは意味が同じだからわける必要がありません。A━B━Cをかいてしまったら、A━C━B、B━A━C、B━C━A、C━A━B、C━B━Aは意味がおなじなので、もうかかなくていいです。
また、A━B━Dをかいたなら、A━D━Bはもうかかなくていいし、A━C━DをかいたならA━D━Cはもうかかなくていいし……というふうに、どんどん減らしていけます。
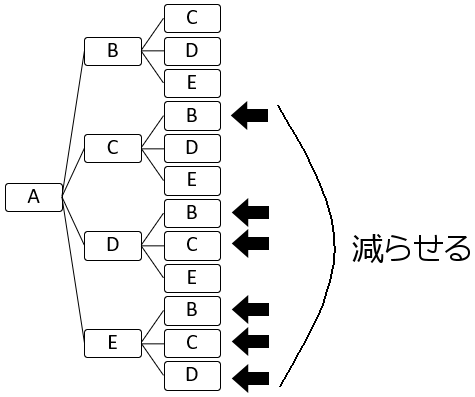
そんな感じで、かかなくていいやつをかかずに樹形図をかくと、けっきょくこうなります。

これでOKです。足の数がかなり減らせます。やみくもに全パターンをかくときとはずいぶん違いますよね。
右側の足の数を数えると、$10$ 本あります。分母は $10$ です。また、赤くチェックをしたところがEさんが選ばれているところです。なので、
$$\cfrac{6}{10}=\cfrac{3}{5}$$
<②の問題>
AさんとEさんの少なくとも $1$ 人が選ばれているところにチェックをするとこうなります。

なので答えは $\cfrac{9}{10}$ です。
「起こらない確率」の考え方を使うと、「AさんとEさんの少なくとも$1$ 人」というのは、「BさんCさんDさんの$3$人が選ばれたとき以外」ということですから、
$$1-\cfrac{1}{10}=\cfrac{9}{10}$$
これでもOKです。
答え(中2 6章 確率 第3回)
 (1)① 同様に確からしい, 同様に確からしい ② $\cfrac{a}{n}$ ③ $1$, $0$ ④ 入る, 入らない, 入らない
(1)① 同様に確からしい, 同様に確からしい ② $\cfrac{a}{n}$ ③ $1$, $0$ ④ 入る, 入らない, 入らない
(2)①$\cfrac{1}{6}$ ②$\cfrac{2}{3}$ ③$\cfrac{1}{2}$ ④$\cfrac{1}{2}$ ⑤$\cfrac{1}{3}$ ⑥$\cfrac{1}{3}$ ⑦$\cfrac{1}{2}$ ⑧$\cfrac{1}{2}$
(3)①$\cfrac{3}{13}$ ②$\cfrac{10}{13}$ ③$\cfrac{1}{4}$ ④$\cfrac{3}{4}$ ⑤$\cfrac{1}{2}$ ⑥$\cfrac{1}{2}$ ⑦$\cfrac{2}{5}$ ⑧$\cfrac{3}{5}$ ⑨$\cfrac{2}{5}$
(4)① 右上図
② $\cfrac{1}{8}$
③ $\cfrac{3}{8}$
④ $\cfrac{7}{8}$
(5)① 右下図
② $\cfrac{1}{3}$
③ $\cfrac{1}{3}$
(6) $\cfrac{7}{9}$
(7)① $\cfrac{1}{12}$
② $\cfrac{1}{6}$
(8)① $\cfrac{1}{6}$ ② $\cfrac{11}{18}$ ③ $\cfrac{5}{9}$
(9)① $\cfrac{25}{49}$ ② $\cfrac{3}{7}$
(10)① $\cfrac{1}{4}$ ② $\cfrac{3}{4}$
(11)① $\cfrac{1}{7}$ ② $\cfrac{6}{7}$
(12)①$\cfrac{3}{5}$ ② $\cfrac{3}{5}$ ③ $\cfrac{1}{10}$ ④ $\cfrac{9}{10}$
(13)① $\cfrac{3}{5}$ ② $\cfrac{9}{10}$