数学 中2 学年末模擬テスト 第1回

ページがちゃんと表示されるまで$10$秒くらいかかります。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
「印刷」をクリックすると同じ内容のpdfファイルが表示されます。また、解答用紙と答えも問題のあとに表示されます。1~7ページが問題、8ページが定義・定理のおさらい、9~12ページが解答用紙、13~16ページが答え、17ページが定義・定理のおさらいの答えです。必要におうじて印刷してください。
問題をクリックすると答えがでます。
ふつうのテストより問題数は多いです。いつも多いですが今回は特に多いです。なのでふつうのテストをやるときよりずっと時間がかかると思います。がんばって!
$\huge{1}$ 次の①~⑧の計算をしなさい。
$\qquad①$ $\quad 5-3\times7\qquad ② \quad \cfrac{3}{4}-1+\cfrac{1}{3}$
答え
$①-16$ $②\cfrac{1}{12}$
\begin{eqnarray*} &①& 5-3\times7\\ &=& 5-21\\ &=&-16 \end{eqnarray*} \begin{eqnarray*} \require{cancel} &②& \cfrac{3}{4}-1+\cfrac{1}{3}\\ &=& \cfrac{9}{12}-\cfrac{12}{12}+\cfrac{4}{12}\\ &=& \cfrac{1}{12} \end{eqnarray*}
$\qquad③$ $\quad -6+2\times\{(-3)^2-5\}\qquad ④ \quad 2(4a-b)-3(7a-3b)$
答え
$③2$ $④-13a+7b$
\begin{eqnarray*} &③& -6+2\times\{(-3)^2-5\}\\ &=& -6+2\times(9-5)\\ &=&-6+2\times4\\ &=&-6+8\\ &=&2 \end{eqnarray*} \begin{eqnarray*} \require{cancel} &④& 2(4a-b)-3(7a-3b)\\ &=& 8a-2b-21a+9b\\ &=& 8a-21a-2b+9b\\ &=& -13a+7b \end{eqnarray*}
$\qquad⑤$ $\quad \cfrac{2x-3y}{6}-\cfrac{x-4y}{4}\qquad ⑥ \quad 12ab^2\times(-5ab)$
答え
$⑤\cfrac{x+6y}{12} \ \left(\cfrac{1}{12}x+\cfrac{1}{2}y\right)$ $⑥-60a^2b^3$
\begin{eqnarray*} &⑤& \cfrac{2x-3y}{6}-\cfrac{x-4y}{4}\\ &=& \cfrac{2(2x-3y)-3(x-4y)}{12}\\ &=& \cfrac{4x-6y-3x+12y}{12}\\ &=& \cfrac{4x-3x-6y+12y}{12}\\ &=& \cfrac{x+6y}{12} \end{eqnarray*} \begin{eqnarray*} \require{cancel} &⑥& 12ab^2\times(-5ab)\\ &=& -60a^2b^3 \end{eqnarray*}
$\qquad⑦$ $\quad 8x\div(-12xy)\times3y^2\qquad ⑧ \quad 6x^2\div\cfrac{12}{5}x^2y^2\times\cfrac{4}{15}y$
答え
$⑦-2y$ $⑧\cfrac{2}{3y}$
\begin{eqnarray*} \require{cancel} &⑦& 8x\div(-12xy)\times3y^2\\ &=& -\cfrac{8x\times3yy}{12xy}\\ &=& -\cfrac{{}^2\bcancel{8}\bcancel{x}\times\bcancel{3}\bcancel{y}y}{{}^{\bcancel{3}}\bcancel{12}\bcancel{x}\bcancel{y}}\\ &=& -2y \end{eqnarray*} \begin{eqnarray*} \require{cancel} &⑧& 6x^2\div\cfrac{12}{5}x^2y^2\times\cfrac{4}{15}y\\ &=& \cfrac{6xx}{1}\div\cfrac{12xxyy}{5}\times\cfrac{4y}{15}\\ &=& \cfrac{6xx}{1}\times\cfrac{5}{12xxyy}\times\cfrac{4y}{15}\\ &=& \cfrac{\bcancel{6}\bcancel{x}\bcancel{x}}{1}\times\cfrac{\bcancel{5}}{\bcancel{12}\bcancel{x}\bcancel{x}\bcancel{y}y}\times\cfrac{{}^2\bcancel{4}\bcancel{y}}{{}^3\bcancel{15}}\\ &=&\cfrac{2}{3y} \end{eqnarray*}
$\huge{2}$ 次の ①~③の連立方程式を解きなさい。また、④の方程式を解きなさい。
\begin{eqnarray*}
① \ \left\{
\begin{array}{l}
y=-2x+5\\
3x-2y=11
\end{array}
\right.
\qquad② \ \left\{
\begin{array}{l}
5(x-3)+2y=-2y-5\\
2x+3y=11
\end{array}
\right.\\
\end{eqnarray*}
答え
$①\phantom{ho}\begin{eqnarray*}
\left\{
\begin{array}{l}
x=3\\
y=-1
\end{array}
\right.
\quad②
\left\{
\begin{array}{l}
x=-2\\
y=5
\end{array}
\right.
\end{eqnarray*}$
①番 代入法で、①の式を②の式に代入して解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
y=-2x+5\quad…①\\
3x-2y=11\quad…②
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*}
3x-2\times(-2x+5)&=&11\\
3x+4x-10&=&11\\
7x&=&21\\
x&=&3
\end{eqnarray*}
$x=3を①に代入$
\begin{eqnarray*}
y&=&-2\times3+5\\
&=&-6+5\\
&=&-1\\
\\
\left\{
\begin{array}{l}
x=3\\
y=-1
\end{array}
\right.
\end{eqnarray*}
②番 ①の式のかっこをはずし、整理します。加減法で、$y$ の係数をそろえて解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
5(x-3)+2y=-2y-5\quad…①\\
2x+3y=11\quad…②
\end{array}
\right.
\end{eqnarray*}
$①を整理$
\begin{eqnarray*}
5(x-3)+2y&=&-2y-5\\
5x-15+2y&=&-2y-5\\
5x+2y+2y&=&-5+15\\
5x+4y&=&10\quad…③
\end{eqnarray*}
$②\times4 \ - \ ③\times3$
\begin{eqnarray*}
8x+12y=44\\
\underline{-) \quad 15x+12y=30}\\
-7x\phantom{++6y}=14\\
x=-2
\end{eqnarray*}
$x=-2を②に代入$
\begin{eqnarray*}
2\times(-2)+3y&=&11\\
-4+3y&=&11\\
3y&=&15\\
y&=&5
\\
\left\{
\begin{array}{l}
x=-2\\
y=5
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*} ③ \ \left\{ \begin{array}{l} \cfrac{2}{3}x+y=2\\ 0.3x-y=-4.9\\ \end{array} \right. \qquad④ \quad 2x-y=x-5y=9 \end{eqnarray*}
答え
$③\phantom{ho}\begin{eqnarray*}
\left\{
\begin{array}{l}
x=-3\\
y=4
\end{array}
\right.
\quad④
\left\{
\begin{array}{l}
x=4\\
y=-1
\end{array}
\right.
\end{eqnarray*}$
③番 分数があるときは分母の公倍数をかけて分母をはらいます。小数があるときは $\times10$ や $\times100$ をして小数を消します。そのへんは $1$ 次方程式のときと同じです。そのあとは $x$ か $y$ の係数をそろえて足すか引くかして、$1$ 文字消去していけばいいです。
\begin{eqnarray*}
\left\{
\begin{array}{l}
\cfrac{2}{3}x+y=2\quad…①\\
0.3x-y=-4.9\quad…②
\end{array}
\right.
\end{eqnarray*}
$①の式に3をかけて分母をはらう$
\begin{eqnarray*}
\cfrac{2}{3}x+y&=&2\\
2x+3y&=&6\qquad…③
\end{eqnarray*}
$②の式に10をかけて小数をなくす$
\begin{eqnarray*}
0.3x-y&=&-4.9\\
3x-10y&=&-49\qquad…④
\end{eqnarray*}
$③\times3\ - \ ④\times2$
\begin{eqnarray*}
6x+\phantom{2}9y=\phantom{-}18\\
\underline{-) \quad 6x-20y=-98}\\
29y=116\phantom{0}\\
y=4\phantom{110}
\end{eqnarray*}
\begin{eqnarray*}
y=4を③に代入\\
2x+3\times4&=&6\\
2x+12&=&6\\
2x&=&-6\\
x&=&-3\\
\\
\left\{
\begin{array}{l}
x=-3\\
y=4
\end{array}
\right.
\end{eqnarray*}
④番 まんなかをかくした式をつくり、①とします。左側をかくした式をつくり、②とします。①の式と②の式を連立させ、$x$ の係数をそろえて加減法で解きます。
まず、まんなかをかくせば、
$2x-y=9$ という式ができます。
それから、左がわをかくせば、
$x-5y=9$ という式ができます。
んで、この $2$ つの式を連立させて解いていくわけです。
\begin{eqnarray*}
\left\{
\begin{array}{l}
2x-y=9\qquad…①\\
x-5y=9\qquad…②
\end{array}
\right.
\end{eqnarray*}
$①-②\times2$
\begin{eqnarray*}
2x-\phantom{10}y=\phantom{1}9\\
\underline{-) \quad 2x-10y=18} \\
9y=-9 \\
y=-1
\end{eqnarray*}
\begin{eqnarray*}
y=-1を①に代入\\
2x-(-1)&=&9\\
2x+1&=&9\\
2x&=&9-1\\
2x&=&8\\
x&=&4
\\
\left\{
\begin{array}{l}
x=4\\
y=-1
\end{array}
\right.
\end{eqnarray*}
$\huge{3}$ 次の $①~③$ の問いに答えなさい。
$①$ 傾きが $-\cfrac{2}{3}$ で点$(-6,2)$を通る直線の式を求めなさい。
答え
$y=-\cfrac{2}{3}x-2$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
傾きというのは1次関数のときは $a$ のことです。だから $a=-\cfrac{2}{3}$ です。これを $y=ax+b$ に代入します。すると
$$y=-\cfrac{2}{3}x+b$$
となります。あと、「点$(-6,2)$を通る」というのは、$x=-6$ のとき $y=2$ という意味です。これをこの $y=-\cfrac{2}{3}x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
2&=&-\cfrac{2}{3}\times(-6)+b\\
2&=&4+b\\
2-4&=&b\\
-2&=&b
\end{eqnarray*}
$②$ $2$ 点$(-2,9),(3,-1)$ を通る $1$ 次関数の式を求めなさい。
答え
$y=-2x+5$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
$2$ 点を通る直線の式をきかれたときは、
$$a=\cfrac{y_2-y_1}{x_2-x_1}$$
という公式を使って $a$ を求めましょう。
$2$ 点の座標 $(-2,9),(3,-1)$ を $(x_1,y_1),(x_2,y_2)$ だということにして、上の公式にあてはめると、
\begin{eqnarray*}
a&=&\cfrac{y_2-y_1}{x_2-x_1}\\
&=&\cfrac{-1-9}{3-(-2)}\\
&=&\cfrac{-10}{5}\\
&=&-2\\
\end{eqnarray*}
これで $a=-2$ だということがわかりました。これを $y=ax+b$ に代入して、
$$y=-2x+b$$
ここに、 $(-2,9),(3,-1)$ のどちらかを代入して $b$ を求めます。代入するのはどっちでもよいです。今回は、 $(3,-1)$ のほうをいれてみましょう。
\begin{eqnarray*}
-1&=&-2\times3+b\\
-1&=&-6+b\\
-1+6&=&b\\
5&=&b
\end{eqnarray*}
これで $a=-2$ , $b=5$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-2x+5$$
$③$ $1$ 次関数 $y=-3x-2$ について、$x$ の変域が $-1 \leqq x \leqq 3$ のとき、$y$ の変域を求めなさい。
答え
$-11 \leqq y \leqq 1$
「$x$ の変域が $p \leqq x \leqq q$ のとき、$y$ の変域を求めなさい。」というお決まりの問題があって、こうきかれたときは、答えの形はこうです。 $$小 \leqq y \leqq 大$$ んで、小と大にそれぞれ、小さい数と大きい数を書いておけばいいです。小さい数と大きい数っていうのは、 $-1 \leqq x \leqq 3$ の $-1$ と $3$ をそれぞれ問題の $y=-3x-2$ の $x$ に代入してえられる数です。じゃあまず、 $x=-1$ を $y=-3x-2$ に代入します。 \begin{eqnarray*} y&=&-3\times(-1)-2\\ &=&3-2\\ &=&1\\ \end{eqnarray*} 次に、 $x=3$ を $y=-3x-2$ に代入します。 \begin{eqnarray*} y&=&-3\times3-2\\ &=&-9-2\\ &=&-11\\ \end{eqnarray*} これで、$1$ と $-11$ というふたつの数がえられました。これを小と大にあてはめればよいです。じゃあ答えを書きましょう。$$-11 \leqq y \leqq 1$$ これでOKです。ただし、 $y$ の変域をきかれたときのこのやり方は、3年生で習う「2乗に比例する関数$y=ax^2$」では通用しないから気をつけてください。
 $\huge{4}$
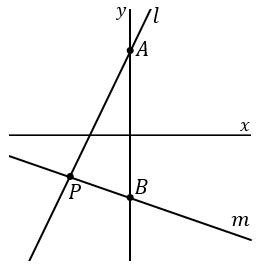
右の図で、直線 $l, \ m$ はそれぞれ $y=2x+4, \ y=-\cfrac{1}{3}x-3$ のグラフである。直線 $l$ と $y$ 軸との交点を $A$ とし、直線 $m$ と $y$ 軸との交点を $B$ とする。直線 $l$ と直線 $m$ との交点を $P$ とする。このとき、以下の問いに答えなさい。
$\huge{4}$
右の図で、直線 $l, \ m$ はそれぞれ $y=2x+4, \ y=-\cfrac{1}{3}x-3$ のグラフである。直線 $l$ と $y$ 軸との交点を $A$ とし、直線 $m$ と $y$ 軸との交点を $B$ とする。直線 $l$ と直線 $m$ との交点を $P$ とする。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(-3, \ -2)$
$2$ 直線の交点は連立方程式の解です。直線 $l, \ m$ の式を連立方程式にして
\begin{eqnarray*}
\left\{
\begin{array}{l}
y=2x+4\\
y=-\cfrac{1}{3}x-3\\
\end{array}
\right.
\end{eqnarray*}
これを解けばいいです。解き方は、この手の連立方程式は代入法で、右辺 $=$ 右辺の式をたてて、$x$ を求めていきましょう。関数の問題でよく使うパターンです。
代入法で、右辺 = 右辺の式にして、これを解きます。
\begin{eqnarray*}
2x+4&=&-\cfrac{1}{3}x-3\qquad(×3)\\
6x+12&=&-x-9\\
6x+x&=&-9-12\\
7x&=&-21\\
x&=&-3\\
\end{eqnarray*}
$y=2x+4$ に $x=-3$ を代入して $y$ を求めます。
\begin{eqnarray*}
y&=&2×(-3)+4\\
&=&-6+4\\
&=&-2\\\\
&&答え\quad
(-3, \ -2)
\end{eqnarray*}
※座標をきかれているのだから、かならず座標の答え方で答えましょう。
$(2)$ $\triangle PAB$ の面積を求めなさい。
答え
$\cfrac{21}{2}$
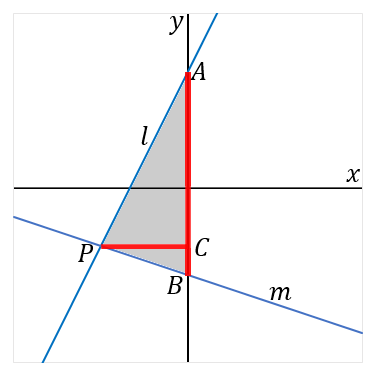 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。すると高さは $P$ から $AB$ におろした垂線と $AB$ との交点を $C$ とでもしておきます。すると $PC$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。すると高さは $P$ から $AB$ におろした垂線と $AB$ との交点を $C$ とでもしておきます。すると $PC$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
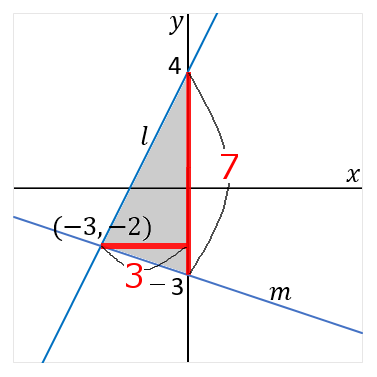
$A$ の $y$ 座標は $y=2x+4$ の切片だから $4$。$B$ の $y$ 座標は $y=-\cfrac{1}{3}x-3$ の切片だから $-3$。だから $AB=7$。長さの話なのですから絶対値で考えるようにしましょう。
 <$PC$ について>
<$PC$ について>
$PC$ の長さは、点 $P$ の $x$ 座標をみればよいです。点 $P$ の $x$ 座標は $-3$ ですから、$PC$ の長さは $3$ です。これも長さの話なのですから絶対値をいうようにしましょう。
これで底辺と高さがわかりました。では面積をだしましょう。
$$7×3×\cfrac{1}{2}=\cfrac{21}{2}$$
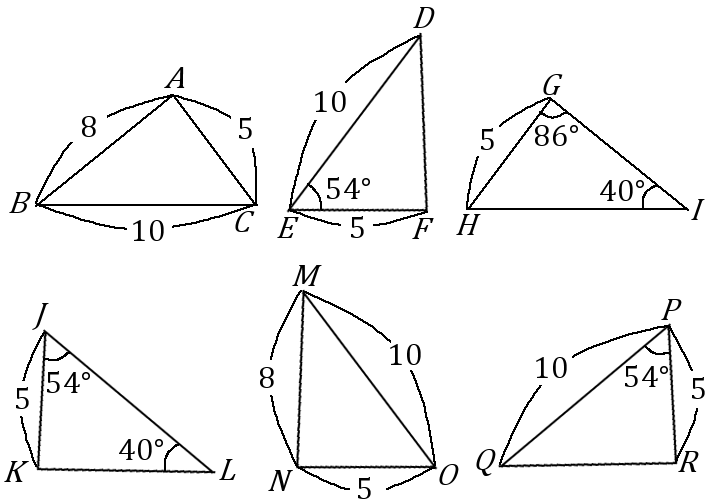
$\huge{5}$ 下の図のなかから、合同な三角形の組をすべて見つけ、記号 $\equiv$ を使って表しなさい。また、そのときに使った合同条件をいいなさい。
答え
$\triangle ABC \ \equiv \ \triangle NMO$…$3$ 組の辺がそれぞれ等しい。
$\triangle DEF \ \equiv \ \triangle QPR$…$2$ 組の辺とその間の角がそれぞれ等しい。
$\triangle GHI \ \equiv \ \triangle KJL$…$1$ 組の辺とその両端の角がそれぞれ等しい。
対応する辺や角に注意する。
$\huge{6}$
以下の①~③について、仮定と結論をいいなさい。
① $\triangle ABC \ \equiv \ \triangle DEF$ ならば、$AB=DE$ である。
② $8x=48$ ならば、$x=6$ である。
③ $\triangle ABC$ において、$AB=AC$ ならば、$\triangle ABC$ は二等辺三角形である。
答え
① 仮定…$\triangle ABC \ \equiv \ \triangle DEF$ 結論…$AB=DE$
② 仮定…$8x=48$ 結論…$x=6$
③ 仮定…$\triangle ABC$ において、$AB=AC$ 結論…$\triangle ABC$ は二等辺三角形
$\huge{7}$
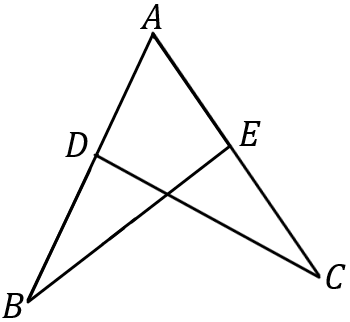
右の図において、$AB=AC, \ AD=AE$ であるならば、$\angle ABE=\angle ACD$ となる。これについて、以下の①,②の問いに答えなさい。
① 仮定と結論をいいなさい。
② $\angle ABE=\angle ACD$ を証明しなさい。
答え
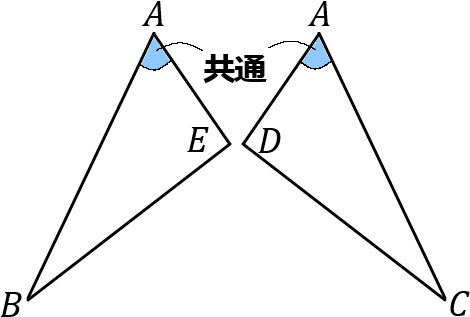
① 〈仮定〉 $AB=AC, \ AD=AE$
〈結論〉 $\angle ABE=\angle ACD$
② 〈証明〉
$\triangle ABE$ と $\triangle ACD$ で、
仮定から、
$AB=AC$ ……①
$AD=AE$ ……②
共通な角だから、$\angle BAE = \angle CAD$ ……③
①②③より、$2$ 組の辺とその間の角がそれぞれ等しいので
$\triangle ABE \ \equiv \ \triangle ACD$
合同な三角形の対応する角なので
$\angle ABE=\angle ACD$

$\huge{8}$
右の図で、$AC=DC=DB$ であるとき、$\angle x$ の大きさを求めなさい。
答え
$\angle x=40^{ \circ }$
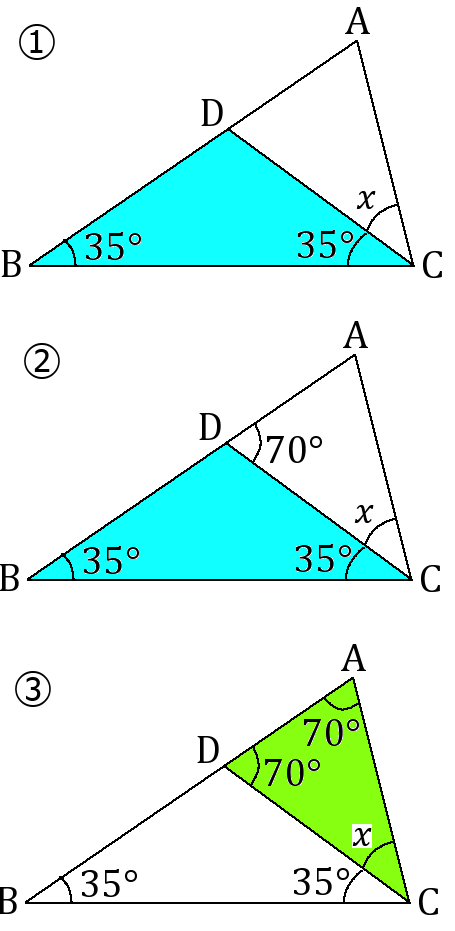
$DB=DC$ なのですから、$\triangle DBC$ は 二等辺三角形です。なので、$\angle DCB=35^{ \circ }$ です。…①
三角形の外角は、それととなり合わない $2$ つの内角の和に等しいです。$\triangle DBC$ で考えて、$\angle ADC=35^{ \circ }+35^{ \circ }=70^{ \circ }$ です。…②
$AC=DC$ なのですから、$\triangle CAD$ は 二等辺三角形です。なので、$\angle CAD=70^{ \circ }$ です。…③
$\triangle CAD$ で考えて、$\angle x=180^{ \circ }-(70^{ \circ }+70^{ \circ })=40^{ \circ }$ です。
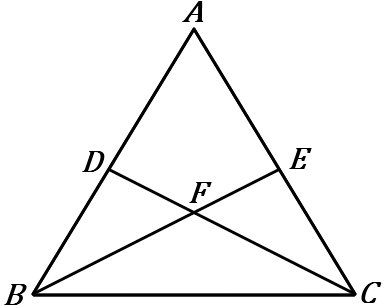
$\huge{9}$
右の図で、$\triangle ABC$ は $AB=AC$ の二等辺三角形である。$DB=EC$ ならば、$\triangle FBC$ は二等辺三角形であることを証明しなさい。
 答え
答え
〈証明〉
$\triangle DBC$ と $\triangle ECB$ で、
仮定から、$DB=EC$ ……①
二等辺三角形の底角だから、$\angle DBC=\angle ECB$ ……②
共通な辺だから、$BC=CB$ ……③
①②③より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle DBC \ \equiv \ \triangle ECB$
合同な図形の対応する角だから、$\angle DCB=\angle EBC$
$2$つの角が等しい三角形だから、$\triangle FBC$ は二等辺三角形である
定理 $2$つの角が等しい三角形は二等辺三角形である。
$\huge{10}$
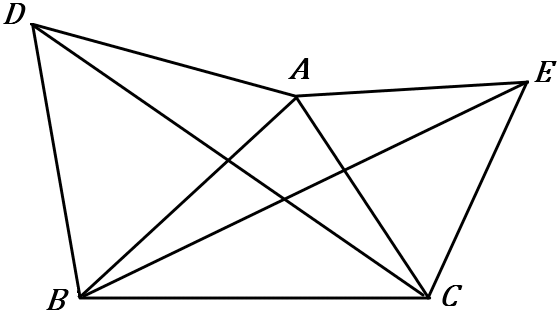
右の図で、$\triangle ADB$ と $\triangle ACE$ はどちらも正三角形である。$DC=BE$ であることを証明しなさい。
 答え
答え
〈証明〉
$\triangle ADC$ と $\triangle ABE$ で、
$\triangle ADB$ は正三角形だから、$AD=AB$ ……①
$\triangle ACE$ は正三角形だから、$AC=AE$ ……②
$\angle DAB=60^{ \circ }$ だから、$\angle DAC=60^{ \circ }+\angle BAC$ ……③
$\angle CAE=60^{ \circ }$ だから、$\angle BAE=60^{ \circ }+\angle BAC$ ……④
③④より、$\angle DAC=\angle BAE$ ……⑤
①②⑤より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle ADC \ \equiv \ \triangle ABE$
合同な図形の対応する辺だから、$DC=BE$
正三角形の $3$つの辺の長さは等しいです。(定義)
正三角形の $3$つの角の大きさは等しくて、すべて $60^{ \circ }$ です。
$\huge{11}$
次の①~③のことがらの逆をいいなさい。また、それは成り立つか。
① $2$直線が平行ならば、同位角は等しい。
② $x=3, \ y=4$ ならば、$x+y=7$
③ $\triangle ABC$で、$AB=AC$ ならば、$\angle B=\angle C$
答え
① 同位角が等しいならば、$2$直線は平行である。 …成り立つ
② $x+y=7$ ならば、$x=3, \ y=4$ …成り立たない
③ $\triangle ABC$で、$\angle B=\angle C$ならば、$AB=AC$ …成り立つ
仮定と結論をいれかえたものを逆といいます。
逆はつねに成り立つとは限りません。成り立つこともあれば、成り立たないこともあります。
$\huge{12}$
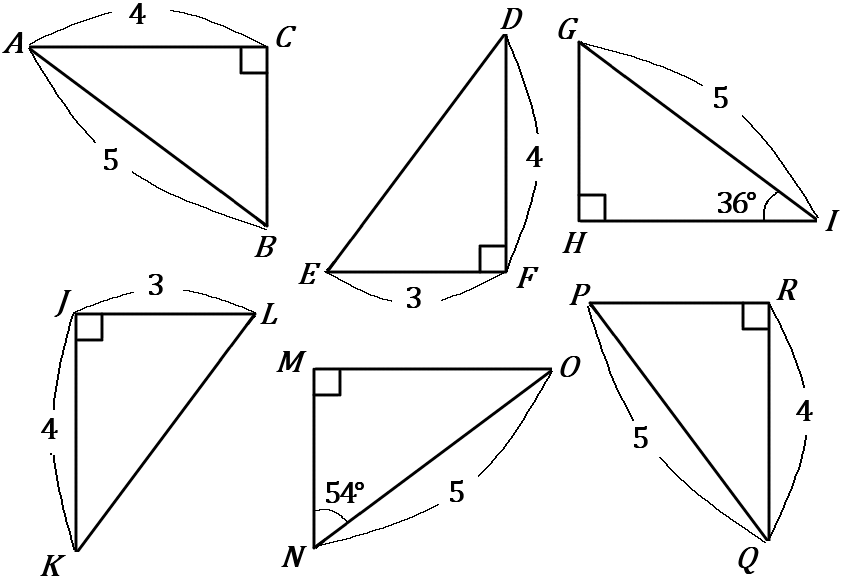
下の図のなかから、合同な三角形の組を見つけ、記号 $\equiv$ を使って表しなさい。また、そのときに使った合同条件をいいなさい。
答え
$\triangle ABC \ \equiv \ \triangle QPR$…直角三角形で、斜辺と他の$1$辺がそれぞれ等しい。
$\triangle DEF \ \equiv \ \triangle KLJ$…$2$ 組の辺とその間の角がそれぞれ等しい。
$\triangle GHI \ \equiv \ \triangle NMO$…直角三角形で、斜辺と$1$鋭角がそれぞれ等しい。
※対応する辺や角に注意しましょう。
※直角三角形の合同条件をいうときは、「直角三角形で」と最初にいうのを忘れないようにしましょう。
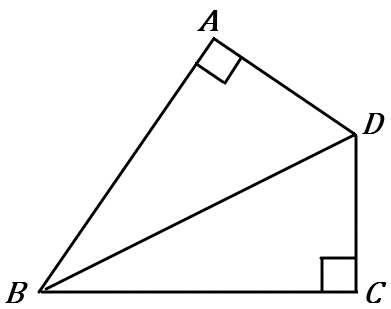 $\huge{13}$
右の図で、$\angle A =\angle C =90^{ \circ },$ $AD=CD$である。
$\huge{13}$
右の図で、$\angle A =\angle C =90^{ \circ },$ $AD=CD$である。
$\angle ABD=\angle CBD$ を証明しなさい。
答え
〈証明〉
$\triangle ABD$ と $\triangle CBD$ で、
仮定から、$\angle A =\angle C =90^{ \circ }$ ……①
$AD=CD$ ……②
共通な辺だから、$BD=BD$ ……③
①②③より、直角三角形で、斜辺と他の$1$辺がそれぞれ等しいので
$\triangle ABD \ \equiv \ \triangle CBD$
合同な図形の対応する角だから、
$\angle ABD=\angle CBD$
$\huge{14}$
下の図の四角形 $ABCD$ と四角形 $EFGH$ はどちらも平行四辺形である。$x, \ y, \ z$ の値をそれぞれ求めなさい。また、そのときに利用した平行四辺形の性質をいいなさい。

答え
$x=10$ 平行四辺形の$2$組の対辺はそれぞれ等しい。
$y=70$ 平行四辺形の$2$組の対角はそれぞれ等しい。
$z=8$ 平行四辺形の$2$つの対角線はぞれぞれの中点で交わる。
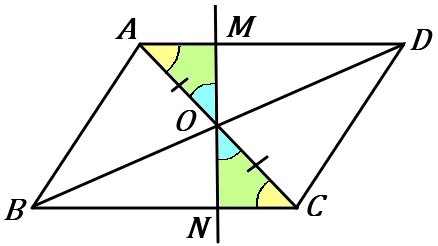
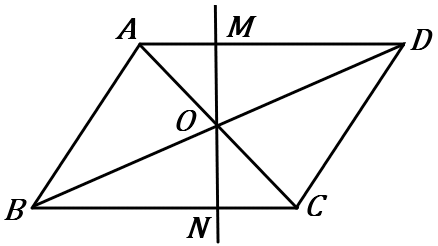 $\huge{15}$ 右の ▱$ABCD$ で、対角線の交点を $O$ とする。$O$ を通る直線と辺 $AD, \ BC$ との交点をそれぞれ $M, \ N$ とする。
$\huge{15}$ 右の ▱$ABCD$ で、対角線の交点を $O$ とする。$O$ を通る直線と辺 $AD, \ BC$ との交点をそれぞれ $M, \ N$ とする。
$AM=CN$ であることを証明しなさい。
答え
 〈証明〉
〈証明〉
$\triangle OAM$ と $\triangle OCN$ で、
対頂角だから、$\angle AOM =\angle CON $ ……①
平行四辺形の対角線はそれぞれの中点で交わるから、$OA=OC$ ……②
平行線の錯角だから、$\angle OAM =\angle OCN $ ……③
①②③より、$1$組の辺とその両端の角がそれぞれ等しいので、
$\triangle OAM \ \equiv \ \triangle OCN$
合同な図形の対応する辺だから、
$ AM= CN$
$\triangle OAM \ \equiv \ \triangle OCN$ を証明すればいいです。合同条件は $1$辺両端角です。
 $\huge{16}$
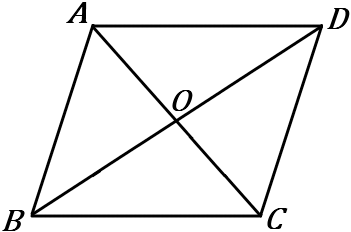
右の四角形 $ABCD$ が①~③の条件をみたすとき、平行四辺形であるといえるか。また、いえるときは、平行四辺形であるための条件をいいなさい。
$\huge{16}$
右の四角形 $ABCD$ が①~③の条件をみたすとき、平行四辺形であるといえるか。また、いえるときは、平行四辺形であるための条件をいいなさい。
① $AB /\!/ DC, \ AD /\!/ BC$
② $OA=OB, \ OC=OD$
③ $AB /\!/ DC, AB=DC$
答え
①…いえる $2$組の対辺がそれぞれ平行(定義)
②…いえない
③…いえる $1$組の対辺が平行で長さが等しい
 $\huge{17}$
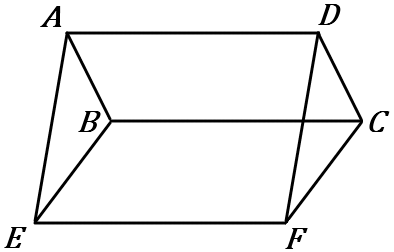
右の図で、四角形$ABCD$ と四角形$BEFC$ はどちらも平行四辺形である。
$\huge{17}$
右の図で、四角形$ABCD$ と四角形$BEFC$ はどちらも平行四辺形である。
四角形 $AEFD$ が平行四辺形であることを証明しなさい。
答え
〈証明〉
▱$ABCD$ で、
$AD=BC, \ AD /\!/ BC$ ……①
▱$BEFC$ で、
$BC=EF, \ BC /\!/ EF$ ……②
①②より、$AD=EF, \ \ AD /\!/ EF$
$1$組の対辺が平行で長さが等しいので、
四角形 $AEFD$ は平行四辺形である。
$\huge{18}$
特別な平行四辺形の $2$つの対角線について、次の表に〇か×をいれなさい。
\begin{array}{c|c|c|c}
\hline
& ひし形 & 長方形 & 正方形 \\
\hline
垂直に交わる & & & \\
\hline
長さが等しい & & & \\
\hline
\end{array}
答え
\begin{array}{c|c|c|c}
\hline
& ひし形 & 長方形 & 正方形 \\
\hline
垂直に交わる & 〇 & × & 〇 \\
\hline
長さが等しい & × & 〇 & 〇 \\
\hline
\end{array}
$\huge{19}$
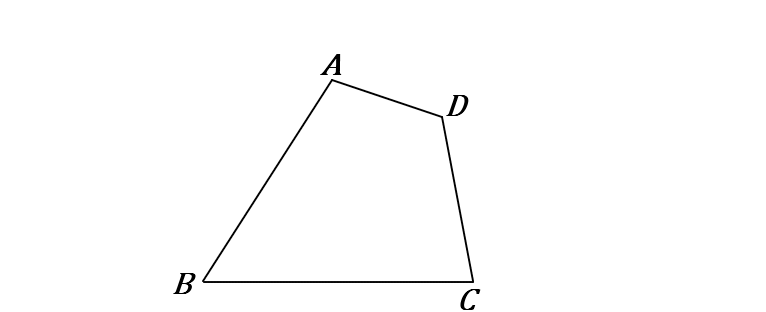
下の四角形$ABCD$ に線をかきくわえて、面積が等しい三角形をかきなさい。また、そのときの手順を説明しなさい。
答え
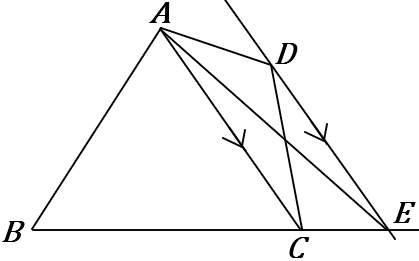
①辺$BC$ を $C$側に延長する。
②$A$ と $C$ をむすぶ。
③$D$ を通り、$AC$ と平行な線をひき、半直線$BC$ との交点を $E$ とする。
④$A$ と $E$ をむすぶ。
$\triangle ABE$ は四角形$ABCD$ と面積が等しい。
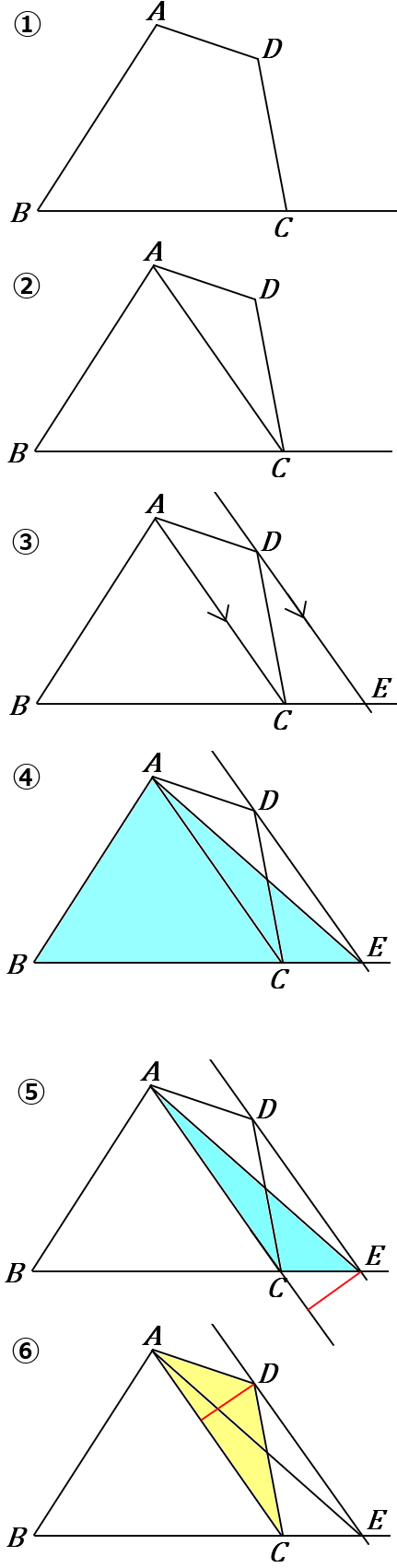 ①辺$BC$ を $C$側に延長します。
①辺$BC$ を $C$側に延長します。
②$A$ と $C$ をむすびます。
③$D$ を通り、$AC$ と平行な線をひき、半直線$BC$ との交点を $E$ とします。平行な線は、だいたい見た感じで平行になってればOKです。コンパスとか使ってなくていいです。そういうことになってます。
④$A$ と $E$ をむすびます。
$\triangle ABE$ と 四角形$ABCD$ の面積は等しいです。理由は、$\triangle ACE =\triangle ACD$ だからです。どちらの三角形も、$AC$ を底辺とすれば、高さの長さ(赤線のところ)が同じになります。(⑤⑥)
この答えでは、辺$BC$ を $C$側に延長して三角形をつくりましたが、このほかにもいくつか、面積の等しい三角形がかけます。同じやり方をしていれば、どれをかいてもOKです。
このようにして、面積の等しい図形をつくることを、数学では等積変形といいます。
この問題の手順を利用するととてもラクになる問題が、関数でよく出題されます。また、この等積変形の考え方を利用しないと、たぶん解けない問題が、特に私立高校の入試問題でよく出題されます。なので、ぜひおぼえておきたい手順です。
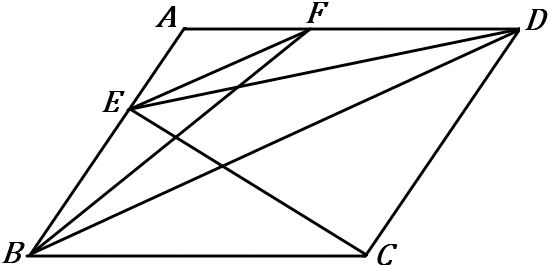 $\huge{20}$
右の ▱$ABCD$ で、$EF /\!/ BD$ である。
$\huge{20}$
右の ▱$ABCD$ で、$EF /\!/ BD$ である。
$\triangle EBC$ と面積が等しい三角形を $2$ついいなさい。
答え $\triangle EBD$ $\triangle FBD$
 $EB$ を底辺とすれば、$\triangle EBC$ と $\triangle EBD$ は面積が等しいことがいえます。
$EB$ を底辺とすれば、$\triangle EBC$ と $\triangle EBD$ は面積が等しいことがいえます。
$BD$ を底辺とすれば、$\triangle EBD$ と $\triangle FBD$ は面積が等しいことがいえます。
$\huge{21}$
次の①~⑧の確率を求めなさい。
①さいころを投げて、$1$ の目が出る確率
②さいころを投げて、$1$ 以上の目が出る確率
③さいころを投げて、$1$ より大きい目が出る確率
④さいころを投げて、$1$ 以下の目が出る確率
⑤さいころを投げて、$1$ より小さい目が出る確率
⑥さいころを投げて、$2$ か $5$ の目が出る確率
⑦さいころを投げて、偶数の目が出る確率
⑧さいころを投げて、$3$ の倍数の目が出る確率
答え
①$\cfrac{1}{6}$ ②$1$ ③$\cfrac{5}{6}$ ④$\cfrac{1}{6}$ ⑤$0$ ⑥$\cfrac{1}{3}$ ⑦$\cfrac{1}{2}$ ⑧$\cfrac{1}{3}$
②「以上」なので $1$ は入ります。$\cfrac{6}{6}=1$
③「より大きい」なので $1$ は入りません。
④「以下」なので $1$ は入ります。
⑤「より小さい」なので $1$ は入りません。$\cfrac{0}{6}=0$
⑥$\cfrac{2}{6}=\cfrac{1}{3}$
⑦偶数は $2, \ 4, \ 6$ の $3$ 通りです。$\cfrac{3}{6}=\cfrac{1}{2}$
⑧$3$ の倍数は $3, \ 6$ の $2$ 通りです。$\cfrac{2}{6}=\cfrac{1}{3}$
$\huge{22}$
次の①~⑧の確率を求めなさい。
①ジョーカーを除いた $52$ 枚のトランプから $1$ 枚引くとき、絵札である確率
②ジョーカーを除いた $52$ 枚のトランプから $1$ 枚引くとき、絵札でない確率
③ジョーカーを除いた $52$ 枚のトランプから $1$ 枚引くとき、スペードである確率
④ジョーカーを除いた $52$ 枚のトランプから $1$ 枚引くとき、スペードでない確率
⑤硬貨を投げて、表が出る確率
⑥硬貨を投げて、裏が出る確率
⑦袋の中に赤玉$3$個と白玉$6$個が入っている。ここから玉を$1$個取り出すとき、赤玉である確率
⑧袋の中に赤玉$3$個と白玉$6$個が入っている。ここから玉を$1$個取り出すとき、赤玉でない確率
⑨箱の中にくじが $9$ 本入っていて、そのうちの $3$ 本が当たりである。ここからくじを $1$ 本引くとき、当たりである確率
答え
①$\cfrac{3}{13}$ ②$\cfrac{10}{13}$ ③$\cfrac{1}{4}$ ④$\cfrac{3}{4}$ ⑤$\cfrac{1}{2}$ ⑥$\cfrac{1}{2}$ ⑦$\cfrac{1}{3}$ ⑧$\cfrac{2}{3}$ ⑨$\cfrac{1}{3}$
①絵札は$12$枚です。$\cfrac{12}{52}=\cfrac{3}{13}$
②絵札でないのは$40$枚です。$\cfrac{40}{52}=\cfrac{10}{13}$
③スペードは$13$枚です。$\cfrac{13}{52}=\cfrac{1}{4}$
④スペードでないのは$39$枚です。$\cfrac{39}{52}=\cfrac{3}{4}$
⑦$\cfrac{3}{9}=\cfrac{1}{3}$
⑧$\cfrac{6}{9}=\cfrac{2}{3}$
⑨$\cfrac{3}{9}=\cfrac{1}{3}$
$\huge{23}$
$1$ 枚の硬貨を $3$ 回投げるとき、次の①~④の問いに答えなさい。
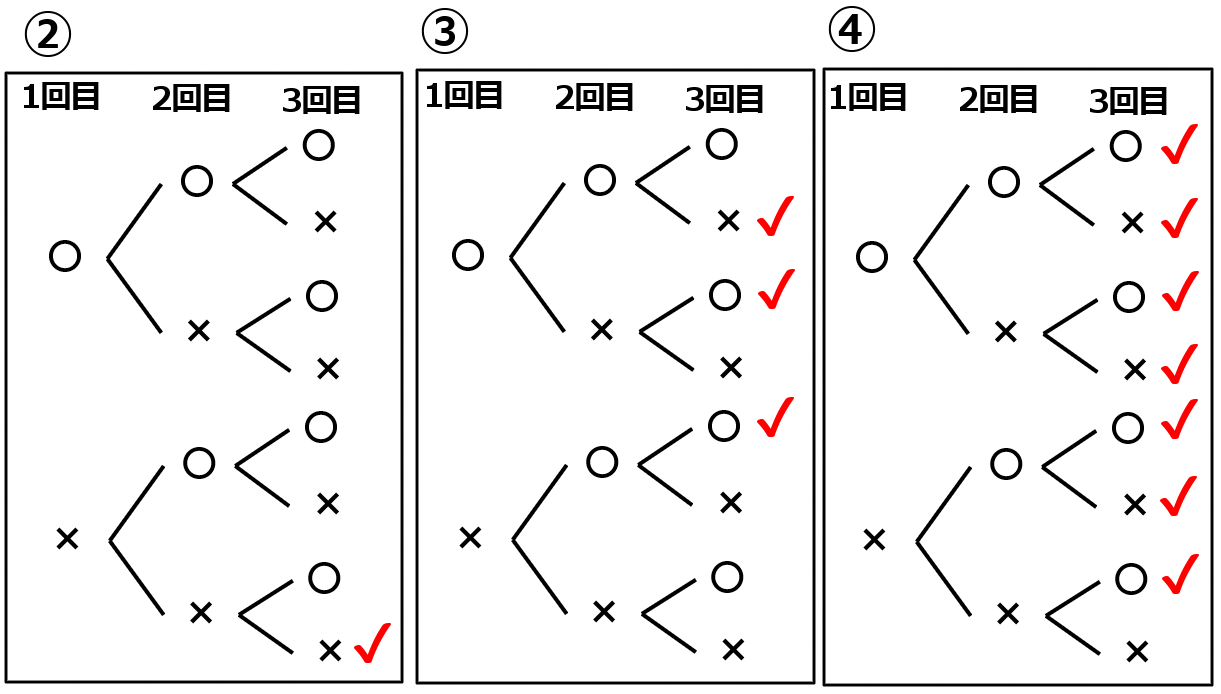
① 表を〇,裏を×として樹形図をかきなさい。
② $3$ 枚とも裏である確率を求めなさい。
③ $2$ 枚が表、$1$ 枚が裏である確率を求めなさい。
④ 少なくとも $1$ 枚が表である確率を求めなさい。
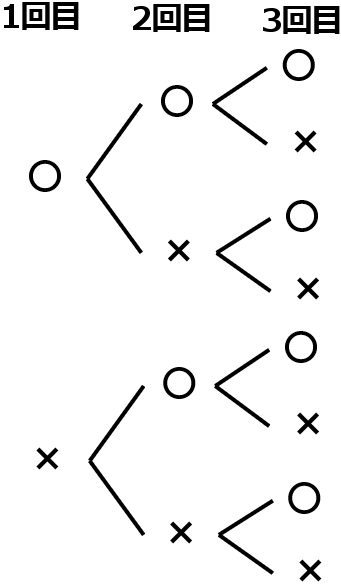 答え
答え
① 右図
② $\cfrac{1}{8}$
③ $\cfrac{3}{8}$
④ $\cfrac{7}{8}$
答えのような図を樹形図といいます。しらみつぶしに全パターンを調べるのに便利です。
右側の足の数を数えてください。それの本数が、全部で何パターンあるか、というのを表すことになります。全部で $8$ 通りのパターンがあります。なので分母は $8$ です。
下の図で、赤でチェックしてあるところが、問題に該当するところです。
$\huge{24}$ $\boxed{\large{\ 0\ }}$$\boxed{\large{\ 1\ }}$$\boxed{\large{\ 2\ }}$$\boxed{\large{\ 3\ }}$ と数字のかかれたカードが全部で $4$ 枚ある。この中から $2$ 枚のカードを抜き取ってならべ、$2$ けたの整数をつくるとき、偶数となる確率を求めなさい。
答え
$\cfrac{5}{9}$
「$2$ 枚のカードを抜き取ってならべ、$2$ けたの整数をつくる」というのは、たとえば、$\boxed{\large{\ 2\ }}$$\boxed{\large{\ 3\ }}$ というのは、$23$ だということになります。左が $10$ の位で、右が $1$ の位です。
気をつけなければならないのは、左側に $\boxed{\large{\ 0\ }}$ のカードは置けない、ということです。
$\boxed{\large{\ 0\ }}$$\boxed{\large{\ 1\ }}$ とか $\boxed{\large{\ 0\ }}$$\boxed{\large{\ 2\ }}$ とかは、$2$ けたの整数とはいえません。
そのようなことをふまえて、樹形図をかきます。
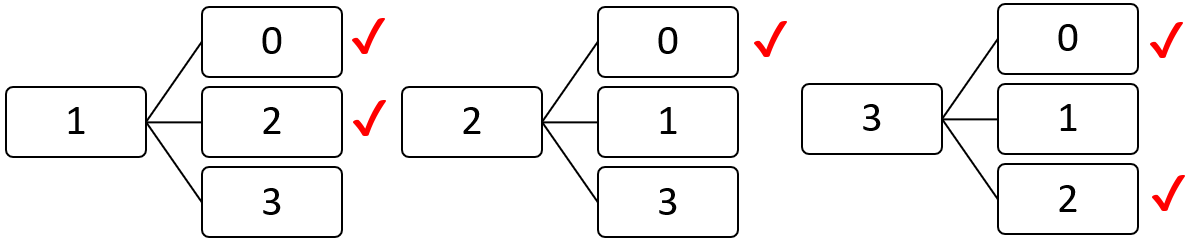 足の本数が、全部で何パターンあるか、というのを表すことになります。全部で $9$ 通りのパターンがあります。なので分母は $9$ です。
足の本数が、全部で何パターンあるか、というのを表すことになります。全部で $9$ 通りのパターンがあります。なので分母は $9$ です。
赤でチェックしてあるところが、問題に該当するところです。
$\huge{25}$
大小 $2$つのさいころを投げるとき、次の①~③の問いに答えなさい。
① 同じ目が出る確率を求めなさい。
② 出る目の和が$5$ 以下になる確率を求めなさい。
③ 出る目の積が$8$ より大きくなる確率を求めなさい。
答え
① $\cfrac{1}{6}$ ② $\cfrac{5}{18}$ ③ $\cfrac{5}{9}$
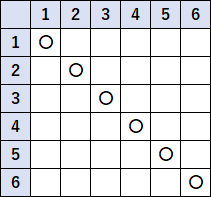 ①樹形図をかいてもいけます。関数の座標のかき方みたいなのをかいてもいいです。右の図のような表をかいてもいいです。すきなやり方でやってください。ここでは表でやっておきます。
①樹形図をかいてもいけます。関数の座標のかき方みたいなのをかいてもいいです。右の図のような表をかいてもいいです。すきなやり方でやってください。ここでは表でやっておきます。
目の出方は、表のマス目の数だけパターンがあります。なので $36$ パターンあります。分母は $36$ です。
表で、出た目がおなじところに〇印をつけます。ここが問題に該当するところです。
なので、
$$\cfrac{6}{36}=\cfrac{1}{6}$$
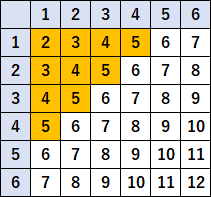 ②出る目の和を表にかきこんでしまいます。「$5$ 以下」というのは、$5$ がふくまれます。なので、色のついているところが問題に該当するところです。なので、
②出る目の和を表にかきこんでしまいます。「$5$ 以下」というのは、$5$ がふくまれます。なので、色のついているところが問題に該当するところです。なので、
$$\cfrac{10}{36}=\cfrac{5}{18}$$
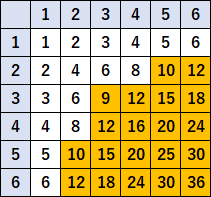 ③出る目の積を表にかきこんでしまいます。「$8$ より大きい」というのは、$8$ はふくまれません。なので、色のついているところが問題に該当するところです。なので、
③出る目の積を表にかきこんでしまいます。「$8$ より大きい」というのは、$8$ はふくまれません。なので、色のついているところが問題に該当するところです。なので、
$$\cfrac{20}{36}=\cfrac{5}{9}$$
 $\huge{26}$
袋の中に赤玉が $2$ 個と白玉が $3$ 個入っている。次の①,②の問いに答えなさい。
$\huge{26}$
袋の中に赤玉が $2$ 個と白玉が $3$ 個入っている。次の①,②の問いに答えなさい。
①袋の中から玉を $1$ 個取り出してからそれを袋にもどし、また玉を $1$ 個取り出す。このとき、取り出した玉の色が同じである確率を求めなさい。
②袋の中から玉を $2$ 個同時に取り出すとき、取り出した玉の色が同じである確率を求めなさい。
答え
① $\cfrac{13}{25}$ ② $\cfrac{2}{5}$
<①の問題>
①,②,③,④,⑤と、$5$ 個の玉に番号をつけてしまいます。そして、①と②が赤玉、③と④と⑤が白玉ということにします。①②③④⑤という感じです。
んで、樹形図をかいてもいけます。または、関数の座標のかき方みたいなのをかいてもいいです。図のような表をかいてもいいです。すきなやり方でやってください。ここでは表でやっていきます。
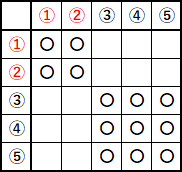 玉の出方は、表のマス目の数だけパターンがあります。なので $25$ パターンあります。分母は $25$ です。
玉の出方は、表のマス目の数だけパターンがあります。なので $25$ パターンあります。分母は $25$ です。
表で、玉の色がおなじところに〇印をつけます。ここが問題に該当するところです。
なので、
$$\cfrac{13}{25}$$
<②の問題>
玉に番号をつけるところは同じです。今回も表でやりますが、はじめの問題とちがうのは、今回は同じ玉を取り出すことはできません。はじめの問題では、たとえば①①というふうに、同じ玉を$2$ 回取り出せますが、今回はそれができません。こういうときは、表に斜めの線がはいります。こんな感じです。
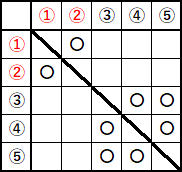 線をいれたのはもちろん、「同じ番号の玉はとり出せない」という意味です。
線をいれたのはもちろん、「同じ番号の玉はとり出せない」という意味です。
玉の出方は、表のマス目の数だけパターンがあります。なので $20$ パターンあります。分母は $20$ です。
表で、玉の色がおなじところに〇印をつけます。ここが問題に該当するところです。
なので、
$$\cfrac{8}{20}=\cfrac{2}{5}$$
$\Large{定義・定理のおさらい}$
合同な図形の性質
① 合同な図形では、対応する線分 の長さはそれぞれ等しい。
② 合同な図形では、 対応する角 の大きさはそれぞれ等しい。
三角形の合同条件
① $3$ 組の辺 がそれぞれ等しい。
② $2$ 組の辺とその間の角 がそれぞれ等しい。
③ $1$ 組の辺とその両端の角 がそれぞれ等しい。
二等辺三角形
① 用語や記号の意味をはっきりとのべたものを 定義 という。
② $2$つの 辺の長さ が等しい三角形を二等辺三角形という。
③ $3$つの辺の長さが等しい三角形を 正三角形 という。
④ すでに証明されたことのうちで、いろいろな証明をするときによく使われるものを 定理 という。
⑤ 二等辺三角形の $2$ つの 低角 は等しい。
⑥ 二等辺三角形の頂角の二等分線は、底辺を 垂直に二等分 する。
直角三角形
① あることがらの仮定と結論をいれかえたものを 逆 という。
② $1$つの角が直角である三角形を直角三角形といい、直角に対する辺を 斜辺 という。
③ $1$つの角が直角である二等辺三角形を 直角二等辺三角形 という。
④ $90^{ \circ }$より小さい角を 鋭角 という。
⑤ $90^{ \circ }$より大きい角を 鈍角 という。
⑥ $3$つの角がすべて $90^{ \circ }$より小さい三角形を 鋭角 三角形という。
⑦ $1$つの角が $90^{ \circ }$より大きい三角形を 鈍角 三角形という。
直角三角形の合同条件
① 斜辺と他の$1$辺 がそれぞれ等しい。
② 斜辺と$1$鋭角 がそれぞれ等しい。
平行四辺形
① 四角形の向かい合う辺を 対辺、向かい合う角を 対角 という。
② $2$組の対辺がそれぞれ 平行な 四角形を平行四辺形という。(定義)
平行四辺形の性質
① $2$組の 対辺 はそれぞれ等しい。
② $2$組の 対角 はそれぞれ等しい。
③ $2$つの 対角線 はそれぞれの 中点 で交わる。
平行四辺形であるための条件
四角形は次のどれかが成り立つとき、平行四辺形である。
① $2$組の対辺がそれぞれ 平行 である。
② $2$組の 対辺 がそれぞれ等しい。
③ $2$組の 対角 がそれぞれ等しい。
④ $2$つの 対角線 がそれぞれの 中点 で交わる。
⑤ $1$組の 対辺 が 平行で長さ が等しい。
特別な平行四辺形
① $4$つの辺が等しい四角形を ひし形 という。(定義)
② $4$つの角が等しい四角形を 長方形 という。(定義)
③ $4$つの辺が等しく、$4$つの角が等しい四角形を 正方形 という。(定義)
また、それぞれの $2$つの対角線は次のような性質がある。
④ ひし形の対角線は、垂直に 交わる。
⑤ 長方形の対角線は、長さが 等しい。
⑥ 正方形の対角線は、垂直 で 長さが 等しい。
答え(中2 学年末模擬テスト 第1回)
1$①-16$ $②\cfrac{1}{12}$ $③2$ $④-13a+7b$ $⑤\cfrac{x+6y}{12} \ \left(\cfrac{1}{12}x+\cfrac{1}{2}y\right)$ $⑥-60a^2b^3$ $⑦-2y$ $⑧\cfrac{2}{3y}$
2$①x=3, \ y=-1$ $②x=-2, \ y=5$ $③x=-3, \ y=4$ $④x=4, \ y=-1$
3$①y=-\cfrac{2}{3}x-2$ $②y=-2x+5$ $③-11 \leqq y \leqq 1$
4$(1) \ (-3, \ -2)$ $(2) \ \cfrac{21}{2}$
5$\triangle ABC \ \equiv \ \triangle NMO$…$3$ 組の辺がそれぞれ等しい。
$\triangle DEF \ \equiv \ \triangle QPR$…$2$ 組の辺とその間の角がそれぞれ等しい。
$\triangle GHI \ \equiv \ \triangle KJL$…$1$ 組の辺とその両端の角がそれぞれ等しい。
6 ① 仮定…$\triangle ABC \ \equiv \ \triangle DEF$ 結論…$AB=DE$
② 仮定…$8x=48$ 結論…$x=6$
③ 仮定…$\triangle ABC$ において、$AB=AC$ 結論…$\triangle ABC$ は二等辺三角形
7① 〈仮定〉 $AB=AC, \ AD=AE$
〈結論〉 $\angle ABE=\angle ACD$
② 〈証明〉
$\triangle ABE$ と $\triangle ACD$ で、
仮定から、
$AB=AC$ ……①
$AD=AE$ ……②
共通な角だから、$\triangle BAE = \triangle CAD$ ……③
①②③より、$2$ 組の辺とその間の角がそれぞれ等しいので
$\triangle ABE \ \equiv \ \triangle ACD$
合同な三角形の対応する角なので
$\angle ABE=\angle ACD$
8 $\angle x=40^{ \circ }$
9 〈証明〉
$\triangle DBC$ と $\triangle ECB$ で、
仮定から、$DB=EC$ ……①
二等辺三角形の底角だから、$\angle DBC=\angle ECB$ ……②
共通な辺だから、$BC=CB$ ……③
①②③より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle DBC \ \equiv \ \triangle ECB$
合同な図形の対応する角だから、$\angle DCB=\angle EBC$
$2$つの角が等しい三角形だから、$\triangle FBC$ は二等辺三角形である
10 〈証明〉
$\triangle ADC$ と $\triangle ABE$ で、
$\triangle ADB$ は正三角形だから、$AD=AB$ ……①
$\triangle ACE$ は正三角形だから、$AC=AE$ ……②
$\angle DAB=60^{ \circ }$ だから、$\angle DAC=60^{ \circ }+\angle BAC$ ……③
$\angle CAE=60^{ \circ }$ だから、$\angle BAE=60^{ \circ }+\angle BAC$ ……④
③④より、$\angle DAC=\angle BAE$ ……⑤
①②⑤より、$2$組の辺とその間の角がそれぞれ等しいので、
$\triangle ADC \ \equiv \ \triangle ABE$
合同な図形の対応する辺だから、$DC=BE$
11 ① 同位角が等しいならば、$2$直線は平行である。 …成り立つ
② $x+y=7$ ならば、$x=3, \ y=4$ …成り立たない
③ $\triangle ABC$で、$\angle B=\angle C$ならば、$AB=AC$ …成り立つ
12 $\triangle ABC \ \equiv \ \triangle QPR$…直角三角形で、斜辺と他の$1$辺がそれぞれ等しい。
$\triangle DEF \ \equiv \ \triangle KLJ$…$2$ 組の辺とその間の角がそれぞれ等しい。
$\triangle GHI \ \equiv \ \triangle NMO$…直角三角形で、斜辺と$1$鋭角がそれぞれ等しい。
13 〈証明〉
$\triangle ABD$ と $\triangle CBD$ で、
仮定から、$\angle A =\angle C =90^{ \circ }$ ……①
$AD=CD$ ……②
共通な辺だから、$BD=BD$ ……③
①②③より、直角三角形で、斜辺と他の$1$辺がそれぞれ等しいので
$\triangle ABD \ \equiv \ \triangle CBD$
合同な図形の対応する角だから、
$\angle ABD=\angle CBD$
14 $x=10$ 平行四辺形の$2$組の対辺はそれぞれ等しい。
$y=70$ 平行四辺形の$2$組の対角はそれぞれ等しい。
$z=8$ 平行四辺形の$2$つの対角線はぞれぞれの中点で交わる。
15 〈証明〉
$\triangle OAM$ と $\triangle OCN$ で、
対頂角だから、$\angle AOM =\angle CON $ ……①
平行四辺形の対角線はそれぞれの中点で交わるから、$OA=OC$ ……②
平行線の錯角だから、$\angle OAM =\angle OCN $ ……③
①②③より、$1$組の辺とその両端の角がそれぞれ等しいので、
$\triangle OAM \ \equiv \ \triangle OCN$
合同な図形の対応する辺だから、
$ AM= CN$
16 ①…いえる $2$組の対辺がそれぞれ平行(定義)
②…いえない
③…いえる $1$組の対辺が平行で長さが等しい
17 〈証明〉
▱$ABCD$ で、
$AD=BC, \ AD /\!/ BC$ ……①
▱$BEFC$ で、
$BC=EF, \ BC /\!/ EF$ ……②
①②より、$AD=EF, \ \ AD /\!/ EF$
$1$組の対辺が平行で長さが等しいので、
四角形 $AEFD$ は平行四辺形である。
18
\begin{array}{c|c|c|c}
\hline
& ひし形 & 長方形 & 正方形 \\
\hline
垂直に交わる & 〇 & × & 〇 \\
\hline
長さが等しい & × & 〇 & 〇 \\
\hline
\end{array}
19
①辺$BC$ を $C$側に延長する。
②$A$ と $C$ をむすぶ。
③$D$ を通り、$AC$ と平行な線をひき、半直線$BC$ との交点を $E$ とする。
④$A$ と $E$ をむすぶ。
$\triangle ABE$ は四角形$ABCD$ と面積が等しい。
20 $\triangle EBD$ $\triangle FBD$
21 ①$\cfrac{1}{6}$ ②$1$ ③$\cfrac{5}{6}$ ④$\cfrac{1}{6}$ ⑤$0$ ⑥$\cfrac{1}{3}$ ⑦$\cfrac{1}{2}$ ⑧$\cfrac{1}{3}$
22 ①$\cfrac{3}{13}$ ②$\cfrac{10}{13}$ ③$\cfrac{1}{4}$ ④$\cfrac{3}{4}$ ⑤$\cfrac{1}{2}$ ⑥$\cfrac{1}{2}$ ⑦$\cfrac{1}{3}$ ⑧$\cfrac{2}{3}$ ⑨$\cfrac{1}{3}$
23 
① 右図
② $\cfrac{1}{8}$
③ $\cfrac{3}{8}$
④ $\cfrac{7}{8}$
24 $\cfrac{5}{9}$
25 ① $\cfrac{1}{6}$ ② $\cfrac{5}{18}$ ③ $\cfrac{5}{9}$
26 ① $\cfrac{13}{25}$ ② $\cfrac{2}{5}$