数学 中3 2章 平方根 第3回)
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
平方根
(1) 次の $ \boxed{\LARGE\phantom{hoge}}$ の中にあてはまる言葉や数や式をいれましょう。
① $x^2=a$ となるとき、$x$ を $a$ の平方根という。正の数には平方根が $ \boxed{\LARGE\phantom{hogeho}}$ の $2$ つあり、絶対値は等しく、符号が異なる。
正の数 $a$ の $2$つの平方根を、記号 $\sqrt{ }$ を使って、 正のほうを$ \boxed{\LARGE\phantom{hoge}}$,負のほうを $ \boxed{\LARGE\phantom{hoge}}$と表す。両方まとめて $ \boxed{\LARGE\phantom{hoge}}$ と表す。
$\sqrt{ }$ を $ \boxed{\LARGE\phantom{hoge}}$ という。読み方は $ \boxed{\LARGE\phantom{hogeho}}$ 。
② $0$ の平方根は $ \boxed{\LARGE\phantom{ho}}$ である。
答え
① $x^2=a$ となるとき、$x$ を $a$ の平方根という。正の数には平方根が $ \boxed{\large正と負}$ の $2$ つあり、絶対値は等しく、符号が異なる。
正の数 $a$ の $2$つの平方根を、記号 $\sqrt{ }$ を使って、 正のほうを$ \boxed{\large\sqrt{a}}$,負のほうを $ \boxed{\large-\sqrt{a}}$と表す。両方まとめて $ \boxed{\large\pm\sqrt{a}}$ と表す。
$\sqrt{ }$ を $ \boxed{\large根号}$ という。読み方は $ \boxed{\largeルート}$ 。
② $0$ の平方根は $ \boxed{\large0}$ である。
「$2$ 乗したら $a$ になる数を 「$a$ の平方根」ていうんだ」と思っちゃえばいいです。たとえば $4$ の平方根は $2$ です。でも、$-2$ も $2$ 乗したら $4$ になりますよね? なのでけっきょく、$4$ の平方根は $2$ と $-2$ の $2$つです。両方まとめて $\pm2$ と表します。「$\pm$」の読み方は「プラスマイナス」です。つちじゃありません。
じゃあ、$2$ 乗したら $2$ になる数はなんですか? ……。こまっちゃいますよね? なので、それを$\sqrt{ }$ を使って表すことにするわけです。$2$ の平方根は $\pm\sqrt{2}$ です。これは、ぴったりした数にはなりません。$\pm1.732...$ とどこまでもつづいていく数になります。
というわけで、$\sqrt{ }$ を使わずに平方根がいえる数と、$\sqrt{ }$ を使わないと平方根が表せない数があるわけです。たとえば $4$ の平方根は $\pm2$ だし、$9$ の平方根は $\pm3$ です。でも $2$ の平方根は $\pm\sqrt{2}$ です。$3$ の平方根は $\pm\sqrt{3}$ です。
正の数には平方根はプラスとマイナスの $2$つあります。
負の数には平方根はありません。$2$ 乗するとマイナスになる数はないからです。なので、ルートの中がマイナスになることはありません。これからいろいろ計算をしていきますが、たとえば$\sqrt{-2}$ とかになっちゃったら、それはおかしいです。どこかでまちがえたと思ってください。
$0$ の平方根は、これだけは $0$ の $1$ つだけです。$\pm0$ とやっちゃダメ。
(2) 次の数の平方根を求めなさい。または、表しなさい。
\begin{eqnarray*}
&①& \quad 1 \quad &②& \quad 16\quad &③& \quad 49 \quad &④& \quad 144 \\
\\
&⑤& \quad \cfrac{4}{9} \quad &⑥& \quad 0.25 \quad &⑦& \quad 0 \quad &⑧& \quad -25
\\
&⑨& \quad 17 \quad &⑩& \quad 0.9 \quad &⑪& \quad \cfrac{3}{10} \quad &⑫& \quad \cfrac{64}{121}
\end{eqnarray*}
答え
$①\pm1$ $②\pm4$ $③\pm7$ $④\pm12$ $⑤\pm\cfrac{2}{3}$ $⑥\pm0.5$ $⑦0$ $⑧ない$ $⑨ \pm\sqrt{17}$ $⑩ \pm\sqrt{0.9}$ $⑪ \pm\sqrt{\cfrac{3}{10}}$ $⑫ \pm\cfrac{8}{11}$
$\large{\pm}$ を忘れないようにしましょう。
⑦$0$ の平方根は $0$ です。$0$ にはプラスもマイナスもないので、これだけは $\large{\pm}$ をつけません。
⑧負の数の平方根はありません。「ない」とか「なし」とか答えましょう。
(3) 次の①~⑥が正しければ〇を書きなさい。誤っていれば、×を書き、下線の部分を正しく書き直しなさい。
\begin{eqnarray*}
&①& \quad 16 の平方根は \underline{ 4 } \quad \qquad &②& \quad \sqrt{16}=\underline{ 4 }\\
\\
&③& \quad \sqrt{4^2}= \underline{ 4 } &④& \quad \sqrt{(-4)^2}=\underline{ -4 }\\
\\
&⑤& \quad (\sqrt{4})^2= \underline{ 4 } &⑥& \quad (-\sqrt{4})^2=\underline{ -4 }\\
\\
\end{eqnarray*}
答え
$①× \ \pm4$ $②〇$ $③〇$ $④×\ 4$ $⑤〇$ $⑥× \ 4$
①平方根は $\pm$ がつきます。
②ぎゃくに、こちらはつけてはいけません。意味を考えましょう。よくわからなかったら、テストのときはこうしてください。
「平方根」と書かれていたら、$\large{\pm}$ をつける。
「平方根」と書かれていなかったら、$\large{\pm}$ をつけない。
それでうまくいきます。漢字三文字で平方根。平と方と根で平方根。この三文字が問題文にあったら $\pm$ をつける。なければつけない。「根には土がついている」とでもおぼえてください。
③⑤$2$ 乗したらルートは消えます。
④⑥マイナスの数にかっこをつけて $2$ 乗したらプラスになります。このことも、あやふやなひとは整理しておきましょう。
$(-2)^2=4, \ -2^2=-4, \ (-2^2)=-4$ という感じです。
(4) 次の①~④の数を、根号を使わずに表しなさい。
$$
① \ \sqrt{25}\qquad ② \ -\sqrt{\cfrac{36}{49}} \qquad ③ \ \sqrt{0.09} \qquad ④ \ (\sqrt{256})^2
$$
答え
$①5$ $②-\cfrac{6}{7}$ $③0.3$ $④256$
④ルートは $2$ 乗すると消えます。
平方根の大小
(5) 次①~③の $2$つの数について、数の大小を不等号を用いて表しなさい。④は不等号をもちいて、小さい順に数をならべなさい。
$$
① \quad \sqrt{10},\quad\sqrt{9.9}\qquad ② \quad 11, \quad \sqrt{120} \qquad ③\quad -\sqrt{35},\quad-6
$$
$$
④ \quad -3,\quad 3,\quad-\sqrt{10},\quad \sqrt{10},\quad-\sqrt{8},\quad\sqrt{8}
$$
答え
$① \sqrt{10}\gt \sqrt{9.9}$ $② 11\gt \sqrt{120}$ $③ -\sqrt{35} \gt -6$ $④ -\sqrt{10}\lt-3\lt-\sqrt{8}\lt\sqrt{8}\lt3\lt\sqrt{10}$
$$正の数 \ a, \ b について、$$ $$\large{a\lt b\qquadならば\qquad\sqrt{a}\lt\sqrt{b}}$$
$\sqrt{ }$ のついている数とついていない数の大小は、$2$ 乗して比べましょう。根号は、$2$ 乗をすると消えます。そして、絶対値の大小関係は、$2$ 乗をしても変わりません。
②$11^2=121, \ (\sqrt{120})^2=120$ なので、$11\gt \sqrt{120}$ です。
③$(\sqrt{35})^2=35, \ 6^2=36$ なので、$\sqrt{35}\lt 6$ です。なので、$-\sqrt{35}\gt -6$ です。
④$3^2=9, \ (\sqrt{10})^2=10, \ (\sqrt{8})^2=8$ なので、$\sqrt{8}\lt 3\lt\sqrt{10}$ です。
素因数分解(おさらい)
(6) 次の①,②の数を素因数分解して、素数の積の形で表しなさい。
$\qquad①30\qquad\qquad\qquad②160$
答え
$①2\times3\times5$ $②2^5\times5$
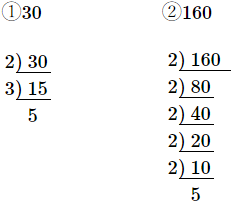
自然数をいくつかの自然数の積に形に表すとき、その $1$ つ $1$ つの自然数を因数という。
その因数が素数のとき、それを素因数という。
自然数を素因数だけの積の形に表すことを素因数分解するという。
素因数分解して表された積の形は、素因数を並べる順序を考えなければ、$1$ 通りだけである。
(7) 次の①,②の問いに答えなさい。
① $350$ にできるだけ小さい自然数をかけて、その答えがある整数の $2$ 乗になるようにしたい。どんな数をかければよいか。
② $294$ をできるだけ小さい自然数で割って、その答えがある整数の $2$ 乗になるようにしたい。どんな数で割ればよいか。
答え
$① 14$ $② 6$
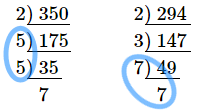 point
point
どちらの問題もやり方はおなじです。
手順1 素因数分解してください。
手順2 同じ数が$2$つあったら、そこを〇でかこんでください。
手順3 〇でかこまれなかった数をかけてください。
その数が答えです。簡単なので、手順をおぼえましょう。
ちなみに、①は $350\times14=4900$ となって、$4900$ は $70$ の $2$ 乗です。
②は $294\div6=49$ となって、$49$ は $7$ の $2$ 乗です。
これの発展問題を、入試でわりと見ます。そちらはこんな甘いもんじゃないです。でも、そういうのを解けるようになるためにも、まずこの基本問題を確実にできるようにしておきましょう。
平方根の乗法・除法
(8) 次の計算をしなさい。
\begin{eqnarray*}
&①& \ \sqrt{5}\times\sqrt{6}
&②& \ 5\times \sqrt{6}
&③& \ 3\sqrt{5}\times2\sqrt{7}\\\\
&④& \ -\sqrt{3}\times(-5\sqrt{2})\quad
&⑤& \ \sqrt{35}\div\sqrt{5}\quad
&⑥& \ 9\sqrt{15}\div\sqrt{3}\\\\
&⑦& \ \sqrt{42}\div3\sqrt{7}
&⑧& \ 20\sqrt{6}\div(-4\sqrt{2})
\end{eqnarray*}
答え
$①\sqrt{30}$ $②5\sqrt{6}$ $③6\sqrt{35}$ $④5\sqrt{6}$ $⑤\sqrt{7}$ $⑥9\sqrt{5}$ $⑦\cfrac{\sqrt{6}}{3}$ $⑧-5\sqrt{3}$
<ルートの掛け算>
ルートの外は外と、ルートの中は中とかけます。
$$③ \ 3\sqrt{5}\times2\sqrt{7}=6\sqrt{35}$$
<ルートの割り算>
ルートはルートで割れます。ミスが心配だと思うなら、分数にして約分する、というのがいいと思います。ルートの外は外と、ルートの中は中と約分できます。
\begin{eqnarray*}
\require{cancel}
&⑤& \ \sqrt{35}\div\sqrt{5}=\cfrac{ \sqrt{\bcancel{35}}}{ \sqrt{\bcancel{5}}}=\sqrt{7}\\
&⑥& \ 9 \sqrt{15}\div\sqrt{3}=\cfrac{ 9 \sqrt{\bcancel{15}}}{ \sqrt{\bcancel3}}=9\sqrt{5}\\
&⑦& \ \sqrt{42}\div3\sqrt{7}=\cfrac{ \sqrt{\bcancel{42}}}{ 3 {\sqrt{\bcancel{7}}}}=\cfrac{\sqrt{6}}{3}\\
&⑧& \ 20 \sqrt{6}\div(-4\sqrt{2})=-\cfrac{ \bcancel{20} \sqrt{\bcancel{6}}}{ \bcancel{4} {\sqrt{\bcancel2}}}=-5\sqrt{3}
\end{eqnarray*}
学校で教わるやり方をちょっとはしょってしまってるかもしれませんが、慣れるとみんなこうやるようになっちゃいます。話がはやいので。
$\sqrt{a}$ の形になおす
(9) 次の①~③の数を、$\sqrt{a}$ の形にしなさい。
$① \ 3\sqrt{10} \qquad ② \ \cfrac{\sqrt{14}}{4} \qquad③ \ 3 \sqrt{\cfrac{ \ 2 \ }{ \ 5 \ }}$
答え
$①\sqrt{90}$ $②\sqrt{\cfrac{ \ 7 \ }{ \ 8 \ }}$ $③\sqrt{\cfrac{ \ 18 \ }{ \ 5 \ }}$
ルートの外にある数をルートの中に入れなさい、という意味の問題です。
ルートの外にある数は、$2$ 乗してルートの中に入れます。
$$① \ 3\sqrt{10}=\sqrt{3^2\times10}=\sqrt{90}$$
$$② \ \cfrac{\sqrt{14}}{4}=\sqrt{\cfrac{14}{4^2}}=\sqrt{\cfrac{ \ 7 \ }{ \ 8 \ }}$$
$$③ \ 3\sqrt{\cfrac{ \ 2 \ }{ \ 5 \ }}=\sqrt{3^2\times \cfrac{ \ 2 \ }{ \ 5 \ }}=\sqrt{\cfrac{ \ 18 \ }{ \ 5 \ }}$$
$a\sqrt{b}$ の形になおす
(10) 次の①~④の数を、$a\sqrt{b}$ の形にするか、根号をなくせるときはなくしなさい。根号の中の数はできるだけ小さい整数となるようにしなさい。
$① \ \sqrt{24} \qquad ② \ \sqrt{50} \qquad③ \ \sqrt{288} \qquad④ \ \sqrt{324}$
答え
$①2\sqrt{6}$ $②5\sqrt{2}$ $③12\sqrt{2}$ $④18$
このことについて教わったあとは、たとえばなにかの問題で、答えが $\sqrt{24}$ になったとして、 $\sqrt{24}$ と答えるとバツになります。$\sqrt{24}=\sqrt{2^2\times6}$ なので、$2\sqrt{6}$ と形をなおして答えなければなりません。ルートの中はなるべく小さい数になおしてないとバツになります。だから、答えにルートがついているときは、ひとつひとつ、なおせるかどうか確かめなければなりません。これは、やらないとだめです。そのうちなにがなおせて、なにがなおせないかをだんだんおぼえてきますので、しばらくがまんして確かめるようにしてください。この問題は、ぜんぶなおせる数です。
$$① \ \sqrt{24}=\sqrt{2^2\times6}=2\sqrt{6}$$
$$② \ \sqrt{50}=\sqrt{5^2\times2}=5\sqrt{2}$$
$$③ \ \sqrt{288}=\sqrt{12^2\times2}=12\sqrt{2}$$
$$④ \ \sqrt{324}=\sqrt{18^2}=18$$
なんの $2$ 乗との積になっているかをぱっぱっと思いつければいいのですが、数が大きくなったりすると、なかなかわかりません。計算力に自信がないひとは、あきらめてすべて素因数分解してください。なおせるか、なおせないか、なおせるとしたらどうなるのか、を確認できます。こんな感じです。
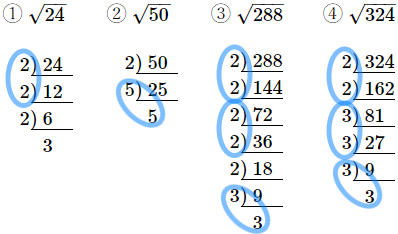
1.素因数分解する
2.同じ数が $2$ 個あったら〇でかこむ
3.〇でかこまれた数が$1$つだけ外に出る(いくつも出てきたときは全部かける)
4.〇でかこまれなかった数は中に残る(いくつも残ったときは全部かける)
というわけで、$\sqrt{24}$ は $2$ が外に出て $2$ と $3$ が残るので $2\sqrt{6}$
$\sqrt{50}$ は $5$ が外に出て $2$ が残るので $5\sqrt{2}$
$\sqrt{288}$ は $2$ と $2$ と $3$ が外に出て $2$ が残るので $12\sqrt{2}$
$\sqrt{324}$ は $2$ と $3$ と $3$ が外に出て 何も残らないので $18$
近似値を求める
(11) $\sqrt{5}=2.236, \ \sqrt{50}=7.071$ として、次の①~④の近似値を求めなさい。
$①\quad \sqrt{500}\qquad$$② \ \sqrt{5000}\qquad$$③ \ \sqrt{0.05}\qquad$$④ \ \sqrt{0.005}$
答え
$①22.36$ $②70.71$ $③0.2236$ $④0.07071$
\begin{eqnarray*}
① \ \sqrt{500}&=&\sqrt{100\times5}\qquad② \ \sqrt{5000}&=&\sqrt{100\times50}\\
&=&10\sqrt{5}&=&10\sqrt{50}\\
&=&10\times2.236&=&10\times7.071\\
&=&22.36&=&70.71\\\\
③ \ \sqrt{0.05}&=&\sqrt{\cfrac{5}{100}}\qquad④ \ \sqrt{0.005}&=&\sqrt{\cfrac{50}{10000}}\\
&=&\cfrac{\sqrt{5}}{10}&=&\cfrac{\sqrt{50}}{100}\\
&=&\cfrac{2.236}{10}&=&\cfrac{7.071}{100}\\
&=&0.2236&=&0.07071
\end{eqnarray*}
この問題で使える数は基本 $100$ か $10000$ です。$10^2=100, \ 100^2=10000$ だからです。
②の問題は、$5000$ を $1000\times5$ とやると失敗です。どうにもなりません。$100\times50$ とやれば、うまくいきます。
④の問題も同じで、$0.005$ をふつうに分数にすると $\cfrac{5}{1000}$ ですが、これだと失敗です。あえて分母を $10000$ にして、$\cfrac{50}{10000}$ とやってしまいます。それでうまくいきます。
平方根のいろいろなかけ算
(12) 次の計算をしなさい。
\begin{eqnarray*}
&①& \quad \sqrt{3}\times\sqrt{6}\qquad &②& \quad 2\times\sqrt{24}\qquad &③& \quad 3\sqrt{10}\times4\sqrt{5}\\\\
&④& \quad \sqrt{32}\times\sqrt{2}\qquad &⑤& \quad 2\sqrt{14}\times\sqrt{21}\qquad &⑥& \quad (5\sqrt{3})^2\\\\
&⑦& \quad \sqrt{11}\sqrt{3}\sqrt{11}\qquad &⑧& \quad \sqrt{26}\sqrt{13}\qquad &⑨& \quad 2\sqrt{40}\times\sqrt{60}
\end{eqnarray*}
答え
$①3\sqrt{2}$ $②4\sqrt{6}$ $③60\sqrt{2}$ $④8$ $⑤14\sqrt{6}$ $⑥75$ $⑦11\sqrt{3}$ $⑧13\sqrt{2}$ $⑨40\sqrt{6}$
$3\sqrt{6}\times\sqrt{12}=$を例に、$3$通りのやり方を解説します。どのやり方でやってもいいです。自分にあってると思うやり方でやってください。
$$\large{3\sqrt{6}\times\sqrt{12}=}$$
やりかた1$\quad3\sqrt{6}\times\sqrt{6\times2}=3\times6\times\sqrt{2}=18\sqrt{2}$
…いちばんかしこいやり方だと思うのですが、なかなか慣れないかもしれません。
やりかた2$\quad3\sqrt{6}\times2\sqrt{3}=6\sqrt{18}=6\times3\sqrt{2}=18\sqrt{2}$
…なおせるルートを全部なおしてからかけます。やり方3よりこっちのほうが、ルートの中の数が大きくならないので、その点はラクです。気をつけなければならないのは、かけたあとにさらにルートがなおることがある、ということです。ひんぱんにあります。そこがこのやり方のめんどうくさいところです。このやり方でやるなら、かけたあとも必ずルートがなおるかどうか確認しましょう。
やりかた3$\quad3\sqrt{72}=3\times6\sqrt{2}=18\sqrt{2}$
…全部かけてしまって、さいごにルートをなおします。単純明快、わかりやすいです。ただ、ときどき、ルートの中の数が大きくなってしまうことがあります。そういうときはルートをなおすのが大変なので、いつもこれでやるのはあまりおすすめできません。
ということで、どれでやってもいいです。すきなやり方でやってください。やりかた2がぶなんでいいのかな、とも思います。でも、やりかた3でもかまいません。私自身、やりかた3でやっちゃうことがいちばん多い気がします。やりかた1は、ときどき絶大な効果を発揮することがあります。はじめのうちはいろいろためすといいかもしれません。そしたら問題によってやり方を使い分けられるようになるからです。
以下、やりかたの例をしめします。
\begin{eqnarray*}
&①&\sqrt{3}\times\sqrt{6}=\sqrt{18}=3\sqrt{2}\\
&②&2\times\sqrt{24}=2\times2\sqrt{6}=4\sqrt{6}\\
&③&3\sqrt{10}\times4\sqrt{5}=12\sqrt{50}=12\times5\sqrt{2}=60\sqrt{2}\\
&④&\sqrt{32}\times\sqrt{2}=\sqrt{64}=8\\
&⑤&2\sqrt{14}\times\sqrt{21}=2\sqrt{2\cdot7}\times\sqrt{3\cdot7}=2\times7\sqrt{2\times3}=14\sqrt{6}\\\
&⑥&(5\sqrt{3})^2=25\times3=75\\
&⑦&\sqrt{11}\sqrt{3}\sqrt{11}=11\sqrt{3}\\
&⑧&\sqrt{26}\sqrt{13}=\sqrt{13\cdot2}\sqrt{13}=13\sqrt{2}\\
&⑨&2\sqrt{40}\times\sqrt{60}=2\sqrt{20\cdot2}\times\sqrt{20\cdot3}=2\times20\sqrt{6}=40\sqrt{6}
\end{eqnarray*}
分母の有理化
(13) 次の①~⑥の分母を有理化しなさい。
\begin{eqnarray*}
&①& \ \cfrac{\sqrt{3}}{\sqrt{2}} \qquad\qquad &②& \ \cfrac{3}{\sqrt{5}} \qquad\qquad &③& \ \cfrac{5}{\sqrt{10}}\\\\
&④& \ \cfrac{\sqrt{12}}{4\sqrt{30}} \qquad\qquad &⑤& \ \cfrac{6\sqrt{17}}{\sqrt{34}} \qquad\qquad &⑥& \ \cfrac{12}{\sqrt{18}}
\end{eqnarray*}
答え
$①\cfrac{\sqrt{6}}{2}$ $②\cfrac{3\sqrt{5}}{5}$ $③\cfrac{\sqrt{10}}{2}$ $④\cfrac{\sqrt{10}}{20}$ $⑤3\sqrt{2}$ $⑥2\sqrt{2}$
$\cfrac{1}{\sqrt{2}}$ とか、$\cfrac{2\sqrt{3}}{\sqrt{5}}$ のように、分母にルートがある場合があります。こういう場合、分母のルートをなくしてしまいます。手順をふめば、そういうことができます。分子にルートがあるのはそのままでいいです。でも、分母にあるときは、なくしてしまいます。これを、分母を有理化する、といいます。
そのやり方は、分母のルートとおなじものを、分母と分子の両方にかけてしまう、というものです。以下に2パターンをしめします。
$$\cfrac{1}{\sqrt{2}}=\cfrac{1\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}=\cfrac{\sqrt{2}}{2}$$
$$\cfrac{2\sqrt{3}}{\sqrt{5}}=\cfrac{2\sqrt{3}\times\sqrt{5}}{\sqrt{5}\times\sqrt{5}}=\cfrac{2\sqrt{15}}{5}$$
こうすれば、分数の値そのものは変えずに、分母のルートをなくすことができます。
このことを教わったあとは、たとえばなにかの問題で答えが $\cfrac{2\sqrt{3}}{\sqrt{5}}$ となったとして、そのように答えるとバツになります。分母を有理化していないからです。分母にルートがある形で答えてはいけません。そういうときは、かならず分母を有理化して答えてください。
分母の有理化にかんして、大きいポイントがひとつ、あります。
約分できるときは、まず約分する。分母を有理化するのはそのあと。
ということです。ルートはルートと約分できます。分母を有理化するまえに、「約分できないかな?」といつも確認するクセをつけるといいです。そして、約分できるときはまず約分してください。そうしないと、すごく損です。答えはおなじになりますが、約分できるときはまず約分したほうがずっとトクです。例をしめします。
\begin{eqnarray*}
&約&分しないで有理化&約&分してから有理化\\
&&\cfrac{\sqrt{15}}{\sqrt{30}}&&\cfrac{\sqrt{15}}{\sqrt{30}}\\
&=&\cfrac{\sqrt{15}\times\sqrt{30}}{\sqrt{30}\times\sqrt{30}}\qquad\qquad&=&\cfrac{1}{\sqrt{2}}\\
&=&\cfrac{\sqrt{450}}{30}&=&\cfrac{1\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}\\
&=&\cfrac{15\sqrt{2}}{30}&=&\cfrac{\sqrt{2}}{2}\\
&=&\cfrac{\sqrt{2}}{2}
\end{eqnarray*}
どう見ても約分してから分母を有理化したほうがラクですよね。
…おもいのほか話が長くなってしまいました。すいません。では問題の解答例です。
\begin{eqnarray*}
&①&\cfrac{\sqrt{3}}{\sqrt{2}}=\cfrac{\sqrt{3}\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}=\cfrac{\sqrt{6}}{2}\\
&②&\cfrac{3}{\sqrt{5}}=\cfrac{3\times\sqrt{5}}{\sqrt{5}\times\sqrt{5}}=\cfrac{3\sqrt{5}}{5}\\
&③&\cfrac{5}{\sqrt{10}}=\cfrac{5\times\sqrt{10}}{\sqrt{10}\times\sqrt{10}}=\cfrac{5\sqrt{10}}{10}=\cfrac{\sqrt{10}}{2}\\
&④&まず約分する\\
&&\cfrac{\sqrt{12}}{4\sqrt{30}}=\cfrac{\sqrt{2}}{4\sqrt{5}}=\cfrac{\sqrt{2}\times\sqrt{5}}{4\sqrt{5}\times\sqrt{5}}=\cfrac{\sqrt{10}}{20}\\
&⑤&まず約分する\\
&&\cfrac{6\sqrt{17}}{\sqrt{34}}=\cfrac{6}{\sqrt{2}}=\cfrac{6\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}=\cfrac{6\sqrt{2}}{2}=3\sqrt{2}\\
&⑥&\cfrac{12}{\sqrt{18}}=\cfrac{12}{3\sqrt{2}}=\cfrac{4}{\sqrt{2}}=\cfrac{4\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}=\cfrac{4\sqrt{2}}{2}=2\sqrt{2}
\end{eqnarray*}
平方根のいろいろな割り算
(14) 次の計算をしなさい。
\begin{eqnarray*}
&①& \quad \sqrt{5}\div\sqrt{35}\qquad\qquad ② \quad 12\div2\sqrt{18}\\\\
&③& \quad 4\sqrt{15}\div6\sqrt{10}
\end{eqnarray*}
答え
$①\cfrac{\sqrt{7}}{7}$ $②\sqrt{2}$ $③\cfrac{\sqrt{6}}{3}$
割り算は、ぴったり割れるんだったら割っておけばいいです。ルートはルートで割れます。ぴったり割れないんだったら、分数にして、もし約分できるなら約分して、ルートがなおせるのならなおして、分母にルートがあったら有理化しましょう。分母を有理化したあとにまた約分できることになることもよくあるので、そこも気をつけましょう。
そのさい、約分ができるかどうかをまず最初に確認して、約分できるなら約分してください。ルートをなおしたり分母を有理化したりするのはそのあとにしましょう。
\begin{eqnarray*}
&①&\sqrt{5}\div\sqrt{35}=\cfrac{\sqrt{5}}{\sqrt{35}}=\cfrac{1}{\sqrt{7}}=\cfrac{\sqrt{7}}{7}\\
&②&12\div2\sqrt{18}=\cfrac{12}{2\sqrt{18}}=\cfrac{6}{\sqrt{18}}=\cfrac{6}{3\sqrt{2}}=\cfrac{2}{\sqrt{2}}=\cfrac{2\sqrt{2}}{2}=\sqrt{2}\\
&③&4\sqrt{15}\div6\sqrt{10}=\cfrac{4\sqrt{15}}{6\sqrt{10}}=\cfrac{2\sqrt{3}}{3\sqrt{2}}=\cfrac{2\sqrt{6}}{6}=\cfrac{\sqrt{6}}{3}
\end{eqnarray*}
平方根のかけ算と割り算のまじった計算
(15) 次の計算をしなさい。
$$
① \quad 12\sqrt{30}\div\sqrt{6}\div6\sqrt{10}\qquad ② \quad 2\sqrt{21}\times\sqrt{\cfrac{ \ 1 \ }{ \ 10 \ }}\div\sqrt{\cfrac{ \ 3 \ }{ \ 5 \ }}
$$
答え
$①\sqrt{2}$ $②\sqrt{14}$
①かけ算と割り算がまじった計算は、ひとつの分数にして、分母と分子にわけてしまいます。$\div$ の直後にかいてあるものは分母にします。
$$12\sqrt{30}\div\sqrt{6}\div6\sqrt{10}=\cfrac{12\sqrt{30}}{\sqrt{6}\times6\sqrt{10}}$$
そして、まず約分できるところを全部約分してしまいます。優先順位はいつも約分が最初です。ルートの外は外と約分、ルートの中は中と約分できます。
$$\cfrac{\bcancel{12}\sqrt{\bcancel{30}}}{\sqrt{\bcancel{6}}\times\bcancel{6}\sqrt{\bcancel{10}}}
=\cfrac{2}{\sqrt{2}}
=\cfrac{2\sqrt{2}}{2}
=\sqrt{2}$$
そのあと、もしルートがなおせるのならなおし、分母にルートが残っていたなら有理化します。ルートをなおしたり、分母を有理化したあと、また約分できることもよくあるので、気をつけましょう。
②分数になっているときも、やり方は同じです。ひとつの分数にして、約分していく、という感じです。分数の割り算は逆数をかける(ひっくり返してかける)んでしたね。というわけで、こんなふうにやっていきます。
\begin{eqnarray*}
&&2\sqrt{21}\times\sqrt{\cfrac{ \ 1 \ }{ \ 10 \ }}\div\sqrt{\cfrac{ \ 3 \ }{ \ 5 \ }}\\
&=&2\sqrt{21}\times\cfrac{1}{\sqrt{10}}\div\cfrac{\sqrt{3}}{\sqrt{5}}\\
&=&2\sqrt{21}\times\cfrac{1}{\sqrt{10}}\times\cfrac{\sqrt{5}}{\sqrt{3}}\\
&=&\cfrac{2\sqrt{21}\times\sqrt{5}}{\sqrt{10}\times\sqrt{3}}
\end{eqnarray*}
そしてまず約分。それからルートをなおしたり分母を有理化したりしていきます。
$$\cfrac{2\sqrt{\bcancel{21}}\times\sqrt{\bcancel{5}}}{\sqrt{\bcancel{10}}\times\sqrt{\bcancel{3}}}
=\cfrac{2\sqrt{7}}{\sqrt{2}}
=\cfrac{2\sqrt{14}}{2}
=\sqrt{14}$$
最終的に答えをかくとき、①もう約分できない、②もうなおせるルートがない、③分母にルートがついていない、の $3$ つを確認しましょう。
平方根の加法・減法
(16) 次の計算をしなさい。
\begin{eqnarray*}
&①& \ 8\sqrt{3}+5\sqrt{3} &②& \ 4+5\sqrt{11}-6\sqrt{11}\\\\
&③& \ -8\sqrt{2}+7\sqrt{3}-9\sqrt{2}\qquad\qquad &④& \ \cfrac{5\sqrt{5}}{4}-\sqrt{5}\\\\
&⑤& \ \cfrac{\sqrt{2}}{2}+2\sqrt{2}-\cfrac{\sqrt{2}}{3}
\end{eqnarray*}
答え
$①13\sqrt{3}$ $②4-\sqrt{11}$ $③-17\sqrt{2}+7\sqrt{3}$ $④\cfrac{\sqrt{5}}{4}$ $⑤\cfrac{13\sqrt{2}}{6}$
平方根の足し算引き算は、ルートの中が同じなら足したり引いたりできます。ルートの中がちがうときは、足したり引いたりできません。
$2\sqrt{2}+3\sqrt{2}=5\sqrt{2}$ ←ルートの中が同じなので足せる
$2\sqrt{2}+3\sqrt{3}$ ←ルートの中がちがうので足せない
ちょうど、$2x+3x=5x$ というふうに、文字が同じなら足せる、$2x+3y$ は文字がちがうから足せない、もうこれ以上できない、というのと似ています。
あともちろん、$\sqrt2+\sqrt3=\sqrt5$ なんていうのはダメですからね。そんなのやっちゃいけません。
\begin{eqnarray*}
&①& \ 8\sqrt{3}+5\sqrt{3}=13\sqrt{3}\\\\
&②& \ 4+5\sqrt{11}-6\sqrt{11}=4-\sqrt{11}\\\\
&③& \ -8\sqrt{2}+7\sqrt{3}-9\sqrt{2}=-17\sqrt{2}+7\sqrt{3}\\\\
&④& \ \cfrac{5\sqrt{5}}{4}-\sqrt{5}=\cfrac{5\sqrt{5}-4\sqrt{5}}{4}=\cfrac{\sqrt{5}}{4}\\\\
&⑤& \ \cfrac{\sqrt{2}}{2}+2\sqrt{2}-\cfrac{\sqrt{2}}{3}\\
&=&\cfrac{3\sqrt{2}+12\sqrt{2}-2\sqrt{2}}{6}\\
&=&\cfrac{13\sqrt{2}}{6}
\end{eqnarray*}
分数で足し算引き算になっていたら、ふつうに通分すればOKです。
平方根のいろいろな足し算・引き算
(17) 次の計算をしなさい。
\begin{eqnarray*}
&①& \ 4\sqrt{3}+\sqrt{27}-2\sqrt{48} \qquad &②& \ \sqrt{216}-2\sqrt{45}-2\sqrt{54}-3\sqrt{125}\\\\
&③& \ \sqrt{80}-\cfrac{80}{\sqrt{5}} \qquad\quad &④& \ 3\sqrt{8}-\sqrt{\cfrac{ \ 1 \ }{ \ 2 \ }}
\end{eqnarray*}
答え
$①-\sqrt{3}$ $②-21\sqrt{5}$ $③-12\sqrt{5}$ $④\cfrac{11\sqrt{2}}{2}$
ルートの中がちがうと足したり引いたりできません。でも、ルートをなおすと、ルートの中が同じになることがあって、そうするとそれは足したり引いたりできます。問題はそういうことになっています。
分母にルートがあるときは、まず分母を有理化して、それから通分して計算していきましょう。
\begin{eqnarray*}
&①& 4\sqrt{3}+\sqrt{27}-2\sqrt{48}\\
&=& 4\sqrt{3}+3\sqrt{3}-8\sqrt{3} \\
&=& -\sqrt{3}\\
\\
&②& \sqrt{216}-2\sqrt{45}-2\sqrt{54}-3\sqrt{125}\\
&=& 6\sqrt{6}-6\sqrt{5}-6\sqrt{6}-15\sqrt{5} \\
&=& -21\sqrt{5}\\
\\
&③& \sqrt{80}-\cfrac{80}{\sqrt{5}}\\
&=& 4\sqrt{5}-\cfrac{80\sqrt{5}}{5} \\
&=& 4\sqrt{5}-16\sqrt{5} \\
&=& -12\sqrt{5}\\
\\
&④& 3\sqrt{8}-\sqrt{\cfrac{ \ 1 \ }{ \ 2 \ }}\\
&=& 6\sqrt{2}-\cfrac{1}{\sqrt{2}} \\
&=& 6\sqrt{2}-\cfrac{\sqrt{2}}{2} \\
&=& \cfrac{12\sqrt{2}-\sqrt{2}}{2} \\
&=& \cfrac{11\sqrt{2}}{2}
\end{eqnarray*}
平方根のいろいろな計算
(18) 次の計算をしなさい。
\begin{eqnarray*}
&①& \ -8\sqrt{6}+2\sqrt{3}\times3\sqrt{2} &②& \ 5\sqrt{2}-\sqrt{6}\div\sqrt{12}\\\\
&③& \ 2\sqrt{5}(\sqrt{10}+3\sqrt{7}) &④& \ (\sqrt{3}+\sqrt{72})\div\sqrt{2}\\\\
&⑤& \ (\sqrt{5}+4)(\sqrt{15}-3) \qquad\qquad &⑥& \ (\sqrt{3}-\sqrt{2})(\sqrt{6}-\sqrt{3})\\\\
&⑦& \ (\sqrt{6}-9)(\sqrt{6}-7) &⑧& \ (2\sqrt{5}-1)(2\sqrt{5}-6)\\\\
&⑨& \ (\sqrt{7}+2)^2 &⑩& \ (2\sqrt{2}-3\sqrt{6})^2\\\\
&⑪& \ (\sqrt{2}+4)(\sqrt{2}-4) &⑫& \ \left(\cfrac{\sqrt{15}}{3}+2\sqrt{2}\right)\left(\cfrac{\sqrt{15}}{3}-2\sqrt{2}\right)
\end{eqnarray*}
1. $ \large{(x+a)(x+b)=x^2+(a+b)x+ab}$
2. $ \large{(x+a)^2=x^2+2ax+a^2}$
3. $ \large{(x-a)^2=x^2-2ax+a^2}$
4. $ \large{(x+a)(x-a)=x^2-a^2}$
答え
$①-2\sqrt{6}$ $②\cfrac{9\sqrt{2}}{2}$ $③10\sqrt{2}+6\sqrt{35}$ $④\cfrac{\sqrt{6}}{2}+6$ $⑤5\sqrt{3}-3\sqrt{5}+4\sqrt{15}-12$ $⑥3\sqrt{2}-3-2\sqrt{3}+\sqrt{6}$ $⑦69-16\sqrt{6}$ $⑧26-14\sqrt{5}$ $⑨11+4\sqrt{7}$ $⑩62-24\sqrt{3}$ $⑪-14$ $⑫-\cfrac{19}{3}$
⑦番以降は乗法公式を使いましょう。テストのとき、わからなかったり、自信がなかったりするときは、分配法則でまんべんなくかけていけば大丈夫です。でもふだんは、なるべく乗法公式を使う練習をしておきましょう。 \begin{eqnarray*} &①& -8\sqrt{6}+2\sqrt{3}\times3\sqrt{2}\\ &=& -8\sqrt{6}+6\sqrt{6}\\ &=& -2\sqrt{6}\\ \\ &②& 5\sqrt{2}-\sqrt{6}\div\sqrt{12}\\ &=& 5\sqrt{2}-\cfrac{\sqrt{6}}{\sqrt{12}}\\ &=& 5\sqrt{2}-\cfrac{1}{\sqrt{2}}\\ &=& 5\sqrt{2}-\cfrac{\sqrt{2}}{2}\\ &=& \cfrac{10\sqrt{2}-\sqrt{2}}{2}\\ &=& \cfrac{9\sqrt{2}}{2}\\ \\ &③& 2\sqrt{5}(\sqrt{10}+3\sqrt{7})\\ &=& 2\sqrt{50}+6\sqrt{35}\\ &=& 10\sqrt{2}+6\sqrt{35}\\ \\ &④& (\sqrt{3}+\sqrt{72})\div\sqrt{2}\\ &=& \cfrac{\sqrt{3}}{\sqrt{2}}+\sqrt{36}\\ &=& \cfrac{\sqrt{6}}{2}+6\\ \\ &⑤& (\sqrt{5}+4)(\sqrt{15}-3)\\ &=& \sqrt{75}-3\sqrt{5}+4\sqrt{15}-12\\ &=& 5\sqrt{3}-3\sqrt{5}+4\sqrt{15}-12\\ \\ &⑥& (\sqrt{3}-\sqrt{2})(\sqrt{6}-\sqrt{3})\\ &=& \sqrt{18}-3-\sqrt{12}+\sqrt{6}\\ &=& 3\sqrt{2}-3-2\sqrt{3}+\sqrt{6}\\ \\ &⑦& (\sqrt{6}-9)(\sqrt{6}-7)\\ &=& (\sqrt{6})^2+(-9-7)\sqrt{6}+63\\ &=& 6-16\sqrt{6}+63\\ &=& 69-16\sqrt{6}\\ \\ &⑧& (2\sqrt{5}-1)(2\sqrt{5}-6)\\ &=& (2\sqrt{5})^2+(-1-6)2\sqrt{5}+6\\ &=& 20-14\sqrt{5}+6\\ &=& 26-14\sqrt{5}\\ \\ &⑨& (\sqrt{7}+2)^2\\ &=& (\sqrt{7})^2+2\cdot\sqrt{7}\cdot2+(2)^2\\ &=& 7+4\sqrt{7}+4\\ &=& 11+4\sqrt{7}\\ \\ &⑩& (2\sqrt{2}-3\sqrt{6})^2\\ &=& (2\sqrt{2})^2-2\cdot2\sqrt{2}\cdot3\sqrt{6}+(3\sqrt{6})^2\\ &=& 8-12\sqrt{12}+54\\ &=& 62-24\sqrt{3}\\ \\ &⑪& (\sqrt{2}+4)(\sqrt{2}-4)\\ &=& (\sqrt{2})^2-(4)^2\\ &=& 2-16\\ &=& -14\\ \\ &⑫& \left(\cfrac{\sqrt{15}}{3}+2\sqrt{2}\right)\left(\cfrac{\sqrt{15}}{3}-2\sqrt{2}\right)\\ &=& \left(\cfrac{\sqrt{15}}{3}\right)^2-(2\sqrt{2})^2\\ &=& \cfrac{15}{9}-8\\ &=& \cfrac{5}{3}-8\\ &=& \cfrac{5-24}{3}\\ &=& -\cfrac{19}{3}\\ \\ \end{eqnarray*}
「~のとき、~の値」の問題
(19) $x=4+2\sqrt{3}, \ y=4-2\sqrt{3}$ のとき、次①,②の式の値を求めなさい。
$\quad①\quad x^2-y^2 \qquad\qquad②\quad x^2-2xy+y^2$
答え
$①32\sqrt{3}$ $②48$
①まず、$x+y$ と $x-y$ を用意しておきます。
$x+y=4+2\sqrt{3}+4-2\sqrt{3}=8$
$x-y=4+2\sqrt{3}-(4-2\sqrt{3})=4+2\sqrt{3}-4+2\sqrt{3}=4\sqrt{3}$
問題の式を因数分解して代入していきます。
\begin{eqnarray*}
&&x^2-y^2\\
&=&(x+y)(x-y)\quad \class{mathbg-r}{(ここで代入する)} \\
&=&8\times4\sqrt{3}\\
&=&32\sqrt{3}
\end{eqnarray*}
②因数分解して代入します。
\begin{eqnarray*}
&&x^2-2xy+y^2\\
&=&(x-y)^2 \quad \class{mathbg-r}{(ここで代入する)} \\
&=&\{ (4+2\sqrt{3})-(4-2\sqrt{3}) \}^2\\
&=&(4+2\sqrt{3}-4+2\sqrt{3})^2\\
&=&(4\sqrt{3})^2\\
&=&48
\end{eqnarray*}
やり方が思いつかないときや、自信がないときは、単に代入して、がんばって計算すれば同じ答えがでます。
\begin{eqnarray*}
&①&x^2-y^2\\
&=&(4+2\sqrt{3})^2-(4-2\sqrt{3})^2\\
&=&16+16\sqrt{3}+12-(16-16\sqrt{3}+12)\\
&=&16+16\sqrt{3}+12-16+16\sqrt{3}-12\\
&=&32\sqrt{3}
\end{eqnarray*}
\begin{eqnarray*}
&②&x^2-2xy+y^2\\
&=&(4+2\sqrt{3})^2-2(4+2\sqrt{3})(4-2\sqrt{3})+(4-2\sqrt{3})^2\\
&=&16+16\sqrt{3}+12-2(16-12)+16-16\sqrt{3}+12\\
&=&16+12-8+16+12\\
&=&48
\end{eqnarray*}
できるだけ小さい整数にする
(20) 次①,②の問いに答えなさい。
① $\sqrt{132n}$ の値ができるだけ小さい整数になるときの、正の整数 $n$ の値を求めなさい。
② $\sqrt{\cfrac{150}{n}}$ の値ができるだけ小さい整数になるときの、正の整数 $n$ の値を求めなさい。
答え
$①33$ $②6$
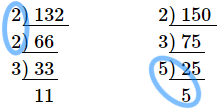 POINT
POINT
(6)の問題と同じようにやればOKです。
どちらの問題もやり方はおなじです。
手順1 素因数分解してください。
手順2 同じ数が$2$つあったら、そこに〇をつけてください。
手順3 〇がつかなかった数をかけてください。
その数が答えです。簡単なので、手順をおぼえましょう。
ちなみに、①は $132\times33=4356$ となって、$\sqrt{4356}=66$ です。
②は $150\div6=25$ となって、$\sqrt{25}=5$ です。
これの発展問題を、入試でわりと見ます。そちらはこんな甘いもんじゃないです。でも、そういうのを解けるようになるためにも、まずこの基本問題を確実にできるようにしておきましょう。
平方根の大小
(21) 次の①,②の不等式を満たす整数 $x$ をすべて求めなさい。
$$
① \quad 3 \ \lt\sqrt{x} \ \lt \ 3.5\qquad② \ 2\sqrt{6} \ \lt x \ \lt \ 5\sqrt{2}
$$
答え
$① x=10,11,12$ $② x=5,6,7$
$$正の数 \ a, \ b について、$$ $$\large{a\lt b\qquadならば\qquad\sqrt{a}\lt\sqrt{b}}$$
$\sqrt{ }$ のついている数とついていない数の大小は、$2$ 乗して比べましょう。根号は、$2$ 乗をすると消えます。そして、絶対値の大小関係は、$2$ 乗をしても変わりません。
\begin{eqnarray*}
① \ 3 \ &\lt&\sqrt{x} \ \lt \ 3.5\\
\ 3^2 \ &\lt&(\sqrt{x})^2 \ \lt \ 3.5^2\\
\ 9 \ &\lt& x \ \lt \ 12.25
\end{eqnarray*}
となるので、$x$ は $10,11,12$ です。
\begin{eqnarray*}
②2\sqrt{6} \ \lt x \ \lt \ 5\sqrt{2}\\
\ (2\sqrt{6})^2 \ &\lt&x^2 \ \lt \ (5\sqrt{2})^2\\
\ 24 \ &\lt& x^2 \ \lt \ 50
\end{eqnarray*}
となるので、$2$ 乗した数が $24$ と $50$ の間にあるのは $5,6,7$ です。
有理数と無理数
(22) 次の $ \boxed{\LARGE\phantom{hoge}}$ の中にあてはまる言葉をいれましょう。
① $0.1$ や $0.125$ などのように、終わりのある小数を $ \boxed{\LARGE\phantom{hogehoge}}$ という。
終わりがなく、どこまでもつづく小数を $ \boxed{\LARGE\phantom{hogehoge}}$ という。
$0.111111...$ や $0.123123123...$ のように、いくつかの数字が同じ順序でくり返し現れる無限小数を $ \boxed{\LARGE\phantom{hogehoge}}$ という。
② 有限小数や循環小数は分数で表すことができる。整数 $a$ と、$0$ でない整数 $b$ を使って、$\cfrac{a}{b}$ の形で表すことのできる数を $ \boxed{\LARGE\phantom{hogeho}}$ という。
有理数でない数を $ \boxed{\LARGE\phantom{hogeho}}$ という。$\sqrt{2}$ や $\pi$ のような、循環しない無限小数は $ \boxed{\LARGE\phantom{hogeho}}$ である。
答え
① $0.1$ や $0.125$ などのように、終わりのある小数を $ \boxed{有限小数}$ という。
終わりがなく、どこまでもつづく小数を $ \boxed{無限小数}$ という。
$0.111111...$ や $0.123123123...$ のように、いくつかの数字が同じ順序でくり返し現れる無限小数を $ \boxed{循環小数}$ という。
② 有限小数や循環小数は分数で表すことができる。整数 $a$ と、$0$ でない整数 $b$ を使って、$\cfrac{a}{b}$ の形で表すことのできる数を $ \boxed{有理数}$ という。
有理数でない数を $ \boxed{無理数}$ という。$\sqrt{2}$ や $\pi$ のような、循環しない無限小数は $ \boxed{無理数}$ である。
有理数と無理数
(23) 次の数を有理数と無理数に分けなさい。
$$
\quad \sqrt{200},\quad -3\sqrt{2},\quad 0.\dot36\dot9,\quad \pi,\quad \cfrac{1}{289},\quad\sqrt{10000}
$$
答え
有理数…$0.\dot36\dot9, \ \cfrac{1}{289}, \ \sqrt{10000}$
無理数…$\sqrt{200}, -3\sqrt{2}, \pi$
$\sqrt{10000}=100$
循環小数
(24) 次の①の分数を循環小数で表しなさい。②,③の循環小数を分数で表しなさい。
$$
① \ \cfrac{12}{13}\qquad② \ 0.\dot{6}\qquad③ \ 0.\dot{3}6\dot{9}
$$
答え
$①0.\dot{9}2307\dot{6}$ $②\cfrac{2}{3}$ $③\cfrac{41}{111}$
①割り算をして、どこが繰り返すかを確認すればOKです。
$$12\div12=0.92307692307692...$$
②小数第一位の数をくり返すときは、分母を $9$ にしておけばいいです。約分できるときは約分します。
③小数第一位から第三位までをくり返すときは、分母を $999$ にしておけばいいです。約分できるときは約分します。
$$\cfrac{369}{999}=\cfrac{41}{111}$$
答え(中3 2章 平方根 第3回)
(1)① $x^2=a$ となるとき、$x$ を $a$ の平方根という。正の数には平方根が $ \boxed{\large正と負}$ の $2$ つあり、絶対値は等しく、符号が異なる。
正の数 $a$ の $2$つの平方根を、記号 $\sqrt{ }$ を使って、 正のほうを$ \boxed{\large\sqrt{a}}$,負のほうを $ \boxed{\large-\sqrt{a}}$と表す。両方まとめて $ \boxed{\large\pm\sqrt{a}}$ と表す。
$\sqrt{ }$ を $ \boxed{\large根号}$ という。読み方は $ \boxed{\largeルート}$ 。
② $0$ の平方根は $ \boxed{\large0}$ である。
(2)①\pm1$ $②\pm4$ $③\pm7$ $④\pm12$ $⑤\pm\cfrac{2}{3}$ $⑥\pm0.5$ $⑦0$ $⑧ない$ $⑨ \pm\sqrt{17}$ $⑩ \pm\sqrt{0.9}$ $⑪ \pm\sqrt{\cfrac{3}{10}}$ $⑫ \pm\cfrac{8}{11}$
(3)$①× \ \pm4$ $②〇$ $③〇$ $④×\ 4$ $⑤〇$ $⑥× \ 4$
(4)$①5$ $②-\cfrac{6}{7}$ $③0.3$ $④256$
(5)① \sqrt{10}\gt \sqrt{9.9}$ $② 11\gt \sqrt{120}$ $③ -\sqrt{35} \gt -6$ $④ -\sqrt{10}\lt-3\lt-\sqrt{8}\lt\sqrt{8}\lt3\lt\sqrt{10}$
(6)$①2\times3\times5$ $②2^5\times5$
(7)$① 14$ $② 6$
(8)$①\sqrt{30}$ $②5\sqrt{6}$ $③6\sqrt{35}$ $④5\sqrt{6}$ $⑤\sqrt{7}$ $⑥9\sqrt{5}$ $⑦\cfrac{\sqrt{6}}{3}$ $⑧-5\sqrt{3}$
(9)$①\sqrt{90}$ $②\sqrt{\cfrac{ \ 7 \ }{ \ 8 \ }}$ $③\sqrt{\cfrac{ \ 18 \ }{ \ 5 \ }}$
(10)$①2\sqrt{6}$ $②5\sqrt{2}$ $③12\sqrt{2}$ $④18$
(11)$①22.36$ $②70.71$ $③0.2236$ $④0.07071$
(12)$①3\sqrt{2}$ $②4\sqrt{6}$ $③60\sqrt{2}$ $④8$ $⑤14\sqrt{6}$ $⑥75$ $⑦11\sqrt{3}$ $⑧13\sqrt{2}$ $⑨40\sqrt{6}$
(13)$①\cfrac{\sqrt{6}}{2}$ $②\cfrac{3\sqrt{5}}{5}$ $③\cfrac{\sqrt{10}}{2}$ $④\cfrac{\sqrt{10}}{20}$ $⑤3\sqrt{2}$ $⑥2\sqrt{2}$
(14)$①\cfrac{\sqrt{7}}{7}$ $②\sqrt{2}$ $③\cfrac{\sqrt{6}}{3}$
(15)$①\sqrt{2}$ $②\sqrt{14}$
(16)$①13\sqrt{3}$ $②4-\sqrt{11}$ $③-17\sqrt{2}+7\sqrt{3}$ $④\cfrac{\sqrt{5}}{4}$ $⑤\cfrac{13\sqrt{2}}{6}$
(17)$①-\sqrt{3}$ $②-21\sqrt{5}$ $③-12\sqrt{5}$ $④\cfrac{11\sqrt{2}}{2}$
(18)$①-2\sqrt{6}$ $②\cfrac{9\sqrt{2}}{2}$ $③10\sqrt{2}+6\sqrt{35}$ $④\cfrac{\sqrt{6}}{2}+6$ $⑤5\sqrt{3}-3\sqrt{5}+4\sqrt{15}-12$ $⑥3\sqrt{2}-3-2\sqrt{3}+\sqrt{6}$ $⑦69-16\sqrt{6}$ $⑧26-14\sqrt{5}$ $⑨11+4\sqrt{7}$ $⑩62-24\sqrt{3}$ $⑪-14$ $⑫-\cfrac{19}{3}$
(19)$①32\sqrt{3}$ $②48$
(20)$①33$ $②6$
(21)$① x=10,11,12$ $② x=5,6,7$
(22)① $0.1$ や $0.125$ などのように、終わりのある小数を $ \boxed{有限小数}$ という。
終わりがなく、どこまでもつづく小数を $ \boxed{無限小数}$ という。
$0.111111...$ や $0.123123123...$ のように、いくつかの数字が同じ順序でくり返し現れる無限小数を $ \boxed{循環小数}$ という。
② 有限小数や循環小数は分数で表すことができる。整数 $a$ と、$0$ でない整数 $b$ を使って、$\cfrac{a}{b}$ の形で表すことのできる数を $ \boxed{有理数}$ という。
有理数でない数を $ \boxed{無理数}$ という。$\sqrt{2}$ や $\pi$ のような、循環しない無限小数は $ \boxed{無理数}$ である。
(23)有理数…$0.\dot36\dot9, \ \cfrac{1}{289}, \ \sqrt{10000}$
無理数…$\sqrt{200}, -3\sqrt{2}, \pi$
(24)$①0.\dot{9}2307\dot{6}$ $②\cfrac{2}{3}$ $③\cfrac{41}{111}$