数学 中3 3章 $2$ 次方程式 第2回)
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
$2$ 次方程式
(1) 次の $ \boxed{\LARGE\phantom{hoge}}$ の中にあてはまる言葉をいれましょう。
$ax^2+bx+c=0$ の形になる方程式を、$2$ 次方程式という。$2$ 次方程式を成り立たせる文字の値を $ \boxed{\LARGE\phantom{ho}}$ といい、すべての解を求めることを $2$ 次方程式を $ \boxed{\LARGE\phantom{hoge}}$ という。
答え
$ax^2+bx+c=0$ の形になる方程式を、$2$ 次方程式という。$2$ 次方程式を成り立たせる文字の値を $ \boxed{解}$ といい、すべての解を求めることを $2$ 次方程式を $ \boxed{解く}$ という。
(2) 次のア~カの方程式の中から、$2$ 次方程式であるものをすべて選びなさい。
\begin{eqnarray*}
&ア& \quad 3x+15=0&イ& \quad 4x^2=2\\\\
&ウ& \quad x^2+3x-1=8+x^2 \quad &エ& \quad x^2-4x+6=\cfrac{1}{2}x^2\\\\
&オ& \quad (x+1)^2=x^2+3x+2\quad&カ& \quad (x+10)(x-9)=0
\end{eqnarray*}
答え
イ,エ,カ
すべてを左辺に移項して($=0$ の形にして)整理したとき、$x^2$ があるものが $2$ 次方程式だと思っちゃっていいです。文字は $x$ でなくちゃいけないのかというと、もちろんそんなことはありません。ナントカの $2$ 乗があれば、それはナントカの $2$ 次方程式です。
アは $1$ 次方程式です。ウはすべてを左辺に移項して整理すると $3x-9=0$ となり、$x^2$ がなくなってしまいます。オもすべてを左辺に移項して整理すると $-x-1=0$ となり、$x^2$ が消えてしまいます。カは展開すると $x^2+x-90=0$ となります。
(3) 次のア~エの $2$ 次方程式のうち、$-3$ と $-5$ がともに解であるものを選びなさい。 \begin{eqnarray*} &ア& \quad x^2-2x-15=0\qquad&イ& \quad x^2+2x-15=0\\\\ &ウ& \quad x^2+8x+15=0&エ& \quad x^2-8x+15=0\\\\ \end{eqnarray*}
答え
ウ
$x$ に $-3$ と $-5$ を代入して、どちらも成り立つ式を選べばいいです。
アは $x=-3$ のときは成り立ちますが、$x=-5$ のとき成り立ちません。
イも $x=-5$ のときは成り立ちますが、$x=-3$ のとき成り立ちません。
ウは $x=-3$ のとき $(-3)^2+8\times(-3)+15=0,$ $x=-5$ のとき $(-5)^2+8\times(-5)+15=0$ となり、どちらも成り立っています。
エは $x=-3$ のときも $x=-5$ のときもどちらも成り立ちません。
(4) 次の①~④の $2$ 次方程式を解きなさい。 \begin{eqnarray*} &①& \quad (x-6)(x+8)=0\qquad&②& \quad (x-10)(x-12)=0\\\\ &③& \quad \left( x+\cfrac{1}{3}\right) \left(x-\cfrac{2}{5}\right)=0&④& \quad (3x+2)(4x-3)=0 \end{eqnarray*}
答え
$①x=6, \ x=-8$ $②x=10, \ x=12$ $③x=-\cfrac{1}{3}, \ x=\cfrac{2}{5}$ $④x=-\cfrac{2}{3}, \ x=\cfrac{3}{4}$
$$\large{AB=0ならば\qquad A=0\quadまたは\quad B=0}$$
問題の式はどれも、左辺を展開すると $x^2$ がでてきますよね。なので $2$ 次方程式です。
んで、かっこの中が $0$ になる数が解です。
④は、$3x+2=0$ と $4x-3=0$ を解いてるわけですが、
「$ax+b$ の形のときは、$-\cfrac{b}{a}$ が解」だと思っちゃうと速いです。符号を逆にするのを忘れずに。
$2$ 次方程式の解き方 ①
(5) 次の $2$ 次方程式を解きなさい。
$$
x^2-8x+7=0
$$
答え
$x=1, \ x=7$
これから $2$ 次方程式の解き方について説明していきます。$2$ 次方程式は、式の形とか条件によって、解き方を使い分けていきます。「こういうときはこう解く」、というふうにパターンをおぼえていきましょう。
基本的に、右辺は「$=0$」になっているようにしましょう。(8)番と(9)番の問題はちがいますが、それ以外はみんな「$=0$」になっています。
解は $2$つでてきます。(7)番の問題だけはちがいますが、それ以外はみんな $2$つでてきます。
ではまずさいしょのパターンの解き方です。
$x^2+5x-6=0$ のような式は、かっこかっこの形に因数分解して解きます。かっこの中を $0$ にする数が解です。
\begin{eqnarray*}
x^2-8x+7&=&0\\
(x-1)(x-7)&=&0\\
x&=&1, \ x=7
\end{eqnarray*}
$2$ 次方程式の解き方 ②
(6) 次の $2$ 次方程式を解きなさい。
$$
x^2-6x=0
$$
答え
$x=0, \ x=6$
$x^2-6x=0$ のような式は、$x$ でくくります。くくったときは、解の $1$ つはかならず $0$ です。もう $1$ つは、かっこの中を $0$ にする数です。 \begin{eqnarray*} x^2-6x&=&0\\ x(x-6)&=&0\\ x&=&0, \ x=6 \end{eqnarray*} くくったときに、かっこの中の $x$ に係数がついているときがあります。そういうときはアレです。「$ax+b$ の形のときは、$-\cfrac{b}{a}$ が解」です。以下、その例です。 \begin{eqnarray*} 3x^2+5x&=&0\\ x(3x+5)&=&0\\ x&=&0, \ x=-\cfrac{5}{3} \end{eqnarray*} ちなみに、かっこの外の $x$ に係数がついているときは、それは気にせんでいいです。 \begin{eqnarray*} 3x(x+2)&=&0\\ x&=&0, \ x=-2 \end{eqnarray*}
$2$ 次方程式の解き方 ③
(7) 次の $2$ 次方程式を解きなさい。
$$
x^2+10x+25=0
$$
答え
$x=-5$
因数分解したときに、「かっこの $2$ 乗 $=0$」の形になるときがあります。この場合は、解は $1$ つしかかかないことになります。こういうときの解を「重解」といいます。 \begin{eqnarray*} x^2+10x+25&=&0\\ (x+5)^2&=&0\\ x&=&-5 \end{eqnarray*}
$2$ 次方程式の解き方 ④
(8) 次の $2$ 次方程式を解きなさい。
$$
x^2=36
$$
答え
$x=\pm6$
$x^2=36$ のような形のときは、こういうときは「$=0$」の形にせず、この形のまま、次の行で $x^2$ の $2$ 乗をとってしまい、右辺を $\pm\sqrt{ }$ の中にいれてしまいます。「$2$ 乗をとってプラスマイナスルート」です。んで、そのあとは、もしルートがなおせるときはなおしたり、分母にルートがあるときは分母の有理化をしたりします。
\begin{eqnarray*}
x^2&=&36\\
x&=&\pm\sqrt{36}\quad \class{mathbg-r}{(2乗をとってプラスマイナスルート)}\\
&=&\pm6
\end{eqnarray*}
$x=\pm6$ というのは、$x=6, \ x=-6$ とかいてもOKです。おなじことです。
このやり方でやるときに注意が必要なのは、左辺は $x^2$ にしておこう、ということです。係数がついていたら、「$2$ 乗をとってプラスマイナスルート」はやめておいたほうがぶなんです。なにかついているときは、それをなくしてから $2$ 乗をとりましょう。以下、その例です。
\begin{eqnarray*}
5x^2&=&36\quad \class{mathbg-r}{(x^2に5がついているので、ここでは2乗はとらない)}\\
x^2&=&\cfrac{36}{5}\quad \class{mathbg-r}{(こうしてから2乗をとろう)}\\
x&=&\pm\sqrt{\cfrac{36}{5}}\quad \class{mathbg-r}{(2乗をとってプラスマイナスルート)}\\
&=&\pm\cfrac{\sqrt{36}}{\sqrt{5}}=\pm\cfrac{6}{\sqrt{5}}=\pm\cfrac{6\sqrt{5}}{5}
\end{eqnarray*}
あとちなみに $x^2=36$ については、「$=0$」の形からかっこかっこに因数分解することにして、
\begin{eqnarray*}
x^2&=&36\\
x^2-36&=&0\\
(x+6)(x-6)&=&0\\
x&=&-6, \ x=6
\end{eqnarray*}
まあ、こんなふうにしてやるのもアリっちゃアリです。答え、おんなじです。でもこれはおすすめしません。
$2$ 次方程式の解き方 ⑤
(9) 次の $2$ 次方程式を解きなさい。
$$
(x-5)^2=12
$$
答え
$x=5\pm2\sqrt{3}$
この形、でおぼえてください。この形、というのは、$a(x+b)^2=c$ の形です。これは展開して整理しないでください。「$2$ 乗をとってプラスマイナスルート」でやってください。でないとひどい目にあうことがあります。 \begin{eqnarray*} (x-5)^2&=&12\\ x-5&=&\pm\sqrt{12}\quad \class{mathbg-r}{(2乗をとってプラスマイナスルート)}\\ x-5&=&\pm2\sqrt{3}\\ x&=&5\pm2\sqrt{3}\\ \end{eqnarray*}
$2$ 次方程式の解き方 ⑥
(10) 次の $2$ 次方程式を解きなさい。
$$
x^2+8x+6=0
$$
答え
$x=-4\pm\sqrt{10}$
$$2次方程式ax^2+bx+c=0の解は$$ $$\qquad\large{ x=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}}$$
かっこかっこの形に因数分解したいのですが、どうにもなりません。ムリです。そういうときは$2$ 次方程式の解の公式です。
$x^2+8x+6=0$ なので、
$a=1, \ b=8, \ c=6$ として、解の公式にあてはめると、
\begin{eqnarray*}
\require{cancel}
x&=&\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\
&=&\cfrac{-8\pm\sqrt{8^2-4\cdot1\cdot6}}{2\cdot1}\\
&=&\cfrac{-8\pm\sqrt{64-24}}{2}\\
&=&\cfrac{-8\pm\sqrt{40}}{2}\\
&=&\cfrac{-8\pm2\sqrt{10}}{2}\\
&=&\cfrac{-\bcancel{8}\pm\bcancel{2}\sqrt{10}}{\bcancel{2}}\\
&=&-4\pm\sqrt{10}
\end{eqnarray*}
解の公式のよいところは、$x=$ ではじまるところ。最後まで計算したら、それが解です。ルートがなおせるときはなおして、ルートがなおせたときは約分できることがあるので、できるときはしましょう。
約分についてですが、たとえば、
$$\cfrac{9\pm5\sqrt{2}}{6}$$
こういうのは約分できません。$9$ と $5$ と $6$ はいっぺんに割れないからです。なのでここでやめてOKです。それから、
$$\cfrac{9\pm\sqrt{2}}{6}$$
こういうのも約分しちゃダメです。これでやめてください。そんで、
$$\cfrac{9\pm3\sqrt{2}}{6}=\cfrac{\bcancel{9}\pm\bcancel{3}\sqrt{2}}{\bcancel{6}}=\cfrac{3\pm\sqrt{2}}{2}$$
こういうときが約分できます。$9$ と $3$ と $6$ は $3$ で割れます。約分してください。約分できるのにしてないと、それはそれでバツになります。
$2$ 次方程式の解の公式は、どんな形で問題がでても、$ax^2+bx+c=0$ の形にすればみんな解けます。オールマイティーです。$x^2+2x=0$ だったら、$a=1, \ b=2, \ c=0$ だということでいけます。あと、$x^2=5$ とかだったら、$x^2-5=0$ にして、$a=1, \ b=0, \ c=-5$ ということでいけます。
でも、$2$ 次方程式の解の公式は、最後の手段です。因数分解や、$2$ 乗をとってプラスマイナスルートってやれば解けるときに、解の公式をやっちゃいけません。めんどくさいからです。以下、因数分解できるのに、解の公式でやるとどうなるかの例をしめします。
\begin{eqnarray*}
&x^2&+x-2=0\quad を解く\\
\\
&解&の公式&因&数分解\\
x&=&\cfrac{-1\pm\sqrt{1^2-4\cdot1\cdot(-2)}}{2\cdot1}\quad&&(x-1)(x+2)=0\\
&=&\cfrac{-1\pm\sqrt{1+8}}{2}&&x=1, \ x=-2\\
&=&\cfrac{-1\pm\sqrt{9}}{2}\\
&=&\cfrac{-1\pm3}{2}\\
&=&\cfrac{-1+3}{2}, \ \cfrac{-1-3}{2}\\
x&=&1, \ x=-2
\end{eqnarray*}
というわけで同じ解がでてきますが、こういうのは解の公式でやっちゃいけません。めんどうくさいです。時間がかかるし、ミスする可能性が高くなります。因数分解できるときは因数分解しましょう。解の公式は最後の手段。どうにもならないときに使ってください。
いろいろな $2$ 次方程式 パート1
(11) 次の $2$次方程式を解きなさい。
\begin{eqnarray*}
&①& \ x^2=50 &②& \ x^2-12x=0\\\\
&③& \ x^2-4x-45=0 &④& \ x^2-121=0\\\\
&⑤& \ x^2-18x+81=0 &⑥& \ -x^2+5x+6=0 \\\\
&⑦& \ 7x^2+2x-20=5(x+1)^2+17 \qquad &⑧& \ (x-10)^2=72\\\\
&⑨& \ x^2-4x+2=0 &⑩& \ 2x^2-5x-3=0
\end{eqnarray*}
答え
$①x=\pm5\sqrt{2}$ $②x=0, \ x=12$ $③x=9, \ x=-5$ $④x=\pm11$ $⑤x=9$ $⑥x=6, \ x=-1$ $⑦x=7, \ x=-3$ $⑧x=10\pm6\sqrt{2}$ $⑨x=2\pm\sqrt{2}$ $⑩x=3, \ x=-\cfrac{1}{2}$
これから $2$ 次方程式の解き方について説明していきます。$2$ 次方程式は、式の形とか条件によって、解き方を使い分けていきます。「こういうときはこう解く」、というふうにパターンをおぼえていきましょう。
基本的に、右辺は「$=0$」になっているようにしましょう。①番④番⑧番の問題はちがいますが、それ以外はみんな「$=0$」になっています。
解は $2$つでてきます。⑤番の問題だけはちがいますが、それ以外はみんな $2$つでてきます。
\begin{eqnarray*}
①
x^2&=&50\quad \class{mathbg-r}{(2乗をとってプラスマイナスルート)}\\
x&=&\pm\sqrt{50}=\pm5\sqrt{2}\\
\end{eqnarray*}
\begin{eqnarray*}
②
x^2-12x&=&0\quad \class{mathbg-r}{(くくる)}\\
x(x-12)&=&0\\
x&=&0, \ x=12\\
\end{eqnarray*}
\begin{eqnarray*}
③
x^2-4x-45&=&0\quad \class{mathbg-r}{(因数分解する)}\\
(x-9)(x+5)&=&0\\
x&=&9, \ x=-5\\
\end{eqnarray*}
\begin{eqnarray*}
④
x^2-121&=&0\\
x^2&=&121\quad \class{mathbg-r}{(2乗をとってプラスマイナスルート)}\\
x&=&\pm\sqrt{121}=\pm11\\
\end{eqnarray*}
\begin{eqnarray*}
⑤
x^2-18x+81&=&0\quad \class{mathbg-r}{(因数分解する)}\\
(x-9)^2&=&0\\
x&=&9\quad \class{mathbg-r}{(重解)}\\
\end{eqnarray*}
\begin{eqnarray*}
⑥
-x^2+5x+6&=&0\quad \class{mathbg-r}{(両辺に\times-1)}\\
x^2-5x-6&=&0\quad \class{mathbg-r}{(因数分解する)}\\
(x-6)(x+1)&=&0\\
x&=&6, \ x=-1\\
\end{eqnarray*}
⑥$-x^2+5x+6=0$ のように、$x^2$ のまえになにかあるときは、それを消すことを考えましょう。この場合は、両辺に $-1$ をかければOKです。
\begin{eqnarray*}
⑦
7x^2+2x-20=5(x+1)^2&+&17\quad \class{mathbg-r}{(展開する)}\\
7x^2+2x-20=5(x^2+2x+1)&+&17\quad \class{mathbg-r}{(展開する)}\\
7x^2+2x-20=5x^2+10x+5&+&17\quad \class{mathbg-r}{(=0にする)}\\
7x^2+2x-20-5x^2-10x-22&=&0\quad \class{mathbg-r}{(整理する)}\\
2x^2-8x-42&=&0\quad \class{mathbg-r}{(両辺を2で割る)}\\
x^2-4x-21&=&0\quad \class{mathbg-r}{(因数分解する)}\\
(x-7)(x+3)&=&0\\
x&=&7, \ x=-3\\
\end{eqnarray*}
⑦ごちゃごちゃしてる$2$ 次方程式は、$=0$ の形にしましょう。展開や整理もして、それからやり方を考えましょう。
\begin{eqnarray*}
⑧
(x-10)^2&=&72\quad \class{mathbg-r}{(2乗をとってプラスマイナスルート)}\\
x-10&=&\pm\sqrt{72}=\pm6\sqrt{2}\\
x&=&10\pm6\sqrt{2}
\end{eqnarray*}
\begin{eqnarray*}
⑨\quad
&x^2&-4x+2=0\quad \class{mathbg-r}{(2次方程式の解の公式)}\\
x&=&\cfrac{-(-4)\pm\sqrt{(-4)^2-4\cdot1\cdot2}}{2\cdot1}\\
&=&\cfrac{4\pm\sqrt{16-8}}{2}\\
&=&\cfrac{4\pm\sqrt{8}}{2}\\
&=&\cfrac{4\pm2\sqrt{2}}{2}\\
&=&\cfrac{\bcancel{4}\pm\bcancel{2}\sqrt{2}}{\bcancel{2}}\\
&=&2\pm\sqrt{2}
\end{eqnarray*}
\begin{eqnarray*}
⑩\quad
&2&x^2-5x-3=0\quad \class{mathbg-r}{(2次方程式の解の公式)}\\
x&=&\cfrac{-(-5)\pm\sqrt{(-5)^2-4\cdot2\cdot(-3)}}{2\cdot2}\\
&=&\cfrac{5\pm\sqrt{25+24}}{4}\\
&=&\cfrac{5\pm\sqrt{49}}{4}\\
&=&\cfrac{5\pm7}{4}\\
&=&\cfrac{12}{4}, \ \cfrac{-2}{4}\\
x&=&3, \ x=-\cfrac{1}{2}
\end{eqnarray*}
⑩$x^2$ に係数がついているのですが、これを消そうとすると、かえってややこしいことになってしまいます。なのでこのままでやります。因数分解を思いつくならしてください。そのほうが速いしラクです。思いつかないときは、$2$ 次方程式の解の公式です。
解の公式を使ったときに、ルートが消えてしまうことがあります。このときは、足したときと引いたときの両方をそれぞれ計算して答えるようにしましょう。
いろいろな $2$ 次方程式 パート2
(12) 次の $2$次方程式を解きなさい。
\begin{eqnarray*}
&①& \ x^2=\cfrac{3}{5} &②& \ 2x^2+15x=0\\\\
&③& \ x^2+20x+36=0 &④& \ x^2-144=0\\\\
&⑤& \ 25x^2+30x+9=0 &⑥& \ 3x^2+9x-54=0 \\\\
&⑦& \ (x-1)^2=3(x+1)^2+4 \qquad &⑧& \ (x-8)^2=18\\\\
&⑨& \ x^2-6x-6=0 &⑩& \ 6x^2-5x-6=0
\end{eqnarray*}
答え
$①x=\pm\cfrac{\sqrt{15}}{5}$ $②x=0, \ x=-\cfrac{15}{2}$ $③x=-18, \ x=-2$ $④x=\pm12$ $⑤x=-\cfrac{3}{5}$ $⑥x=-6, \ x=3$ $⑦x=-1, \ x=-3$ $⑧x=8\pm3\sqrt{2}$ $⑨x=3\pm\sqrt{15}$ $⑩x=\cfrac{3}{2}, \ x=-\cfrac{2}{3}$
これから $2$ 次方程式の解き方について説明していきます。$2$ 次方程式は、式の形とか条件によって、解き方を使い分けていきます。「こういうときはこう解く」、というふうにパターンをおぼえていきましょう。
基本的に、右辺は「$=0$」になっているようにしましょう。①番④番⑧番の問題はちがいますが、それ以外はみんな「$=0$」になっています。
解は $2$つでてきます。⑤番の問題だけはちがいますが、それ以外はみんな $2$つでてきます。
\begin{eqnarray*}
①
x^2&=&\cfrac{3}{5}\quad \class{mathbg-r}{(2乗をとってプラスマイナスルート)}\\
x&=&\pm\sqrt{\cfrac{3}{5}}=\pm\cfrac{\sqrt{3}}{\sqrt{5}}=\pm\cfrac{\sqrt{15}}{5}\\
\end{eqnarray*}
\begin{eqnarray*}
②
2x^2+15x&=&0\quad \class{mathbg-r}{(くくる)}\\
x(2x+15)&=&0\\
x&=&0, \ x=-\cfrac{15}{2}\\
\end{eqnarray*}
\begin{eqnarray*}
③
x^2+20x+36&=&0\quad \class{mathbg-r}{(因数分解する)}\\
(x+18)(x+2)&=&0\\
x&=&-18, \ x=-2\\
\end{eqnarray*}
\begin{eqnarray*}
④
x^2-144&=&0\\
x^2&=&144\quad \class{mathbg-r}{(2乗をとってプラスマイナスルート)}\\
x&=&\pm\sqrt{144}=\pm12\\
\end{eqnarray*}
\begin{eqnarray*}
⑤
25x^2+30x+9&=&0\quad \class{mathbg-r}{(因数分解する)}\\
(5x+3)^2&=&0\\
x&=&-\cfrac{3}{5}\quad \class{mathbg-r}{(重解)}\\
\end{eqnarray*}
\begin{eqnarray*}
⑥
3x^2+9x-54&=&0\quad \class{mathbg-r}{(両辺を3で割る)}\\
x^2+3x-18&=&0\quad \class{mathbg-r}{(因数分解する)}\\
(x+6)(x-3)&=&0\\
x&=&-6, \ x=3\\
\end{eqnarray*}
⑥$3x^2+9x-54=0$ のように、$x^2$ のまえになにかあるときは、それを消すことを考えましょう。この場合は、両辺を $3$ で割ればOKです。
\begin{eqnarray*}
⑦
(x-1)^2=3(x+1)^2+4&&\quad \class{mathbg-r}{(展開する)}\\
x^2-2x+1=3(x^2+2x+1)+4&&\quad \class{mathbg-r}{(展開する)}\\
x^2-2x+1=3x^2+6x+3+4&&\quad \class{mathbg-r}{(=0にする)}\\
x^2-2x+1-3x^2-6x-3-4=0&&\quad \class{mathbg-r}{(整理する)}\\
-2x^2-8x-6=0&&\quad \class{mathbg-r}{(両辺を-2で割る)}\\
x^2+4x+3=0&&\quad \class{mathbg-r}{(因数分解する)}\\
(x+1)(x+3)=0&&\\
x=-1, \ x=-3&&
\end{eqnarray*}
⑦ごちゃごちゃしてる$2$ 次方程式は、$=0$ の形にしましょう。展開や整理もして、それからやり方を考えましょう。
\begin{eqnarray*}
⑧
(x-8)^2&=&18\quad \class{mathbg-r}{(2乗をとってプラスマイナスルート)}\\
x-8&=&\pm\sqrt{18}=\pm3\sqrt{2}\\
x&=&8\pm3\sqrt{2}
\end{eqnarray*}
\begin{eqnarray*}
⑨\quad
&x^2&-6x-6=0\quad \class{mathbg-r}{(2次方程式の解の公式)}\\
x&=&\cfrac{-(-6)\pm\sqrt{(-6)^2-4\cdot1\cdot(-6)}}{2\cdot1}\\
&=&\cfrac{6\pm\sqrt{36+24}}{2}\\
&=&\cfrac{6\pm\sqrt{60}}{2}\\
&=&\cfrac{6\pm2\sqrt{15}}{2}\\
&=&\cfrac{\bcancel{6}\pm\bcancel{2}\sqrt{15}}{\bcancel{2}}\\
&=&3\pm\sqrt{15}
\end{eqnarray*}
\begin{eqnarray*}
⑩\quad
&&6x^2-5x-6=0\quad \class{mathbg-r}{(2次方程式の解の公式)}\\
x&=&\cfrac{-(-5)\pm\sqrt{(-5)^2-4\cdot6\cdot(-6)}}{2\cdot6}\\
&=&\cfrac{5\pm\sqrt{25+144}}{12}\\
&=&\cfrac{5\pm\sqrt{169}}{12}\\
&=&\cfrac{5\pm13}{12}\\
&=&\cfrac{18}{12}, \ \cfrac{-8}{12}\\
x&=&\cfrac{3}{2}, \ x=-\cfrac{2}{3}
\end{eqnarray*}
⑩$x^2$ に係数がついているのですが、これを消そうとすると、かえってややこしいことになってしまいます。なのでこのままでやります。因数分解を思いつくならしてください。そのほうが速いしラクです。思いつかないときは、$2$ 次方程式の解の公式です。
解の公式を使ったときに、ルートが消えてしまうことがあります。このときは、足したときと引いたときの両方をそれぞれ計算して答えるようにしましょう。
平方完成
(13) 次の①,②の $2$ 次方程式を、$(x+a)^2=b$ の形になおして解きなさい。計算の過程もかくこと。
$$
①x^2+10x=-5\qquad\quad②x^2-5x=1
$$
答え
\begin{eqnarray*}
①
x^2+10x&=&-5\\
x^2+10x+25&=&-5+25\\
(x+5)^2&=&20\\
x+5&=&\pm\sqrt{20}=\pm2\sqrt{5}\\
x&=&-5\pm2\sqrt{5}\\
\end{eqnarray*}
\begin{eqnarray*}
②
x^2-5x&=&1\\
x^2-5x+\cfrac{25}{4}&=&1+\cfrac{25}{4}\\
\left(x-\cfrac{5}{2}\right)^2&=&\cfrac{29}{4}\\
x-\cfrac{5}{2}&=&\pm\sqrt{\cfrac{29}{4}}=\pm\cfrac{\sqrt{29}}{\sqrt{4}}=\pm\cfrac{\sqrt{29}}{2}\\
x&=&\cfrac{5}{2}\pm\cfrac{\sqrt{29}}{2}\\
\end{eqnarray*}
「$2$ 乗をとってプラスマイナスルート」の考え方を利用して、左辺をかっこの $2$ 乗の形にして解く、という $2$ 次方程式の解き方があります。「平方完成する」とか「完全平方の形にする」とかいいます。
中学では平方完成を利用する機会があまりないのですが、$2$ 次方程式について教わった直後のテストでは、このことについて出題されることが多いので、理解しておきましょう。
ポイントは、「$x$ の項の係数を $2$ で割って $2$乗 した数を両辺に加える」ということです。①は $x$ の係数は $10$ ですから、これをを $2$ で割って $2$乗 すると $25$ になります。この数を両辺に加えると、左辺は因数分解できることになって、しかもかっこの $2$ 乗になってくれます。これでうまくいくわけです。
\begin{eqnarray*}
①
x^2+10x&=&-5\\
&&\class{mathbg-r}{(x の係数を2で割って2乗した数を両辺に加える)}\\
x^2+10x+25&=&-5+25\\
(x+5)^2&=&20\\
x+5&=&\pm\sqrt{20}\quad \class{mathbg-r}{(2乗をとってプラスマイナスルート)}\\
x&=&-5\pm2\sqrt{5}\\
\end{eqnarray*}
②もやり方はおなじですが、$x$ の項の係数が奇数のときは分数になるので、計算がとたんにめんどうくさくなってしまいます。
\begin{eqnarray*}
②
x^2-5x&=&1\\
&&\class{mathbg-r}{(x の係数を2で割って2乗した数を両辺に加える)}\\
x^2-5x+\cfrac{25}{4}&=&1+\cfrac{25}{4}\\
\left(x-\cfrac{5}{2}\right)^2&=&\cfrac{29}{4}\quad \class{mathbg-r}{(2乗をとってプラスマイナスルート)}\\
x-\cfrac{5}{2}&=&\pm\sqrt{\cfrac{29}{4}}=\pm\cfrac{\sqrt{29}}{\sqrt{4}}=\pm\cfrac{\sqrt{29}}{2}\\
x&=&\cfrac{5}{2}\pm\cfrac{\sqrt{29}}{2}\\
\end{eqnarray*}
$2$ 次方程式の利用
(14) ある正の整数を $2$ 乗するところを、あやまって $2$ 倍しために、計算の結果が $99$ 小さくなった。ある正の整数を求めなさい。
答え
$11$
ある正の整数を $x$ として、問題文のように式をたてて解きます。
\begin{eqnarray*}
x^2&=&2x+99\\
x^2-2x-99&=&0\\
(x-11)(x+9)&=&0\\
x&=&11, \ x=-9
\end{eqnarray*}
ここで注意が必要です。正の整数を求めなさい、というのですから、$-9$ というのは、問題の答えとしてはいけません。ということで、答えは
$$11$$
このように、$2$ 次方程式の文章題は、答えが $2$ 通りあって、そのうちのかたほうしか答えてはいけない、ということがよくあります。解を求めたあと、答えとしてよいのかどうかをしっかり確認するようにしましょう。
(15) 連続する $3$ つの自然数がある。まん中の数の $2$ 乗は、残りの $2$ つの数の和の $8$ 倍より $15$ 小さい。この連続する $3$ つの自然数を求めなさい。
答え
$14, \ 15, \ 16$
連続する $3$ つの自然数を、$x-1, \ x, \ x+1$ とします。もちろんほかにも表せますが、今回はそういうことにしてやっていきましょう。
まん中の数の $2$ 乗というのは、$x^2$ です。
残りの $2$ つの数の和の $8$ 倍より $15$ 小さい数というのは、
$(x-1+x+1)\times8-15$ と表せます。
ということで、式をたてて解きます。
\begin{eqnarray*}
x^2&=&8(x-1+x+1)-15\\
x^2&=&16x-15\\
x^2-16x+15&=&0\\
(x-15)(x-1)&=&0\\
x&=&15, \ x=1
\end{eqnarray*}
連続する $3$ つの自然数のうち、まん中の数を $x$ としているのですから、この連続する $3$ つの自然数は、$14, \ 15, \ 16$ と、$0, \ 1, \ 2$ ということになります。ここで注意が必要です。自然数というのは、$1$ からはじまります。$0$ は自然数にははいりません。なので、$0, \ 1, \ 2$ というのは、「連続する $3$ つの自然数」とはいえません。問題の答えとしてはいけません。ということで、答えは
$$14, \ 15, \ 16$$
このように、$2$ 次方程式の文章題は、答えが $2$ 通りあって、そのうちのかたほうしか答えてはいけない、ということがよくあります。解を求めたあと、答えとしてよいのかどうかをしっかり確認するようにしましょう。

(16) 縦が $20m$,横が $22m$ の長方形の土地がある。この土地に、右の図のように、縦と横に垂直になるように、幅の等しい $2$ 本の道をつくり、道をのぞいた土地の面積が $360m^2$ になるようにしたい。道幅は何$m$ にしたらよいか。
答え
$2m$
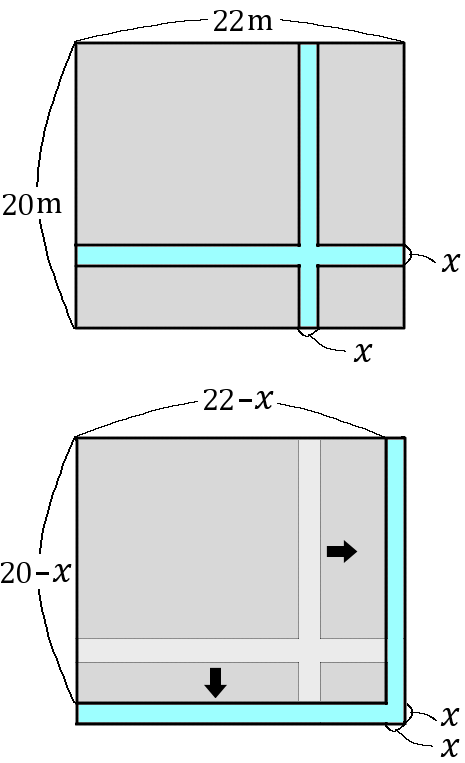 道幅を $xm$ ということにします。そして、下の図のように、道を右と下にぴったりよせてしまいます。これがこの問題の古来からの由緒正しいやり方なので、まあ、よせておきましょう。すると縦の長さは$(20-x)m,$ 横の長さは $(22-x)m$ ということになります。道をのぞいた土地の面積を $360m^2$ にしたい、というのですから、
\begin{eqnarray*}
(20-x)(22-x)&=&360\\
440-42x+x^2-360&=&0\\
x^2-42x+80&=&0\\
(x-40)(x-2)&=&0\\
x&=&40, \ x=2
\end{eqnarray*}
道幅を $xm$ ということにして式をたてて、$x$ が求められましたが、ここで注意が必要です。土地は縦が $20m$,横が $22m$ なのですから、ここに幅が $40m$ の道はつくれません。なのでこれは答えてはいけません。ということで、答えは
道幅を $xm$ ということにします。そして、下の図のように、道を右と下にぴったりよせてしまいます。これがこの問題の古来からの由緒正しいやり方なので、まあ、よせておきましょう。すると縦の長さは$(20-x)m,$ 横の長さは $(22-x)m$ ということになります。道をのぞいた土地の面積を $360m^2$ にしたい、というのですから、
\begin{eqnarray*}
(20-x)(22-x)&=&360\\
440-42x+x^2-360&=&0\\
x^2-42x+80&=&0\\
(x-40)(x-2)&=&0\\
x&=&40, \ x=2
\end{eqnarray*}
道幅を $xm$ ということにして式をたてて、$x$ が求められましたが、ここで注意が必要です。土地は縦が $20m$,横が $22m$ なのですから、ここに幅が $40m$ の道はつくれません。なのでこれは答えてはいけません。ということで、答えは
$$2m$$
このように、$2$ 次方程式の文章題は、答えが $2$ 通りあって、そのうちのかたほうしか答えてはいけない、ということがよくあります。解を求めたあと、答えとしてよいのかどうかをしっかり確認するようにしましょう。
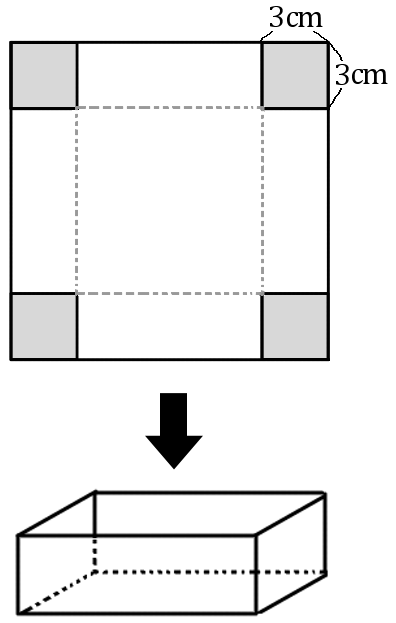 (17) 正方形の紙の四すみから、右の図のように、$1$ 辺が $3cm$ の正方形を切り取って箱をつくる。箱の容積が $588cm^3$ のとき、もとの正方形の紙の $1$ 辺の長さは何$cm$ だったか。
(17) 正方形の紙の四すみから、右の図のように、$1$ 辺が $3cm$ の正方形を切り取って箱をつくる。箱の容積が $588cm^3$ のとき、もとの正方形の紙の $1$ 辺の長さは何$cm$ だったか。
答え
$20cm$
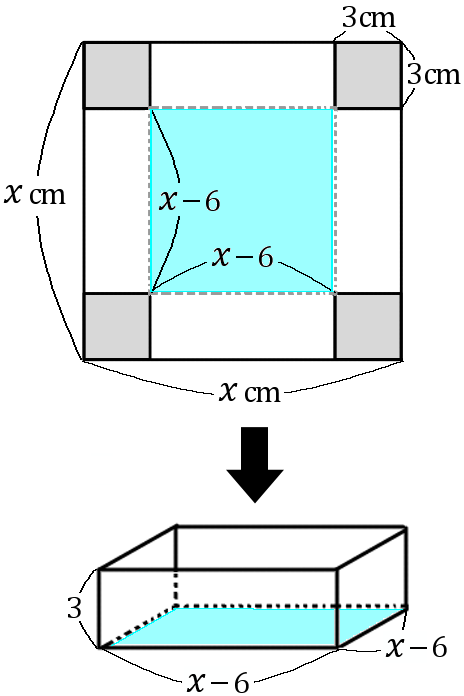
もとの正方形の紙の $1$ 辺を $xcm$ ということにします。
箱は直方体ですから、その容積は縦$\times$横$\times$高さです。縦と横はどちらも $(x-6)cm,$ 高さは $3cm$ になります。なので、
\begin{eqnarray*}
3(x-6)^2&=&588\\
(x-6)^2&=&196\\
(2乗をと&っ&て\pm\sqrt{\phantom{ho}})\\
x-6&=&\pm\sqrt{196}=\pm14\\
x&=&6\pm14\\
x&=&20, \ x=-8
\end{eqnarray*}
もとの正方形の紙の $1$ 辺を $xcm$ ということにして式をたてて、$x$ が求められましたが、ここで注意が必要です。$x$ は $6$ より大きい数でなければいけません。なので、$-8$ は答えてはいけません。ということで、答えは
$$20cm$$
このように、$2$ 次方程式の文章題は、答えが $2$ 通りあって、そのうちのかたほうしか答えてはいけない、ということがよくあります。解を求めたあと、答えとしてよいのかどうかをしっかり確認するようにしましょう。
答え(中3 3章 $2$ 次方程式 第2回)
(1)解,解く (2)イ,エ,カ (3)ウ
(4)$①x=6, \ x=-8$ $②x=10, \ x=12$ $③x=-\cfrac{1}{3}, \ x=\cfrac{2}{5}$ $④x=-\cfrac{2}{3}, \ x=\cfrac{3}{4}$
(5)$x=1, \ x=7$ (6)$x=0, \ x=6$ (7)$x=-5$ (8)$x=\pm6$ (9)$x=x=5\pm2\sqrt{3}$ (10)$x=-4\pm\sqrt{10}$
(11)$①x=\pm5\sqrt{2}$ $②x=0, \ x=12$ $③x=9, \ x=-5$ $④x=\pm11$ $⑤x=9$ $⑥x=6, \ x=-1$ $⑦x=7, \ x=-3$ $⑧x=10\pm6\sqrt{2}$ $⑨x=2\pm\sqrt{2}$ $⑩x=3, \ x=-\cfrac{1}{2}$
(12)$①x=\pm\cfrac{\sqrt{15}}{5}$ $②x=0, \ x=-\cfrac{15}{2}$ $③x=-18, \ x=-2$ $④x=\pm12$ $⑤x=-\cfrac{3}{5}$ $⑥x=-6, \ x=3$ $⑦x=-1, \ x=-3$ $⑧x=8\pm3\sqrt{2}$ $⑨x=3\pm\sqrt{15}$ $⑩x=\cfrac{3}{2}, \ x=-\cfrac{2}{3}$
(13)\begin{eqnarray*}
①
x^2+10x&=&-5\\
x^2+10x+25&=&-5+25\\
(x+5)^2&=&20\\
x+5&=&\pm\sqrt{20}=\pm2\sqrt{5}\\
x&=&-5\pm2\sqrt{5}\\
\end{eqnarray*}
\begin{eqnarray*}
②
x^2-5x&=&1\\
x^2-5x+\cfrac{25}{4}&=&1+\cfrac{25}{4}\\
\left(x-\cfrac{5}{2}\right)^2&=&\cfrac{29}{4}\\
x-\cfrac{5}{2}&=&\pm\sqrt{\cfrac{29}{4}}=\pm\cfrac{\sqrt{29}}{\sqrt{4}}=\pm\cfrac{\sqrt{29}}{2}\\
x&=&\cfrac{5}{2}\pm\cfrac{\sqrt{29}}{2}\\
\end{eqnarray*}
(14)$11$ (15)$14, \ 15, \ 16$ (16)$2m$ (17)$20cm$