数学 中3 1学期期末模擬テスト 第2回
 ページがちゃんと表示されるまで$10$秒くらいかかります。
ページがちゃんと表示されるまで$10$秒くらいかかります。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
「印刷」をクリックすると同じ内容のpdfファイルが表示されます。また、解答用紙と答えも問題のあとに表示されます。1~5ページが問題、6~8ページが解答用紙、9~11ページが答えです。必要におうじて印刷してください。
ふつうのテストより問題数は多いです。単純に $2$ 倍くらいはあります。$50$ 分がふつうのテストの制限時間だと思いますが、ぜんぶ終わらせるのにその倍くらい時間がかかるかも。がんばって。
問題をクリックすると答えがでます。
$\huge{1}$ 次の①~③の計算をしなさい。④~⑧の各問いに答えなさい。
\begin{eqnarray*}
&①& \quad -5-3\times(-4) \qquad ② \quad -3xy\div\cfrac{18}{5}x^2y\times(-3xy)\\
\\
&③& \quad -2(4x+3)-3(2x-5)
\end{eqnarray*}
答え
$①7$ $②\cfrac{5}{2}y$ $③-14x+9$
\begin{eqnarray*} &①& -5-3\times(-4)\\ &=& -5+12\\ &=&7 \end{eqnarray*} \begin{eqnarray*} \require{cancel} &②& -3xy\div\cfrac{18}{5}x^2y\times(-3xy)\\ &=&\cfrac{\bcancel{3}\bcancel{x}\bcancel{y}}{1}\times\cfrac{5}{{}^2\bcancel{{}^6}\bcancel{18}\bcancel{x}\bcancel{x}\bcancel{y}}\times\cfrac{\bcancel{3}\bcancel{x}y}{1}\\ &=&\cfrac{5}{2}y \end{eqnarray*} \begin{eqnarray*} &③& -2(4x+3)-3(2x-5)\\ &=& -8x-6-6x+15\\ &=& -8x-6x-6+15\\ &=&-14x+9 \end{eqnarray*}
$\qquad$④ $1$ 次方程式 $x-\cfrac{5}{6}=\cfrac{2-x}{3}$ を解きなさい。
答え $x=\cfrac{9}{8}$
\begin{eqnarray*} x-\cfrac{5}{6}&=&\cfrac{2-x}{3}\quad(両辺に\times6) \\ 6x-5&=&4-2x \\ 6x+2x&=&4+5\\ 8x&=&9\\ x&=&\cfrac{9}{8} \end{eqnarray*}
$\qquad$⑤ $S=\cfrac{(a+b)h}{2}$ を $h$ について解きなさい。
答え $h=\cfrac{2S}{a+b}$
\begin{eqnarray*} S&=&\cfrac{(a+b)h}{2}\quad(左辺と右辺をとりかえる) \\ \cfrac{(a+b)h}{2}&=&S\quad(\times2) \\ (a+b)h&=&2S\\ h&=&\cfrac{2S}{a+b} \end{eqnarray*}
$\qquad$⑥ 連立方程式 $\left\{\begin{array}{l} 4x+3y=9\\ 3x+3(y-3)=y+1 \end{array}\right.$ を解きなさい。
答え $x=12,y=-13$
\begin{eqnarray*} \left\{ \begin{array}{l} 4x+3y=9\qquad…①\\ 3x+3(y-3)=y+1\qquad…② \end{array} \right. \end{eqnarray*} $②を整理$ \begin{eqnarray*} 3x+3y-9&=&y+1\\ 3x+3y-y&=&1+9\\ 3x+2y&=&10\qquad…③ \end{eqnarray*} $①\times2-③\times3$ \begin{eqnarray*} 8x+6y=\phantom{-}18\\ \underline{-) \quad 9x+6y=\phantom{-}30} \\ -x\phantom{-0y}=-12\\ x=\phantom{-}12 \end{eqnarray*} \begin{eqnarray*} x=12を③に代入\\ 36+2y&=&10\\ 2y&=&10-36\\ 2y&=&-26\\ y&=&-13\\ \\ \left\{ \begin{array}{l} x=12\\ y=-13 \end{array} \right. \end{eqnarray*}
$\qquad$⑦ $2$ 点 $(-2,\ 4),\ (8,\ -1)$ を通る直線の式を求めなさい。
答え $y=-\cfrac{1}{2}x+3$
直線の式の形は $y=ax+b$ \begin{eqnarray*} a&=&\cfrac{y_2-y_1}{x_2-x_1}\\ &=&\cfrac{-1-4}{8-(-2)}=\cfrac{-5}{10}=-\cfrac{1}{2}\\ \end{eqnarray*} $y=-\cfrac{1}{2}x+b$ に $x=-2,\ y=4$ を代入 \begin{eqnarray*} 4&=&-\cfrac{1}{2}\times(-2)+b\\ 4&=&1+b\\ 3&=&b \end{eqnarray*}
$\qquad$⑧ 大小 $2$ 個のサイコロを投げるとき、出る目の和が $6$ の約数になる確率を求めなさい。
答え $\cfrac{2}{9}$
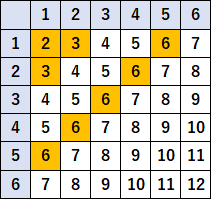
出る目の和を表にするとこうなる。
オレンジ色のところが $6$ の約数。
$$ \cfrac{8}{36}=\cfrac{2}{9}$$
$\huge{2}$ 次の計算をしなさい。
\begin{eqnarray*}
&①& \quad 4x(3x-7y) \qquad &②& \quad (24x^2y-16xy^2)\div4xy
\end{eqnarray*}
答え
$①12x^2-28xy$ $②6x-4y$
\begin{eqnarray*} &①& 4x(3x-7y)\\ &=& 12x^2-28xy \end{eqnarray*} \begin{eqnarray*} &②& (24x^2y-16xy^2)\div4xy\\ &=& 6x-4y \end{eqnarray*}
\begin{eqnarray*} &③& \quad (24x^2-18x)\div\cfrac{6}{5}x \qquad &④& \quad (a+b)(x+y) \end{eqnarray*}
答え
$③20x-15$ $④ax+ay+bx+by$
\begin{eqnarray*} &③& (24x^2-18x)\div\cfrac{6}{5}x\\ &=& (24x^2-18x)\times\cfrac{5}{6x}\\ &=& 20x-15 \end{eqnarray*} \begin{eqnarray*} &④& (a+b)(x+y)\\ &=& ax+ay+bx+by \end{eqnarray*}
\begin{eqnarray*} &⑤& \quad (3x-1)(x-2) \qquad &⑥& \quad (2a+b)(a-b-1)\ \end{eqnarray*}
答え
$⑤3x^2-7x+2$ $⑥2a^2-ab-2a-b^2-b$
\begin{eqnarray*} &⑤& (3x-1)(x-2)\\ &=& 3x^2-6x-x+2\\ &=& 3x^2-7x+2 \end{eqnarray*} \begin{eqnarray*} &⑥& (2a+b)(a-b-1)\\ &=& 2a^2-2ab-2a+ab-b^2-b\\ &=& 2a^2-ab-2a-b^2-b \end{eqnarray*}
\begin{eqnarray*} &⑦& \quad 2(x-3)(x-4)-(x-5)(x+4) \end{eqnarray*}
答え
$⑦x^2-13x+44$
\begin{eqnarray*} &⑦& 2(x-3)(x-4)-(x-5)(x+4)\\ &=& 2(x^2-7x+12)-(x^2-x-20)\\ &=& 2x^2-14x+24-x^2+x+20\\ &=& x^2-13x+44 \end{eqnarray*}
\begin{eqnarray*} &⑧& \quad (2x+3y)(2x-3y)+3(x-2y)^2 \end{eqnarray*}
答え
$⑧7x^2-12xy+3y^2$
\begin{eqnarray*} &⑧& (2x+3y)(2x-3y)+3(x-2y)^2\\ &=& 4x^2-9y^2+3(x^2-4xy+4y^2)\\ &=& 4x^2-9y^2+3x^2-12xy+12y^2\\ &=& 7x^2-12xy+3y^2 \end{eqnarray*}
\begin{eqnarray*} &⑨& \quad (x+2y-1)^2 \qquad &⑩& \quad (3x-y+7)(3x-y-7) \end{eqnarray*}
答え
$⑨x^2+4xy+4y^2-2x-4y+1$ $⑩9x^2-6xy+y^2-49$
\begin{eqnarray*}
&⑨& (x+2y-1)^2\\
&&x+2y=Aとすると\\
&=& (A-1)^2\\
&=& A^2-2A+1\\
&=& (x+2y)^2-2(x+2y)+1\\
&=& x^2+4xy+4y^2-2x-4y+1
\end{eqnarray*}
⑨については、がんばって $9$ 回かければおなじ答えがでます。やりかたが思いつかないときや自信がないときはこれでもOKです。
\begin{eqnarray*}
&⑨& (x+2y-1)^2\\
&=& (x+2y-1)(x+2y-1)\\
&=& x^2+2xy-x+2xy+4y^2-2y-x-2y+1\\
&=& x^2+4xy-2x+4y^2-4y+1
\end{eqnarray*}
\begin{eqnarray*}
&⑩& (3x-y+7)(3x-y-7)\\
&&3x-y=Aとすると\\
&=&(A+7)(A-7)\\
&=&A^2-49\\
&=& (3x-y)^2-49\\
&=& 9x^2-6xy+y^2-49
\end{eqnarray*}
⑩についても、がんばって $9$ 回かければおなじ答えがでます。やりかたが思いつかないときや自信がないときはこれでもOKです。
\begin{eqnarray*}
&⑩& (3x-y+7)(3x-y-7)\\
&=& 9x^2-3xy-21x-3xy+y^2+7y+21x-7y-49\\
&=& 9x^2-6xy+y^2-49
\end{eqnarray*}
$\huge{3}$ 次の式を因数分解しなさい。
\begin{eqnarray*}
&①& \quad ma+mb+m \qquad &②& \quad 36a^2b-18ab^2
\end{eqnarray*}
答え
$①m(a+b+1)$ $②18ab(2a-b)$
\begin{eqnarray*} &③& \quad x^2-7x-60 \qquad &④& \quad a^2-6a+9\ \end{eqnarray*}
答え
$③(x+5)(x-12)$ $④(a-3)^2$
\begin{eqnarray*} &⑤& \quad 49x^2+154xy+121y^2 \qquad &⑥& \quad \cfrac{4}{9}a^2-\cfrac{4}{3}a+1 \end{eqnarray*}
答え
$⑤(7x+11y)^2$ $⑥\left(\cfrac{2}{3}a-1\right)^2$
\begin{eqnarray*} &⑦& \quad 25x^2-4y^2 \qquad &⑧& \quad \cfrac{1}{36}x^2-\cfrac{1}{169} \end{eqnarray*}
答え
$⑦(5x+2y)(5x-2y)$ $⑧\left(\cfrac{1}{6}x+\cfrac{1}{13}\right)\left(\cfrac{1}{6}x-\cfrac{1}{13}\right)$
\begin{eqnarray*} &⑨& \quad 3x^2-3x-60 \qquad &⑩& \quad 100x^2-25y^2 \end{eqnarray*}
答え
$⑨3(x+4)(x-5)$ $⑩25(2x+y)(2x-y)$
\begin{eqnarray*}
&⑨& 3x^2-3x-60\\
&=& 3(x^2-x-20)\\
&=& 3(x+4)(x-5)
\end{eqnarray*}
\begin{eqnarray*}
&⑩& 100x^2-25y^2\\
&=& 25(4x^2-y^2)\\
&=& 25(2x+y)(2x-y)
\end{eqnarray*}
⑩の問題はまちがえやすいです。気をつけて。
$(10x+5y)(10x-5y)$ と答えるとバツになります。因数分解は、くくれるときはまずくくるというのがお約束です。
\begin{eqnarray*} &⑪& \quad a(x-1)+(x-1) \qquad &⑫& \quad (2a+b)^2+5(2a+b)+6 \end{eqnarray*}
答え
$⑪(x-1)(a+1)$ $⑫(2a+b+2)(2a+b+3)$
\begin{eqnarray*} &⑪& a(x-1)+(x-1)\\ &&(x-1)=Aとすると\\ &=& aA+A\\ &=& A(a+1)\\ &=& (x-1)(a+1) \end{eqnarray*} \begin{eqnarray*} &⑫& (2a+b)^2+5(2a+b)+6\\ &&(2a+b)=Aとすると\\ &=& A^2+5A+6\\ &=& (A+2)(A+3)\\ &=& (2a+b+2)(2a+b+3)\\ \end{eqnarray*}
\begin{eqnarray*} &⑬& \quad ac+bc+ad+bd \end{eqnarray*}
答え
$⑬(a+b)(c+d)$
\begin{eqnarray*} &⑬& ac+bc+ad+bd\\ &=& c(a+b)+d(a+b)\\ &&(a+b)=Aとすると\\ &=& cA+dA\\ &=& A(c+d)\\ &=& (a+b)(c+d) \end{eqnarray*}
$\huge{4}$ 次の $(1)~(5)$ の問いに答えなさい。
$\qquad(1)$
乗法公式や因数分解を使って次の①~④の計算をしなさい。計算の過程をかいておくこと。
\begin{eqnarray*}
① \quad 104^2\qquad ② \quad 99^2\qquad
③ \quad 52\times48 \qquad ④13.5^2-3.5^2
\end{eqnarray*}
答え
\begin{eqnarray*}
&①& 104^2\\
&=& (100+4)^2\\
&=& 10000+800+16\\
&=& 10816
\end{eqnarray*}
\begin{eqnarray*}
&②& 99^2\\
&=& (100-1)^2\\
&=& 10000-200+1\\
&=& 9801
\end{eqnarray*}
\begin{eqnarray*}
&③& 52\times48\\
&=& (50+2)(50-2)\\
&=& 2500-4\\
&=& 2496
\end{eqnarray*}
\begin{eqnarray*}
&④& 13.5^2-3.5^2\\
&=& (13.5+3.5)(13.5-3.5)\\
&=& 17\times10\\
&=& 170
\end{eqnarray*}
$\qquad(2)$ $x=4, \ y=-\cfrac{1}{3}$ のとき、次の式の値を求めなさい。 \begin{eqnarray*} \quad -(x+2y)(x-y)+(x+y)^2 \end{eqnarray*}
答え
$-1$
問題の式にいきなり $x$ と $y$ の値を代入しても答えは出ますが、めんどうくさいことになります。いったん展開して整理してから代入するとラクになります。この問題はそれほどラクになってるような気がしないですけど、変形したほうがラクになる問題が多いですので、そういうものだと思っておきましょう。 \begin{eqnarray*} && -(x+2y)(x-y)+(x+y)^2\\ &=& -(x^2+xy-2y^2)+x^2+2xy+y^2\\ &=& -x^2-xy+2y^2+x^2+2xy+y^2\\ &=& xy+3y^2 \quad \class{mathbg-r}{(ここまでやってから代入する)} \\ &=& 4\times\left(-\cfrac{1}{3}\right)+3\times\left(-\cfrac{1}{3}\right)^2\\ &=& -\cfrac{4}{3}+\cfrac{1}{3}\\ &=& -1 \end{eqnarray*}
$\qquad(3)$ $x=43, \ y=23$ のとき、次の式の値を求めなさい。 $$x^2-2xy+y^2$$
答え
$400$
問題の式に $x$ や $y$ の値を代入すれば答えは出ますが、めんどうくさいことになります。因数分解をしてから代入するとラクになる問題というのがあります。夢のようにラクになることさえあります。 \begin{eqnarray*} && x^2-2xy+y^2\\ &=& (x-y)^2\quad \class{mathbg-r}{(ここで代入する)} \\ &=& (43-23)^2\\ &=& 20^2\\ &=& 400 \end{eqnarray*}
$\qquad(4)$ $x+2y=\cfrac{3}{5}, \ x-2y=-10$ のとき、次の式の値を求めなさい。 $$x^2-4y^2$$
答え
$-6$
与えられた式を連立方程式にして、
\begin{eqnarray*}
\left\{
\begin{array}{l}
x+2y=\cfrac{3}{5}\\
x-2y=-10
\end{array}
\right.
\end{eqnarray*}
これを解けば $x, \ y$ が求められて、それを代入すれば答えが求められるのですが、この問題の場合はちょっと損なやりかたです。
因数分解をすればもっとラクにやれます。
\begin{eqnarray*}
&& x^2-4y^2\\
&=& (x+2y)(x-2y)\quad \class{mathbg-r}{(こうすれば代入できる)} \\
&=& \cfrac{3}{5}\times(-10)\\
&=& -6
\end{eqnarray*}
$\qquad(5)$ 次の $ \boxed{\Large\phantom{hoge}}$ の中にあてはまる数や式をいれなさい。 \begin{eqnarray*} &①& \quad (x+7)(x-\boxed{\Large\phantom{hoge}}) \qquad &②& \quad (5x-\boxed{\Large\phantom{hoge}})^2\\ &=& \quad x^2+\boxed{\Large\phantom{hoge}}-35&=& \quad 25x^2-\boxed{\Large\phantom{hogeho}}+144y^2 \\ \end{eqnarray*}
答え
\begin{eqnarray*}
&①& \quad (x+7)(x-\boxed{\large{ \ 5 \ }}) \quad &②& \quad (5x-\boxed{\large{ \ 12y \ }})^2\\
&=& \quad x^2+\boxed{\large{ \ 2x \ }}-35&=& \quad 25x^2-\boxed{\large{ \ 120xy \ }}+144y^2
\\
\end{eqnarray*}
\begin{eqnarray*} &③& \quad x^2-\boxed{\Large\phantom{hoge}}-39\qquad\quad &④& \quad 4x^2-\boxed{\Large\phantom{hoge}}+9y^2\\ &=& \quad (x+3)(x-\boxed{\Large\phantom{hoge}})&=& \quad (2x-\boxed{\Large\phantom{hoge}})^2 \\ \end{eqnarray*}
答え
\begin{eqnarray*}
&③& \quad x^2-\boxed{\large{ \ 10x \ }}-39\qquad &④& \quad 4x^2-\boxed{\large{ \ 12xy \ }}+9y^2\\
&=& \quad (x+3)(x-\boxed{\large{ \ 13 \ }})&=& \quad (2x-\boxed{\large{ \ 3y \ }})^2
\\
\end{eqnarray*}
$\huge{5}$ 次の $(1)~(11)$ の問いに答えなさい。
$\qquad(1)$ 次の数の平方根を求めなさい。または、根号を使って表しなさい。
\begin{eqnarray*}
&①& \quad 1 \quad &②& \quad 16\quad &③& \quad \cfrac{4}{25} \quad &④& \quad 0.01 \\
\\
&⑤& \quad 0 \quad &⑥& \quad -9 \quad &⑦& \quad 15 \quad &&
\end{eqnarray*}
答え
$①\pm1$ $②\pm4$ $③\pm\cfrac{2}{5}$ $④\pm0.1$ $⑤0$ $⑥ない$ $⑦\pm\sqrt{15}$
$\large{\pm}$ を忘れないようにしましょう。
⑤$0$ の平方根は $0$ です。$0$ にはプラスもマイナスもないので、これだけは $\large{\pm}$ をつけません。
⑥負の数の平方根はありません。「ない」とか「なし」とか答えましょう。ヘンな問題だなあと思うんですけど、もしかしたらテストに出るかもしれないので、いちおう出題しておきました。
$\qquad(2)$ 次の①~④が正しければ〇を書きなさい。誤っていれば、×を書き、下線の部分を正しく書き直しなさい。
\begin{eqnarray*}
&①& \quad 64 の平方根は \underline{ 8 } \quad \qquad &②& \quad \sqrt{64}=\underline{ \pm8 }\\
\\
&③& \quad -\sqrt{8^2}= \underline{ -8 } &④& \quad \left(-\sqrt{8}\right)^2=\underline{ -8 }\\
\\
\end{eqnarray*}
答え
$①×\ \pm8$ $②×\ 8$ $③〇 $ $④×\ 8$
①平方根は $\pm$ がつきます。
②ぎゃくに、こちらはつけてはいけません。意味を考えましょう。よくわからなかったら、テストのときはこうしてください。
「平方根」と書かれていたら、$\large{\pm}$ をつける。
「平方根」と書かれていなかったら、$\large{\pm}$ をつけない。
それでうまくいきます。漢字三文字で平方根。平と方と根で平方根。この三文字が問題文にあったら $\pm$ をつける。なければつけない。「根には土がついている」とでもおぼえてください。
③$2$ 乗したらルートは消えます。
④マイナスの数にかっこをつけて $2$ 乗したらプラスになります。このことも、あやふやなひとは整理しておきましょう。
$(-2)^2=4, \ -2^2=-4, \ (-2^2)=-4$ という感じです。
$\qquad(3)$ $30$ 以下の素数をすべて答えなさい。
答え
$2,$ $3,$ $5,$ $7,$ $11,$ $13,$ $17,$ $19,$ $23,$ $29$
素数は $2$ からはじまります。$1$ とその数自身以外の約数がない自然数を素数といいます。
$\qquad(4)$ 次の①,②の数を素因数分解しなさい。
$$①20\qquad\qquad\qquad②144$$
答え
$①2^2\times5$ $②2^4\times3^2$
\begin{eqnarray*} 2&&\underline{)20} \\ 2&&\underline{)10} \\ &&\phantom{)1}5 \end{eqnarray*} \begin{eqnarray*} 2&&\underline{)144} \\ 2&&\underline{)72} \\ 2&&\underline{)36} \\ 2&&\underline{)18} \\ 3&&\underline{)\phantom{1}9} \\ &&\phantom{)1}3 \end{eqnarray*}
$\qquad(5)$ $120$ をできるだけ小さい自然数で割って、商がある自然数の $2$ 乗になるようにしたい。その自然数を求めなさい。
答え
$30$
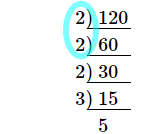 ①素因数分解して、$2$ つあるところにはマルをします。マルがつかなかったところをかければOKです。それでつじつまがあってます。$2\times3\times5=30$ が答えです。
①素因数分解して、$2$ つあるところにはマルをします。マルがつかなかったところをかければOKです。それでつじつまがあってます。$2\times3\times5=30$ が答えです。
$120\div30=4$ となって、これは $2$ の $2$ 乗になっています。
$\qquad(6)$ $\sqrt{\cfrac{135}{n}}$ の値ができるだけ小さい整数になるときの、正の整数 $n$ の値を求めなさい。
答え
$15$
(5)の問題と同じようにやればOKです。
どちらの問題もやり方はおなじです。
手順1 素因数分解してください。
手順2 同じ数が$2$つあったら、そこに〇をつけてください。
手順3 〇がつかなかった数をかけてください。
その数が答えです。簡単なので、手順をおぼえましょう。
ちなみに $\cfrac{135}{15}=9$ となって、$\sqrt{9}=3$ です。
$\qquad(7)$ ①の $2$つの数について、数の大小を不等号を用いて表しなさい。②の $4$つの数について、不等号をもちいて、小さい順に数をならべなさい。
$$
①\quad -\sqrt{20},\quad-5
$$
$$
② \quad 3.4,\quad-\sqrt{11},\quad \sqrt{11},\quad-\sqrt{15}
$$
答え
$① -\sqrt{20} \gt -5$ $② -\sqrt{15}\lt-\sqrt{11}\lt\sqrt{11}\lt3.4$
$\sqrt{ }$ のついている数とついていない数の大小は、$2$ 乗して比べましょう。根号は、$2$ 乗をすると消えます。そして、絶対値の大小関係は、$2$ 乗をしても変わりません。
①$(\sqrt{20})^2=20, \ 5^2=25$ なので、$\sqrt{20}\lt 25$ です。なので、$-\sqrt{20}\gt -5$ です。
②$(\sqrt{11})^2=11, \ 3.4^2=11.56$ なので、$\sqrt{11}\lt 3.4$ です。
$\qquad(8)$ 次の①~③の数を、$\sqrt{a}$ の形にしなさい。
$$① \ 3\sqrt{2} \qquad ② \ \cfrac{\sqrt{15}}{5} \qquad③ \ 2 \sqrt{\cfrac{ \ 3 \ }{ \ 14 \ }}$$
答え
$①\sqrt{18}$ $②\sqrt{\cfrac{ \ 3 \ }{ \ 5 \ }}$ $③\sqrt{\cfrac{ \ 6 \ }{ \ 7 \ }}$
ルートの外にある数をルートの中に入れなさい、という意味の問題です。
ルートの外にある数は、$2$ 乗してルートの中に入れます。
$$① \ 3\sqrt{2}=\sqrt{3^2\times2}=\sqrt{18}$$
$$② \ \cfrac{\sqrt{15}}{5}=\sqrt{\cfrac{15}{5^2}}=\sqrt{\cfrac{ \ 3 \ }{ \ 5 \ }}$$
$$③ \ 2 \sqrt{\cfrac{ \ 3 \ }{ \ 14 \ }}=\sqrt{2^2\times \cfrac{ \ 3 \ }{ \ 14 \ }}=\sqrt{\cfrac{ \ 6 \ }{ \ 7 \ }}$$
$\qquad(9)$ 次の①~②の数を、$a\sqrt{b}$ の形にしなさい。根号の中の数はできるだけ小さい整数となるようにしなさい。
$$① \ \sqrt{54} \qquad ② \ \sqrt{162}$$
答え
$①3\sqrt{6}$ $②9\sqrt{2}$
$$① \ \sqrt{54}=\sqrt{3^2\times6}=3\sqrt{6}$$
$$② \ \sqrt{162}=\sqrt{9^2\times2}=9\sqrt{2}$$
なんの $2$ 乗との積になっているかをぱっぱっと思いつければいいのですが、数が大きくなったりすると、なかなかわかりません。計算力に自信がないひとは、あきらめてすべて素因数分解してください。なおせるか、なおせないか、なおせるとしたらどうなるのか、を確認できます。こんな感じです。
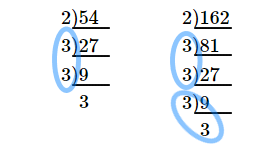
1.素因数分解する
2.同じ数が $2$ 個あったら〇でかこむ
3.〇でかこまれた数が$1$つだけ外に出る(いくつも出てきたときは全部かける)
4.〇でかこまれなかった数は中に残る(いくつも残ったときは全部かける)
というわけで、$\sqrt{54}$ は $3$ が外に出て $2$ と $3$ が残るので $2\sqrt{3}$
$\sqrt{162}$ は $3$ と $3$ が外に出て $2$ が残るので $9\sqrt{2}$
$\qquad(10)$ $\sqrt{3}=1.732, \ \sqrt{30}=5.477$ として、次の①~④の近似値を求めなさい。
$$①\quad \sqrt{300}\qquad② \ \sqrt{3000}\qquad③ \ \sqrt{0.03}\qquad④ \ \sqrt{0.003}$$
答え
$①17.32$ $②54.77$ $③0.1732$ $④0.05477$
\begin{eqnarray*}
① \ \sqrt{300}&=&\sqrt{100\times3}\qquad② \ \sqrt{3000}&=&\sqrt{100\times30}\\
&=&10\sqrt{3}&=&10\sqrt{30}\\
&=&10\times1.732&=&10\times5.477\\
&=&17.32&=&54.77\\\\
③ \ \sqrt{0.03}&=&\sqrt{\cfrac{3}{100}}\qquad④ \ \sqrt{0.003}&=&\sqrt{\cfrac{30}{10000}}\\
&=&\cfrac{\sqrt{3}}{10}&=&\cfrac{\sqrt{30}}{100}\\
&=&\cfrac{1.732}{10}&=&\cfrac{5.477}{100}\\
&=&0.1732&=&0.05477
\end{eqnarray*}
この問題で使える数は基本 $100$ か $10000$ です。$10^2=100, \ 100^2=10000$ だからです。
②の問題は、$3000$ を $1000\times3$ とやると失敗です。どうにもなりません。$100\times30$ とやれば、うまくいきます。
④の問題も同じで、$0.003$ をふつうに分数にすると $\cfrac{3}{1000}$ ですが、これだと失敗です。あえて分母を $10000$ にして、$\cfrac{30}{10000}$ とやってしまいます。それでうまくいきます。
$\qquad(11)$ 次の①~③の分母を有理化しなさい。 \begin{eqnarray*} &①& \ \cfrac{\sqrt{3}}{\sqrt{5}} \qquad\qquad &②& \ \cfrac{7}{\sqrt{14}} \qquad\qquad &③& \ \cfrac{4\sqrt{13}}{\sqrt{26}} \end{eqnarray*}
答え
$①\cfrac{\sqrt{15}}{5}$ $②\cfrac{\sqrt{14}}{2}$ $③2\sqrt{2}$
\begin{eqnarray*}
&①&\cfrac{\sqrt{3}}{\sqrt{5}}=\cfrac{\sqrt{3}\times\sqrt{5}}{\sqrt{5}\times\sqrt{5}}=\cfrac{\sqrt{15}}{5}\\
&②&\cfrac{7}{\sqrt{14}}=\cfrac{7\times\sqrt{14}}{\sqrt{14}\times\sqrt{14}}=\cfrac{7\sqrt{14}}{14}=\cfrac{\sqrt{14}}{2}\\
&③&まず約分する\\
&&\cfrac{4\sqrt{13}}{\sqrt{26}}=\cfrac{4}{\sqrt{2}}=\cfrac{4\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}=\cfrac{4\sqrt{2}}{2}=2\sqrt{2}\\
\end{eqnarray*}
$\cfrac{1}{\sqrt{2}}$ とか、$\cfrac{2\sqrt{3}}{\sqrt{5}}$ のように、分母にルートがある場合があります。こういう場合、分母のルートをなくしてしまいます。手順をふめば、そういうことができます。分子にルートがあるのはそのままでいいです。でも、分母にあるときは、なくしてしまいます。これを、分母を有理化する、といいます。
そのやり方は、分母のルートとおなじものを、分母と分子の両方にかけてしまう、というものです。以下に2パターンをしめします。
$$\cfrac{1}{\sqrt{2}}=\cfrac{1\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}=\cfrac{\sqrt{2}}{2}$$
$$\cfrac{2\sqrt{3}}{\sqrt{5}}=\cfrac{2\sqrt{3}\times\sqrt{5}}{\sqrt{5}\times\sqrt{5}}=\cfrac{2\sqrt{15}}{5}$$
こうすれば、分数の値そのものは変えずに、分母のルートをなくすことができます。
分母の有理化にかんして、大きいポイントがひとつ、あります。
約分できるときは、まず約分する。分母を有理化するのはそのあと。
ということです。ルートはルートと約分できます。分母を有理化するまえに、「約分できないかな?」といつも確認するクセをつけるといいです。そして、約分できるときはまず約分してください。そうしないと、すごく損になってしまうことがあります。答えはおなじになりますが、約分できるときはまず約分したほうがトクです。例をしめします。
\begin{eqnarray*}
&約&分しないで有理化&約&分してから有理化\\
&&\cfrac{\sqrt{15}}{\sqrt{30}}&&\cfrac{\sqrt{15}}{\sqrt{30}}\\
&=&\cfrac{\sqrt{15}\times\sqrt{30}}{\sqrt{30}\times\sqrt{30}}\qquad\qquad&=&\cfrac{1}{\sqrt{2}}\\
&=&\cfrac{\sqrt{450}}{30}&=&\cfrac{1\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}\\
&=&\cfrac{15\sqrt{2}}{30}&=&\cfrac{\sqrt{2}}{2}\\
&=&\cfrac{\sqrt{2}}{2}
\end{eqnarray*}
どう見ても約分してから分母を有理化したほうがラクですよね。
$\huge{6}$ 次の計算をしなさい。 \begin{eqnarray*} &①& \ \sqrt{2}\times\sqrt{5}\qquad &②& \ 6\sqrt{6}\div(-3\sqrt{2}) \end{eqnarray*}
答え
$①\sqrt{10}$ $②-2\sqrt{3}$
\begin{eqnarray*} \require{cancel} &①& \ \sqrt{2}\times\sqrt{5}=\sqrt{10}\\ &②& \ 6\sqrt{6}\div(-3\sqrt{2})=-\cfrac{6\sqrt{6}}{3\sqrt{2}}=-2\sqrt{3} \end{eqnarray*}
\begin{eqnarray*} &③& \ 2\sqrt{12}\times\sqrt{2}\qquad &④& \ 15\div(-5\sqrt{6}) \end{eqnarray*}
答え
$③4\sqrt{6}$ $④-\cfrac{\sqrt{6}}{2}$
\begin{eqnarray*} \require{cancel} &③& \ 2\sqrt{12}\times\sqrt{2}=2\sqrt{24}=2\cdot2\sqrt{6}=4\sqrt{6}\\ &④& \ 15\div(-5\sqrt{6})=-\cfrac{15}{5\sqrt{6}}=-\cfrac{3}{\sqrt{6}}=-\cfrac{3\sqrt{6}}{6}=-\cfrac{\sqrt{6}}{2} \end{eqnarray*}
\begin{eqnarray*} &⑤& \ 8\sqrt{35}\times\sqrt{3}\div6\sqrt{30}\qquad &⑥& \ \sqrt{\cfrac{3}{10}}\div2\sqrt{6}\div\sqrt{\cfrac{2}{5}} \end{eqnarray*}
答え
$⑤\cfrac{2\sqrt{14}}{3}$ $⑥\cfrac{\sqrt{2}}{8}$
\begin{eqnarray*} &⑤& \ 8\sqrt{35}\times\sqrt{3}\div6\sqrt{30}=\cfrac{\bcancel{8}\sqrt{\bcancel{35}}\times\sqrt{\bcancel{3}}}{\bcancel{6}\sqrt{\bcancel{30}}}=\cfrac{4\sqrt{7}}{3\sqrt{2}}\\ &=&\cfrac{4\sqrt{14}}{6}=\cfrac{2\sqrt{14}}{3}\\ &⑥& \ \sqrt{\cfrac{3}{10}}\div2\sqrt{6}\div\sqrt{\cfrac{2}{5}}\\ &=&\cfrac{\sqrt{3}}{\sqrt{10}}\div2\sqrt{6}\div\cfrac{\sqrt{2}}{\sqrt{5}}\\ &=&\cfrac{\sqrt{\bcancel{3}}}{\sqrt{\bcancel{10}}}\times\cfrac{1}{2\sqrt{\bcancel{6}}}\times\cfrac{\sqrt{\bcancel{5}}}{\sqrt{2}}\\ &=&\cfrac{1}{\sqrt{2}}\times\cfrac{1}{2\sqrt{2}}\times\cfrac{1}{\sqrt{2}}\\ &=&\cfrac{1}{4\sqrt{2}}=\cfrac{\sqrt{2}}{8} \end{eqnarray*}
\begin{eqnarray*} &⑦& \ \sqrt{20}-5\sqrt{10}+\sqrt{45}+3\sqrt{40}\qquad &⑧& \ \sqrt{27}+\cfrac{12}{\sqrt{3}} \end{eqnarray*}
答え
$⑦5\sqrt{5}+\sqrt{10}$ $⑧7\sqrt{3}$
\begin{eqnarray*} &⑦& \ \sqrt{20}-5\sqrt{10}+\sqrt{45}+3\sqrt{40}\\ &=&2\sqrt{5}-5\sqrt{10}+3\sqrt{5}+6\sqrt{10}\\ &=&5\sqrt{5}+\sqrt{10}\\ &⑧& \ \sqrt{27}+\cfrac{12}{\sqrt{3}}=3\sqrt{3}+\cfrac{12\sqrt{3}}{3}\\ &=&3\sqrt{3}+4\sqrt{3}=7\sqrt{3} \end{eqnarray*}
\begin{eqnarray*} &⑨& \ \sqrt{54}-\sqrt{\cfrac{2}{3}}\qquad &⑩& \ -8\sqrt{5}+\sqrt{15}\times\sqrt{3} \end{eqnarray*}
答え
$⑨\cfrac{8\sqrt{6}}{3}$ $⑩-5\sqrt{5}$
\begin{eqnarray*} &⑨& \ \sqrt{54}-\sqrt{\cfrac{2}{3}}=3\sqrt{6}-\cfrac{\sqrt{2}}{\sqrt{3}}=3\sqrt{6}-\cfrac{\sqrt{6}}{3}\\ &=&\cfrac{9\sqrt{6}}{3}-\cfrac{\sqrt{6}}{3}=\cfrac{8\sqrt{6}}{3}\\ &⑩& \ -8\sqrt{5}+\sqrt{15}\times\sqrt{3}=-8\sqrt{5}+\sqrt{45}\\ &=&-8\sqrt{5}+3\sqrt{5}=-5\sqrt{5} \end{eqnarray*}
\begin{eqnarray*} &⑪& \ \sqrt{2}(\sqrt{10}-2\sqrt{3})\qquad &⑫& \ (3\sqrt{10}+\sqrt{18})\div\sqrt{2} \end{eqnarray*}
答え
$⑪2\sqrt{5}-2\sqrt{6}$ $⑫3\sqrt{5}+3$
\begin{eqnarray*} &⑪& \ \sqrt{2}(\sqrt{10}-2\sqrt{3})=\sqrt{20}-2\sqrt{6}=2\sqrt{5}-2\sqrt{6}\\ &⑫& \ (3\sqrt{10}+\sqrt{18})\div\sqrt{2}=3\sqrt{5}+\sqrt{9}=3\sqrt{5}+3 \end{eqnarray*}
\begin{eqnarray*} &⑬& \ (\sqrt{5}-5)(\sqrt{5}-4)\qquad &⑭& \ (\sqrt{6}-\sqrt{3})(\sqrt{15}-\sqrt{2}) \end{eqnarray*}
答え
$⑬25-9\sqrt{5}$ $⑭3\sqrt{10}-2\sqrt{3}-3\sqrt{5}+\sqrt{6}$
\begin{eqnarray*} &⑬& \ (\sqrt{5}-5)(\sqrt{5}-4)=5-9\sqrt{5}+20=25-9\sqrt{5}\\ &⑭& \ (\sqrt{6}-\sqrt{3})(\sqrt{15}-\sqrt{2})=\sqrt{90}-\sqrt{12}-\sqrt{45}+\sqrt{6}\\ &=&3\sqrt{10}-2\sqrt{3}-3\sqrt{5}+\sqrt{6} \end{eqnarray*}
\begin{eqnarray*} &⑮& \ (3\sqrt{2}-2\sqrt{3})^2\qquad &⑯& \ (2\sqrt{10}+3)(2\sqrt{10}-3) \end{eqnarray*}
答え
$⑮30-12\sqrt{6}$ $⑯31$
\begin{eqnarray*} &⑮& \ (3\sqrt{2}-2\sqrt{3})^2=18-12\sqrt{6}+12=30-12\sqrt{6}\\ &⑯& \ (2\sqrt{10}+3)(2\sqrt{10}-3)=40-9=31 \end{eqnarray*}
$\huge{7}$ 次の $(1)~(5)$ の問いに答えなさい。
$\qquad(1)$ $x=3+2\sqrt{2}, \ y=3-2\sqrt{2}$ のとき、次①,②の式の値を求めなさい。
$$①\quad xy \qquad\qquad②\quad x^2-2xy+y^2$$
答え
$①1$ $②32$
① \begin{eqnarray*} xy&=&(3+2\sqrt{2})(3-2\sqrt{2})\\ &=&9-8\\ &=&1 \end{eqnarray*} ② \begin{eqnarray*} &&x^2-2xy+y^2\\ &=&(x-y)^2\quad \class{mathbg-r}{(ここで代入する)} \\ &=&\{(3+2\sqrt{2})-(3-2\sqrt{2})\}^2\\ &=&(3+2\sqrt{2}-3+2\sqrt{2})^2\\ &=&(4\sqrt{2})^2\\ &=&32 \end{eqnarray*} ②については、やり方が思いつかないときや、自信がないときは、単に代入して、がんばって計算すれば同じ答えがでます。 \begin{eqnarray*} &②&x^2-2xy+y^2\\ &=&(3+2\sqrt{2})^2-2(3+2\sqrt{2})((3-2\sqrt{2})+(3-2\sqrt{2})^2\\ &=&9+12\sqrt{2}+8-2(9-8)+9-12\sqrt{2}+8\\ &=&32 \end{eqnarray*}
$\qquad(2)$ $\sqrt{50-a}$ の値が自然数となるような $a$ をすべて求めなさい。ただし、$a$ は自然数とする。
答え
$1, \ 14, \ 25, \ 34, \ 41, \ 46, \ 49$
自然数は $1, \ 2, \ 3, \cdots$ です。$1$ からはじまります。
ルートの中は負の数だといけませんので、$a$ は $50$ 以下の自然数だということになります。あとは、$a$ がいくつのときに $\sqrt{50-a}$ が自然数になるかを確認すればよいです。
$a=1$ のとき、$\sqrt{50-1}=\sqrt{49}=7$
$a=14$ のとき、$\sqrt{50-14}=\sqrt{36}=6$
$a=25$ のとき、$\sqrt{50-25}=\sqrt{25}=5$
$a=34$ のとき、$\sqrt{50-34}=\sqrt{16}=4$
$a=41$ のとき、$\sqrt{50-41}=\sqrt{9}=3$
$a=46$ のとき、$\sqrt{50-46}=\sqrt{4}=2$
$a=49$ のとき、$\sqrt{50-49}=\sqrt{1}=1$
$\sqrt{50-a}$ が自然数になるのはこの $7$ 通りです。
$a=1$ のとき、$a=2$ のとき、$a=3$ のとき…といくつかためしてみたら、「ああ、ルートの中が $1$ とか $4$ とか $9$ とかの $2$ 乗の数になればいいのか」と気づくのではないでしょうか。
$a=50$ のときは、$\sqrt{50-50}=\sqrt{0}=0$ となってルートはなくなるのですが、$0$ は自然数ではないのでダメです。問題にあいません。
$\qquad(3)$ $7\lt \sqrt{n} \lt8$ を満たす $n$ は何個あるか。ただし $n$ は自然数とする。
答え
$14$ 個
自然数は $1, \ 2, \ 3, \cdots$ です。$1$ からはじまります。
平方根の大小に関する問題は、$2$ 乗をしてくらべます。問題の式の $7$ と $\sqrt{n}$ と $8$ をすべて $2$ 乗すると、
$49\lt n \lt64$ となります。
$2$ 乗をしても大小関係は変わりません。なので、$n$ は $50$ から $63$ までの $14$ 個ということになります。
ところで、$50$ から $63$ まで、いくつの自然数がありますか、ときかれて、単純に $63-50=13$ だから $13$ 個と答えたりはしてませんか? それ、ダメですよ。ためしに $50, \ 51, \ 52,\cdots 62, \ 63$ と指を折って数えてみてください。$14$ 個あるはずです。
$50$ から $63$ まで、いくつの自然数がありますか、ときかれたときは、$63-50+1=14$ なので $14$ 個と答えなくちゃいけません。$+1$ しないといけません。小学校のときに教わることだと思うんだけど、忘れちゃっているひと、けっこう多いです。
$\qquad(4)$ 次の数を有理数と無理数に分けなさい。 $$ \cfrac{2}{27},\quad 2-\sqrt{2},\quad 0.\dot789\dot0,\quad \cfrac{\pi}{3},\quad \sqrt{225} $$
答え
有理数…$\cfrac{2}{27}, \ 0.\dot789\dot0, \ \sqrt{225}$
無理数…$2-\sqrt{2}, \ \cfrac{\pi}{3}$
$\sqrt{225}=15$ です。
循環小数は有理数です。
絶対にまちがえたくないなら、そりゃちゃんと言葉の定義と意味を理解しなきゃいけませんが、よくわからないなあというときは、「ルートと $\pi$ が無理数で、あとは有理数」と思っときゃたいていあたります。
$\qquad(5)$ ①の分数を循環小数で表しなさい。②,③の循環小数を分数で表しなさい。 $$ ① \ \cfrac{2}{7}\qquad② \ 0.\dot{5}\qquad③ \ 0.\dot{3}0\dot{0} $$
答え
$①0.\dot{2}8571\dot{4}$ $②\cfrac{5}{9}$ $③\cfrac{100}{333}$
①割り算をして、どこが繰り返すかを確認すればOKです。
$$2\div7=0.2857142857...$$
②小数第一位の数をくり返すときは、分母を $9$ にしておけばいいです。
③小数第一位から第三位までをくり返すときは、分母を $999$ にしておけばいいです。約分できるときは約分します。
$$\cfrac{300}{999}=\cfrac{100}{333}$$
$\huge{8}$ 連続する $3$つの整数がある。いちばん小さい数といちばん大きい数の積に $1$ を加えると、真ん中の数の $2$ 乗になることを証明しなさい。
答え
連続する $3$つの整数を $n-1, \ n, \ n+1$ とすると、
\begin{eqnarray*}
&& (n-1)(n+1)+1\\
&=& n^2-1+1\\
&=& n^2
\end{eqnarray*}
よって、連続する $3$つの整数で、いちばん小さい数といちばん大きい数の積に $1$ を加えると、真ん中の数の $2$ 乗になる。
<おぼえておきたい数学のおやくそく>
偶数…$2n$
奇数…$2n+1 \quad (2n-1)$
$3$の倍数…$3n$
$5$の倍数…$5n$
連続する $2$つの数…$n, \ n+1$
連続する $3$つの数…$n-1, \ n, \ n+1 \quad (n, \ n+1, \ n+2)$
連続する $2$つの偶数…$2n, \ 2n+2$
連続する $2$つの奇数…$2n-1, \ 2n+1$
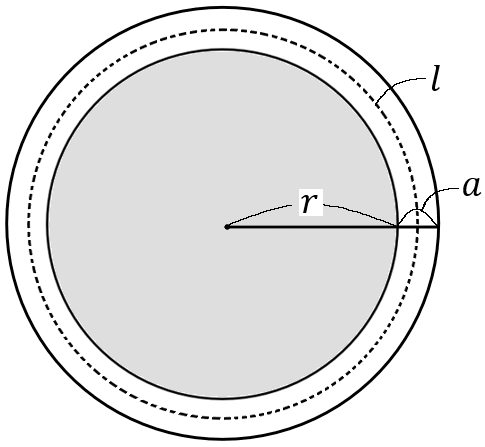
$\huge{9}$ 半径が $r$ m の花壇の周囲に、幅 $a$ mの道がある。道の中央を通る円周の長さを $l$ mとし、道の面積を $S$ ㎡とすると、$S=al$ となることを証明しなさい。
答え
\begin{eqnarray*}
S&=& \pi(r+a)^2-\pi r^2\\
&=& \pi(r^2+2ar+a^2)-\pi r^2\\
&=& \pi r^2+2\pi ar+\pi a^2-\pi r^2\\
&=& 2\pi ar+\pi a^2\quad …①
\end{eqnarray*}
道の中央を通る円周の半径の長さは $r+\cfrac{1}{2}a$ だから、
\begin{eqnarray*}
l&=& 2\pi (r+\cfrac{1}{2}a)\\
&=& 2\pi r+ \pi a\
\end{eqnarray*}
よって、
\begin{eqnarray*}
al&=& a(2\pi r+ \pi a)\\
&=& 2\pi ar+\pi a^2\quad…②
\end{eqnarray*}
①,②から、$S=al$
$S=al$ を証明しなさい、というのだから、「①$S$ について」と、「②$al$ について」、それぞれを式で表すことを考えていきます。
<①$S$ について>
$S$ というのは道の面積なのですから、いちばん大きい円からいちばん小さい円を引いたものになります。また、円の面積は $\pi \times(半径)^2$ です。
なのでいちばん小さい円の面積は $\pi r^2$ です。
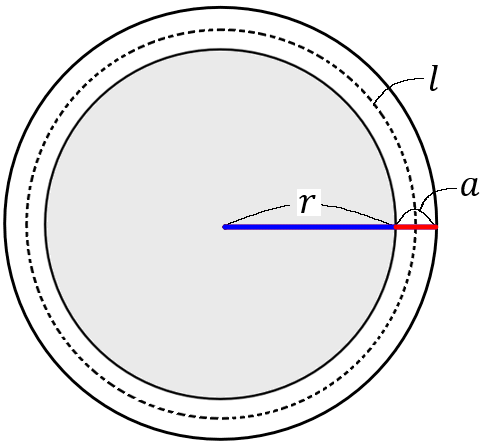 いちばん大きい円の半径は、右の図のように考えると、青い部分と赤い部分の和です。青の長さは$r,$ 赤は $a$ ですから、半径の長さは $(r+a)$ ということになります。
いちばん大きい円の半径は、右の図のように考えると、青い部分と赤い部分の和です。青の長さは$r,$ 赤は $a$ ですから、半径の長さは $(r+a)$ ということになります。
なので、大きい円の面積は
\begin{eqnarray*}
&& \pi (r+a)^2\\
&=& \pi (r^2+2ar+a^2) \\
&=& \pi r^2+2\pi ar+\pi a^2
\end{eqnarray*}
なので、
\begin{eqnarray*}
S&=& \pi r^2+2\pi ar+\pi a^2-\pi r^2\\
&=& 2\pi ar+\pi a^2
\end{eqnarray*}
<②$al$ について>
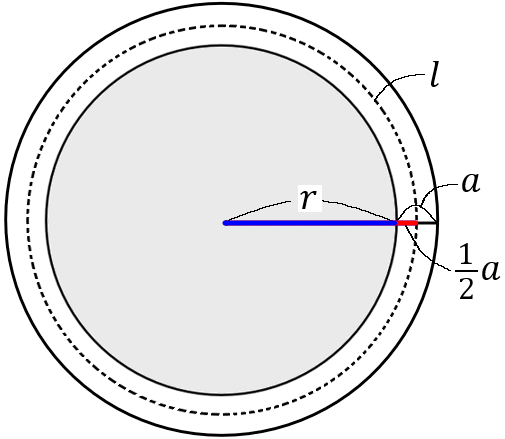 $l$ というのは、点線の円の周囲の長さのことです。点線の円の半径の長さは、右の図のように考えると、青い部分と赤い部分の和です。青の長さは$r,$ 赤は $\cfrac{1}{2}a$ ですから、点線の円の半径の長さは $\left(r+\cfrac{1}{2}a\right)$ ということになります。
$l$ というのは、点線の円の周囲の長さのことです。点線の円の半径の長さは、右の図のように考えると、青い部分と赤い部分の和です。青の長さは$r,$ 赤は $\cfrac{1}{2}a$ ですから、点線の円の半径の長さは $\left(r+\cfrac{1}{2}a\right)$ ということになります。
円周は $2\pi \times 半径$ ですから、
\begin{eqnarray*}
l&=& 2\pi \left(r+\cfrac{1}{2}a\right)\\
&=& 2\pi r+\pi a
\end{eqnarray*}
なので、
\begin{eqnarray*}
al&=& a(2\pi r+\pi a)\\
&=& 2\pi ar+\pi a^2
\end{eqnarray*}
これで①も②もどちらも $2\pi ar+\pi a^2$ になりました。なので、
$$S=al$$
答え(中3 1学期期末模擬テスト 第1回)
1$①7$ $②\cfrac{5}{2}y$ $-14x+9$ $④x=\cfrac{9}{8}$ $⑤h=\cfrac{2S}{a+b}$ $⑥x=12, \ y=-13$ $⑦y=-\cfrac{1}{2}x+3$ $⑧\cfrac{2}{9}$
2$①12x^2-28xy$ $②6x-4y$ $③20x-15$ $④ax+ay+bx+by$ $⑤3x^2-7x+2$ $⑥2a^2-ab-2a-b^2-b$ $⑦x^2-13x+44$ $⑧7x^2-12xy+3y^2$ $⑨x^2+4xy+4y^2-2x-4y+1$ $⑩9x^2-6xy+y^2-49$
3$①m(a+b+1)$ $②18ab(2a-b)$ $③(x+5)(x-12)$ $④(a-3)^2$ $⑤(7x+11y)^2$ $⑥\left(\cfrac{2}{3}a-1\right)^2$ $⑦(5x+2y)(5x-2y)$ $⑧\left(\cfrac{1}{6}x+\cfrac{1}{13}\right)\left(\cfrac{1}{6}x-\cfrac{1}{13}\right)$ $⑨3(x+4)(x-5)$ $⑩25(2x+y)(2x-y)$ $⑪(x-1)(a+1)$ $⑫(2a+b+2)(2a+b+3)$ $⑬(a+b)(c+d)$
4
\begin{eqnarray*}
(1)&①& 104^2&②& 99^2&③& 52\times48\\
&=& (100+4)^2&=& (100-1)^2&=& (50+2)(50-2)\\
&=& 10000+800+16\qquad&=& 10000-200+1\qquad&=& 2500-4\\
&=& 10816&=& 9801&=& 2496
\end{eqnarray*}
\begin{eqnarray*}
&④& 13.5^2-3.5^2\\
&=& (13.5+3.5)(13.5-3.5)\\
&=& 17\times10\\
&=& 170
\end{eqnarray*}
(2)$-1$ (3)$400$ (4)$-6$
\begin{eqnarray*}
(5)&①& \quad (x+7)(x-\boxed{\large{ \ 5 \ }}) \quad &②& \quad (5x-\boxed{\large{ \ 12y \ }})^2\\
&=& \quad x^2+\boxed{\large{ \ 2x \ }}-35&=& \quad 25x^2-\boxed{\large{ \ 120xy \ }}+144y^2
\\
\end{eqnarray*}
\begin{eqnarray*}
&③& \quad x^2-\boxed{\large{ \ 10x \ }}-39\qquad &④& \quad 4x^2-\boxed{\large{ \ 12xy \ }}+9y^2\\
&=& \quad (x+3)(x-\boxed{\large{ \ 13 \ }})&=& \quad (2x-\boxed{\large{ \ 3y \ }})^2
\\
\end{eqnarray*}
5(1)$①\pm1$ $②\pm4$ $③\pm\cfrac{2}{5}$ $④\pm0.1$ $⑤0$ $⑥ない$ $⑦\pm\sqrt{15}$
(2)$①×\ \pm8$ $②×\ 8$ $③〇 $ $④×\ 8$
(3)$2,$ $3,$ $5,$ $7,$ $11,$ $13,$ $17,$ $19,$ $23,$ $29$
(4)$①2^2\times5$ $②2^4\times3^2$
(5)$30$
(6)$15$
(7)$① -\sqrt{20} \gt -5$ $② -\sqrt{15}\lt-\sqrt{11}\lt\sqrt{11}\lt3.4$
(8)$①\sqrt{18}$ $②\sqrt{\cfrac{ \ 3 \ }{ \ 5 \ }}$ $③\sqrt{\cfrac{ \ 6 \ }{ \ 7 \ }}$
(9)$①3\sqrt{6}$ $②9\sqrt{2}$
(10)$①17.32$ $②54.77$ $③0.1732$ $④0.05477$
(11)$①\cfrac{\sqrt{15}}{5}$ $②\cfrac{\sqrt{14}}{2}$ $③2\sqrt{2}$
6$①\sqrt{10}$ $②-2\sqrt{3}$ $③4\sqrt{6}$ $④-\cfrac{\sqrt{6}}{2}$ $⑤\cfrac{2\sqrt{14}}{3}$ $⑥\cfrac{\sqrt{2}}{8}$ $⑦5\sqrt{5}+\sqrt{10}$ $⑧7\sqrt{3}$ $⑨\cfrac{8\sqrt{6}}{3}$ $⑩-5\sqrt{5}$ $⑪2\sqrt{5}-2\sqrt{6}$ $⑫3\sqrt{5}+3$ $⑬25-9\sqrt{5}$ $⑭3\sqrt{10}-2\sqrt{3}-3\sqrt{5}+\sqrt{6}$ $⑮30-12\sqrt{6}$ $⑯31$
7(1)$①1$ $②32$
(2)$1, \ 14, \ 25, \ 34, \ 41, \ 46, \ 49$
(3)$14$ 個
(4)有理数…$\cfrac{2}{27}, \ 0.\dot789\dot0, \ \sqrt{225}$
無理数…$2-\sqrt{2}, \ \cfrac{\pi}{3}$
(5)$①0.\dot{2}8571\dot{4}$ $②\cfrac{5}{9}$ $③\cfrac{100}{333}$
8
連続する $3$つの整数を $n-1, \ n, \ n+1$ とすると、
\begin{eqnarray*}
&& (n-1)(n+1)+1\\
&=& n^2-1+1\\
&=& n^2
\end{eqnarray*}
よって、連続する $3$つの整数で、いちばん小さい数といちばん大きい数の積に $1$ を加えると、真ん中の数の $2$ 乗になる。
9
\begin{eqnarray*}
S&=& \pi(r+a)^2-\pi r^2\\
&=& \pi(r^2+2ar+a^2)-\pi r^2\\
&=& \pi r^2+2\pi ar+\pi a^2-\pi r^2\\
&=& 2\pi ar+\pi a^2\quad …①
\end{eqnarray*}
道の中央を通る円周の半径の長さは $r+\cfrac{1}{2}a$ だから、
\begin{eqnarray*}
l&=& 2\pi (r+\cfrac{1}{2}a)\\
&=& 2\pi r+ \pi a\
\end{eqnarray*}
よって、
\begin{eqnarray*}
al&=& a(2\pi r+ \pi a)\\
&=& 2\pi ar+\pi a^2\quad…②
\end{eqnarray*}
①,②から、$S=al$