数学 中3 6章 円 第1回(全12問)
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
(1) 次の $ \boxed{\LARGE\phantom{hoge}}$ の中にあてはまる言葉をいれましょう。

答え

半径の長さはみんな同じ。
接点を通る半径と接線は垂直。
弦と垂直な半径は弦を二等分する。
(2) 円周角の定理
① $1$ つの弧に対する円周角の大きさは、その弧に対する中心角の大きさの $ \boxed{\LARGE\phantom{hoge}}$ である。
② $1$ つの弧に対する円周角の大きさは
$\boxed{\LARGE\phantom{hogehogehoge}}$ 。
答え
① 半分 ② すべて等しい

※円周角がどうして中心角の半分になるのかを問われることもあるので、なぜそうなるのかも説明できるようにしておきましょう。
(3) 下の①の図で、$x$ の値を求めなさい。②③の図で、$x, \ y$ の値を求めなさい。

答え
①$x=61$ ②$x=116, \ y=58$
③$x=90, \ y=60$
③…半円の弧に対する円周角は$90^{ \circ }$ です。
(4) 下の①~⑭の図で、$x$ の値を求めなさい。
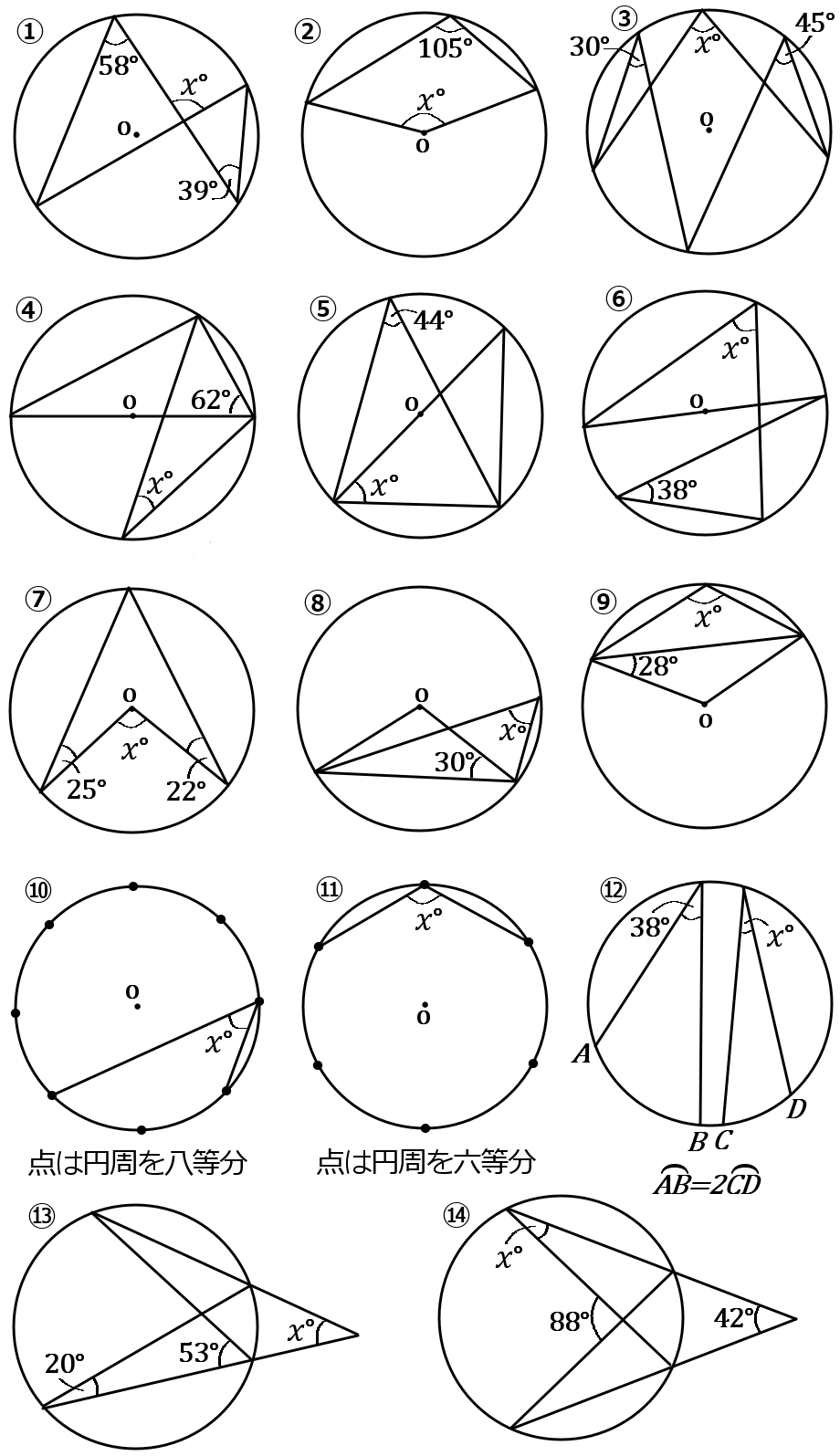
答え
①$x=97$
②$x=150$
③$x=75$
④$x=28$
⑤$x=46$
⑥$x=52$
⑦$x=94$
⑧$x=60$
⑨$x=118$
⑩$x=45$
⑪$x=120$
⑫$x=19$
⑬$x=33$
⑭$x=23$
 ①$x^{ \circ }=58^{ \circ }+39^{ \circ }=97^{ \circ }$
①$x^{ \circ }=58^{ \circ }+39^{ \circ }=97^{ \circ }$
②$x^{ \circ }=360^{ \circ }-(105^{ \circ } \times2)$
$=360^{ \circ }-210^{ \circ }=150^{ \circ }$
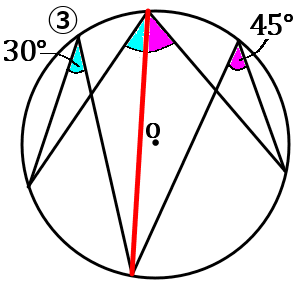
③図のように補助線をひいて考えます。円周角の定理から、色のついた部分はどちらも同じ大きさです。$x^{ \circ }=30^{ \circ }+45^{ \circ }=75^{ \circ }$
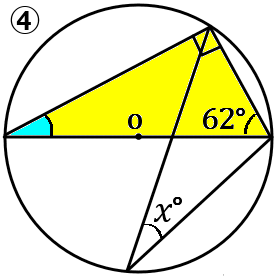 ④半円の弧に対する円周角は$90^{ \circ }$ です。黄色の直角三角形で考えて、青の部分は $180^{ \circ }-(90^{ \circ }+62^{ \circ })=28^{ \circ }$。青の部分と $x$ は同じです。
④半円の弧に対する円周角は$90^{ \circ }$ です。黄色の直角三角形で考えて、青の部分は $180^{ \circ }-(90^{ \circ }+62^{ \circ })=28^{ \circ }$。青の部分と $x$ は同じです。
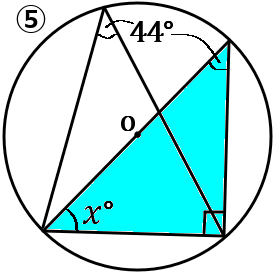 ⑤半円の弧に対する円周角は$90^{ \circ }$ です。青の直角三角形で考えて、$x^{ \circ }=180^{ \circ }-(90^{ \circ }+44^{ \circ })=46^{ \circ }$
⑤半円の弧に対する円周角は$90^{ \circ }$ です。青の直角三角形で考えて、$x^{ \circ }=180^{ \circ }-(90^{ \circ }+44^{ \circ })=46^{ \circ }$
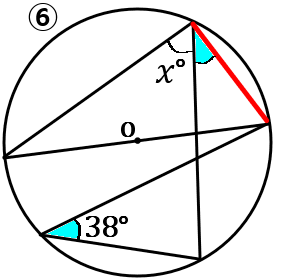 ⑥図のように補助線をひいて考えます。半円の弧の円周角は$90^{ \circ }$ です。また、青の部分の大きさは同じです。なので、$x^{ \circ }=90^{ \circ }-38^{ \circ }=52^{ \circ }$
⑥図のように補助線をひいて考えます。半円の弧の円周角は$90^{ \circ }$ です。また、青の部分の大きさは同じです。なので、$x^{ \circ }=90^{ \circ }-38^{ \circ }=52^{ \circ }$
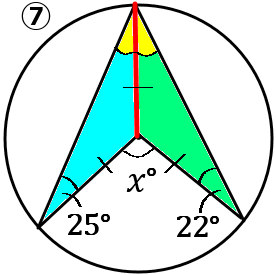 ⑦図のように補助線をひいて考えます。色のついた三角形はどちらも二等辺三角形なので、底角が等しいです。なので黄色の部分の大きさは $25^{ \circ }+22^{ \circ }$ です。$x^{ \circ }=(25^{ \circ }+22^{ \circ })\times2=94^{ \circ }$
⑦図のように補助線をひいて考えます。色のついた三角形はどちらも二等辺三角形なので、底角が等しいです。なので黄色の部分の大きさは $25^{ \circ }+22^{ \circ }$ です。$x^{ \circ }=(25^{ \circ }+22^{ \circ })\times2=94^{ \circ }$
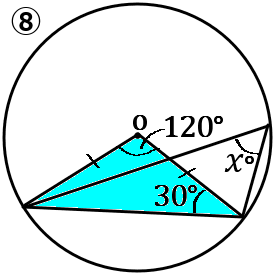 ⑧色のついた三角形は二等辺三角形になるので、底角が等しいです。なので頂角は $180^{ \circ }-(30^{ \circ }\times2)=120^{ \circ }$ となります。$x^{ \circ }=120^{ \circ }\times\cfrac{1}{2}=60^{ \circ }$
⑧色のついた三角形は二等辺三角形になるので、底角が等しいです。なので頂角は $180^{ \circ }-(30^{ \circ }\times2)=120^{ \circ }$ となります。$x^{ \circ }=120^{ \circ }\times\cfrac{1}{2}=60^{ \circ }$
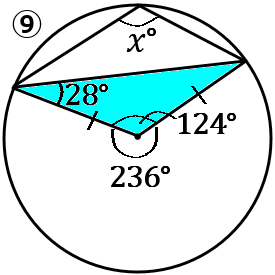 ⑨色のついた三角形は二等辺三角形になるので、底角が等しいです。なので頂角は $180^{ \circ }-(28^{ \circ }\times2)=124^{ \circ }$ となります。$x^{ \circ }=(360^{ \circ }-124^{ \circ })\times\cfrac{1}{2}=236^{ \circ }\times\cfrac{1}{2}=118^{ \circ }$
⑨色のついた三角形は二等辺三角形になるので、底角が等しいです。なので頂角は $180^{ \circ }-(28^{ \circ }\times2)=124^{ \circ }$ となります。$x^{ \circ }=(360^{ \circ }-124^{ \circ })\times\cfrac{1}{2}=236^{ \circ }\times\cfrac{1}{2}=118^{ \circ }$
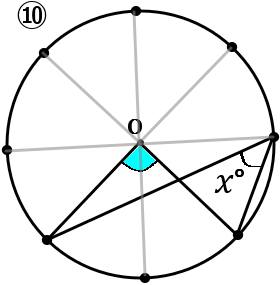 ⑩色のついた部分の大きさは、$360^{ \circ }\times\cfrac{2}{8}=90^{ \circ }$
⑩色のついた部分の大きさは、$360^{ \circ }\times\cfrac{2}{8}=90^{ \circ }$
なので $x^{ \circ }=90^{ \circ }\times\cfrac{1}{2}=45^{ \circ }$
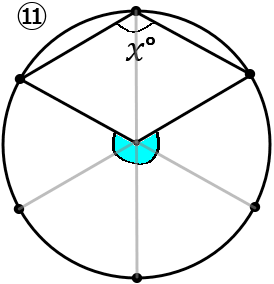 ⑪色のついた部分の大きさは、$360^{ \circ }\times\cfrac{4}{6}=240^{ \circ }$
⑪色のついた部分の大きさは、$360^{ \circ }\times\cfrac{4}{6}=240^{ \circ }$
なので $x^{ \circ }=240^{ \circ }\times\cfrac{1}{2}=120^{ \circ }$
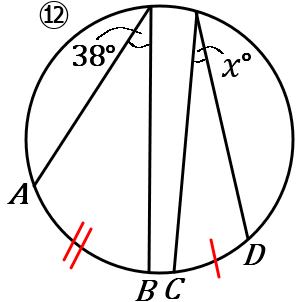 ⑫弧の長さは、その弧に対する円周角の大きさに比例します。なので、$38^{ \circ }:x^{ \circ }=\stackrel{ \Large \frown }{ AB } : \stackrel{ \Large \frown }{ CD }=2:1$
⑫弧の長さは、その弧に対する円周角の大きさに比例します。なので、$38^{ \circ }:x^{ \circ }=\stackrel{ \Large \frown }{ AB } : \stackrel{ \Large \frown }{ CD }=2:1$
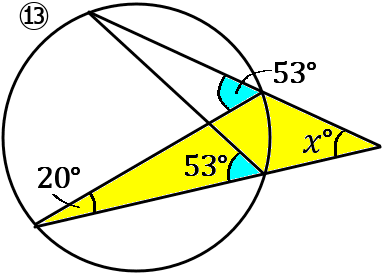 ⑬水色の部分の大きさは同じです。黄色の三角形で考えて、$x^{ \circ }+20^{ \circ }=53^{ \circ }$
⑬水色の部分の大きさは同じです。黄色の三角形で考えて、$x^{ \circ }+20^{ \circ }=53^{ \circ }$
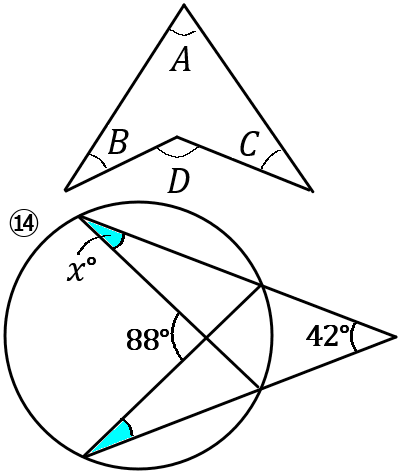 ⑭右の形で、$\angle A + \angle B + \angle C = \angle D$ というのを利用すると簡単です。
⑭右の形で、$\angle A + \angle B + \angle C = \angle D$ というのを利用すると簡単です。
⑭の図で、色のついた部分の角の大きさは同じなので、$42^{ \circ }+x^{ \circ }+x^{ \circ }=88^{ \circ }$
(5) 円周角の定理の逆
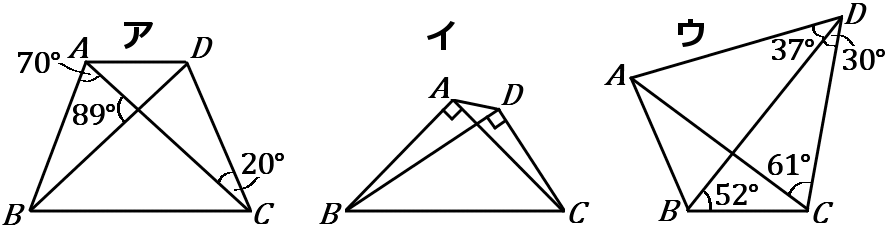
下のア~ウのうち、$4$ 点 $A,B,C,D$ が $1$つの円周上にあるものをすべて選びなさい。
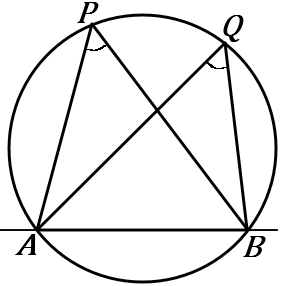 $2$ 点 $P,Q$ が直線 $AB$ の同じ側にあって、$\angle APB=\angle AQB$ ならば、$4$ 点 $A,B,P,Q$ は、$1$つの円周上にある。
$2$ 点 $P,Q$ が直線 $AB$ の同じ側にあって、$\angle APB=\angle AQB$ ならば、$4$ 点 $A,B,P,Q$ は、$1$つの円周上にある。
答え
イ,ウ
 ア…色のついた三角形で考えると、$\angle ABD=21^{ \circ }$ です。$\angle ABD \neq \angle ACD$ なので、$4$ 点 $A,B,C,D$ は $1$つの円周上にはありません。
ア…色のついた三角形で考えると、$\angle ABD=21^{ \circ }$ です。$\angle ABD \neq \angle ACD$ なので、$4$ 点 $A,B,C,D$ は $1$つの円周上にはありません。
イ…$\angle BAC = \angle BDC =90^{ \circ }$ です。なので、$4$ 点 $A,B,C,D$ は $1$つの円周上にあります。
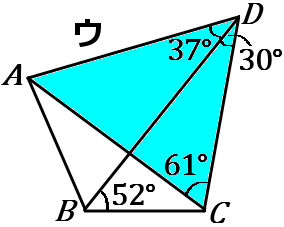 ウ…色のついた三角形で考えると、$\angle DAC=180^{ \circ }-(37^{ \circ }+30^{ \circ }+61^{ \circ })$
ウ…色のついた三角形で考えると、$\angle DAC=180^{ \circ }-(37^{ \circ }+30^{ \circ }+61^{ \circ })$
=$52^{ \circ }$ です。$\angle DAC = \angle DBC$ なので、$4$ 点 $A,B,C,D$ は $1$つの円周上にあります。
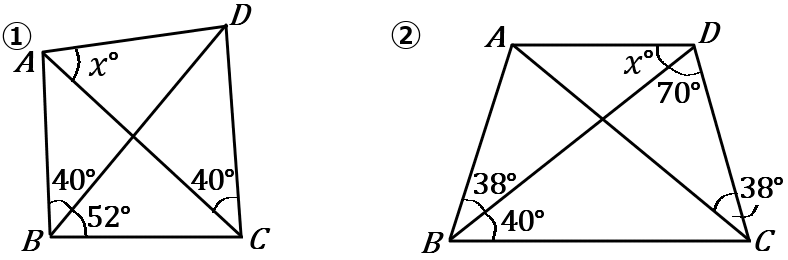
(6) 下の①②の図で、$x$ の値を求めなさい。
答え
① $x=52$ ② $x=32$
 ①$\angle ABD=\angle ACD$ ですから、$4$ 点 $A,B,C,D$ は $1$つの円周上にあります。円周角の定理より、$\angle x=\angle DBC=52^{ \circ }$
①$\angle ABD=\angle ACD$ ですから、$4$ 点 $A,B,C,D$ は $1$つの円周上にあります。円周角の定理より、$\angle x=\angle DBC=52^{ \circ }$
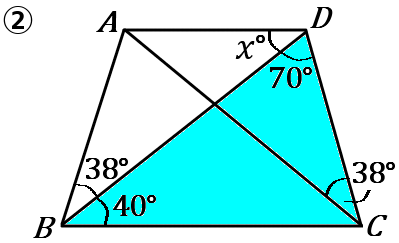
②$\angle ABD=\angle ACD$ ですから、$4$ 点 $A,B,C,D$ は $1$つの円周上にあります。色のついた三角形で考えると、$\angle ACB+70^{ \circ }+40^{ \circ }+38^{ \circ }=180^{ \circ }$ ですから、$\angle ACB=32^{ \circ }$ です。んで、円周角の定理より、$\angle x=\angle ACB$ です。
 (7) 方べきの定理
(7) 方べきの定理
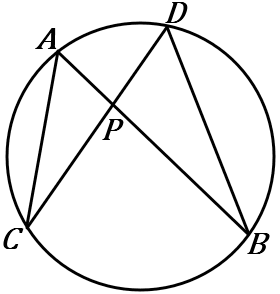
右の図で、$4$ 点 $A,B,C,D$ は $1$つの円周上にある。
$PA\times PB=PC\times PD$を証明しなさい。
答え
〈証明〉
$\triangle PAC$ と $\triangle PDB$ で、
対頂角だから、$\angle APC=\angle DPB$ ……①
$\stackrel{ \Large \frown }{ AD }$ に対する円周角だから、$\angle ACP=\angle DBP$ ……②
①②より、$2$ 組の角がそれぞれ等しいので
$\triangle PAC$ ∽$\ \triangle PDB$
よって、$PA:PD=PC:PB$
したがって、$PA\times PB=PC\times PD$
$\triangle PAC$ ∽$\ \triangle PDB$ を証明すればいいです。
ちなみに、この $PA\times PB=PC\times PD$ を方べきの定理といいます。こんなふうにできた $2$つの三角形はかならず相似で、$PA\times PB=PC\times PD$ です。
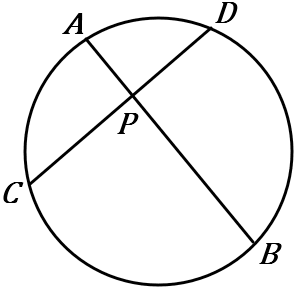 右の図のように、円の内部に点 $P$ をとり、$P$ を通る $2$ 本の直線をひいて、円との交点を $A,B,C,D$ とすると、
右の図のように、円の内部に点 $P$ をとり、$P$ を通る $2$ 本の直線をひいて、円との交点を $A,B,C,D$ とすると、
$PA\times PB=PC\times PD$
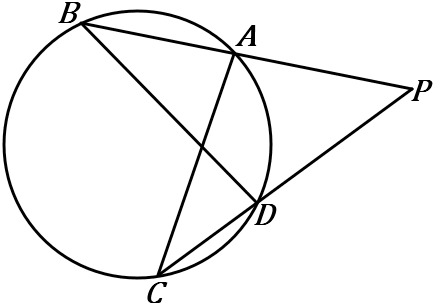 (8) 右の図で、$4$ 点 $A,B,C,D$ は $1$つの円周上にある。
(8) 右の図で、$4$ 点 $A,B,C,D$ は $1$つの円周上にある。
$PA\times PB=PC\times PD$を証明しなさい。
答え
〈証明〉
$\triangle PAC$ と $\triangle PDB$ で、
共通な角だから、$\angle APC=\angle DPB$ ……①
$\stackrel{ \Large \frown }{ AD }$ に対する円周角だから、$\angle ACD=\angle DBA$ ……②
①②より、$2$ 組の角がそれぞれ等しいので
$\triangle PAC$ ∽$\ \triangle PDB$
よって、$PA:PD=PC:PB$
したがって、$PA\times PB=PC\times PD$
$\triangle PAC$ ∽$\ \triangle PDB$ を証明すればいいです。
ちなみに、この $PA\times PB=PC\times PD$ を方べきの定理といいます。(7)の問題も方べきの定理ですが、こっちもそうです。パート2みたいなもんです。こんなふうにできた $2$つの三角形はかならず相似で、$PA\times PB=PC\times PD$ です。
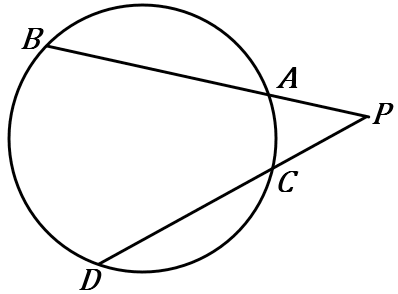 右の図のように、円の外部に点 $P$ をとり、$P$ を通る $2$ 本の直線をひいて、円との交点を $A,B,C,D$ とすると、
右の図のように、円の外部に点 $P$ をとり、$P$ を通る $2$ 本の直線をひいて、円との交点を $A,B,C,D$ とすると、
$PA\times PB=PC\times PD$
(9)
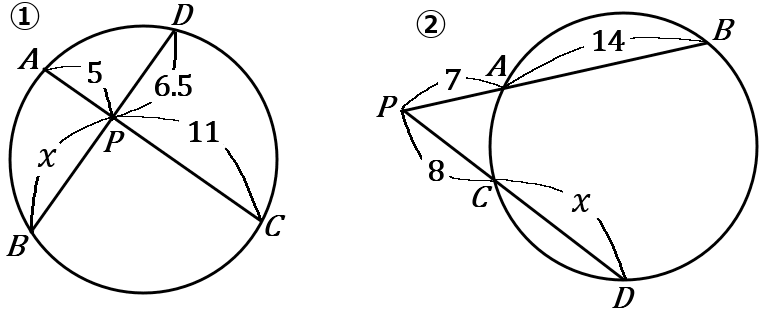
下の①、②の図で、$x$ の値を求めなさい。
答え
① $x=\cfrac{110}{13}$ ② $x=\cfrac{83}{8}$
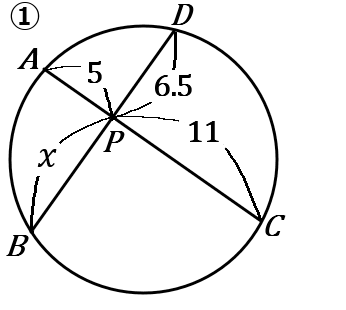 ①方べきの定理より、
\begin{eqnarray*}
AP\times PC&=&DP\times PB\\
5\times11&=&6.5\times x\\
55&=&6.5x\\
x&=&\cfrac{55}{6.5}=\cfrac{110}{13}
\end{eqnarray*}
※$\triangle PAB$ ∽$\ \triangle PDC$ や、$\triangle PAD$ ∽$\ \triangle PBC$ で比例式をたててもいけます。好きなやり方でやってください。
①方べきの定理より、
\begin{eqnarray*}
AP\times PC&=&DP\times PB\\
5\times11&=&6.5\times x\\
55&=&6.5x\\
x&=&\cfrac{55}{6.5}=\cfrac{110}{13}
\end{eqnarray*}
※$\triangle PAB$ ∽$\ \triangle PDC$ や、$\triangle PAD$ ∽$\ \triangle PBC$ で比例式をたててもいけます。好きなやり方でやってください。
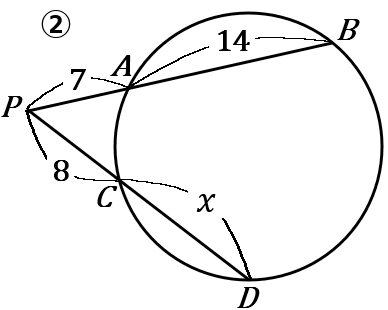 ②方べきの定理より、
\begin{eqnarray*}
PA\times PB&=&PC\times PD\\
7\times(7+14)&=&8\times(8+x)\\
147&=&64+8x\\
8x&=&147-64\\
x&=&\cfrac{83}{8}
\end{eqnarray*}
※$\triangle PAD$ ∽$\ \triangle PCB$ や、$\triangle PAC$ ∽$\ \triangle PDB$ で比例式をたててもいけます。好きなやり方でやってください。
②方べきの定理より、
\begin{eqnarray*}
PA\times PB&=&PC\times PD\\
7\times(7+14)&=&8\times(8+x)\\
147&=&64+8x\\
8x&=&147-64\\
x&=&\cfrac{83}{8}
\end{eqnarray*}
※$\triangle PAD$ ∽$\ \triangle PCB$ や、$\triangle PAC$ ∽$\ \triangle PDB$ で比例式をたててもいけます。好きなやり方でやってください。
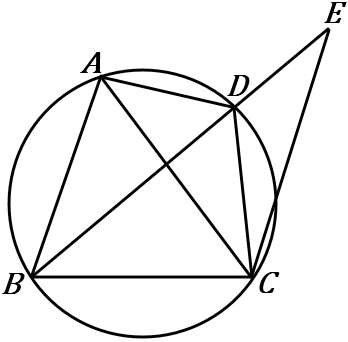 (10) 右の図で、$4$ 点 $A,B,C,D$ は $1$つの円周上にある。また、$AB /\!/ EC$ である。$\triangle ACD$ ∽$\ \triangle BEC$ を証明しなさい。
(10) 右の図で、$4$ 点 $A,B,C,D$ は $1$つの円周上にある。また、$AB /\!/ EC$ である。$\triangle ACD$ ∽$\ \triangle BEC$ を証明しなさい。
答え
〈証明〉
$\triangle ACD$ と $\triangle BEC$ で、
$\stackrel{ \Large \frown }{ CD }$ に対する円周角だから、$\angle CAD=\angle DBC$ ……①
$\stackrel{ \Large \frown }{ AD }$ に対する円周角だから、$\angle ACD=\angle ABD$ ……②
平行線の錯角だから、$\angle BEC=\angle ABD$ ……③
②③より、$\angle ACD=\angle BEC$ ……④
①④より、$2$ 組の角がそれぞれ等しいので
$\triangle ACD$ ∽$\ \triangle BEC$
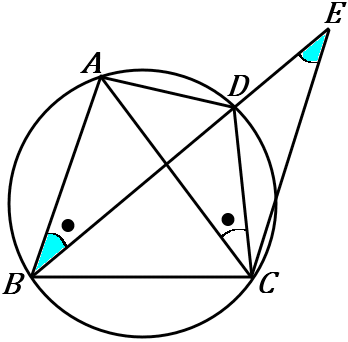 平行線の錯角なので、色のついた角の大きさは同じです。そして、円周角の定理より、$\angle ACD=\angle ABD$ です。なので、$\angle ACD=\angle BEC$ となります。
平行線の錯角なので、色のついた角の大きさは同じです。そして、円周角の定理より、$\angle ACD=\angle ABD$ です。なので、$\angle ACD=\angle BEC$ となります。
 (11) 円に内接する四角形の性質
(11) 円に内接する四角形の性質
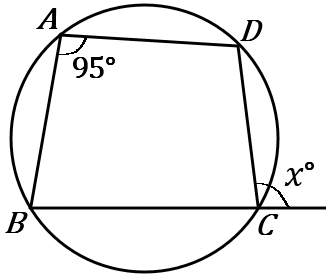
右の図で、$4$ 点 $A,B,C,D$ は $1$つの円周上にある。$x$ の値を求めなさい。
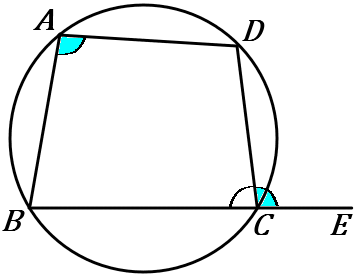 ①対角の和は$180^{ \circ }$ である。
①対角の和は$180^{ \circ }$ である。
②外角はそれととなりあう内角の対角に等しい。
①…$\angle A+\angle DCB=180^{ \circ }$
$\angle B+\angle D=180^{ \circ }$
②…$\angle A=\angle DCE$
答え
$x=95$
この問題は、円周角の定理を利用すればできるのですが、円に内接する四角形の性質を利用すれば、すごく簡単です。ていうか、即答できちゃう問題です。
円に内接する四角形の性質を利用するとラクになる問題がよく出題されるので、この性質はおぼえておきたいです。
 (12) 接弦定理
(12) 接弦定理
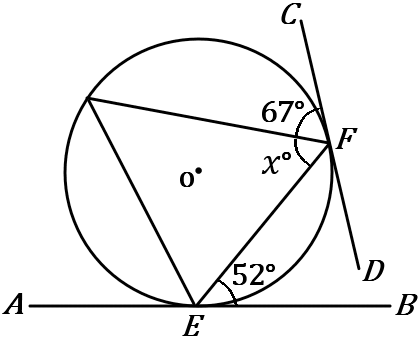
右の図で、$AB, \ CD$ は円$O$ の接線であり、$E,F$ はその接点である。$x$ の値を求めなさい。
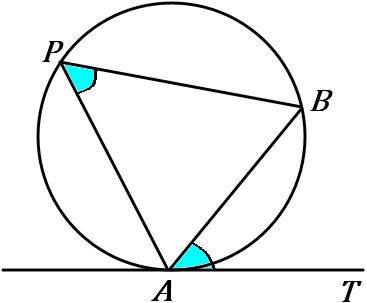 円の接線と接点を通る弦とがつくる角は、その角内にある弧に対する円周角に等しい。
円の接線と接点を通る弦とがつくる角は、その角内にある弧に対する円周角に等しい。
$\angle TAB=\angle P$
答え
$x=61$
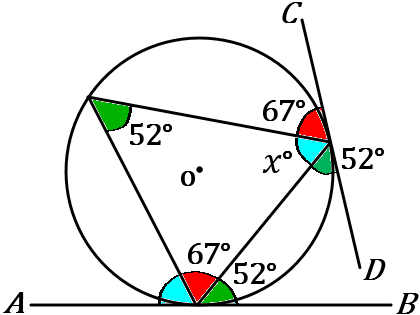 接弦定理といわれてる定理がありまして、それは上の通りです。「接線と弦がつくる角の性質」というタイトルですが、これ、接弦定理というやつです。言葉でいうとややこしいですが、上の図の水色の角が等しくなります。接線と弦がつくる角と、その弦の弧がつくる円周角が等しくなります。
接弦定理といわれてる定理がありまして、それは上の通りです。「接線と弦がつくる角の性質」というタイトルですが、これ、接弦定理というやつです。言葉でいうとややこしいですが、上の図の水色の角が等しくなります。接線と弦がつくる角と、その弦の弧がつくる円周角が等しくなります。
この定理により、この問題の緑の部分と赤の部分と水色の部分の角の大きさはそれぞれ等しいです。
なので $x=61$ です。
接弦定理も、知っているとすんなりできてしまう問題がよく出題されるので、おぼえておきたいです。ちょっとおぼえづらいです。図をよく見ておぼえてくださいね。
答え(中3 6章 円 第1回)
(1)
(2)① 半分 ② すべて等しい
(3)①$x=61$ ②$x=116, \ y=58$
③$x=90, \ y=60$
(4)①$x=97$
②$x=150$
③$x=75$
④$x=28$
⑤$x=46$
⑥$x=52$
⑦$x=94$
⑧$x=60$
⑨$x=118$
⑩$x=45$
⑪$x=120$
⑫$x=19$
⑬$x=33$
⑭$x=23$
(5)イ,ウ
(6)① $x=52$ ② $x=32$
(7)〈証明〉
$\triangle PAC$ と $\triangle PDB$ で、
対頂角だから、$\angle APC=\angle DPB$ ……①
$\stackrel{ \Large \frown }{ AD }$ に対する円周角だから、$\angle ACP=\angle DBP$ ……②
①②より、$2$ 組の角がそれぞれ等しいので
$\triangle PAC$ ∽$\ \triangle PDB$
よって、$PA:PD=PC:PB$
したがって、$PA\times PB=PC\times PD$
$\triangle PAC$ と $\triangle PDB$ で、
共通な角だから、$\angle APC=\angle DPB$ ……①
$\stackrel{ \Large \frown }{ AD }$ に対する円周角だから、$\angle ACD=\angle DBA$ ……②
①②より、$2$ 組の角がそれぞれ等しいので
$\triangle PAC$ ∽$\ \triangle PDB$
よって、$PA:PD=PC:PB$
したがって、$PA\times PB=PC\times PD$
(9)① $x=\cfrac{110}{13}$ ② $x=\cfrac{83}{8}$
(10)〈証明〉
$\triangle ACD$ と $\triangle BEC$ で、
$\stackrel{ \Large \frown }{ CD }$ に対する円周角だから、$\angle CAD=\angle DBC$ ……①
$\stackrel{ \Large \frown }{ AD }$ に対する円周角だから、$\angle ACD=\angle ABD$ ……②
平行線の錯角だから、$\angle BEC=\angle ABD$ ……③
②③より、$\angle ACD=\angle BEC$ ……④
①④より、$2$ 組の角がそれぞれ等しいので
$\triangle ACD$ ∽$\ \triangle BEC$
(11)$x=95$
(12)$x=61$