数学 中3 7章 三平方の定理 第1回(全16問)
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
(1) 次の $ \boxed{\LARGE\phantom{hoge}}$ の中にあてはまる言葉や式をいれましょう。
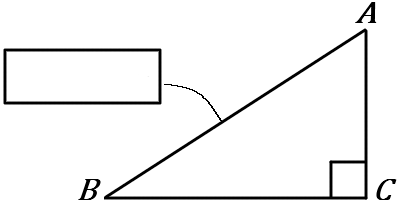
① $1$つの角が直角である三角形を直角三角形といい、直角に対する辺を $ \boxed{\LARGE\phantom{hoge}}$ という。
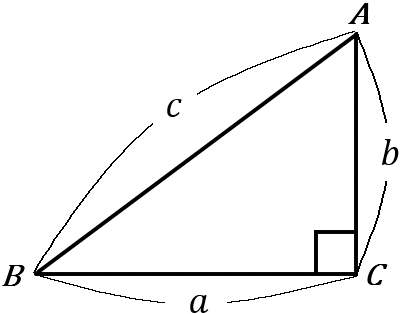
三平方の定理
② 右の直角三角形$ABC$ で、$3$ 辺 $a, \ b, \ c$ の長さの関係は、 $ \boxed{\LARGE\phantom{hogehogehogehoge}}$
答え
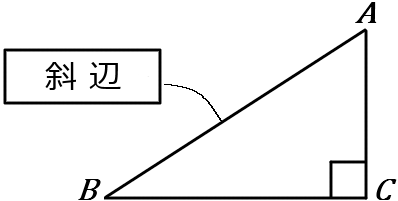
① 斜辺 ② $a^2+b^2=c^2$
 直角三角形の直角をはさむ$2$ 辺の長さを$a, \ b$, 斜辺の長さを$c$ とすると、
直角三角形の直角をはさむ$2$ 辺の長さを$a, \ b$, 斜辺の長さを$c$ とすると、
$\quad \large{a^2+b^2=c^2}$
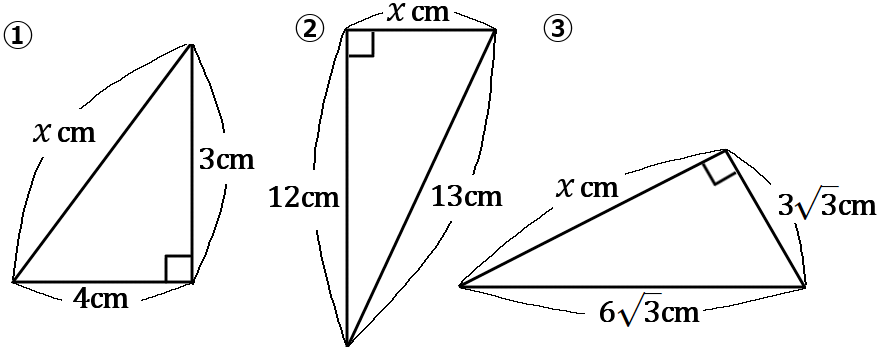
(2) 下の①~③の図で、$x$ の値を求めなさい。
答え
① $x=5$ ② $x=5$ ③ $x=9$
\begin{eqnarray*} ①x^2&=&3^2+4^2 \\ &=&25 \\ x&=&\pm \sqrt{25} =\pm 5 \\ x&\gt&0 \ だから \\ x&=&5\\ \end{eqnarray*} \begin{eqnarray*} ②x^2&=&13^2-12^2 \\ &=&25 \\ x&=&\pm \sqrt{25} =\pm 5 \\ x&\gt&0 \ だから \\ x&=&5\\ \end{eqnarray*} \begin{eqnarray*} ③x^2&=&(6\sqrt{3})^2-(3\sqrt{3})^2 \\ &=&81 \\ x&=&\pm \sqrt{81} =\pm 9 \\ x&\gt&0 \ だから \\ x&=&9\\ \end{eqnarray*}
三平方の定理の逆
(3) 次のア~ウの中から、直角三角形であるものをすべて選びなさい。
ア $3cm, \ 4cm, \ 5cm$
イ $4cm, \ 5cm, \ 6cm$
ウ $6cm, \ 6\sqrt{2}cm, \ 6cm$
答え
ア,ウ
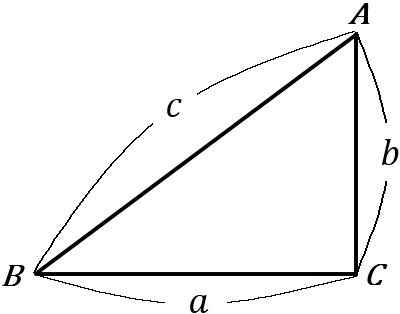 $3$ 辺の長さが $a, \ b, \ c$ の三角形で、
$a^2+b^2=c^2$ ならば、その三角形は $c$ を斜辺とする直角三角形である。
$3$ 辺の長さが $a, \ b, \ c$ の三角形で、
$a^2+b^2=c^2$ ならば、その三角形は $c$ を斜辺とする直角三角形である。
ア $3^2=9, \ 4^2=16, \ 5^2=25$
$9+16=25$ なので、アは $5cm$ の辺を斜辺とする直角三角形
イ $4^2=16, \ 5^2=25, \ 6^2=36$
$16+25\neq 36$ なので、直角三角形ではない
ウ $6^2=36, \ (6\sqrt{2})^2=72, \ 6^2=36$
$36+36=72$ なので、ウは $6\sqrt{2}cm$ の辺を斜辺とする直角三角形
$30^{ \circ }, \ 60^{ \circ }, \ 90^{ \circ }$ の直角三角形
(4) 下の①~③の図で、$x$ の値を求めなさい。④は $\triangle ABC$ の面積を求めなさい。
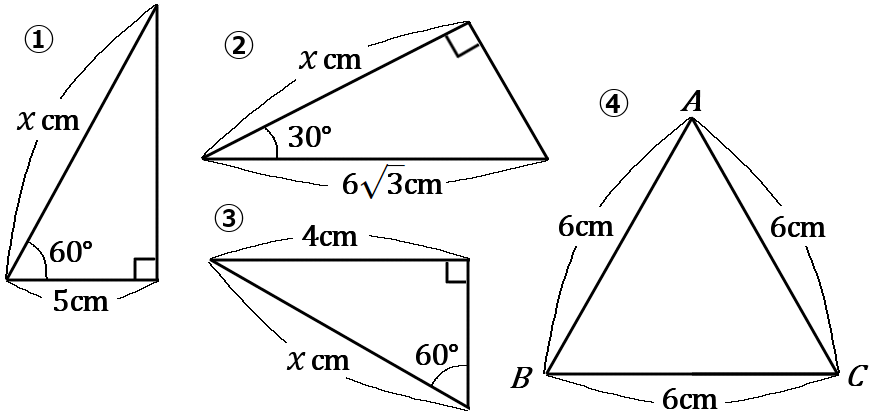
答え
①$x=10$
②$x=9$
③$x=\cfrac{8\sqrt{3}}{3}$
④$9\sqrt{3}cm^2$
 $30^{ \circ }, \ 60^{ \circ }, \ 90^{ \circ }$ の直角三角形の辺の比は
$30^{ \circ }, \ 60^{ \circ }, \ 90^{ \circ }$ の直角三角形の辺の比は
$\quad \large{1:2:\sqrt{3}}$
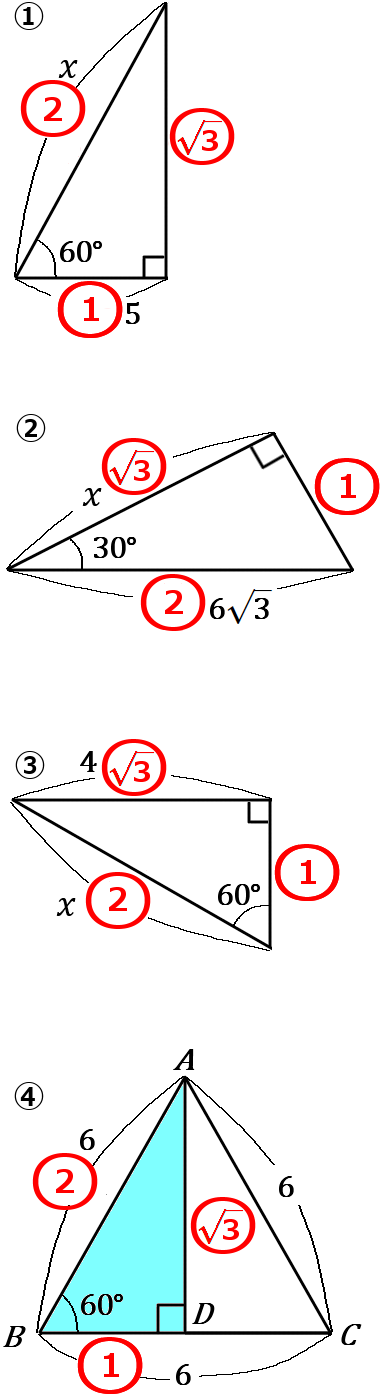 ① $30^{ \circ }, \ 60^{ \circ }, \ 90^{ \circ }$ の直角三角形なので、$1:2:\sqrt{3}$ の比が使えます。
\begin{eqnarray*}
x:2&=&5:1 \\
x&=&10
\end{eqnarray*}
① $30^{ \circ }, \ 60^{ \circ }, \ 90^{ \circ }$ の直角三角形なので、$1:2:\sqrt{3}$ の比が使えます。
\begin{eqnarray*}
x:2&=&5:1 \\
x&=&10
\end{eqnarray*}
② $30^{ \circ }, \ 60^{ \circ }, \ 90^{ \circ }$ の直角三角形なので、$1:2:\sqrt{3}$ の比が使えます。
\begin{eqnarray*}
x:\sqrt{3}&=&6\sqrt{3}:2\\
2x&=&18 \\
x&=&9
\end{eqnarray*}
③ $30^{ \circ }, \ 60^{ \circ }, \ 90^{ \circ }$ の直角三角形なので、$1:2:\sqrt{3}$ の比が使えます。
\begin{eqnarray*}
x:2&=&4:\sqrt{3}\\
\sqrt{3}x&=&8 \\
x&=&\cfrac{8}{\sqrt{3}}=\cfrac{8\sqrt{3}}{3}\\
\end{eqnarray*}
④三角形の面積は、底辺$\times$高さ$\times \cfrac{1}{2}$ です。
また、二等辺三角形の頂角の二等分線は、底辺を垂直に二等分します。
正三角形の $1$つの角の大きさは $60^{ \circ }$ です。
なので、$A$ から辺$BC$ におろした垂線と $BC$ との交点を $D$ とすると、$\triangle ABD$ は、$30^{ \circ }, \ 60^{ \circ }, \ 90^{ \circ }$ の直角三角形となり、$1:2:\sqrt{3}$ の辺の比が利用できることになります。
\begin{eqnarray*}
AD:\sqrt{3}&=&6:2\\
AD&=&3\sqrt{3}
\end{eqnarray*}
これで $AD$(高さ)が $3 \sqrt{3}$ だと求められました。なので面積は、$6\times 3\sqrt{3} \times \cfrac{1}{2}=9\sqrt{3}$
※正三角形は、$1$ 辺の長さがわかれば、高さを求められます。なので、面積も求められます。このことは、入試でよく問われます。
直角二等辺三角形($45^{ \circ }, \ 45^{ \circ }, \ 90^{ \circ }$ の三角形)
(5) 下の①~③の図で、$x$ の値を求めなさい。
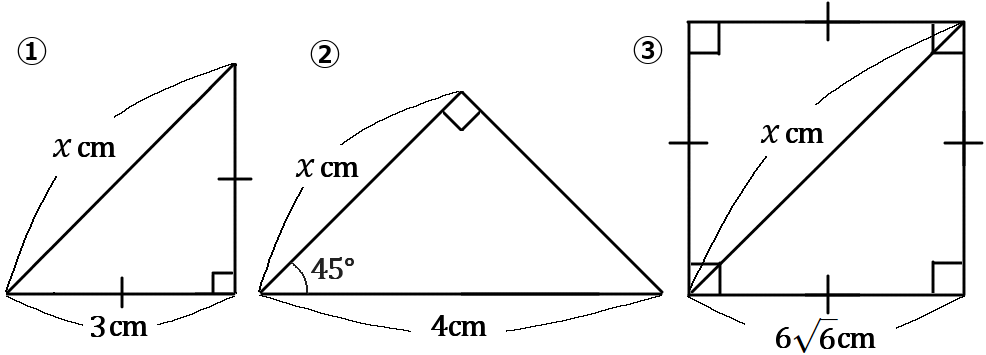
答え
①$x=3\sqrt{2}$
②$x=2\sqrt{2}$
③$x=12\sqrt{3}$
 直角二等辺三角形($45^{ \circ }, \ 45^{ \circ }, \ 90^{ \circ }$ の三角形)の辺の比は
直角二等辺三角形($45^{ \circ }, \ 45^{ \circ }, \ 90^{ \circ }$ の三角形)の辺の比は
$\quad \large{1:1:\sqrt{2}}$
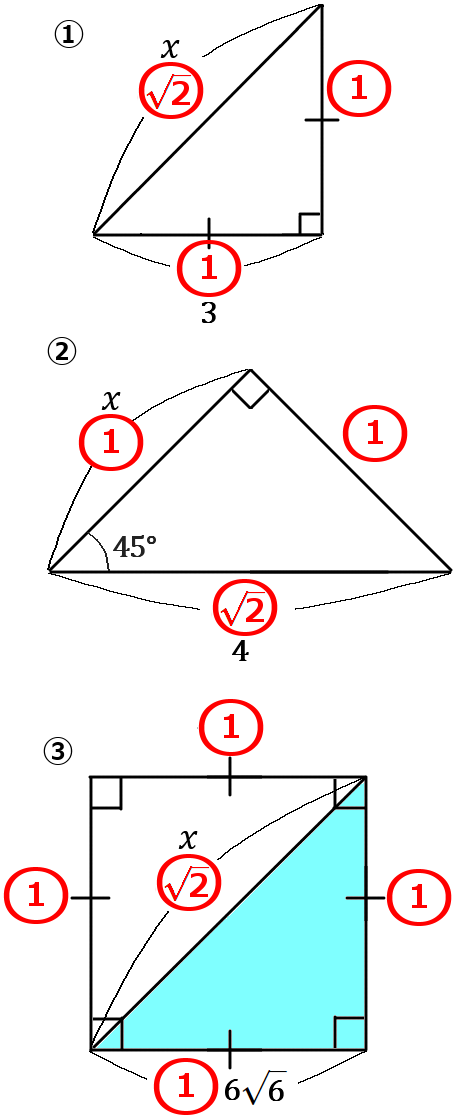 ① 直角二等辺三角形なので、$1:1:\sqrt{2}$ の比が使えます。
\begin{eqnarray*}
x:\sqrt{2}&=&3:1 \\
x&=&3\sqrt{2}
\end{eqnarray*}
① 直角二等辺三角形なので、$1:1:\sqrt{2}$ の比が使えます。
\begin{eqnarray*}
x:\sqrt{2}&=&3:1 \\
x&=&3\sqrt{2}
\end{eqnarray*}
② 直角二等辺三角形なので、$1:1:\sqrt{2}$ の比が使えます。
\begin{eqnarray*}
x:1&=&4:\sqrt{2}\\
\sqrt{2}x&=&4 \\
x&=&\cfrac{4}{\sqrt{2}}=2\sqrt{2}
\end{eqnarray*}
③ 水色の三角形は直角二等辺三角形なので、$1:1:\sqrt{2}$ の比が使えます。
\begin{eqnarray*}
x:\sqrt{2}&=&6\sqrt{6}:1\\
x&=&\sqrt{2} \times 6\sqrt{6}=12\sqrt{3}
\end{eqnarray*}
※正方形は、対角線で $2$つの三角形にわけると、$45^{ \circ }, \ 45^{ \circ }, \ 90^{ \circ }$ の合同な直角二等辺三角形になっています。
二等辺三角形の面積
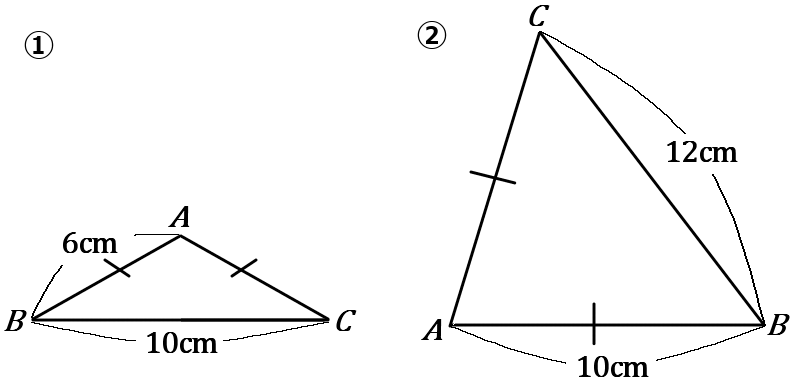
(6) 下の①②の三角形はどちらも $AB=AC$ の二等辺三角形である。それぞれの三角形の面積を求めなさい。
答え
①$5\sqrt{11}cm^2$
②$48cm^2$
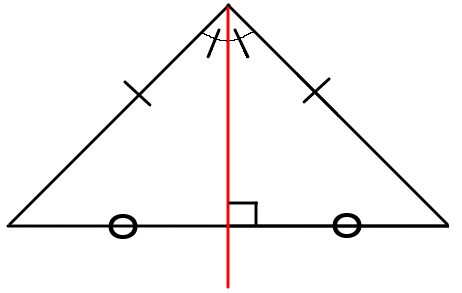 二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する。
二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する。
三角形の面積は底辺 $\times$ 高さ $ \times \cfrac{1}{2}$ です。また、二等辺三角形の頂角の二等分線をひいて、三角形を $2$つにわけると、合同な直角三角形ができています。
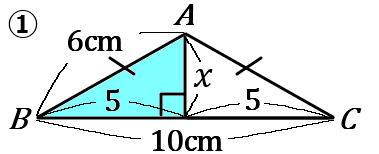 ① 頂角$A$ の二等分線を底辺におろしたときの長さを $x$ とします。水色の三角形は直角三角形なので、
\begin{eqnarray*}
x^2&=&6^2-5^2\\
&=&11\\
x&=&\pm \sqrt{11}\\
x&\gt&0 \ だから \\
x&=&\sqrt{11}\\
\end{eqnarray*}
なので、$\triangle ABC$ の面積は、$BC$ を底辺として、
① 頂角$A$ の二等分線を底辺におろしたときの長さを $x$ とします。水色の三角形は直角三角形なので、
\begin{eqnarray*}
x^2&=&6^2-5^2\\
&=&11\\
x&=&\pm \sqrt{11}\\
x&\gt&0 \ だから \\
x&=&\sqrt{11}\\
\end{eqnarray*}
なので、$\triangle ABC$ の面積は、$BC$ を底辺として、
$10 \times \sqrt{11} \times \cfrac{1}{2}=5\sqrt{11}$
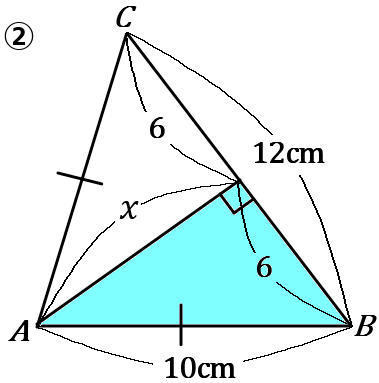 ② 頂角$A$ の二等分線を底辺におろしたときの長さを $x$ とします。水色の三角形は直角三角形なので、
\begin{eqnarray*}
x^2&=&10^2-6^2\\
&=&64\\
x&=&\pm 8\\
x&\gt&0 \ だから \\
x&=&8\\
\end{eqnarray*}
なので、$\triangle ABC$ の面積は、$BC$ を底辺として、
② 頂角$A$ の二等分線を底辺におろしたときの長さを $x$ とします。水色の三角形は直角三角形なので、
\begin{eqnarray*}
x^2&=&10^2-6^2\\
&=&64\\
x&=&\pm 8\\
x&\gt&0 \ だから \\
x&=&8\\
\end{eqnarray*}
なので、$\triangle ABC$ の面積は、$BC$ を底辺として、
$12 \times 8 \times \cfrac{1}{2}=48$
台形の面積
(7) 次の①②の図の四角形の面積を求めなさい。ただし、②は $AD /\!/ BC$ とする。
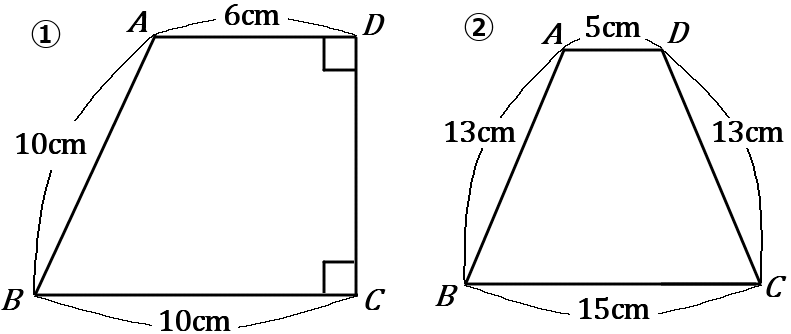
答え
① $16\sqrt{21}cm^2$ ② $120cm^2$
台形の面積は、(上底$+$下底)$\times$高さ$\times \cfrac{1}{2}$ です。
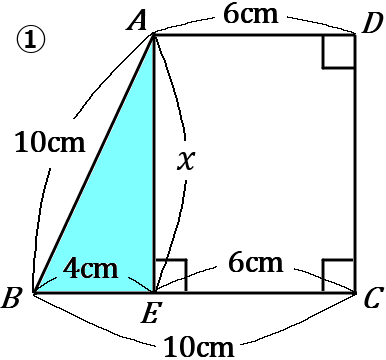 ①頂点$A$ から 辺$BC$ におろした垂線と $BC$ との交点を $E$ とすると、$\triangle ABE$ は直角三角形なので、三平方の定理が使えます。
①頂点$A$ から 辺$BC$ におろした垂線と $BC$ との交点を $E$ とすると、$\triangle ABE$ は直角三角形なので、三平方の定理が使えます。
また、四角形 $AECD$ は長方形になるので、$EC=6$ です。なので $BE$ の長さは、$10-6=4$ です。
$\triangle ABE$ で、$AE$ の長さを $x$ とすると、
\begin{eqnarray*}
x^2&=&10^2-4^2\\
&=&84\\
x&=&\pm \sqrt{84}=\pm 2\sqrt{21}\\
x&\gt&0 \ だから \\
x&=&2\sqrt{21}\\
\end{eqnarray*}
これで台形の高さが求められました。面積をだしましょう。
$(6+10)\times 2\sqrt{21} \times \cfrac{1}{2}=16 \sqrt{21}$
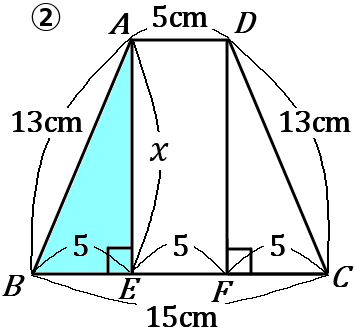 ②頂点$A, \ D$ から辺 $BC$ に垂線をおろし、それぞれの交点を $E, \ F$ とします。すると$\triangle ABE$ は直角三角形なので、三平方の定理が使えます。
②頂点$A, \ D$ から辺 $BC$ に垂線をおろし、それぞれの交点を $E, \ F$ とします。すると$\triangle ABE$ は直角三角形なので、三平方の定理が使えます。
また、四角形 $AEFD$ は長方形なので、$AD=EF$ です。それから、$\triangle ABE \ \equiv \ \triangle DCF$ なので、$BE=CF$ です。なので、$BE=EF=FC=5$ となります。
$\triangle ABE$ で、$AE$ の長さを $x$ とすると、
\begin{eqnarray*}
x^2&=&13^2-5^2\\
&=&144\\
x&=&\pm \sqrt{144}=\pm 12\\
x&\gt&0 \ だから \\
x&=&12\\
\end{eqnarray*}
これで台形の高さが求められました。面積をだしましょう。
$(5+15)\times 12 \times \cfrac{1}{2}=120$
※$AB=DC$ のような台形を等脚台形といいます。三平方の定理を使った求積問題でよくでてきます。
 三角形の面積
三角形の面積
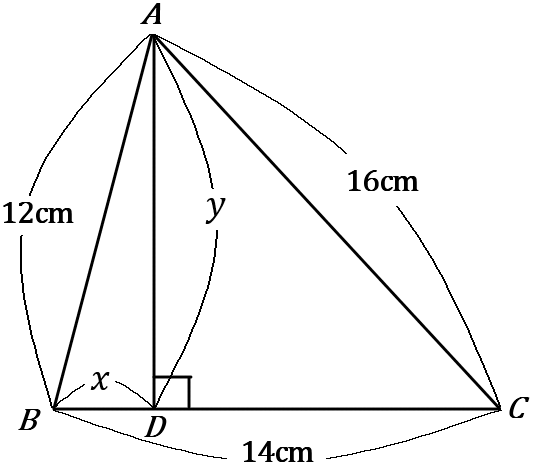
(8) 右の図のような $\triangle ABC$ がある。また、頂点$A$ から辺$BC$ に垂線をおろして、$BC$ との交点を $D$ とする。$BD=xcm,$ $AD=ycm$ として、$x, \ y$ の値を求めなさい。また、$\triangle ABC$ の面積を求めなさい。
答え
$x=3$ $y=3\sqrt{15}$ 面積 $21\sqrt{15}cm^2$
 これ、計算が大変です。がんばってください。
これ、計算が大変です。がんばってください。
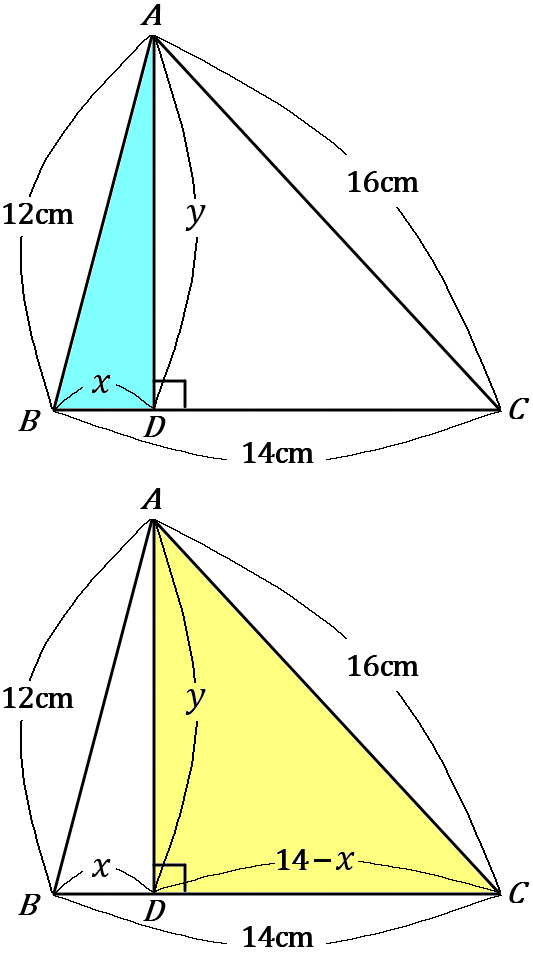
水色の三角形で、三平方の定理から、
$y^2=12^2-x^2$ …①
黄色の三角形で、$DC=14-x$ だから、
$y^2=16^2-(14-x)^2$ …②
どちらも $y^2=$ で式をたてるのがポイントです。
①②の式はどちらも左辺が $y^2$ です。なので、右辺$=$右辺の式をたてて解いていきます。
\begin{eqnarray*}
12^2-x^2&=&16^2-(14-x)^2\\
144-x^2&=&256-(196-28x+x^2)\\
144-x^2&=&256-196+28x-x^2\\
-28x&=&256-196-144\\
-28x&=&-84\\
x&=&\cfrac{-84}{-28}=3
\end{eqnarray*}
$x=3$ を①の式に代入
\begin{eqnarray*}
y^2&=&12^2-x^2\\
&=&12^2-3^2\\
&=&144-9\\
&=&135\\
y&=&\pm \sqrt{135}=\pm 3\sqrt{15}\\
y&\gt&0 \ だから \\
y&=&3\sqrt{15}
\end{eqnarray*}
これで高さが $3\sqrt{15}$ だと求められました。なので面積は、
$14 \times 3\sqrt{15} \times \cfrac{1}{2}=21\sqrt{15}$
半径と弦,半径と接線
(9) 下の①,②の図について、次の①,②の問いに答えなさい。
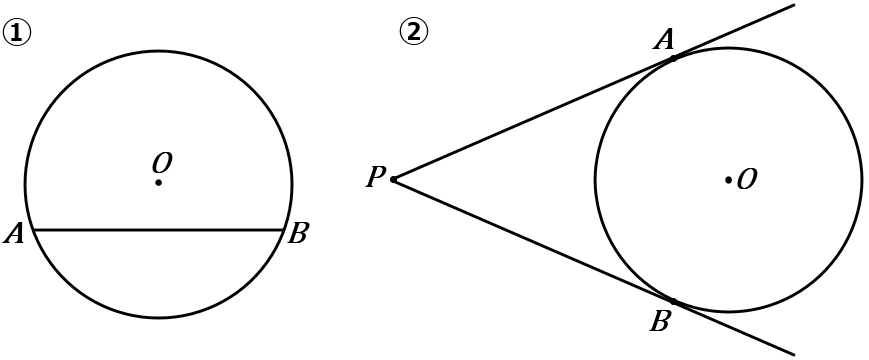
① 線分 $AB$ は円$O$ の弦である。円$O$ の半径が $3cm,$ 円の中心 $O$ と弦$AB$ との距離が $1cm$ であるとき、弦$AB$ の長さを求めなさい。
② $PA, \ PB$ はともに円$O$ の接線であり、点$A, \ B$ はその接点である。円$O$ の半径が$5cm,$ $PA=12cm$ であるとき、点$P$ と $O$ の距離を求めなさい。
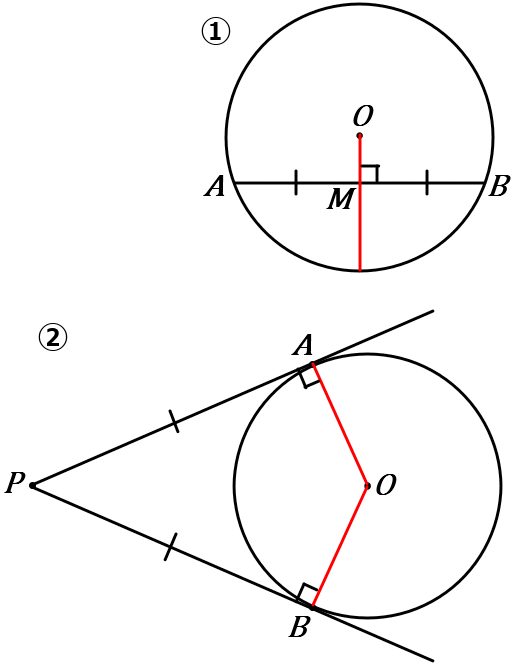 ①円の中心から弦にひいた垂線は、その弦を二等分する。
①円の中心から弦にひいた垂線は、その弦を二等分する。
$AB \perp OM$ ならば、$AM=BM$
②円外の点 $P$ から円$O$ にひいた$2$ 本の接線の、$P$ から接点までの長さは等しい。また、接線は接点を通る半径と垂直である。
$$PA=PB\\
PA \perp OA, \ PB \perp OB$$
答え
① $4\sqrt{2}cm$ ② $13cm$
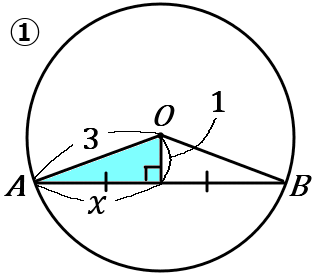 ①不親切な問題というのがありまして、線の長さだとか、考え方のヒントみたいなものがいっさい図にかきこまれていないときがあります。そういうときは、自分でどんどん図に情報をかきくわえてしまいましょう。右の図みたいな感じです。
①不親切な問題というのがありまして、線の長さだとか、考え方のヒントみたいなものがいっさい図にかきこまれていないときがあります。そういうときは、自分でどんどん図に情報をかきくわえてしまいましょう。右の図みたいな感じです。
$O$ から弦に垂線をおろすと、その線は弦を二等分します。$A$ から垂線と $AB$ との交点までの長さを $x$ とすると、水色の三角形で考えて、
\begin{eqnarray*}
x^2&=&3^2-1^2\\
&=&8\\
x&=&\pm \sqrt{8}=\pm 2\sqrt{2}\\
x&\gt&0 \ だから \\
x&=&2\sqrt{2}
\end{eqnarray*}
なので、
$AB=2\sqrt{2} \times 2=4 \sqrt{2}$
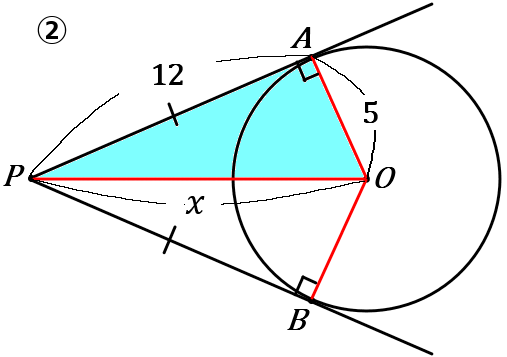 ②この問題も図にいろいろ線や長さをかきくわえてしまいます。接線と、接点を通る半径が垂直、というのがポイントで、これで三平方の定理が使えます。
②この問題も図にいろいろ線や長さをかきくわえてしまいます。接線と、接点を通る半径が垂直、というのがポイントで、これで三平方の定理が使えます。
$PO=x$ として、水色の三角形で考えて、
\begin{eqnarray*}
x^2&=&5^2+12^2\\
=&169\\
x&=&\pm \sqrt{169}=\pm 13\\
x&\gt&0 \ だから \\
x&=&13
\end{eqnarray*}
$2$ 点間の距離
(10) 座標平面上で、次の①②の $2$ 点間の距離を求めなさい。
① $A(2, \ 1), \ B(6, \ 4)$
② $A(-3, \ 2), \ B(1, \ -2)$
座標平面上の $2$ 点 $(x_1, \ y_1), \ (x_2, \ y_2)$ の間の距離は
$\qquad \large{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}$
答え
① $5$ ② $4\sqrt{2}$
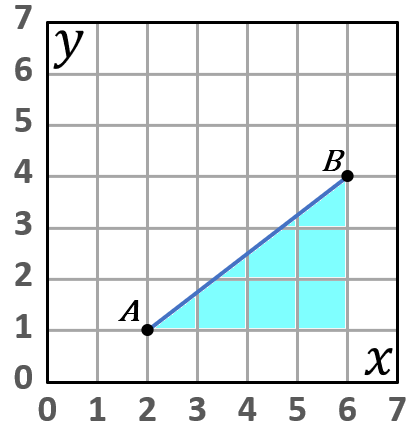 ①$2$ 点 $A(2, \ 1), \ B(6, \ 4)$ の座標は右の図で確認してください。$AB$ 間の距離、というのは、$AB$ の長さだと思っちゃえばいいです。なので、水色の三角形で、三平方の定理を使えば求められます。$AB^2=3^2+4^2$ でいけます。なのですが。
①$2$ 点 $A(2, \ 1), \ B(6, \ 4)$ の座標は右の図で確認してください。$AB$ 間の距離、というのは、$AB$ の長さだと思っちゃえばいいです。なので、水色の三角形で、三平方の定理を使えば求められます。$AB^2=3^2+4^2$ でいけます。なのですが。
これ、これから先、高校生になったあともでてきます。こういう長さを求めるのが必要になる問題がいろいろあるんです。なので、そのつどいちいち三角形を思いえがいてやるのではめんどうなので、公式をおぼえてしまいましょう。
$2$ 点間の距離
$$\large{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}$$
です。$A(2, \ 1), \ B(6, \ 4)$ をこの公式にあてはめると、
\begin{eqnarray*}
AB&=&\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\
&=&\sqrt{(6-2)^2+(4-1)^2}\\
&=&\sqrt{16+9}\\
&=&\sqrt{25}\\
&=&5\\
\end{eqnarray*}
②$A(-3, \ 2), \ B(1, \ -2)$ を $2$ 点間の距離 の公式にあてはめて、
\begin{eqnarray*}
AB&=&\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\
&=&\sqrt{\{1-(-3)\}^2+(-2-2)^2}\\
&=&\sqrt{16+16}\\
&=&\sqrt{32}\\
&=&4\sqrt{2}\\
\end{eqnarray*}
※符号に気をつけて。
 直方体の対角線
直方体の対角線
(11) 右の直方体 $ABCD-EFGH$ について、頂点$ D, \ F$ 間の距離を求めなさい。
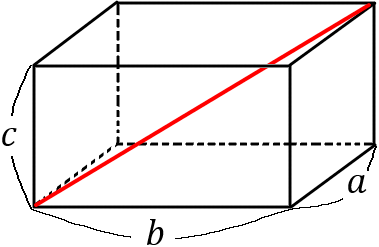 直方体の縦、横、高さをそれぞれ $a, \ b, \ c$ とすると、対角線の長さは
$$ \large{ \sqrt{a^2+b^2+c^2} } $$
直方体の縦、横、高さをそれぞれ $a, \ b, \ c$ とすると、対角線の長さは
$$ \large{ \sqrt{a^2+b^2+c^2} } $$
答え
$\sqrt{29}cm$
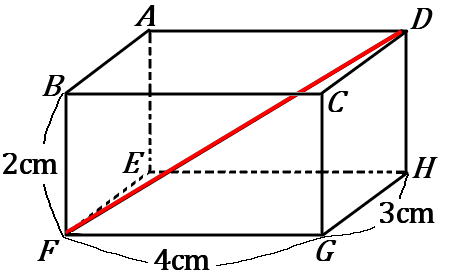 頂点$ D, \ F$ 間の距離というのは、$DF$ の長さのことです。直方体の対角線の公式にあてはめて、
$$DF=\sqrt{3^2+4^2+2^2}=\sqrt{29}$$
これが答えです。この公式はわかりやすいというか、おぼえやすいです。なのでおぼえておきたいです。
頂点$ D, \ F$ 間の距離というのは、$DF$ の長さのことです。直方体の対角線の公式にあてはめて、
$$DF=\sqrt{3^2+4^2+2^2}=\sqrt{29}$$
これが答えです。この公式はわかりやすいというか、おぼえやすいです。なのでおぼえておきたいです。
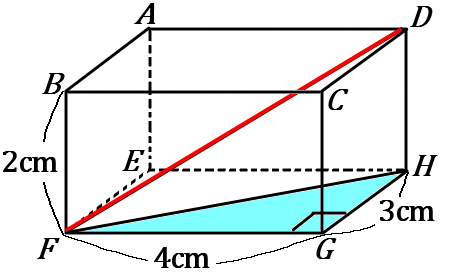 公式を使わずに求めるのもやってみましょう。
公式を使わずに求めるのもやってみましょう。
まず、水色の三角形は$G$ のところが直角なので、三平方の定理から、
\begin{eqnarray*}
FH^2&=&3^2+4^2\\
&=&25\\
FH&=&\pm \sqrt{25}=\pm 5\\
FH&\gt&0 \ だから \\
FH&=&5
\end{eqnarray*}
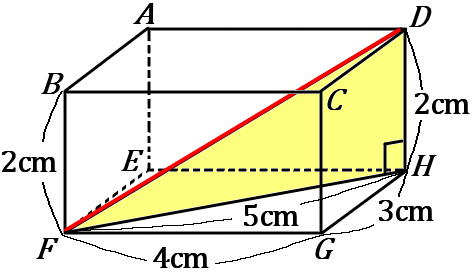 つぎに黄色の三角形は$H$ のところが直角なので、
つぎに黄色の三角形は$H$ のところが直角なので、
\begin{eqnarray*}
FD^2&=&5^2+2^2\\
&=&29\\
FD&=&\pm \sqrt{29}\\
FD&\gt&0 \ だから \\
FD&=&\sqrt{29}
\end{eqnarray*}
最短距離
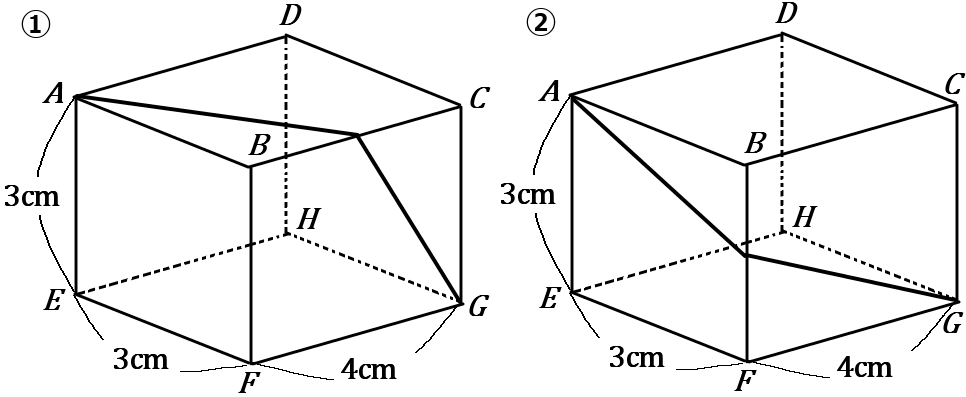
(12) 下の図のような直方体 $ABCD-EFGH$ について、頂点$ A$ から $G$ まで、表面上にひもをかける。
①ひもが辺 $BC$ 上を通るとき、ひもの長さがもっとも短くなるのは何$cm$か。
②ひもが辺 $BF$ 上を通るとき、ひもの長さがもっとも短くなるのは何$cm$か。
答え
① $2\sqrt{13}cm$ ② $\sqrt{58}cm$
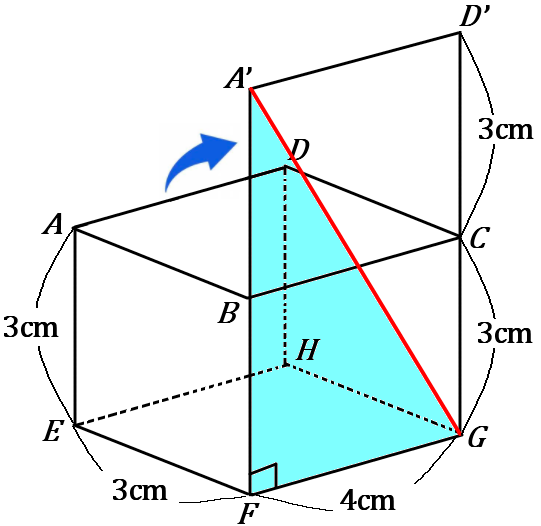 ①直方体の内部は通りません。表面上を通る最短距離の問題です。この問題も定番で、展開図で考えます。いっそ箱だと思ってください。パカっとフタがあくんです。こんなふうに。そう考えるといいです。そんで、フタがまっすぐになるまで開いて、$A'$ から $G$ までの直線をひけばいいです。水色の三角形で、$F$ のところが直角ですから、三平方の定理が使えますね。$A'F$ の長さは $3+3=6$ です。なので、
\begin{eqnarray*}
A'G^2&=&6^2+4^2\\
&=&52\\
A'G&=&\pm \sqrt{52}=\pm 2\sqrt{13}\\
A'G&\gt&0 \ だから \\
A'G&=&2\sqrt{13}
\end{eqnarray*}
①直方体の内部は通りません。表面上を通る最短距離の問題です。この問題も定番で、展開図で考えます。いっそ箱だと思ってください。パカっとフタがあくんです。こんなふうに。そう考えるといいです。そんで、フタがまっすぐになるまで開いて、$A'$ から $G$ までの直線をひけばいいです。水色の三角形で、$F$ のところが直角ですから、三平方の定理が使えますね。$A'F$ の長さは $3+3=6$ です。なので、
\begin{eqnarray*}
A'G^2&=&6^2+4^2\\
&=&52\\
A'G&=&\pm \sqrt{52}=\pm 2\sqrt{13}\\
A'G&\gt&0 \ だから \\
A'G&=&2\sqrt{13}
\end{eqnarray*}
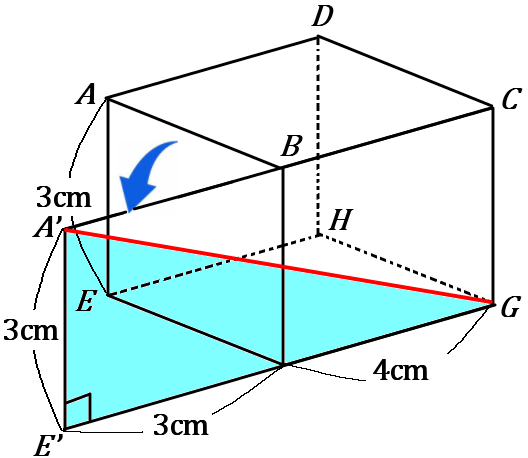 ②こちらは横向きにパカっとフタがあくわけです。こんなふうに。すると、$E'$ のところが直角ですから、三平方の定理が使えます。$E'G$ の長さは $3+4=7$ なので、
②こちらは横向きにパカっとフタがあくわけです。こんなふうに。すると、$E'$ のところが直角ですから、三平方の定理が使えます。$E'G$ の長さは $3+4=7$ なので、
\begin{eqnarray*}
A'G^2&=&3^2+7^2\\
&=&58\\
A'G&=&\pm \sqrt{58}\\
A'G&\gt&0 \ だから \\
A'G&=&\sqrt{58}
\end{eqnarray*}
折る問題
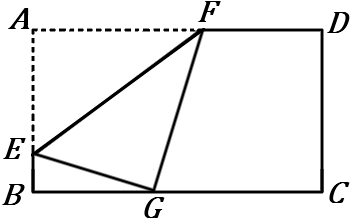 (13) 右の図の長方形 $ABCD$ を、$EF$ のところで折り曲げて、頂点 $A$ を辺 $BC$ に重ねる。$A$ が $BC$ に重なったところを $G$ とする。
(13) 右の図の長方形 $ABCD$ を、$EF$ のところで折り曲げて、頂点 $A$ を辺 $BC$ に重ねる。$A$ が $BC$ に重なったところを $G$ とする。
$AB=5cm, \ BG=3cm$ のとき、$EB$ の長さを求めなさい。
答え
$1.6cm \ \left( \cfrac{8}{5}cm \right)$
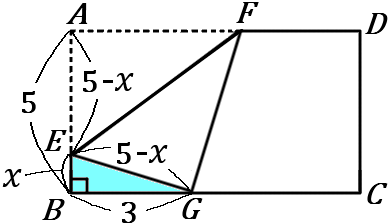 $EB=x$ とすると、$AE=5-x$ です。んで、折ったわけですから、$AE=GE$ になっています。「折る問題」は、たぶんかならず、このパターンをどこかで使います。折ったんだからこことここは同じだろう、というパターンです。
$EB=x$ とすると、$AE=5-x$ です。んで、折ったわけですから、$AE=GE$ になっています。「折る問題」は、たぶんかならず、このパターンをどこかで使います。折ったんだからこことここは同じだろう、というパターンです。
というわけで、$GE=5-x$ ということにして、水色の三角形で三平方の定理をやっていきます。
\begin{eqnarray*}
x^2+3^2&=&(5-x)^2\\
x^2+9&=&25-10x+x^2\\
10x&=&25-9\\
x&=&1.6
\end{eqnarray*}
正四角すいの表面積と体積
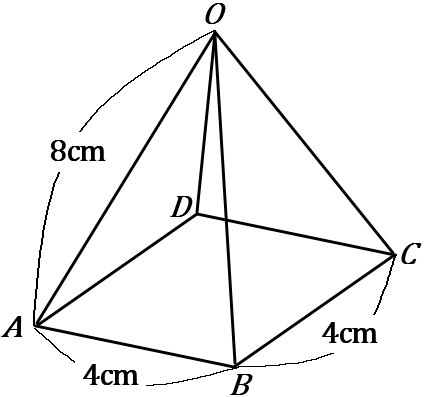 (14) 底面が $1$ 辺 $4cm$ の正方形、側面がすべて二等辺三角形で等しい辺の長さが $8cm$ である正四角すいの体積と表面積を求めなさい。
(14) 底面が $1$ 辺 $4cm$ の正方形、側面がすべて二等辺三角形で等しい辺の長さが $8cm$ である正四角すいの体積と表面積を求めなさい。
答え
体積 $\cfrac{32\sqrt{14}}{3}cm^3$ 表面積 $16+ 16\sqrt{15}cm^2$
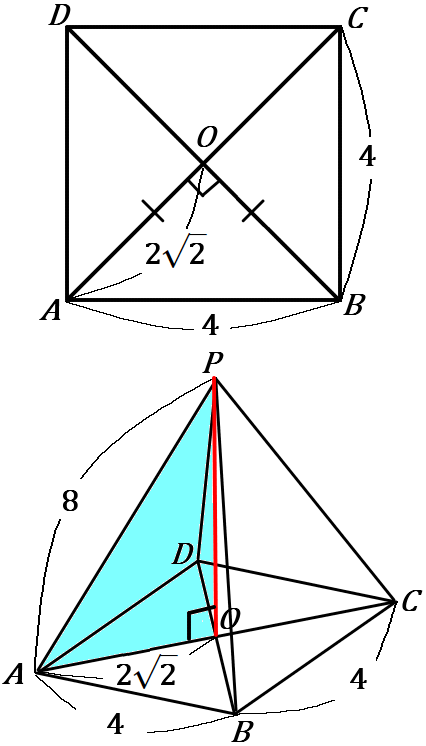 <体積>
<体積>
すい体の体積は、
底面積 $\times$ 高さ $\times\cfrac{1}{3}$ です。
底面積は $1$ 辺が $4cm$ の正方形ですから、$16cm^2$ です。
高さは、右の図の水色の三角形で求めていきます。
底面の正方形の対角線の交点を $O$ とすると、正方形の対角線は垂直に交わるので、$\triangle OAB$ は直角二等辺三角形になるので、$1:1:\sqrt{2}$ の辺の比が使えて、$OA=2\sqrt{2}$ となります。(上の図)
頂点 $P$ から底面に垂線をおろすと $O$ を通るはず、と考えて、水色の三角形で三平方の定理より、
\begin{eqnarray*}
PO^2&=&8^2-(2\sqrt{2})^2\\
&=&56\\
PO&=&\pm \sqrt{56}=\pm 2\sqrt{14}\\
PO&\gt&0 \ だから \\
PO&=&2\sqrt{14}
\end{eqnarray*}
これで高さ $PO$ の長さが求められました。体積をだしましょう。
$16\times 2\sqrt{14} \times \cfrac{1}{3}=\cfrac{32\sqrt{14}}{3}$
 <表面積>
<表面積>
立体の表面積は、底面積 $+$ 側面積です。
この立体は、$1$つの底面と、$4$つの側面があります。
底面積は $16cm^2$ です。
側面は、各辺がそれぞれ $8cm,$ $8cm,$ $4cm$ の、$4$つの合同な二等辺三角形です。右の図の $\triangle PAB$ で、頂点 $P$ から底辺におろした垂線と 底辺との交点を $M$ とすると、三平方の定理より、
\begin{eqnarray*}
PM^2&=&8^2-2^2\\
&=&60\\
PM&=&\pm \sqrt{60}=\pm 2\sqrt{15}\\
PM&\gt&0 \ だから \\
PM&=&2\sqrt{15}
\end{eqnarray*}
なので、$\triangle PAB$ の面積は、
$4 \times 2\sqrt{15} \times \cfrac{1}{2}=4\sqrt{15}$
なので、表面積は、
$16+4\sqrt{15} \times 4=16+ 16\sqrt{15}$
円すいの体積と表面積
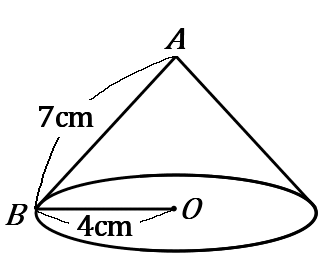 (15) 底面の半径が $4cm,$ 母線の長さが $7cm$ である円すいの体積と表面積を求めなさい。
(15) 底面の半径が $4cm,$ 母線の長さが $7cm$ である円すいの体積と表面積を求めなさい。
答え
体積 $\cfrac{16\sqrt{33}}{3} \large{{\pi}} \ cm^3$ 表面積 $44\pi \ cm^2$
 <体積>
<体積>
すい体の体積は、
底面積 $\times$ 高さ $\times\cfrac{1}{3}$ です。
円の面積は $\pi r^2$ です。なので底面積は
$\pi \times 4^2=16\pi$ です。
高さは水色の三角形で求めます。三平方の定理を使って、
\begin{eqnarray*}
AO^2&=&7^2-4^2\\
&=&33\\
AO&=&\pm \sqrt{33}\\
AO&\gt&0 \ だから \\
AO&=&\sqrt{33}
\end{eqnarray*}
これで高さ $AO$ の長さが求められました。体積をだしましょう。
$16\pi \times \sqrt{33} \times \cfrac{1}{3}=\cfrac{16\sqrt{33}}{3}\large{\pi}$
<表面積>
円すいの表面積は、底面積 $+$ 側面積です。
底面積は $16\pi$ です。
円すいの側面積は、底面の半径と母線がわかっているときは、
母線 $\times$ 底面の半径 $\times \pi$ でOKです。なので、
$4 \times 7 \times \pi=28\pi$
ということで表面積は
$16\pi +28\pi=44\pi$
※円すいの母線を $l,$ 底面の半径を $r,$ 側面積を $S$ とすると、
$$\large{S=lr\pi}$$
円すいの最短距離
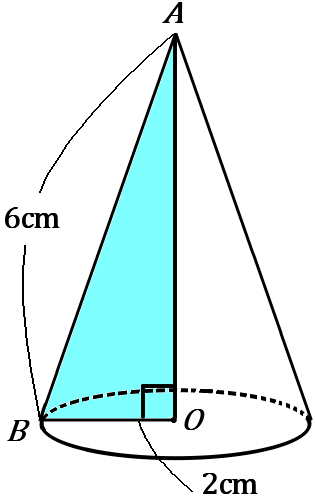
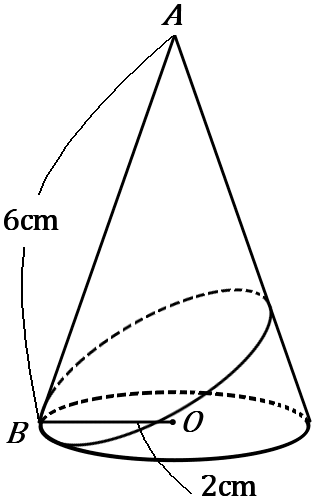 (16) 右の図のような、底面の半径が $2cm,$ 母線の長さが $6cm$ である円すいがある。次の①②の問いに答えなさい。
(16) 右の図のような、底面の半径が $2cm,$ 母線の長さが $6cm$ である円すいがある。次の①②の問いに答えなさい。
①円すいの体積を求めなさい。
②底面の円周上の点$B$ から円すいの側面にあわせて、$1$ 周してもとの点までもどるようにひもをかける。ひもの長さがもっとも短くなるのは何$cm$ か。
答え
体積 $\cfrac{16\sqrt{2}}{3} \large{{\pi}} \ cm^3$ ひもの長さ $6\sqrt{3}cm$
 <体積>
<体積>
すい体の体積は、
底面積 $\times$ 高さ $\times\cfrac{1}{3}$ です。
円の面積は $\pi r^2$ です。なので底面積は
$\pi \times 2^2=4\pi$ です。
高さは水色の三角形で求めます。三平方の定理を使って、
\begin{eqnarray*}
AO^2&=&6^2-2^2\\
&=&32\\
AO&=&\pm 4\sqrt{2}\\
AO&\gt&0 \ だから \\
AO&=&4\sqrt{2}
\end{eqnarray*}
これで高さ $AO$ の長さが求められました。体積をだしましょう。
$4\pi \times 4\sqrt{2} \times \cfrac{1}{3}=\cfrac{16\sqrt{2}}{3}\large{\pi}$
 <ひもの長さ>
<ひもの長さ>
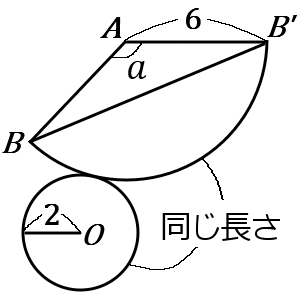
右の図のような展開図をかいて考えます。ひもの最短距離は、$B$ から $B'$ までまっすぐにひいた線の長さになっています。だからといって、このままではどうにもならなさそうなのですが、おうぎ形の中心角 $\angle a$ の大きさが、どうにかしてくれる大きさになっています。そう信じて、おうぎ形の中心角の大きさをだしてみましょう。
底面の円の円周とおうぎ形の弧は同じ長さです。その長さは底面の円の円周で考えて、$4\pi$ です。
おうぎ形のもとになっている円の円周は $12\pi$ なので、弧はその $\cfrac{1}{3}$ になっています。じゃあ中心角も $\cfrac{1}{3}$ だろうということで、
$\quad \angle a= 360^{ \circ } \times \cfrac{1}{3}=120^{ \circ }$
これがおうぎ形の中心角の大きさです。ちなみに、円すいの母線と底面の半径がわかっているときは、展開図のおうぎ形の中心角の大きさは $360^{ \circ }\times$ 底面の半径 $\div$ 母線とやれば一発です。もしかしたら $1$ 年生のときに教わっているかもしれません。
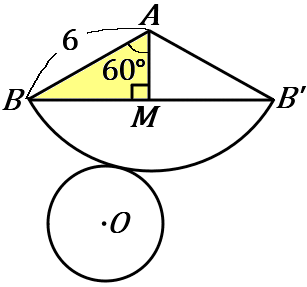 おうぎ形の中心角が $120^{ \circ }$ だと求められたので、もういちど、展開図をかきます。こんどは中心角を $120^{ \circ }$ だとおもってかきます。
おうぎ形の中心角が $120^{ \circ }$ だと求められたので、もういちど、展開図をかきます。こんどは中心角を $120^{ \circ }$ だとおもってかきます。
$\triangle ABB'$ は二等辺三角形です。頂角の二等分線をひくと、その線は $120^{ \circ }$ を $60^{ \circ }$ ずつにわけることになります。こんな感じで、円すいの最短距離の問題は、展開図のおうぎ形の中心角がかならずなんとかなる角度になっています。また、二等辺三角形の頂角の二等分線は底辺を垂直に二等分します。
黄色の三角形で考えれば、$30^{ \circ },$ $60^{ \circ },$ $90^{ \circ }$ の三角形ですから、$1:2:\sqrt{3}$ の比が使えることになって、$BM=3\sqrt{3}$ です。なので、
$BB'=3\sqrt{3} \times 2=6\sqrt{3}$
答え(中3 7章 三平方の定理 第1回(全16問))

(1)① 斜辺 ② $a^2+b^2=c^2$
(2)① $x=5$ ② $x=5$ ③ $x=9$
(3)ア,ウ
(4)①$x=10$
②$x=9$
③$x=\cfrac{8\sqrt{3}}{3}$
④$9\sqrt{3}cm^2$
(5)①$x=3\sqrt{2}$
②$x=2\sqrt{2}$
③$x=12\sqrt{3}$
(6)①$5\sqrt{11}cm^2$
②$48cm^2$
(7)①$16\sqrt{21}cm^2$ ②$120cm^2$
(8)$x=3$ $y=3\sqrt{15}$ 面積 $21\sqrt{15}cm^2$
(9)①$4\sqrt{2}cm$ ②$13cm$
(10)①$5$ ②$4\sqrt{2}$
(11)$\sqrt{29}cm$
(12)①$2\sqrt{13}cm$ ②$\sqrt{58}$
(13)$1.6cm \ \left( \cfrac{8}{5}cm \right)$
(14)体積 $\cfrac{32\sqrt{14}}{3}cm^3$ 表面積 $16+ 16\sqrt{15}cm^2$
(15)体積 $\cfrac{16\sqrt{33}}{3} \large{{\pi}} \ cm^3$ 表面積 $44\pi \ cm^2$
(16)体積 $\cfrac{16\sqrt{2}}{3} \large{{\pi}} \ cm^3$ ひもの長さ $6\sqrt{3}cm$