中3数学 1学期の計算 第17回 全32問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
① $-5-(+2)\times(-3)$
答え $1$
\begin{eqnarray*} &&-5-(+2)\times(-3)\\ &=&-5-2\times(-3)\\ &=&-5+6\\ &=&1 \end{eqnarray*}② $\cfrac{2}{3}-1-\left(-\cfrac{1}{6}\right)$
答え $-\cfrac{1}{6}$
\begin{eqnarray*} &&\cfrac{2}{3}-1+\cfrac{1}{6}\\ &=&\cfrac{4}{6}-\cfrac{6}{6}+\cfrac{1}{6}\\ &=&-\cfrac{1}{6} \end{eqnarray*}③ $-3-2\times\{(-5)^2+(-3)^3\}$
答え $1$
\begin{eqnarray*} &&-3-2\times\{(-5)^2+(-3)^3\}\\ &=&-3-2\times(25-27)\\ &=&-3-2\times(-2)\\ &=&-3+4\\ &=&1 \end{eqnarray*}④ $\left(\cfrac{12}{13}a^2+\cfrac{11}{12}a\right)-\left(\cfrac{25}{26}a^2+a\right)$
答え $-\cfrac{1}{26}a^2-\cfrac{1}{12}a$
\begin{eqnarray*} &&\cfrac{12}{13}a^2+\cfrac{11}{12}a-\cfrac{25}{26}a^2-a\\ &=&\cfrac{12}{13}a^2-\cfrac{25}{26}a^2+\cfrac{11}{12}a-a\\ &=&\cfrac{24}{26}a^2-\cfrac{25}{26}a^2+\cfrac{11}{12}a-\cfrac{12}{12}a\\ &=&-\cfrac{1}{26}a^2-\cfrac{1}{12}a \end{eqnarray*}⑤ $(8x^2+12x-4)\div(-4)$
答え $-2x^2-3x+1$
⑥ $(18x^2y-27xy^2)\div\left(-\cfrac{9}{4}xy\right)$
答え $-8x+12y$
\begin{eqnarray*} &&(18x^2y-27xy^2)\times\left(-\cfrac{4}{9xy}\right)\\ &=&18x^2y\times\left(-\cfrac{4}{9xy}\right)-27xy^2\times\left(-\cfrac{4}{9xy}\right)\\ &=&-8x+12y \end{eqnarray*}⑦ $-5x(2x-4y)-2x(-6x+7y)$
答え $2x^2+6xy$
\begin{eqnarray*} &&-10x^2+20xy+12x^2-14xy\\ &=&-10x^2+12x^2+20xy-14xy\\ &=&2x^2+6xy \end{eqnarray*}⑧ $\cfrac{1}{12}(24a+36b)-\cfrac{1}{6}(36a+30b)$
答え $-4a-2b$
\begin{eqnarray*} &&2a+3b-6a-5b\\ &=&2a-6a+3b-5b\\ &=&-4a-2b \end{eqnarray*}⑨ $\cfrac{5x-4y}{6}-\cfrac{11x-2y}{12}$
答え $\cfrac{-x-6y}{12}\quad\left(-\cfrac{x+6y}{12},-\cfrac{1}{12}x-\cfrac{1}{2}yも可\right)$
\begin{eqnarray*} &&\cfrac{2(5x-4y)-(11x-2y)}{12}\\ &=&\cfrac{10x-8y-11x+2y}{12}\\ &=&\cfrac{10x-11x-8y+2y}{12}\\ &=&\cfrac{-x-6y}{12} \end{eqnarray*}⑩ $51ab^2\times(-8ab)\div(-34a^2b^2)$
答え $12b$
\begin{eqnarray*} &&\cfrac{51abb\times8ab}{34aabb}\\ &=&12b \end{eqnarray*}⑪ $-27xy\div\left(-\cfrac{72}{5}x^2y^3\right)\times(-16xy)$
答え $-\cfrac{30}{y}$
\begin{eqnarray*} &&-\cfrac{27xy}{1}\times\left(-\cfrac{5}{72xxyyy}\right)\times\left(-\cfrac{16xy}{1}\right)\\ &=&-\cfrac{30}{y} \end{eqnarray*}⑫ $(x-14)(x+2)$
答え $x^2-12x-28$
⑬ $\left(\cfrac{1}{2}a-\cfrac{1}{3}b\right)^2$
答え $\cfrac{1}{4}a^2-\cfrac{1}{3}ab+\cfrac{1}{9}b^2$
⑭ $\left(\cfrac{15}{16}x+\cfrac{17}{18}y\right)\left(\cfrac{15}{16}x-\cfrac{17}{18}y\right)$
答え $\cfrac{225}{256}x^2-\cfrac{289}{324}y^2$
⑮ $(5x-8)(5x+10)$
答え $25x^2+10x-80$
⑯ $7\sqrt{30}\div14\sqrt{180}\times\sqrt{8}$
答え $\cfrac{\sqrt{3}}{3}$
\begin{eqnarray*} \require{cancel} &&\cfrac{\bcancel{7}\sqrt{\bcancel{30}}\times\sqrt{\bcancel{8}}}{\bcancel{14}\sqrt{\bcancel{180}}}\\ &=&\cfrac{\sqrt{4}}{2\sqrt{3}}\\ &=&\cfrac{2\sqrt{3}}{6}\\ &=&\cfrac{\sqrt{3}}{3} \end{eqnarray*}※まず約分。
⑰ $-3\sqrt{8}-4\sqrt{27}+5\sqrt{12}-\sqrt{18}$
答え $-9\sqrt{2}-2\sqrt{3}$
\begin{eqnarray*} &&-3\cdot2\sqrt{2}-4\cdot3\sqrt{3}+5\cdot2\sqrt{3}-3\sqrt{2}\\ &=&-6\sqrt{2}-12\sqrt{3}+10\sqrt{3}-3\sqrt{2}\\ &=&-6\sqrt{2}-3\sqrt{2}-12\sqrt{3}+10\sqrt{3}\\ &=&-9\sqrt{2}-2\sqrt{3} \end{eqnarray*}⑱ $\sqrt{54}\div\sqrt{\cfrac{72}{5}}\div\sqrt{6}$
答え $\cfrac{\sqrt{10}}{4}$
\begin{eqnarray*} &&\sqrt{54}\div\cfrac{\sqrt{72}}{\sqrt{5}}\div\sqrt{6}\\ &=&\cfrac{\sqrt{54}}{1}\times\cfrac{\sqrt{5}}{\sqrt{72}}\times\cfrac{1}{\sqrt{6}}\\ &=&\cfrac{\sqrt{\bcancel{54}}}{1}\times\cfrac{\sqrt{5}}{\sqrt{\bcancel{72}}}\times\cfrac{1}{\sqrt{\bcancel{6}}}\\ &=&\cfrac{\sqrt{5}}{\sqrt{8}}\\ &=&\cfrac{\sqrt{5}}{2\sqrt{2}}\\ &=&\cfrac{\sqrt{10}}{4} \end{eqnarray*}⑲ $\cfrac{\sqrt{54}}{2}-\sqrt{\cfrac{ \ 2 \ }{ \ 3 \ }}$
答え $\cfrac{7\sqrt{6}}{6}$
\begin{eqnarray*} &&\cfrac{\sqrt{54}}{2}-\sqrt{\cfrac{ \ 2 \ }{ \ 3 \ }}\\ &=& \cfrac{3\sqrt{6}}{2}-\cfrac{\sqrt{2}}{\sqrt{3}} \\ &=& \cfrac{3\sqrt{6}}{2}-\cfrac{\sqrt{6}}{3} \\ &=& \cfrac{9\sqrt{6}}{6}-\cfrac{2\sqrt{6}}{6} \\ &=& \cfrac{7\sqrt{6}}{6} \end{eqnarray*}⑳ $(1+2\sqrt{2})^2$
答え $9+4\sqrt{2}$
\begin{eqnarray*} &&1^2+2\cdot1\cdot2\sqrt{2}+(2\sqrt{2})^2\\ &=& 1+4\sqrt{2}+8\\ &=&9+4\sqrt{2} \end{eqnarray*}① $75x^2y-25xy^2+125xy$
答え $25xy(3x-y+5)$
② $x^2-17x+60$
答え $(x-12)(x-5)$
③ $\cfrac{1}{25}a^2-\cfrac{2}{5}ab+b^2$
答え $\left(\cfrac{1}{5}a-b\right)^2$
④ $\cfrac{1}{36}x^2-y^2$
答え $\left(\cfrac{1}{6}x+y\right)\left(\cfrac{1}{6}x-y\right)$
① $3x+2=-\cfrac{3}{2}x-1$
答え $x=-\cfrac{2}{3}$
\begin{eqnarray*} 3x+2&=&-\cfrac{3}{2}x-1\quad(\times2)\\ 6x+4&=&-3x-2 \\ 6x+3x&=&-2-4\\ 9x&=&-6\\ x&=&-\cfrac{6}{9}=-\cfrac{2}{3} \end{eqnarray*}② $\left\{\begin{array}{l} 3x+2y=0\\ 4x-10=5y+13 \end{array}\right.$
答え $x=2,y=-3$
\begin{eqnarray*} \left\{ \begin{array}{l} 3x+2y=0\qquad…①\\ 4x-10=5y+13\qquad…② \end{array} \right. \end{eqnarray*} $②を整理$ \begin{eqnarray*} 4x-5y&=&13+10\\ 4x-5y&=&23\qquad…③ \end{eqnarray*} $①\times4-③\times3$ \begin{eqnarray*} 12x+\phantom{1}8y=\phantom{-6}0\\ \underline{-) \quad 12x-15y=\phantom{-}69} \\ 23y=-69 \\ y=-3\phantom{6} \end{eqnarray*} \begin{eqnarray*} y=-3を①に代入\\ 3x+2\times(-3)&=&0\\ 3x-6&=&0\\ 3x&=&6\\ x&=&2 \\ \left\{ \begin{array}{l} x=2\\ y=-3 \end{array} \right. \end{eqnarray*}次の式を$[\phantom{y}]$内の文字について解きなさい。
①
$-4x=\cfrac{6y-z}{2}\quad[y]$
答え $y=\cfrac{-8x+z}{6}\\ \left(-\cfrac{8x-z}{6},-\cfrac{4}{3}x+\cfrac{1}{6}zも可\right)$
\begin{eqnarray*} -4x&=&\cfrac{6y-z}{2}\quad(\times2) \\ -8x&=&6y-z\quad(左辺と右辺をとりかえる) \\ 6y-z&=&-8x \\ 6y&=&-8x+z \\ y&=&\cfrac{-8x+z}{6} \end{eqnarray*}$x=3+3\sqrt{3}$ のとき、次の式の値を求めなさい。
②
$x^2-6x+9$
答え $27$
\begin{eqnarray*} &&x^2-6x+9 \\ &=&(x-3)^2\quad \class{mathbg-r}{(ここで代入する)} \\ &=&(3+3\sqrt{3}-3)^2\\ &=&(3\sqrt{3})^2\\ &=&27 \end{eqnarray*} やり方が思いつかないときや、自信がないときは、単に代入して、がんばって計算すれば同じ答えがでます \begin{eqnarray*} &&x^2-6x+9\\ &=&(3+3\sqrt{3})^2-6(3+3\sqrt{3})+9\\ &=&9+18\sqrt{3}+27-18-18\sqrt{3}+9\\ &=&27 \end{eqnarray*}③ $y$ が $x$ に比例し、$x=6$ のとき、$y=8$ である。$x=-9$ のときの $y$ の値を求めなさい。
答え $-12$
比例の式の形は $y=ax$ $$a=\cfrac{8}{6}=\cfrac{4}{3}$$ $y=\cfrac{4}{3}x$ に $x=-9$ を代入する $$y=\cfrac{4}{3}\times(-9)=-12$$④ $y$ が $x$ に反比例し、$x=6$ のとき、$y=8$ である。$x=-9$ のときの $y$ の値を求めなさい。
答え $-\cfrac{16}{3}$
反比例の式の形は $y=\cfrac{a}{x}$ $$a=x \times y=6\times8=48$$ $y=\cfrac{48}{x}$ に $x=-9$ を代入する $$y=\cfrac{48}{-9}=-\cfrac{16}{3}$$⑤ $2$ 点 $(-2,\ 4),\ (2,\ 6)$ を通る直線の式を求めなさい。
答え $y=\cfrac{1}{2}x+5$
直線の式の形は $y=ax+b$ \begin{eqnarray*} a&=&\cfrac{y_2-y_1}{x_2-x_1}\\ &=&\cfrac{6-4}{2-(-2)}=\cfrac{2}{4}=\cfrac{1}{2}\\ \end{eqnarray*} $y=\cfrac{1}{2}x+b$ に $x=2,\ y=6$ を代入 \begin{eqnarray*} 6&=&\cfrac{1}{2}\times2+b\\ 6&=&1+b\\ 6-1&=&b\\ 5&=&b \end{eqnarray*}⑥ 袋の中に赤玉が $2$ 個と白玉が $4$ 個はいっている。袋の中から玉を $2$ 個同時に取り出すとき、取り出した玉の色が少なくとも $1$ 個は赤である確率を求めなさい。
答え $\cfrac{3}{5}$
①,②,③,④,⑤,⑥と、$6$ 個の玉に番号をつけてしまいます。そして、①と②が赤玉、③と④と⑤と⑥が白玉ということにします。①②③④⑤⑥という感じ。んで、樹形図をかいてもいけます。または、さいころの問題のときのような表をかいてもいいです。ここでは表でやることにすると、
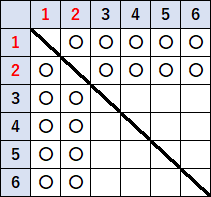
「玉を同時に取り出す」ときは、同じ玉を取り出せないので、表にナナメ線がはいります。〇をつけたところが問題にあうところで、 $$\cfrac{18}{30}=\cfrac{3}{5}$$
答え
$\boxed{\large{\ 1\ }}①1②-\cfrac{1}{6}③1④-\cfrac{1}{26}a^2-\cfrac{1}{12}a\\ ⑤-2x^2-3x+1 ⑥-8x+12y⑦2x^2+6xy⑧-4a-2b\\ ⑨\cfrac{-x-6y}{12}\quad\left(-\cfrac{x+6y}{12},-\cfrac{1}{12}x-\cfrac{1}{2}yも可\right)\\ ⑩12b ⑪-\cfrac{30}{y}⑫x^2-12x-28⑬\cfrac{1}{4}a^2-\cfrac{1}{3}ab+\cfrac{1}{9}b^2\\ ⑭\cfrac{225}{256}x^2-\cfrac{289}{324}y^2 ⑮25x^2+10x-80⑯\cfrac{\sqrt{3}}{3}\\ ⑰-9\sqrt{2}-2\sqrt{3}⑱\cfrac{\sqrt{10}}{4}⑲\cfrac{7\sqrt{6}}{6}⑳9+4\sqrt{2}\\ \boxed{\large{\ 2\ }}①25xy(3x-y+5)②(x-12)(x-5)\\ ③\left(\cfrac{1}{5}a-b\right)^2 ④\left(\cfrac{1}{6}x+y\right)\left(\cfrac{1}{6}x-y\right)\\ \boxed{\large{\ 3\ }}①x=-\cfrac{2}{3}②x=2,y=-3\\ \boxed{\large{\ 4\ }}①y=\cfrac{-8x+z}{6} \left(-\cfrac{8x-z}{6},-\cfrac{4}{3}x+\cfrac{1}{6}zも可\right)\\ ②27 ③-12④-\cfrac{16}{3}⑤y=\cfrac{1}{2}x+5⑥\cfrac{3}{5} $