中3数学 冬休みの計算 第8回 全35問
謹賀新年。
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
① $6-4\div2$
答え $4$
\begin{eqnarray*} &&6-4\div2\\ &=&6-2\\ &=&4 \end{eqnarray*}② $-\cfrac{7}{3}\div\cfrac{7}{2}+\cfrac{3}{4}$
答え $\cfrac{1}{12}$
\begin{eqnarray*} &&-\cfrac{7}{3}\div\cfrac{7}{2}+\cfrac{3}{4}\\ &=&-\cfrac{7}{3}\times\cfrac{2}{7}+\cfrac{3}{4}\\ &=&-\cfrac{2}{3}+\cfrac{3}{4}\\ &=&-\cfrac{8}{12}+\cfrac{9}{12}\\ &=&\cfrac{1}{12} \end{eqnarray*}③ $(-2)^2+(-1^2)\times(-3)$
答え $7$
\begin{eqnarray*} &&(-2)^2+(-1^2)\times(-3)\\ &=&4-1\times(-3)\\ &=&4+3\\ &=&7 \end{eqnarray*}④ $(5x-8)-(3x-11)$
答え $2x+3$
\begin{eqnarray*} &&5x-8-3x+11\\ &=&5x-3x-8+11\\ &=&2x+3 \end{eqnarray*}⑤ $(12x^2y-18xy^3)\div\cfrac{3}{2}xy$
答え $8x-12y^2$
\begin{eqnarray*} &&(12x^2y-18xy^3)\div\cfrac{3}{2}xy\\ &=&(12x^2y-18xy^3)\times\cfrac{2}{3xy}\\ &=&12x^2y\times\cfrac{2}{3xy}-18xy^3\times\cfrac{2}{3xy}\\ &=&8x-12y^2 \end{eqnarray*}⑥ $-\cfrac{x+2y}{3}-\cfrac{3x-2y}{12}$
答え $\cfrac{-7x-6y}{12}\\ \quad\left(-\cfrac{7x+6y}{12},\ -\cfrac{7}{12}x-\cfrac{1}{2}yも可\right)$
\begin{eqnarray*} &&-\cfrac{x+2y}{3}-\cfrac{3x-2y}{12}\\ &=&\cfrac{-4(x+2y)-(3x-2y)}{12}\\ &=&\cfrac{-4x-8y-3x+2y}{12}\\ &=&\cfrac{-7x-6y}{12} \end{eqnarray*}⑦ $-5(x-5)(x+5)$
答え $-5x^2+125$
\begin{eqnarray*} &&-5(x-5)(x+5)\\ &=&-5(x^2-25)\\ &=&-5x^2+125 \end{eqnarray*}⑧ $\left(3x-\cfrac{7}{6}y\right)^2$
答え $9x^2-7xy+\cfrac{49}{36}y^2$
⑨ $\left(\cfrac{7}{8}a+\cfrac{9}{10}b\right)\left(\cfrac{7}{8}a-\cfrac{9}{10}b\right)$
答え $\cfrac{49}{64}a^2-\cfrac{81}{100}b^2$
⑩ $\cfrac{\sqrt{32}}{4}+\cfrac{20\sqrt{5}}{\sqrt{10}}-\cfrac{1}{\sqrt{8}}$
答え $\cfrac{43\sqrt{2}}{4}$
\begin{eqnarray*} &&\cfrac{4\sqrt{2}}{4}+\cfrac{20}{\sqrt{2}}-\cfrac{1}{2\sqrt{2}}\\ &=&\cfrac{4\sqrt{2}}{4}+\cfrac{20\sqrt{2}}{2}-\cfrac{\sqrt{2}}{4}\\ &=&\cfrac{4\sqrt{2}}{4}+\cfrac{40\sqrt{2}}{4}-\cfrac{\sqrt{2}}{4}\\ &=&\cfrac{43\sqrt{2}}{4} \end{eqnarray*}⑪ $\sqrt{35}\div\sqrt{\cfrac{7}{15}}\times\sqrt{\cfrac{12}{5}}$
答え $6\sqrt{5}$
\begin{eqnarray*} \require{cancel} &&\sqrt{35}\times\sqrt{\cfrac{15}{7}}\times\sqrt{\cfrac{12}{5}}\\ &&\sqrt{{}^5\bcancel{35}}\times\cfrac{\sqrt{{}^3\bcancel{15}}}{\bcancel{\sqrt{7}}}\times\cfrac{\sqrt{12}}{\bcancel{\sqrt{5}}}\\ &=&\sqrt{5}\times\sqrt{3}\times2\sqrt{3}\\ &=&6\sqrt{5} \end{eqnarray*}⑫ $\left(3\sqrt2-2\sqrt{10}\right)^2$
答え $58-24\sqrt{5}$
\begin{eqnarray*} &&\left(3\sqrt2-2\sqrt{10}\right)^2\\ &=&18-12\sqrt{20}+40\\ &=&58-24\sqrt{5} \end{eqnarray*}① $35x^3y-50x^2y^2+25xy$
答え $5xy(7x^2-10xy+5)$
② $x^2-17x-60$
答え $(x+3)(x-20)$
③ $25x^2-90xy+81y^2$
答え $(5x-9y)^2$
④ $\cfrac{9}{49}x^2-144y^2$
答え $\left(\cfrac{3}{7}x+12y\right)\left(\cfrac{3}{7}x-12y\right)$
⑤ $2a^2-8a+8$
答え $2(a-2)^2$
\begin{eqnarray*} &&2a^2-8a+8\\ &=&2(a^2-4a+4)\\ &=&2(a-2)^2 \end{eqnarray*}① $\cfrac{2}{3}x-1=\cfrac{4}{9}x-\cfrac{3}{2}$
答え $x=-\cfrac{9}{4}$
\begin{eqnarray*} \cfrac{2}{3}x-1&=&\cfrac{4}{9}x-\cfrac{3}{2}\quad(\times18) \\ 12x-18&=&8x-27 \\ 12x-8x&=&-27+18\\ 4x&=&-9\\ x&=&-\cfrac{9}{4} \end{eqnarray*}② $\left\{\begin{array}{l} 0.3x+0.2y=0.7\\ 5x+3(y-2)=3 \end{array}\right.$
答え $x=-3,\ y=8$
\begin{eqnarray*} \left\{ \begin{array}{l} 0.3x+0.2y=0.7\qquad…①\\ 5x+3(y-2)=3\qquad…② \end{array} \right. \end{eqnarray*} \begin{eqnarray*} ①\times10\\ 0.3x+0.2y&=&0.7 \\ 3x+2y&=&7\qquad…③ \end{eqnarray*}\begin{eqnarray*} ②を整理\\ 5x+3(y-2)&=&3 \\ 5x+3y-6&=&3 \\ 5x+3y&=&9\qquad…④ \end{eqnarray*}
\begin{eqnarray*} ④\times2-③\times3\\ 10x+6y=18\\ \underline{-) \quad 9x+6y=21} \\ x\phantom{-5y}=-3 \end{eqnarray*}
\begin{eqnarray*} x=-3を&③&に代入\\ 3\times(-3)+2y&=&7\\ -9+2y&=&7\\ 2y&=&16\\ y&=&8 \\ \left\{ \begin{array}{l} x=-3\\ y=8 \end{array} \right. \end{eqnarray*}
③ $x^2-8x=20$
答え $x=10,\ x=-2$
\begin{eqnarray*} x^2-8x&=&20 \\ x^2-8x-20&=&0\\ (x-10)(x+2)&=&0\\ x&=&10,\ x=-2 \end{eqnarray*}④ $15x^2-20=0$
答え $x=\pm\cfrac{2\sqrt{3}}{3}$
\begin{eqnarray*} 15x^2-20&=&0 \\ 15x^2&=&20 \\ x^2&=&\cfrac{20}{15}=\cfrac{4}{3}\\ x&=&\pm \sqrt {\frac{\ 4\ }{\ 3\ }}=\pm \cfrac{\sqrt4}{\sqrt3}=\pm \cfrac{2\sqrt3}{3} \end{eqnarray*}⑤ $-12x^2=-15x$
答え $x=0 ,\ x=\cfrac{5}{4}$
\begin{eqnarray*} -12x^2&=&-15x \\ -12x^2+15x&=&0\quad(両辺を-3で割る)\\ 4x^2-5x&=&0\\ x(4x-5)&=&0\\ x&=&0,\ x=\cfrac{5}{4} \end{eqnarray*}⑥ $2x^2+6x+3=0$
答え $x=\cfrac{-3\pm\sqrt{3}}{2}$
\begin{eqnarray*} x&=&\cfrac{-6\pm\sqrt{6^2-4\times2\times3}}{2\times2}\\ &=&\cfrac{-6\pm\sqrt{36-24}}{4}\\ &=&\cfrac{-6\pm\sqrt{12}}{4}\\ &=&\cfrac{-6\pm2\sqrt{3}}{4}\\ &=&\cfrac{-3\pm\sqrt{3}}{2} \end{eqnarray*}次の式を$[\phantom{x}]$内の文字について解きなさい。
①
$3y=-\cfrac{9}{8}x-2\quad[x]$
答え $x=\cfrac{-24y-16}{9}\\ \left(x=-\cfrac{24y+16}{9}, \ x=-\cfrac{8}{3}y-\cfrac{16}{9}も可\right)$
\begin{eqnarray*} 3y&=&-\cfrac{9}{8}x-2\quad(左辺と右辺をとりかえる） \\ -\cfrac{9}{8}x-2&=&3y\quad(\times-8) \\ 9x+16&=&-24y\\ 9x&=&-24y-16 \\ x&=&\cfrac{-24y-16}{9} \end{eqnarray*}$x=6+\sqrt{5}$, $y=3+\sqrt{5}$ のとき、次の式の値を求めなさい。
②
$x^2-4xy+4y^2$
答え $5$
\begin{eqnarray*} &&x^2-4xy+4y^2\\ &=&(6+\sqrt{5})^2-4(6+\sqrt{5})(3+\sqrt{5})+4(3+\sqrt{5})^2\\ &=&36+12\sqrt{5}+5-4(18+9\sqrt{5}+5)+4(9+6\sqrt{5}+5)\\ &=&36+12\sqrt{5}+5-4(23+9\sqrt{5})+4(14+6\sqrt{5})\\ &=&36+12\sqrt{5}+5-92-36\sqrt{5}+56+24\sqrt{5}\\ &=&5 \end{eqnarray*} ＜別解＞ \begin{eqnarray*} &&x^2-4xy+4y^2\\ &=&(x-2y)^2\\ &=&\{(6+\sqrt{5})-2(3+\sqrt{5})\}^2\\ &=&(6+\sqrt{5}-6-2\sqrt{5})^2\\ &=&(-\sqrt{5})^2\\ &=&5 \end{eqnarray*}③ $y$ が $x$ に比例し、$x=-15$ のとき、$y=-4$ である。$x=-5$ のときの $y$ の値を求めなさい。
答え $y=-\cfrac{4}{3}$
比例の式の形は $y=ax$ $$a=\cfrac{-4}{-15}=\cfrac{4}{15}\\ y=\cfrac{4}{15}x\ に\ x=-5 を代入する\\ y=\cfrac{4}{15}\times(-5)=-\cfrac{4}{3}$$④ $y$ が $x$ に反比例し、$x=-7$ のとき、$y=4$ である。$x=6$ のときの $y$ の値を求めなさい。
答え $y=-\cfrac{14}{3}$
反比例の式の形は $y=\cfrac{a}{x}$ $$a=x \times y=-7\times4=-28\\ y=-\cfrac{28}{x}\ に\ x=6\ を代入する\\ y=-\cfrac{28}{6}=-\cfrac{14}{3}$$⑤ $2$ 点 $(-1,\ 3),\ (2,\ -3)$ を通る直線の式を求めなさい。
答え $y=-2x+1$
直線の式の形は $y=ax+b$ \begin{eqnarray*} a&=&\cfrac{y_2-y_1}{x_2-x_1}\\ &=&\cfrac{-3-3}{2-(-1)}=\cfrac{-6}{3}=-2\\ \end{eqnarray*} $y=-2x+b$ に $x=-1,\ y=3$ を代入 \begin{eqnarray*} 3&=&-2\times(-1)+b\\ 3&=&2+b\\ 1&=&b \end{eqnarray*}⑥ $y$ が $x$ の $2$ 乗に比例し、$x=4$ のとき、$y=8$ である。$x=-5$ のときの $y$ の値を求めなさい。
答え $y=\cfrac{25}{2}$
$2$ 乗に比例する式の形は $y=ax^2$ $$y=ax^2 に x=4,\ y=8 を代入する$$ \begin{eqnarray*} 8&=&a\times4^2\\ 8&=&16a\\ \cfrac{1}{2}&=&a \end{eqnarray*} $$y=\cfrac{1}{2}x^2\ に\ x=-5 を代入する\\ y=\cfrac{1}{2}\times(-5)^2=\cfrac{1}{2}\times25=\cfrac{25}{2}$$⑦ $8$ 人の生徒があるテストを受けた。得点はそれぞれ、$96$ 点、$87$ 点、$75$ 点、$88$ 点、$69$ 点、$80$ 点、$16$ 点、$77$ 点だった。このときの中央値（メジアン）を求めなさい。
答え $78.5\ 点$
得点を低い順にならべると、$$16,\ 69,\ 75,\ 77,\ 80,\ 87,\ 88,\ 96$$ $8$ 人の中央値（メジアン）は $4$ 番目と $5$ 番目の平均だから、 $$(77+80)\div2=78.5$$
⑧ $2$ 個のサイコロを同時に投げるとき、出る目の積が $3$ の倍数となる確率を求めなさい。
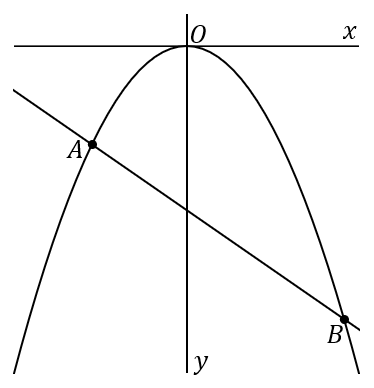
$①$ $2$ 点 $A, \ B$ の座標をそれぞれ求めなさい。
答え
$A(-3,-3) \quad , \quad B\left(5,-\cfrac{25}{3}\right)$
2つの線の交点の座標は連立方程式の解です。放物線と直線についてもおなじこと。つまり、
\begin{eqnarray*}
\left\{
\begin{array}{l}
y=-\cfrac{1}{3}x^2\\
y=-\cfrac{2}{3}x-5
\end{array}
\right.
\end{eqnarray*}
を解けばいいです。代入法で、（上の式の右辺）＝（下の式の右辺）という式をたてて解いていきましょう。2次方程式になります。そして、解は2つでてきます。なぜならグラフが2か所で交わっているからです。
\begin{eqnarray*}
-\cfrac{1}{3}x^2&=&-\cfrac{2}{3}x-5\\
-\cfrac{1}{3}x^2+\cfrac{2}{3}x+5&=&0\quad両辺に\times(-3)\\
x^2-2x-15&=&0\\
(x-5)(x+3)&=&0\\
x&=&5,\quad x=-3
\end{eqnarray*}
こんなふうに2つの $x$ が求められました。こんどはそれぞれの $x$ について、$y$ をだしていきましょう。使う式は $y=-\cfrac{1}{3}x^2$ と $y=-\cfrac{2}{3}x-5$ のどっちでもいいです。どっちを使っても同じ答えになります。今回は $y=-\cfrac{1}{3}x^2$ を使ってみましょう。
$x=5$ のとき
$$y=-\cfrac{1}{3}\times5^2=-\cfrac{25}{3}$$
$x=-3$ のとき
$$y=-\cfrac{1}{3}\times(-3)^2=-3$$
こうして、$x=5$ のとき $y=-\cfrac{25}{3}$ , $x=-3$ のとき $y=-3$ というふうに、$x$ と $y$ の2つの組が求められました。じゃあ答えを書きましょう。
$$A(-3,-3) \quad , \quad B\left(5,-\cfrac{25}{3}\right)$$
$A$ は $x$ がマイナスのほう、$B$ は $x$ がプラスのほうを答えましょう。それはグラフを見て判断しましょう。
$②$ $\triangle OAB$ の面積を求めなさい。
答え
$20$
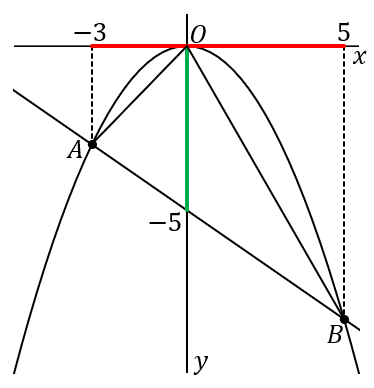$\triangle OAB$ の面積は、赤 $\times$ 緑 $\times\cfrac{1}{2}$ です。
直線の $y$ 切片は $-5$ なので、緑線の長さは $5$ です。赤の長さは、$2$ 点 $A, \ B$ の $x$ 座標をみればよいです。なので、
$$8×5×\cfrac{1}{2}=20$$
$③$ 点 $A$ を通り、$\triangle OAB$ の面積を $2$ 等分する直線の式を求めなさい。
答え
$y=-\cfrac{7}{33}x-\cfrac{40}{11}$
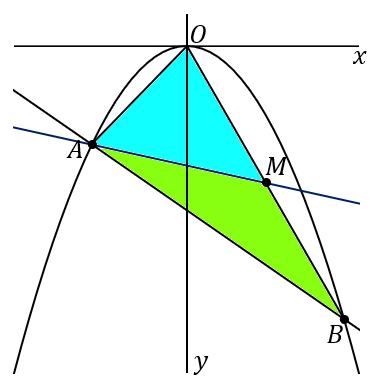＜中線＞
三角形の $1$ つの頂点から、むかいあう辺の中点を通るようにひいた線を中線といいます。三角形の中線は、その三角形の面積を二等分します。
なので、$OB$ の中点を求めて、そこと点 $A$ を通る直線の式を答えればよいです。
＜中点＞
中点の座標は、「足して $2$ で割る」です。$x$ 座標と $y$ 座標のそれぞれを足して $2$ で割ればよいです。
点 $O$ の座標は $(0, \ 0),$ 点 $B$ の座標は $\left(5, \ -\cfrac{25}{3}\right)$ です。なのでその中点を $M$ とすると、その座標は、
\begin{eqnarray*}
&&\left(\cfrac{x+x}{2}, \ \cfrac{y+y}{2}\right)\\
&=&\left(\cfrac{0+5}{2}, \ \cfrac{0+\left(-\cfrac{25}{3}\right)}{2}\right)\\
&=&\left(\cfrac{5}{2}, \ \cfrac{-\cfrac{25}{3}}{2}\right)\\
&=&\left(\cfrac{5}{2}, \ -\cfrac{25}{3}\times\cfrac{1}{2}\right)\\
&=&\left(\cfrac{5}{2}, \ -\cfrac{25}{6}\right)
\end{eqnarray*}
というわけで中点 $M$ の座標は $\left(\cfrac{5}{2}, \ -\cfrac{25}{6}\right)$ です。
では答えをだしていきましょう。点 $A \ (-3,-3)$ と点 $M \ \left(\cfrac{5}{2}, \ -\cfrac{25}{6}\right)$ を通る直線の式を求めればよいです。
直線の式の形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標です。
\begin{eqnarray*}
a&=&\cfrac{y_2-y_1}{x_2-x_1}\\
&=&\cfrac{-\cfrac{25}{6}-(-3)}{\cfrac{5}{2}-(-3)}\\
&=&\cfrac{-\cfrac{25}{6}+3}{\cfrac{5}{2}+3}\\
&=&\cfrac{-\cfrac{25}{6}+\cfrac{18}{6}}{\cfrac{5}{2}+\cfrac{6}{2}}\\
&=&\cfrac{-\cfrac{7}{6}}{\cfrac{11}{2}}\\
&=&-\cfrac{7}{6}\div\cfrac{11}{2}\\
&=&-\cfrac{7}{6}\times\cfrac{2}{11}\\
&=&-\cfrac{7}{33}
\end{eqnarray*}
$y=-\cfrac{7}{33}x+b$ に $x=-3,\ y=-3$ を代入
\begin{eqnarray*}
-3&=&-\cfrac{7}{33}\times(-3)+b\\
-3&=&\cfrac{7}{11}+b\\
-3-\cfrac{7}{11}&=&b\\
-\cfrac{33}{11}-\cfrac{7}{11}&=&b\\
-\cfrac{40}{11}&=&b
\end{eqnarray*}
これで $a$ と $b$ がわかりました。では答えです。
$$y=-\cfrac{7}{33}x-\cfrac{40}{11}$$
$④$ 関数 $y=-\cfrac{1}{3}x^2$ 上に点 $P$ をとる。$\triangle PAB$ の面積が $\triangle OAB$ の面積と等しくなるとき、点 $P$ の座標を求めなさい。ただし、$x$ の範囲は $0\lt x \lt5$ とする。
答え
$\left(2,-\cfrac{4}{3}\right)$
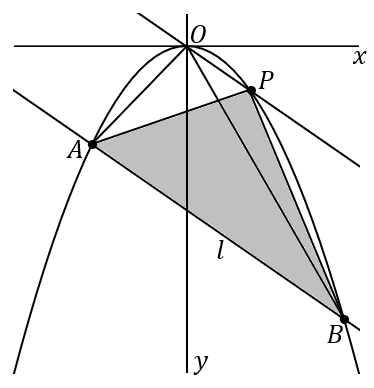直線 $y=-\cfrac{2}{3}x-5$ を $l$ ということにします。点 $O$ を通って直線 $l$ と平行な直線をひきます。この直線と放物線との交点が、$P$ です。こうやって $P$ をとれば、$\triangle OAB$ と $\triangle PAB$ は面積がおなじです。底辺を $AB$ だということにしたとき、底辺が共通で、高さが等しいからです。
じゃあ点 $P$ の座標を求めていきましょう。
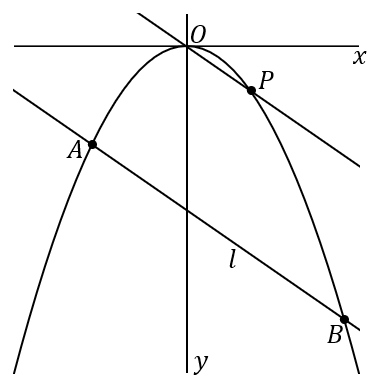＜点 $O$ を通って 直線 $l$ と平行な直線＞
原点を通る直線の式を求めるのだから、式の形は $y=ax$ です。
傾きが等しいとき、$2$ 直線は平行になるのだから、$l$ と平行な直線というのは、傾きが $l$ と等しくなります。$l$ の傾きは $-\cfrac{2}{3}$ だから、求めたい直線の傾きも $-\cfrac{2}{3}$ です。$a=-\cfrac{2}{3}$ です。
というわけで、$O$ を通って $l$ に平行な直線の式は、
$$y=-\cfrac{2}{3}x$$
となります。
＜直線と放物線の交点＞
2つの線の交点の座標は連立方程式の解です。放物線と直線についてもおなじこと。つまり、
\begin{eqnarray*}
\left\{
\begin{array}{l}
y=-\cfrac{1}{3}x^2\\
y=-\cfrac{2}{3}x
\end{array}
\right.
\end{eqnarray*}
を解けばいいです。代入法で、（上の式の右辺）＝（下の式の右辺）という式をたてて解いていきましょう。2次方程式になります。そして、解は2つでてきます。なぜならグラフが2か所で交わっているからです。
\begin{eqnarray*}
-\cfrac{1}{3}x^2&=&-\cfrac{2}{3}x\\
-\cfrac{1}{3}x^2+\cfrac{2}{3}x&=&0\quad両辺に\times(-3)\\
x^2-2x&=&0\\
x(x-2)&=&0\\
x&=&0,\quad x=2
\end{eqnarray*}
こんなふうに2つの $x$ が求められました。点 $P$ の $x$ 座標は、$2$ のほうです。こんどは $x=2$ のときの $y$ をだしていきましょう。使う式は $y=-\cfrac{1}{3}x^2$ と $y=-\cfrac{2}{3}x$ のどっちでもいいです。どっちを使っても同じ答えになります。今回は $y=-\cfrac{2}{3}x$ のほうを使うことにすると、
\begin{eqnarray*}
y=-\cfrac{2}{3}\times2=-\cfrac{4}{3}
\end{eqnarray*}
こうして、$x=2$ のとき $y=-\cfrac{4}{3}$ というふうに、$x$ と $y$ の組が求められました。じゃあ答えを書きましょう。
$$\left(2,-\cfrac{4}{3}\right)$$
$P$ の座標が $\left(2,-\cfrac{4}{3}\right)$ のとき、$\triangle OAB$ と $\triangle PAB$ は面積がおなじです。底辺が共通で、高さが等しいからです。
答え
$\boxed{\large{\ 1\ }}①4②\cfrac{1}{12}③7④2x+3\\ ⑤8x-12y^2 ⑥\cfrac{-7x-6y}{12}\\ \quad\left(-\cfrac{7x+6y}{12},\ -\cfrac{7}{12}x-\cfrac{1}{2}yも可\right)\\ ⑦-5x^2+125 ⑧9x^2-7xy+\cfrac{49}{36}y^2\\⑨\cfrac{49}{64}a^2-\cfrac{81}{100}b^2 ⑩\cfrac{43\sqrt{2}}{4}⑪6\sqrt{5}⑫58-24\sqrt{5}\\ \boxed{\large{\ 2\ }}①5xy(7x^2-10xy+5)②(x+3)(x-20)\\ ③(5x-9y)^2④\left(\cfrac{3}{7}x+12y\right)\left(\cfrac{3}{7}x-12y\right)\\ ⑤2(a-2)^2\\ \boxed{\large{\ 3\ }}①x=-\cfrac{9}{4}②x=-3,y=8\\ ③x=10,-2④x=\pm\cfrac{2\sqrt{3}}{3}⑤x=0,\cfrac{5}{4}\\ ⑥x=\cfrac{-3\pm\sqrt{3}}{2}\\ \boxed{\large{\ 4\ }}①x=\cfrac{-24y-16}{9}\\ \left(x=-\cfrac{24y+16}{9}, \ x=-\cfrac{8}{3}y-\cfrac{16}{9}も可\right)\\②5③y=-\cfrac{4}{3}\\ ④y=-\cfrac{14}{3}⑤y=-2x+1⑥y=\cfrac{25}{2}\\ ⑦78.5点⑧\cfrac{5}{9}\\ \boxed{\large{\ 5\ }}①A(-3,-3) \quad , \quad B\left(5,-\cfrac{25}{3}\right)\\②20③y=-\cfrac{7}{33}x-\cfrac{40}{11} ④\left(2,-\cfrac{4}{3}\right) $