中3数学 夏休みの計算 第4回 全32問
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
① $-7-3\times(+8)$
答え $-31$
\begin{eqnarray*} &&-7-3\times(+8)\\ &=&-7-24\\ &=&-31 \end{eqnarray*}② $2-\cfrac{1}{2}-\cfrac{4}{3}$
答え $\cfrac{1}{6}$
\begin{eqnarray*} &&2-\cfrac{1}{2}-\cfrac{4}{3}\\ &=&\cfrac{12}{6}-\cfrac{3}{6}-\cfrac{8}{6}\\ &=&\cfrac{1}{6} \end{eqnarray*}③ $(-2^2)+\{(-5)-4\}\times(-2)^2$
答え $-40$
\begin{eqnarray*} &&(-2^2)+\{(-5)-4\}\times(-2)^2\\ &=&-4+\{(-5)-4\}\times4\\ &=&-4-9\times4\\ &=&-4-36\\ &=&-40 \end{eqnarray*}④ $(5x-4)+(3x+4)$
答え $8x$
\begin{eqnarray*} &&(5x-4)+(3x+4)\\ &=&5x-4+3x+4\\ &=&8x \end{eqnarray*}⑤ $(12a^2b-6ab^2)\div\left(-\cfrac{6}{7}ab\right)$
答え $-14a+7b$
\begin{eqnarray*} &&(12a^2b-6ab^2)\div\left(-\cfrac{6}{7}ab\right)\\ &=&(12a^2b-6ab^2)\times\left(-\cfrac{7}{6ab}\right)\\ &=&12a^2b\times\left(-\cfrac{7}{6ab}\right)-6ab^2\times\left(-\cfrac{7}{6ab}\right)\\ &=&-14a+7b \end{eqnarray*}⑥ $\cfrac{x-2y}{5}-\cfrac{3x-4y}{3}$
答え $\cfrac{-12x+14y}{15}\\\quad\left(-\cfrac{12x-14y}{15},-\cfrac{4}{5}x+\cfrac{14}{15}yも可\right)$
\begin{eqnarray*} &&\cfrac{x-2y}{5}-\cfrac{3x-4y}{3}\\ &=&\cfrac{3(x-2y)-5(3x-4y)}{15}\\ &=&\cfrac{3x-6y-15x+20y}{15}\\ &=&\cfrac{-12x+14y}{15} \end{eqnarray*}⑦ $(x-8)(x-10)$
答え $x^2-18x+80$
⑧ $\left(9a-\cfrac{2}{3}b\right)^2$
答え $81a^2-12ab+\cfrac{4}{9}b^2$
⑨ $(x+11y)(x-11y)$
答え $x^2-121y^2$
⑩ $-(2x-3)^2+2(x+2)(5x-2)$
答え $6x^2+28x-17$
\begin{eqnarray*} &&-(4x^2-12x+9)+2(5x^2+8x-4)\\ &=&-4x^2+12x-9+10x^2+16x-8\\ &=&6x^2+28x-17 \end{eqnarray*}⑪ $\sqrt{\cfrac{3}{2}}-\sqrt{\cfrac{2}{3}}$
答え $\cfrac{\sqrt{6}}{6}$
\begin{eqnarray*} &&\sqrt{\cfrac{3}{2}}-\sqrt{\cfrac{2}{3}}\\ &=&\cfrac{\sqrt{3}}{\sqrt{2}}-\cfrac{\sqrt{2}}{\sqrt{3}}\\ &=&\cfrac{\sqrt{6}}{2}-\cfrac{\sqrt{6}}{3}\\ &=&\cfrac{3\sqrt{6}}{6}-\cfrac{2\sqrt{6}}{6}\\ &=&\cfrac{\sqrt{6}}{6} \end{eqnarray*}⑫ $5\sqrt{75}\div10\sqrt{125}\times5\sqrt{6}$
答え $\cfrac{3\sqrt{10}}{2}$
\begin{eqnarray*} &&5\sqrt{75}\div10\sqrt{125}\times5\sqrt{6}\\ &=&\cfrac{5\sqrt{75}\times5\sqrt{6}}{10\sqrt{125}}\\ &=&\cfrac{5\sqrt{18}}{2\sqrt{5}}\\ &=&\cfrac{15\sqrt{2}}{2\sqrt{5}}\\ &=&\cfrac{15\sqrt{10}}{10}\\ &=&\cfrac{3\sqrt{10}}{2} \end{eqnarray*}⑬ $\left(1-2\sqrt{2}\right)^2$
答え $9-4\sqrt{2}$
\begin{eqnarray*} &&\left(1-2\sqrt{2}\right)^2\\ &=&1-4\sqrt{2}+8\\ &=&9-4\sqrt{2} \end{eqnarray*}① $16a^2b-24ab$
答え $8ab(2a-3)$
② $x^2-12x-28$
答え $(x-14)(x+2)$
③ $25x^2-\cfrac{20}{3}xy+\cfrac{4}{9}y^2$
答え $\left(5x-\cfrac{2}{3}y\right)^2$
④ $\cfrac{1}{49}x^2-4y^2$
答え $\left(\cfrac{1}{7}x+2y\right)\left(\cfrac{1}{7}x-2y\right)$
⑤ $2x^2+4xy+2y^2$
答え $2(x+y)^2$
\begin{eqnarray*} &&2x^2+4xy+2y^2\\ &=&2(x^2+2xy+y^2)\\ &=&2(x+y)^2 \end{eqnarray*}① $\cfrac{2}{3}x-2=-x+\cfrac{1}{4}$
答え $x=\cfrac{27}{20}$
\begin{eqnarray*} \cfrac{2}{3}x-2&=&-x+\cfrac{1}{4}\quad(\times12) \\ 8x-24&=&-12x+3 \\ 8x+12x&=&3+24\\ 20x&=&27\\ x&=&\cfrac{27}{20} \end{eqnarray*}② $\left\{\begin{array}{l} 10(x+y)=y+8\\ 7x-5y=-17 \end{array}\right.$
答え $x=-1,y=2$
\begin{eqnarray*} \left\{ \begin{array}{l} 10(x+y)=y+8\qquad…①\\ 7x-5y=-17\qquad…② \end{array} \right. \end{eqnarray*} $①を整理$ \begin{eqnarray*} 10x+10y&=&y+8\\ 10x+10y-y&=&8\\ 10x+9y&=&8\qquad…③ \end{eqnarray*} $②\times9+③\times5$ \begin{eqnarray*} 63x-45y=-153\\ \underline{+) \quad 50x+45y=\phantom{-1}40} \\ 113x\phantom{-15y}=-113 \\ x=-1\phantom{16} \end{eqnarray*} \begin{eqnarray*} x=-1を②に代入\\ 7\times(-1)-5y&=&-17\\ -7-5y&=&-17\\ -5y&=&-17+7\\ -5y&=&-10\\ y&=&2 \\ \left\{ \begin{array}{l} x=-1\\ y=2 \end{array} \right. \end{eqnarray*}③ $x^2-13x+36=0$
答え $x=4 ,\ x=9$
\begin{eqnarray*} x^2-13x+36&=&0 \\ (x-4)(x-9)&=&0\\ x&=&4,\ x=9 \end{eqnarray*}④ $25x^2+40x+16=0$
答え $x=-\cfrac{4}{5}$
\begin{eqnarray*} 25x^2+40x+16&=&0 \\ (5x+4)^2&=&0\\ x&=&-\cfrac{4}{5} \end{eqnarray*}⑤ $2x^2=3$
答え $x=\pm \cfrac{\sqrt{6}}{2}$
\begin{eqnarray*} 2x^2&=&3 \\ x^2&=&\cfrac{3}{2}\\ x&=&\pm \sqrt {\frac{\ 3\ }{\ 2\ }}=\pm \cfrac{\sqrt{3}}{\sqrt{2}}=\pm \cfrac{\sqrt{6}}{2} \end{eqnarray*}⑥ $2x^2=3x$
答え $x=0 ,\ x=\cfrac{3}{2}$
\begin{eqnarray*} 2x^2&=&3x \\ 2x^2-3x&=&0\\ x(2x-3)&=&0\\ x&=&0,\ x=\cfrac{3}{2} \end{eqnarray*}⑦ $2x^2=3x-1$
答え $x=1,\ x=\cfrac{1}{2}$
\begin{eqnarray*} 2x^2&=&3x-1\\ 2x^2-3x+1&=&0 \end{eqnarray*} $2$ 次方程式の解の公式により、 \begin{eqnarray*} x&=&\cfrac{-(-3)\pm\sqrt{(-3)^2-4\times2\times1}}{2\times2}\\ &=&\cfrac{3\pm\sqrt{9-8}}{4}\\ &=&\cfrac{3\pm\sqrt{1}}{4}\\ &=&\cfrac{3\pm1}{4}\\ x&=&\cfrac{4}{4},\ x=\cfrac{2}{4}\\ x&=&1,\ x=\cfrac{1}{2} \end{eqnarray*}次の式を$[\phantom{x}]$内の文字について解きなさい。
①
$\cfrac{1}{3}y=-\cfrac{3}{4}x+2\quad[x]$
答え $x=\cfrac{-4y+24}{9}\\ \left(-\cfrac{4y-24}{9},-\cfrac{4}{9}y+\cfrac{8}{3}も可\right)$
\begin{eqnarray*} \cfrac{1}{3}y&=&-\cfrac{3}{4}x+2\quad(\times12) \\ 4y&=&-9x+24 \\ 9x&=&-4y+24\\ x&=&\cfrac{-4y+24}{9} \end{eqnarray*}$x=1+\sqrt{5}, \ y=-1+\sqrt{5}$ のとき、次の式の値を求めなさい。
②
$x^2+2xy+y^2$
答え $20$
\begin{eqnarray*} &&x^2+2xy+y^2\\ &=&(x+y)^2\quad \class{mathbg-r}{(ここで代入する)} \\ &=&\{(1+\sqrt{5})+(-1+\sqrt{5})\}^2\\ &=&(2\sqrt{5})^2\\ &=&20 \end{eqnarray*} やり方が思いつかないときや、自信がないときは、単に代入して、がんばって計算すれば同じ答えがでます \begin{eqnarray*} &&x^2+2xy+y^2\\ &=&(1+\sqrt{5})^2+2(1+\sqrt{5})(-1+\sqrt{5})+(-1+\sqrt{5})^2\\ &=&1+2\sqrt{5}+5+2(-1+5)+1-2\sqrt{5}+5\\ &=&20 \end{eqnarray*}③ $y$ が $x$ に比例し、$x=-4$ のとき、$y=-6$ である。$x=6$ のときの $y$ の値を求めなさい。
答え $y=9$
比例の式の形は $y=ax$ $$a=\cfrac{y}{x}=\cfrac{-6}{-4}=\cfrac{3}{2}\\ y=\cfrac{3}{2}xに\ x=6\ を代入する\\ y=\cfrac{3}{2}\times6=9$$④ $y$ が $x$ に反比例し、$x=-4$ のとき、$y=-6$ である。$x=6$ のときの $y$ の値を求めなさい。
答え $y=4$
反比例の式の形は $y=\cfrac{a}{x}$ $$a=x \times y=-4\times(-6)=24\\ y=\cfrac{24}{x}\ に\ x=6\ を代入する\\ y=\cfrac{24}{6}=4$$⑤ 下の直線の式を求めなさい。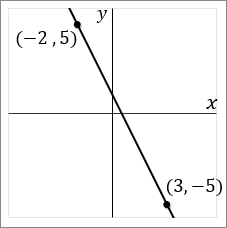
答え $y=-2x+1$
直線の式の形は $y=ax+b$ \begin{eqnarray*} a&=&\cfrac{y_2-y_1}{x_2-x_1}\\ &=&\cfrac{5-(-5)}{-2-3}=\cfrac{10}{-5}=-2\\ \end{eqnarray*} $y=-2x+b$ に $x=-2,\ y=5$ を代入 \begin{eqnarray*} 5&=&-2\times(-2)+b\\ 5&=&4+b\\ 1&=&b \end{eqnarray*}⑥ $A, B, C, D, E$ の $5$ 人の生徒があるテストをうけた。表はその得点の結果である。$5$ 人の平均点が $61.2$ 点であるとき、$C$ さんの得点は何点か。 \begin{array}{|cccccc|} \hline & A & B & C & D & E & \\ \hline & 62 & 75 & & 48 & 66 & \\ \hline \end{array}
答え 55点
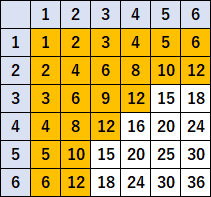
$C$ さんの得点を $x$ とすると、 \begin{eqnarray*} \cfrac{62+75+x+48+66}{5}&=&61.2 \quad(両辺に\times5)\\ 62+75+x+48+66&=&306\\ 251+x&=&306\\ x&=&306-251\\ x&=&55 \end{eqnarray*}⑦ $2$ 個のサイコロを同時に投げるとき、出る目の積が $12$ 以下になる確率を求めなさい。
答え
$\boxed{\large{\ 1\ }}①-31②\cfrac{1}{6}③-40④8x⑤-14a+7b\\ ⑥\cfrac{-12x+14y}{15}\quad\left(-\cfrac{12x-14y}{15},-\cfrac{4}{5}x+\cfrac{14}{15}yも可\right)\\ ⑦x^2-18x+80 ⑧81a^2-12ab+\cfrac{4}{9}b^2⑨x^2-121y^2\\ ⑩6x^2+28x-17 ⑪\cfrac{\sqrt{6}}{6}⑫\cfrac{3\sqrt{10}}{2}⑬9-4\sqrt{2}\\ \boxed{\large{\ 2\ }}①8ab(2a-3)②(x-14)(x+2)\\ ③\left(5x-\cfrac{2}{3}y\right)^2④\left(\cfrac{1}{7}x+2y\right)\left(\cfrac{1}{7}x-2y\right)\\ ⑤2(x+y)^2\\ \boxed{\large{\ 3\ }}①x=\cfrac{27}{20}②x=-1,y=2③x=4,x=9\\ ④x=-\cfrac{4}{5}⑤x=\pm\cfrac{\sqrt{6}}{2}⑥x=0,x=\cfrac{3}{2}\\ ⑦x=1,x=\cfrac{1}{2}\\ \boxed{\large{\ 4\ }}①x=\cfrac{-4y+24}{9} \left(-\cfrac{4y-24}{9},-\cfrac{4}{9}y+\cfrac{8}{3}も可\right)\\ ②20③y=9 ④y=4⑤y=-2x+1⑥55点⑦\cfrac{23}{36} $