数学 中1 3章 $1$ 次方程式 第4回(全20問)
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
方程式とその解
$(1)$ 次の $ \boxed{\LARGE\phantom{hoge}}$ の中にあてはまる言葉をいれましょう。
①方程式を成り立たせる値を、その方程式の $ \boxed{\LARGE\phantom{ho}}$ という。解を求めることを、その方程式を $ \boxed{\LARGE\phantom{hoge}}$ という。
②たとえば、
\begin{eqnarray*}
\begin{array}{l}
3x+5&=&8\\
3x&=&8-5
\end{array}
\end{eqnarray*}
上の $2$ つの式の $+5$ と $-5$ のように、一方の辺の項を、符号を変えて、他方の辺に移すことを $ \boxed{\LARGE\phantom{hoge}}$ という。
答え
①方程式を成り立たせる値を、その方程式の $ \boxed{解}$ という。解を求めることを、その方程式を $ \boxed{解く}$ という。
②たとえば、
\begin{eqnarray*}
\begin{array}{l}
3x+5&=&8\\
3x&=&8-5
\end{array}
\end{eqnarray*}
上の $2$ つの式の $+5$ と $-5$ のように、一方の辺の項を、符号を変えて、他方の辺に移すことを $ \boxed{移項}$ という。
$1$ 次方程式の解き方
次の $(1)$ ~ $(7)$ の $1$ 次方程式を解きなさい。また、$(8)$ の比例式を解きなさい。
$(1)\qquad -6+3x=8x-21$
答え
$x=3$
\begin{eqnarray*}
-6+3x&=&8x-21 \quad \class{mathbg-r}{(移項する)} \\
3x-8x&=&-21+6 \quad \class{mathbg-r}{(計算する)} \\
-5x&=&-15 \class{mathbg-r}{(xの係数で割る)} \\
x&=&\cfrac{-15}{-5}=3 \quad \class{mathbg-r}{(解)} \\
\end{eqnarray*}
1次方程式の解き方は、
①移項→ ②計算→ ③解
です。この手順を身につけましょう。あと、「方程式を解け」という問題に答えるときはかならず「$x=3$」というふうに、「文字$=$数」 の形で答えるようにしましょう。数だけ答えちゃだめです。
$(2)\qquad \cfrac{1}{7}x=21$
答え
$x=147$
\begin{eqnarray*}
\cfrac{1}{7}x&=&21 \quad \class{mathbg-r}{(両辺に7をかける)} \\
\cfrac{7}{7}x&=&21\times7\\
x&=&147
\end{eqnarray*}
「1次方程式を解きなさい」といわれたら、やり方は①移項、②計算、③解、なのですが、この問題の場合は単純すぎて移項の出番がないです。
方程式で分数があったら、まず、分数を整数になおしましょう。方程式はそれができます。「分母をはらう」といいます。分母の数をかけちゃって、分数を消します。
ところでこれ、$x=3$ と答えてしまうひとがいます。
$7x=21$ の解が $x=3$ なのであって、
$\cfrac{1}{7}x=21$ の解は $x=3$ ではないです。気をつけてくださいね。
$(3)\qquad -2(x-1)=-9+5(2x+3)$
答え
$x=-\cfrac{1}{3}$
\begin{eqnarray*} -2(x-1)&=&-9+5(2x+3) \class{mathbg-r}{(かっこをはずす)} \\ -2x+2&=&-9+10x+15 \class{mathbg-r}{(移項する)} \\ -2x-10x&=&-9+15-2 \class{mathbg-r}{(計算する)} \\ -12x&=&4 \quad \class{mathbg-r}{(xの係数で割る)} \\ x&=&\cfrac{4}{-12}=-\cfrac{1}{3} \quad \class{mathbg-r}{(解)} \\ \end{eqnarray*} 1次方程式の解き方は、①移項、②計算、③解。…なのですが、問題にかっこがあるときは、まず最初にかっこをはずしましょう。分配法則でかっこをはずしたら、①移項、②計算、③解、をやっていきます。
$(4)\qquad 0.2(x+1)=x+0.6 $
答え
$x=\cfrac{1}{2}$
その1(先に小数をなくす)
\begin{eqnarray*}
0.2(x+1)&=&x+0.6 \quad \class{mathbg-r}{(両辺に×10)} \\
2(x+1)&=&10x+6 \quad \class{mathbg-r}{(かっこをはずす)} \\
2x+2&=&10x+6 \quad \class{mathbg-r}{(移項する)} \\
2x-10x&=&6-2 \quad \class{mathbg-r}{(計算する)} \\
-8x&=&-4 \class{mathbg-r}{(xの係数で割る)} \\
x&=&\cfrac{-4}{-8}=\cfrac{1}{2} \quad \class{mathbg-r}{(解)} \\
\end{eqnarray*}
その2(先にかっこをはずす)
\begin{eqnarray*}
0.2(x+1)&=&x+0.6 \quad \class{mathbg-r}{(かっこをはずす)} \\
0.2x+0.2&=&x+0.6 \quad \class{mathbg-r}{(両辺に×10)} \\
2x+2&=&10x+6 \quad \class{mathbg-r}{(移項する)} \\
2x-10x&=&6-2 \quad \class{mathbg-r}{(計算する)} \\
-8x&=&-4 \class{mathbg-r}{(xの係数で割る)} \\
x&=&\cfrac{-4}{-8}=\cfrac{1}{2} \quad \class{mathbg-r}{(解)} \\
\end{eqnarray*}
1次方程式の解き方は、①移項、②計算、③解。…なのですが、問題にかっこがあるときはまずかっこをはずしましょう。
小数があるときはまず小数を整数になおしましょう。
じゃあかっこと小数の両方があるときはどうする? っていう話なのですが、最初にかっこをはずしても、小数をなくしても、それはどちらでもいいです。上の「その1」と「その2」のように、結果はおなじです。
ただ、最初に小数をなくすときはちょっと注意が必要です。
いまからまちがってる例をかきます。
\begin{eqnarray*}
0.2(x+1)&=&x+0.6 \quad \class{mathbg-r}{(両辺に×10)} \\
2(10x+10)&=&10x+6
\end{eqnarray*}
これはやっちゃダメです。これはかけすぎです。まちがっています。正しいのは上の「その1」の2行目です。
こういうミスが心配だったら、最初にかっこをはずすようにしてればまちがいないです。
$(5)\qquad -\cfrac{5}{3}x+2=3-\cfrac{1}{6}x $
答え
$x=-\cfrac{2}{3}$
\begin{eqnarray*}
-\cfrac{5}{3}x+2&=&3-\cfrac{1}{6}x
\class{mathbg-r}{(両辺に×6)}\\
\left(-\cfrac{5}{3}x+2\right)×6&=&\left(3-\cfrac{1}{6}x\right)×6\\
-10x+12&=&18-x
\quad \class{mathbg-r}{(移項する)} \\
-10x+x&=&18-12
\quad \class{mathbg-r}{(計算する)}\\
-9x&=&6
\class{mathbg-r}{(xの係数で割る)}\\
x&=&\cfrac{6}{-9}=-\cfrac{2}{3} \quad \class{mathbg-r}{(解)} \\
\end{eqnarray*}
1次方程式の解き方は、①移項、②計算、③解。…なのですが、問題に分数があるときは、まず最初に分数を整数になおしましょう。方程式はそれができます。
やり方は単純で、分母の公倍数を両辺にかけます。すると分数が消えるので、わかりやすくなりますね。「分母をはらう」といいます。
あと、公倍数ならなんでもいいのですが、数が小さいほうが計算がラクなので、なるべく最小公倍数をかけるようにしましょう。
この問題の場合は、分母の数は $3$ と $6$ なので、最小公倍数は $6$ です。その数をすべての項にかけていきます。必ず約分できて、必ず分母は $1$ になって、かけ終えたら分数がなくなっています。そうなる数をかけているんだから、そのつもりでかけていきましょう。
分数がなくなったら、①移項、②計算、③解、をやっていきましょう。
$(6)\qquad \cfrac{3x+1}{4}=3-\cfrac{x+3}{2} $
答え
$x=1$
\begin{eqnarray*}
\cfrac{3x+1}{4}&=&3-\cfrac{x+3}{2}
\class{mathbg-r}{(両辺に×4)} \\
\cfrac{3x+1}{4}×4&=&\left(3-\cfrac{x+3}{2}\right)×4 \quad(ア)\\
3x+1&=&12-2(x+3) \quad(イ)
\class{mathbg-r}{(かっこをはずす)} \\
3x+1&=&12-2x-6
\class{mathbg-r}{(移項する)} \\
3x+2x&=&12-6-1
\class{mathbg-r}{(計算する)} \\
5x&=&5
\class{mathbg-r}{(xの係数で割る)} \\
x&=&\cfrac{5}{5}=1\\
\end{eqnarray*}
分数があるのでまず分母をはらいましょう。この問題の場合は、分母の数は $4$ と $2$ なので、最小公倍数は $4$ です。その数を両辺にかけていきます。必ず約分できて、必ず分母は $1$ になって、かけ終えたら分数がなくなります。そうなる数をかけているんだから、そのつもりでかけていきましょう。
さて、この問題は、分子が式になっています。こういうときは、約分をしたあとかっこをつけて分子を書いておきましょう。ええと。言葉だとわかりづらいので、下の(ア)と(イ)の式を見くらべてください。約分をしたあと、でてきた数のうしろに、かっこをつけて分子の式を書いています。意味がわかるまで考えながら見てください。
\begin{eqnarray*}
\cfrac{3x+1}{4}×4&=&\left(3-\cfrac{x+3}{2}\right)×4 \quad(ア)\\
3x+1&=&12-2(x+3) \quad(イ)
\end{eqnarray*}
分数がなくなったら、今度はかっこが残っています。だからかっこをはずしましょう。そして、①移項、②計算、③解、をやっていきましょう。
$(7)\qquad \cfrac{1}{2}(3x-2)-\cfrac{2}{3}(x-1)=3 $
答え
$x=4$
\begin{eqnarray*}
\cfrac{1}{2}(3x-2)-\cfrac{2}{3}(x-1)&=&3
\quad \class{mathbg-r}{(両辺に×6)} \\
\Bigl\{ \cfrac{1}{2}(3x-2)-\cfrac{2}{3}(x-1) \Bigr\} ×6&=&3\times6 \quad(ア)\\
3(3x-2)-4(x-1)&=&18 \quad(イ)
\quad \class{mathbg-r}{(かっこをはずす)} \\
9x-6-4x+4&=&18
\quad \class{mathbg-r}{(移項する)} \\
9x-4x&=&18+6-4
\quad \class{mathbg-r}{(計算する)} \\
5x&=&20
\quad \class{mathbg-r}{(xの係数で割る)} \\
x&=&\cfrac{20}{5}=4 \quad \class{mathbg-r}{(解)} \\
\end{eqnarray*}
「分数があったらまず分数を消す」「かっこがあったらまずかっこをはずす」というのが1次方程式のやり方なのですが、「じゃあ分数とかっこがあったらどっちが先なの?」っていう話になりますよね。これは、どっちが先でもいいです。どっちからやってもいけます。先に分数を消したほうが、ちょっとラクなことが多いかもしれません。でも、最初のうちは、いろいろためしてみてください。とにかくまず、分数もかっこもない式をつくる、というのが目標になります。
で、ここでは先に分数を消していくことにします。この問題の場合は、分母の数は $2$ と $3$ なので、最小公倍数は $6$ ですね。その数を両辺にかけていきます。必ず約分できて、必ず分母は $1$ になって、かけ終えたら分数がなくなります。そうなる数をかけているんだから、そのつもりでかけていきましょう。
さて、この問題は、分子のうしろがかっこのついた式になっています。こういうときは、約分をしたあと、かっことその中身はそのまま書いておきましょう。ええと。言葉だとわかりづらいので、下の(ア)と(イ)の式を見くらべてください。約分をしたあと、でてきた数のうしろに、かっこの式をそのまま書いています。意味がわかるまで考えながら見てください。
\begin{eqnarray*}
\Bigl\{ \cfrac{1}{2}(3x-2)-\cfrac{2}{3}(x-1) \Bigr\} ×6&=&3\times6 \quad(ア)\\
3(3x-2)-4(x-1)&=&18 \quad(イ)
\end{eqnarray*}
分数がなくなったら、今度はかっこが残っています。だからかっこをはずしましょう。そして、①移項、②計算、③解、をやっていきましょう。
あと、いちおう先にかっこをはずしちゃうパターンもやっておきます。
\begin{eqnarray*}
\cfrac{1}{2}(3x-2)-\cfrac{2}{3}(x-1)&=&3
\quad \class{mathbg-r}{(かっこをはずす)} \\
\cfrac{3}{2}x-1-\cfrac{2}{3}x+\cfrac{2}{3}&=&3
\quad \class{mathbg-r}{(両辺に×6)} \\
9x-6-4x+4&=&18
\quad \class{mathbg-r}{(移項する)} \\
9x-4x&=&18+6-4
\quad \class{mathbg-r}{(計算する)} \\
5x&=&20
\quad \class{mathbg-r}{(xの係数で割る)} \\
x&=&\cfrac{20}{5}=4 \quad \class{mathbg-r}{(解)} \\
\end{eqnarray*}
というわけで、先に分数を消しても、先にかっこをはずしても、どちらでもいけます。似たようなもんです。ただ、先にかっこをはずしちゃうと、ちょっと手間がかかって損なことがあります。たくさん練習して、どうすればラクかを見つけていきましょう。
次の比例式を解きなさい。
$(8)\qquad 3:(x-2)=5:(\cfrac{1}{2}x-1) $
答え
$x=2$
\begin{eqnarray*} 3:(x-2)&=&5:(\cfrac{1}{2}x-1) \class{mathbg-r}{(変形する)} \\ 3(\cfrac{1}{2}x-1)&=&5(x-2) \class{mathbg-r}{(かっこをはずす)} \\ \cfrac{3}{2}x-3&=&5x-10 \quad \class{mathbg-r}{(両辺に×2)} \\ 3x-6&=&10x-20 \class{mathbg-r}{(移項する)} \\ 3x-10x&=&-20+6 \class{mathbg-r}{(計算する)} \\ -7x&=&-14 \quad \class{mathbg-r}{(xの係数で割る)} \\ x&=&\cfrac{-14}{-7}=2 \end{eqnarray*} 比の性質は、$$a:b=c:d \quad ならば\quad ad=bc$$です。言葉では「内項の積は外項の積に等しい」といって、内項の積というのはこの場合は $bc$ で、外項の積というのは $ad$ のことになります。これにこの問題をあてはめると、 \begin{eqnarray*} 3:(x-2)&=&5:(\cfrac{1}{2}x-1)\\ 3(\cfrac{1}{2}x-1)&=&5(x-2)\\ \end{eqnarray*} となります。左辺と右辺については、どっちにどっちの式を書いてもいいので、左辺のほうに $x$ の式を書くようにしましょう。両辺にでてきちゃうときは、もうほんとにどっちがどっちでもいいです。んで、あとは解くだけです。この問題はかっこがあるからまずかっこをはずして、それから①移項、②計算、③解。
ここからは文章題になります。文章題はムリだ、というひとは、①番から⑧番までの問題を繰り返して、確実にできるようになりましょう。
ムリかもしれないけどやってみる、というひとはここから先へ進みましょう。がんばって!
$(9)$ $1$ 匹 $120$ 円のめだかと、$1$ 匹 $160$ 円の金魚を、あわせて $15$ 匹と、$1$ つ $220$ 円の水草を $2$ つ買ったら、代金の合計が全部で $2400$ 円になった。めだかと金魚はそれぞれ何匹ずつ買ったか。
答え
めだか 11匹
金魚 4匹
方程式をたてて解きます。まず何を $x$ にするかを決めるのですが、きかれたことを $x$ にするのが基本です。この問題はめだかと金魚のそれぞれの数をきかれているので、こういう場合はどちらかを $x$ にします。それはどちらでもいいです。
今回は、めだかを $x$ 匹買ったことにしましょう。すると金魚は $(15-x)$ 匹買ったことになります。
$1$ 匹 $120$ 円のめだか $x$ 匹の代金の合計は $120x$ 円です。
$1$ 匹 $160$ 円の金魚 $(15-x)$ 匹の代金の合計は $160(15-x)$ 円です。
それから、$220$ 円の水草を $2$ つ買ったから、その代金は $220\times2=440$ 円になります。
それらをすべて足したら $2400$ 円、ということで式をたてます。
$$120x+160(15-x)+440=2400$$
($1$ 匹 $120$ 円のめだかの代金の合計)+($1$ 匹 $160$ 円の金魚の代金の合計)+($1$ つ $220$ 円の水草 $2$ つの代金の合計)$=2400$ 円、という式になっています。じゃあ、解いていきましょう。
\begin{eqnarray*}
120x+160(15-x)+440&=&2400\\
120x+2400-160x+440&=&2400\\
120x-160x&=&2400-2400-440\\
-40x&=&-440\\
x&=&\cfrac{-440}{-40}=11
\end{eqnarray*}
<ここから先は確かめの話>
というわけで $x=11$ というふうに解が求められました。 $x$ というのはめだかの匹数だから、それを $11$ 匹買ったことになります。めだかと金魚は全部で$15$ 匹買ったんだから、金魚は $4$ 匹買ったことになります。
$1$ 匹 $120$ 円のめだかは $11$ 匹で $1320$ 円。
$1$ 匹 $160$ 円の金魚は $4$ 匹で $640$ 円。
$1$ つ $220$ 円の水草が $2$ つで $440$ 円。
$1320$ 円と $640$ 円と $440$ 円をあわせて $2400$ 円。ぴったりですね。じゃあ答えましょう。
めだか 11匹
金魚 4匹
$(10)$ ある施設の入場料は、大人 $1$ 人ぶんの金額が子ども $1$ 人ぶんの金額の $1.5$ 倍である。この施設に、子ども $8$ 人と大人 $5$ 人で入場したら、入場料の合計が $2790$ 円だった。この施設の子ども $1$ 人ぶんの入場料はいくらか。
答え
180円
方程式をたてて解きます。まず何を $x$ にするかを決めるのですが、きかれたことを $x$ にするのが基本です。この問題は、子ども $1$ 人ぶんの入場料をきかれてるから、これを $x$ 円ということにします。
子どもの $1$ 人ぶんの入場料を $x$ 円とすると、大人 $1$ 人ぶんの入場料は、子ども $1$ 人ぶんの $1.5$ 倍だから、 $1.5x$ 円ということになります。
この問題では子ども $8$ 人と大人 $5$ 人で入場したのですから、その場合について考えましょう。まず、子ども$8$ 人ぶんの入場料は $8x$ 円です。
大人 $5$ 人ぶんの入場料の合計は $1.5x\times5=7.5x$ 円です。
子ども $8$ 人と大人 $5$ 人の入場料を足したら $2790$ 円。ということで式をたてます。
$$8x+7.5x=2790$$
(子ども $8$ 人ぶん)+(大人 $5$ 人ぶん)$=2790$ という式です。じゃあ解いていきましょう。
\begin{eqnarray*}
8x+7.5x&=&2790\quad \quad\class{mathbg-r}{(両辺に×10)} \\
80x+75x&=&27900\\
155x=27900\\
x&=&\cfrac{27900}{155}=180
\end{eqnarray*}
<ここから先は確かめの話>
というわけで $x=180$ というふうに解が求められました。 $x$ というのは子ども $1$ 人ぶんの入場料のことでしたね。すると大人 $1$ 人ぶんの入場料は、$180\times1.5=270$ 円ということになります。
子どもは $8$ 人入場したからその入場料はぜんぶで $180\times8=1440$ 円。
大人は $5$ 人入場したからその入場料はぜんぶで $270\times5=1350$ 円。
あわせて $2790$ 円。ぴったりですね。じゃあ答えましょう。
180円
$(11)$ プリントを、生徒 $1$ 人に $2$ 枚ずつ配ると $45$ 枚余り、生徒 $1$ 人に $3$ 枚ずつ配ろうとすると $75$ 枚足りない。生徒の人数とプリントの枚数を求めなさい。
答え
生徒 120人
プリント 285枚
方程式をたてて解きます。まず何を $x$ にするかを決めるのですが、きかれたことを $x$ にするのが基本です。ところがこの問題は生徒の人数とプリントをきかれていて、どちらを $x$ にするかというのはちょっとなやみどころです。
生徒の人数を $x$ として式をたてるのと、プリントの枚数を $x$ として式をたてるのと、どっちでやってもいけます。でもこれ、たててみればすぐにわかるのですが、生徒の人数を $x$ にしてやったほうがぜんぜんラクです。プリントを $x$ にしてやるのは、じぶんの修行のためならゼヒやってみるといいですけど、単に問題を解きたいときにはやめておいたほうがいいです。
というわけで生徒の人数を $x$ にして、「$2$ 枚ずつ配った時のプリントの枚数 $=$ $3$ 枚ずつ配った時のプリントの枚数」という式をたてていきます。
まず、生徒 $1$ 人に $2$ 枚ずつプリントを配ると $45$ 枚余るんだから、生徒の人数を $x$ 人とするとプリントの枚数は $2x+45$ とあらわせます。
つぎに、生徒 $1$ 人に $3$ 枚ずつ配ろうとすると $75$ 枚足りないんだから、生徒の人数を $x$ 人とするとプリントの枚数は $3x-75$ とあらわせます。
どちらもプリントの枚数をあらわしているんだから、じゃあそれは等しいだろうということで式をたてます。
$$2x+45=3x-75$$
($2$ 枚ずつ配った時のプリントの枚数)=($3$ 枚ずつ配った時のプリントの枚数)という式になっています。じゃあ解いてみましょう。
\begin{eqnarray*}
2x+45&=&3x-75\\
2x-3x&=&-75-45\\
-x&=&-120\\
x&=&120
\end{eqnarray*}
<ここから先は確かめの話>
というわけで $x=120$ というふうに解が求められました。 $x$ というのは生徒の人数のことでしたね。
するとプリントの枚数は、生徒 $1$ 人に $2$ 枚ずつ配ったときには $45$ 枚余るんだから、 $120\times2+45=285$ 枚。
生徒 $1$ 人に $3$ 枚ずつ配った時には $75$ 枚足りなくなるんだから、$120\times3-75=285$ 枚。
どちらで計算してもおなじ $285$ 枚になっています。じゃあ答えましょう。
生徒 120人
プリント 285枚
ところでこれ、生徒の人数ではなくて、プリントの枚数を $x$ 枚ということにしてやってみたらどうなるか、というのをやっておきます。興味のあるひとは下の説明ボタンを押して読んでみてください。
このへんからけっこう難易度があがります。こりゃムリだ、というひとは、①番から⑪番までの問題を繰り返して、確実にできるようになりましょう。
しんどいけどやり通す、というひとはここから先へ進みましょう。がんばって!
$(12)$ 妹が家を出てから $16$ 分後に、兄が分速 $750$ mの速さで追いかけた。妹の速さを分速 $150$ m、家から駅までの距離を $2900$ mとすると、妹が駅に着くまでに兄は妹に追いつけるか。追いつけるならば、兄が家を出てから何分後か。
答え
追いつけない
方程式をたてて解きます。まず何を $x$ にするかを決めるのですが、きかれたことを $x$ にするのが基本です。この問題は「兄は妹に追いつけるか。追いつけるならば、兄が家を出てから何分後か」ということですから、兄は妹に追いつけるとしたら $x$ 分後に追いつく、ということにします。
こういう「追いつく」問題は、「先に出発したひとのすすんだ距離=あとから追いかけるひとのすすんだ距離」という式をたてて解いていくというのが定番です。「先に出発したひとのすすんだ距離と、あとから追いかけるひとのすすんだ距離が等しい」ということは、いい方をかえると「追いついた」ということになるからです。
兄が妹に $x$ 分後に追いついたとすると、兄のすすんだ距離は $750x$mです。速さ×時間=距離です。
つぎに、妹のすすんだ距離は、$150(x+16)$m。速さ×時間をやったのですが、妹のすすんだ時間は兄より $16$ 分多いということに注意しましょう。
これが等しいということで、式をたてます。
$$750x=150(x+16)$$
(兄のすすんだ距離)=(妹のすすんだ距離)という式です。じゃあ解きましょう。
\begin{eqnarray*}
750x&=&150(x+16)\\
750x&=&150x+2400\\
750x-150x&=&2400\\
600x&=&2400\\
x&=&\cfrac{2400}{600}=4
\end{eqnarray*}
<ここから先は確かめの話>
というわけで $x=4$ というふうに解が求められました。 $x$ というのは兄が妹に追いつくまでにかかる時間だから、兄は $4$ 分後に追いつくことになります。
すると兄は追いつくまでに $750\times4=3000$mすすむことになります。
妹は $150\times(16+4)=3000$mすすむことになる。 $2$ 人のすすんだ距離が等しいから、これはOKってことになるのですが。
答えるまえにもういちど問題を確認しましょう。家から駅までの距離が $2900$ mだとかいてあります。$3000$ mすすんだところで追いつくってことは、これは、残念パターンですね。というわけで、答えましょう。
追いつけない
ところでこれ、この「追いかける」パターンの問題っていうのは、 $2$ 人の速さをひいちゃって、その速さで $2$ 人のあいだの距離をすすむのにどれくらいかかるか、ってやってしまうやり方があります。興味があったら下の説明ボタンを押して読んでみてください。
$(13)$ 家から学校まで行くのに、分速 $50$ mの速さで行くと、分速 $160$ mの速さで行くより $11$ 分遅く着く。家から学校までの距離を求めなさい。
答え
800m
方程式をたてて解きます。まず何を $x$ にするかを決めるのですが、きかれたことを $x$ にするのが基本です。この問題は、家から学校までの距離を求めなさい、ということですから、家から学校までの距離を $x$ mということにします。
速さがわかっているので、時間で式をたてます。
「分速$50$mで行ったときにかかる時間=分速$160$mで行ったときにかかる時間+$11$分」
という感じです。
$時間=\cfrac{距離}{速さ}$ ですから、家から学校までの $x$mを分速 $50$mで行ったときにかかる時間は、$\cfrac{x}{50}$ 分。
どうように、分速 $160$mで行ったときにかかる時間は、$\cfrac{x}{160}$ 分。
分速 $50$mで行ったら$11$分遅いんだから、分速 $160$mで行ったときにかかった時間に $11$ を足せば式が成り立つはず。というわけで、式をたてます。
$$\cfrac{x}{50}=\cfrac{x}{160}+11$$
(分速$50$mで行ったときにかかる時間)=(分速$160$mで行ったときにかかる時間$+11$)という式です。じゃあ解きましょう。
\begin{eqnarray*}
\cfrac{x}{50}&=&\cfrac{x}{160}+11\class{mathbg-r}{(両辺に×800)} \\
16x&=&5x+8800\\
16x-5x&=&8800\\
11x&=&8800\\
x&=&\cfrac{8800}{11}=800
\end{eqnarray*}
<ここから先は確かめの話>
というわけで $x=800$ というふうに解が求められました。 $x$ というのは家から学校までの距離だから、それが $800$mだ、ということになります。すると、分速 $50$mで行ったときにかかる時間は、$800\div 50=16$分。
また、分速 $160$mで行ったときにかかる時間は、$800\div 160=5$分。
分速 $50$mで行ったときのほうが、分速 $160$mで行ったときより $11$ 分遅く着きます。問題にある通りのことになるので、じゃあ答えを書きましょう。
800m
$(14)$ ふもとから山頂まで、自動車で山を往復するのに、登りは時速 $25$ kmで登り、下りは時速 $40$ kmでおりたら、全部で $2$ 時間 $36$ 分かかった。ふもとから山頂までの距離を求めなさい。
答え
40km
方程式をたてて解きます。まず何を $x$ にするかを決めるのですが、きかれたことを $x$ にするのが基本です。この問題は、ふもとから山頂までの距離を求めなさい、ということですから、ふもとから山頂までの距離を $x$ kmということにします。
速さがわかっているので、時間で式をたてます。
「登るのにかかった時間+下りるのにかかった時間= $2$ 時間 $36$ 分」
という感じです。
$時間=\cfrac{距離}{速さ}$ ですから、ふもとから山頂まで $x$kmを時速 $25$kmで登ったときにかかる時間は、$\cfrac{x}{25}$ 時間。
どうように、山頂からふもとまで $x$kmを時速 $40$kmで下りたときにかかる時間は、$\cfrac{x}{40}$ 時間。
かかった時間が$2$ 時間 $36$ 分。この、$36$ 分というところは、時間になおさなくてはいけません。この問題は「時速」ということで話をすすめているので、分は時間になおさないとおかしくなってしまいます。
$時間=\cfrac{分}{60}$だから、 $36$ 分 $=\cfrac{36}{60}$ 時間 $=\cfrac{3}{5}$ 時間。なので、 $2$ 時間 $36$ 分 $=2\cfrac{3}{5}$ 時間 $=\cfrac{13}{5}$ 時間ということになります。
では式をたてます。
登った時間+下った時間 $=\cfrac{13}{5}$ 時間ですから、
$$\cfrac{x}{25}+\cfrac{x}{40}=\cfrac{13}{5}$$
こういう式になりますね。では解きます。
\begin{eqnarray*}
\cfrac{x}{25}+\cfrac{x}{40}&=&\cfrac{13}{5} \class{mathbg-r}{(両辺に×200)} \\
8x+5x&=&520\\
13x&=&520\\
x&=&\cfrac{520}{13}=40
\end{eqnarray*}
<ここから先は確かめの話>
というわけで $x=40$ というふうに解が求められました。 $x$ というのはふもとから山頂までの距離ですから、それが $40$kmだ、ということになります。
すると、時速 $25$kmで登ったときにかかる時間は、$40\div 25=\cfrac{8}{5}=1\cfrac{3}{5}=1$ 時間 $36$ 分($\cfrac{3}{5}$ 時間は $36$ 分)。
また、時速 $40$kmで下りたときにかかる時間は、$40\div 40=1$ 時間。
$1$ 時間 $36$ 分+ $1$ 時間 =$2$ 時間 $36$ 分。ということになるので、すなわち、問題にある通りのことになるので、じゃあ答えを書きましょう。
40km
$(15)$ A地点からB地点をへてC地点まで、$320$ kmの道のりを行くのに、A~B間を時速 $100$ km、B~C間を時速$60$ kmで走ると $4$ 時間$ 24$ 分かかった。A~B間の道のりと、B~C間の道のりをそれぞれ求めなさい。
答え
A~B間の道のり 140km
B~C間の道のり 180km
方程式をたてて解きます。まず何を $x$ にするかを決めるのですが、きかれたことを $x$ にするのが基本です。この問題は、A~B間の道のりと、B~C間の道のりをそれぞれ求めなさい、ということですから、A~B間の道のりか、B~C間の道のりか、どっちかを $x$ kmということにします。それはどっちでもいいです。
今回は、A~B間の道のりを $x$ kmということにしよう。するとB~C間の道のりは、 $(320-x)$ kmということになるね。
それから、この問題は図をかいて考えましょう。そんなに美しい図なんてかく必要ないです。まあだいたいこんな感じの図をかきます。
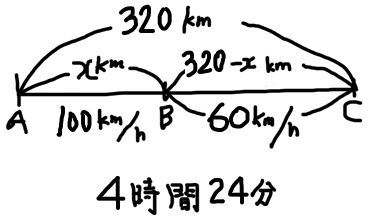
この問題も、時間で式をたてるのがおすすめです。
「A~B間にかかった時間+B~C間にかかった時間= $4$ 時間 $24$ 分」
という感じです。
$時間=\cfrac{距離}{速さ}$ だから、A~B間の $x$kmを時速 $100$kmで走ったときにかかる時間は、$\cfrac{x}{100}$ 時間。
B~C間の $(320-x)$kmを時速 $60$kmで走ったときにかかる時間は、$\cfrac{320-x}{60}$ 時間。
あともちろん、かかった時間の $4$ 時間 $24$ 分の、$24$ 分というところは、時間になおさなくてはいけません。この問題は「時速」ということで話をすすめているので、分は時間になおさないとおかしくなってしまいます。
$時間=\cfrac{分}{60}$ですから、 $24$ 分 $=\cfrac{24}{60}$ 時間 $=\cfrac{2}{5}$ 時間。なので、 $4$ 時間 $24$ 分 $=4\cfrac{2}{5}$ 時間 $=\cfrac{22}{5}$ 時間ということになります。
では式をたててみましょう。A~B間の時間+B~C間の時間 $=\cfrac{22}{5}$ ですから、
$$\cfrac{x}{100}+\cfrac{320-x}{60}=\cfrac{22}{5}$$
こんな式になりますね。解きましょう。
\begin{eqnarray*}
\cfrac{x}{100}+\cfrac{320-x}{60}&=&\cfrac{22}{5} \class{mathbg-r}{(両辺に×300)} \\
3x+5(320-x)&=&1320\\
3x+1600-5x&=&1320\\
3x-5x&=&1320-1600\\
-2x&=&-280\\
x&=&\cfrac{-280}{-2}=140
\end{eqnarray*}
<ここから先は確かめの話>
というわけで $x=140$ というふうに解が求められました。 $x$ というのはA~B間の道のりですから、A~B間が $140$kmで、じゃあB~C間は $320-140=180$kmだということになります。
すると、時速 $100$kmでA~B間の $140$kmを走ったときにかかる時間は、$140\div 100=1.4=1$ 時間 $24$ 分($0.4$ 時間は $24$ 分)。
また、時速 $60$kmでB~C間の $180$kmを走ったときにかかる時間は、$180\div 60=3$ 時間。
$1$ 時間 $24$ 分+ $3$ 時間 $=4$ 時間 $24$ 分。ということになるので、すなわち、問題にある通りのことになるので、じゃあ答えを書きましょう。
A~B間の道のり 140km
B~C間の道のり 180km
ところでこれ、この問題では「A~B間の道のりと、B~C間の道のりをそれぞれ求めなさい」ときかれたわけですが、「A~B間を行くのにかかった時間と、B~C間を行くのにかかった時間をそれぞれ求めなさい」ときかれるときがあって、その場合がちょっと考えどころだったりします。きかれたことを $x$ にして式をたてて解いていくのが基本なんだから、じゃあその場合はA~B間にかかった時間を $x$ 時間ということにして解いていけばいいんじゃないの?という話なのですが、たとえ時間をきかれていても、道のりを $x$ ということにして解いちゃって、そこから時間を求めていくというのもアリです。この問題でやったみたいに。最後のところでほら、A~B間は $1$ 時間 $24$ 分で、B~C間は $3$ 時間てだしてるじゃないですか。こんなふうに、道のりをだせば時間もでてきます。もちろん基本にのっとって、A~B間にかかった時間をきかれたなら、その時間を $x$ にして式をたてて解いていく、というのもぜんぜんアリですけど。いちおう時間を $x$ にしてやったらどういう感じか、やっておきますので、興味があったら下の説明ボタンを押して読んでみてください。
$(16)$ 現在、父は $48$ 歳、姉は $23$ 歳、妹は $19$ 歳である。父の年齢が姉妹の年齢の和の $5$ 倍であるのはいつか。
答え
18年前
見るからに違和感のある問題です。姉妹の年齢の和の $5$ 倍、って、それ、ムリじゃない? という気がすごくするんですけど、まあとりあえず方程式をたてて解いていきましょう。
まず何を $x$ にするかを決めるですが、きかれたことを $x$ にしちゃうのが基本です。この問題は、父の年齢が姉妹の年齢の和の $5$ 倍であるのはいつか、ということですから、$x$ 年後にそうであるということにします。
$x$ 年後の父の年齢は $48+x$ 歳、姉の年齢は $23+x$ 歳、妹の年齢は $19+x$ 歳です。
父の年齢$=5\times$(姉の年齢+妹の年齢)という式をたてると、
$$48+x=5\times(23+x+19+x)\\$$
こうなりますね。では解きます。
\begin{eqnarray*}
48+x&=&5\times(23+x+19+x)\\
48+x&=&115+5x+95+5x\\
x-5x-5x&=&115+95-48\\
-9x&=&162\\
x&=&\cfrac{162}{-9}=-18
\end{eqnarray*}
<ここから先は確かめの話>
というわけで $x=-18$ というふうに解が求められました。父の年齢が $x$ 年後に姉妹の年齢の和の $5$ 倍になる、ということで $x$ を求めたわけですから、じゃあそれは $-18$ 年後だということになります。なんだか変だなあ、と最初に問題を見て違和感をおぼえたのはこのせいだったんですね。$-18$ 年後というのは、$18$ 年前、という意味です。$18$ 年前に父は $30$ 歳、姉は $5$ 歳、妹は $1$ 歳。$(5+1)\times6=30$ だから、問題にあいます。ということで答えを書きます。
18年前
$(17)$ $18$ %の食塩水 $300$ gに $10$ %の食塩水を何gか加えて、$15$ %の食塩水をつくりたい。$10$ %の食塩水は何g加えればよいか。
答え
180g
方程式をたてて解きます。まず何を $x$ にするかを決めるのですが、きかれたことを $x$ にするのが基本です。この問題は「$10$%の食塩水は何g加えればよいか」ということだから、$10$%の食塩水を$x$g加える、ということにします。
食塩水の問題を解くときにおぼえておかなくちゃならない基本の式があって、
$$食塩水の濃度=\cfrac{食塩の重さ}{食塩水全体の重さ}$$
です。理科の質量パーセント濃度のところでもでてきましたね。おなじ式です。で、これを変形すると、
$$食塩の重さ= 食塩水の濃度 \times 食塩水全体の重さ$$
となります。中学生になると、むしろこっちの式のほうがよく使います。これを使って、食塩の重さで式をたてていきます。図をかいておくと、
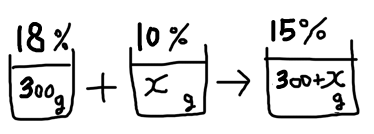
こんな感じで、$18$%の食塩水にふくまれる食塩の重さと $10$%の食塩水にふくまれる食塩の重さを足したらば、$15$%の食塩水にふくまれる食塩の重さという式をたてていきます。
まず、$18$%の食塩水 $300$gにふくまれる食塩の重さは、$\cfrac{18}{100}\times300$ g。
つぎに、$10$%の食塩水 $x$gにふくまれる食塩の重さは、$\cfrac{10}{100}x$ g。
そして、$15$%の食塩水 $(300+x)$ gにふくまれる食塩の重さは、$\cfrac{15}{100}(300+x)$ g。
さあ、これをもとにして、食塩+食塩=食塩の式をたてます。
$$\cfrac{18}{100}\times300+\cfrac{10}{100}x=\cfrac{15}{100}(300+x)$$
これは、($18$%の食塩水にふくまれる食塩)+($10$%の食塩水にふくまれる食塩)=($15$%の食塩水にふくまれる食塩)という意味の式です「食塩+食塩=食塩」は、これから先も何度もよく使う式の形です。特に2年生のときによく使います。
じゃあ解きます。
\begin{eqnarray*}
\cfrac{18}{100}\times300+\cfrac{10}{100}x&=&\cfrac{15}{100}(300+x)\\
\class{mathbg-r}{(両辺に×100)} \\
18\times300+10x&=&15(300+x)\\
5400+10x&=&4500+15x\\
10x-15x&=&4500-5400\\
-5x&=&-900\\
x&=&\cfrac{-900}{-5}=180
\end{eqnarray*}
<ここから先は確かめの話>
というわけで $x=180$ というふうに解が求められました。$10$%の食塩水を$x$g加える、ということにして $x$ を求めたわけですから、じゃあ$10$%の食塩水を$180$g加えるということになります。「確かめ」もやっぱり食塩の重さでやっていきます。
$18$%の食塩水$300$gにふくまれる食塩の重さは$54$g。
$10$%の食塩水$180$gにふくまれる食塩の重さは$18$g。
$15$%の食塩水$480$gにふくまれる食塩の重さは$72$g。
$54+18=72$だから、これはつじつまがあいますね。ということで答えを書きます。
180g
$(18)$ 生徒を長いすに座らせるのに、長いす $1$ 脚に $7$ 人ずつ座ると $4$ 人が座れず、$8$ 人ずつ座ると $7$ 人だけ座った長いすが $1$ 脚できて、誰もすわっていない長いすが $1$ 脚できた。長いすの数と生徒の人数を求めなさい。
答え
長いすの数 13脚
生徒の人数 95人
方程式をたてて解きます。まず何を $x$ にするかを決めるのですが、この問題は「長いすの数」と「生徒の人数」のふたつのことをきかれています。どっちを $x$ にしてもいけるんですが、この手の問題のときは「長いすの数」を $x$ にするのがいいです。「生徒の人数」を $x$ にするとどうしても式が分数になってしまうからです。
ということで長いすの数を $x$ 人ということにします。そのうえで(生徒の人数)=(生徒の人数)という式をたてていきます。
まず、生徒が $7$ 人ずつ長いすに座ったときの生徒の人数は、長いすが $x$ 脚あるとすると、 $7x+4$ 人です。ひとつのいすに $7$ 人ずつ座って、あと $4$ 人が座れなかった、という意味です。
 つぎに、生徒が $8$ 人ずつ長いすに座ったときの生徒の人数は、 $8x-9$ 人です。「ひとつのいすに $8$ 人ずつ座ったら、最後のいすには $7$ 人しか座っていなくて、誰もすわっていないいすが $1$ つできた」というのを、「全部のいすに $8$ 人ずつ座るには、あと $9$ 人足りない」という意味にとらえて $-9$ しています。わかるでしょうか。長いすの問題はここがやっかいなところです。
つぎに、生徒が $8$ 人ずつ長いすに座ったときの生徒の人数は、 $8x-9$ 人です。「ひとつのいすに $8$ 人ずつ座ったら、最後のいすには $7$ 人しか座っていなくて、誰もすわっていないいすが $1$ つできた」というのを、「全部のいすに $8$ 人ずつ座るには、あと $9$ 人足りない」という意味にとらえて $-9$ しています。わかるでしょうか。長いすの問題はここがやっかいなところです。
ちなみにこれ、「ひとつのいすに $8$ 人ずつ座ったら、最後のいすには $7$ 人しか座っていなくて、誰もすわっていないいすが $1$ つできた」というのを素直に式にすると、 $8(x-2)+7$ 人となります。これでもいけます。問題ありません。いけます。だけど、こっちの式は $(x-1)$ のところがちょっと、わかりづらいですよねえ。う~ん。どうでしょうか。
なのでまあ、 $8x-9$ 人のほうをおすすめしています。
さあ、そんなわけで、これをもとにして、生徒の人数=生徒の人数という式をたてます。
$$7x+4=8x-9$$
これはもちろん、( $7$ 人ずつ座ったときの人数)=( $8$ 人ずつ座ったときの人数)という意味です。じゃあ解きましょう。
\begin{eqnarray*}
7x+4&=&8x-9\\
7x-8x&=&-9-4\\
-x&=&-13\\
x&=&13
\end{eqnarray*}
<ここから先は確かめの話>
というわけで $x=13$ というふうに解が求められました。長いすの数を$x$ 脚、ということにして $x$ を求めたわけですから、長いすの数は $13$ 脚ということになります。
この数のいすに $7$ 人ずつ座ったらあと $4$ 人が座れなかったということは、生徒の人数は $7\times13+4=95$ 人。
また、 $8$ 人ずつ座ったら最後のいすは $7$ 人しか座っておらず、誰もすわっていないいすが $1$ つできた、ということは、$9$ 人ぶんの空席ができた、ということですから、生徒の人数は $8\times13-9=95$ 人。
どちらで計算しても $95$ 人てでてきます。じゃあ答え書きます。
長いすの数 13脚
生徒の人数 95人
あとこれ、生徒の人数を $x$ 人ということにして式をたてたらどうなるか、というのもやっておきます。興味があったら下の説明ボタンを押して読んでみてください。
$(19)$ ある高校の全校生徒数は $1282$ 人で、男子生徒の $16$ %と女子生徒の $25$ %の合計は $244$ 人である。男子生徒の人数と女子生徒の人数をそれぞれ求めなさい。
答え
男子生徒 850人
女子生徒 432人
方程式をたてて解きます。まず何を $x$ にするかを決めるのですが、この問題は「男子生徒の人数」と「女子生徒の人数」のふたつのことをきかれています。どっちを $x$ にしてもいけます。これはどっちでもいいです。んで、今回は男子生徒の人数を $x$ ということにしてやっていきましょう。めざすのは(男子生徒の$16$%)+(女子生徒の$25$%)$=244$人、という感じです。
まず、男子生徒の $16$%というのは、$\cfrac{16}{100}x$です。もちろん $0.16x$ ってあらわしてもいいです。それはどっちでもいけます。
つぎに女子生徒。生徒数全体が $1282$ 人で、男子の人数を $x$ 人ということにしたので、女子生徒全体の人数は、 $1282-x$ 人とあらわすことになります。じゃあ女子生徒の $25$%というのは、$\cfrac{25}{100}(1282-x)$です。もちろん $0.25(1282-x)$ ってあらわしてもいいです。
さて、そんなわけで、これをもとにして、(男子生徒の $16$ %)+(女子生徒の $25$ %)= $244$ 人という式をたてると、
$$\cfrac{16}{100}x+\cfrac{25}{100}(1282-x)=244$$
こうなりますね。じゃあ解きましょう。
\begin{eqnarray*}
\cfrac{16}{100}x+\cfrac{25}{100}(1282-x)&=&244\\
\class{mathbg-r}{(両辺に\times100)} \\
16x+25(1282-x)&=&24400\\
16x+32050-25x&=&24400\\
16x-25x&=&24400-32050\\
-9x&=&-7650\\
x&=&\cfrac{-7650}{-9}=850
\end{eqnarray*}
<ここから先は確かめの話>
というわけで $x=850$ というふうに解が求められました。男子生徒の人数を$x$ 人、ということにして $x$ を求めたわけですから、男子生徒の人数は $850$ 人ということになります。
すると女子生徒の人数は $1282-850=432$ 人ということになります。
男子生徒の $16$%は、$850\times\cfrac{16}{100}=136$人。
女子生徒の $25$%は、$432\times\cfrac{25}{100}=108$人。
$136+108=244$ ですから、問題とぴったりですね。では答えです。
男子生徒 850人
女子生徒 432人
$(20)$ ふたつの本棚A,Bがある。Aの本棚には本が $620$ 冊はいっている。Bの本棚には本が $340$ 冊はいっている。本棚Aから本棚Bに本を何冊か移して、AとBの本の比が $5:7$ になるようにしたい。何冊移せばよいか。
答え
220冊
比例式をたてて解きます。まず何を $x$ にするかを決めるのですが、この問題はふつうに「Aの本棚からBの本棚にうつす本の数」を $x$ ということにしてやっていきましょう。めざすのは(Aの本棚の本)$:$(Bの本棚の本)=$5:7$ 、という感じです。
まず、Aの本棚から、 $x$ 冊の本をBの本棚に移したら、それだけ本が減ることになって、Aの本棚に残っている本の数は $620-x$ 冊です。
つぎに、Bの本棚には、$x$ 冊の本が移ってくるのですから、それだけ本が増えることになって、Bの本棚にならぶ本の数は $340+x$ 冊ということになります。
これをもとにして、(Aの本棚の本)$:$(Bの本棚の本)=$5:7$ という式をたてると、
$$620-x:340+x=5:7$$
こうなりますね。じゃあ解きましょう。比の性質は $a:b=c:d$ ならば $ad=bc$ でしたね。
\begin{eqnarray*}
620-x:340+x&=&5:7 \\
7(620-x)&=&5(340+x)\\
4340-7x&=&1700+5x\\
-7x-5x&=&1700-4340\\
-12x&=&-2640\\
x&=&\cfrac{-2640}{-12}=220
\end{eqnarray*}
<ここから先は確かめの話>
というわけで $x=220$ というふうに解が求められました。Aの本棚からBの本棚にうつす本の数、ということにして $x$ を求めたわけですから、Aの本棚からBの本棚に、$220$ 冊の本を移すということになります。
するとAの本棚に残っている本の数は $620-220=400$ 冊ということになります。
Bの本棚にならぶ本の数は $340+220=560$ 冊ということになります。
$400:560$ という比は $80$ で割れば $5:7$ になりますね。では答えです。
220冊
答え(中1 3章 $1$ 次方程式 第4回)
$(1)$ $x=3$
$(2)$ $x=147$
$(3)$ $x=-\cfrac{1}{3}$
$(4)$ $x=\cfrac{1}{2}$
$(5)$ $x=-\cfrac{2}{3}$
$(6)$ $x=1$
$(7)$ $x=4$
$(8)$ $x=2$
$(9)$ めだか 11匹
金魚 4匹
$(10)$ 180円
$(11)$ 生徒 120人
プリント 285枚
$(12)$ 追いつけない
$(13)$ 800m
$(14)$ 40km
$(15)$ A~B間の道のり 140km
B~C間の道のり 180km
$(16)$ 18年前
$(17)$ 180g
$(18)$ 長いすの数 13脚
生徒の人数 95人
$(19)$ 男子生徒 850人
女子生徒 432人
$(20)$ 220冊