数学 中2 2学期中間模擬テスト 第2回
 ページがちゃんと表示されるまで$10$秒くらいかかります。
ページがちゃんと表示されるまで$10$秒くらいかかります。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
「印刷」をクリックすると同じ内容のpdfファイルが表示されます。また、解答用紙と答えも問題のあとに表示されます。1~6ページが問題、7~8ページが解答用紙、9~10ページが答えです。必要におうじて印刷してください。
問題をクリックすると答えがでます。
ふつうのテストより問題数は多いです。なのでふつうのテストをやるときより時間がかかると思います。がんばって!
$\huge{1}$ 次の①~⑧の計算をしなさい。
$\qquad①$ $\quad 8+16\div(-4)\qquad ② \quad \cfrac{1}{3}-1+\cfrac{3}{4}$
答え
$①4$ $②\cfrac{1}{12}$
\begin{eqnarray*} &①& 8+16\div(-4)\\ &=& 8-4\\ &=&4 \end{eqnarray*} \begin{eqnarray*} \require{cancel} &②& \cfrac{1}{3}-1+\cfrac{3}{4}\\ &=& \cfrac{4}{12}-\cfrac{12}{12}+\cfrac{9}{12}\\ &=& \cfrac{1}{12} \end{eqnarray*}
$\qquad③$ $\quad 6\times(-2)+(-4)^2\qquad ④ \quad 3(2a-b)-(7a-8b)$
答え
$③4$ $④-a+5b$
\begin{eqnarray*} &③& 6\times(-2)+(-4)^2\\ &=& 6\times(-2)+16\\ &=&-12+16\\ &=&4 \end{eqnarray*} \begin{eqnarray*} \require{cancel} &④& 3(2a-b)-(7a-8b)\\ &=& 6a-3b-7a+8b\\ &=& 6a-7a-3b+8b\\ &=& -a+5b \end{eqnarray*}
$\qquad⑤$ $\quad \cfrac{2x-y}{3}-\cfrac{x-4y}{4}\qquad ⑥ \quad 5ab\times(-4ab^2)$
答え
$⑤\cfrac{5x+8y}{12}$ $⑥-20a^2b^3$
\begin{eqnarray*} &⑤& \cfrac{2x-y}{3}-\cfrac{x-4y}{4}\\ &=& \cfrac{4(2x-y)-3(x-4y)}{12}\\ &=& \cfrac{8x-4y-3x+12y}{12}\\ &=& \cfrac{8x-3x-4y+12y}{12}\\ &=& \cfrac{5x+8y}{12} \end{eqnarray*} \begin{eqnarray*} \require{cancel} &⑥& 5ab\times(-4ab^2)\\ &=& -20a^2b^3 \end{eqnarray*}
$\qquad⑦$ $\quad 6x^2\div(-18xy)\times9y\qquad ⑧ \quad 9x\div\cfrac{27}{2}x^2y^2\times\cfrac{3}{4}y^2$
答え
$⑦-3x$ $⑧\cfrac{1}{2x}$
\begin{eqnarray*} \require{cancel} &⑦& 6x^2\div(-18xy)\times9y\\ &=& -\cfrac{6xx\times9y}{18xy}\\ &=& -\cfrac{\bcancel{6}\bcancel{x}x\times{}^3\bcancel{9}\bcancel{y}}{{}^{\bcancel{3}}\bcancel{18}\bcancel{x}\bcancel{y}}\\ &=& -3x \end{eqnarray*} \begin{eqnarray*} \require{cancel} &⑧& 9x\div\cfrac{27}{2}x^2y^2\times\cfrac{3}{4}y^2\\ &=& \cfrac{9x}{1}\div\cfrac{27xxyy}{2}\times\cfrac{3yy}{4}\\ &=& \cfrac{9x}{1}\times\cfrac{2}{27xxyy}\times\cfrac{3yy}{4}\\ &=& \cfrac{\bcancel{9}\bcancel{x}\bcancel{x}}{1}\times\cfrac{\bcancel{2}}{\bcancel{27}\bcancel{x}x\bcancel{y}\bcancel{y}}\times\cfrac{\bcancel{9}\bcancel{y}\bcancel{y}}{{}^2\bcancel{4}}\\ &=&\cfrac{1}{2x} \end{eqnarray*}
$\huge{2}$ 次の ①~⑤の連立方程式を解きなさい。また、⑥の方程式を解きなさい。
\begin{eqnarray*}
① \ \left\{
\begin{array}{l}
5x+9y=12\\
y=-\cfrac{2}{3}x
\end{array}
\right.
\qquad② \ \left\{
\begin{array}{l}
y=4x-12\\
3x-2y=-6
\end{array}
\right.\\
\end{eqnarray*}
答え
$①\phantom{ho}\begin{eqnarray*}
\left\{
\begin{array}{l}
x=-12\\
y=8
\end{array}
\right.
\quad②
\left\{
\begin{array}{l}
x=6\\
y=12
\end{array}
\right.
\end{eqnarray*}$
①番 代入法で、②の式を①の式に代入して解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
5x+9y=12\quad…①\\
y=-\cfrac{2}{3}x\quad…②
\end{array}
\right.
\end{eqnarray*}
$②を①に代入$
\begin{eqnarray*}
5x+9\times\left(-\cfrac{2}{3}x\right)&=&12\\
5x-6x&=&12\\
-x&=&12\\
x&=&-12
\end{eqnarray*}
$x=-12を②に代入$
\begin{eqnarray*}
y&=&-\cfrac{2}{3}\times(-12)\\
&=&8
\\
\left\{
\begin{array}{l}
x=-12\\
y=8
\end{array}
\right.
\end{eqnarray*}
②番 代入法で、①の式を②の式に代入して解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
y=4x-12\quad…①\\
3x-2y=-6\quad…②
\end{array}
\right.\\
\end{eqnarray*}
$①を②に代入$
\begin{eqnarray*}
3x-2(4x-12)&=&-6\\
3x-8x+24&=&-6\\
-5x&=&-30\\
x&=&6
\end{eqnarray*}
$x=6を①に代入$
\begin{eqnarray*}
y&=&4\times6-12\\
&=&12
\\
\left\{
\begin{array}{l}
x=6\\
y=12
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*} ③ \ \left\{ \begin{array}{l} 2(x-2y)=-y+1\\ 5x-7y=1 \end{array} \right. \qquad④ \ \left\{ \begin{array}{l} 0.7x+0.2y=-0.5\\ -13x-3y=15 \end{array} \right.\\ \end{eqnarray*}
答え
$③\phantom{ho}\begin{eqnarray*}
\left\{
\begin{array}{l}
x=-4\\
y=-3
\end{array}
\right.
\quad④
\left\{
\begin{array}{l}
x=-3\\
y=8
\end{array}
\right.
\end{eqnarray*}$
③番 ①の式のかっこをはずし、整理します。加減法で、$x$ の係数をそろえて解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
2(x-2y)=-y+1\quad①\\
5x-7y=1\quad…②
\end{array}
\right.
\end{eqnarray*}
$①を整理$
\begin{eqnarray*}
2(x-2y)&=&-y+1\\
2x-4y&=&-y+1\\
2x-4y+y&=&1\\
2x-3y&=&1\quad…③
\end{eqnarray*}
$②\times2 \ - \ ③\times5$
\begin{eqnarray*}
10x-14y=\phantom{-}2\\
\underline{-) \quad 10x-15y=\phantom{-}5}\\
y=-3
\end{eqnarray*}
$y=-3を③に代入$
\begin{eqnarray*}
2x-3\times(-3)&=&1\\
2x+9&=&1\\
2x&=&-8\\
x&=&-4
\\
\left\{
\begin{array}{l}
x=-4\\
y=-3
\end{array}
\right.
\end{eqnarray*}
④番 ①の式を $10$ 倍して小数をなくします。加減法で、$y$ の係数をそろえて解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
0.7x+0.2y=-0.5\quad…①\\
-13x-3y=15\quad…②
\end{array}
\right.\\
\end{eqnarray*}
$①\times10$
\begin{eqnarray*}
7x+2y&=&-5…③
\end{eqnarray*}
$②\times2 \ + \ ③\times3$
\begin{eqnarray*}
-26x-6y=\phantom{-}30\\
\underline{+) \quad 21x+6y=-15}\\
-5x\phantom{4xyz}=\phantom{-}15\\
x=-3\phantom{-}
\end{eqnarray*}
$x=-3を③に代入$
\begin{eqnarray*}
7\times(-3)+2y&=&-5\\
-21+2y&=&-5\\
2y&=&16\\
y&=&8
\\
\left\{
\begin{array}{l}
x=-3\\
y=8
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*} ⑤ \ \left\{ \begin{array}{l} \cfrac{1}{3}x+\cfrac{5}{2}y=12\\ 5x+6y=-9 \end{array} \right. \qquad⑥ \ 3x+2y=9x+5y-3=3 \end{eqnarray*}
答え
$⑤\phantom{ho}\begin{eqnarray*}
\left\{
\begin{array}{l}
x=-9\\
y=6
\end{array}
\right.
\quad⑥
\left\{
\begin{array}{l}
x=-1\\
y=3
\end{array}
\right.
\end{eqnarray*}$
⑤番 ①の式を $6$ 倍して分母をはらいます。加減法で、$y$ を消去して解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
\cfrac{1}{3}x+\cfrac{5}{2}y=12\quad…①\\
5x+6y=-9…\quad②
\end{array}
\right.
\end{eqnarray*}
$①\times6$
\begin{eqnarray*}
2x+15y&=&72\quad…③
\end{eqnarray*}
$②\times5 \ - \ ③\times2$
\begin{eqnarray*}
25x+30y=-45\\
\underline{-) \quad 4x+30y=\phantom{1}144}\\
21x\phantom{+30y}=-189\\
x=-9\phantom{18}
\end{eqnarray*}
$x=-9を②に代入$
\begin{eqnarray*}
5\times(-9)+6y&=&-9\\
-45+6y&=&-9\\
6y&=&36\\
y&=&6
\\
\left\{
\begin{array}{l}
x=-9\\
y=6
\end{array}
\right.
\end{eqnarray*}
⑥番 まんなかをかくした式をつくり、①とします。左側をかくした式をつくって整理し、②とします。①の式と②の式を連立させ、$x$ の係数をそろえて加減法で解きます。
\begin{eqnarray*}
&& \ 3x+2y=9x+5y-3=3
\end{eqnarray*}
$まんなかをかくした式をたてる$
\begin{eqnarray*}
3x+2y&=&3\quad…①
\end{eqnarray*}
$左側をかくした式をたてて整理する$
\begin{eqnarray*}
9x+5y-3&=&3\\
9x+5y&=&6\quad…②
\end{eqnarray*}
$①と②を連立させる$
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
3x+2y=3\quad…①\\
9x+5y=6\quad…②
\end{array}
\right.
\end{eqnarray*}
$①\times3 \ - \ ②\times2$
\begin{eqnarray*}
9x+6y=9\\
\underline{-) \quad 9x+5y=6}\\
y=3
\end{eqnarray*}
$y=3を①に代入$
\begin{eqnarray*}
3x+2\times(3)&=&3\\
3x+6&=&3\\
3x&=&-3\\
x&=&-1
\\
\left\{
\begin{array}{l}
x=-1\\
y=3
\end{array}
\right.
\end{eqnarray*}
$\huge{3}$ 次の①~⑤のことがらについて、$y$ を $x$ の式であらわしなさい。また、$y$ が $x$ の $1$ 次関数である場合は〇、そうでない場合は×をかきなさい。
$①\quad 1$ 個 $120$ 円のパンを $x$ 個買い、$1000$ 円をはらったときのおつりが $y$ 円
答え
$y=-120x+1000\quad 〇$
$(y=1000-120xも可)$
$y=ax+b$ の形なので $1$ 次関数です。
$②\quad 3000m$ の道のりを、分速 $xm$ で歩いたときにかかった時間が $y$ 分
答え
$y=\cfrac{3000}{x}\quad ×$
$y=\cfrac{a}{x}$ の形なので、この式は反比例です。反比例は $1$ 次関数ではありません。
$③\quad$半径$ xcm$ の円の面積が $ycm^2$
答え
$y=\pi x^2\quad ×$
$x^2$ なので、$1$ 次関数ではありません。
$④\quad$ 水槽に水が $300L$ 入っている。この水槽から、 $1$ 分につき $15L$ ずつ $ x$ 分間水を抜いたときの残りの水が $yL$
答え
$y=-15x+300\quad 〇$
$(y=300-15xも可)$
$⑤\quad1$ 辺が $xcm$ の立方体の体積 $ycm$
答え
$y=x^3\quad ×$
$x^3$ なので、$1$ 次関数ではありません。
$\huge{4}$ $1$ 次関数 $y=-\cfrac{1}{2}x+3$ について、次の $①~③$ の問いに答えなさい。
$①\quad x$ の値が $-4$ から$8$ まで増加するときの変化の割合を求めなさい。
答え
$-\cfrac{1}{2}$
$1$ 次関数 $y=ax+b$ で変化の割合をきかれたときは、$a$ を答えといてください。計算もなんもありません。$a$ を答えておけばいいんです。テストのときはそうやっちゃってください。
$②\quad x$ の値が $-4$ から$8$ まで増加するときの $y$ の増加量を求めなさい。
答え
$-6$
$yの増加量=xの増加量\times変化の割合$ です。
この問題の場合、$x$ の増加量は、$x$ の値が $-4$ から$8$ まで増加したのですから $12$ です。
変化の割合は $-\cfrac{1}{2}$ です。なので、
$$yの増加量=xの増加量\times変化の割合=12\times\left(-\cfrac{1}{2}\right)=-6$$
$③\quad x$ の変域が $-4 \leqq x \leqq 8$ のとき、$y$ の変域を求めなさい。
答え
$-1 \leqq y \leqq 5$
「$x$ の変域が $a \leqq x \leqq b$ のとき、$y$ の変域を求めなさい。」というお決まりの問題があって、こうきかれたときは、答えの形はこうです。 $$小 \leqq y \leqq 大$$ んで、小と大にそれぞれ、小さい数と大きい数を書いておけばいいです。小さい数と大きい数っていうのは、 $-4 \leqq x \leqq 8$ の $-4$ と $8$ をそれぞれ問題の $y=-\cfrac{1}{2}x+3$ の $x$ に代入してえられる数です。じゃあまず、 $x=-4$ を $y=-\cfrac{1}{2}x+3$ に代入します。 \begin{eqnarray*} y&=&-\cfrac{1}{2}×(-4)+3\\ &=&2+3\\ &=&5\\ \end{eqnarray*} 次に、 $x=8$ を $y=-\cfrac{1}{2}x+3$ に代入します。 \begin{eqnarray*} y&=&-\cfrac{1}{2}×8+3\\ &=&-4+3\\ &=&-1\\ \end{eqnarray*} これで、$5$ と $-1$ というふたつの数がえられました。これを小と大にあてはめればよいです。じゃあ答えを書きましょう。$$-1 \leqq y \leqq 5$$ これでOKです。ただし、 $y$ の変域をきかれたときのこのやり方は、3年生で習う「2乗に比例する関数$y=ax^2$」では通用しないから気をつけてください。
$\huge{5}$ 次の $①~⑧$ の直線の式を求めなさい。
$①$ 変化の割合が $-\cfrac{1}{3}$ で、点$(6,2)$を通る。
答え
$y=-\cfrac{1}{3}x+4$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
変化の割合というのは1次関数のときは $a$ のことです。だから $a=-\cfrac{1}{3}$ です。これを $y=ax+b$ に代入します。すると
$$y=-\cfrac{1}{3}x+b$$
となります。あと、「点$(6,2)$を通る」というのは、$x=6$ のとき $y=2$ という意味です。これをこの $y=-\cfrac{1}{3}x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
2&=&-\cfrac{1}{3}×6+b\\
2&=&-2+b\\
2+2&=&b\\
4&=&b
\end{eqnarray*}
$b$ は右辺においたままにして解いていくのがおすすめです。たぶんこういうやり方って、このあたりで初めて見るのかもしれません。最初はとまどうと思いますが、1次関数で $b$ を求めるときは、このやり方のほうがミスが少ないです。だからこれがおすすめです。まあどうしてもなじめなかったら由緒正しく $b$ を左辺にもってって解いてもいいです。
ともかく、これでめでたく $a=-\cfrac{1}{3}$ , $b=4$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-\cfrac{1}{3}x+4$$
$②$ 傾きが $-2$ で、 $x=3$ のとき $y=-2$ となる。
答え
$y=-2x+4$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
傾きというのは $a$ のことです。だから $a=-2$ です。これを $y=ax+b$ に代入します。すると
$$y=-2x+b$$
となります。 $x=3$ , $y=-2$ をこの $y=-2x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
-2&=&-2×3+b\\
-2&=&-6+b\\
-2+6&=&b\\
4&=&b
\end{eqnarray*}
これで $a=-2$ , $b=4$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-2x+4$$
$③$ \(\cfrac{yの増加量\phantom{増加}}{xの増加量\phantom{増加}}\) が $\cfrac{1}{2}$ で、点 $(6,2)$ を通る。
答え
$y=\cfrac{1}{2}x-1$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
\(\cfrac{yの増加量\phantom{増加}}{xの増加量\phantom{増加}}\)というのは1次関数のときは $a$ のことです。だから $a=\cfrac{1}{2}$ です。これを $y=ax+b$ に代入します。すると
$$y=\cfrac{1}{2}x+b$$
となります。 $x=6$ , $y=2$ をこの $y=\cfrac{1}{2}x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
2&=&\cfrac{1}{2}×6+b\\
2&=&3+b\\
2-3&=&b\\
-1&=&b
\end{eqnarray*}
これで $a=\cfrac{1}{2}$ , $b=-1$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=\cfrac{1}{2}x-1$$
$④$ $x$ の値が $3$ 増加すると $y$ の値が $6$ 増加し、$x=1$ のとき $y=5$ となる。
答え
$y=2x+3$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
1次関数のときは \(a=\cfrac{yの増加量\phantom{増加}}{xの増加量\phantom{増加}}\)だから、この問題の場合は $a=\cfrac{6}{3}=2$ となります。これを $y=ax+b$ に代入すると
$$y=2x+b$$
となります。 $x=1$ , $y=5$ をこの $y=3x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
5&=&2\times1+b\\
5&=&2+b\\
5-2&=&b\\
3&=&b
\end{eqnarray*}
これで $a=2$ , $b=3$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=2x+3$$
$⑤$ 直線 $y=\cfrac{1}{2}x-3$ に平行で、点$(4,-3)$ を通る。
答え
$y=\cfrac{1}{2}x-5$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
傾きが等しいとき、2直線は平行になります。$y=\cfrac{1}{2}x-3$ に平行ということは、求めたい直線の傾きは $\cfrac{1}{2}$ だということになります。つまり $a=\cfrac{1}{2}$ です。これを $y=ax+b$ に代入すると
$$y=\cfrac{1}{2}x+b$$
となります。 $x=4$ , $y=-3$ をこの $y=\cfrac{2}{3}x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
-3&=&\cfrac{1}{2}×4+b\\
-3&=&2+b\\
-3-2&=&b\\
-5&=&b
\end{eqnarray*}
これで $a=\cfrac{1}{2}$ , $b=-5$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=\cfrac{1}{2}x-5$$
$⑥$ $y$ 切片が $2$ で、点$(3,3)$ を通る。
答え
$y=\cfrac{1}{3}x+2$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
$y$ 切片というのは $b$ のことです。だから $b=2$ です。これを $y=ax+b$ に代入します。すると
$$y=ax+2$$
となります。 $x=3$ , $y=3$ をこの $y=ax+2$ に代入して、 $a$ を求めます。
\begin{eqnarray*}
3&=&3a+2\\
-3a&=&2-3\\
-3a&=&-1\\
a&=&\cfrac{1}{3}
\end{eqnarray*}
これで $a=\cfrac{1}{3}$ , $b=2$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=\cfrac{1}{3}x+2$$
$⑦$ 2点$(-6,-5),(-2,-3)$ を通る。
答え
$y=\cfrac{1}{2}x-2$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
$2$ 点を通る直線の式をきかれたときは、
$$a=\cfrac{y_2-y_1}{x_2-x_1}$$
という公式を使って $a$ を求めましょう。
$2$ 点の座標 $(-6,-5),(-2,-3)$ を $(x_1,y_1),(x_2,y_2)$ だということにして、上の公式にあてはめると、
\begin{eqnarray*}
a&=&\cfrac{y_2-y_1}{x_2-x_1}\\
&=&\cfrac{-3-(-5)}{-2-(-6)}\\
&=&\cfrac{2}{4}\\
&=&\cfrac{1}{2}\\
\end{eqnarray*}
これで $a=\cfrac{1}{2}$ だということがわかりました。これを $y=ax+b$ に代入して、
$$y=\cfrac{1}{2}x+b$$
ここに、 $(-6,-5),(-2,-3)$ のどちらかを代入して $b$ を求めます。代入するのはどっちでもよいです。計算さえまちがえなければ、どっちをいれても答えは同じになります。だから、計算がラクそうなほうをいれるのが得。今回は、 $(-2,-3)$ のほうをいれてみましょう。
\begin{eqnarray*}
-3&=&\cfrac{1}{2}\times(-2)+b\\
-3&=&-1+b\\
-3+1&=&b\\
-2&=&b
\end{eqnarray*}
これで $a=\cfrac{1}{2}$ , $b=-2$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=\cfrac{1}{2}x-2$$
ところで、この問題に関してはもうひとつ、連立方程式をたてて $a$ と $b$ を求めていく、という定番のやり方があります。ここで紹介しているやり方と、連立方程式をたてるのと、両方ためして、好きなほうでやってください。連立方程式をたててやるやり方は、次の問題で説明します。
$⑧$ $x=2$ のとき $y=5$ で、$x=4$ のとき $y=9$ となる。
答え
$y=2x+1$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
$y=ax+b$ に $x=2,y=5$ を代入すると
$$5=2a+b$$
$y=ax+b$ に $x=4,y=9$ を代入すると
$$9=4a+b$$
こうしてできたふたつの式を連立させて解きます。引き算をすれば $b$ が消えます。
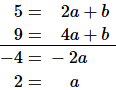
$a=2$ を $5=2a+b$ に代入して $b$ を求めます。
\begin{eqnarray*}
5&=&2×2+b\\
5&=&4+b\\
5-4&=&b\\
1&=&b
\end{eqnarray*}
これで $a=2$ , $b=1$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=2x+1$$
ところで、この問題に関してはもうひとつ、前の問題で説明した $a=\cfrac{y_2-y_1}{x_2-x_1}$ という公式を使って、まず $a$ を求めてしまう、というやり方でもいけます。どっちでもいけます。テストのときは好きなほうでやってください。
$\huge{6}$ $y$ が $x$ の1次関数であるとき、表のア~ウにあてはまる数をこたえなさい。また、$y$ を $x$ の式で表しなさい。
\begin{array}{c|ccccc}
\hline
x & -6 & -3 & 1 & 6 & ウ \\
\hline
y & ア & 6 & イ & 0 & -4 \\
\hline
\end{array}
答え
ア…$8$, イ…$\cfrac{10}{3}$, ウ…$12$, 式 $y=-\cfrac{2}{3}x+4$
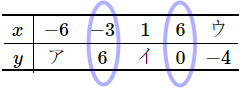 まず、$y$ を $x$ の式で表してしまいましょう。そのために、$x$ と $y$ がわかっている組を $2$ 組、見つけます。必ず $2$ 組はあるはずです。この問題の場合は、$x=-3$ のとき $y=6$, $x=6$ のとき $y=0$ というのがありますね。これで $a$ を求めることができます。$(-3, 6), (6, 0)$ だと思ってもいいです。$a$ が求まりますよね?
まず、$y$ を $x$ の式で表してしまいましょう。そのために、$x$ と $y$ がわかっている組を $2$ 組、見つけます。必ず $2$ 組はあるはずです。この問題の場合は、$x=-3$ のとき $y=6$, $x=6$ のとき $y=0$ というのがありますね。これで $a$ を求めることができます。$(-3, 6), (6, 0)$ だと思ってもいいです。$a$ が求まりますよね?
$\quad a=\cfrac{y_2-y_1}{x_2-x_1}$ を使って、
$\quad a=\cfrac{0-6}{6-(-3)}=\cfrac{-6}{9}=-\cfrac{2}{3}$
$y=-\cfrac{2}{3}x+b$ に $(6, 0)$ を代入して、
\begin{eqnarray*}
0&=&-\cfrac{2}{3}\times6+b\\
0&=&-4+b\\
4&=&b
\end{eqnarray*}
これで、式は $y=-\cfrac{2}{3}x+4$ だと求められました。あとはアとイとウをだしていきましょう。
アは $x=-6$ のときの $y$ の値のことだから、
\begin{eqnarray*}
y&=&-\cfrac{2}{3}\times(-6)+4=4+4=8
\end{eqnarray*}
イは $x=1$ のときの $y$ の値のことだから、
\begin{eqnarray*}
y=-\cfrac{2}{3}\times1+4=-\cfrac{2}{3}+\cfrac{12}{3}=\cfrac{10}{3}
\end{eqnarray*}
ウは $y=-4$ のときの $x$ の値のことだから、
\begin{eqnarray*}
-4&=&-\cfrac{2}{3}x+4 \quad(\times3)\\
-12&=&-2x+12\\
2x&=&12+12\\
2x&=&24\\
x&=&12
\end{eqnarray*}
これですべて求まりました。答えを書きましょう。
ア…$8$, イ…$\cfrac{10}{3}$, ウ…$12$, 式 $y=-\cfrac{2}{3}x+4$
$\huge{7}$
次の $①~④$ にあてはまるものを下のア~カのなかからすべて選び、記号で答えなさい。
$①$ グラフが右下がりの直線である。
答え
イ,エ,カ
$y=ax+b$ の 形のものが直線のグラフになります。
$a\lt0$ のとき、グラフは右下がりになります。
$②$ グラフが点 $(-3, \ 1)$ を通る。
答え
ウ,オ
ア~カの式に $x=-3$ を代入して、$y=1$ となるものが答えです。めんどくさいですが、ひとつひとつ全部確かめなきゃだめです。 \begin{eqnarray*} &ア& \quad y=3\times(-3)=-9\\ &イ& \quad y=-3\times(-3)-2=7\\ &ウ& \quad y=\cfrac{1}{3}\times(-3)+2=1\\ &エ& \quad y=-\cfrac{1}{3}\times(-3)-2=-1\\ &オ& \quad y=-\cfrac{3}{-3}=1\\ &カ& \quad y=-3\times(-3)=9 \end{eqnarray*}
$③$ グラフが平行である。
答え
イとカ
オは式の形が反比例なので、グラフは直線ではないので気にしなくていいです。んで、あとのグラフは直線の式なのですが、$y=ax+b$ の $a$ の値がおなじだとグラフが平行になります。なのでこの問題の答えはイとカです。
$④$ グラフが $y$ 軸上で交わる。 \begin{eqnarray*} &ア& \quad y=3x \qquad &イ& \quad y=-3x-2 \qquad &ウ& \quad y=\cfrac{1}{3}x+2\\ &エ& \quad y=-\cfrac{1}{3}x-2 \qquad &オ& \quad y=-\cfrac{3}{x} \qquad &カ& \quad y=-3x \end{eqnarray*}
答え
アとカ,イとエ
オは式の形が反比例なので、グラフは双曲線なので、$y$ 軸上は通らないので気にしなくていいです。んで、あとのグラフは $y$ 軸上を通るのですが、$y=ax+b$ の $b$ の値がおなじだと $y$ 軸上で交わります。なのでこの問題の答えはアとカ,イとエです。
アとカはどちらも比例のグラフで、どちらも原点を通ります。$y$ 軸上で交わっているといえます。どちらも $b=0$ なんだから $b$ が等しい、とおもっちゃってもいいです。
$\huge{8}$
次の $①~⑥$ のグラフをかきなさい。
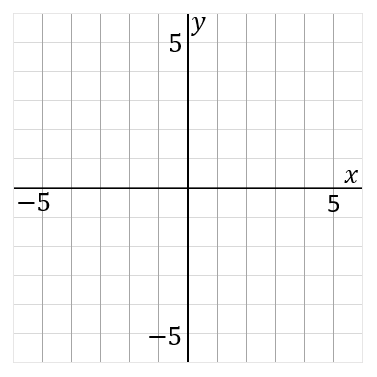 \begin{eqnarray*}
&&① \quad y=x-2\\
&&② \quad y=-3x+3\\
&&③ \quad 3x-9y=9\\
&&④ \quad y=-\cfrac{1}{4}x-\cfrac{3}{4}\\
&&⑤ \quad x=2\\
&&⑥ \quad y=-3
\end{eqnarray*}
\begin{eqnarray*}
&&① \quad y=x-2\\
&&② \quad y=-3x+3\\
&&③ \quad 3x-9y=9\\
&&④ \quad y=-\cfrac{1}{4}x-\cfrac{3}{4}\\
&&⑤ \quad x=2\\
&&⑥ \quad y=-3
\end{eqnarray*}
答え
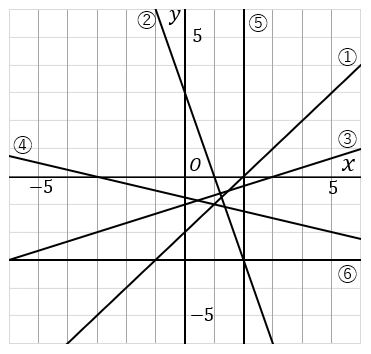
$①$ 切片が $-2$ なので、$y$ 軸の $-2$ をスタート地点にします。傾きが $1$ なので、$\cfrac{1}{1}$ なので、右に $1$ 歩行って上に $1$ 歩行く点をとっていきます。点を定規で結びます。
$②$ 切片が $3$ なので、$y$ 軸の $3$ をスタート地点にします。傾きが $-3$ なので、$\cfrac{-3}{1}$ なので、右に $1$ 歩行って下に $3$ 歩行く点をとっていきます。点を定規で結びます。
$③$ まず式を $y$ について解きます。
\begin{eqnarray*}
3x-9y&=&9\\
-9y&=&-3x+9\quad両辺に-1をかける\\
9y&=&3x-9\quad両辺に\cfrac{1}{9}をかける\\
y&=&\cfrac{1}{3}x-1\\
\end{eqnarray*}
これで $y=ax+b$ の形になったので、あとはこのグラフをかけばよいです。切片が $-1$ なので、$y$ 軸の $-1$ をスタート地点にします。傾きが $\cfrac{1}{3}$ なので、右に $3$ 歩行って上に $1$ 歩行く点をとっていきます。点を定規で結びます。
$④$ 切片が分数なので、$x$ と $y$ がどちらも整数になるところを探します。はじめはテキトーです。テキトーに $x$ に整数を代入していって、$y$ も整数になるやつをさがします。たとえば $x$ に $1$ を代入すると、$y=-1$ となります。なので、点 $(1, \ -1)$ をスタート地点にします。傾きが $-\cfrac{1}{4}$ なので、右に $4$ 歩行って下に $1$ 歩行く点をとります。点を定規で結びます。
$⑤$ $y$ 軸に平行な線です。たて線です。$x$ 軸の $2$ を通るようにします。
$⑤$ $x$ 軸に平行な線です。よこ線です。$y$ 軸の $-3$ を通るようにします。
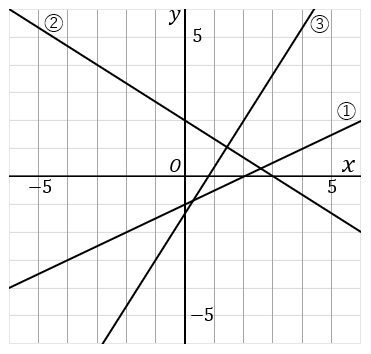
$\huge{9}$ 下の $①~③$ の直線の式を求めなさい。
答え
\begin{eqnarray*}
&&①\quad y=\cfrac{1}{2}x-1\\
&&②\quad y=-\cfrac{2}{3}x+2\\
&&③\quad y=\cfrac{5}{3}x-\cfrac{4}{3}
\end{eqnarray*}
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
$①$ $y$ 軸上の $-1$ を通っています。なので $b=-1$ です。そこから右に $2$ 歩行って上に $1$ 歩行っています。$a=\cfrac{縦}{右}$ なので $a=\cfrac{1}{2}$ です。なので式は$$y=\cfrac{1}{2}x-1$$
$②$ $y$ 軸上の $2$ を通っています。なので $b=2$ です。そこから右に $3$ 歩行って下に $2$ 歩行っています。$a=\cfrac{縦}{右}$ なので $a=\cfrac{-2}{3}$ です。なので式は$$y=-\cfrac{2}{3}x+2$$
$③$ $y$ 軸上のぴったりしたところを通っていません。こういうときは、カドを通っているところを $2$ か所さがします。この直線の場合は、点 $(-1, \ -3)$ と点 $(2, \ 2)$ を通っています。この $2$ 点を通る直線の式、ということで計算で求めればよいです。
\begin{eqnarray*}
a&=&\cfrac{y_2-y_1}{x_2-x_1}\\
&=&\cfrac{2-(-3)}{2-(-1)}\\
&=&\cfrac{5}{3}
\end{eqnarray*}
これで $a=\cfrac{5}{3}$ だということがわかりました。これを $y=ax+b$ に代入して、
$$y=\cfrac{5}{3}x+b$$
ここに、 $(-1,-3),(2,2)$ のどちらかを代入して $b$ を求めます。今回は、 $(2,2)$ のほうをいれてみましょう。
\begin{eqnarray*}
2&=&\cfrac{5}{3}×2+b\\
2&=&\cfrac{10}{3}+b\\
2-\cfrac{10}{3}&=&b\\
\cfrac{6}{3}-\cfrac{10}{3}&=&b\\
-\cfrac{4}{3}&=&b
\end{eqnarray*}
これで $a=\cfrac{5}{3}$ , $b=-\cfrac{4}{3}$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=\cfrac{5}{3}x-\cfrac{4}{3}$$
$\huge{10}$
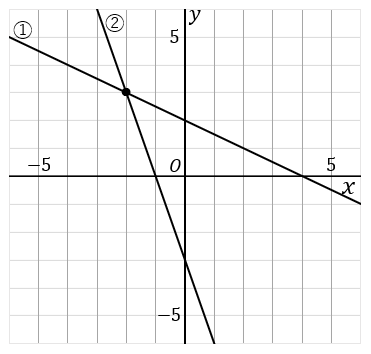
次の連立方程式の解を、グラフをかいて求めなさい。
 \begin{eqnarray*}
\left\{
\begin{array}{l}
x+2y=4\\
3x+y=-3
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*}
\left\{
\begin{array}{l}
x+2y=4\\
3x+y=-3
\end{array}
\right.
\end{eqnarray*}
 \begin{eqnarray*}
\left\{
\begin{array}{l}
x=-2\\
y=3
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*}
\left\{
\begin{array}{l}
x=-2\\
y=3
\end{array}
\right.
\end{eqnarray*}
加減法や代入法を使って解いてしまうこともできますが、それだとテストのとき点数はもらえません。グラフをかいていなければダメです。というわけでグラフをかきます。このままでは傾きや切片がわかりませんので、こういうときは、それぞれの式を $y$ について解きます。
\begin{eqnarray*}
x+2y&=&4\\
2y&=&-x+4\quad 両辺に \times\cfrac{1}{2}\\
y&=&-\cfrac{1}{2}x+2\qquad\cdots①
\end{eqnarray*}
\begin{eqnarray*}
3x+y&=&-3\\
y&=&-3x-3\qquad\cdots②
\end{eqnarray*}
こうしてできた $2$ つの式をおなじグラフ上にかいて、その交点を座標を答えればいいです。交点の座標は点$(-2, \ 3)$ ですね。$x=-2, \ y=3$ が解です。
$\huge{11}$ 2つの直線 $y=2x+4$ と $y=-\cfrac{2}{3}x-4$ の交点の座標を計算して求めなさい。
答え
$(-3,-2)$
2直線の交点の座標は連立方程式の解です。
連立方程式\begin{eqnarray*}
\left\{
\begin{array}{l}
y=2x+4\\
y=-\cfrac{2}{3}x-4
\end{array}
\right.
\end{eqnarray*}
を解いて、その解がこの問題の答えです。代入法で、
(上の式の右辺)=(下の式の右辺)という式をたてて解いていきましょう。
\begin{eqnarray*}
2x+4&=&-\cfrac{2}{3}x-4\quad 両辺に\times3\\
6x+12&=&-2x-12\\
6x+2x&=&-12-12\\
8x&=&-24\\
x&=&-3\\
\end{eqnarray*}
$y=2x+4$ に $x=-3$ を代入して $y$ を求めます。
\begin{eqnarray*}
y&=&2×(-3)+4\\
&=&-6+4\\
&=&-2\\
\end{eqnarray*}
これで $x=-3$ , $y=-2$ というふうに、解が求められました。じゃあ答えを書きましょう。
$$(-3,-2)$$
この問題は「座標を求めよ」といわれているのだから、座標の書きかたで答えるようにしましょう。
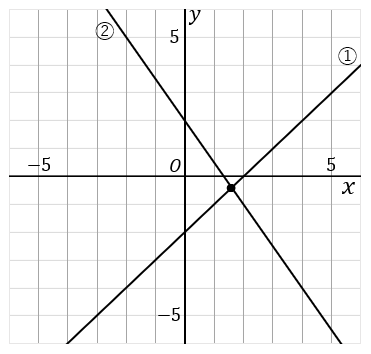
$\huge{12}$ 下の $①, \ ②$ の2つの直線の交点の座標を求めなさい。
答え
$\left(\cfrac{8}{5},-\cfrac{2}{5}\right)$
2直線の交点の座標は連立方程式の解です。まず、2つの直線の式をグラフから求めます。 $①, \ ②$ の直線の式はそれぞれ
$$y=x-2\qquad\cdots①$$
$$y=-\cfrac{3}{2}x+2\qquad\cdots②$$
もしわからなかったら、$9$ 番の問題のやり方を確認してください。
んで、この問題に答えるには、連立方程式
\begin{eqnarray*}
\left\{
\begin{array}{l}
y=x-2\\
y=-\cfrac{3}{2}x+2
\end{array}
\right.
\end{eqnarray*}
を解けばいいです。代入法で、
$①$の式の右辺=$②$の式の右辺
という式をたてて解いていきましょう。
\begin{eqnarray*}
x-2&=&-\cfrac{3}{2}x+2\qquad(×2)\\
2x-4&=&-3x+4\\
2x+3x&=&4+4\\
5x&=&8\\
x&=&\cfrac{8}{5}\\
\end{eqnarray*}
$y=x-2$ に $x=\cfrac{8}{5}$ を代入して $y$ を求めます。
\begin{eqnarray*}
y&=&\cfrac{8}{5}-2\\
&=&\cfrac{8}{5}-\cfrac{10}{5}\\
&=&-\cfrac{2}{5}\\
\end{eqnarray*}
これで $x=\cfrac{8}{5}$ , $y=-\cfrac{2}{5}$ というふうに、解が求められました。じゃあ答えを書きましょう。
$$\left(\cfrac{8}{5},-\cfrac{2}{5}\right)$$
この問題の答えは整数にはなりません。交点はぴったりとしたカドにはないからです。答えは分数になるはず。そう思って解いていきましょう。
$\huge{13}$ $10$ 円玉と $50$ 円玉があわせて $21$ 枚あり、合計金額は $450$ 円である。$10$ 円玉と $50$ 円玉はそれぞれ何枚ずつあるか
答え
$10$円玉…$15$枚 $50$円玉…$6$枚
$10$ 円玉が $x$ 枚、$50$ 円玉が $y$ 枚あることにします。文字を $2$ つ使うので、式も $2$ つたてなければ解けません。文字の数だけ式がいります。
$1$ つ目の式は、$10$ 円玉と $50$ 円玉 はあわせて $21$ 枚あるのですから、
$$x+y=21$$
$2$ つ目の式は、金額で式をたてます。あわせて $450$ 円なのですから、
$$10x+50y=450$$
この$2$ つの式を連立させて解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
x+y=21\quad…①\\
10x+50y=450\quad…②
\end{array}
\right.
\end{eqnarray*}
加減法で、$x$ の係数をそろえて解きます。
$① \ - \ ②\div10$
\begin{eqnarray*}
x+\phantom{5}y=\phantom{-}21\\
\underline{-) \quad x+5y=\phantom{-}45}\\
-4y=-24\\
y=6\phantom{-2}
\end{eqnarray*}
$y=6を①に代入$
\begin{eqnarray*}
x+6&=&21\\
x&=&15
\\
\left\{
\begin{array}{l}
x=15\\
y=6
\end{array}
\right.
\end{eqnarray*}
※かならず、きかれていることに答えましょう。$x=15, \ y=6$ なんて答えてしまったら、マルになりません。$10$ 円玉が $15$ 枚、$50$ 円玉が $6$ 枚と答えましょう。
$\huge{14}$ $A$ 地点から $C$ 地点まで $3400m$ の道のりを、$A$ 地点から途中の $B$ 地点までは分速 $120m$ の速さで進み、$B$ 地点から $C$ 地点までは分速 $80m$ の速さで進んだところ、全部で $35$ 分かかった。$A$ 地点から $B$ 地点までの道のりと、$B$ 地点から $C$ 地点までの道のりをそれぞれ求めなさい。
答え
$A$ 地点から $B$ 地点までの道のり…$1800m$
$B$ 地点から $C$ 地点までの道のり…$1600m$
$A$ 地点から $B$ 地点までの道のりを $xm$、$B$ 地点から $C$ 地点までの道のりを $ym$ とします。文字を $2$ つ使うので、式も $2$ つたてなければ解けません。文字の数だけ式がいります。
$1$ つ目の式は、道のりは全部で $3400m$ ですから、
$$x+y=3400$$
$2$ つ目の式は、$A~B$ 間にかかった時間と $B~C$ 間にかかった時間をあわせたら $35$ 分で式をたてます。
「時間$=$道のり$\div$速さ」ですから、
$$\cfrac{x}{120}+\cfrac{y}{80}=35$$
この$2$ つの式を連立させて解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
x+y=3400\quad…①\\
\cfrac{x}{120}+\cfrac{y}{80}=35\quad…②
\end{array}
\right.
\end{eqnarray*}
$②の分母をはらう\\
\begin{eqnarray*}
\qquad\cfrac{x}{120}+\cfrac{y}{80}&=&35\quad \class{mathbg-r}{(両辺に\times240)}\\
2x+3y&=&8400\quad…③
\end{eqnarray*}
$
加減法で解きます。
$③ \ - \ ①\times2$
\begin{eqnarray*}
2x+3y=8400\\
\underline{-) \quad 2x+2y=6800}\\
y=1600
\end{eqnarray*}
$y=1600を①に代入$
\begin{eqnarray*}
x+1600&=&3400\\
x&=&3400-1600\\
x&=&1800
\\
\left\{
\begin{array}{l}
x=1800\\
y=1600
\end{array}
\right.
\end{eqnarray*}
$\huge{15}$ $12$ %の食塩水と $7$ %の食塩水をまぜて、$10$ %の食塩水を $150g$ つくりたい。$12$ %の食塩水と $7$ %の食塩水は、それぞれ何 $g$ ずつまぜればよいか。
答え
$12$ %の食塩水…$90g$
$\phantom{1}7$ %の食塩水…$60g$
$12$ %の食塩水を $xg$、$7$ %の食塩水を $yg$ まぜることにします。文字を $2$ つ使うので、式も $2$ つたてなければ解けません。文字の数だけ式がいります。
$1$ つ目の式は、食塩水全体の重さは $150g$ ですから、
$$x+y=150$$
$2$ つ目の式は、$12$ %の食塩水 $xg$ にふくまれる食塩の重さと $7$ %の食塩水 $yg$ にふくまれる食塩の重さをあわせたら、全体の食塩水 $150g$ にふくまれる食塩の重さということで式をたてます。
「食塩$=$食塩水$\times$濃度」ですから、
$$\cfrac{12}{100}x+\cfrac{7}{100}y=\cfrac{10}{100}\times150$$
この$2$ つの式を連立させて解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
x+y=150\quad…①\\
\cfrac{12}{100}x+\cfrac{7}{100}y=\cfrac{10}{100}\times150\quad…②
\end{array}
\right.
\end{eqnarray*}
$②の分母をはらう\\
\begin{eqnarray*}
\qquad12x+7y&=&1500\quad…③
\end{eqnarray*}
$
加減法で、$y$ を消去します。
$③ \ - ①\times7$
\begin{eqnarray*}
12x+7y=1500\\
\underline{-) \quad 7x+7y=1050}\\
5x\phantom{+3y}=\phantom{0}450\\
x=90\phantom{3y}
\end{eqnarray*}
$x=90を①に代入$
\begin{eqnarray*}
90+y&=&150\\
y&=&60
\\
\left\{
\begin{array}{l}
x=90\\
y=60
\end{array}
\right.
\end{eqnarray*}
$\huge{16}$ ある学校の昨年度の生徒数は $530$ 人だったが、今年度は昨年度にくらべて男子は $6$ %減り、女子は $5$ %増えたため、$529$ 人となった。昨年度の男子、女子の生徒数をそれぞれ求めなさい。
答え
男子…$250$ 人
女子…$280$ 人
昨年度の男子生徒を $x$ 人、女子生徒を $y$ 人ということにします。文字を $2$ つ使うので、式も $2$ つたてなければ解けません。文字の数だけ式がいります。
$1$ つ目の式は、昨年度の生徒数は $530$ 人ですから、
$$x+y=530$$
$2$ つ目は、男子の $6$ %減と、女子の $5$ %増をあわせたら、全体としては $1$ 人減っている、ということで式をたてます。
$$-\cfrac{6}{100}x+\cfrac{5}{100}y=-1$$
この$2$ つの式を連立させて解きます。
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
x+y=530\quad…①\\
-\cfrac{6}{100}x+\cfrac{5}{100}y=-1\quad…②
\end{array}
\right.
\end{eqnarray*}
$②の分母をはらう\\
\begin{eqnarray*}
\qquad-6x+5y&=&-100\quad…③
\end{eqnarray*}
$
加減法で、$y$ の係数をそろえて解きます。
$①\times5 \ + \ ③$
\begin{eqnarray*}
5x+5y=2650\\
\underline{-) \quad -6x+5y=-100}\\
11x\phantom{+55y}=2750\\
x=250\phantom{0}
\end{eqnarray*}
昨年度の男子生徒数を $x$ ということにして、$x$ が求められました。きかれているのは、昨年度の男子と女子です。昨年度の生徒数は全体で $530$ 人ですから、
$$530-250=280$$
となって、昨年度の女子生徒は $280$ 人です。
答え(中2 2学期中間模擬テスト 第2回)
1$①4$ $②\cfrac{1}{12}$ $③4$ $④-a+5b$ $⑤\cfrac{5x+8y}{12}$ $⑥-20a^2b^3$ $⑦-3x$ $⑧\cfrac{1}{2x}$
2$①x=-12, \ y=8$ $②x=6, \ y=12$ $③x=-4, \ y=-3$ $④x=-3, \ y=8$ $⑤x=-9, \ y=6$ $⑥x=-1, \ y=3$
3$①y=-120x+1000$ 〇 $②y=\cfrac{3000}{x}$ × $③y=\pi x^2$ × $④y=-15x+300$ 〇 $⑤y=x^3$ ×
4$①-\cfrac{1}{2}$ $②-6$ $③-1 \leqq y \leqq 5$
5$①y=-\cfrac{1}{3}x+4$ $②y=-2x+4$ $③y=\cfrac{1}{2}x-1$ $④y=2x+3$ $⑤y=\cfrac{1}{2}x-5$ $⑥y=\cfrac{1}{3}x+2$ $⑦y=\cfrac{1}{2}x-2$ $⑧y=2x+1$
 6ア…$8$, イ…$\cfrac{10}{3}$, ウ…$12$, 式 $y=-\cfrac{2}{3}x+4$
6ア…$8$, イ…$\cfrac{10}{3}$, ウ…$12$, 式 $y=-\cfrac{2}{3}x+4$
7①イ,エ,カ ②ウ,オ ③イとカ ④アとカ,イとエ
8 右上図
9$①y=\cfrac{1}{2}x-1$ $②y=-\cfrac{2}{3}x+2$ $③y=\cfrac{5}{3}-\cfrac{4}{3}$
10 $x=-2, \ y=3$ グラフ右下図
 11$(-3, \ -2)$
11$(-3, \ -2)$
12 $\left(\cfrac{8}{5}, \ -\cfrac{2}{5}\right)$
13 $10$円玉…$15$枚 $50$円玉…$6$枚
14 $A$ 地点から $B$ 地点までの道のり…$1800m$
$B$ 地点から $C$ 地点までの道のり…$1600m$
15 $12$ %の食塩水…$90g$
$7$ %の食塩水…$60g$
16 男子…$250$ 人
女子…$280$ 人