数学 中3 1章 展開・因数分解 第1回)
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
展開
(1) 次の式を計算しなさい。
\begin{eqnarray*}
&①& \quad 3x(2x-3y)&②& \quad \cfrac{2}{3}x(6x-12y)\\
\\
&③& \quad (-4x+7y)\times (-2x)&④& \quad -5a(6a+2b-3c)\\
\\
&⑤& \quad (15xy+20x)\div 5x&⑥& \quad (3ax-4x)\div(-x)\\
\\
&⑦& \quad (8x^2y-6xy^2)\div(2xy)\quad&⑧& \quad (-12x^2+6x)\div \cfrac{3}{2}x
\end{eqnarray*}
$$ \large{a(b+c)=ab+ac \qquad (a+b)c=ac+bc}$$
答え
$①6x^2-9xy$ $②4x^2-8xy$ $③8x^2-14xy$
$④-30a^2-10ab+15ac$ $⑤3y+4$ $⑥-3a+4$ $⑦4x-3y$ $⑧-8x+4$
⑧分数の割り算は逆数をかけます。いわゆる「ひっくり返して掛ける」というやつです。そのさい、注意点があります。$x$ は分母のほうにいきます。
$\qquad \cfrac{3}{2}x=\cfrac{3x}{2}$ なので、逆数にすると$\cfrac{2}{3x}$
なので、
\begin{eqnarray*}
&& (-12x^2+6x)\div \cfrac{3}{2}x\\
&=& (-12x^2+6x)\times \cfrac{2}{3x}\\
&=& -12x^2\times \cfrac{2}{3x} +6x\times \cfrac{2}{3x}\\
&=& -8x+4
\end{eqnarray*}
まちがえやすい注意点なので、もういちど整理しておきますね。
$\qquad \cfrac{3}{2}x$ を逆数にすると $\cfrac{2}{3}x$ ←まちがい
$\qquad \cfrac{3}{2}x$ を逆数にすると $\cfrac{2}{3x}$ ←正しい
(2) 次の式を展開しなさい。
\begin{eqnarray*}
&①& \quad (a+b)(c+d)&②& \quad (4x+3)(2x-1)\\
\\
&③& \quad (3x+y)(2x-7y)&④& \quad (x+y)(2x-3y+1)\\
\\
&⑤& \quad (x+3)(x+5)&⑥& \quad (a+5)(a-8)\\
\\
&⑦& \quad (y-4)(y-6)&⑧& \quad (x+4)^2\\
\\
&⑨& \quad (2x-5)^2&⑩& \quad \left( \cfrac{2}{3}x+3 \right)^2\\
\\
&⑪& \quad (2x+11)(2x-11)\qquad&⑫& \quad \left( \cfrac{3}{5}x+12y\right) \left( \cfrac{3}{5}x-12y \right)\\
\\
&⑬& \quad (-2a+3)(2a+3)&⑭& \quad (x+4y)(4y-x)\\
\end{eqnarray*}
1. $ \large{(x+a)(x+b)=x^2+(a+b)x+ab}$
2. $ \large{(x+a)^2=x^2+2ax+a^2}$
3. $ \large{(x-a)^2=x^2-2ax+a^2}$
4. $ \large{(x+a)(x-a)=x^2-a^2}$
答え
$①ac+ad+bc+bd$ $②8x^2+2x-3$ $③6x^2-19xy-7y^2$ $④2x^2-xy+x-3y^2+y$ $⑤x^2+8x+15$ $⑥a^2-3a-40$ $⑦y^2-10y+24$ $⑧x^2+8x+16$ $⑨4x^2-20x+25$ $⑩\cfrac{4}{9}x^2+4x+9$ $⑪4x^2-121$ $⑫\cfrac{9}{25}x^2-144y^2$ $⑬-4a^2+9$ $⑭-x^2+16y^2$
分配法則でまんべんなく掛ければすべて正答できるのですが、⑤番以降は乗法公式でやりましょう。中3でおぼえるべき乗法公式は $4$つです。必ずおぼえて使えるようになり、慣れておきましょう。でないといろいろこまったことになります。
⑬と⑭は、かっこの中の順番を変えれば公式$4$が使えます。
\begin{eqnarray*}
&⑬& (-2a+3)(2a+3)\\
&=& (3-2a)(3+2a)\\
&=& 9-4a^2
\end{eqnarray*}
\begin{eqnarray*}
&⑭& (x+4y)(4y-x)\\
&=& (4y+x)(4y-x)\\
&=& 16y^2-x^2
\end{eqnarray*}
(3) 次の式を展開しなさい。
\begin{eqnarray*}
&①& \quad -(x+2)(x-3)&②& \quad 2(x+1)^2\\
\\
&③& \quad 3(x-4)(x+6)-(x-2)(x-3)\\
\\
&④& \quad (x+2y)(x-2y)+2(3x-y)^2\\
\\
&⑤& \quad (x+y-2)^2&⑥& \quad (x-y+5)(x-y-5)\\
\\
&⑦& \quad (2x+y-3)(2x-y+3)
\end{eqnarray*}
答え
$①-x^2+x+6$ $②2x^2+4x+2$ $③2x^2+11x-78$ $④19x^2-12xy-2y^2$ $⑤x^2+2xy-4x+y^2-4y+4$ $⑥x^2-2xy+y^2-25$ $⑦4x^2-y^2+6y-9$
\begin{eqnarray*} &①& -(x+2)(x-3)\\ &=& -(x^2-x-6)\\ &=& -x^2+x+6 \end{eqnarray*} \begin{eqnarray*} &②& 2(x+1)^2\\ &=& 2(x^2+2x+1)\\ &=& 2x^2+4x+2 \end{eqnarray*} \begin{eqnarray*} &③& 3(x-4)(x+6)-(x-2)(x-3)\\ &=& 3(x^2+2x-24)-(x^2-5x+6)\\ &=& 3x^2+6x-72-x^2+5x-6\\ &=& 2x^2+11x-78 \end{eqnarray*} \begin{eqnarray*} &④& (x+2y)(x-2y)+2(3x-y)^2\\ &=& x^2-4y^2+2(9x^2-6xy+y^2)\\ &=& x^2-4y^2+18x^2-12xy+2y^2\\ &=& 19x^2-12xy-2y^2 \end{eqnarray*} \begin{eqnarray*} &⑤& (x+y-2)^2\\ &=& (x+y)^2-4(x+y)+4\\ &=& x^2+2xy+y^2-4x-4y+4\\ &=& x^2+2xy-4x+y^2-4y+4 \end{eqnarray*} \begin{eqnarray*} &⑥& (x-y+5)(x-y-5)\\ &=& (x-y)^2-25\\ &=& x^2-2xy+y^2-25 \end{eqnarray*} \begin{eqnarray*} &⑦& (2x+y-3)(2x-y+3)\\ &=& \{2x+(y-3)\} \{2x-(y-3)\}\\ &=& 4x^2-(y-3)^2\\ &=& 4x^2-(y^2-6y+9)\\ &=& 4x^2-y^2+6y-9 \end{eqnarray*}
(4) 乗法公式を使って次の計算をしなさい。計算の過程をかいておくこと。
\begin{eqnarray*}
&①& \quad 101^2\qquad&②& \quad 97^2\\
\\
&③& \quad 105\times95
\end{eqnarray*}
答え
\begin{eqnarray*}
&①& 101^2\\
&=& (100+1)^2\\
&=& 10000+200+1\\
&=& 10201
\end{eqnarray*}
\begin{eqnarray*}
&②& 97^2\\
&=& (100-3)^2\\
&=& 10000-600+9\\
&=& 9409
\end{eqnarray*}
\begin{eqnarray*}
&③& 105\times95\\
&=& (100+5)(100-5)\\
&=& 10000-25\\
&=& 9975
\end{eqnarray*}
(5) $x=-2, \ y=\cfrac{1}{2}$ のとき、次の式の値を求めなさい。 \begin{eqnarray*} &①& \quad (x-2y)(x+y)+2y^2\\ \\ &②& \quad (x+y)^2-(x+y)(y-x) \end{eqnarray*}
答え
$①5$ $②6$
問題の式に $x$ や $y$ の値を代入すれば答えは出ますが、めんどうくさいことになります。いったん展開して整理してから代入するとラクになります。 \begin{eqnarray*} &①& (x-2y)(x+y)+2y^2\\ &=& x^2-xy-2y^2+2y^2\\ &=& x^2-xy \quad \class{mathbg-r}{(ここまでやってから代入する)} \\ &=& (-2)^2-(-2)\times \cfrac{1}{2}\\ &=& 4+1\\ &=& 5 \end{eqnarray*} \begin{eqnarray*} &②& (x+y)^2-(x+y)(y-x)\\ &=& (x+y)^2-(y+x)(y-x)\\ &=& x^2+2xy+y^2-(y^2-x^2)\\ &=& x^2+2xy+y^2-y^2+x^2\\ &=& 2x^2+2xy \quad \class{mathbg-r}{(ここまでやってから代入する)} \\ &=& 2 \times(-2)^2+2 \times(-2) \times \cfrac{1}{2}\\ &=& 8-2\\ &=& 6 \end{eqnarray*}
(6) 次の $ \boxed{\Large\phantom{hoge}}$ の中にあてはまる数や式をいれなさい。 \begin{eqnarray*} &①& \quad (x+3)(x+\boxed{\Large\phantom{hoge}}) \qquad &②& \quad (x-\boxed{\Large\phantom{hoge}})^2\\ &=& \quad x^2+\boxed{\Large\phantom{hoge}}+12&=& \quad x^2-\boxed{\Large\phantom{hoge}}+16y^2 \\ \end{eqnarray*}
答え
\begin{eqnarray*}
&①& \quad (x+3)(x+\boxed{\large{ \ 4 \ }}) \qquad &②& \quad (x-\boxed{\large{ \ 4y \ }})^2\\
&=& \quad x^2+\boxed{\large{ \ 7x \ }}+12&=& \quad x^2-\boxed{\large{ \ 8xy \ }}+16y^2
\\
\end{eqnarray*}
素数
(7) 30以下の素数をすべていいなさい。
答え
$$2,3,5,7,11,13,17,19,23,29$$
$1$ より大きい自然数で、正の約数が $1$ とその数しかない数を素数(そすう)という。
※$1$ は素数じゃないです。素数は $2$ からはじまります。しっかりおぼえて。
素因数分解
(8) 次の①,②の数を素因数分解して、素数の積の形で表しなさい。
$$①18\qquad\qquad\qquad②90$$
答え
$①2\times3^2$ $②2\times3^2\times5$
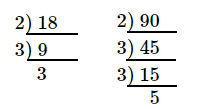
自然数をいくつかの自然数の積に形に表すとき、その $1$ つ $1$ つの自然数を因数という。
その因数が素数のとき、それを素因数という。
自然数を素因数だけの積の形に表すことを素因数分解するという。
素因数分解して表された積の形は、素因数を並べる順序を考えなければ、$1$ 通りだけである。
因数分解
(9) 次の式を因数分解しなさい。
\begin{eqnarray*}
&①& \quad ax+ay&②& \quad 24x^2-12x\\
\\
&③& \quad -3x^2y+9xy^2\qquad&④& \quad 8a^2-16ab+12ac
\end{eqnarray*}
$$ \large{ab+ac=a(b+c)}$$
答え
$①a(x+y)$ $②12x(2x-1)$ $③-3xy(x-3y)$
$④4a(2a-4b+3c)$
くくるのは因数分解です。そのさい、かっこの外がなるべく大きくなるようにします。なので、たとえば②の問題は、
\begin{eqnarray*}
&②& 24x^2-12x\\
&=& 2x(12x-6)
\end{eqnarray*}
こういうのは×です。かっこの中がまだ $6$ でくくれるからです。
③番の問題は、
\begin{eqnarray*}
&③& -3x^2y+9xy^2\\
&=& 3xy(-x+3y)
\end{eqnarray*}
これでも〇になるとおもいますが、こういうのは
$$-3xy(x-3y)$$
とかくのが数学のおやくそくです。$(-$ というふうにはかきません。別にダメというわけじゃないんですけど、まあ、ふつうそうすることになってます。
(10) 次の式を因数分解しなさい。 \begin{eqnarray*} &①& \quad x^2+5x+6 &②& \quad a^2-5a-24\\ \\ &③& \quad x^2+x-30 &④& \quad m^2-7m+12\\ \\ &⑤& \quad x^2+4x+4 &⑥& \quad m^2+2m+1\\ \\ &⑦& \quad 9x^2+12xy+4y^2 &⑧& \quad \cfrac{1}{9}x^2+\cfrac{4}{3}x+4\\ \\ &⑨& \quad x^2-6x+9 &⑩& \quad a^2-10a+25\\ \\ &⑪& \quad 4x^2-12xy+9y^2 \qquad &⑫& \quad \cfrac{1}{4}m^2-m+1\\ \\ &⑬& \quad x^2-4 &⑭& \quad a^2-36\\ \\ &⑮& \quad 9a^2-16b^2 &⑯& \quad \cfrac{1}{16}x^2-\cfrac{4}{9}y^2\\ \end{eqnarray*}
1. $ \large{x^2+(a+b)x+ab}=(x+a)(x+b)$
2. $ \large{x^2+2ax+a^2=(x+a)^2}$
3. $ \large{x^2-2ax+a^2=(x-a)^2}$
4. $ \large{x^2-a^2=(x+a)(x-a)}$
答え
$①(x+2)(x+3)$ $②(a+3)(a-8)$ $③(x+6)(x-5)$
$④(x-3)(x-4)$ $⑤(x+2)^2$ $⑥(m+1)^2$ $⑦(3x+2y)^2$ $⑧(\cfrac{1}{3}x+2)^2$ $⑨(x-3)^2$ $⑩(a-5)^2$ $⑪(2x-3y)^2$ $⑫(\cfrac{1}{2}m-1)^2$ $⑬(x+2)(x-2)$ $⑭(a+6)(a-6)$ $⑮(3a+4b)(3a-4b)$ $⑯\left(\cfrac{1}{4}x+\cfrac{2}{3}y\right)\left(\cfrac{1}{4}x-\cfrac{2}{3}y\right)$
さあ、数学はこれから、$2$ 乗の数に気をつけるようにしましょう。$2$ 乗の数 というのは、 $$\large{1,4,9,16,25,36,49,64,81,100,121,144,169...}$$ こういう数のことです。問題の中にこういう数があるときは、公式の②番③番④番のことを考えましょう。
(11) 次の $ \boxed{\Large\phantom{hoge}}$ の中にあてはまる数や式をいれなさい。 \begin{eqnarray*} &①& \quad x^2+\boxed{\Large\phantom{hoge}}+24\qquad &②& \quad x^2-\boxed{\Large\phantom{hoge}}+49y^2\\ &=& \quad (x+3)(x+\boxed{\Large\phantom{hoge}})&=& \quad (x-\boxed{\Large\phantom{hoge}})^2 \\ \end{eqnarray*}
答え
\begin{eqnarray*}
&①& \quad x^2+\boxed{\large{ \ 11x \ }}+24\qquad &②& \quad x^2-\boxed{\large{ \ 14xy \ }}+49y^2\\
&=& \quad (x+3)(x+\boxed{\large{ \ 8 \ }})&=& \quad (x-\boxed{\large{ \ 7y \ }})^2
\\
\end{eqnarray*}
(12) 因数分解を使って次の計算をしなさい。計算の過程をかいておくこと。
$$①\quad 76^2-24^2 \qquad\qquad\qquad ②\quad243\times233-233^2$$
答え
\begin{eqnarray*}
&①& 76^2-24^2\\
&=& (76+24)(76-24)\\
&=& 100\times52\\
&=& 5200
\end{eqnarray*}
\begin{eqnarray*}
&②& 243\times233-233^2\\
&=& 233(243-233)\\
&=& 233\times10\\
&=& 2330
\end{eqnarray*}
(13) 次の式を因数分解しなさい。 \begin{eqnarray*} &①& \quad 2x^2-6x-20 &②& \quad a^3-8a^2+16a\\ \\ &③& \quad 16x^2-64y^2 &④& \quad x(a+b)-2y(a+b)\\ \\ &⑤& \quad a(x+y)+x+y &⑥& \quad (x+1)^2+4(x+1)+3\\ \\ &⑦& \quad (x-y)^2-6(x-y)+9 \quad &⑧& \quad (x-6)^2-9\\ \\ &⑨& \quad ax+ay+bx+by \end{eqnarray*}
答え
$①2(x+2)(x-5)$ $②a(a-4)^2$ $③16(x+2y)(x-2y)$
$④(a+b)(x-2y)$ $⑤(x+y)(a+1)$ $⑥(x+2)(x+4)$ $⑦(x-y-3)^2$ $⑧(x-3)(x-9)$ $⑨(x+y)(a+b)$
\begin{eqnarray*} &①& 2x^2-6x-20\\ &=& 2(x^2-3x-10)\\ &=& 2(x+2)(x-5) \end{eqnarray*} \begin{eqnarray*} &②& a^3-8a^2+16a\\ &=& a(a^2-8a+16)\\ &=& a(a-4)^2 \end{eqnarray*} \begin{eqnarray*} &③& 16x^2-64y^2\\ &=& 16(x^2-4y^2)\\ &=& 16(x+2y)(x-2y) \end{eqnarray*} \begin{eqnarray*} &④& a+b \ を \ A \ とおくと、\\ &&x(a+b)-2y(a+b)\\ &=& xA-2yA\\ &=& A(x-2y)\\ &=& (a+b)(x-2y) \end{eqnarray*} \begin{eqnarray*} &⑤& x+y \ を \ A \ とおくと、\\ &&a(x+y)+x+y\\ &=& aA+A\\ &=& A(a+1)\\ &=& (x+y)(a+1) \end{eqnarray*} \begin{eqnarray*} &⑥& x+1 \ を \ A \ とおくと、\\ &&(x+1)^2+4(x+1)+3\\ &=& A^2+4A+3\\ &=& (A+1)(A+3)\\ &=& (x+1+1)(x+1+3)\\ &=& (x+2)(x+4) \end{eqnarray*} \begin{eqnarray*} &⑦& x-y \ を \ A \ とおくと、\\ &&(x-y)^2-6(x-y)+9\\ &=& A^2-6A+9\\ &=& (A-3)^2\\ &=& (x-y-3)^2 \end{eqnarray*} \begin{eqnarray*} &⑧& x-6 \ を \ A \ とおくと、\\ &&(x-6)^2-9\\ &=& A^2-9\\ &=& (A+3)(A-3)\\ &=& (x-6+3)(x-6-3)\\ &=& (x-3)(x-9) \end{eqnarray*} \begin{eqnarray*} &⑨&ax+ay+bx+by\\ &=& a(x+y)+b(x+y)\\ &&x+y \ を \ A \ とおくと、\\ &=& aA+bA\\ &=& A(a+b)\\ &=& (x+y)(a+b) \end{eqnarray*}
(14) $x=1.7, \ y=8.3$ のとき、次の式の値を求めなさい。 $$x^2+2xy+y^2$$
答え
$100$
問題の式に $x$ や $y$ の値を代入すれば答えは出ますが、めんどうくさいことになります。因数分解をしてから代入するとラクになる問題というのがあります。夢のようにラクになることさえあります。 \begin{eqnarray*} && x^2+2xy+y^2\\ &=& (x+y)^2\quad \class{mathbg-r}{(ここで代入する)} \\ &=& (1.7+8.3)^2\\ &=& 10^2\\ &=& 100 \end{eqnarray*}
(15) $x+y=5, \ x-y=-7$ のとき、次の式の値を求めなさい。 $$x^2-y^2$$
答え
$-35$
与えられた式を連立方程式にして、
\begin{eqnarray*}
\left\{
\begin{array}{l}
x+y=5\\
x-y=-7
\end{array}
\right.
\end{eqnarray*}
これを解けば $x, \ y$ が求められて、それを代入すれば答えが求められるのですが、この問題の場合はちょっと損なやりかたです。
因数分解をすればもっとラクにやれます。
\begin{eqnarray*}
&& x^2-y^2\\
&=& (x+y)(x-y)\quad \class{mathbg-r}{(こうすれば代入できる)} \\
&=& 5\times(-7)\\
&=& -35
\end{eqnarray*}
展開・因数分解の利用
(16) 連続する $2$つの整数がある。それぞれの平方の和から $1$ をひくと、もとの $2$つの数の積の $2$倍になることを証明しなさい。
答え
連続する $2$つの整数を $n, \ n+1$ とすると、
\begin{eqnarray*}
&& n^2+(n+1)^2-1\\
&=& n^2+n^2+2n+1-1\\
&=& 2n^2+2n\\
&=& 2n(n+1)
\end{eqnarray*}
よって、連続する $2$つの整数で、それぞれの平方の和から $1$ をひくと、もとの $2$つの数の積の $2$倍になる。
<おぼえておきたい数学のおやくそく>
偶数…$2n$
奇数…$2n+1 \quad (2n-1)$
$3$の倍数…$3n$
$5$の倍数…$5n$
連続する $2$つの数…$n, \ n+1$
連続する $3$つの数…$n-1, \ n, \ n+1 \quad (n, \ n+1, \ n+2)$
連続する $2$つの偶数…$2n, \ 2n+2$
連続する $2$つの奇数…$2n-1, \ 2n+1$
(17) 連続する $2$つの奇数がある。大きいほうの奇数の平方から、小さいほうの奇数の平方をひくと、$8$ の倍数になることを証明しなさい。
答え
連続する $2$つの奇数を $2n-1, \ 2n+1$ とすると、
\begin{eqnarray*}
&& (2n+1)^2-(2n-1)^2\\
&=& 4n^2+4n+1-(4n^2-4n+1)\\
&=& 4n^2+4n+1-4n^2+4n-1\\
&=& 8n
\end{eqnarray*}
よって、連続する $2$つの奇数で、大きいほう奇数の平方から、小さいほうの奇数の平方をひくと、$8$ の倍数になる。
<おぼえておきたい数学のおやくそく>
偶数…$2n$
奇数…$2n+1 \quad (2n-1)$
$3$の倍数…$3n$
$5$の倍数…$5n$
連続する $2$つの数…$n, \ n+1$
連続する $3$つの数…$n-1, \ n, \ n+1 \quad (n, \ n+1, \ n+2)$
連続する $2$つの偶数…$2n, \ 2n+2$
連続する $2$つの奇数…$2n-1, \ 2n+1$
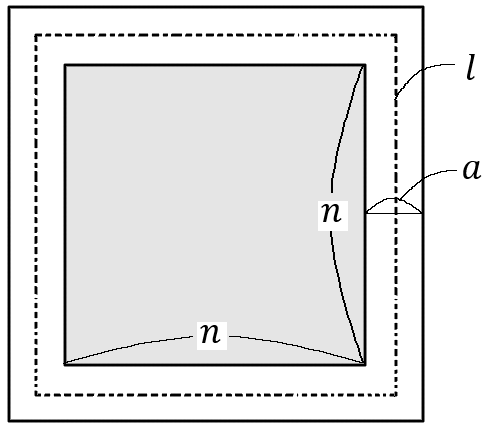
(18) $1$ 辺が $n$ mの正方形の土地の周囲に、幅 $a$ mの道がある。道の中央を通る周の長さを $l$ mとし、道の面積を $S$ ㎡とすると、$S=al$ となることを証明しなさい。
答え
\begin{eqnarray*}
S&=& (n+2a)^2-n^2\\
&=& n^2+4an+4a^2-n^2\\
&=& 4an+4a^2\quad …①
\end{eqnarray*}
道の中央を通る周は正方形となり、その $1$ 辺の長さは $n+a$ だから、
\begin{eqnarray*}
l&=& (n+a)\times4\\
&=& 4n+4a
\end{eqnarray*}
よって、
\begin{eqnarray*}
al&=& a(4n+4a)\\
&=& 4an+4a^2\quad…②
\end{eqnarray*}
①,②から、$S=al$
$S=al$ を証明しなさい、というのだから、「①$S$ について」と、「②$al$ について」、それぞれを式で表すことを考えていきます。
<①$S$ について>
$S$ というのは道の面積なのですから、いちばん大きい正方形からいちばん小さい正方形を引いたものになります。
いちばん小さい正方形の面積は $n^2$ です。
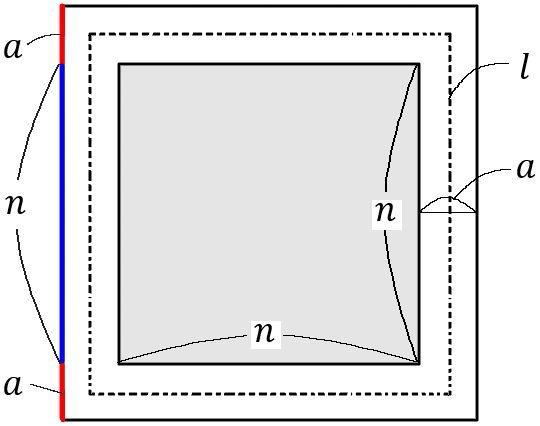 いちばん大きい正方形の $1$ 辺は、右の図のように考えると、赤い部分と青い部分の和です。赤の長さは$a\times2=2a,$ 青は $n$ ですから、大きい正方形の $1$ 辺の長さは $(n+2a)$ ということになります。なので、大きい正方形の面積は
$$(n+2a)^2=n^2+4an+4a^2$$
なので、
$$S=n^2+4an+4a^2-n^2=4an+4a^2$$
<②$al$ について>
いちばん大きい正方形の $1$ 辺は、右の図のように考えると、赤い部分と青い部分の和です。赤の長さは$a\times2=2a,$ 青は $n$ ですから、大きい正方形の $1$ 辺の長さは $(n+2a)$ ということになります。なので、大きい正方形の面積は
$$(n+2a)^2=n^2+4an+4a^2$$
なので、
$$S=n^2+4an+4a^2-n^2=4an+4a^2$$
<②$al$ について>
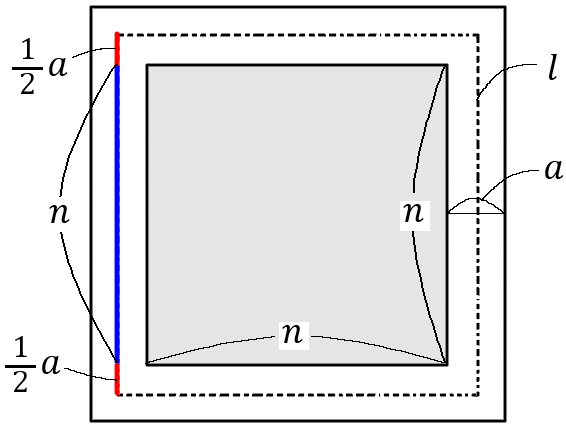 $l$ というのは、点線の正方形の周囲の長さのことです。点線の正方形の $1$ 辺は、右の正方形のように考えると、赤い部分と青い部分の和です。赤の長さは$\cfrac{1}{2}a\times2=a,$ 青は $n$ ですから、点線の正方形の $1$ 辺の長さは $(n+a)$ ということになります。$l$ の長さはその $4$ 倍なので、
$$l=(n+a)\times4=4n+4a$$
なので、
$$al=a(4n+4a)=4an+4a^2$$
これで①も②もどちらも $4an+4a^2$ になりました。なので、
$$S=al$$
$l$ というのは、点線の正方形の周囲の長さのことです。点線の正方形の $1$ 辺は、右の正方形のように考えると、赤い部分と青い部分の和です。赤の長さは$\cfrac{1}{2}a\times2=a,$ 青は $n$ ですから、点線の正方形の $1$ 辺の長さは $(n+a)$ ということになります。$l$ の長さはその $4$ 倍なので、
$$l=(n+a)\times4=4n+4a$$
なので、
$$al=a(4n+4a)=4an+4a^2$$
これで①も②もどちらも $4an+4a^2$ になりました。なので、
$$S=al$$
答え(中3 1章 展開・因数分解 第1回)
(1)$①6x^2-9xy$ $②4x^2-8xy$ $③8x^2-14xy$ $④-30a^2-10ab+15ac$ $⑤3y+4$ $⑥-3a+4$ $⑦4x-3y$ $⑧-8x+4$
(2)$①ad+ac+bc+bd$ $②8x^2+2x-3$ $③6x^2-19xy-7y^2$ $④2x^2-xy+x-3y^2+y$ $⑤x^2+8x+15$ $⑥a^2-3a-40$ $⑦y^2-10y+24$ $⑧x^2+8x+16$ $⑨4x^2-20x+25$ $⑩\cfrac{4}{9}x^2+4x+9$ $⑪4x^2-121$ $⑫\cfrac{9}{25}x^2-144y^2$ $⑬-4a^2+9$ $⑭-x^2+16y^2$
(3)$①-x^2+x+6$ $②2x^2+4x+2$ $③2x^2+11x-78$ $④19x^2-12xy-2y^2$ $⑤x^2+2xy-4x+y^2-4y+4$ $⑥x^2-2xy+y^2-25$ $⑦4x^2-y^2+6y-9$
\begin{eqnarray*}
(4)&①& 101^2&②& 97^2&③& 105\times95\\
&=& (100+1)^2&=& (100-3)^2&=& (100+5)(100-5)\\
&=& 10000+200+1\qquad&=& 10000-600+9\qquad&=& 10000-25\\
&=& 10201&=& 9409&=& 9975
\end{eqnarray*}
(5)$①5$ $②6$
\begin{eqnarray*}
(6)&①& \quad (x+3)(x+\boxed{\large{ \ 4 \ }}) \qquad &②& \quad (x-\boxed{\large{ \ 4y \ }})^2\\
&=& \quad x^2+\boxed{\large{ \ 7x \ }}+12&=& \quad x^2-\boxed{\large{ \ 8xy \ }}+16y^2
\\
\end{eqnarray*}
(7)$2,3,5,7,11,13,17,19,23,29$ (8)$①2\times3^2$ $②2\times3^2\times5$
(9)$①a(x+y)$ $②12x(2x-1)$ $③-3xy(x-3y)$ $④4a(2a-4b+3c)$
(10)$①(x+2)(x+3)$ $②(x+3)(x-8)$ $③(x+6)(x-5)$
$④(x-3)(x-4)$ $⑤(x+2)^2$ $⑥(m+1)^2$ $⑦(3x+2y)^2$ $⑧(\cfrac{1}{3}x+2)^2$ $⑨(x-3)^2$ $⑩(a-5)^2$ $⑪(2x-3y)^2$ $⑫(\cfrac{1}{2}m-1)^2$ $⑬(x+2)(x-2)$ $⑭(a+6)(a-6)$ $⑮(3a+4b)(3a-4b)$ $⑯\left(\cfrac{1}{4}x+\cfrac{2}{3}y\right)\left(\cfrac{1}{4}x-\cfrac{2}{3}y\right)$
\begin{eqnarray*}
(11)&①& \quad x^2+\boxed{\large{ \ 11x \ }}+24\qquad &②& \quad x^2-\boxed{\large{ \ 14xy \ }}+49y^2\\
&=& \quad (x+3)(x+\boxed{\large{ \ 8 \ }})&=& \quad (x-\boxed{\large{ \ 7y \ }})^2
\\
\end{eqnarray*}
\begin{eqnarray*}
(12)&①& 76^2-24^2&②& 243\times233-233^2\\
&=& (76+24)(76-24)\qquad&=& 233(243-233)\\
&=& 100\times52&=& 233\times10\\
&=& 5200&=& 2330
\end{eqnarray*}
(13)$①2(x+2)(x-5)$ $②a(a-4)^2$ $③16(x+2y)(x-2y)$
$④(a+b)(x-2y)$ $⑤(x+y)(a+1)$ $⑥(x+2)(x+4)$ $⑦(x-y-3)^2$ $⑧(x-3)(x-9)$ $⑨(x+y)(a+b)$
(14)$100$ (15)$-35$
(16)連続する $2$つの整数を $n, \ n+1$ とすると、
\begin{eqnarray*}
&& n^2+(n+1)^2-1\\
&=& n^2+n^2+2n+1-1\\
&=& 2n^2+2n\\
&=& 2n(n+1)
\end{eqnarray*}
よって、連続する $2$つの整数で、それぞれの平方の和から $1$ をひくと、もとの $2$つの数の積の $2$倍になる。
(17)連続する $2$つの奇数を $2n-1, \ 2n+1$ とすると、
\begin{eqnarray*}
&& (2n+1)^2-(2n-1)^2\\
&=& 4n^2+4n+1-(4n^2-4n+1)\\
&=& 4n^2+4n+1-4n^2+4n-1\\
&=& 8n
\end{eqnarray*}
よって、連続する $2$つの奇数で、大きいほう奇数の平方から、小さいほうの奇数の平方をひくと、$8$ の倍数になる。
\begin{eqnarray*}
(18)S&=& (n+2a)^2-n^2\\
&=& n^2+4an+4a^2-n^2\\
&=& 4an+4a^2\quad …①
\end{eqnarray*}
道の中央を通る周は正方形となり、その $1$ 辺の長さは $n+a$ だから、
$$
l= (n+a)\times4
= 4n+4a
$$
よって、
$$
al= a(4n+4a)
= 4an+4a^2\quad…②
$$
①,②から、$S=al$