数学 中3 5章 相似 第1回(全22問)
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
(1)
相似な図形の性質
① 相似な図形では、対応する $ \boxed{\LARGE\phantom{hogehoge}}$ はすべて等しい。
② 相似な図形では、対応する $ \boxed{\LARGE\phantom{hoge}}$ はそれぞれ等しい。
答え
①線分の比 ②角
(2) 「三角形$ABC$と三角形$DEF$は相似である」というのを記号でかくと、
$\qquad \qquad \boxed{\LARGE\phantom{hogehogehogehoge}}$
三角形の相似条件
① $ \boxed{\LARGE\phantom{hogehogehogehoge}}$ がすべて等しい。
② $ \boxed{\LARGE\phantom{hogehogehogehogehogehoge}}$ が等しい。
③ $ \boxed{\LARGE\phantom{hogehoge}}$ がそれぞれ等しい。
答え
$\triangle ABC$ ∽$\triangle DEF$
① $3$ 組の辺の比
② $2$ 組の辺の比が等しく、その間の角
③ $2$ 組の角
(3) 下の図のなかから、相似な三角形の組を見つけ、記号 ∽ を使って表しなさい。また、そのときに使った相似条件をいいなさい。
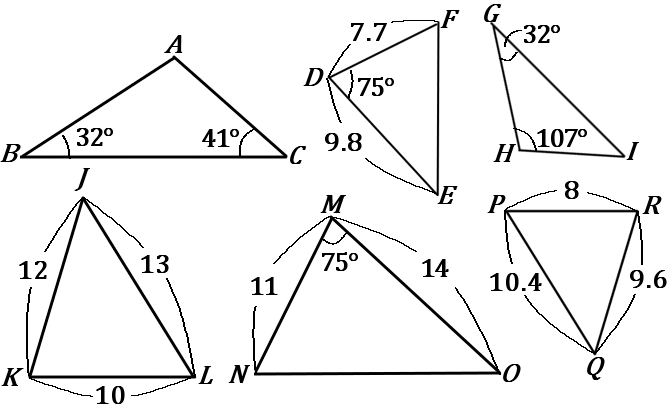
答え
$\triangle ABC$ ∽$\triangle HGI$…$2$ 組の角がそれぞれ等しい。
$\triangle DEF$ ∽$\triangle MON$…$2$ 組の辺の比とその間の角が等しい。
$\triangle JKL$ ∽$\triangle QRP$…$3$ 組の辺の比がすべて等しい。
対応する辺や角に注意する。
(4) 次の①~③の図で、相似な三角形を見つけ、 記号 ∽ を使って表しなさい。また、そのときに使った相似条件をいいなさい。

答え
①$\triangle ABC$ ∽$\ \triangle ADE$…$2$ 組の角がそれぞれ等しい。
②$\triangle ABC$ ∽$\triangle EBD$…$2$ 組の角がそれぞれ等しい。
③$\triangle ABC$ ∽$\ \triangle EDC$…$2$ 組の辺の比とその間の角が等しい。
対応する辺や角に注意する。
① $\angle A$ は共通、平行線の同位角だから $\angle B \ = \ \angle ADE$
② $\angle B$ は共通、仮定から $\angle A \ = \ \angle DEB$
③ 対頂角だから $\angle ACB \ = \ \angle ECD, \ AC:BC=EC:DC=5:6$
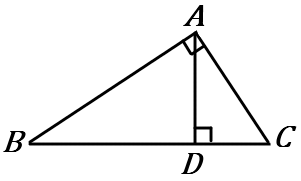
(5) $\angle A=90^{ \circ }$ の直角三角形で、頂点 $A$ から $BC$ におろした垂線と $BC$ との交点を $D$ とする。
$\triangle ABC$ ∽$\ \triangle DBA$を証明しなさい。
答え
〈証明〉
$\triangle ABC$ と $\triangle DBA$ で、
仮定から、$\angle BAC=\angle BDA$ ……①
共通な角だから、$\angle ABC=\angle DBA$ ……②
①②より、$2$ 組の角がそれぞれ等しいので
$\triangle ABC$ ∽$\ \triangle DBA$
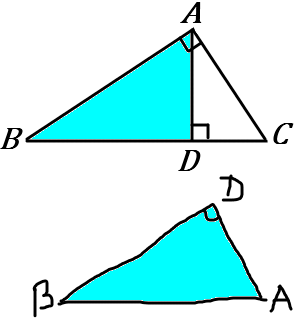 対応する辺や角に注意しましょう。
対応する辺や角に注意しましょう。
相似な図形どうしを、対応する辺や角に注意して、向きをそろえてかいてしまうのがよいです。問題の図の下や横に、こんな感じで図をかき加えてしまいましょう。→
すると、辺や角のいい方のミスが少なくなります。
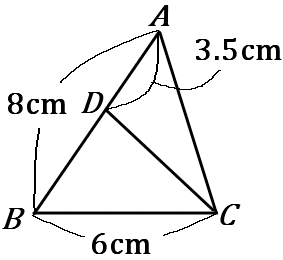 (6) 右の図で、$AB=8cm,$ $\ BC=6cm,$ $\ AD=3.5cm$ である。
(6) 右の図で、$AB=8cm,$ $\ BC=6cm,$ $\ AD=3.5cm$ である。
$\triangle ABC$ ∽$\ \triangle CBD$を証明しなさい。
答え
〈証明〉
$\triangle ABC$ と $\triangle CBD$ で、
仮定から、$AB:BC=8:6=4:3$ ……①
$CB:BD=6:4.5=4:3$ ……②
共通な角だから、$\angle ABC=\angle CBD$ ……③
①②③より、$2$ 組の辺の比とその間の角が等しいので
$\triangle ABC$ ∽$\ \triangle CBD$
 対応する辺や角に注意しましょう。
対応する辺や角に注意しましょう。
相似な図形どうしを、対応する辺や角に注意して、向きをそろえてかいてしまうのがよいです。問題の図の下や横に、こんな感じで図をかき加えてしまいましょう。→
すると、辺や角のいい方のミスが少なくなります。
※$BD=8-3.5=4.5$
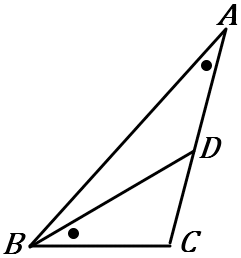 (7) 右の図で、$\angle BAC=\angle DBC$ である。
(7) 右の図で、$\angle BAC=\angle DBC$ である。
$\triangle ABC$ ∽$\ \triangle BDC$を証明しなさい。
答え
〈証明〉
$\triangle ABC$ と $\triangle BDC$ で、
仮定から、$\angle BAC=\angle DBC$ ……①
共通な角だから、$\angle ACB=\angle BCD$ ……②
①②より、$2$ 組の角がそれぞれ等しいので
$\triangle ABC$ ∽$\ \triangle BDC$
 対応する辺や角に注意しましょう。
対応する辺や角に注意しましょう。
相似な図形どうしを、対応する辺や角に注意して、向きをそろえてかいてしまうのがよいです。問題の図の下や横に、こんな感じで図をかき加えてしまいましょう。→
すると、辺や角のいい方のミスが少なくなります。

(8) $\angle A=90^{ \circ }$ の直角三角形で、頂点 $A$ から $BC$ におろした垂線と $BC$ との交点を $D$ とする。
$\triangle ABD$ ∽$\ \triangle CAD$を証明しなさい。
答え
〈証明〉
$\triangle ABD$ と $\triangle CAD$ で、
仮定から、$\angle ADB=\angle CDA$ ……①
$\triangle ABD$ で、
$\angle ABD+\angle BAD+90^{ \circ }=180^{ \circ }$
したがって、$\angle ABD=90^{ \circ }-\angle BAD$ ……②
また、$\angle CAD=90^{ \circ }-\angle BAD$ ……③
②③より、$\angle ABD=\angle CAD$ ……④
①④より、$2$ 組の角がそれぞれ等しいので
$\triangle ABD$ ∽$\ \triangle CAD$
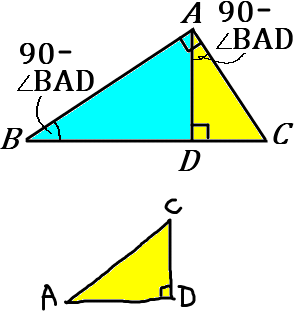 対応する辺や角に注意しましょう。
対応する辺や角に注意しましょう。
相似な図形どうしを、対応する辺や角に注意して、向きをそろえてかいてしまうのがよいです。問題の図の下や横に、こんな感じで図をかき加えてしまいましょう。→
すると、辺や角のいい方のミスが少なくなります。
直角三角形や正方形や長方形で、$\angle ABD=\angle CAD$ であることを証明していくこのパターンは、入試でよく見かけます。どちらも $90^{ \circ }-\angle BAD$ になっている、ということをいえばいいです。できるようにしておきたいパターンです。
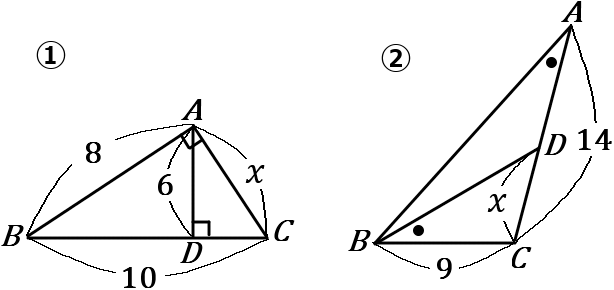
(9)
下の①、②の図で、$x$ の値を求めなさい。ただし、①は $\angle BAC=\angle ADC=90^{ \circ },$ ②は $\angle BAC=\angle DBC$ とする。
答え
① $x=\cfrac{15}{2}$ ② $x=\cfrac{81}{14}$
 どちらも
相似な図形どうしを、対応する辺や角に注意して、向きをそろえてかいてしまうのがよいです。問題の図の下や横に、図をかき加えてしまいましょう。すると、わかりやすくなりますよね。
どちらも
相似な図形どうしを、対応する辺や角に注意して、向きをそろえてかいてしまうのがよいです。問題の図の下や横に、図をかき加えてしまいましょう。すると、わかりやすくなりますよね。
①$\triangle ABC$ ∽$\ \triangle DAC$
\begin{eqnarray*}
8:6&=&10:x\\
4:3&=&10:x\\
4x&=&30\\
x&=&\cfrac{30}{4}=\cfrac{15}{2}
\end{eqnarray*}
②$\triangle ABC$ ∽$\ \triangle BDC$
\begin{eqnarray*}
14:9&=&9:x\\
14x&=&81\\
x&=&\cfrac{81}{14}
\end{eqnarray*}
(10)
下の①~⑤の図で、$x, \ y$ の値を求めなさい。ただし、①~⑤まで、すべて $\ DE /\!/ BC$ とする。

答え
① $x=\cfrac{15}{2}, \ y=\cfrac{16}{3}$
② $x=1.2, \ y=3$
③ $x=6, \ y=16$
④ $x=\cfrac{5}{4}, \ y=\cfrac{15}{2}$
⑤ $x=\cfrac{72}{5}, \ y=\cfrac{25}{3}$
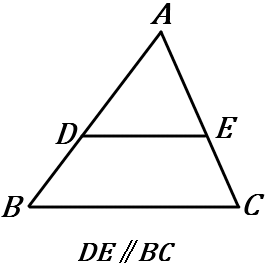 $\triangle ABC$ で、辺 $AB, \ AC$ 上の点をそれぞれ $D, \ E$ とする。
$\triangle ABC$ で、辺 $AB, \ AC$ 上の点をそれぞれ $D, \ E$ とする。
1 $\ DE /\!/ BC$ ならば、
$\quad AD:AB=AE:AC=DE:BC$
2 $\ DE /\!/ BC$ ならば、
$\quad AD:DB=AE:EC$
※すべて上の定理を利用しています。以下のやり方は一例です。このほかにもいろんな式のたて方があります。
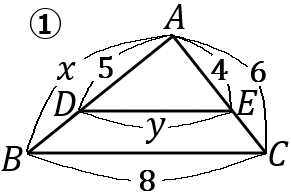 \begin{eqnarray*}
①
5:x&=&4:6\\
5:x&=&2:3\\
2x&=&15\\
x&=&\cfrac{15}{2}
\end{eqnarray*}
\begin{eqnarray*}
y:8&=&4:6\\
y:8&=&2:3\\
3y&=&16\\
y&=&\cfrac{16}{3}
\end{eqnarray*}
\begin{eqnarray*}
①
5:x&=&4:6\\
5:x&=&2:3\\
2x&=&15\\
x&=&\cfrac{15}{2}
\end{eqnarray*}
\begin{eqnarray*}
y:8&=&4:6\\
y:8&=&2:3\\
3y&=&16\\
y&=&\cfrac{16}{3}
\end{eqnarray*}
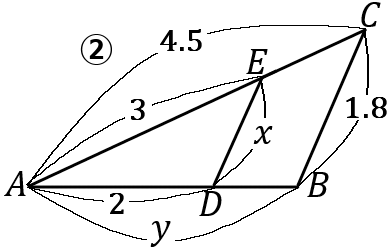 \begin{eqnarray*}
②
3:4.5&=&x:1.8\\
2:3&=&x:1.8\\
3x&=&3.6\\
x&=&1.2
\end{eqnarray*}
\begin{eqnarray*}
3:4.5&=&2:y\\
2:3&=&2:y\\
y&=&3
\end{eqnarray*}
\begin{eqnarray*}
②
3:4.5&=&x:1.8\\
2:3&=&x:1.8\\
3x&=&3.6\\
x&=&1.2
\end{eqnarray*}
\begin{eqnarray*}
3:4.5&=&2:y\\
2:3&=&2:y\\
y&=&3
\end{eqnarray*}
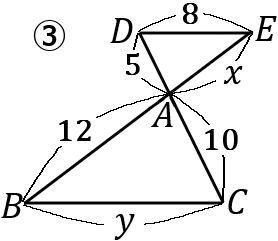 \begin{eqnarray*}
③
5:10&=&x:12\\
10x&=&60\\
x&=&6
\end{eqnarray*}
\begin{eqnarray*}
8:y&=&5:10\\
8:y&=&1:2\\
y&=&16
\end{eqnarray*}
\begin{eqnarray*}
③
5:10&=&x:12\\
10x&=&60\\
x&=&6
\end{eqnarray*}
\begin{eqnarray*}
8:y&=&5:10\\
8:y&=&1:2\\
y&=&16
\end{eqnarray*}
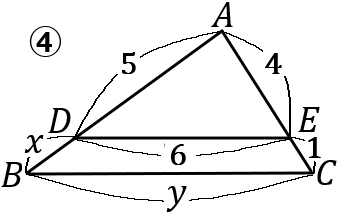 \begin{eqnarray*}
④
5:x&=&4:1\\
4x&=&5\\
x&=&\cfrac{5}{4}
\end{eqnarray*}
\begin{eqnarray*}
6:y&=&4:4+1\\
6:y&=&4:5\\
4y&=&30\\
y&=&\cfrac{30}{4}=\cfrac{15}{2}
\end{eqnarray*}
\begin{eqnarray*}
④
5:x&=&4:1\\
4x&=&5\\
x&=&\cfrac{5}{4}
\end{eqnarray*}
\begin{eqnarray*}
6:y&=&4:4+1\\
6:y&=&4:5\\
4y&=&30\\
y&=&\cfrac{30}{4}=\cfrac{15}{2}
\end{eqnarray*}
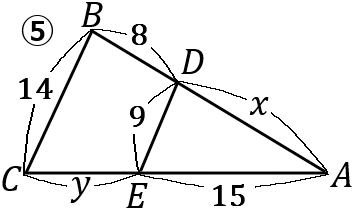 \begin{eqnarray*}
⑤
14:9&=&8+x:x\\
14x&=&9(8+x)\\
14x&=&72+9x\\
14x-9x&=&72\\
5x&=&72\\
x&=&\cfrac{72}{5}
\end{eqnarray*}
\begin{eqnarray*}
14:9&=&y+15:15\\
9(y+15)&=&210\\
9y+135&=&210\\
9y&=&210-135\\
9y&=&75\\
y&=&\cfrac{75}{9}=\cfrac{25}{3}
\end{eqnarray*}
\begin{eqnarray*}
⑤
14:9&=&8+x:x\\
14x&=&9(8+x)\\
14x&=&72+9x\\
14x-9x&=&72\\
5x&=&72\\
x&=&\cfrac{72}{5}
\end{eqnarray*}
\begin{eqnarray*}
14:9&=&y+15:15\\
9(y+15)&=&210\\
9y+135&=&210\\
9y&=&210-135\\
9y&=&75\\
y&=&\cfrac{75}{9}=\cfrac{25}{3}
\end{eqnarray*}
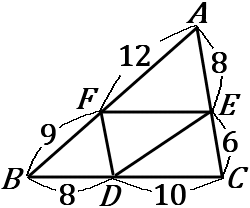 (11) 右の図で、平行な線分の組はどれか。
(11) 右の図で、平行な線分の組はどれか。
答え
$FE$ と $BC$
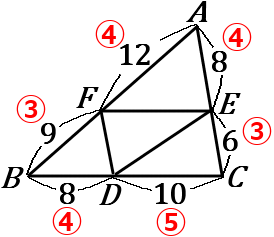 それぞれの比をもっとも簡単な整数比になおして、マルつきの数字で書きくわえてしまうのがよいです。
それぞれの比をもっとも簡単な整数比になおして、マルつきの数字で書きくわえてしまうのがよいです。
$AF:FB=12:9=4:3$
$BD:DC=8:10=4:5$
$AE:EC=8:6=4:3$
$AF:FB=AE:EC$ なので、$\ FE /\!/ BC$
(12)
下の①、②の図で、$x$ の値を求めなさい。ただし、$\angle BAD=\angle CAD$ とする。

答え
① $x=6$ ② $x=\cfrac{9}{2}$
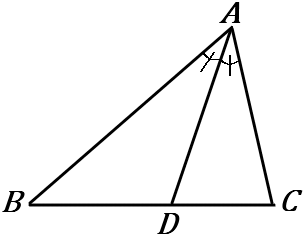 $\triangle ABC$ で、$\angle A$ の二等分線と辺 $BC$ との交点を $D$ とすると、
$\triangle ABC$ で、$\angle A$ の二等分線と辺 $BC$ との交点を $D$ とすると、
$\quad AB:AC=BD:CD$
上の定理を利用します。
 ①
\begin{eqnarray*}
6:9&=&4:x\\
2:3&=&4:x\\
2x&=&12\\
x&=&6
\end{eqnarray*}
①
\begin{eqnarray*}
6:9&=&4:x\\
2:3&=&4:x\\
2x&=&12\\
x&=&6
\end{eqnarray*}
 ②
\begin{eqnarray*}
x:6&=&3:4\\
4x&=&18\\
x&=&\cfrac{18}{4}=\cfrac{9}{2}
\end{eqnarray*}
②
\begin{eqnarray*}
x:6&=&3:4\\
4x&=&18\\
x&=&\cfrac{18}{4}=\cfrac{9}{2}
\end{eqnarray*}
(13)
下の①,③の図で、$x$ の値を求めなさい。②の図で、$x, \ y$ の値を求めなさい。ただし、どの図も$\ l /\!/ m /\!/ n$ とする。
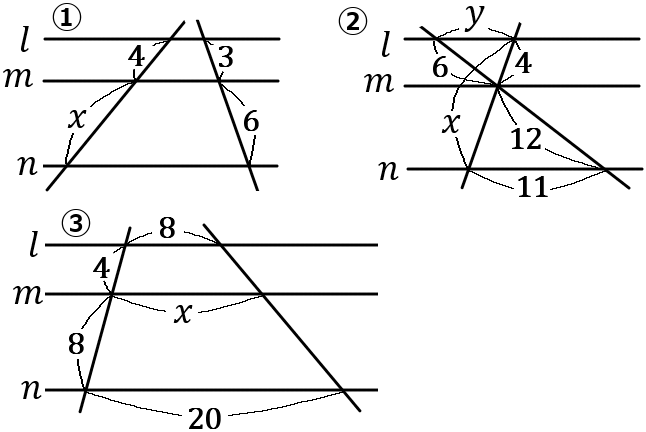
答え
① $x=8$ ② $x=12, \ y=\cfrac{11}{2}$ ③$x=12$
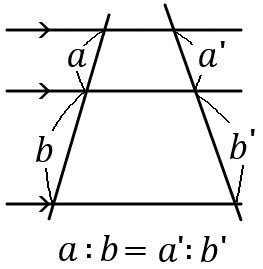 $3$ つ以上の平行線に、$1$ つの直線がどのように交わっても、その直線は平行線によって一定の比に分けられる。
$3$ つ以上の平行線に、$1$ つの直線がどのように交わっても、その直線は平行線によって一定の比に分けられる。
 ①
\begin{eqnarray*}
4:x&=&3:6\\
4:x&=&1:2\\
x&=&8
\end{eqnarray*}
①
\begin{eqnarray*}
4:x&=&3:6\\
4:x&=&1:2\\
x&=&8
\end{eqnarray*}
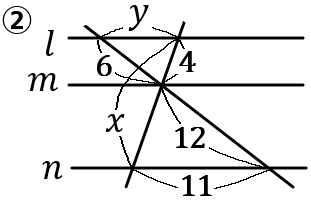 ②
\begin{eqnarray*}
6:12&=&4:x-4\\
1:2&=&4:x-4\\
x-4&=&8\\
x&=&8+4\\
x&=&12
\end{eqnarray*}
②
\begin{eqnarray*}
6:12&=&4:x-4\\
1:2&=&4:x-4\\
x-4&=&8\\
x&=&8+4\\
x&=&12
\end{eqnarray*}
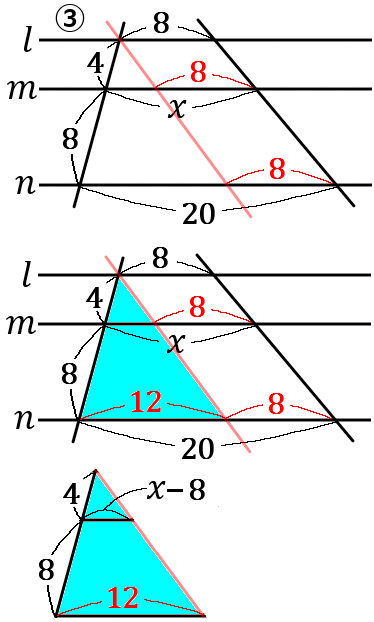 \begin{eqnarray*}
6:12&=&y:11\\
1:2&=&y:11\\
2y&=&11\\
y&=&\cfrac{11}{2}
\end{eqnarray*}
③右の図のように、補助線をひきます。で、青い部分の相似な三角形で式をたてていきます。
\begin{eqnarray*}
4:4+8&=&x-8:12\\
4:12&=&x-8:12\\
1:3&=&x-8:12\\
3(x-8)&=&12\\
3x-24&=&12\\
3x&=&12+24\\
3x&=&36\\
x&=&12
\end{eqnarray*}
\begin{eqnarray*}
6:12&=&y:11\\
1:2&=&y:11\\
2y&=&11\\
y&=&\cfrac{11}{2}
\end{eqnarray*}
③右の図のように、補助線をひきます。で、青い部分の相似な三角形で式をたてていきます。
\begin{eqnarray*}
4:4+8&=&x-8:12\\
4:12&=&x-8:12\\
1:3&=&x-8:12\\
3(x-8)&=&12\\
3x-24&=&12\\
3x&=&12+24\\
3x&=&36\\
x&=&12
\end{eqnarray*}
(14)
下の①,②の図で、$x$ の値を求めなさい。ただし、①の図は $\ AD /\!/ EF /\!/ BC$ , ②の図は $\ AB /\!/ EF /\!/ CD$ とする。
答え
① $x=11$ ② $x=\cfrac{18}{5}$
 ①右の図のように、補助線をひきます。で、青い部分の相似な三角形で式をたてていきます。
\begin{eqnarray*}
8:8+4&=&x-5:9\\
8:12&=&x-5:9\\
2:3&=&x-5:9\\
3(x-5)&=&18\\
3x-15&=&18\\
3x&=&18+15\\
3x&=&33\\
x&=&11
\end{eqnarray*}
①右の図のように、補助線をひきます。で、青い部分の相似な三角形で式をたてていきます。
\begin{eqnarray*}
8:8+4&=&x-5:9\\
8:12&=&x-5:9\\
2:3&=&x-5:9\\
3(x-5)&=&18\\
3x-15&=&18\\
3x&=&18+15\\
3x&=&33\\
x&=&11
\end{eqnarray*}
 ②$\triangle EAB$ ∽$\ \triangle EDC$ (青いところ)で、その相似比は $6:9=2:3$ です。なので、$BE:EC=2:3$ です。
②$\triangle EAB$ ∽$\ \triangle EDC$ (青いところ)で、その相似比は $6:9=2:3$ です。なので、$BE:EC=2:3$ です。
この比を、$\triangle BEF$ ∽$\ \triangle BCD$ (黄色いところ)に使って $x$ を求めていきます。
\begin{eqnarray*}
2:2+3&=&x:9\\
2:5&=&x:9\\
5x&=&18\\
x&=&\cfrac{18}{5}
\end{eqnarray*}
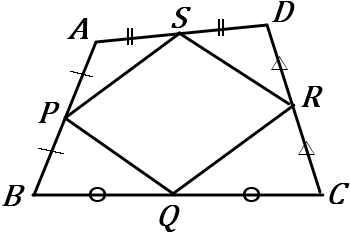
(15) 右の図で、線分 $AB,$ $BC,$ $CD,$ $DA$ の中点をそれぞれ $P,Q,R,S$ とする。四角形 $PQRS$ は平行四辺形となることを証明しなさい。
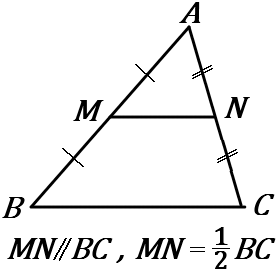 三角形の $2$ つの辺の中点を結ぶ線分は、残りの辺に平行で、長さはその半分である。
三角形の $2$ つの辺の中点を結ぶ線分は、残りの辺に平行で、長さはその半分である。
答え
〈証明〉
$B$ と $D$ を結ぶ。
$\triangle ABD$ で、中点連結定理より、
$\quad PS /\!/ BD, \ PS=\cfrac{1}{2}BD$ …①
$\triangle CBD$ で、中点連結定理より、
$\quad QR /\!/ BD, \ QR=\cfrac{1}{2}BD$ …②
四角形 $PQRS$ で、①②より、
$\quad PS /\!/ QR, \ PS=QR$
$1$ 組の対辺が平行で長さが等しいので、
四角形 $PQRS$ は平行四辺形である。
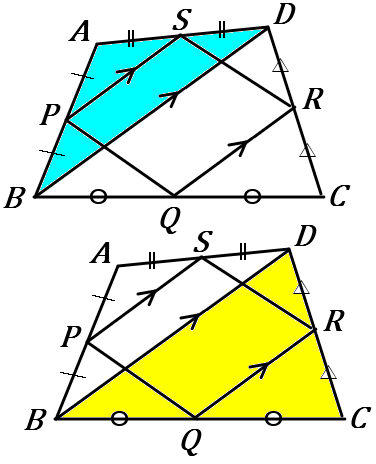 中点連結定理を使った証明です。
中点連結定理を使った証明です。
青い三角形で、$\quad PS /\!/ BD, \ PS=\cfrac{1}{2}BD$
黄色い三角形で、$\quad QR /\!/ BD, \ QR=\cfrac{1}{2}BD$
したがって $\quad PS /\!/ QR, \ PS=QR$ となります。
平行四辺形になるための条件は $4$つありましたね(定義をふくめれば $5$つ)。その最後のやつです。「$1$ 組の対辺が平行で長さが等しい」。これでうまくいきます。

(16) 右の図で、$x$ の値を求めなさい。ただし、$AD=DE=EB, \ AF=FC$ とする。
答え
$x=9$
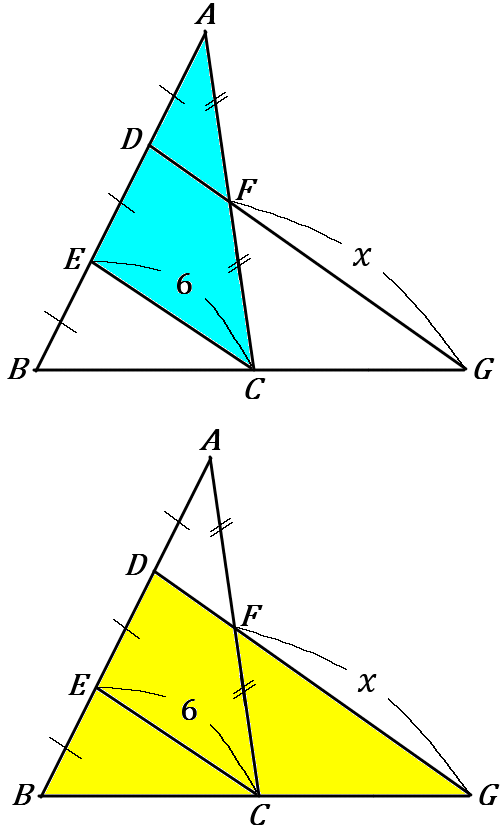 $\triangle AEC$ で、$AD:DE=AF:FC=1:1$
$\triangle AEC$ で、$AD:DE=AF:FC=1:1$
中点連結定理より、$DF=\cfrac{1}{2}EC=3$ …①
また、$DF /\!/ EC, \ DE:EB=1:1$ だから、$BC:CG=1:1$
$\triangle DBG$ で、中点連結定理より、
$DG=2EC=12$ …②
①②より、$x=DG-DF=12-3=9$
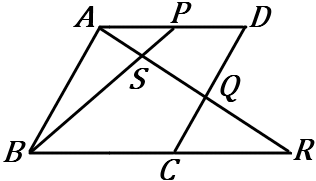
(17) 右の平行四辺形$ABCD$ で、$AP=PD, \ DQ:QC=5:4$ とする。
$AS:SR$ の比を求めなさい。
答え
$5:18$
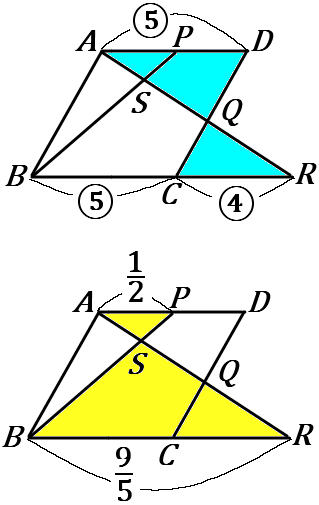 $\triangle QAD$ ∽$\ \triangle QRC$ です。
$\triangle QAD$ ∽$\ \triangle QRC$ です。
相似比は $5:4$ なので、$AD:CR=5:4$です。
$AD=BC$ なので、$BR=\cfrac{9}{5}BC$ です。
$\triangle SAP$ ∽$\ \triangle SRB$ です。
$AP=PD$ だから、$AP=\cfrac{1}{2}AD$ です。
なので、$AP:BR=\cfrac{1}{2}:\cfrac{9}{5}=5:18$
$AP:BR=AS:AR$ だから、$AS:SR=5:18$
(18)
相似な図形の面積の比
① 相似比が $m:n$ である $2$つの図形の面積の比は、 $ \boxed{\LARGE\phantom{hogeho}}$ である。
相似な立体の表面積の比
② 相似比が $m:n$ である $2$つの立体の表面積の比は、 $ \boxed{\LARGE\phantom{hogeho}}$ である。
相似な立体の体積の比
③ 相似比が $m:n$ である $2$つの立体の体積の比は、 $ \boxed{\LARGE\phantom{hogeho}}$ である。
答え
①$m^2:n^2$ ②$m^2:n^2$ ③$m^3:n^3$
(19) 右の図で、$\triangle ABC$ ∽$\ \triangle DEF$ であり、その相似比は $2:3$ である。
$\triangle ABC$ の面積が $16cm^2$ のとき、$\triangle DEF$ の面積を求めなさい。
答え
$36cm^2$
$\triangle DEF$ の面積を $x$ とすると、 \begin{eqnarray*} 2^2:3^2&=&16:x\\ 4:9&=&16:x\\ 4x&=&9\times16\\ x&=&\cfrac{9\times16}{4}=36 \end{eqnarray*}
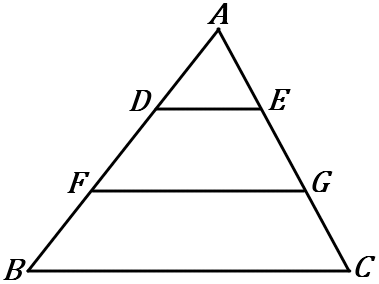
(20) 右の図の $\triangle ABC$ で、$AD=DF=FB, \ DE /\!/ FG /\!/ BC$ である。以下の①~③の問いに答えなさい。
①$\triangle ADE$ と $\triangle AFG$ と $\triangle ABC$ の面積の比をいいなさい。
 ②$\triangle ADE$ の面積を $x$ とする。
②$\triangle ADE$ の面積を $x$ とする。
台形$DFGE$ の面積を $y$ とする。
台形$FBCG$ の面積を $z$ とする。
$x:y:z$ の比を求めなさい。
③$\triangle ABC$ の面積が $12cm^2$ であるとき、台形$FBCG$ の面積を求めなさい。
答え
①$1:4:9$ ②$1:3:5$ ③$\cfrac{20}{3}cm^2$
①仮定から、$\triangle ADE$ ∽$\ \triangle AFG$ ∽$\ \triangle ABC$ です。相似比は $1:2:3$ です。
なので、面積比は $1^2:2^2:3^2=1:4:9$ です。
 ② ①の問題の答えから、$x=1$ とすると、$\triangle AFG$ の面積は $4$ です。また、$\triangle ABC$ の面積は $9$ です。
② ①の問題の答えから、$x=1$ とすると、$\triangle AFG$ の面積は $4$ です。また、$\triangle ABC$ の面積は $9$ です。
なので、
$\quad y=4-1=3$
$\quad z=9-4=5$
なので、$x:y:z=1:3:5$
③台形$FBCG$ の面積は全体($\triangle ABC$)の $\cfrac{5}{9}$ です。なので、
$\quad 12\times \cfrac{5}{9}=\cfrac{20}{3}$
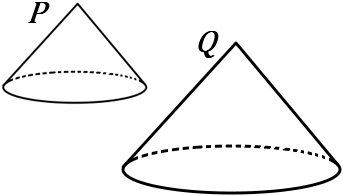
(21) 右の図で、円すい$P$ と円すい$Q$ は相似であり、その相似比は $2:3$ である。以下の①②の問いに答えなさい。
①円すい$P$ の表面積が $24 \large{\pi}$ $cm^2$ のとき、円すい$Q$ の表面積を求めなさい。
②円すい$P$ の体積が $56 \large{\pi}$ $cm^3$ のとき、円すい$Q$ の体積を求めなさい。
答え
①$54 \large{\pi}$ $cm^2$ ②$189 \large{\pi}$ $cm^3$
①$Q$ の表面積を $x$ とすると、 \begin{eqnarray*} 2^2:3^2&=&24 \pi:x\\ 4:9&=&24 \pi:x\\ 4x&=&24 \pi \times 9\\ x&=&\cfrac{24 \pi \times9}{4}=54 \large{\pi} \end{eqnarray*} ②$Q$ の体積を $y$ とすると、 \begin{eqnarray*} 2^3:3^3&=&56 \pi:y\\ 8:27&=&56 \pi:y\\ 8y&=&56 \pi \times 27\\ y&=&\cfrac{56 \pi \times27}{8}=189 \pi \end{eqnarray*}
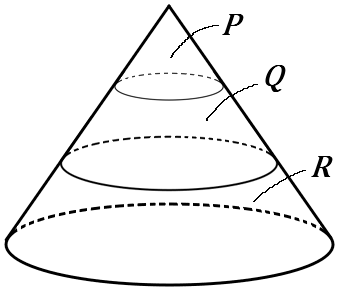
(22) 右の図のように、円すいを、底面に平行で高さを $3$等分する $2$つの平面で切り、$3$つの部分をそれぞれ$P, \ Q, \ R$ とする。以下の①~③の問いに答えなさい。
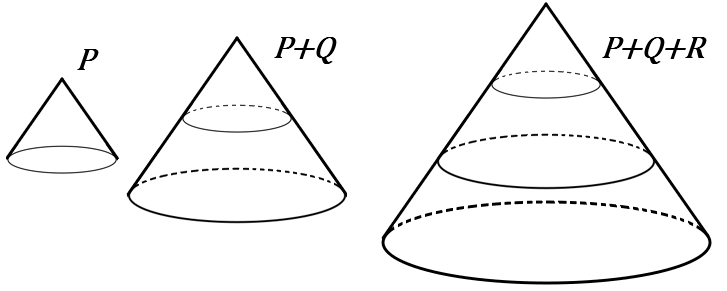
①$P$ と $P+Q$ と$P+Q+R$ の体積の比をいいなさい。
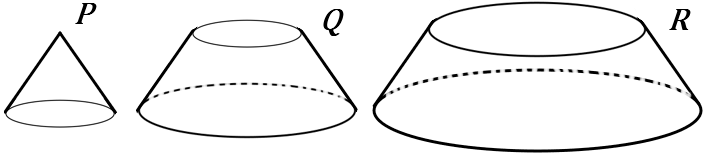
②$P$ の体積を $x$, $Q$ の体積を $y$, $R$ の体積を $z$ とする。
$x:y:z$ の比を求めなさい。
③$P$ の体積が $5 \pi cm^3$ であるとき、$Q$ の体積を求めなさい。
また、$R$ の体積を求めなさい。
答え
①$1:8:27$ ②$1:7:19$ ③$y=35\pi cm^3, \ z=95\pi cm^3$

①$P+Q$ と $P+Q+R$ をそれぞれ底面どうしがぴったり重なるように積み重ねると、仮定から、$P$ ∽ $P+Q$ ∽ $P+Q+R$ です。相似比は $1:2:3$ です。
なので、体積比は $1^3:2^3:3^3=1:8:27$ です。

② ①の問題の答えから、$x=1$ とすると、$P+Q$ の体積は $8$ です。また、$P+Q+R$ の体積は $27$ です。
なので、
$\quad y=8-1=7$
$\quad z=27-8=19$
なので、$x:y:z=1:7:19$
③ ②の問題の答えから、
\begin{eqnarray*}
x:y&=&1:7\\
5\pi:y&=&1:7\\
y&=&35\pi
\end{eqnarray*}
\begin{eqnarray*}
x:z&=&1:19\\
5\pi:z&=&1:19\\
z&=&95\pi
\end{eqnarray*}
答え(中3 5章 相似 第1回)
(1)①線分の比 ②角
(2)$\triangle ABC$ ∽$\triangle DEF$
① $3$ 組の辺の比
② $2$ 組の辺の比が等しく、その間の角
③ $2$ 組の角
(3)$\triangle ABC$ ∽$\triangle HGI$…$2$ 組の角がそれぞれ等しい。
$\triangle DEF$ ∽$\triangle MON$…$2$ 組の辺の比とその間の角が等しい。
$\triangle JKL$ ∽$\triangle QRP$…$3$ 組の辺の比がすべて等しい。
(4)①$\triangle ABC$ ∽$\ \triangle ADE$…$2$ 組の角がそれぞれ等しい。
②$\triangle ABC$ ∽$\triangle EBD$…$2$ 組の角がそれぞれ等しい。
③$\triangle ABC$ ∽$\ \triangle EDC$…$2$ 組の辺の比とその間の角が等しい。
(5)〈証明〉
$\triangle ABC$ と $\triangle DBA$ で、
仮定から、$\angle BAC=\angle BDA$ ……①
共通な角だから、$\angle ABC=\angle DBA$ ……②
①②より、$2$ 組の角がそれぞれ等しいので
$\triangle ABC$ ∽$\ \triangle DBA$
(6)〈証明〉
$\triangle ABC$ と $\triangle CBD$ で、
仮定から、$AB:BC=8:6=4:3$ ……①
$CB:BD=6:4.5=4:3$ ……②
共通な角だから、$\angle ABC=\angle CBD$ ……③
①②③より、$2$ 組の辺の比とその間の角が等しいので
$\triangle ABC$ ∽$\ \triangle CBD$
(7)〈証明〉
$\triangle ABC$ と $\triangle BDC$ で、
仮定から、$\angle BAC=\angle DBC$ ……①
共通な角だから、$\angle ACB=\angle BCD$ ……②
①②より、$2$ 組の角がそれぞれ等しいので
$\triangle ABC$ ∽$\ \triangle BDC$
$\triangle ABD$ と $\triangle CAD$ で、
仮定から、$\angle ADB=\angle CDA$ ……①
$\triangle ABD$ で、
$\angle ABD+\angle BAD+90^{ \circ }=180^{ \circ }$
したがって、$\angle ABD=90^{ \circ }-\angle BAD$ ……②
また、$\angle CAD=90^{ \circ }-\angle BAD$ ……③
②③より、$\angle ABD=\angle CAD$ ……④
①④より、$2$ 組の角がそれぞれ等しいので
$\triangle ABD$ ∽$\ \triangle CAD$
(9)① $x=\cfrac{15}{2}$ ② $x=\cfrac{81}{14}$
(10) ① $x=\cfrac{15}{2}, \ y=\cfrac{16}{3}$
② $x=1.2, \ y=3$
③ $x=6, \ y=16$
④ $x=\cfrac{5}{4}, \ y=\cfrac{15}{2}$
⑤ $x=\cfrac{72}{5}, \ y=\cfrac{25}{3}$
(11) $FE$ と $BC$
(12)① $x=6$ ② $x=\cfrac{9}{2}$
(13)① $x=8$ ② $x=12, \ y=\cfrac{11}{2}$ ③$x=12$
(14)① $x=11$ ② $x=\cfrac{18}{5}$
(15)〈証明〉
$B$ と $D$ を結ぶ。
$\triangle ABD$ で、中点連結定理より、
$\quad PS /\!/ BD, \ PS=\cfrac{1}{2}BD$ …①
$\triangle CBD$ で、中点連結定理より、
$\quad QR /\!/ BD, \ QR=\cfrac{1}{2}BD$ …②
四角形 $PQRS$ で、①②より、
$\quad PS /\!/ QR, \ PS=QR$
$1$ 組の対辺が平行で長さが等しいので、 四角形 $PQRS$ は平行四辺形である。
(16) $x=9$
(17) $5:18$
(18)①$m^2:n^2$ ②$m^2:n^2$ ③$m^3:n^3$
(19) $36cm^2$
(20)①$1:4:9$ ②$1:3:5$ ③$\cfrac{20}{3}cm^2$
(21)①$54 \large{\pi}$ $cm^2$ ②$189 \large{\pi}$ $cm^3$
(22)①$1:8:27$ ②$1:7:19$ ③$y=35\pi cm^3, \ z=95\pi cm^3$