数学 中3 2学期期末模擬テスト 第1回
 ページがちゃんと表示されるまで$10$秒くらいかかります。
ページがちゃんと表示されるまで$10$秒くらいかかります。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
「印刷」をクリックすると同じ内容のpdfファイルが表示されます。また、解答用紙と答えも問題のあとに表示されます。1~6ページが問題、7~8ページが解答用紙、9~10ページが答えです。必要におうじて印刷してください。
問題をクリックすると答えがでます。
ふつうのテストより問題数は多いです。なのでふつうのテストをやるときより時間がかかると思います。がんばって!
$\huge{1}$ 次の①~⑥の計算をしなさい。⑦~⑨の各問いに答えなさい。
$\qquad①$ $\quad -7+2\times5 \qquad ② \quad (-3)\times(-2^2)+6\times(-5)$
答え
$①3$ $②-18$
\begin{eqnarray*} &①& -7+2\times5\\ &=&-7+10\\ &=& 3 \end{eqnarray*} \begin{eqnarray*} \require{cancel} &②& (-3)\times(-2^2)+6\times(-5)\\ &=& (-3)\times(-4)+6\times(-5)\\ &=& 12-30\\ &=& -18 \end{eqnarray*}
$\qquad③$ $-\cfrac{1}{4}+\left(-\cfrac{3}{7}\right)\div\left(-\cfrac{9}{14}\right) \qquad ④ \quad 3(2x+3y)-4(3x-y) $
答え
$③cfrac{5}{12}$ $④-6x+13y$
\begin{eqnarray*} \require{cancel} &③& -\cfrac{1}{4}+\left(-\cfrac{3}{7}\right)\div\left(-\cfrac{9}{14}\right) \\ &=& -\cfrac{1}{4}+\left(-\cfrac{3}{7}\right)\times\left(-\cfrac{14}{9}\right) \\ &=& -\cfrac{1}{4}+\left(-\cfrac{\bcancel{3}}{\bcancel{7}}\right)\times\left(-\cfrac{{}^2\bcancel{14}}{{}^3\bcancel{9}}\right) \\ &=& -\cfrac{1}{4}+\cfrac{2}{3}\\ &=& -\cfrac{3}{12}+\cfrac{8}{12}\\ &=& \cfrac{5}{12} \end{eqnarray*} \begin{eqnarray*} \require{cancel} &④& 3(2x+3y)-4(3x-y)\\ &=& 6x+9y-12x+4y\\ &=& -6x+13y \end{eqnarray*}
$\qquad⑤$ $3\sqrt{6}\div6\sqrt{24}\times3\sqrt{10} \qquad ⑥ \quad -\cfrac{4}{\sqrt{2}}+\sqrt{3}\times\sqrt{6} $
答え
$⑤\cfrac{3\sqrt{10}}{4}$ $⑥\sqrt{2}$
\begin{eqnarray*} \require{cancel} &⑤& 3\sqrt{6}\div6\sqrt{24}\times3\sqrt{10}\\ &=&\cfrac{3\sqrt{6}\times3\sqrt{10}}{6\sqrt{24}}\\ &=&\cfrac{\bcancel{3}\sqrt{\bcancel{6}}\times3\sqrt{\bcancel{10}}}{\bcancel{6}\sqrt{\bcancel{24}}}\\ &=&\cfrac{3\sqrt{5}}{2\sqrt{2}}\\ &=&\cfrac{3\sqrt{10}}{4} \end{eqnarray*} \begin{eqnarray*} \require{cancel} &⑥& -\cfrac{4}{\sqrt{2}}+\sqrt{3}\times\sqrt{6}\\ &=&-\cfrac{4\sqrt{2}}{2}+\sqrt{18}\\ &=&-2\sqrt{2}+3\sqrt{2}\\ &=&\sqrt{2} \end{eqnarray*}
$\qquad$⑦ $x^2-9x+20$ を因数分解しなさい。
答え
$(x-4)(x-5)$
$\qquad$⑧ 連立方程式 $\left\{\begin{array}{l} 5x-4y=5\\ \cfrac{2x+3y}{3}=-7 \end{array}\right.$ を解きなさい。
答え
$x=-3,y=-5$
\begin{eqnarray*} \left\{ \begin{array}{l} 5x-4y=5\qquad…①\\ \cfrac{2x+3y}{3}=-7\qquad…② \end{array} \right. \end{eqnarray*} $②の分母をはらう$ \begin{eqnarray*} \cfrac{2x+3y}{3}&=&-7\quad(両辺に\times3)\\ 2x+3y&=&-21\qquad…③ \end{eqnarray*} $①\times3+③\times4$ \begin{eqnarray*} 15x-12y=\phantom{-}15\\ \underline{+) \quad 8x+12y=-84} \\ 23x\phantom{-12y}=-69\\ x=-3\phantom{1} \end{eqnarray*} \begin{eqnarray*} x=-3を①に代入\\ 5\times(-3)-4y&=&5\\ -15-4y&=&5\\ -4y&=&5+15\\ -4y&=&20\\ y&=&-5 \\ \left\{ \begin{array}{l} x=-3\\ y=-5 \end{array} \right. \end{eqnarray*}
$\qquad$⑨ $2$ 次方程式 $x^2-2x-2=0$ を解きなさい。
答え
$x=1\pm\sqrt{3}$
\begin{eqnarray*} x^2&-&2x-2=0\\ &2&次方程式の解の公式により\\ x&=&\cfrac{-(-2)\pm\sqrt{(-2)^2-4\times1\times(-2)}}{2\times1}\\ &=&\cfrac{2\pm\sqrt{4+8}}{2}\\ &=&\cfrac{2\pm\sqrt{12}}{2}\\ &=&\cfrac{2\pm2\sqrt{3}}{2}\\ &=&1\pm\sqrt{3} \end{eqnarray*}
$\huge{2}$ 次の①~③の各問いに答えなさい。
$①$ $x$ と $y$ の関係が $y=ax^2$ で表され、$x=2$ のとき $y=-\cfrac{4}{3}$ である。$x=-3$ のときの $y$ の値を求めなさい。
答え
$y=-3$
$y=ax^2$ に $x=2$ , $y=-\cfrac{4}{3}$ を代入すると、
\begin{eqnarray*}
-\cfrac{4}{3}&=&a×(2)^2\\
-\cfrac{4}{3}&=&4a\qquad\qquad(\times3)\\
-4&=&12a\\
-\cfrac{4}{12}&=&a\\
-\cfrac{1}{3}&=&a
\end{eqnarray*}
これで $a=-\cfrac{1}{3}$ というふうに、 $a$ が求められました。$y=ax^2$ に $a=-\cfrac{1}{3}$ を代入して、
$$y=-\cfrac{1}{3}x^2$$
この式に $x=-3$ を代入して、
$y=-\cfrac{1}{3}×(-3)^2=-\cfrac{1}{3}×9=-3$
$②$ 関数 $y=ax^2$ について、$x$ の値が $-6$ から $3$ まで増加するときの、変化の割合が $-12$ である。$a$ の値を求めなさい。
答え
$a=4$
関数 $y=ax^2$ について、$x$ の値が $p$ から $q$ まで増加するときの変化の割合は $$(p+q)\times a=変化の割合$$ を利用します。この問題の場合は、 $$(-6+3)\times a=-12$$ となります。あとはこれを解くだけ。 \begin{eqnarray*} (-6+3)\times a&=&-12\\ -3a&=&-12\\ a&=&4 \end{eqnarray*}
$③$ 関数 $y=2x^2$ について、$x$ の変域が $-3 \leqq x \leqq 2$ のとき、$y$ の変域を求めなさい。
答え
$0 \leqq y \leqq 18$
「関数 $y=ax^2$ について、$x$ の変域が $p \leqq x \leqq q$ のとき、$y$ の変域を求めなさい」ときかれたら、
<手順①>まず $p \leqq x \leqq q$ が $0$ をまたいでいるかを確認します。この問題の場合は、 $-3 \leqq x \leqq 2$ なのでまたいでいます。
<手順②>またいでいるときは、 $y=ax^2$ の $a$ の符号を確認します。
$a$ がプラスの時は、答えの形は $0 \leqq y \leqq 〇$ です。
$a$ がマイナスの時は、答えの形は $〇 \leqq y \leqq 0$ です。
〇のところには数がはいります。
この問題の場合は、$a$ はプラスです。
<手順③>〇のところにはいる数は、 $p \leqq x \leqq q$ の $p$ と $q$ のうち、$0$ から遠いほうを $y=ax^2$ の $x$ に代入してでてきた数です。
この問題の場合は、$-3 \leqq x \leqq 2$ ですから $0$ から遠いのは $-3$ です。$-3$ を $y=2x^2$ の $x$ に代入して、
$$y=2\times(-3)^2=18$$
なので答えは
$$0 \leqq y \leqq 18$$
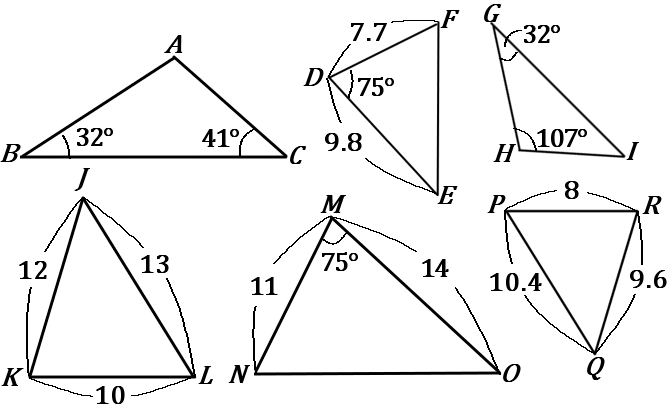
$\huge{3}$ 下の図のなかから、相似な三角形の組を見つけ、記号 ∽ を使って表しなさい。また、そのときに使った相似条件をいいなさい。
答え
$\triangle ABC$ ∽$\triangle HGI$…$2$ 組の角がそれぞれ等しい。
$\triangle DEF$ ∽$\triangle MON$…$2$ 組の辺の比とその間の角が等しい。
$\triangle JKL$ ∽$\triangle QRP$…$3$ 組の辺の比がすべて等しい。
対応する辺や角に注意する。
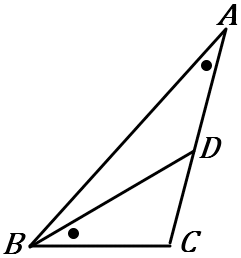 $\huge{4}$ 右の図で、$\angle BAC=\angle DBC$ である。
$\huge{4}$ 右の図で、$\angle BAC=\angle DBC$ である。
$\triangle ABC$ ∽$\ \triangle BDC$を証明しなさい。
答え
〈証明〉
$\triangle ABC$ と $\triangle BDC$ で、
仮定から、$\angle BAC=\angle DBC$ ……①
共通な角だから、$\angle ACB=\angle BCD$ ……②
①②より、$2$ 組の角がそれぞれ等しいので
$\triangle ABC$ ∽$\ \triangle BDC$
 対応する辺や角に注意しましょう。
対応する辺や角に注意しましょう。
相似な図形どうしを、対応する辺や角に注意して、向きをそろえてかいてしまうのがよいです。問題の図の下や横に、こんな感じで図をかき加えてしまいましょう。→
すると、辺や角のいい方のミスが少なくなります。
$\huge{5}$ 下の①~⑤の図で、$x, \ y$ の値を求めなさい。ただし、①~⑤まで、すべて $\ DE /\!/ BC$ とする。

答え
① $x=\cfrac{15}{2}, \ y=\cfrac{16}{3}$
② $x=1.2, \ y=3$
③ $x=6, \ y=16$
④ $x=\cfrac{5}{4}, \ y=\cfrac{15}{2}$
⑤ $x=\cfrac{72}{5}, \ y=\cfrac{25}{3}$
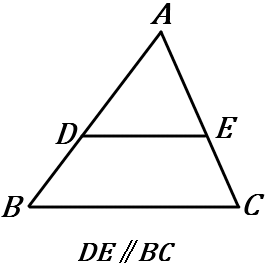 $\triangle ABC$ で、辺 $AB, \ AC$ 上の点をそれぞれ $D, \ E$ とする。
$\triangle ABC$ で、辺 $AB, \ AC$ 上の点をそれぞれ $D, \ E$ とする。
1 $\ DE /\!/ BC$ ならば、
$\quad AD:AB=AE:AC=DE:BC$
2 $\ DE /\!/ BC$ ならば、
$\quad AD:DB=AE:EC$
※すべて上の定理を利用しています。以下のやり方は一例です。このほかにもいろんな式のたて方があります。
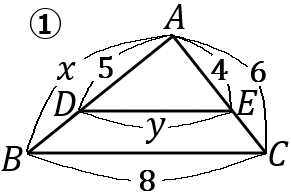 \begin{eqnarray*}
①
5:x&=&4:6\\
5:x&=&2:3\\
2x&=&15\\
x&=&\cfrac{15}{2}
\end{eqnarray*}
\begin{eqnarray*}
y:8&=&4:6\\
y:8&=&2:3\\
3y&=&16\\
y&=&\cfrac{16}{3}
\end{eqnarray*}
\begin{eqnarray*}
①
5:x&=&4:6\\
5:x&=&2:3\\
2x&=&15\\
x&=&\cfrac{15}{2}
\end{eqnarray*}
\begin{eqnarray*}
y:8&=&4:6\\
y:8&=&2:3\\
3y&=&16\\
y&=&\cfrac{16}{3}
\end{eqnarray*}
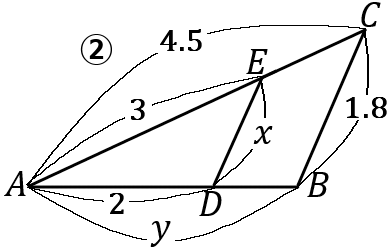 \begin{eqnarray*}
②
3:4.5&=&x:1.8\\
2:3&=&x:1.8\\
3x&=&3.6\\
x&=&1.2
\end{eqnarray*}
\begin{eqnarray*}
3:4.5&=&2:y\\
2:3&=&2:y\\
y&=&3
\end{eqnarray*}
\begin{eqnarray*}
②
3:4.5&=&x:1.8\\
2:3&=&x:1.8\\
3x&=&3.6\\
x&=&1.2
\end{eqnarray*}
\begin{eqnarray*}
3:4.5&=&2:y\\
2:3&=&2:y\\
y&=&3
\end{eqnarray*}
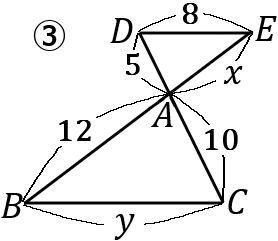 \begin{eqnarray*}
③
5:10&=&x:12\\
10x&=&60\\
x&=&6
\end{eqnarray*}
\begin{eqnarray*}
8:y&=&5:10\\
8:y&=&1:2\\
y&=&16
\end{eqnarray*}
\begin{eqnarray*}
③
5:10&=&x:12\\
10x&=&60\\
x&=&6
\end{eqnarray*}
\begin{eqnarray*}
8:y&=&5:10\\
8:y&=&1:2\\
y&=&16
\end{eqnarray*}
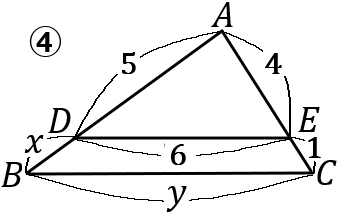 \begin{eqnarray*}
④
5:x&=&4:1\\
4x&=&5\\
x&=&\cfrac{5}{4}
\end{eqnarray*}
\begin{eqnarray*}
6:y&=&4:4+1\\
6:y&=&4:5\\
4y&=&30\\
y&=&\cfrac{30}{4}=\cfrac{15}{2}
\end{eqnarray*}
\begin{eqnarray*}
④
5:x&=&4:1\\
4x&=&5\\
x&=&\cfrac{5}{4}
\end{eqnarray*}
\begin{eqnarray*}
6:y&=&4:4+1\\
6:y&=&4:5\\
4y&=&30\\
y&=&\cfrac{30}{4}=\cfrac{15}{2}
\end{eqnarray*}
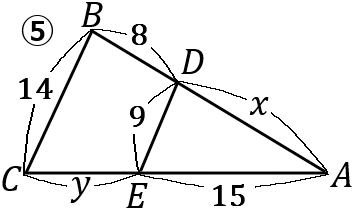 \begin{eqnarray*}
⑤
14:9&=&8+x:x\\
14x&=&9(8+x)\\
14x&=&72+9x\\
14x-9x&=&72\\
5x&=&72\\
x&=&\cfrac{72}{5}
\end{eqnarray*}
\begin{eqnarray*}
14:9&=&y+15:15\\
9(y+15)&=&210\\
9y+135&=&210\\
9y&=&210-135\\
9y&=&75\\
y&=&\cfrac{75}{9}=\cfrac{25}{3}
\end{eqnarray*}
\begin{eqnarray*}
⑤
14:9&=&8+x:x\\
14x&=&9(8+x)\\
14x&=&72+9x\\
14x-9x&=&72\\
5x&=&72\\
x&=&\cfrac{72}{5}
\end{eqnarray*}
\begin{eqnarray*}
14:9&=&y+15:15\\
9(y+15)&=&210\\
9y+135&=&210\\
9y&=&210-135\\
9y&=&75\\
y&=&\cfrac{75}{9}=\cfrac{25}{3}
\end{eqnarray*}
$\huge{6}$
下の①、②の図で、$x$ の値を求めなさい。ただし、$\angle BAD=\angle CAD$ とする。

答え
① $x=6$ ② $x=\cfrac{9}{2}$
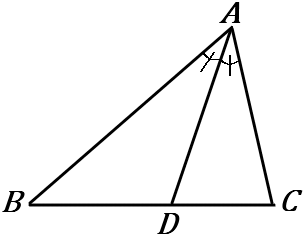 $\triangle ABC$ で、$\angle A$ の二等分線と辺 $BC$ との交点を $D$ とすると、
$\triangle ABC$ で、$\angle A$ の二等分線と辺 $BC$ との交点を $D$ とすると、
$\quad AB:AC=BD:CD$
上の定理を利用します。
 ①
\begin{eqnarray*}
6:9&=&4:x\\
2:3&=&4:x\\
2x&=&12\\
x&=&6
\end{eqnarray*}
①
\begin{eqnarray*}
6:9&=&4:x\\
2:3&=&4:x\\
2x&=&12\\
x&=&6
\end{eqnarray*}
 ②
\begin{eqnarray*}
x:6&=&3:4\\
4x&=&18\\
x&=&\cfrac{18}{4}=\cfrac{9}{2}
\end{eqnarray*}
②
\begin{eqnarray*}
x:6&=&3:4\\
4x&=&18\\
x&=&\cfrac{18}{4}=\cfrac{9}{2}
\end{eqnarray*}
$\huge{7}$
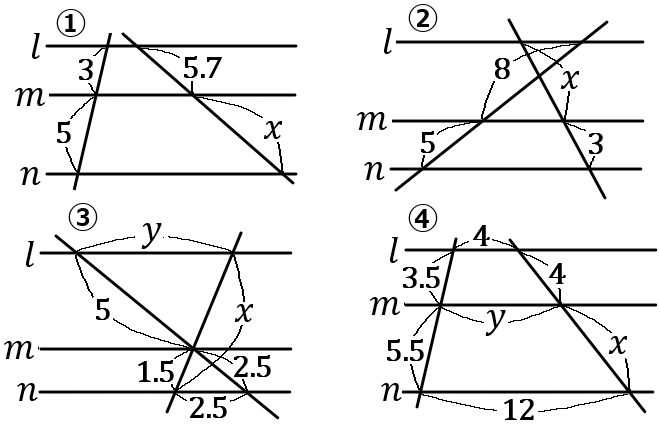
下の①,②の図で、$x$ の値を求めなさい。③,④の図で、$x, \ y$ の値を求めなさい。ただし、どの図も$\ l /\!/ m /\!/ n$ とする。
答え
① $x=9.5$ ② $x=\cfrac{24}{5}$ ③ $x=4.5, \ y=5$ ④$x=\cfrac{44}{7}, \ y=\cfrac{64}{9}$
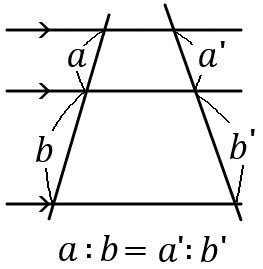 $3$ つ以上の平行線に、$1$ つの直線がどのように交わっても、その直線は平行線によって一定の比に分けられる。
$3$ つ以上の平行線に、$1$ つの直線がどのように交わっても、その直線は平行線によって一定の比に分けられる。
 ①
\begin{eqnarray*}
3:5&=&5.7:x\\
3x&=&5.7\times5\\
x&=&\cfrac{5.7\times5}{3}=9.5
\end{eqnarray*}
①
\begin{eqnarray*}
3:5&=&5.7:x\\
3x&=&5.7\times5\\
x&=&\cfrac{5.7\times5}{3}=9.5
\end{eqnarray*}
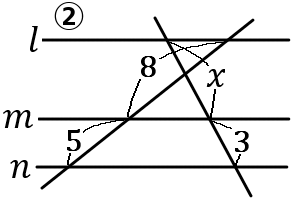 ②
\begin{eqnarray*}
8:5&=&x:3\\
5x&=&24\\
x&=&\cfrac{24}{5}
\end{eqnarray*}
②
\begin{eqnarray*}
8:5&=&x:3\\
5x&=&24\\
x&=&\cfrac{24}{5}
\end{eqnarray*}
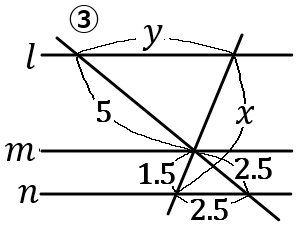 ③
\begin{eqnarray*}
5:2.5&=&x-1.5:1.5\\
2:1&=&x-1.5:1.5\\
x-1.5&=&3\\
x&=&3+1.5\\
x&=&4.5
\end{eqnarray*}
\begin{eqnarray*}
5:2.5&=&y:2.5\\
y&=&5
\end{eqnarray*}
③
\begin{eqnarray*}
5:2.5&=&x-1.5:1.5\\
2:1&=&x-1.5:1.5\\
x-1.5&=&3\\
x&=&3+1.5\\
x&=&4.5
\end{eqnarray*}
\begin{eqnarray*}
5:2.5&=&y:2.5\\
y&=&5
\end{eqnarray*}
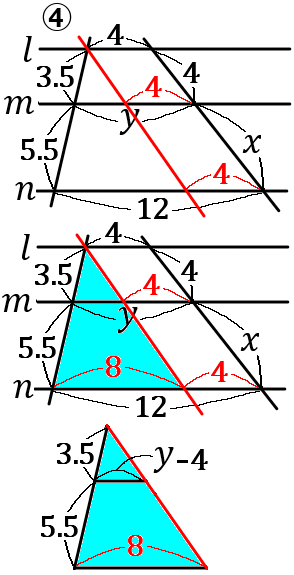 ④
\begin{eqnarray*}
3.5:5.5&=&4:x\\
7:11&=&4:x\\
7x&=&44\\
x&=&\cfrac{44}{7}
\end{eqnarray*}
〈$y$ の求め方〉
右の図のように、補助線をひきます。で、青い部分の相似な三角形で式をたてていきます。
\begin{eqnarray*}
3.5:3.5+5.5&=&y-4:12-4\\
3.5:9&=&y-4:8\\
9(y-4)&=&28\\
9y-36&=&28\\
9y&=&28+36\\
9y&=&64\\
y&=&\cfrac{64}{9}
\end{eqnarray*}
④
\begin{eqnarray*}
3.5:5.5&=&4:x\\
7:11&=&4:x\\
7x&=&44\\
x&=&\cfrac{44}{7}
\end{eqnarray*}
〈$y$ の求め方〉
右の図のように、補助線をひきます。で、青い部分の相似な三角形で式をたてていきます。
\begin{eqnarray*}
3.5:3.5+5.5&=&y-4:12-4\\
3.5:9&=&y-4:8\\
9(y-4)&=&28\\
9y-36&=&28\\
9y&=&28+36\\
9y&=&64\\
y&=&\cfrac{64}{9}
\end{eqnarray*}
$\huge{8}$
下の①,②の図で、$x$ の値を求めなさい。ただし、①の図は $\ AD /\!/ EF /\!/ BC$ , ②の図は $\ AB /\!/ EF /\!/ CD$ とする。
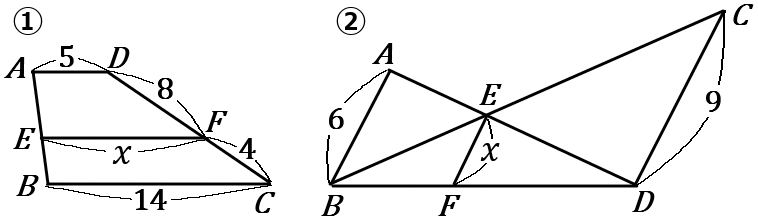
答え
① $x=11$ ② $x=\cfrac{18}{5}$
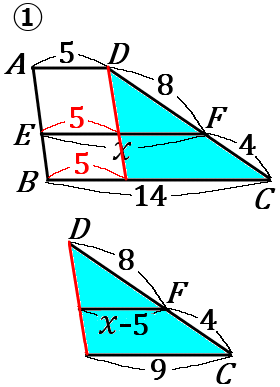 ①右の図のように、補助線をひきます。で、青い部分の相似な三角形で式をたてていきます。
\begin{eqnarray*}
8:8+4&=&x-5:9\\
8:12&=&x-5:9\\
2:3&=&x-5:9\\
3(x-5)&=&18\\
3x-15&=&18\\
3x&=&18+15\\
3x&=&33\\
x&=&11
\end{eqnarray*}
①右の図のように、補助線をひきます。で、青い部分の相似な三角形で式をたてていきます。
\begin{eqnarray*}
8:8+4&=&x-5:9\\
8:12&=&x-5:9\\
2:3&=&x-5:9\\
3(x-5)&=&18\\
3x-15&=&18\\
3x&=&18+15\\
3x&=&33\\
x&=&11
\end{eqnarray*}
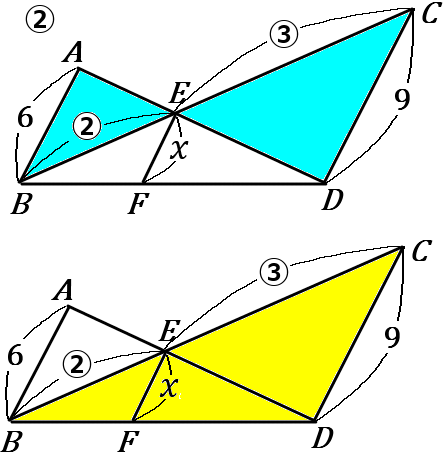 ②$\triangle EAB$ ∽$\ \triangle EDC$ (青いところ)で、その相似比は $6:9=2:3$ です。なので、$BE:EC=2:3$ です。
②$\triangle EAB$ ∽$\ \triangle EDC$ (青いところ)で、その相似比は $6:9=2:3$ です。なので、$BE:EC=2:3$ です。
この比を、$\triangle BEF$ ∽$\ \triangle BCD$ (黄色いところ)に使って $x$ を求めていきます。
\begin{eqnarray*}
2:2+3&=&x:9\\
2:5&=&x:9\\
5x&=&18\\
x&=&\cfrac{18}{5}
\end{eqnarray*}
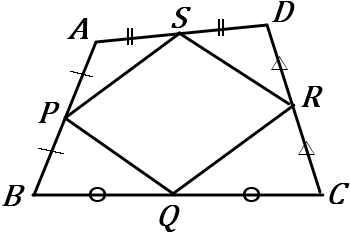
$\huge{9}$ 右の図で、線分 $AB,$ $BC,$ $CD,$ $DA$ の中点をそれぞれ $P,Q,R,S$ とする。四角形 $PQRS$ は平行四辺形となることを証明しなさい。
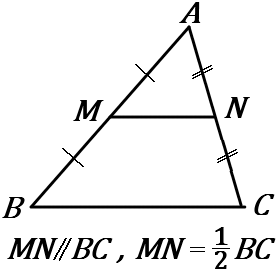 三角形の $2$ つの辺の中点を結ぶ線分は、残りの辺に平行で、長さはその半分である。
三角形の $2$ つの辺の中点を結ぶ線分は、残りの辺に平行で、長さはその半分である。
答え
〈証明〉
$B$ と $D$ を結ぶ。
$\triangle ABD$ で、中点連結定理より、
$\quad PS /\!/ BD, \ PS=\cfrac{1}{2}BD$ …①
$\triangle CBD$ で、中点連結定理より、
$\quad QR /\!/ BD, \ QR=\cfrac{1}{2}BD$ …②
四角形 $PQRS$ で、①②より、
$\quad PS /\!/ QR, \ PS=QR$
$1$ 組の対辺が平行で長さが等しいので、
四角形 $PQRS$ は平行四辺形である。
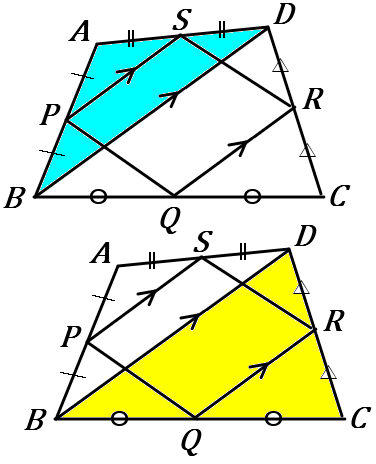 中点連結定理を使った証明です。
中点連結定理を使った証明です。
青い三角形で、$\quad PS /\!/ BD, \ PS=\cfrac{1}{2}BD$
黄色い三角形で、$\quad QR /\!/ BD, \ QR=\cfrac{1}{2}BD$
したがって $\quad PS /\!/ QR, \ PS=QR$ となります。
平行四辺形になるための条件は $4$つありましたね(定義をふくめれば $5$つ)。その最後のやつです。「$1$ 組の対辺が平行で長さが等しい」。これでうまくいきます。

$\huge{10}$ 右の図で、$x$ の値を求めなさい。ただし、$AD=DE=EB, \ AF=FC$ とする。
答え
$x=9$
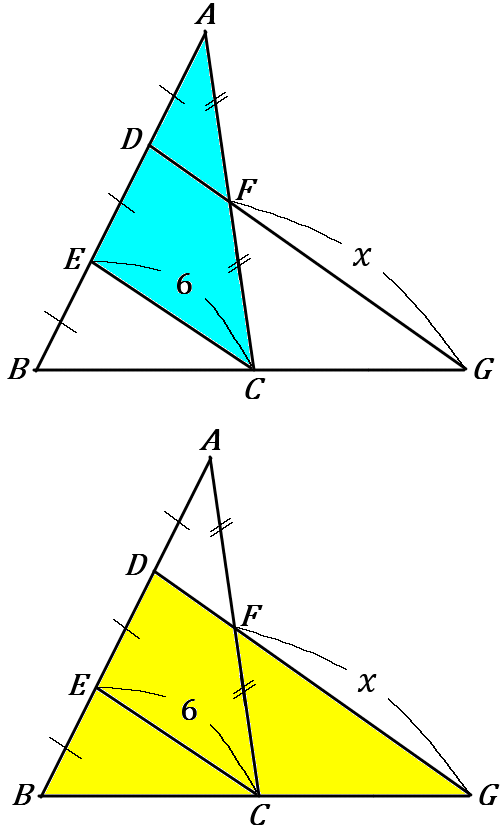 $\triangle AEC$ で、$AD:DE=AF:FC=1:1$
$\triangle AEC$ で、$AD:DE=AF:FC=1:1$
中点連結定理より、$DF=\cfrac{1}{2}EC=3$ …①
また、$DF /\!/ EC, \ DE:EB=1:1$ だから、$BC:CG=1:1$
$\triangle DBG$ で、中点連結定理より、
$DG=2EC=12$ …②
①②より、$x=DG-DF=12-3=9$
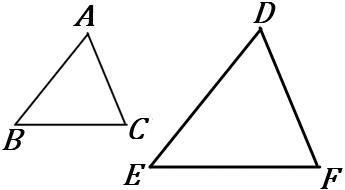
$\huge{11}$ 右の図で、$\triangle ABC$ ∽$\ \triangle DEF$ であり、その相似比は $2:3$ である。
$\triangle ABC$ の面積が $16cm^2$ のとき、$\triangle DEF$ の面積を求めなさい。
相似比が $m:n$ である $2$ つの図形の面積の比は、$m^2:n^2$ である。
答え
$36cm^2$
$\triangle DEF$ の面積を $x$ とすると、 \begin{eqnarray*} 2^2:3^2&=&16:x\\ 4:9&=&16:x\\ 4x&=&9\times16\\ x&=&\cfrac{9\times16}{4}=36 \end{eqnarray*}
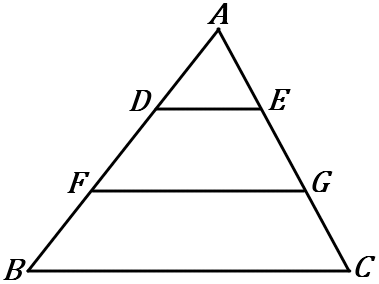
$\huge{12}$ 右の図の $\triangle ABC$ で、$AD=DF=FB, \ DE /\!/ FG /\!/ BC$ である。以下の①~③の問いに答えなさい。
①$\triangle ADE$ と $\triangle AFG$ と $\triangle ABC$ の面積の比をいいなさい。
相似比が $m:n$ である $2$ つの図形の面積の比は、$m^2:n^2$ である。
答え
$1:4:9$
仮定から、$\triangle ADE$ ∽$\ \triangle AFG$ ∽$\ \triangle ABC$ です。相似比は $1:2:3$ です。
なので、面積比は $1^2:2^2:3^2=1:4:9$ です。
 $②$ $\triangle ADE$ の面積を $x$ とする。
$②$ $\triangle ADE$ の面積を $x$ とする。
台形$DFGE$ の面積を $y$ とする。
台形$FBCG$ の面積を $z$ とする。
$x:y:z$ の比を求めなさい。
答え
$1:3:5$
 ①の問題の答えから、$x=1$ とすると、$\triangle AFG$ の面積は $4$ です。また、$\triangle ABC$ の面積は $9$ です。
①の問題の答えから、$x=1$ とすると、$\triangle AFG$ の面積は $4$ です。また、$\triangle ABC$ の面積は $9$ です。
なので、
$\quad y=4-1=3$
$\quad z=9-4=5$
なので、$x:y:z=1:3:5$
$③$ $\triangle ABC$ の面積が $12cm^2$ であるとき、台形$FBCG$ の面積を求めなさい。
答え
$\cfrac{20}{3}cm^2$
台形$FBCG$ の面積は全体($\triangle ABC$)の $\cfrac{5}{9}$ です。なので、
$\quad 12\times \cfrac{5}{9}=\cfrac{20}{3}$
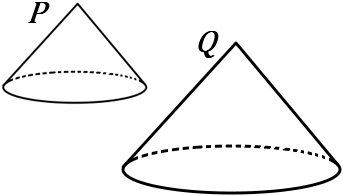
$\huge{13}$ 右の図で、円すい$P$ と円すい$Q$ は相似であり、その相似比は $2:3$ である。以下の①②の問いに答えなさい。
①円すい$P$ の表面積が $24 \large{\pi}$ $cm^2$ のとき、円すい$Q$ の表面積を求めなさい。
相似比が $m:n$ である $2$ つの立体の表面積の比は、$m^2:n^2$ である。
答え
$54 \large{\pi}$ $cm^2$
$Q$ の表面積を $x$ とすると、 \begin{eqnarray*} 2^2:3^2&=&24 \pi:x\\ 4:9&=&24 \pi:x\\ 4x&=&24 \pi \times 9\\ x&=&\cfrac{24 \pi \times9}{4}=54 \large{\pi} \end{eqnarray*}
$②$ 円すい$P$ の体積が $56 \large{\pi}$ $cm^3$ のとき、円すい$Q$ の体積を求めなさい。
相似比が $m:n$ である $2$ つの立体の体積の比は、$m^3:n^3$ である。
答え
$189 \large{\pi}$ $cm^3$
$Q$ の体積を $y$ とすると、 \begin{eqnarray*} 2^3:3^3&=&56 \pi:y\\ 8:27&=&56 \pi:y\\ 8y&=&56 \pi \times 27\\ y&=&\cfrac{56 \pi \times27}{8}=189 \pi \end{eqnarray*}
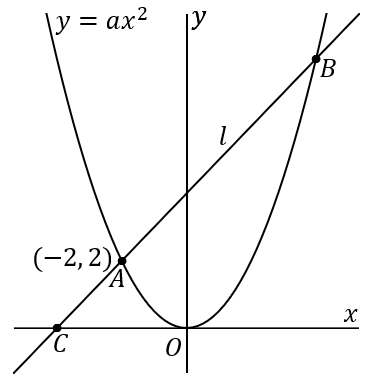 $\huge{14}$ 右の図のように、関数$y=ax^2$ のグラフと直線 $l$ が $2$ 点 $A$,$B$ で交わっていて、点 $A$ の座標は $(-2, \ 2)$ である。直線 $l$ と $x$ 軸との交点を $C$ とする。$CA:AB=1:3$ であるとき、以下の $(1)~(4)$ の問いに答えなさい。
$\huge{14}$ 右の図のように、関数$y=ax^2$ のグラフと直線 $l$ が $2$ 点 $A$,$B$ で交わっていて、点 $A$ の座標は $(-2, \ 2)$ である。直線 $l$ と $x$ 軸との交点を $C$ とする。$CA:AB=1:3$ であるとき、以下の $(1)~(4)$ の問いに答えなさい。
$(1)$ $a$ の値を求めなさい。
答え
$a=\cfrac{1}{2}$
$y=ax^2$ に、$x=-2, \ y=2$ を代入して、$a$ を求めればよいです。
\begin{eqnarray*}
2&=&a\times(-2)^2\\
2&=&4a\\
\cfrac{2}{4}&=&a\\
\cfrac{1}{2}&=&a\\
\end{eqnarray*}
$(2)$ 点 $B$ の座標を求めなさい。
答え
$(4, \ 8)$
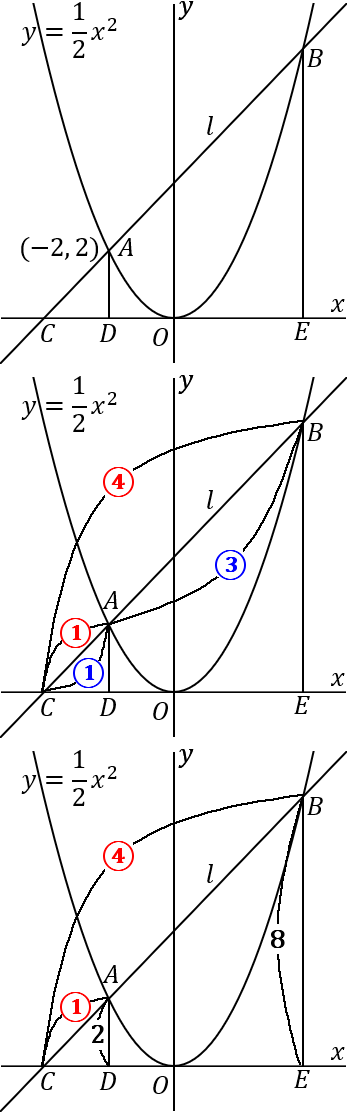 右の図のように、点 $A, \ B$ から $x$ 軸へ垂線をおろし、その交点をそれぞれ $D, \ E$ とします。$ AD /\!/ BE$ ですから、$\triangle CAD$ ∽$\ \triangle CBE$ になります。
右の図のように、点 $A, \ B$ から $x$ 軸へ垂線をおろし、その交点をそれぞれ $D, \ E$ とします。$ AD /\!/ BE$ ですから、$\triangle CAD$ ∽$\ \triangle CBE$ になります。
こんなふうに、この問題は三角形の相似を利用して考えます。
$CA:AB=1:3$ なのですから、$CA:CB=1:4$ です。なので、$\triangle CAD$ と $\triangle CBE$ の相似比は、$1:4$ です。
なので、$AD:BE=1:4$ となります。
点 $A$ の $y$ 座標は $2$ なのですから、$AD=2$ です。なので、$BE=2\times4=8$ となります。点 $B$ の $y$ 座標は、$8$ です。
次に $x$ 座標を求めます。$(1)$ の問題で、この放物線の式は $y=\cfrac{1}{2}x^2$ だということがわかっています。この式に $y=8$ を代入して、
\begin{eqnarray*}
8&=&\cfrac{1}{2}x^2\quad両辺に\times2\\
16&=&x^2\\
\pm\sqrt{16}&=&x\\
\pm4&=&x\\
\end{eqnarray*}
$x\gt0$ ですから、$x=4$ です。
$(3)$ $\triangle OAB$ の面積を求めなさい。
答え
$12$
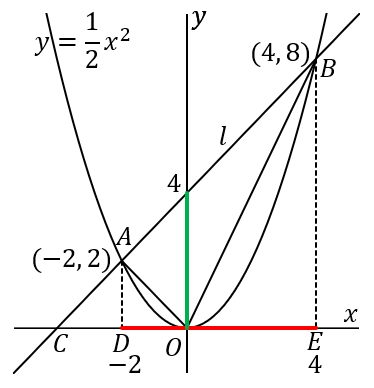
この三角形の面積は、赤 $\times$ 緑 $\times\cfrac{1}{2}$ です。赤のほうは、点 $D$ と 点 $E$ の $x$ 座標はそれぞれ $-2, \ 4$ なので、長さは $6$ です。
このように赤の長さはすぐにわかるですが、緑のほうは、直線 $l$ の $y$ 切片を求める必要があります。
直線 $l$ の式は、点 $(-2, \ 2), \ (4, \ 8)$ の $2$ 点を通る直線の式、ということで求めていきます。
\begin{eqnarray*}
a&=&\cfrac{y_2-y_1}{x_2-x_1}\\
&=&\cfrac{8-2}{4-(-2)}\\
&=&\cfrac{6}{6}\\
&=&1
\end{eqnarray*}
$y=x+b$ に $x=-2, \ y=2$ を代入する
\begin{eqnarray*}
2&=&-2+b\\
2-2&=&b\\
4&=&b
\end{eqnarray*}
これで直線 $l$ の $y$ 切片は $4$ だとわかりました。
なのでこの問題の答えは
$$\triangle OAB=6\times4\times\cfrac{1}{2}=12$$
この三角形の面積が、なぜ「赤×緑×$\cfrac{1}{2}$」とすればうまくいくのかがわからないときは、下の説明ボタンを押して考えてみてください。
$(4)$ 原点を通り、$\triangle OAB$ の面積を $2$ 等分する直線の式を求めなさい。
答え
$y=5x$
 <中線>
<中線>
三角形の $1$ つの頂点から、むかいあう辺の中点を通るようにひいた線を中線といいます。三角形の中線は、その三角形の面積を二等分します。
<中点>
中点の座標は、「足して $2$ で割る」です。$x$ 座標と $y$ 座標のそれぞれを足して $2$ で割ればよいです。「中点は、足して $2$ で割る」。わりとよく使う知識なので、おぼえちゃったほうが話が早いです。
この問題の場合は、点 $A$ と 点 $B$ の中点の座標を知りたいわけです。点 $A$ の座標は $(-2, \ 2),$ 点 $B$ の座標は $(4, \ 8)$ です。なのでその中点の座標は、
\begin{eqnarray*}
&&\left(\cfrac{x+x}{2}, \ \cfrac{y+y}{2}\right)\\
&=&\left(\cfrac{-2+4}{2}, \ \cfrac{2+8}{2}\right)\\
&=&(1, \ 5)
\end{eqnarray*}
となります。中点 $M$ の座標は $(1, \ 5)$ です。
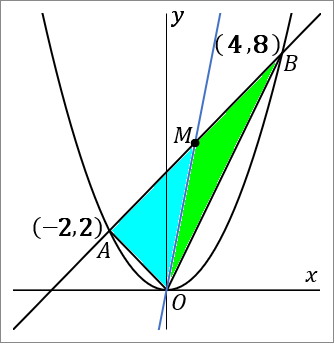
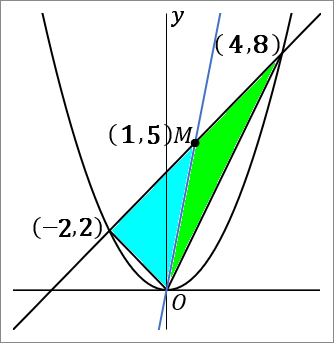 では答えをだしていきましょう。もう一回おなじ図をはっておきます。原点と点 $M(1, \ 5)$ を通る直線の式を求めればよいです。図の青い線です。原点を通る直線なのですから、比例の式をいえばよくて、答えの形は $y=ax$ です。
では答えをだしていきましょう。もう一回おなじ図をはっておきます。原点と点 $M(1, \ 5)$ を通る直線の式を求めればよいです。図の青い線です。原点を通る直線なのですから、比例の式をいえばよくて、答えの形は $y=ax$ です。
$y=ax$ に $x=1, \ y=5$ を代入して、
\begin{eqnarray*}
5&=&a
\end{eqnarray*}
これで $a$ がわかりました。では答えです。
$$y=5x$$
答え(中3 2学期期末模擬テスト 第1回)
1$①3$ $②-18$ $③\cfrac{5}{12}$ $④-6x+13y$ $⑤\cfrac{3\sqrt{10}}{4}$ $⑥\sqrt{2}$ $⑦(x-4)(x-5)$ $⑧x=-3, \ y=-5$ $⑨x=1\pm\sqrt{3}$
2$①y=-3$ $②a=4$ $③0 \leqq y \leqq 18$
3$\triangle ABC$ ∽$\triangle HGI$…$2$ 組の角がそれぞれ等しい。
$\triangle DEF$ ∽$\triangle OMN$…$2$ 組の辺の比とその間の角が等しい。
$\triangle JKL$ ∽$\triangle QRP$…$3$ 組の辺の比がすべて等しい。
4〈証明〉
$\triangle ABC$ と $\triangle BDC$ で、
仮定から、$\angle BAC=\angle DBC$ ……①
共通な角だから、$\angle ACB=\angle BCD$ ……②
①②より、$2$ 組の角がそれぞれ等しいので
$\triangle ABC$ ∽$\ \triangle BDC$
5① $x=\cfrac{15}{2}, \ y=\cfrac{16}{3}$
② $x=1.2, \ y=3$
③ $x=6, \ y=16$
④ $x=\cfrac{5}{4}, \ y=\cfrac{15}{2}$
⑤ $x=\cfrac{72}{5}, \ y=\cfrac{25}{3}$
6$①x=6$ $②x=\cfrac{9}{2}$
7$①x=9.5$ $②x=\cfrac{12}{5}$ $③x=4.5, \ y=5$ $④x=\cfrac{44}{7}, \ y=\cfrac{64}{9}$
8$①x=11$ $②x=\cfrac{18}{5}$
9〈証明〉
$B$ と $D$ を結ぶ。
$\triangle ABD$ で、中点連結定理より、
$\quad PS /\!/ BD, \ PS=\cfrac{1}{2}BD$ …①
$\triangle CBD$ で、中点連結定理より、
$\quad QR /\!/ BD, \ QR=\cfrac{1}{2}BD$ …②
四角形 $PQRS$ で、①②より、
$\quad PS /\!/ QR, \ PS=QR$
$1$ 組の対辺が平行で長さが等しいので、
四角形 $PQRS$ は平行四辺形である。
10 $x=9$
11 $36cm^2$
12 $①1:4:9$ $②1:3:5$ $③\cfrac{20}{3}cm^2$
13 $①54\pi cm^2$ $②189\pi cm^3$
14 (1)$a=\cfrac{1}{2}$ (2)$ \ (4, \ 8)$ (3)$12$ (4)$y=5x$