数学 中3 2学期期末模擬テスト 第2回
 ページがちゃんと表示されるまで10秒くらいかかります。
ページがちゃんと表示されるまで10秒くらいかかります。
ho←ここに四角形が表示されていたら準備OKです。
「印刷」をクリックすると同じ内容のpdfファイルが表示されます。また、解答用紙と答えも問題のあとに表示されます。1~6ページが問題、7~8ページが解答用紙、9~10ページが答えです。必要におうじて印刷してください。
問題をクリックすると答えがでます。
ふつうのテストより問題数は多いです。なのでふつうのテストをやるときより時間がかかると思います。がんばって!
1 次の①~⑥の計算をしなさい。⑦~⑨の各問いに答えなさい。
① 4+5×(−2)②5×(−32)−7×(−8)
答え
①−6 ②11
①4+5×(−2)=4−10=−6 \begin{eqnarray*} \require{cancel} &②& 5\times(-3^2)-7\times(-8)\\ &=& 5\times(-9)-7\times(-8)\\ &=& -45+56\\ &=& 11 \end{eqnarray*}
\qquad③ -\cfrac{3}{4}+\left(-\cfrac{15}{16}\right)\div\left(-\cfrac{9}{8}\right) \qquad ④ \quad -2(4x+3y)+3(5x-2y)
答え
①\cfrac{1}{12} ④7x-12y
\begin{eqnarray*} \require{cancel} &③& -\cfrac{3}{4}+\left(-\cfrac{15}{16}\right)\div\left(-\cfrac{9}{8}\right) \\ &=& -\cfrac{3}{4}+\left(-\cfrac{15}{16}\right)\times\left(-\cfrac{8}{9}\right) \\ &=& -\cfrac{3}{4}+\left(-\cfrac{{}^5\bcancel{15}}{{}^2\bcancel{16}}\right)\times\left(-\cfrac{\bcancel{8}}{{}^3\bcancel{9}}\right) \\ &=& -\cfrac{3}{4}+\cfrac{5}{6}\\ &=& -\cfrac{9}{12}+\cfrac{10}{12}\\ &=& \cfrac{1}{12} \end{eqnarray*} \begin{eqnarray*} \require{cancel} &④& -2(4x+3y)+3(5x-2y)\\ &=& -8x-6y+15x-6y\\ &=& 7x-12y \end{eqnarray*}
\qquad⑤ \sqrt{\cfrac{8}{9}}-\sqrt{\cfrac{9}{8}} \qquad ⑥ \quad 6\sqrt{48}\div\sqrt{6}\div\sqrt{12}
答え
⑤-\cfrac{\sqrt{2}}{12} ⑥2\sqrt{6}
\begin{eqnarray*} \require{cancel} &⑤& \sqrt{\cfrac{8}{9}}-\sqrt{\cfrac{9}{8}}\\ &=&\cfrac{\sqrt{8}}{\sqrt{9}}-\cfrac{\sqrt{9}}{\sqrt{8}}\\ &=&\cfrac{2\sqrt{2}}{3}-\cfrac{3}{2\sqrt{2}}\\ &=&\cfrac{2\sqrt{2}}{3}-\cfrac{3\sqrt{2}}{4}\\ &=&\cfrac{8\sqrt{2}}{12}-\cfrac{9\sqrt{2}}{12}\\ &=&-\cfrac{\sqrt{2}}{12} \end{eqnarray*} \begin{eqnarray*} \require{cancel} &⑥& 6\sqrt{48}\div\sqrt{6}\div\sqrt{12}\\ &=&\cfrac{6\sqrt{48}}{\sqrt{6}\times\sqrt{12}}\\ &=&\cfrac{6\sqrt{2}}{\sqrt{3}}\\ &=&\cfrac{6\sqrt{6}}{3}\\ &=&2\sqrt{6} \end{eqnarray*}
\qquad⑦ x^2-12xy+36y^2 を因数分解しなさい。
答え
(x-6y)^2
\qquad⑧ 方程式 2x-3y=3x-4y+2=7 を解きなさい。
答え
x=-13,y=-11
まんなかをかくした式をつくり、①とします。左側をかくした式をつくって整理し、②とします。①の式と②の式を連立させ、x の係数をそろえて加減法で解きます。
\begin{eqnarray*}
&& \ 2x-3y=3x-4y+2=7
\end{eqnarray*}
まんなかをかくした式をたてる
\begin{eqnarray*}
2x-3y&=&7\quad…①
\end{eqnarray*}
左側をかくした式をたてて整理する
\begin{eqnarray*}
3x-4y+2&=&7\\
3x-4y&=&5\quad…②
\end{eqnarray*}
①と②を連立させる
\begin{eqnarray*}
&& \ \left\{
\begin{array}{l}
2x-3y=7\quad…①\\
3x-4y=5\quad…②
\end{array}
\right.
\end{eqnarray*}
①\times3 \ - \ ②\times2
\begin{eqnarray*}
6x-9y=21\\
\underline{-) \quad 6x-8y=10}\\
-y=11\\
y=-11
\end{eqnarray*}
y=-11を①に代入
\begin{eqnarray*}
2x-3\times(-11)&=&7\\
2x+33&=&7\\
2x&=&-26\\
x&=&-13
\\
\left\{
\begin{array}{l}
x=-13\\
y=-11
\end{array}
\right.
\end{eqnarray*}
\qquad⑨ 2 次方程式 4x^2-14=0 を解きなさい。
答え
x=\pm\cfrac{\sqrt{14}}{2}
\begin{eqnarray*} 4x^2-14&=&0 \quad(\div2)\\ 2x^2-7&=&0 \\ 2x^2&=&7 \\ x^2&=&\cfrac{7}{2}\\ x&=&\pm \sqrt{\cfrac{7}{2}}=\pm\cfrac{\sqrt{7}}{\sqrt{2}}=\pm\cfrac{\sqrt{14}}{2} \end{eqnarray*}
\huge{2} 次の①~③の各問いに答えなさい。
① y が x の 2 乗に比例し、x=-5 のとき y=-\cfrac{15}{2} である。x=-2 のときの y の値を求めなさい。
答え
y=-\cfrac{6}{5}
y=ax^2 に x=-5 , y=-\cfrac{15}{2} を代入すると、
\begin{eqnarray*}
-\cfrac{15}{2}&=&a×(-5)^2\\
-\cfrac{15}{2}&=&25a\qquad\qquad(\times2)\\
-15&=&50a\\
-\cfrac{15}{50}&=&a\\
-\cfrac{3}{10}&=&a
\end{eqnarray*}
これで a=-\cfrac{3}{10} というふうに、 a が求められました。y=ax^2 に a=-\cfrac{3}{10} を代入して、
y=-\cfrac{3}{10}x^2
この式に x=-2 を代入して、
y=-\cfrac{3}{10}×(-2)^2=-\cfrac{3}{{}^5\bcancel{10}}×{}^2\bcancel{4}=-\cfrac{6}{5}
② 関数 y=ax^2 について、x の値が -4 から 3 まで増加するときの、変化の割合が -1 である。a の値を求めなさい。
答え
a=1
関数 y=ax^2 について、x の値が p から q まで増加するときの変化の割合は (p+q)\times a=変化の割合 を利用します。この問題の場合は、 (-4+3)\times a=-1 となります。あとはこれを解くだけ。 \begin{eqnarray*} (-4+3)\times a&=&-1\\ -a&=&-1\\ a&=&1 \end{eqnarray*}
③ 関数 y=-\cfrac{1}{2}x^2 について、x の変域が -\cfrac{7}{2} \leqq x \leqq 3 のとき、y の変域を求めなさい。
答え
-\cfrac{49}{8} \leqq y \leqq 0
「関数 y=ax^2 について、x の変域が p \leqq x \leqq q のとき、y の変域を求めなさい」ときかれたら、
<手順①>まず p \leqq x \leqq q が 0 をまたいでいるかを確認します。この問題の場合は、 -\cfrac{7}{2} \leqq x \leqq 3 なのでまたいでいます。
<手順②>またいでいるときは、 y=ax^2 の a の符号を確認します。
a がプラスの時は、答えの形は 0 \leqq y \leqq 〇 です。
a がマイナスの時は、答えの形は 〇 \leqq y \leqq 0 です。
〇のところには数がはいります。
この問題の場合は、a はマイナスです。
<手順③>〇のところにはいる数は、 p \leqq x \leqq q の p と q のうち、0 から遠いほうを y=ax^2 の x に代入してでてきた数です。
この問題の場合は、-\cfrac{7}{2} \leqq x \leqq 3 ですから 0 から遠いのは -\cfrac{7}{2} です。-\cfrac{7}{2} を y=-\cfrac{1}{2}x^2 の x に代入して、
\begin{eqnarray*}
y&=&-\cfrac{1}{2}\times\left(-\cfrac{7}{2}\right)^2\\
&=&-\cfrac{1}{2}\times\cfrac{49}{4}\\
&=&-\cfrac{49}{8}
\end{eqnarray*}
なので答えは
-\cfrac{49}{8} \leqq y \leqq 0
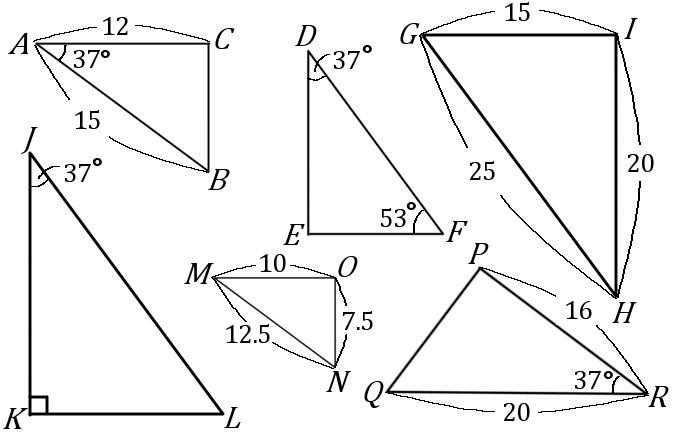
\huge{3} 下の図のなかから、相似な三角形の組を見つけ、記号 ∽ を使って表しなさい。また、そのときに使った相似条件をいいなさい。
答え
\triangle ABC ∽\triangle RQP…2 組の辺の比とその間の角が等しい。
\triangle DEF ∽\triangle JKL…2 組の角がそれぞれ等しい。
\triangle GHI ∽\triangle NMO…3 組の辺の比がすべて等しい。
対応する辺や角に注意する。
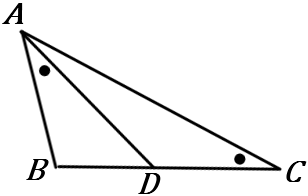 \huge{4} 右の図で、\angle ACB=\angle DAB である。
\huge{4} 右の図で、\angle ACB=\angle DAB である。
\triangle ABC ∽\ \triangle DBAを証明しなさい。
答え
〈証明〉
\triangle ABC と \triangle DBA で、
仮定から、\angle ACB=\angle DAB ……①
共通な角だから、\angle ABC=\angle DBA ……②
①②より、2 組の角がそれぞれ等しいので
\triangle ABC ∽\ \triangle DBA
 対応する辺や角に注意しましょう。
対応する辺や角に注意しましょう。
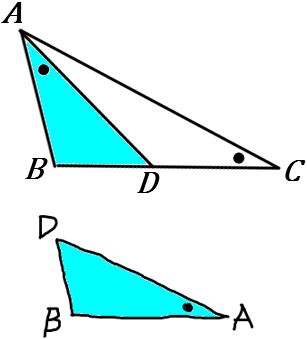
相似な図形どうしを、対応する辺や角に注意して、向きをそろえてかいてしまうのがよいです。問題の図の下や横に、こんな感じで図をかき加えてしまいましょう。→
すると、辺や角のいい方のミスが少なくなります。
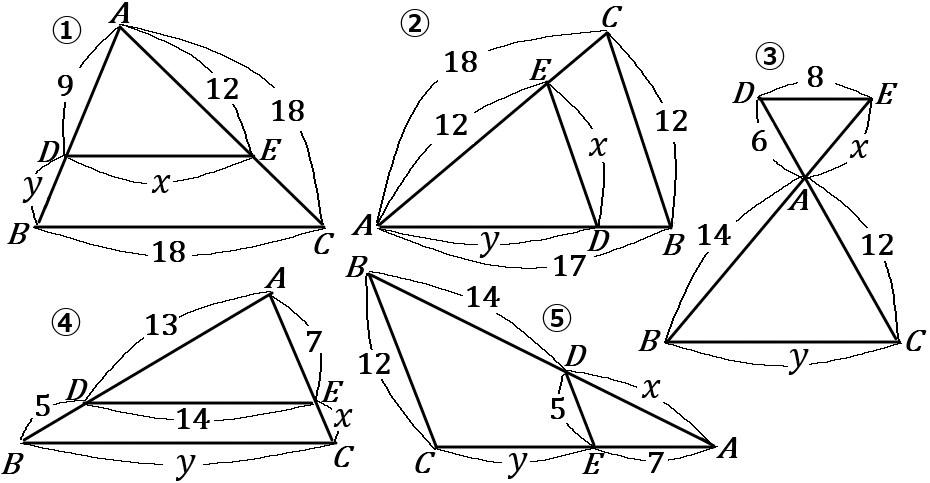
\huge{5} 下の①~⑤の図で、x, \ y の値を求めなさい。ただし、①~⑤まで、すべて \ DE /\!/ BC とする。
答え
① x=12, \ y=\cfrac{9}{2}
② x=8, \ y=\cfrac{34}{3}
③ x=7, \ y=16
④ x=\cfrac{35}{13}, \ y=\cfrac{252}{13}
⑤ x=10, \ y=\cfrac{49}{5}
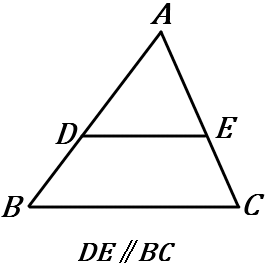 \triangle ABC で、辺 AB, \ AC 上の点をそれぞれ D, \ E とする。
\triangle ABC で、辺 AB, \ AC 上の点をそれぞれ D, \ E とする。
1 \ DE /\!/ BC ならば、
\quad AD:AB=AE:AC=DE:BC
2 \ DE /\!/ BC ならば、
\quad AD:DB=AE:EC
※すべて上の定理を利用しています。以下のやり方は一例です。このほかにもいろんな式のたて方があります。
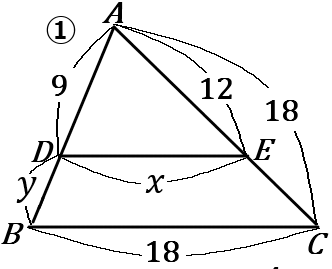 \begin{eqnarray*}
①
12:18&=&x:18\\
x&=&12
\end{eqnarray*}
\begin{eqnarray*}
9:y&=&12:18-12\\
9:y&=&12:6\\
9:y&=&2:1\\
2y&=&9\\
y&=&\cfrac{9}{2}
\end{eqnarray*}
\begin{eqnarray*}
①
12:18&=&x:18\\
x&=&12
\end{eqnarray*}
\begin{eqnarray*}
9:y&=&12:18-12\\
9:y&=&12:6\\
9:y&=&2:1\\
2y&=&9\\
y&=&\cfrac{9}{2}
\end{eqnarray*}
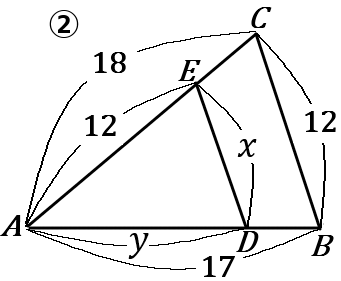 \begin{eqnarray*}
②
12:18&=&x:12\\
2:3&=&x:12\\
3x&=&24\\
x&=&8
\end{eqnarray*}
\begin{eqnarray*}
12:18&=&y:17\\
2:3&=&y:17\\
3y&=&y:34\\
y&=&\cfrac{34}{3}
\end{eqnarray*}
\begin{eqnarray*}
②
12:18&=&x:12\\
2:3&=&x:12\\
3x&=&24\\
x&=&8
\end{eqnarray*}
\begin{eqnarray*}
12:18&=&y:17\\
2:3&=&y:17\\
3y&=&y:34\\
y&=&\cfrac{34}{3}
\end{eqnarray*}
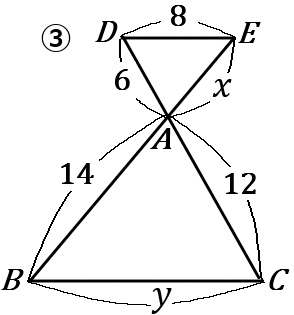 \begin{eqnarray*}
③
6:12&=&x:14\\
1:2&=&x:14\\
x&=&7
\end{eqnarray*}
\begin{eqnarray*}
6:12&=&8:y\\
1:2&=&8:y\\
y&=&16
\end{eqnarray*}
\begin{eqnarray*}
④
13:5&=&7:x\\
13x&=&35\\
x&=&\cfrac{35}{13}
\end{eqnarray*}
\begin{eqnarray*}
③
6:12&=&x:14\\
1:2&=&x:14\\
x&=&7
\end{eqnarray*}
\begin{eqnarray*}
6:12&=&8:y\\
1:2&=&8:y\\
y&=&16
\end{eqnarray*}
\begin{eqnarray*}
④
13:5&=&7:x\\
13x&=&35\\
x&=&\cfrac{35}{13}
\end{eqnarray*}
 \begin{eqnarray*}
13:13+5&=&14:y\\
13:18&=&14:y\\
13y&=&252\\
y&=&\cfrac{252}{13}
\end{eqnarray*}
\begin{eqnarray*}
13:13+5&=&14:y\\
13:18&=&14:y\\
13y&=&252\\
y&=&\cfrac{252}{13}
\end{eqnarray*}
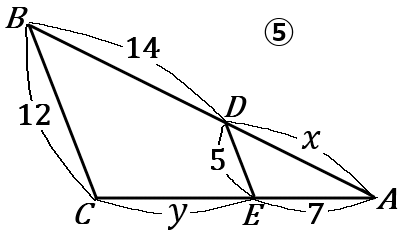 \begin{eqnarray*}
⑤
12:5&=&14+x:x\\
12x&=&5(14+x)\\
12x&=&70+5x\\
12x-5x&=&70\\
7x&=&70\\
x&=&10
\end{eqnarray*}
(x=10 を利用して)
\begin{eqnarray*}
14:10&=&y:7\\
7:5&=&y:7\\
5y&=&49\\
y&=&\cfrac{49}{5}
\end{eqnarray*}
\begin{eqnarray*}
⑤
12:5&=&14+x:x\\
12x&=&5(14+x)\\
12x&=&70+5x\\
12x-5x&=&70\\
7x&=&70\\
x&=&10
\end{eqnarray*}
(x=10 を利用して)
\begin{eqnarray*}
14:10&=&y:7\\
7:5&=&y:7\\
5y&=&49\\
y&=&\cfrac{49}{5}
\end{eqnarray*}
\huge{6}
下の①、②の図で、x の値を求めなさい。ただし、\angle BAD=\angle CAD とする。
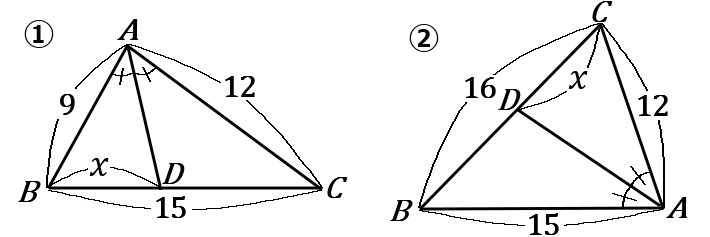
答え
① x=\cfrac{45}{7} ② x=\cfrac{64}{9}
 \triangle ABC で、\angle A の二等分線と辺 BC との交点を D とすると、
\triangle ABC で、\angle A の二等分線と辺 BC との交点を D とすると、
\quad AB:AC=BD:CD
上の定理を利用します。
 ①
\begin{eqnarray*}
9:12&=&x:15-x\\
3:4&=&x:15-x\\
4x&=&3(15-x)\\
4x&=&45-3x\\
4x+3x&=&45\\
7x&=&45\\
x&=&\cfrac{45}{7}
\end{eqnarray*}
①
\begin{eqnarray*}
9:12&=&x:15-x\\
3:4&=&x:15-x\\
4x&=&3(15-x)\\
4x&=&45-3x\\
4x+3x&=&45\\
7x&=&45\\
x&=&\cfrac{45}{7}
\end{eqnarray*}
 ②
\begin{eqnarray*}
12:15&=&x:16-x\\
4:5&=&x:16-x\\
5x&=&4(16-x)\\
5x&=&64-4x\\
5x+4x&=&64\\
9x&=&64\\
x&=&\cfrac{64}{9}
\end{eqnarray*}
②
\begin{eqnarray*}
12:15&=&x:16-x\\
4:5&=&x:16-x\\
5x&=&4(16-x)\\
5x&=&64-4x\\
5x+4x&=&64\\
9x&=&64\\
x&=&\cfrac{64}{9}
\end{eqnarray*}
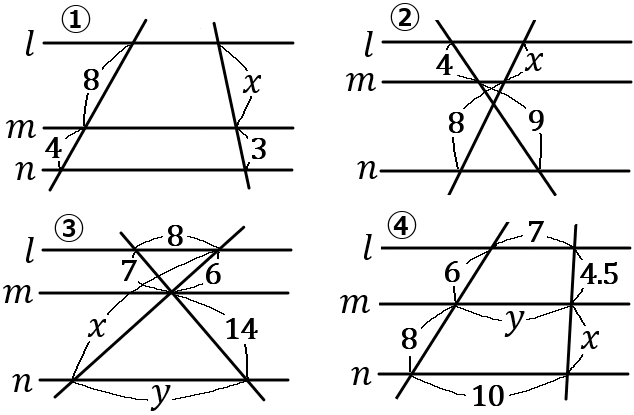
\huge{7}
下の①,②の図で、x の値を求めなさい。③,④の図で、x, \ y の値を求めなさい。ただし、どの図も\ l /\!/ m /\!/ n とする。
答え
① x=6 ② x=\cfrac{32}{9} ③ x=18, \ y=16 ④x=6, \ y=\cfrac{58}{7}
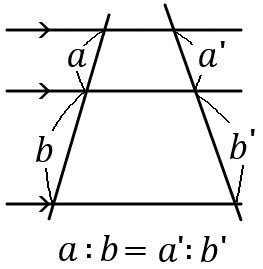 3 つ以上の平行線に、1 つの直線がどのように交わっても、その直線は平行線によって一定の比に分けられる。
3 つ以上の平行線に、1 つの直線がどのように交わっても、その直線は平行線によって一定の比に分けられる。
 ①
\begin{eqnarray*}
8:4&=&x:3\\
2:1&=&x:3\\
x&=&6
\end{eqnarray*}
①
\begin{eqnarray*}
8:4&=&x:3\\
2:1&=&x:3\\
x&=&6
\end{eqnarray*}
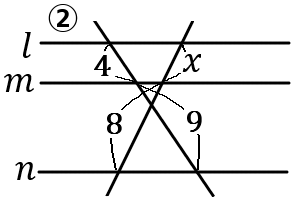 ②
\begin{eqnarray*}
4:9&=&x:8\\
9x&=&32\\
x&=&\cfrac{32}{9}
\end{eqnarray*}
②
\begin{eqnarray*}
4:9&=&x:8\\
9x&=&32\\
x&=&\cfrac{32}{9}
\end{eqnarray*}
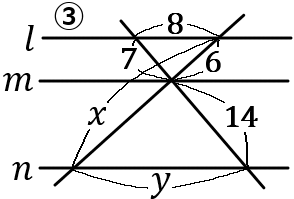 ③
\begin{eqnarray*}
7:14&=&6:x-6\\
1:2&=&6:x-6\\
x-6&=&12\\
x&=&12+6\\
x&=&18
\end{eqnarray*}
\begin{eqnarray*}
7:14&=&8:y\\
1:2&=&8:y\\
y&=&16
\end{eqnarray*}
③
\begin{eqnarray*}
7:14&=&6:x-6\\
1:2&=&6:x-6\\
x-6&=&12\\
x&=&12+6\\
x&=&18
\end{eqnarray*}
\begin{eqnarray*}
7:14&=&8:y\\
1:2&=&8:y\\
y&=&16
\end{eqnarray*}
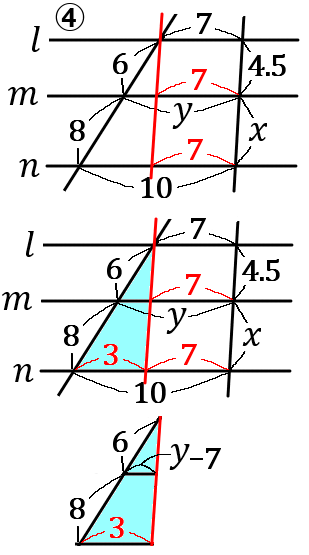 ④
\begin{eqnarray*}
6:8&=&4.5:x\\
3:4&=&4.5:x\\
3x&=&18\\
x&=&6
\end{eqnarray*}
〈y の求め方〉
右の図のように、補助線をひきます。で、青い部分の相似な三角形で式をたてていきます。
\begin{eqnarray*}
6:6+8&=&y-7:10-7\\
6:14&=&y-7:3\\
3:7&=&y-7:3\\
7(y-7)&=&9\\
7y-49&=&9\\
7y&=&9+49\\
7y&=&58\\
y&=&\cfrac{58}{7}
\end{eqnarray*}
④
\begin{eqnarray*}
6:8&=&4.5:x\\
3:4&=&4.5:x\\
3x&=&18\\
x&=&6
\end{eqnarray*}
〈y の求め方〉
右の図のように、補助線をひきます。で、青い部分の相似な三角形で式をたてていきます。
\begin{eqnarray*}
6:6+8&=&y-7:10-7\\
6:14&=&y-7:3\\
3:7&=&y-7:3\\
7(y-7)&=&9\\
7y-49&=&9\\
7y&=&9+49\\
7y&=&58\\
y&=&\cfrac{58}{7}
\end{eqnarray*}
\huge{8}
下の①,②の図で、x の値を求めなさい。ただし、①の図は \ AD /\!/ EF /\!/ BC , ②の図は \ AB /\!/ EF /\!/ CD とする。

答え
① x=10 ② x=3
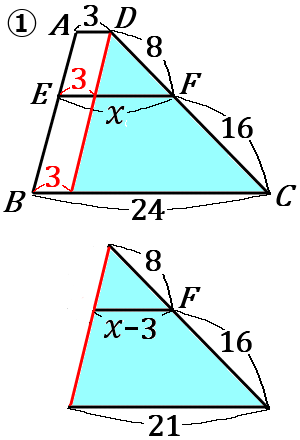 ①右の図のように、補助線をひきます。で、青い部分の相似な三角形で式をたてていきます。
\begin{eqnarray*}
8:8+16&=&x-3:21\\
8:24&=&x-3:21\\
1:3&=&x-3:21\\
3(x-3)&=&21\\
3x-9&=&21\\
3x&=&21+9\\
3x&=&30\\
x&=&10
\end{eqnarray*}
①右の図のように、補助線をひきます。で、青い部分の相似な三角形で式をたてていきます。
\begin{eqnarray*}
8:8+16&=&x-3:21\\
8:24&=&x-3:21\\
1:3&=&x-3:21\\
3(x-3)&=&21\\
3x-9&=&21\\
3x&=&21+9\\
3x&=&30\\
x&=&10
\end{eqnarray*}
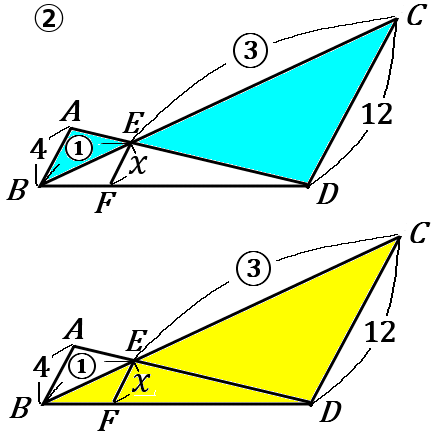 ②\triangle EAB ∽\ \triangle EDC (青いところ)で、その相似比は 4:12=1:3 です。なので、BE:EC=1:3 です。
②\triangle EAB ∽\ \triangle EDC (青いところ)で、その相似比は 4:12=1:3 です。なので、BE:EC=1:3 です。
この比を、\triangle BEF ∽\ \triangle BCD (黄色いところ)に使って x を求めていきます。
\begin{eqnarray*}
1:1+3&=&x:12\\
1:4&=&x:12\\
4x&=&12\\
x&=&3
\end{eqnarray*}
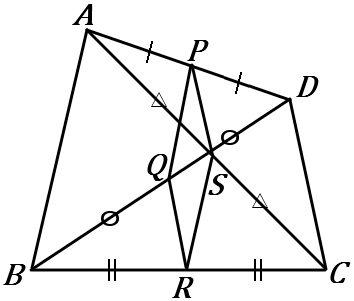
\huge{9} 右の図で、線分 AD, BD, BC, AC の中点をそれぞれ P,Q,R,S とする。四角形 PQRS は平行四辺形となることを証明しなさい。
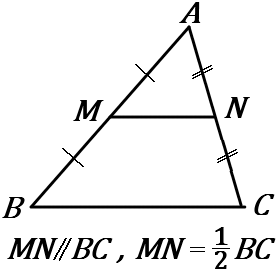 三角形の 2 つの辺の中点を結ぶ線分は、残りの辺に平行で、長さはその半分である。
三角形の 2 つの辺の中点を結ぶ線分は、残りの辺に平行で、長さはその半分である。
答え
〈証明〉
\triangle ABD で、中点連結定理より、
\quad PQ /\!/ AB, \ PQ=\cfrac{1}{2}AB …①
\triangle ABC で、中点連結定理より、
\quad SR /\!/ AB, \ SR=\cfrac{1}{2}AB …②
四角形 PQRS で、①②より、
\quad PQ /\!/ SR, \ PQ=SR
1 組の対辺が平行で長さが等しいので、
四角形 PQRS は平行四辺形である。
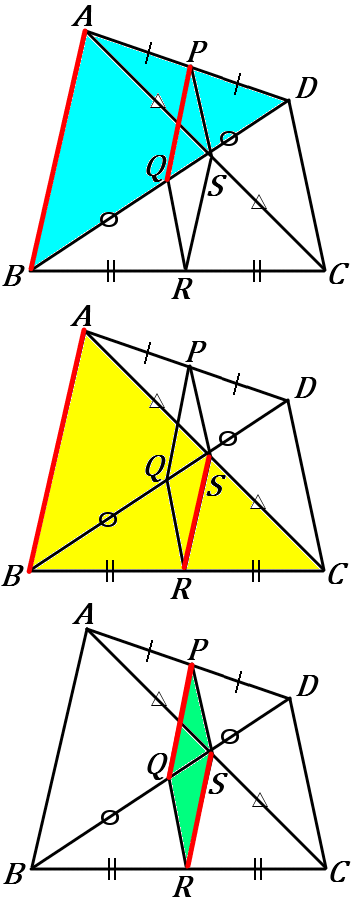 中点連結定理を使った証明です。
中点連結定理を使った証明です。
青い三角形で、\quad PQ /\!/ AB, \ PQ=\cfrac{1}{2}AB
黄色い三角形で、\quad SR /\!/ AB, \ SR=\cfrac{1}{2}AB
PQ と SR は、どちらも AB と平行で、長さが AB の半分。したがって、\quad PQ /\!/ SR, \ PQ=SR となります。
平行四辺形になるための条件は 4つありましたね(定義をふくめれば 5つ)。その最後のやつです。「1 組の対辺が平行で長さが等しい」。これでうまくいきます。

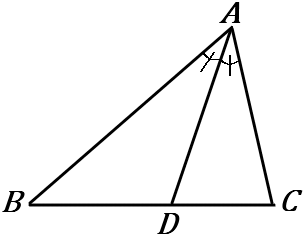
\huge{10} 右の図で、x の値を求めなさい。ただし、AD=DB, \ AE=EC=CG とする。
答え
x=15
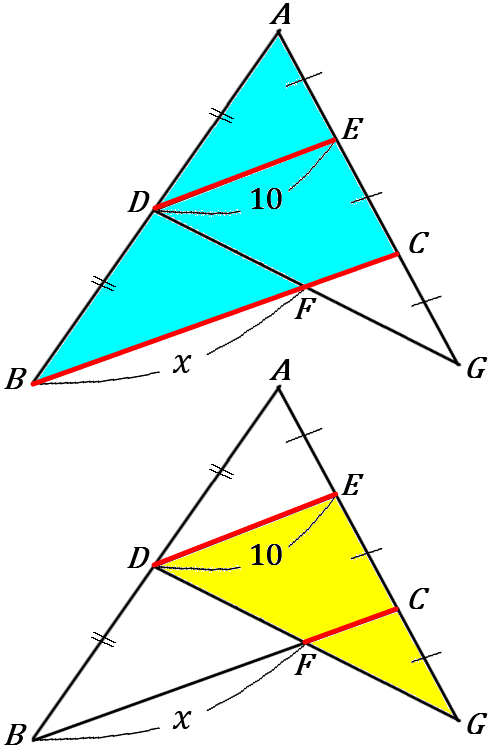 \triangle ABC で、AD:DB=AE:EC=1:1
\triangle ABC で、AD:DB=AE:EC=1:1
中点連結定理より、BC=2DE=20 …①
また、DE /\!/ BC, \ EC:CG=1:1 だから、DF:FG=1:1
\triangle DGE で、中点連結定理より、
FC=\cfrac{1}{2}DE=5 …②
①②より、x=BC-FC=20-5=15
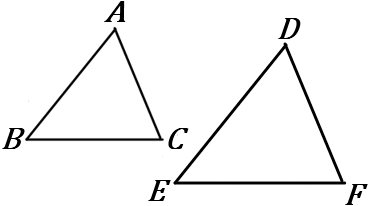
\huge{11} 右の図で、\triangle ABC ∽\ \triangle DEF であり、その相似比は 4:5 である。
\triangle ABC の面積が 8cm^2 のとき、\triangle DEF の面積を求めなさい。
相似比が m:n である 2 つの図形の面積の比は、m^2:n^2 である。
答え
\cfrac{25}{2}cm^2
\triangle DEF の面積を x とすると、 \begin{eqnarray*} 4^2:5^2&=&8:x\\ 16:25&=&8:x\\ 16x&=&25\times8\\ x&=&\cfrac{25\times8}{16}=\cfrac{25}{2} \end{eqnarray*}
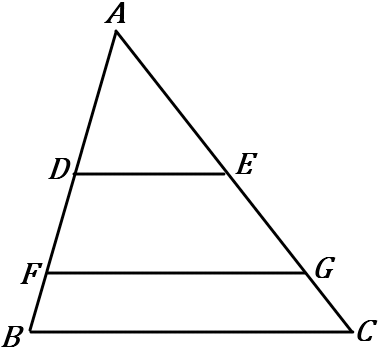
\huge{12} 右の図の \triangle ABC で、AD:DF:FB=3:2:1, \ DE /\!/ FG /\!/ BC である。以下の①~③の問いに答えなさい。
① \triangle ADE と \triangle AFG と \triangle ABC の面積の比をいいなさい。
相似比が m:n である 2 つの図形の面積の比は、m^2:n^2 である。
答え
9:25:36
仮定から、\triangle ADE ∽\ \triangle AFG ∽\ \triangle ABC です。相似比は 3:5:6 です。
なので、面積比は 3^2:5^2:6^2=9:25:36 です。
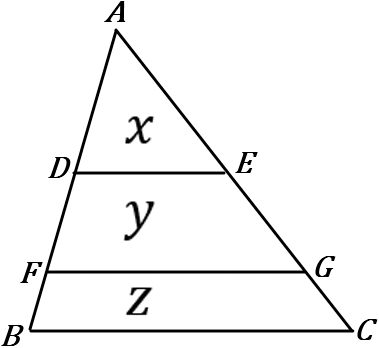 ② \triangle ADE の面積を x とする。
② \triangle ADE の面積を x とする。
台形DFGE の面積を y とする。
台形FBCG の面積を z とする。
x:y:z の比を求めなさい。
答え
9:16:11
 ①の問題の答えから、x=9 とすると、\triangle AFG の面積は 25 です。また、\triangle ABC の面積は 36 です。
①の問題の答えから、x=9 とすると、\triangle AFG の面積は 25 です。また、\triangle ABC の面積は 36 です。
なので、
\quad y=25-9=16
\quad z=36-25=11
なので、x:y:z=9:16:11
③ \triangle ABC の面積が 30cm^2 であるとき、台形FBCG の面積を求めなさい。
答え
\cfrac{55}{6}cm^2
台形FBCG の面積は全体(\triangle ABC)の \cfrac{11}{36} です。なので、
\quad 30\times \cfrac{11}{36}=\cfrac{55}{6}
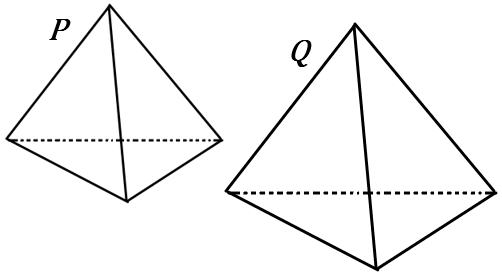
\huge{13} 右の図で、三角すいP と三角すいQ は相似であり、その相似比は 4:5 である。以下の①②の問いに答えなさい。
① 三角すいP の表面積が 32cm^2 のとき、三角すいQ の表面積を求めなさい。
相似比が m:n である 2 つの立体の表面積の比は、m^2:n^2 である。
答え
50cm^2
Q の表面積を x とすると、 \begin{eqnarray*} 4^2:5^2&=&32:x\\ 16:25&=&32:x\\ 16x&=&25\times 32\\ x&=&\cfrac{25\times32}{16}=50 \end{eqnarray*}
② 三角すいP の体積が 128cm^3 のとき、三角すいQ の体積を求めなさい。
相似比が m:n である 2 つの立体の体積の比は、m^3:n^3 である。
答え
250cm^3
Q の体積を y とすると、 \begin{eqnarray*} 4^3:5^3&=&128:y\\ 64:125&=&128:y\\ 64y&=&125\times128\\ y&=&\cfrac{125\times128}{64}=250 \end{eqnarray*}
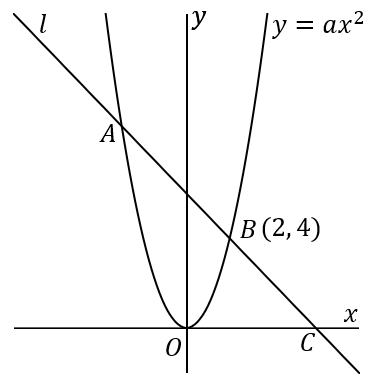 \huge{14} 右の図のように、関数y=ax^2 のグラフと直線 l が 2 点 A,B で交わっていて、点 B の座標は (2, \ 4) である。直線 l と x 軸との交点を C とする。AB:BC=5:4 であるとき、以下の (1)~(4) の問いに答えなさい。
\huge{14} 右の図のように、関数y=ax^2 のグラフと直線 l が 2 点 A,B で交わっていて、点 B の座標は (2, \ 4) である。直線 l と x 軸との交点を C とする。AB:BC=5:4 であるとき、以下の (1)~(4) の問いに答えなさい。
(1) a の値を求めなさい。
答え
a=1
y=ax^2 に、x=2, \ y=4 を代入して、a を求めればよいです。
\begin{eqnarray*}
4&=&a\times2^2\\
4&=&4a\\
1&=&a\\
\end{eqnarray*}
(2) 点 A の座標を求めなさい。
答え
(-3, \ 9)
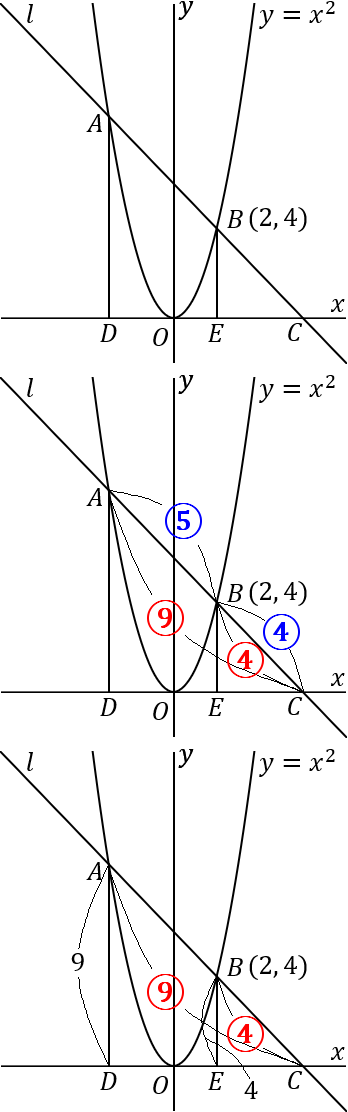 右の図のように、点 A, \ B から x 軸へ垂線をおろし、その交点をそれぞれ D, \ E とします。 AD /\!/ BE ですから、\triangle CAD ∽\ \triangle CBE になります。
右の図のように、点 A, \ B から x 軸へ垂線をおろし、その交点をそれぞれ D, \ E とします。 AD /\!/ BE ですから、\triangle CAD ∽\ \triangle CBE になります。
こんなふうに、この問題は三角形の相似を利用して考えます。
AB:BC=5:4 なのですから、AC:BC=9:4 です。なので、\triangle CAD と \triangle CBE の相似比は、9:4 です。
なので、AD:BE=9:4 となります。
点 B の y 座標は 4 なのですから、BE=4 です。なので、AD=9 となります。点 A の y 座標は、9 です。
次に x 座標を求めます。(1) の問題で、この放物線の式は y=x^2 だということがわかっています。この式に y=9 を代入して、
\begin{eqnarray*}
9&=&x^2\\
\pm\sqrt{9}&=&x\\
\pm3&=&x\\
\end{eqnarray*}
x\lt0 ですから、x=-3 です。
(3) \triangle OAB の面積を求めなさい。
答え
15
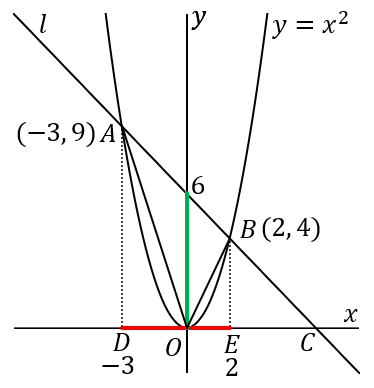
この三角形の面積は、赤 \times 緑 \times\cfrac{1}{2} です。赤のほうは、点 D と 点 E の x 座標はそれぞれ -3, \ 2 なので、長さは 5 です。
このように赤の長さはすぐにわかるですが、緑のほうは、直線 l の y 切片を求める必要があります。
直線 l の式は、点 (-3, \ 9), \ (2, \ 4) の 2 点を通る直線の式、ということで求めていきます。
\begin{eqnarray*}
a&=&\cfrac{y_2-y_1}{x_2-x_1}\\
&=&\cfrac{4-9}{2-(-3)}\\
&=&\cfrac{-5}{5}\\
&=&-1
\end{eqnarray*}
y=-x+b に x=2, \ y=4 を代入する
\begin{eqnarray*}
4&=&-2+b\\
4+2&=&b\\
6&=&b
\end{eqnarray*}
これで直線 l の y 切片は 6 だとわかりました。
なのでこの問題の答えは
\triangle OAB=5\times6\times\cfrac{1}{2}=15
この三角形の面積が、なぜ「赤×緑×\cfrac{1}{2}」とすればうまくいくのかがわからないときは、下の説明ボタンを押して考えてみてください。
(4) 点 A を通り、\triangle OAB の面積を 2 等分する直線の式を求めなさい。
答え
y=-\cfrac{7}{4}x+\cfrac{15}{4}
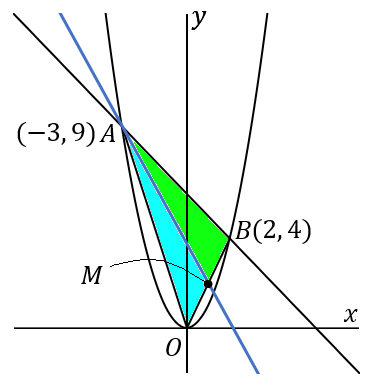 <中線>
<中線>
三角形の 1 つの頂点から、むかいあう辺の中点を通るようにひいた線を中線といいます。三角形の中線は、その三角形の面積を二等分します。
<中点>
中点の座標は、「足して 2 で割る」です。x 座標と y 座標のそれぞれを足して 2 で割ればよいです。「中点は、足して 2 で割る」。わりとよく使う知識なので、おぼえちゃったほうが話が早いです。
この問題の場合は、点 O と 点 B の中点の座標を知りたいわけです。点 O の座標は (0, \ 0), 点 B の座標は (2, \ 4) です。なのでその中点の座標は、
\begin{eqnarray*}
&&\left(\cfrac{x+x}{2}, \ \cfrac{y+y}{2}\right)\\
&=&\left(\cfrac{0+2}{2}, \ \cfrac{0+4}{2}\right)\\
&=&(1, \ 2)
\end{eqnarray*}
となります。中点 M の座標は (1, \ 2) です。
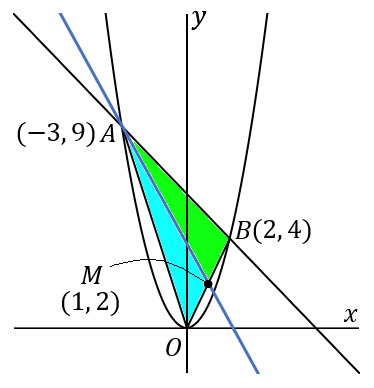 では答えをだしていきましょう。もう一回おなじ図をはっておきます。点 A(-3, \ 9) と点 M(1, \ 2) を通る直線の式を求めればよいです。図の青い線です。
では答えをだしていきましょう。もう一回おなじ図をはっておきます。点 A(-3, \ 9) と点 M(1, \ 2) を通る直線の式を求めればよいです。図の青い線です。
直線の式を求めるときは、答えの形は y=ax+b で、 a と b を求めるのが目標になります。
a=\cfrac{y_2-y_1}{x_2-x_1} に 2 点 A(-3, \ 9) と M(1, \ 2) をあてはめて、
\begin{eqnarray*}
a&=&\cfrac{y_2-y_1}{x_2-x_1}\\
&=&\cfrac{2-9}{1-(-3)}\\
&=&-\cfrac{7}{4}
\end{eqnarray*}
これで a=-\cfrac{7}{4} だということがわかりました。これを y=ax+b に代入して、
y=-\cfrac{7}{4}x+b
この式に、x=1, \ y=2 を代入して b を求めます。
\begin{eqnarray*}
2&=&-\cfrac{7}{4}+b\\
2+\cfrac{7}{4}&=&b\\
\cfrac{8}{4}+\cfrac{7}{4}&=&b\\
\cfrac{15}{4}&=&b
\end{eqnarray*}
これで、a=-\cfrac{7}{4}, \ b=\cfrac{15}{4} だとわかりました。答えは
y=-\cfrac{7}{4}x+\cfrac{15}{4}
答え(中3 2学期期末模擬テスト 第2回)
1①-6 ②11 ③\cfrac{1}{12} ④7x-12y ⑤-\cfrac{\sqrt{2}}{12} ⑥2\sqrt{6} ⑦(x-6y)^2 ⑧x=-13, \ y=-11 ⑨x=\pm\cfrac{\sqrt{14}}{2}
2①y=-\cfrac{6}{5} ②a=1 ③-\cfrac{49}{8} \leqq y \leqq 0
3\triangle ABC ∽\triangle RQP…2 組の辺の比とその間の角が等しい。
\triangle DEF ∽\triangle JKL…2 組の角がそれぞれ等しい。
\triangle GHI ∽\triangle NMO…3 組の辺の比がすべて等しい。
4〈証明〉
\triangle ABC と \triangle DBA で、
仮定から、\angle ACB=\angle DAB ……①
共通な角だから、\angle ABC=\angle DBA ……②
①②より、2 組の角がそれぞれ等しいので
\triangle ABC ∽\ \triangle DBA
5① x=12, \ y=\cfrac{9}{2}
② x=8, \ y=\cfrac{34}{3}
③ x=7, \ y=16
④ x=\cfrac{35}{13}, \ y=\cfrac{252}{13}
⑤ x=10, \ y=\cfrac{49}{5}
6①x=\cfrac{45}{7} ②x=\cfrac{64}{9}
7①x=6 ②x=\cfrac{32}{9} ③x=18, \ y=16 ④x=8, \ y=\cfrac{58}{7}
8①x=10 ②x=3
9〈証明〉
\triangle ABD で、中点連結定理より、
\quad PQ /\!/ AB, \ PQ=\cfrac{1}{2}AB …①
\triangle ABC で、中点連結定理より、
\quad SR /\!/ AB, \ SR=\cfrac{1}{2}AB …②
四角形 PQRS で、①②より、
\quad PQ /\!/ SR, \ PQ=SR
1 組の対辺が平行で長さが等しいので、
四角形 PQRS は平行四辺形である。
10 x=15
11 \cfrac{25}{2}cm^2
12 ①9:25:36 ②9:16:11 ③\cfrac{55}{6}cm^2
13 ①50cm^2 ②250cm^3
14 (1)a=1 (2) \ (-3, \ 9) (3)15 (4)y=-\cfrac{7}{4}x+\cfrac{15}{4}