数学 中3夏期講習 第2回 1次関数と面積
 ページがちゃんと表示されるまで$10$秒くらいかかります。
ページがちゃんと表示されるまで$10$秒くらいかかります。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
「印刷」をクリックすると同じ内容のpdfファイルが表示されます。
 $\huge{1}$
$y$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
$\huge{1}$
$y$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
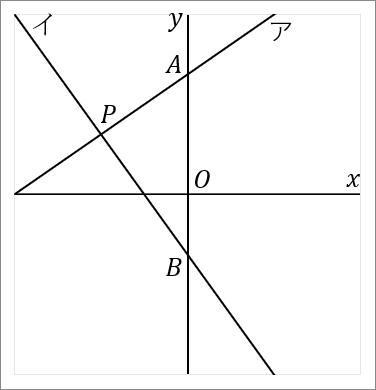
右の図で、直線アは関数 $y=\cfrac{2}{3}x+4$ のグラフであり、直線イは関数 $y=-\cfrac{4}{3}x-2$ のグラフである。直線アと $y$ 軸との交点を $A$ とし、直線イと $y$ 軸との交点を $B$ とする。直線アと直線イとの交点を $P$ とする。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(-3, \ 2)$
$2$ 直線の交点は連立方程式の解です。ア、イの式を連立方程式にして \begin{eqnarray*} && \ \left\{ \begin{array}{l} y=\cfrac{2}{3}x+4\quad…①\\ y=-\cfrac{4}{3}x-2\quad…② \end{array} \right. \end{eqnarray*} これを解けばいいです。解き方は、この手の連立方程式は代入法で、右辺 $=$ 右辺の式をたてて、$x$ を求めていきましょう。関数の問題でよく使うパターンです。 \begin{eqnarray*} 代入法で、右辺 &=& 右辺の式にする。\\\\ \cfrac{2}{3}x+4&=&-\cfrac{4}{3}x-2\quad(両辺に\times3)\\ 2x+12&=&-4x-6\\ 2x+4x&=&-6-12\\ 6x&=&-18\\ x&=&-3 \end{eqnarray*} $x=-3を①に代入$ \begin{eqnarray*} y&=&\cfrac{2}{3}\times(-3)+4\\ &=&-2+4\\ &=&2 \\\\ 答え\\ (-3, \ 2) \end{eqnarray*} ※座標をきかれているのだから、かならず座標の答え方で答えましょう。
$(2)$ $\triangle PAB$ の面積を求めなさい。
答え
$9$
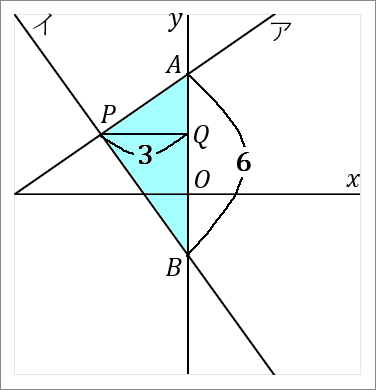 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
点 $A$ の座標は、直線ア $y=\cfrac{2}{3}x+4$ の切片ですから、$(0, \ 4)$ です。
点 $B$ の座標は、直線イ $y=-\cfrac{4}{3}x-2$ の切片ですから、$(0, \ -2)$ です。
なので、$AB$ の長さは $4+2=6$ です。点 $B$ の $y$ 座標は $-2$ ですが、長さの話なのですから絶対値をいうようにしましょう。
<$PQ$ について>
$PQ$ の長さは、点 $P$ の $x$ 座標をみればよいです。点 $P$ の $x$ 座標は $-3$ ですから、$PQ$ の長さは $3$ です。長さの話なのですから、絶対値でいうようにしましょう。
これで底辺と高さがわかりました。では面積をだしましょう。
$$6\times3\times\cfrac{1}{2}=9$$
※答えがでたあと、$9cm^2$ とかいうふうに、やみくもになんにでも単位をつけて答えてしまうひとがいますが、なんでもつけてはいけません。問題によります。この問題は単位をつけてはいけません。問題のどこにも $cm$ とはかかれていないからです。こういうときは答えに単位をつけてはいかんのです。気をつけて。
$(3)$ 点 $P$ を通り、$\triangle PAB$ の面積を二等分する直線の式を求めなさい。
答え
$y=-\cfrac{1}{3}x+1$
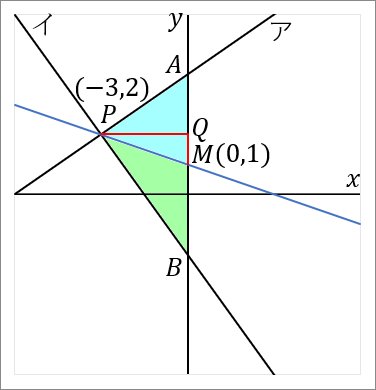 <中線>
<中線>
三角形の $1$ つの頂点から、むかいあう辺の中点を通るようにひいた線を中線といいます。三角形の中線は、その三角形の面積を二等分します。
リクツはこうです。右の図で、$M$ は $AB$ の中点だということにします。すると、水色の三角形と緑色の三角形は、どちらも底辺と高さが等しくなります。それぞれ $AM$ と $MB$ が底辺だとすると、どちらも高さは $PQ$ です。$AM=MB$ なのだから底辺は等しいです。高さは共通なんだから、おなじにきまってます。底辺と高さがおなじなんだから、じゃあ面積はおなじだろうと、こういう話です。
<中点>
中点の座標は、「足して $2$ で割る」です。$x$ 座標と $y$ 座標のそれぞれを足して $2$ で割ればよいです。「中点は、足して $2$ で割る」。わりとよく使う知識なので、おぼえちゃったほうが話が早いです。
この問題の場合は、点 $A$ と 点 $B$ の中点の座標を知りたいわけです。点 $A$ の座標は $(0, \ 4),$ 点 $B$ の座標は $(0, \ -2)$ です。なのでその中点の座標は、
\begin{eqnarray*}
&&\left(\cfrac{x+x}{2}, \ \cfrac{y+y}{2}\right)\\
&=&\left(\cfrac{0+0}{2}, \ \cfrac{4+(-2)}{2}\right)\\
&=&(0, \ 1)
\end{eqnarray*}
となります。中点 $M$ の座標は $(0, \ 1)$ です。
 では答えをだしていきましょう。もう一回おなじ図をはっておきます。点 $P(-3, \ 2)$ と点 $M(0, \ 1)$ を通る直線の式を求めればよいです。図の青い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
では答えをだしていきましょう。もう一回おなじ図をはっておきます。点 $P(-3, \ 2)$ と点 $M(0, \ 1)$ を通る直線の式を求めればよいです。図の青い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$a$ は、点 $P$ と点 $M$ の座標をみくらべて、$P$ から $M$ へいくには、右に $3$ 歩いって下に $1$ 歩いけばいいのだから、$a=-\cfrac{1}{3}$ です。
「$a=\cfrac{縦}{右}$」でやってます。こういうときはこれが速いです。
切片 $b$ は、$y$ 軸上のどこを通るか、ということですからもちろん $1$ です。
これで $a$ も $b$ もわかりました。では答えです。
$$y=-\cfrac{1}{3}x+1$$
※上の $a$ のだしかたがよくわからないときは、「点 $P(-3, \ 2)$ と点 $M(0, \ 1)$ の $2$ 点を通る直線の式を求める」ということで、$a=\cfrac{y-y}{x-x}$ で $a$ を求めていったりとか、連立方程式にして $a$ を求めていったりとか、いつもやってるやり方でやってもOKです。まあ、こういうやり方もあるよね、っていうことです。
 $\huge{2}$
$x$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
$\huge{2}$
$x$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
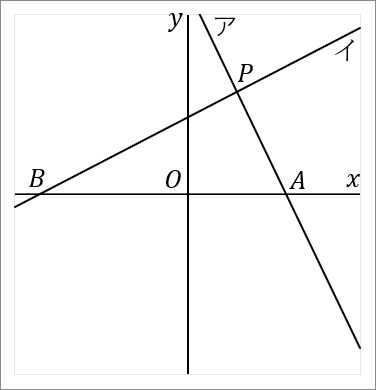
右の図で、直線アと直線イの交点を $P$ とする。直線ア,イと $x$ 軸との交点をそれぞれ $A, \ B$ とする。直線アは関数 $y=-2x+8$ のグラフである。点 $P$ の $x$ 座標が $2,$ 点 $B$ の座標が $(-6, \ 0)$ である。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(2, \ 4)$
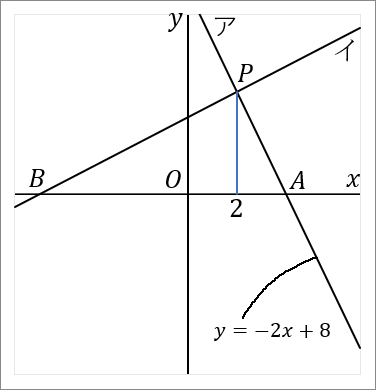 点 $P$ の $x$ 座標は $2$ だと問題にかかれています。あとは $y$ 座標がわかればよいです。また、点 $P$ は直線ア上の点です。アの式はわかっているので、この式を使えば $y$ 座標が求められます。
\begin{eqnarray*}
y&=&-2x+8 に、x=2を代入\\\\
y&=&-2\times2+8\\
&=&-4+8\\
&=&4
\end{eqnarray*}
これで $y=4$ だとわかりました。なので答えは $(2, \ 4)$ です。
点 $P$ の $x$ 座標は $2$ だと問題にかかれています。あとは $y$ 座標がわかればよいです。また、点 $P$ は直線ア上の点です。アの式はわかっているので、この式を使えば $y$ 座標が求められます。
\begin{eqnarray*}
y&=&-2x+8 に、x=2を代入\\\\
y&=&-2\times2+8\\
&=&-4+8\\
&=&4
\end{eqnarray*}
これで $y=4$ だとわかりました。なので答えは $(2, \ 4)$ です。
$(2)$ 直線イの式を求めなさい。
答え
$y=\cfrac{1}{2}x+3$
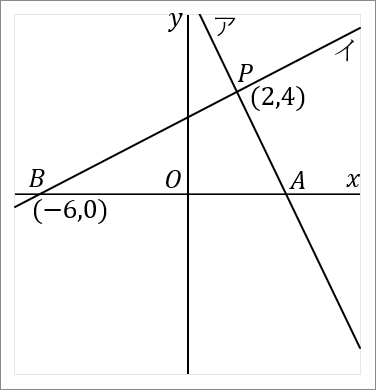 イの式は、点 $B(-6, \ 0)$ を通っています。また、点 $P$ も通っているのですが、その座標は $(1)$ の問題で $(2, \ 4)$ だと求めました。この $2$ 点を通る直線の式だということでやれば、イの式がでます。
イの式は、点 $B(-6, \ 0)$ を通っています。また、点 $P$ も通っているのですが、その座標は $(1)$ の問題で $(2, \ 4)$ だと求めました。この $2$ 点を通る直線の式だということでやれば、イの式がでます。
直線の式を求めなさいといわれたら、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$2$ 点 $(-6, \ 0), \ (2, \ 4)$ を通る直線の式を求めます。
\begin{eqnarray*}
a&=&\cfrac{y-y}{x-x}\\
&=&\cfrac{0-4}{-6-2}=\cfrac{-4}{-8}=\cfrac{1}{2}\\\\
y&=&\cfrac{1}{2}x+bにx=-6,y=0 を代入する\\
0&=&\cfrac{1}{2}\times(-6)+b\\
0&=&-3+b\\
3&=&b\\
\end{eqnarray*}
これで $a$ と $b$ がでました。答えは $y=\cfrac{1}{2}x+3$ です。
$(3)$ $\triangle PAB$ の面積を求めなさい。
答え
$20$
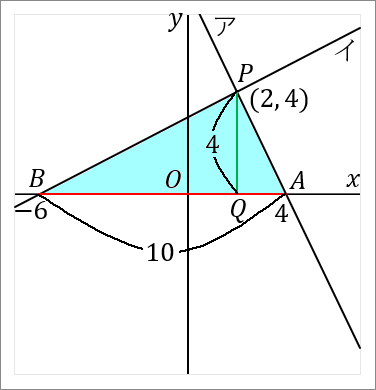 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
点 $A$ の座標は、直線アと $x$ 軸との交点だということで求めます。
ここでポイントがあります。$x$ 軸上の点というのは、$y$ 座標がかならず $0$ です。あたりまえです。$y$ がかならず $0$ なんです。このことを利用して、アの式に $y=0$ を代入すれば、点 $A$ の $x$ 座標が求められます。
\begin{eqnarray*}
y&=&-2x+8にy=0 を代入\\
0&=&-2x+8\\
2x&=&8\\
x&=&4
\end{eqnarray*}
なので点 $A$ の座標は、$(4, \ 0)$ です。
点 $B$ の座標は、$(-6, \ 0)$ です。
というわけで、$AB$ の長さは $4+6=10$ です。点 $B$ の $x$ 座標は $-6$ ですが、長さの話なのですから絶対値をいうようにしましょう。
<$PQ$ について>
$PQ$ の長さは、点 $P$ の $y$ 座標をみればよいです。点 $P$ の $y$ 座標は $4$ ですから、$PQ$ の長さは $4$ です。
これで底辺と高さがわかりました。では面積をだしましょう。
$$10\times4\times\cfrac{1}{2}=20$$
$(4)$ 点 $P$ を通り、$\triangle PAB$ の面積を二等分する直線の式を求めなさい。
答え
$y=\cfrac{4}{3}x+\cfrac{4}{3}$
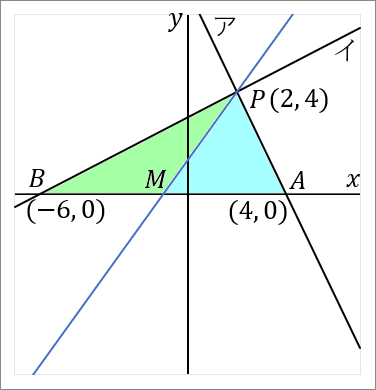 <中線>
<中線>
三角形の $1$ つの頂点から、むかいあう辺の中点を通るようにひいた線を中線といいます。三角形の中線は、その三角形の面積を二等分します。
右の図で、$M$ は $AB$ の中点だということにします。すると、水色の三角形と緑色の三角形は、面積が等しくなります。$\triangle PAB$ の面積は、$PM$ で二等分されています。
<中点>
というわけで、$AB$ の中点 $M$ の座標を求めましょう。中点の座標は、「足して $2$ で割る」です。$x$ 座標と $y$ 座標のそれぞれを足して $2$ で割ればよいです。
点 $A$ の座標は $(4, \ 0),$ 点 $B$ の座標は $(-6, \ 0)$ です。なのでその中点の座標は、
\begin{eqnarray*}
&&\left(\cfrac{x+x}{2}, \ \cfrac{y+y}{2}\right)\\
&=&\left(\cfrac{4+(-6)}{2}, \ \cfrac{0+0}{2}\right)\\
&=&(-1, \ 0)
\end{eqnarray*}
となります。中点 $M$ の座標は $(-1, \ 0)$ です。
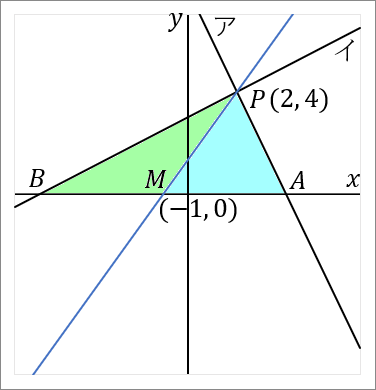 では答えをだしていきましょう。点 $P(2, \ 4)$ と点 $M(-1, \ 0)$ を通る直線の式を求めればよいです。図の青い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
では答えをだしていきましょう。点 $P(2, \ 4)$ と点 $M(-1, \ 0)$ を通る直線の式を求めればよいです。図の青い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$a$ は、点 $M$ と点 $P$ の座標をみくらべて、$M$ から $P$ へいくには、右に $3$ 歩いって上に $4$ 歩いけばいいのだから、$a=\cfrac{4}{3}$ です。
「$a=\cfrac{縦}{右}$」でやってます。こういうときはこれが速いです。
傾き $a$ がわかったので、つぎに、$y=\cfrac{4}{3}x+b$ に点 $P$ か点 $M$ の座標を代入して切片 $b$ を求めます。ここでは点 $M(-1, \ 0)$ を代入することにすると、
\begin{eqnarray*}
0&=&\cfrac{4}{3}\times(-1)+b\\
0&=&-\cfrac{4}{3}+b\\
\cfrac{4}{3}&=&b\\
\end{eqnarray*}
これで $a$ も $b$ もわかりました。では答えです。
$$y=\cfrac{4}{3}x+\cfrac{4}{3}$$
※上の $a$ のだしかたがよくわからないときは、「点 $P(2, \ 4)$ と点 $M(-1, \ 0)$ の $2$ 点を通る直線の式を求める」ということで、$a=\cfrac{y-y}{x-x}$ で $a$ を求めていったりとか、連立方程式にして $a$ を求めていったりとか、いつもやってるやり方でやってもぜんぜんOKです。
 $\huge{3}$
$y$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
$\huge{3}$
$y$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
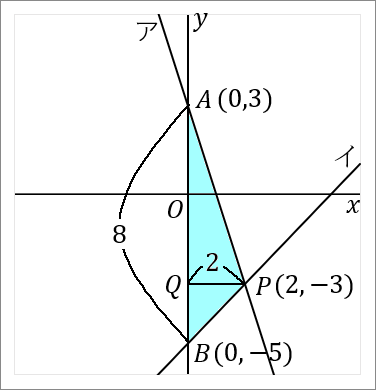
右の図で、直線アは関数 $y=-3x+3$ のグラフであり、直線イは関数 $y=x-5$ のグラフである。直線アと $y$ 軸との交点を $A$ とし、直線イと $y$ 軸との交点を $B$ とする。直線アと直線イとの交点を $P$ とする。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(2, \ -3)$
$2$ 直線の交点は連立方程式の解です。ア、イの式を連立方程式にして \begin{eqnarray*} && \ \left\{ \begin{array}{l} y=-3x+3\quad…①\\ y=x-5\quad…② \end{array} \right. \end{eqnarray*} これを解けばいいです。解き方は、この手の連立方程式は代入法で、右辺 $=$ 右辺の式をたてて、$x$ を求めていきましょう。関数の問題でよく使うパターンです。 \begin{eqnarray*} 代入法で、右辺 &=& 右辺の式にする。\\\\ -3x+3&=&x-5\\ -3x-x&=&-5-3\\ -4x&=&-8\\ x&=&2 \end{eqnarray*} $x=2を②に代入$ \begin{eqnarray*} y&=&2-5\\ &=&-3 \\\\ 答え\\ (2, \ -3) \end{eqnarray*} ※座標をきかれているのだから、かならず座標の答え方で答えましょう。
$(2)$ $\triangle PAB$ の面積を求めなさい。
答え
$8$
 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
点 $A$ の座標は、直線ア $y=-3x+3$ の切片ですから、$(0, \ 3)$ です。
点 $B$ の座標は、直線イ $y=x-5$ の切片ですから、$(0, \ -5)$ です。
なので、$AB$ の長さは $3+5=8$ です。点 $B$ の $y$ 座標は $-5$ ですが、長さの話なのですから絶対値をいうようにしましょう。
<$PQ$ について>
$PQ$ の長さは、点 $P$ の $x$ 座標をみればよいです。点 $P$ の $x$ 座標は $2$ ですから、$PQ$ の長さは $2$ です。
これで底辺と高さがわかりました。では面積をだしましょう。
$$8\times2\times\cfrac{1}{2}=8$$
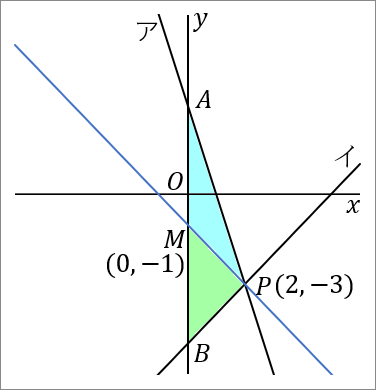
$(3)$ 点 $P$ を通り、$\triangle PAB$ の面積を二等分する直線の式を求めなさい。
答え
$y=-x-1$
 <中線>
<中線>
三角形の $1$ つの頂点から、むかいあう辺の中点を通るようにひいた線を中線といいます。三角形の中線は、その三角形の面積を二等分します。
右の図で、$M$ は $AB$ の中点だということにします。すると、水色の三角形と緑色の三角形は、面積が等しくなります。$\triangle PAB$ の面積は、$PM$ で二等分されています。
<中点>
というわけで、$AB$ の中点 $M$ の座標を求めましょう。中点の座標は、「足して $2$ で割る」です。$x$ 座標と $y$ 座標のそれぞれを足して $2$ で割ればよいです。
点 $A$ の座標は $(0, \ 3),$ 点 $B$ の座標は $(0, \ -5)$ です。なのでその中点の座標は、
\begin{eqnarray*}
&&\left(\cfrac{x+x}{2}, \ \cfrac{y+y}{2}\right)\\
&=&\left(\cfrac{0+0}{2}, \ \cfrac{3+(-5)}{2}\right)\\
&=&(0, \ -1)
\end{eqnarray*}
となります。中点 $M$ の座標は $(0, \ -1)$ です。
 では答えをだしていきましょう。もう一回おなじ図をはっておきます。点 $P(2, \ -3)$ と点 $M(0, \ -1)$ を通る直線の式を求めればよいです。図の青い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
では答えをだしていきましょう。もう一回おなじ図をはっておきます。点 $P(2, \ -3)$ と点 $M(0, \ -1)$ を通る直線の式を求めればよいです。図の青い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$a$ は、点 $P$ と点 $M$ の座標をみくらべて、$M$ から $P$ へいくには、右に $2$ 歩いって下に $2$ 歩いけばいいのだから、$a=-\cfrac{2}{2}=-1$ です。
「$a=\cfrac{縦}{右}$」でやってます。こういうときはこれが速いです。
切片 $b$ は、$y$ 軸上のどこを通るか、ということですからもちろん $-1$ です。
これで $a$ も $b$ もわかりました。では答えです。
$$y=-x-1$$
※上の $a$ のだしかたがよくわからないときは、「点 $P(2, \ -3)$ と点 $M(0, \ -1)$ の $2$ 点を通る直線の式を求める」ということで、$a=\cfrac{y-y}{x-x}$ で $a$ を求めていったりとか、連立方程式にして $a$ を求めていったりとか、いつもやってるやり方でやってもぜんぜんOKです。
 $\huge{4}$
$x$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
$\huge{4}$
$x$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
右の図で、直線アと直線イの交点を $P$ とする。直線ア,イと $x$ 軸との交点をそれぞれ $A, \ B$ とする。直線アは関数 $y=-\cfrac{5}{4}x+\cfrac{5}{2}$ のグラフである。点 $P$ の $x$ 座標が $6,$ 点 $B$ の座標が $(-6, \ 0)$ である。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(6, \ -5)$
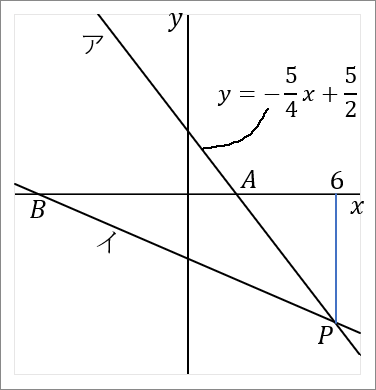 点 $P$ の $x$ 座標は $6$ だと問題にかかれています。あとは $y$ 座標がわかればよいです。また、点 $P$ は直線ア上の点です。アの式はわかっているので、この式を使えば $y$ 座標が求められます。
\begin{eqnarray*}
y&=&-\cfrac{5}{4}x+\cfrac{5}{2} に、x=6を代入\\\\
y&=&-\cfrac{5}{4}\times6+\cfrac{5}{2}\\
y&=&-\cfrac{15}{2}+\cfrac{5}{2}\\
&=&-\cfrac{10}{2}=-5
\end{eqnarray*}
これで $y=-5$ だとわかりました。なので答えは $(6, \ -5)$ です。
点 $P$ の $x$ 座標は $6$ だと問題にかかれています。あとは $y$ 座標がわかればよいです。また、点 $P$ は直線ア上の点です。アの式はわかっているので、この式を使えば $y$ 座標が求められます。
\begin{eqnarray*}
y&=&-\cfrac{5}{4}x+\cfrac{5}{2} に、x=6を代入\\\\
y&=&-\cfrac{5}{4}\times6+\cfrac{5}{2}\\
y&=&-\cfrac{15}{2}+\cfrac{5}{2}\\
&=&-\cfrac{10}{2}=-5
\end{eqnarray*}
これで $y=-5$ だとわかりました。なので答えは $(6, \ -5)$ です。
$(2)$ 直線イの式を求めなさい。
答え
$y=-\cfrac{5}{12}x-\cfrac{5}{2}$
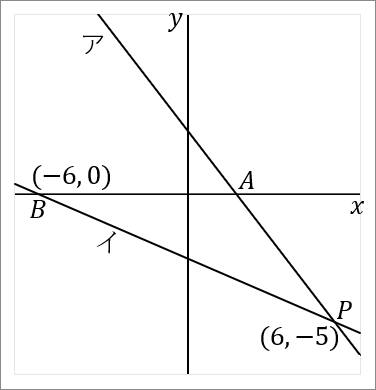 イの式は、点 $B(-6, \ 0)$ を通っています。また、点 $P$ も通っているのですが、その座標は $(1)$ の問題で $(6, \ -5)$ だと求めました。この $2$ 点を通る直線の式だということでやれば、イの式がでます。
イの式は、点 $B(-6, \ 0)$ を通っています。また、点 $P$ も通っているのですが、その座標は $(1)$ の問題で $(6, \ -5)$ だと求めました。この $2$ 点を通る直線の式だということでやれば、イの式がでます。
直線の式を求めなさいといわれたら、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$2$ 点 $(-6, \ 0), \ (6, \ -5)$ を通る直線の式を求めます。
\begin{eqnarray*}
a&=&\cfrac{y-y}{x-x}\\
&=&\cfrac{0-(-5)}{-6-6}=\cfrac{5}{-12}=-\cfrac{5}{12}\\\\
y&=&-\cfrac{5}{12}x+bにx=-6,y=0 を代入する\\
0&=&-\cfrac{5}{12}\times(-6)+b\\
0&=&\cfrac{5}{2}+b\\
-\cfrac{5}{2}&=&b\\
\end{eqnarray*}
これで $a$ と $b$ がでました。答えは $y=-\cfrac{5}{12}x-\cfrac{5}{2}$ です。
$(3)$ $\triangle PAB$ の面積を求めなさい。
答え
$20$
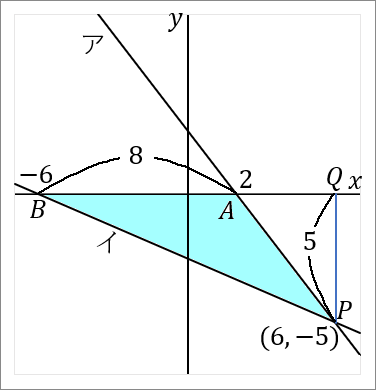 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $x$ 軸におろした垂線と $x$ 軸との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $x$ 軸におろした垂線と $x$ 軸との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
点 $A$ の座標は、直線アと $x$ 軸との交点だということで求めます。
ここでポイントがあります。$x$ 軸上の点というのは、$y$ 座標がかならず $0$ です。あたりまえです。$y$ がかならず $0$ なんです。このことを利用して、アの式に $y=0$ を代入すれば、点 $A$ の $x$ 座標が求められます。
\begin{eqnarray*}
y&=&-\cfrac{5}{4}x+\cfrac{5}{2}にy=0 を代入\\
0&=&-\cfrac{5}{4}x+\cfrac{5}{2}\quad(両辺に\times4)\\
0&=&-5x+10\\
5x&=&10\\
x&=&2
\end{eqnarray*}
なので点 $A$ の座標は、$(2, \ 0)$ です。
点 $B$ の座標は、$(-6, \ 0)$ です。
というわけで、$AB$ の長さは $2+6=8$ です。点 $B$ の $x$ 座標は $-6$ ですが、長さの話なのですから絶対値をいうようにしましょう。
<$PQ$ について>
$PQ$ の長さは、点 $P$ の $y$ 座標をみればよいです。点 $P$ の $y$ 座標は $-5$ ですから、$PQ$ の長さは $5$ です。これも長さの話なのですから絶対値をいうようにしましょう。
これで底辺と高さがわかりました。では面積をだしましょう。
$$8\times5\times\cfrac{1}{2}=20$$
$(4)$ 点 $P$ を通り、$\triangle PAB$ の面積を二等分する直線の式を求めなさい。
答え
$y=-\cfrac{5}{8}x-\cfrac{5}{4}$
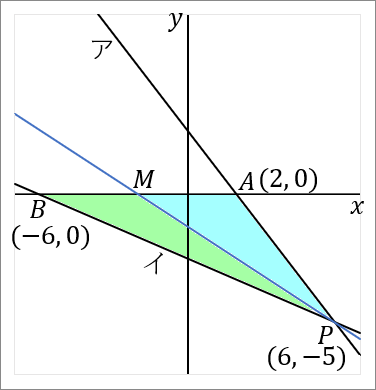 <中線>
<中線>
三角形の $1$ つの頂点から、むかいあう辺の中点を通るようにひいた線を中線といいます。三角形の中線は、その三角形の面積を二等分します。
右の図で、$M$ は $AB$ の中点だということにします。すると、水色の三角形と緑色の三角形は、面積が等しくなります。$\triangle PAB$ の面積は、$PM$ で二等分されています。
<中点>
というわけで、$AB$ の中点 $M$ の座標を求めましょう。中点の座標は、「足して $2$ で割る」です。$x$ 座標と $y$ 座標のそれぞれを足して $2$ で割ればよいです。
点 $A$ の座標は $(2, \ 0),$ 点 $B$ の座標は $(-6, \ 0)$ です。なのでその中点の座標は、
\begin{eqnarray*}
&&\left(\cfrac{x+x}{2}, \ \cfrac{y+y}{2}\right)\\
&=&\left(\cfrac{2+(-6)}{2}, \ \cfrac{0+0}{2}\right)\\
&=&(-2, \ 0)
\end{eqnarray*}
となります。中点 $M$ の座標は $(-2, \ 0)$ です。
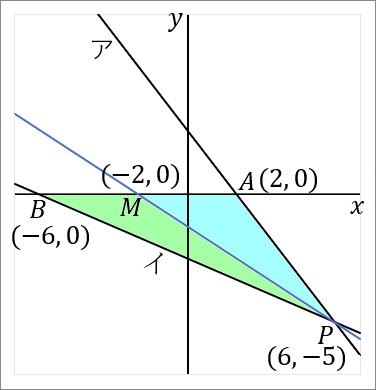 では答えをだしていきましょう。点 $P(6, \ -5)$ と点 $M(-2, \ 0)$ を通る直線の式を求めればよいです。図の青い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
では答えをだしていきましょう。点 $P(6, \ -5)$ と点 $M(-2, \ 0)$ を通る直線の式を求めればよいです。図の青い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$a$ は、点 $M$ と点 $P$ の座標をみくらべて、$M$ から $P$ へいくには、右に $8$ 歩いって下に $5$ 歩いけばいいのだから、$a=-\cfrac{5}{8}$ です。
「$a=\cfrac{縦}{右}$」でやってます。こういうときはこれが速いです。
傾き $a$ がわかったので、つぎに、$y=-\cfrac{5}{8}x+b$ に点 $P$ か点 $M$ の座標を代入して切片 $b$ を求めます。ここでは点 $M(-2, \ 0)$ を代入することにすると、
\begin{eqnarray*}
0&=&-\cfrac{5}{8}\times(-2)+b\\
0&=&\cfrac{5}{4}+b\\
-\cfrac{5}{4}&=&b\\
\end{eqnarray*}
これで $a$ も $b$ もわかりました。では答えです。
$$y=-\cfrac{5}{8}x-\cfrac{5}{4}$$
※上の $a$ のだしかたがよくわからないときは、「点 $P(6, \ -5)$ と点 $M(-2, \ 0)$ の $2$ 点を通る直線の式を求める」ということで、$a=\cfrac{y-y}{x-x}$ で $a$ を求めていったりとか、連立方程式にして $a$ を求めていったりとか、いつもやってるやり方でやってもぜんぜんOKです。
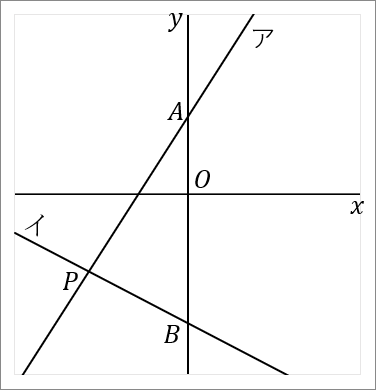 $\huge{5}$
$y$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
$\huge{5}$
$y$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
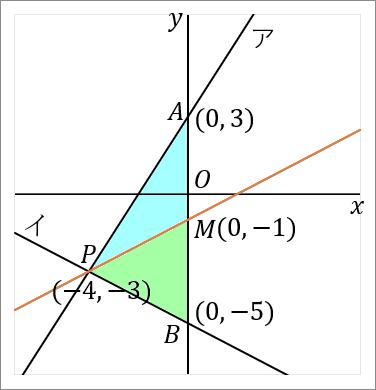
右の図で、直線アは関数 $y=\cfrac{3}{2}x+3$ のグラフであり、直線イは関数 $y=-\cfrac{1}{2}x-5$ のグラフである。直線アと $y$ 軸との交点を $A$ とし、直線イと $y$ 軸との交点を $B$ とする。直線アと直線イとの交点を $P$ とする。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(-4, \ -3)$
$2$ 直線の交点は連立方程式の解です。ア、イの式を連立方程式にして \begin{eqnarray*} && \ \left\{ \begin{array}{l} y=\cfrac{3}{2}x+3\quad…①\\ y=-\cfrac{1}{2}x-5\quad…② \end{array} \right. \end{eqnarray*} これを解けばいいです。解き方は、この手の連立方程式は代入法で、右辺 $=$ 右辺の式をたてて、$x$ を求めていきましょう。関数の問題でよく使うパターンです。 \begin{eqnarray*} 代入法で、右辺 &=& 右辺の式にする。\\\\ \cfrac{3}{2}x+3&=&-\cfrac{1}{2}x-5\quad(両辺に\times2)\\ 3x+6&=&-x-10\\ 3x+x&=&-10-6\\ 4x&=&-16\\ x&=&-4 \end{eqnarray*} $x=-4を①に代入$ \begin{eqnarray*} y&=&\cfrac{3}{2}\times(-4)+3\\ &=&-6+3\\ &=&-3 \\\\ 答え\\ (-4, \ -3) \end{eqnarray*} ※座標をきかれているのだから、かならず座標の答え方で答えましょう。
$(2)$ $\triangle PAB$ の面積を求めなさい。
答え
$16$
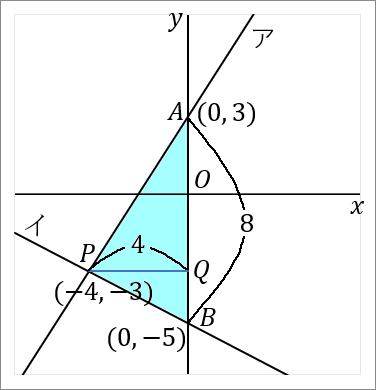 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $AB$ におろした垂線と $AB$ との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
点 $A$ の座標は、直線ア $y=\cfrac{3}{2}x+3$ の切片ですから、$(0, \ 3)$ です。
点 $B$ の座標は、直線イ $y=-\cfrac{1}{2}x-5$ の切片ですから、$(0, \ -5)$ です。
なので、$AB$ の長さは $3+5=8$ です。点 $B$ の $y$ 座標は $-5$ ですが、長さの話なのですから絶対値をいうようにしましょう。
<$PQ$ について>
$PQ$ の長さは、点 $P$ の $x$ 座標をみればよいです。点 $P$ の $x$ 座標は $-4$ ですから、$PQ$ の長さは $4$ です。これも長さの話なのですから絶対値をいうようにしましょう。
これで底辺と高さがわかりました。では面積をだしましょう。
$$8\times4\times\cfrac{1}{2}=16$$
$(3)$ 点 $P$ を通り、$\triangle PAB$ の面積を二等分する直線の式を求めなさい。
答え
$y=\cfrac{1}{2}x-1$
 <中線>
<中線>
三角形の $1$ つの頂点から、むかいあう辺の中点を通るようにひいた線を中線といいます。三角形の中線は、その三角形の面積を二等分します。
右の図で、$M$ は $AB$ の中点だということにします。すると、水色の三角形と緑色の三角形は、面積が等しくなります。$\triangle PAB$ の面積は、$PM$ で二等分されています。
<中点>
というわけで、$AB$ の中点 $M$ の座標を求めましょう。中点の座標は、「足して $2$ で割る」です。$x$ 座標と $y$ 座標のそれぞれを足して $2$ で割ればよいです。
点 $A$ の座標は $(0, \ 3),$ 点 $B$ の座標は $(0, \ -5)$ です。なのでその中点の座標は、
\begin{eqnarray*}
&&\left(\cfrac{x+x}{2}, \ \cfrac{y+y}{2}\right)\\
&=&\left(\cfrac{0+0}{2}, \ \cfrac{3+(-5)}{2}\right)\\
&=&(0, \ -1)
\end{eqnarray*}
となります。中点 $M$ の座標は $(0, \ -1)$ です。
 では答えをだしていきましょう。点 $P(-4, \ -3)$ と点 $M(0, \ -1)$ を通る直線の式を求めればよいです。図の赤い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
では答えをだしていきましょう。点 $P(-4, \ -3)$ と点 $M(0, \ -1)$ を通る直線の式を求めればよいです。図の赤い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$a$ は、点 $P$ と点 $M$ の座標をみくらべて、$P$ から $M$ へいくには、右に $4$ 歩いって上に $2$ 歩いけばいいのだから、$a=\cfrac{2}{4}=\cfrac{1}{2}$ です。
「$a=\cfrac{縦}{右}$」でやってます。こういうときはこれが速いです。
切片 $b$ は、$y$ 軸上のどこを通るか、ということですからもちろん $-1$ です。
これで $a$ も $b$ もわかりました。では答えです。
$$y=\cfrac{1}{2}x-1$$
※上の $a$ のだしかたがよくわからないときは、「点 $P(-4, \ -3)$ と点 $M(0, \ -1)$ の $2$ 点を通る直線の式を求める」ということで、$a=\cfrac{y-y}{x-x}$ で $a$ を求めていったりとか、連立方程式にして $a$ を求めていったりとか、いつもやってるやり方でやってもぜんぜんOKです。
 $\huge{6}$
$x$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
$\huge{6}$
$x$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
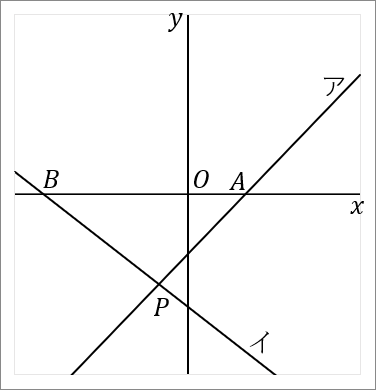
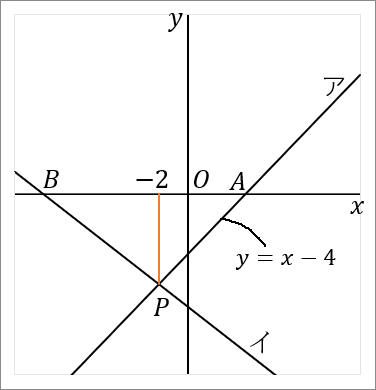
右の図で、直線アと直線イの交点を $P$ とする。直線ア,イと $x$ 軸との交点をそれぞれ $A, \ B$ とする。直線アは関数 $y=x-4$ のグラフである。点 $P$ の $x$ 座標が $-2,$ 点 $B$ の座標が $(-10, \ 0)$ である。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(-2, \ -6)$
 点 $P$ の $x$ 座標は $-2$ だと問題にかかれています。あとは $y$ 座標がわかればよいです。また、点 $P$ は直線ア上の点です。アの式はわかっているので、この式を使えば $y$ 座標が求められます。
\begin{eqnarray*}
y&=&x-4 に、x=-2を代入\\\\
y&=&-2-4\\
&=&-6
\end{eqnarray*}
これで $y=-6$ だとわかりました。なので答えは $(-2, \ -6)$ です。
点 $P$ の $x$ 座標は $-2$ だと問題にかかれています。あとは $y$ 座標がわかればよいです。また、点 $P$ は直線ア上の点です。アの式はわかっているので、この式を使えば $y$ 座標が求められます。
\begin{eqnarray*}
y&=&x-4 に、x=-2を代入\\\\
y&=&-2-4\\
&=&-6
\end{eqnarray*}
これで $y=-6$ だとわかりました。なので答えは $(-2, \ -6)$ です。
$(2)$ 直線イの式を求めなさい。
答え
$y=-\cfrac{3}{4}x-\cfrac{15}{2}$
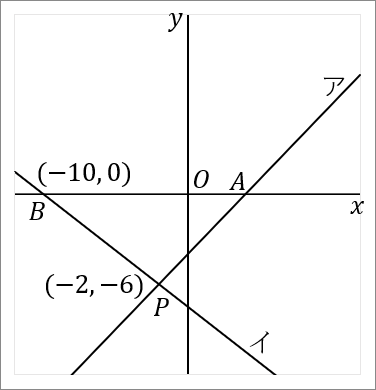 イの式は、点 $B(-10, \ 0)$ を通っています。また、点 $P$ も通っているのですが、その座標は $(1)$ の問題で $(-2, \ -6)$ だと求めました。この $2$ 点を通る直線の式だということでやれば、イの式がでます。
イの式は、点 $B(-10, \ 0)$ を通っています。また、点 $P$ も通っているのですが、その座標は $(1)$ の問題で $(-2, \ -6)$ だと求めました。この $2$ 点を通る直線の式だということでやれば、イの式がでます。
直線の式を求めなさいといわれたら、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$2$ 点 $(-10, \ 0), \ (-2, \ -6)$ を通る直線の式を求めます。
\begin{eqnarray*}
a&=&\cfrac{y-y}{x-x}\\
&=&\cfrac{0-(-6)}{-10-(-2)}=\cfrac{6}{-8}=-\cfrac{3}{4}\\\\
y&=&-\cfrac{3}{4}x+bにx=-10,y=0 を代入する\\
0&=&-\cfrac{3}{4}\times(-10)+b\\
0&=&\cfrac{15}{2}+b\\
-\cfrac{15}{2}&=&b\\
\end{eqnarray*}
これで $a$ と $b$ がでました。答えは $y=-\cfrac{3}{4}x-\cfrac{15}{2}$ です。
$(3)$ $\triangle PAB$ の面積を求めなさい。
答え
$42$
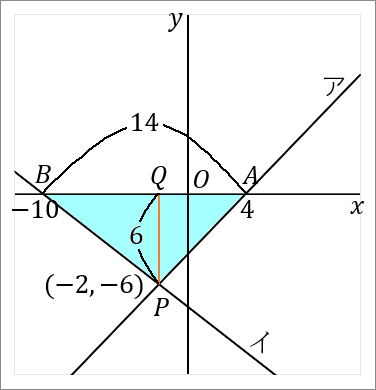 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $x$ 軸におろした垂線と $x$ 軸との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $x$ 軸におろした垂線と $x$ 軸との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
点 $A$ の座標は、直線アと $x$ 軸との交点だということで求めます。
ここでポイントがあります。$x$ 軸上の点というのは、$y$ 座標がかならず $0$ です。あたりまえです。$y$ がかならず $0$ なんです。このことを利用して、アの式に $y=0$ を代入すれば、点 $A$ の $x$ 座標が求められます。
\begin{eqnarray*}
y&=&x-4にy=0 を代入\\
0&=&x-4\\
4&=&x
\end{eqnarray*}
なので点 $A$ の座標は、$(4, \ 0)$ です。
点 $B$ の座標は、$(-10, \ 0)$ です。
というわけで、$AB$ の長さは $4+10=14$ です。点 $B$ の $x$ 座標は $-10$ ですが、長さの話なのですから絶対値をいうようにしましょう。
<$PQ$ について>
$PQ$ の長さは、点 $P$ の $y$ 座標をみればよいです。点 $P$ の $y$ 座標は $-6$ ですから、$PQ$ の長さは $6$ です。これも長さの話なのですから絶対値をいうようにしましょう。
これで底辺と高さがわかりました。では面積をだしましょう。
$$14\times6\times\cfrac{1}{2}=42$$
$(4)$ 点 $B$ を通り、$\triangle PAB$ の面積を二等分する直線の式を求めなさい。
答え
$y=-\cfrac{3}{11}x-\cfrac{30}{11}$
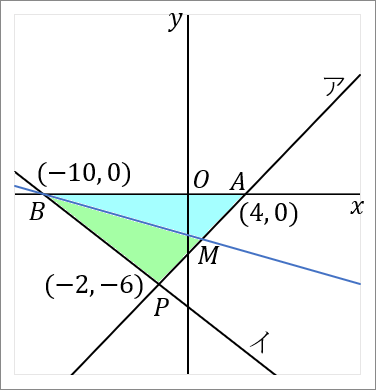 <中線>
<中線>
三角形の $1$ つの頂点から、むかいあう辺の中点を通るようにひいた線を中線といいます。三角形の中線は、その三角形の面積を二等分します。
右の図で、$M$ は $AP$ の中点だということにします。すると、水色の三角形と緑色の三角形は、面積が等しくなります。$\triangle PAB$ の面積は、$BM$ で二等分されています。
<中点>
というわけで、$AP$ の中点 $M$ の座標を求めましょう。中点の座標は、「足して $2$ で割る」です。$x$ 座標と $y$ 座標のそれぞれを足して $2$ で割ればよいです。
点 $A$ の座標は $(4, \ 0),$ 点 $P$ の座標は $(-2, \ -6)$ です。なのでその中点の座標は、
\begin{eqnarray*}
&&\left(\cfrac{x+x}{2}, \ \cfrac{y+y}{2}\right)\\
&=&\left(\cfrac{4+(-2)}{2}, \ \cfrac{0+(-6)}{2}\right)\\
&=&(1, \ -3)
\end{eqnarray*}
となります。中点 $M$ の座標は $(1, \ -3)$ です。
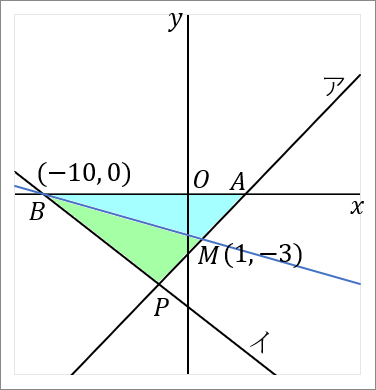 では答えをだしていきましょう。点 $B(-10, \ 0)$ と点 $M(1, \ -3)$ を通る直線の式を求めればよいです。図の青い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
では答えをだしていきましょう。点 $B(-10, \ 0)$ と点 $M(1, \ -3)$ を通る直線の式を求めればよいです。図の青い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$a$ は、点 $B$ と点 $M$ の座標をみくらべて、$B$ から $M$ へいくには、右に $11$ 歩いって下に $3$ 歩いけばいいのだから、$a=-\cfrac{3}{11}$ です。
「$a=\cfrac{縦}{右}$」でやってます。こういうときはこれが速いです。
傾き $a$ がわかったので、つぎに、$y=-\cfrac{3}{11}x+b$ に点 $B$ か点 $M$ の座標を代入して切片 $b$ を求めます。ここでは点 $B(-10, \ 0)$ を代入することにすると、
\begin{eqnarray*}
0&=&-\cfrac{3}{11}\times(-10)+b\\
0&=&\cfrac{30}{11}+b\\
-\cfrac{30}{11}&=&b\\
\end{eqnarray*}
これで $a$ も $b$ もわかりました。では答えです。
$$y=-\cfrac{3}{11}x-\cfrac{30}{11}$$
※上の $a$ のだしかたがよくわからないときは、「点 $B(-10, \ 0)$ と点 $M(1, \ -3)$ の $2$ 点を通る直線の式を求める」ということで、$a=\cfrac{y-y}{x-x}$ で $a$ を求めていったりとか、連立方程式にして $a$ を求めていったりとか、いつもやってるやり方でやってもぜんぜんOKです。
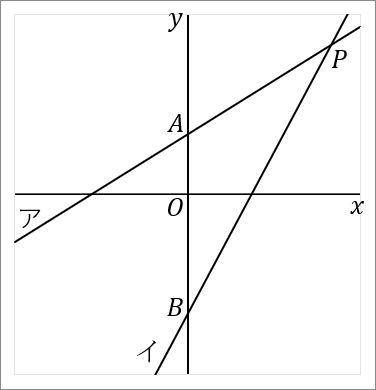 $\huge{7}$
$y$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
$\huge{7}$
$y$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
右の図で、直線アは関数 $y=\cfrac{3}{5}x+4$ のグラフであり、直線イは関数 $y=\cfrac{9}{5}x-8$ のグラフである。直線アと $y$ 軸との交点を $A$ とし、直線イと $y$ 軸との交点を $B$ とする。直線アと直線イとの交点を $P$ とする。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(10, \ 10)$
$2$ 直線の交点は連立方程式の解です。ア、イの式を連立方程式にして \begin{eqnarray*} && \ \left\{ \begin{array}{l} y=\cfrac{3}{5}x+4\quad…①\\ y=\cfrac{9}{5}x-8\quad…② \end{array} \right. \end{eqnarray*} これを解けばいいです。解き方は、この手の連立方程式は代入法で、右辺 $=$ 右辺の式をたてて、$x$ を求めていきましょう。関数の問題でよく使うパターンです。 \begin{eqnarray*} 代入法で、右辺 &=& 右辺の式にする。\\\\ \cfrac{3}{5}x+4&=&\cfrac{9}{5}x-8\quad(両辺に\times5)\\ 3x+20&=&9x-40\\ 3x-9x&=&-40-20\\ -6x&=&-60\\ x&=&10 \end{eqnarray*} $x=10を①に代入$ \begin{eqnarray*} y&=&\cfrac{3}{5}\times10+4\\ &=&6+4\\ &=&10 \\\\ 答え\\ (10, \ 10) \end{eqnarray*} ※座標をきかれているのだから、かならず座標の答え方で答えましょう。
$(2)$ $\triangle PAB$ の面積を求めなさい。
答え
$60$
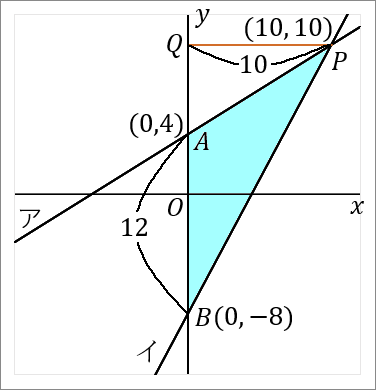 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $y$ 軸におろした垂線と $y$ 軸との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $y$ 軸におろした垂線と $y$ 軸との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
点 $A$ の座標は、直線ア $y=\cfrac{4}{5}x+4$ の切片ですから、$(0, \ 4)$ です。
点 $B$ の座標は、直線イ $y=\cfrac{9}{5}x-8$ の切片ですから、$(0, \ -8)$ です。
なので、$AB$ の長さは $4+8=12$ です。点 $B$ の $y$ 座標は $-8$ ですが、長さの話なのですから絶対値をいうようにしましょう。
<$PQ$ について>
$PQ$ の長さは、点 $P$ の $x$ 座標をみればよいです。点 $P$ の $x$ 座標は $10$ ですから、$PQ$ の長さは $10$ です。
これで底辺と高さがわかりました。では面積をだしましょう。
$$12\times10\times\cfrac{1}{2}=60$$
$(3)$ 点 $A$ を通り、$\triangle PAB$ の面積を二等分する直線の式を求めなさい。
答え
$y=-\cfrac{3}{5}x+4$
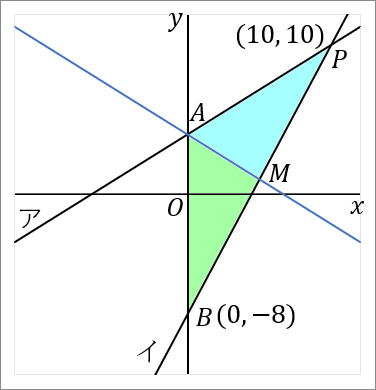 <中線>
<中線>
三角形の $1$ つの頂点から、むかいあう辺の中点を通るようにひいた線を中線といいます。三角形の中線は、その三角形の面積を二等分します。
右の図で、$M$ は $PB$ の中点だということにします。すると、水色の三角形と緑色の三角形は、面積が等しくなります。$\triangle PAB$ の面積は、$AM$ で二等分されています。
<中点>
というわけで、$PB$ の中点 $M$ の座標を求めましょう。中点の座標は、「足して $2$ で割る」です。$x$ 座標と $y$ 座標のそれぞれを足して $2$ で割ればよいです。
点 $P$ の座標は $(10, \ 10),$ 点 $B$ の座標は $(0, \ -8)$ です。なのでその中点の座標は、
\begin{eqnarray*}
&&\left(\cfrac{x+x}{2}, \ \cfrac{y+y}{2}\right)\\
&=&\left(\cfrac{10+0}{2}, \ \cfrac{10+(-8)}{2}\right)\\
&=&(5, \ 1)
\end{eqnarray*}
となります。中点 $M$ の座標は $(5, \ 1)$ です。
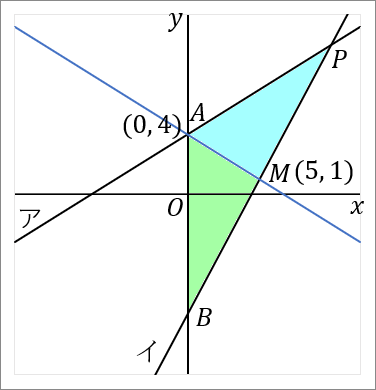 では答えをだしていきましょう。点 $A(0, \ 4)$ と点 $M(5, \ 1)$ を通る直線の式を求めればよいです。図の青い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
では答えをだしていきましょう。点 $A(0, \ 4)$ と点 $M(5, \ 1)$ を通る直線の式を求めればよいです。図の青い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$a$ は、点 $A$ と点 $M$ の座標をみくらべて、$A$ から $M$ へいくには、右に $5$ 歩いって下に $3$ 歩いけばいいのだから、$a=-\cfrac{3}{5}$ です。
「$a=\cfrac{縦}{右}$」でやってます。こういうときはこれが速いです。
切片 $b$ は、$y$ 軸上のどこを通るか、ということですからもちろん $4$ です。
これで $a$ も $b$ もわかりました。では答えです。
$$y=-\cfrac{3}{5}x+4$$
※上の $a$ のだしかたがよくわからないときは、「点 $A(0, \ 4)$ と点 $M(5, \ 1)$ の $2$ 点を通る直線の式を求める」ということで、$a=\cfrac{y-y}{x-x}$ で $a$ を求めていったりとか、連立方程式にして $a$ を求めていったりとか、いつもやってるやり方でやってもぜんぜんOKです。
 $\huge{8}$
$x$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
$\huge{8}$
$x$ 軸と $2$ 直線で囲まれた三角形の面積を求める問題
右の図で、直線アと直線イの交点を $P$ とする。直線ア,イと $x$ 軸との交点をそれぞれ $A, \ B$ とする。直線アは関数 $y=-\cfrac{1}{2}x+\cfrac{11}{2}$ のグラフである。点 $P$ の $x$ 座標が $-9,$ 点 $B$ の座標が $(-5, \ 0)$ である。このとき、以下の問いに答えなさい。
$(1)$ 点 $P$ の座標を求めなさい。
答え
$(-9, \ 10)$
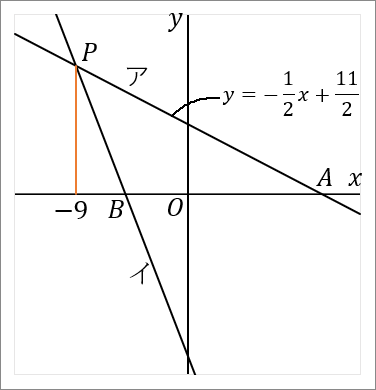 点 $P$ の $x$ 座標は $-9$ だと問題にかかれています。あとは $y$ 座標がわかればよいです。また、点 $P$ は直線ア上の点です。アの式はわかっているので、この式を使えば $y$ 座標が求められます。
\begin{eqnarray*}
y&=&-\cfrac{1}{2}x+\cfrac{11}{2} に、x=-9を代入\\\\
y&=&-\cfrac{1}{2}\times(-9)+\cfrac{11}{2}\\
y&=&\cfrac{9}{2}+\cfrac{11}{2}\\
&=&\cfrac{20}{2}=10
\end{eqnarray*}
これで $y=2$ だとわかりました。なので答えは $(-9, \ 10)$ です。
点 $P$ の $x$ 座標は $-9$ だと問題にかかれています。あとは $y$ 座標がわかればよいです。また、点 $P$ は直線ア上の点です。アの式はわかっているので、この式を使えば $y$ 座標が求められます。
\begin{eqnarray*}
y&=&-\cfrac{1}{2}x+\cfrac{11}{2} に、x=-9を代入\\\\
y&=&-\cfrac{1}{2}\times(-9)+\cfrac{11}{2}\\
y&=&\cfrac{9}{2}+\cfrac{11}{2}\\
&=&\cfrac{20}{2}=10
\end{eqnarray*}
これで $y=2$ だとわかりました。なので答えは $(-9, \ 10)$ です。
$(2)$ 直線イの式を求めなさい。
答え
$y=-\cfrac{5}{2}x-\cfrac{25}{2}$
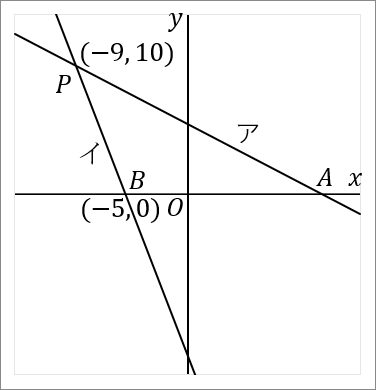 イの式は、点 $B(-5, \ 0)$ を通っています。また、点 $P$ も通っているのですが、その座標は $(1)$ の問題で $(-9, \ 10)$ だと求めました。この $2$ 点を通る直線の式だということでやれば、イの式がでます。
イの式は、点 $B(-5, \ 0)$ を通っています。また、点 $P$ も通っているのですが、その座標は $(1)$ の問題で $(-9, \ 10)$ だと求めました。この $2$ 点を通る直線の式だということでやれば、イの式がでます。
直線の式を求めなさいといわれたら、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$2$ 点 $(-5, \ 0), \ (-9, \ 10)$ を通る直線の式を求めます。
\begin{eqnarray*}
a&=&\cfrac{y-y}{x-x}\\
&=&\cfrac{0-10}{-5-(-9)}=\cfrac{-10}{4}=-\cfrac{5}{2}\\\\
y&=&-\cfrac{5}{2}x+bにx=-5,y=0 を代入する\\
0&=&-\cfrac{5}{2}\times(-5)+b\\
0&=&\cfrac{25}{2}+b\\
-\cfrac{25}{2}&=&b\\
\end{eqnarray*}
これで $a$ と $b$ がでました。答えは $y=-\cfrac{5}{2}x-\cfrac{25}{2}$ です。
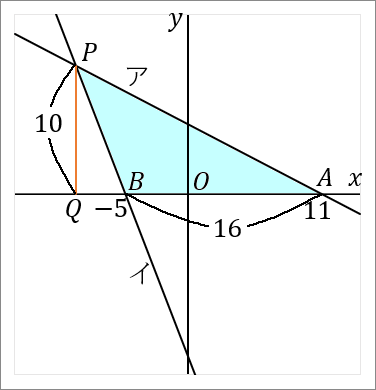
$(3)$ $\triangle PAB$ の面積を求めなさい。
答え
$80$
 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $x$ 軸におろした垂線と $x$ 軸との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。
$AB$ を底辺とします。$P$ から $x$ 軸におろした垂線と $x$ 軸との交点を $Q$ とでもしておきます。すると $PQ$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$AB$ について>
点 $A$ の座標は、直線アと $x$ 軸との交点だということで求めます。
ここでポイントがあります。$x$ 軸上の点というのは、$y$ 座標がかならず $0$ です。あたりまえです。$y$ がかならず $0$ なんです。このことを利用して、アの式に $y=0$ を代入すれば、点 $A$ の $x$ 座標が求められます。
\begin{eqnarray*}
y&=&-\cfrac{1}{2}x+\cfrac{11}{2}にy=0 を代入\\
0&=&-\cfrac{1}{2}x+\cfrac{11}{2}\quad(両辺に\times2)\\
0&=&-x+11\\
x&=&11
\end{eqnarray*}
なので点 $A$ の座標は、$(11, \ 0)$ です。
点 $B$ の座標は、$(-5, \ 0)$ です。
というわけで、$AB$ の長さは $11+5=16$ です。点 $B$ の $x$ 座標は $-5$ ですが、長さの話なのですから絶対値をいうようにしましょう。
<$PQ$ について>
$PQ$ の長さは、点 $P$ の $y$ 座標をみればよいです。点 $P$ の $y$ 座標は $10$ ですから、$PQ$ の長さは $10$ です。
これで底辺と高さがわかりました。では面積をだしましょう。
$$16\times10\times\cfrac{1}{2}=80$$
$(4)$ 点 $B$ を通り、$\triangle PAB$ の面積を二等分する直線の式を求めなさい。
答え
$y=\cfrac{5}{6}x+\cfrac{25}{6}$
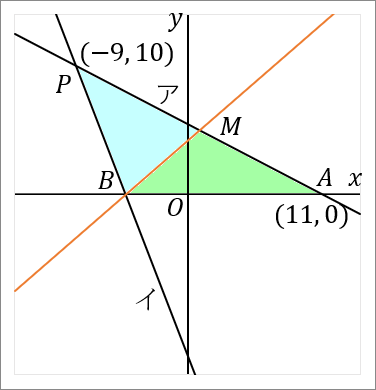 <中線>
<中線>
三角形の $1$ つの頂点から、むかいあう辺の中点を通るようにひいた線を中線といいます。三角形の中線は、その三角形の面積を二等分します。
右の図で、$M$ は $AP$ の中点だということにします。すると、水色の三角形と緑色の三角形は、面積が等しくなります。$\triangle PAB$ の面積は、$BM$ で二等分されています。
<中点>
というわけで、$AP$ の中点 $M$ の座標を求めましょう。中点の座標は、「足して $2$ で割る」です。$x$ 座標と $y$ 座標のそれぞれを足して $2$ で割ればよいです。
点 $A$ の座標は $(11, \ 0),$ 点 $P$ の座標は $(-9, \ 10)$ です。なのでその中点の座標は、
\begin{eqnarray*}
&&\left(\cfrac{x+x}{2}, \ \cfrac{y+y}{2}\right)\\
&=&\left(\cfrac{11+(-9)}{2}, \ \cfrac{0+10}{2}\right)\\
&=&(1, \ 5)
\end{eqnarray*}
となります。中点 $M$ の座標は $(1, \ 5)$ です。
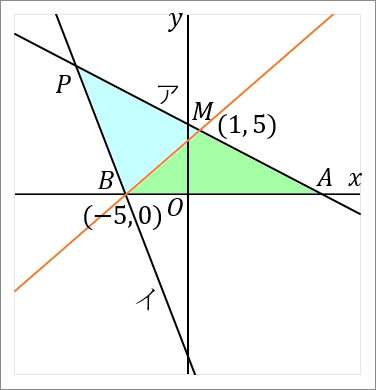 では答えをだしていきましょう。点 $B(-5, \ 0)$ と点 $M(1, \ 5)$ を通る直線の式を求めればよいです。図の赤い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
では答えをだしていきましょう。点 $B(-5, \ 0)$ と点 $M(1, \ 5)$ を通る直線の式を求めればよいです。図の赤い線です。直線の式を求めるときは、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$a$ は、点 $B$ と点 $M$ の座標をみくらべて、$B$ から $M$ へいくには、右に $6$ 歩いって上に $5$ 歩いけばいいのだから、$a=\cfrac{5}{6}$ です。
「$a=\cfrac{縦}{右}$」でやってます。こういうときはこれが速いです。
傾き $a$ がわかったので、つぎに、$y=\cfrac{5}{6}x+b$ に点 $B$ か点 $M$ の座標を代入して切片 $b$ を求めます。ここでは点 $B(-5, \ 0)$ を代入することにすると、
\begin{eqnarray*}
0&=&\cfrac{5}{6}\times(-5)+b\\
0&=&-\cfrac{25}{6}+b\\
\cfrac{25}{6}&=&b\\
\end{eqnarray*}
これで $a$ も $b$ もわかりました。では答えです。
$$y=\cfrac{5}{6}x+\cfrac{25}{6}$$
※上の $a$ のだしかたがよくわからないときは、「点 $B(-5, \ 0)$ と点 $M(1, \ 5)$ の $2$ 点を通る直線の式を求める」ということで、$a=\cfrac{y-y}{x-x}$ で $a$ を求めていったりとか、連立方程式にして $a$ を求めていったりとか、いつもやってるやり方でやってもぜんぜんOKです。
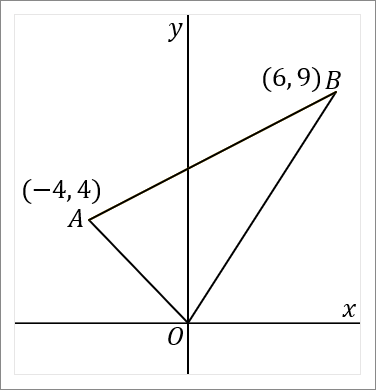 $\huge{9}$
原点を通る $2$ 直線を使った三角形の面積を求める問題
$\huge{9}$
原点を通る $2$ 直線を使った三角形の面積を求める問題
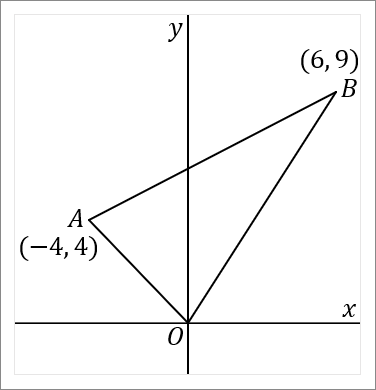
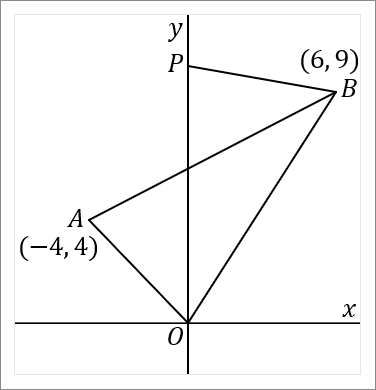
右の図で、$2$ 点 $A, \ B$ の座標はそれぞれ $(-4, \ 4) \ , \ (6, \ 9)$ である。このとき、以下の問いに答えなさい。
$(1)$ $2$ 点 $A, \ B$ を通る直線の式を求めなさい。
答え
$y=\cfrac{1}{2}x+6$
直線の式を求めなさいといわれたら、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$2$ 点 $(-4, \ 4), \ (6, \ 9)$ を通る直線の式を求めます。
\begin{eqnarray*}
a&=&\cfrac{y-y}{x-x}\\
&=&\cfrac{4-9}{-4-6}=\cfrac{-5}{-10}=\cfrac{1}{2}\\\\
y&=&\cfrac{1}{2}x+bにx=-4,y=4 を代入する\\
4&=&\cfrac{1}{2}\times(-4)+b\\
4&=&-2+b\\
6&=&b\\
\end{eqnarray*}
これで $a$ と $b$ がでました。答えは $y=\cfrac{1}{2}x+6$ です。
$(2)$ $\triangle OAB$ の面積を求めなさい。
答え
$30$
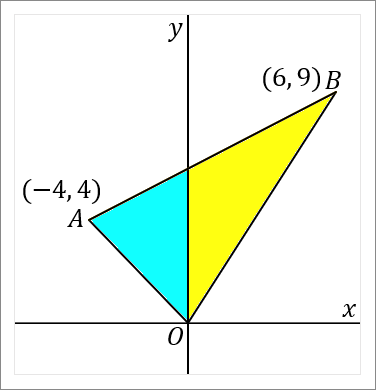 三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。が、$OA$ や $OB$ や $AB$ のどれを底辺にすることにしても、なかなかうまくいきません。この問題の場合は、$y$ 軸で $2$ つの三角形にわけてしまい、それぞれの面積を求めていくのがよいです。図の、水色の三角形の面積と黄色の三角形の面積をそれぞれ求めて、それらを足したのが答え、という感じです。
三角形の面積は「底辺 $\times$ 高さ $\times\cfrac{1}{2}$」です。が、$OA$ や $OB$ や $AB$ のどれを底辺にすることにしても、なかなかうまくいきません。この問題の場合は、$y$ 軸で $2$ つの三角形にわけてしまい、それぞれの面積を求めていくのがよいです。図の、水色の三角形の面積と黄色の三角形の面積をそれぞれ求めて、それらを足したのが答え、という感じです。
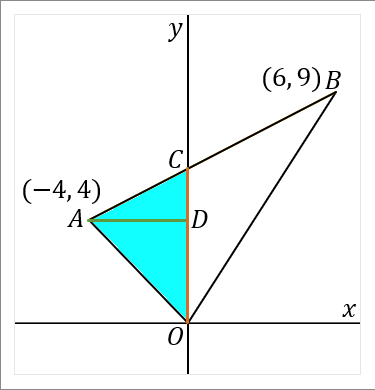 <水色の三角形>
<水色の三角形>
$2$ 点 $A, \ B$ を通る直線と $y$ 軸との交点を $C$ とします。また、点 $A$ から $y$ 軸に垂線をおろして、$y$ 軸との交点を $D$ とします。
$CO$ を底辺とします。すると $AD$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$CO$ について>
点 $C$ の座標は、$2$ 点 $A, \ B$ を通る直線の切片をいえばよいです。$(1)$ の問題の答えをみてください。切片は $6$ です。なので $CO$ の長さは $6$ です。
<$AD$ について>
$AD$ の長さは、点 $A$ の $x$ 座標をみればよいです。なので $AD$ の長さは $4$ です。座標は $-4$ ですが、長さの話なので絶対値をいうようにしましょう。
これで底辺と高さがわかったので、水色の三角形の面積がだせます。
\begin{eqnarray*}
\triangle OAC&=&6\times4\times\cfrac{1}{2}=12
\end{eqnarray*}
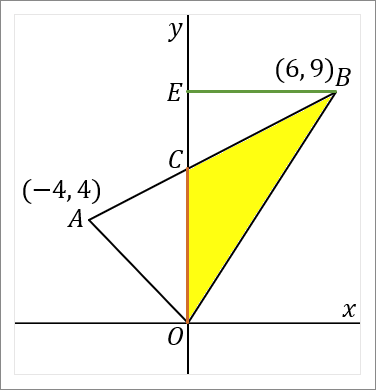 <黄色の三角形>
<黄色の三角形>
点 $B$ から $y$ 軸に垂線をおろして、$y$ 軸との交点を $E$ とします。
$CO$ を底辺とします。すると $BE$ が高さということになります。それぞれの長さを求めて面積をだしましょう。
<$CO$ について>
さきほど説明したように、$CO$ の長さは $6$ です。
<$BE$ について>
$BE$ の長さは、点 $B$ の $x$ 座標をみればよいです。なので $BE$ の長さは $6$ です。
これで底辺と高さがわかったので、黄色の三角形の面積がだせます。
\begin{eqnarray*}
\triangle OBC&=&6\times6\times\cfrac{1}{2}=18
\end{eqnarray*}
 <$\triangle OAB$ について>
<$\triangle OAB$ について>
$\triangle OAB$ の面積は、水色の三角形の面積と黄色の三角形の面積を足せばよいわけですから、
\begin{eqnarray*}
\triangle OAB&=&12+18=30
\end{eqnarray*}
これが答えです。
<このやりかたをおぼえましょう>
この問題はよく出題されます。そんで、もっとてっとり早いやり方があります。なのでそれをおぼえてしまいましょう。
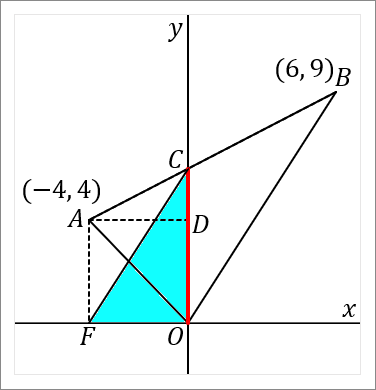 まず、$\triangle OAB$ を $y$ 軸のところでわけるところまではおなじです。ここで、左側の、水色の三角形を等積変形します。点 $A$ から $x$ 軸に垂線をおろして、$x$ 軸との交点を $F$ とします。すると、$\triangle OAC$ と $\triangle OFC$ は面積がおなじです。$CO$ を底辺とすれば、高さはどちらの三角形も長さがおなじになっているからです。底辺が共通で高さの長さがおなじなのだから、面積はおなじです。わかるでしょうか。最初の図で水色だった部分の三角形の面積と、右の図の水色の三角形の面積はおなじです。わからなかったら、わかるまで見てください。時間がかかってもよいので、わかるまで見てください。
まず、$\triangle OAB$ を $y$ 軸のところでわけるところまではおなじです。ここで、左側の、水色の三角形を等積変形します。点 $A$ から $x$ 軸に垂線をおろして、$x$ 軸との交点を $F$ とします。すると、$\triangle OAC$ と $\triangle OFC$ は面積がおなじです。$CO$ を底辺とすれば、高さはどちらの三角形も長さがおなじになっているからです。底辺が共通で高さの長さがおなじなのだから、面積はおなじです。わかるでしょうか。最初の図で水色だった部分の三角形の面積と、右の図の水色の三角形の面積はおなじです。わからなかったら、わかるまで見てください。時間がかかってもよいので、わかるまで見てください。
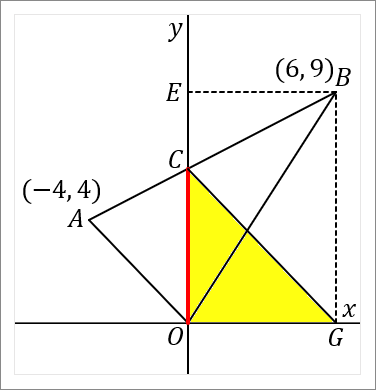 右側の黄色の三角形も、おなじように等積変形します。点 $B$ から $x$ 軸に垂線をおろして、$x$ 軸との交点を $G$ とします。すると、$\triangle OBC$ と $\triangle OGC$ は面積がおなじです。$CO$ を底辺とすれば、高さはどちらの三角形も長さがおなじになっているからです。底辺が共通で高さの長さがおなじなのだから、面積はおなじです。最初の図で黄色だった部分の三角形の面積と、右の図の黄色の三角形の面積はおなじです。
右側の黄色の三角形も、おなじように等積変形します。点 $B$ から $x$ 軸に垂線をおろして、$x$ 軸との交点を $G$ とします。すると、$\triangle OBC$ と $\triangle OGC$ は面積がおなじです。$CO$ を底辺とすれば、高さはどちらの三角形も長さがおなじになっているからです。底辺が共通で高さの長さがおなじなのだから、面積はおなじです。最初の図で黄色だった部分の三角形の面積と、右の図の黄色の三角形の面積はおなじです。
 というわけで、話が長くなってしまいましたが、まとめです。これから説明することをおぼえて、テストではこうやってください。
というわけで、話が長くなってしまいましたが、まとめです。これから説明することをおぼえて、テストではこうやってください。
右の図の $\triangle OAB$ のような三角形の面積をきかれることがよくあります。そうしたら、下の図の $\triangle CFG$ の三角形の面積を考えてください。その面積は、底辺が $FG$ で、高さが $CO$ だということにすればよいわけですから、
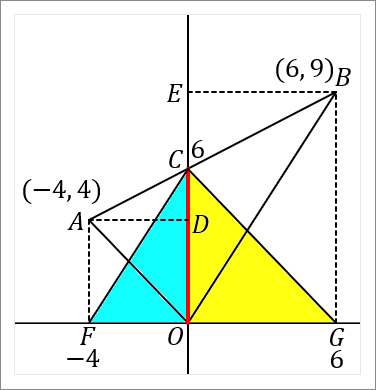 \begin{eqnarray*}
&&\triangle OAB\\
&=&\triangle CFG\\
&=&10\times6\times\cfrac{1}{2}\\
&=&30
\end{eqnarray*}
\begin{eqnarray*}
&&\triangle OAB\\
&=&\triangle CFG\\
&=&10\times6\times\cfrac{1}{2}\\
&=&30
\end{eqnarray*}
 $\huge{10}$
原点を通る $2$ 直線を使った三角形の面積を求める問題
$\huge{10}$
原点を通る $2$ 直線を使った三角形の面積を求める問題
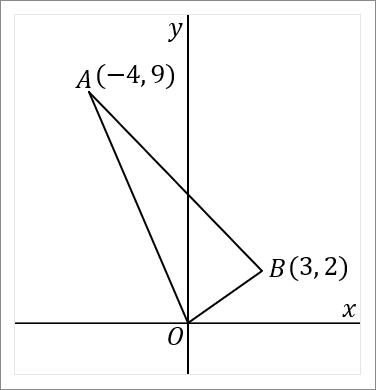
右の図で、$2$ 点 $A, \ B$ の座標はそれぞれ $(-4, \ 9) \ , \ (3, \ 2)$ である。このとき、以下の問いに答えなさい。
$(1)$ $2$ 点 $A, \ B$ を通る直線の式を求めなさい。
答え
$y=-x+5$
直線の式を求めなさいといわれたら、答えの形は $y=ax+b$ で、$a$ と $b$ を求めるのが目標になります。
$2$ 点 $(-4, \ 9), \ (3, \ 2)$ を通る直線の式を求めます。
\begin{eqnarray*}
a&=&\cfrac{y-y}{x-x}\\
&=&\cfrac{9-2}{-4-3}=\cfrac{7}{-7}=-1\\\\
y&=&-x+bにx=-4,y=9 を代入する\\
9&=&-1\times(-4)+b\\
9&=&4+b\\
5&=&b
\end{eqnarray*}
これで $a$ と $b$ がでました。答えは $y=-x+5$ です。
$(2)$ $\triangle OAB$ の面積を求めなさい。
答え
$\cfrac{35}{2}$
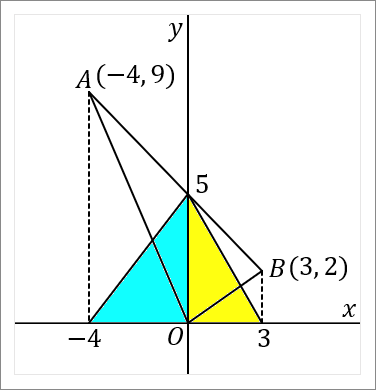 $\triangle OAB$ の面積をきかれたら、右の図の水色の三角形と黄色の三角形をあわせたものをひとつの三角形と考えて、その面積を求めます。その面積は、
\begin{eqnarray*}
7\times5\times\cfrac{1}{2}=\cfrac{35}{2}
\end{eqnarray*}
$\triangle OAB$ の面積をきかれたら、右の図の水色の三角形と黄色の三角形をあわせたものをひとつの三角形と考えて、その面積を求めます。その面積は、
\begin{eqnarray*}
7\times5\times\cfrac{1}{2}=\cfrac{35}{2}
\end{eqnarray*}
 $\huge{11}$
面積がおなじになる三角形をつくる問題
$\huge{11}$
面積がおなじになる三角形をつくる問題
右の図で、$2$ 点 $A, \ B$ の座標はそれぞれ $(-4, \ 4) \ , \ (6, \ 9)$ である。 $y$ 軸上に点 $P$ をとり、その座標を $(0, \ p)$ とする。$\triangle OAB$ と $\triangle OPB$ の面積が等しくなるときの $p$ の値を求めなさい。ただし、$p\gt 0$ とする。
答え
$p=10$
 $y$ 軸上のどこかに点 $P$ をとって、$\triangle OPB$ をつくりなさい。ただし、$\triangle OPB$ の面積は $\triangle OAB$ とおなじであるようにしてください、という問題です。
$y$ 軸上のどこかに点 $P$ をとって、$\triangle OPB$ をつくりなさい。ただし、$\triangle OPB$ の面積は $\triangle OAB$ とおなじであるようにしてください、という問題です。
はじめに、三角形の等積変形の基本的な考え方について、もういちどおさらいしておきましょう。
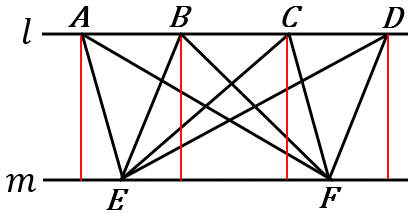 右の図で、$l /\!/ m$ とすると、$\triangle AEF$ と $\triangle BEF$ と $\triangle CEF$ と $\triangle DEF$ の面積はどれも同じす。$EF$ を底辺とすると、どれも底辺が共通で高さの長さが同じだからです。このことをふまえて、
右の図で、$l /\!/ m$ とすると、$\triangle AEF$ と $\triangle BEF$ と $\triangle CEF$ と $\triangle DEF$ の面積はどれも同じす。$EF$ を底辺とすると、どれも底辺が共通で高さの長さが同じだからです。このことをふまえて、
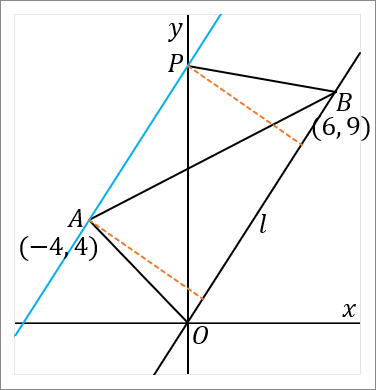 $2$ 点 $O, \ B$ を通る直線を $l$ とします。点 $A$ を通って $l$ と平行な直線をひきます。右の水色の線がそうです。この線と $y$ 軸との交点が、$P$ です。こうやって $P$ をとれば、$\triangle OAB$ と $\triangle OPB$ は面積がおなじです。$OB$ を底辺だということにすれば、底辺が共通で、高さが等しいからです。
$2$ 点 $O, \ B$ を通る直線を $l$ とします。点 $A$ を通って $l$ と平行な直線をひきます。右の水色の線がそうです。この線と $y$ 軸との交点が、$P$ です。こうやって $P$ をとれば、$\triangle OAB$ と $\triangle OPB$ は面積がおなじです。$OB$ を底辺だということにすれば、底辺が共通で、高さが等しいからです。
この、「~を通って~と平行な直線をひく」というのがでてくるかどうかが、この手の問題が解けるかどうかのわかれめです。
それでは $p$ の値を求めましょう。まず、$2$ 点 $O, \ B$ を通る直線の式を求めます。これは原点を通る直線ですから、比例の式です。式の形は $y=ax$ です。この式に $(6, \ 9)$ という座標を代入して、
\begin{eqnarray*}
9&=&6a\\
\cfrac{9}{6}&=&a\\
\cfrac{3}{2}&=&a
\end{eqnarray*}
これで $2$ 点 $O, \ B$ を通る直線の式は $y=\cfrac{3}{2}x$ だということがわかりました。
次に、この直線と平行で点 $A$ を通る直線の式を求めます。
傾きが等しいとき、$2$ 直線は平行になるのだから、求めたい直線の傾きは $\cfrac{3}{2}$ です。なので求めたい直線の式は、
$y=\cfrac{3}{2}x+b$
とおくことができます。この直線が点 $A(-4, \ 4)$ を通るのだから、この座標を代入して、
\begin{eqnarray*}
4&=&\cfrac{3}{2}\times(-4)+b\\
4&=&-6+b\\
10&=&b
\end{eqnarray*}
 というわけで、$2$ 点 $O, \ B$ を通る直線と平行で、点 $A(-4, \ 4)$ を通る直線の式は、
というわけで、$2$ 点 $O, \ B$ を通る直線と平行で、点 $A(-4, \ 4)$ を通る直線の式は、
$y=\cfrac{3}{2}x+10$
です。
この直線と $y$ 軸との交点が $P$ です。その座標は、$y=\cfrac{3}{2}x+10$ の切片をみればよいです。切片は $10$ ですから、その座標は $(0, \ 10)$ です。
これで答えがでました。$p=10$ です。
$P$ の座標が $(0,10)$ のとき、$\triangle OAB$ と $\triangle OPB$ は面積がおなじです。底辺が共通で、高さが等しいからです。
 $\huge{12}$
面積がおなじになる三角形をつくる問題
$\huge{12}$
面積がおなじになる三角形をつくる問題
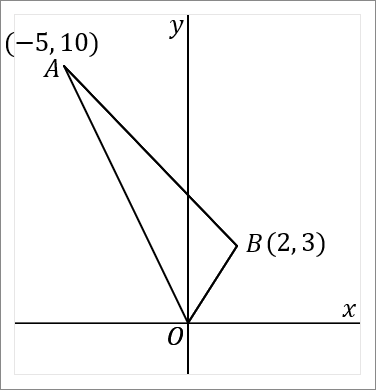
右の図で、$2$ 点 $A, \ B$ の座標はそれぞれ $(-5, \ 10) \ , \ (2, \ 3)$ である。 $y$ 軸上に点 $P$ をとり、その座標を $(0, \ p)$ とする。$\triangle OAB$ と $\triangle OAP$ の面積が等しくなるときの $p$ の値を求めなさい。ただし、$p\gt 0$ とする。
答え
$p=7$
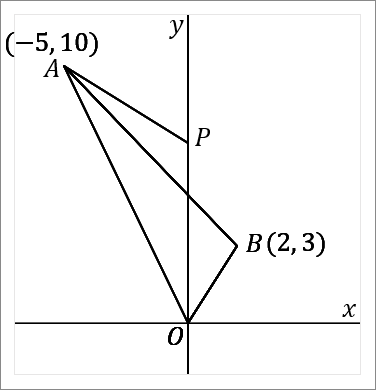 $y$ 軸上のどこかに点 $P$ をとって、$\triangle OAP$ をつくりなさい。ただし、$\triangle OAP$ の面積は $\triangle OAB$ とおなじであるようにしてください、という問題です。
$y$ 軸上のどこかに点 $P$ をとって、$\triangle OAP$ をつくりなさい。ただし、$\triangle OAP$ の面積は $\triangle OAB$ とおなじであるようにしてください、という問題です。
$11$ 番の問題とおなじようにやっていけばOKです。
$2$ 点 $O, \ A$ を通る直線を $l$ とします。点 $B$ を通って $l$ と平行な直線をひきます。下の図の水色の線がそうです。この線と $y$ 軸との交点が、$P$ です。こうやって $P$ をとれば、$\triangle OAB$ と $\triangle OAP$ は面積がおなじです。$OA$ を底辺だということにすれば、底辺が共通で、高さが等しいからです。
この、「~を通って~と平行な直線をひく」というのがでてくるかどうかが、この手の問題が解けるかどうかのわかれめです。
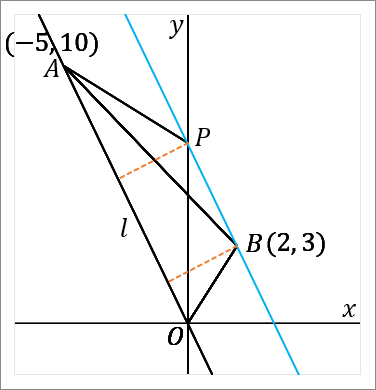
それでは $p$ の値を求めましょう。まず、$2$ 点 $O, \ A$ を通る直線の式を求めます。これは原点を通る直線ですから、比例の式です。式の形は $y=ax$ です。この式に $(-5, \ 10)$ という座標を代入して、
\begin{eqnarray*}
10&=&-5a\\
-\cfrac{10}{5}&=&a\\
-2&=&a
\end{eqnarray*}
これで $2$ 点 $O, \ A$ を通る直線の式は $y=-2x$ だということがわかりました。
次に、この直線と平行で点 $B$ を通る直線の式を求めます。
傾きが等しいとき、$2$ 直線は平行になるのだから、求めたい直線の傾きは $-2$ です。なので求めたい直線の式は、
$y=-2x+b$
とおくことができます。この直線が点 $B(2, \ 3)$ を通るのだから、この座標を代入して、
\begin{eqnarray*}
3&=&-2\times2+b\\
3&=&-4+b\\
7&=&b
\end{eqnarray*}
 というわけで、$2$ 点 $O, \ A$ を通る直線と平行で、点 $B(2, \ 3)$ を通る直線の式は、
というわけで、$2$ 点 $O, \ A$ を通る直線と平行で、点 $B(2, \ 3)$ を通る直線の式は、
$y=-2x+7$
です。
この直線と $y$ 軸との交点が $P$ です。その座標は、$y=-2x+7$ の切片をみればよいです。切片は $7$ ですから、その座標は $(0, \ 7)$ です。
これで答えがでました。$p=7$ です。
$P$ の座標が $(0,7)$ のとき、$\triangle OAB$ と $\triangle OAP$ は面積がおなじです。底辺が共通で、高さが等しいからです。
答え( 中3夏期講習 第2回 1次関数と面積
1(1)$(-3, \ 2)$
(2)$9$
(3)$y=-\cfrac{1}{3}x+1$
2
(1)$(2, \ 4)$
(2)$y=\cfrac{1}{2}x+3$
(3)$20$
(4)$y=\cfrac{4}{3}x+\cfrac{4}{3}$
3(1)$(2, \ -3)$
(2)$8$
(3)$y=-x-1$
4
(1)$(6, \ -5)$
(2)$y=-\cfrac{5}{12}x-\cfrac{5}{2}$
(3)$20$
(4)$y=-\cfrac{5}{8}x-\cfrac{5}{4}$
5(1)$(-4, \ -3)$
(2)$16$
(3)$y=\cfrac{1}{2}x-1$
6
(1)$(-2, \ -6)$
(2)$y=-\cfrac{3}{4}x-\cfrac{15}{2}$
(3)$42$
(4)$y=-\cfrac{3}{11}x-\cfrac{30}{11}$
7(1)$(10, \ 10)$
(2)$60$
(3)$y=-\cfrac{3}{5}x+4$
8
(1)$(-9, \ 10)$
(2)$y=-\cfrac{5}{2}x-\cfrac{25}{2}$
(3)$80$
(4)$y=\cfrac{5}{6}x+\cfrac{25}{6}$
9(1)$y=\cfrac{1}{2}x+6$
(2)$30$
10(1)$y=-x+5$
(2)$\cfrac{35}{2}$
11 $p=10$
12 $p=7$