中3数学 3学期の計算 第8回 全33問
ページがちゃんと表示されるまで10秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
ho←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
① 2−8
答え −6
② −32×2−4×(−6)
③ 76÷(−73)−(−34)
④ −2(2x−y)−(−3x+9y)
⑤ x−3y3−x−4y2
⑥ (x−3)(x+7)−(2x+3)2
⑦ 6√2−4√10÷√5
① 4x2yz−8xy2z
答え 4xyz(x−2y)
② x2−13x+36
答え (x−4)(x−9)
③ x2−12xy+36y2
答え (x−6y)2
④ 49x2−y2
答え (7x+y)(7x−y)
⑤ ax+ay+bx+by
① x+32=8x−1
② {2x−3y=6x+y=−7
答え x=−3,y=−4
{2x−3y=6…①x+y=−7…② ①+②×3 2x−3y=−16+)3x+3y=−21_5x+11y=−15x=−31 x=−3を②に代入−3+y=−7y=−7+3y=−4{x=−3y=−4③ 2x+y=3x+2y−1=5
答え x=4,y=−3
2x+y=3x+2y−1=5 のまんなかを隠した式をつくり、①とする。左側を隠した式をつくり、②とする。
①と②を連立方程式として解く。 {2x+y=5…①3x+2y−1=5…② ②を整理 3x+2y−1=53x+2y=6…③ ①×2−③×3 4x+2y=10−)3x+2y=16_x+44y=14 x=4を①に代入2×4+y=58+y=5y=5−8y=−3{x=4y=−3
④ x2+15x+54=0
⑤ x2−8=0
⑥ 4x2+1=4x
⑦ 3x2=2x
⑧ (x−12)2=1
⑨ x2−2x−1=0
① 1000L の水がはいった水槽から、毎分 50L ずつ水を抜く。 x 分間水を抜いたときの、残りの水の量が yL 以下であった。この数量の関係を不等式で表しなさい。
②次の式を[x]内の文字について解きなさい。
4a+3b=6[b]
③ a=√2+1 のとき、次の式の値を求めなさい。
a2−2a
④ y が x に比例し、x=−3 のとき、y=12 である。x=18 のときの y の値を求めなさい。
⑤ y が x に反比例し、x=−3 のとき、y=12 である。x=18 のときの y の値を求めなさい。
⑥ 関数 y=−2x2 について、x の変域が −3≦x≦2 のとき、y の変域を求めなさい。
答え −18≦y≦0
まず、答えの形はこうです。
小≦y≦大
んで、小と大にそれぞれ、小さい数と大きい数を書いておけばいいです。それを求めるためには、場合分けをしていきます。
①x の変域が 0 をまたいでいるか。
②x の変域が 0 をまたいでいるのなら、a はプラスかマイナスか。
この問題は、x の変域が −3≦x≦2 だから、0 をまたいでいます。この場合は、次に y=ax2 の a の符号がプラスかマイナスかをみます。この問題は、−2 だからマイナス。 a がマイナスのときは答えは
数≦y≦0
となります。 a がマイナスのときは、右側(最大値)が 0 です。左側の数(最小値)は、x の変域、 −3≦x≦2 の両はじの数のうち、0 から遠いほうを y=−2x2 に代入してでてくる数です。−3 と 2 は、どちらのほうが 0 から遠いかといえば、もちろん −3 です。この −3 を y=−2x2 に代入します。
y=−2×(−3)2=−2×9=−18
この −18 というのが、答えの左側の数(最小値)です。
⑦ 関数 y=ax2 で、x の値が x=−4 から x=2 まで変化するときの、変化の割合が 3 であるとき、a の値を求めなさい。
答え a=−32
「関数 y=ax2 について、x の値が x1 から x2 まで変化するときの、変化の割合は?」ときかれたら、 変化の割合=(x1+x2)×a この問題は、どれとどれを足して、どれを掛けたら変化の割合になっているか、やってみると、 {(−4)+2}×a=3 あとは解くだけです。 {(−4)+2}×a=3−2a=3a=−32
⑧ √150n の値ができるだけ小さい整数になるときの、正の整数 n の値を求めなさい。
答え n=6
2)150_3)175_5)125_5
やりかた
手順1 素因数分解してください。
手順2 同じ数が2つあったら、そこを〇で囲ってください。
手順3 〇がつかなかった数をかけてください。
その数が答えです。ルートを直すときとおなじような感じです。アレをやればいいです。
この問題の場合は、6 が答えだとすると、√150×6=√900=30 となります。
⑨ 大小 2 個のサイコロを同時に投げる時、大,小のサイコロの出た目をそれぞれ a, b とする。20≦a2+b2≦50 となる確率を求めなさい。
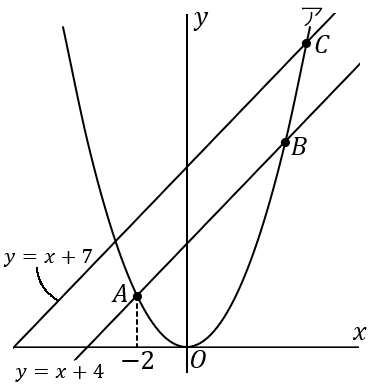
① 曲線アの方程式を y=ax2 とする。a の値を求めなさい。
答え
a=12
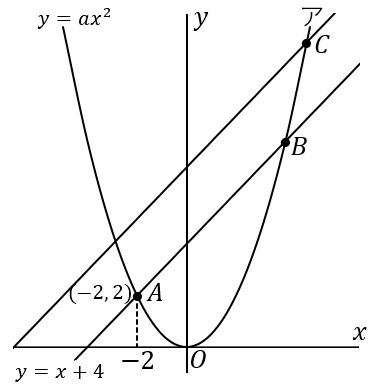 点 A は直線 y=x+4 上の点です。この式に x=−2 を代入して、
y=−2+4=2
点 A の座標は (−2, 2) です。
点 A は直線 y=x+4 上の点です。この式に x=−2 を代入して、
y=−2+4=2
点 A の座標は (−2, 2) です。
y=ax2 がこの点を通るわけですから、y=ax2 に x=−2, y=2 を代入して、
2=a×(−2)22=4a12=a
② △ABC の面積を求めなさい。
答え
9
等積変形をして、△ABC を面積を求めやすい三角形にします。そうして面積を求めていきます。
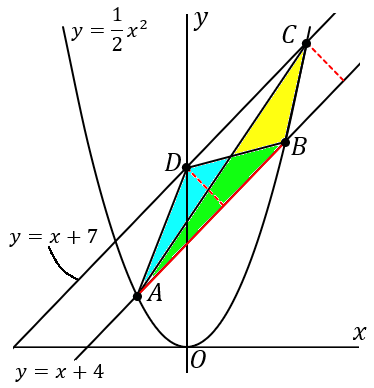 直線 y=x+7 と y 軸との交点を D とします。すると △ABC=△ABD です。直線 y=x+4 と y=x+7 は、傾きが等しいので平行です。なので、どちらの三角形も、AB を底辺とすれば、高さが等しくなります。なので面積は同じです。△ABC の面積を求めたいのなら、△ABD の面積を求めればいいです。そしてこっちのほうがずっと楽です。
直線 y=x+7 と y 軸との交点を D とします。すると △ABC=△ABD です。直線 y=x+4 と y=x+7 は、傾きが等しいので平行です。なので、どちらの三角形も、AB を底辺とすれば、高さが等しくなります。なので面積は同じです。△ABC の面積を求めたいのなら、△ABD の面積を求めればいいです。そしてこっちのほうがずっと楽です。
それでは △ABD の面積を求めていきましょう。
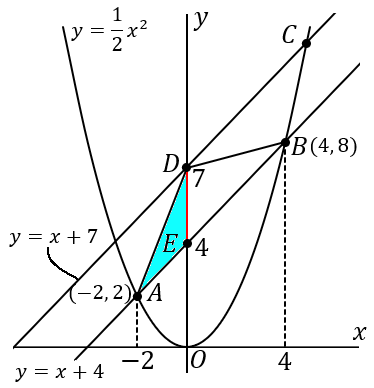 直線 y=x+4 と y 軸との交点を E とします。△ABD を y 軸のところで、右と左にわけます。△DEA と △DEB という 2 つの三角形の面積をそれぞれだして、足せばOKです。
直線 y=x+4 と y 軸との交点を E とします。△ABD を y 軸のところで、右と左にわけます。△DEA と △DEB という 2 つの三角形の面積をそれぞれだして、足せばOKです。
<△DEA>
DE を底辺とします。その長さは 7−4=3 です。また、点 A の座標は (−2, 2) なので、この三角形の高さは 2 です。なので面積は、
3×2×12=3
<△DEB>
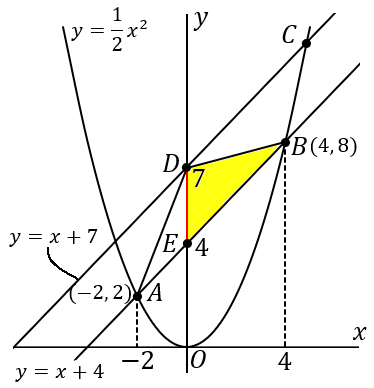 DE を底辺とします。その長さは 3 です。
DE を底辺とします。その長さは 3 です。
高さがわからないので、点 B の x 座標を求めていきます。点 B は y=x+4 と y=12x2 の交点なのですから、
12x2=x+4x2−2x−8=0(x−4)(x+2)=0x=4, x=−2
x=−2 というのは点 A の x 座標のことです。なので点 B の x 座標は 4 です。(ついでに y 座標も求めておくと、y=8 になります。)というわけで、△DEB の高さは 4 です。なので面積は
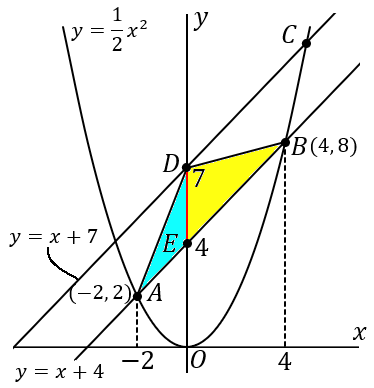 3×4×12=6
なので △ABD の面積は、
△ABD=△DEA+△DEB=3+6=9
3×4×12=6
なので △ABD の面積は、
△ABD=△DEA+△DEB=3+6=9
<もうちょっとラクに>
△ABD をさらに等積変形して、右下の図の水色のような三角形を考えてしまえば、その面積は
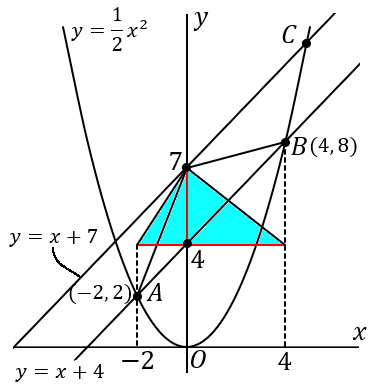 6×3×12=9
これでダイジョブです。ツジツマあってます。水色の三角形は △ABD と面積がおなじです。
6×3×12=9
これでダイジョブです。ツジツマあってます。水色の三角形は △ABD と面積がおなじです。
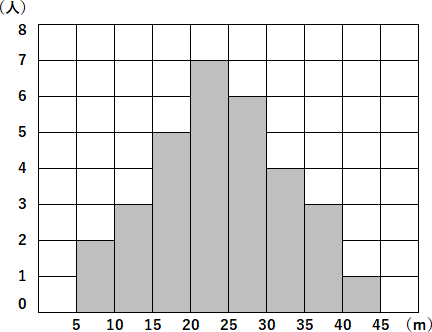
ア この記録は全部で 30 人の生徒によるものである。
イ 階級の幅は 40 である。
ウ 最頻値(モード)と中央値(メジアン)の値は同じである。
エ 記録が 20 m以上 30 m未満の生徒の相対度数は 0.4 以上である。
答え
ウ,エ
ア…生徒は 31 人です。
イ…階級の幅は 5 です。
ウ…最頻値(モード)の階級は 20~25 のところです。なので最頻値は 22.5 です。
また、31 人の生徒による記録なのですから、中央値(メジアン)は 16 番目の生徒の記録となります。16 番目の生徒の記録がふくまれる階級は 20~25 のところです。なので中央値(メジアン)は 22.5 です。
エ…記録が 20 m以上 25 m未満の生徒の度数は 7 です。記録が 25 m以上 30 m未満の生徒の度数は 6 です。なので記録が 20 m以上 30 m未満の生徒の度数は 7+6=13 です。なのでその相対度数は、
13÷31=0.41…
答え
1 ①−6②6③14④−x−7y⑤−x+6y6(−x−6y6,−16x+yも可)⑥−3x2−8x−30⑦−√2 2 ①4xyz(x−2y)②(x−4)(x−9)③(x−6y)2④(7x+y)(7x−y)⑤(x+y)(a+b) 3 ①x=13②x=−3, y=−4③x=4, y=−3④x=−6, x=−9⑤x=±2√2⑥x=12⑦x=0, x=23⑧x=32, x=−12⑨x=1±√2 4 ①1000−50x≦y②b=−4a+63(−4a−63, −43a+2も可)③1④y=−72⑤y=−2⑥−18≦y≦0⑦a=−32⑧6⑨59 5 ①a=12②9 6 ウ,エ