数学 中2 3章 $1$ 次関数 第3回(全25問)
ページがちゃんと表示されるまで$10$秒くらいかかります。印刷するときは、ちょっと待ってからにしてください。
$ \boxed{\phantom{ho}}$←ここに四角形が表示されていたら準備OKです。
問題をクリックすると答えがでます。
(1) $1$ 次関数の式の形は $ \boxed{\LARGE\phantom{hogehoge}}$
$a$ の呼び方は
$\boxed{\LARGE\phantom{hogehoge}}$ $\boxed{\LARGE\phantom{hogehoge}}$ $\boxed{\Huge\phantom{hogehoge}}$
$b$ の呼び方は $\boxed{\LARGE\phantom{hogehoge}}$
$a \gt 0$ のとき、グラフは $\boxed{\LARGE\phantom{hogehoge}}$ の直線
$a \lt 0$ のとき、グラフは $\boxed{\LARGE\phantom{hogehoge}}$ の直線
答え
$y=ax+b$, 傾き, 変化の割合, $\cfrac{xの増加量\phantom{ }}{yの増加量\phantom{ }}$,
切片($y$ 切片), 右上がり, 右下がり
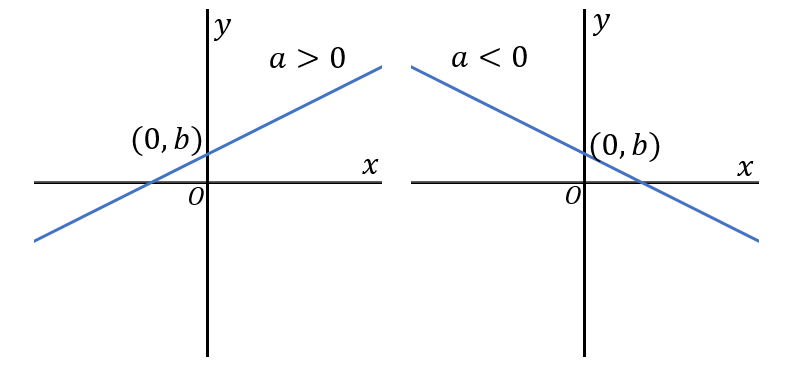 $a\gt0$ ($a$ がプラス)のとき、右上がりの直線になります。
$a\gt0$ ($a$ がプラス)のとき、右上がりの直線になります。
$a\lt0$ ($a$ がマイナス)のとき、右下がりの直線になります。
$b$ は $y$ 軸上のどこを通るか、と思ってしまうといいです。
(2) 1次関数 $y=-\cfrac{1}{3}x-2$ について、 $x$ の値が $-1$ から $5$ まで増加したときの、次の値を求めなさい。
① $x$ の増加量
② $y$ の増加量
③変化の割合
答え
① $6$
② $-2$
③ $-\cfrac{1}{3}$
① $x$ の増加量をきかれたときは、問題の「 $x$ の値が $-1$ から $5$ まで増加したときの」という部分を見て答えればよいです。$-1$ が $5$ になったわけだから、$6$ 増えましたよね? だから $6$ と答えればOKです。
③ ②の問題をとばして、さきにこちらを答えてしまいます。変化の割合というのは1次関数のときは $y=ax+b$ の $a$ のことだとおもっちゃえばいいです。だから $y=-\cfrac{1}{3}x-2$ の $-\cfrac{1}{3}$ の部分を答えれば正解です。テストのときはそう答えてしまいましょう。計算もなんもないです。 $x$ の直前に書いてある数を答えればいいです。ただし、変化の割合をきかれたときのこの答え方は1次関数のときだけしか通用しないから気をつけてください。
②1次関数で $y$ の増加量をきかれたときは、
$y$ の増加量 = $x$ の増加量 × 変化の割合
です。理由は単純で、「$変化の割合=\cfrac{yの増加量\phantom{増加}}{xの増加量\phantom{増加}}$」だからです。変形したら $y$ の増加量 = $x$ の増加量 × 変化の割合 になりますよね? 1次関数のときはこれでうまくいくので、テストのときはこれでやっちゃいましょう。そのほうがラクだしはやいしミスもすくない。というわけでこの問題は $6 \times \left(-\cfrac{1}{3}\right) = -2$ が答えです。ただし、$y$ の増加量をきかれたときのこのやり方は、これも1次関数のときしか通用しないやり方だから気をつけてください。
(3) 変化の割合が $-\cfrac{1}{4}$ で、点$(8,3)$を通る直線の式を求めなさい。
答え
$y=-\cfrac{1}{4}x+5$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
変化の割合というのは1次関数のときは $a$ のことです。だから $a=-\cfrac{1}{4}$ です。これを $y=ax+b$ に代入します。すると
$$y=-\cfrac{1}{4}x+b$$
となります。あと、「点$(6,2)$を通る」というのは、$x=8$ のとき $y=3$ という意味です。これをこの $y=-\cfrac{1}{4}x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
3&=&-\cfrac{1}{4}×8+b\\
3&=&-2+b\\
3+2&=&b\\
5&=&b
\end{eqnarray*}
$b$ は右辺においたままにして解いていくのがおすすめです。たぶんこういうやり方って、このあたりで初めて見るのかもしれません。最初はとまどうと思いますが、1次関数で $b$ を求めるときは、このやり方のほうがミスが少ないです。だからこれがおすすめです。まあどうしてもなじめなかったら由緒正しく $b$ を左辺にもってって解いてもいいです。
ともかく、これでめでたく $a=-\cfrac{1}{4}$ , $b=5$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-\cfrac{1}{4}x+5$$
(4) 傾きが $-1$ で、 $x=-1$ のとき $y=-2$ となる1次関数の式を求めなさい。
答え
$y=-x-3$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
傾きというのは $a$ のことです。だから $a=-1$ です。これを $y=ax+b$ に代入します。すると
$$y=-x+b$$
となります。 $x=-1$ , $y=2$ をこの $y=-x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
-2&=&-1×(-1)+b\\
-2&=&1+b\\
-2-1&=&b\\
-3&=&b
\end{eqnarray*}
これで $a=-1$ , $b=-3$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-x-3$$
(5) \(\cfrac{yの増加量\phantom{増加}}{xの増加量\phantom{増加}}\) が $2$ で、点 $(4,3)$ を通る1次関数の式を求めなさい。
答え
$y=2x-5$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
\(\cfrac{yの増加量\phantom{増加}}{xの増加量\phantom{増加}}\)というのは1次関数のときは $a$ のことです。だから $a=2$ です。これを $y=ax+b$ に代入します。すると
$$y=2x+b$$
となります。 $x=4$ , $y=3$ をこの $y=2x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
3&=&2×4+b\\
3&=&8+b\\
3-8&=&b\\
-5&=&b
\end{eqnarray*}
これで $a=2$ , $b=-5$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$y=2x-5$
(6) $x$ の値が $5$ 増加すると $y$ の値が $10$ 増加し、$x=4$ のとき $y=-2$ となる直線の式を求めなさい。
答え
$y=2x-10$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
1次関数のときは \(a=\cfrac{yの増加量\phantom{増加}}{xの増加量\phantom{増加}}\)だから、この問題の場合は $a=\cfrac{10}{5}=2$ となります。これを $y=ax+b$ に代入すると
$$y=2x+b$$
となります。 $x=4$ , $y=-2$ をこの $y=3x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
-2&=&2×4+b\\
-2&=&8+b\\
-2-8&=&b\\
-10&=&b
\end{eqnarray*}
これで $a=2$ , $b=-10$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=2x-10$$
(7) 直線 $y=-2x-5$ に平行で、点$(-1,-2)$ を通る直線の式を求めなさい。
答え
$y=-2x-4$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
傾きが等しいとき、2直線は平行になります。$y=-2x-5$ に平行ということは、求めたい直線の傾きは $-2$ だということになります。つまり $a=-2$ です。これを $y=ax+b$ に代入すると
$$y=-2x+b$$
となります。 $x=-1$ , $y=-2$ をこの $y=-2x+b$ に代入して、 $b$ を求めます。
\begin{eqnarray*}
-2&=&-2×(-1)+b\\
-2&=&2+b\\
-2-2&=&b\\
-4&=&b
\end{eqnarray*}
これで $a=-2$ , $b=-4$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-2x-4$$
(8) $y$ 切片が $3$ で、点$(-3,2)$ を通る1次関数の式を求めなさい。
答え
$y=\cfrac{1}{3}x+3$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
$y$ 切片というのは $b$ のことです。だから $b=3$ です。これを $y=ax+b$ に代入します。すると
$$y=ax+3$$
となります。 $x=-3$ , $y=2$ をこの $y=ax+2$ に代入して、 $a$ を求めます。
\begin{eqnarray*}
2&=&-3a+3\\
3a&=&3-2\\
3a&=&1\\
a&=&\cfrac{1}{3}
\end{eqnarray*}
これで $a=\cfrac{1}{3}$ , $b=3$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=\cfrac{1}{3}x+3$$
(9) 2点$(-6,-3),(-2,1)$ を通る直線の式を求めなさい。
答え
$y=x+3$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
$2$ 点を通る直線の式をきかれたときは、
$$a=\cfrac{y_2-y_1}{x_2-x_1}$$
という公式を使って $a$ を求めましょう。
$2$ 点の座標 $(-6,-3),(-2,1)$ を $(x_1,y_1),(x_2,y_2)$ だということにして、上の公式にあてはめると、
\begin{eqnarray*}
a&=&\cfrac{y_2-y_1}{x_2-x_1}\\
&=&\cfrac{1-(-3)}{-2-(-6)}\\
&=&\cfrac{4}{4}\\
&=&1\\
\end{eqnarray*}
これで $a=1$ だということがわかりました。これを $y=ax+b$ に代入して、
$$y=x+b$$
ここに、 $(-6,-3),(-2,1)$ のどちらかを代入して $b$ を求めます。代入するのはどっちでもよいです。計算さえまちがえなければ、どっちをいれても答えは同じになります。だから、計算がラクそうなほうをいれるのが得。今回は、 $(-2,1)$ のほうをいれてみましょう。
\begin{eqnarray*}
1&=&-2+b\\
1+2&=&b\\
3&=&b
\end{eqnarray*}
これで $a=1$ , $b=3$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=x+3$$
ところで、この問題に関してはもうひとつ、連立方程式をたてて $a$ と $b$ を求めていく、という定番のやり方があります。ここで紹介しているやり方と、連立方程式をたてるのと、両方ためして、好きなほうでやってください。連立方程式をたててやるやり方は、次の問題で説明します。
(10) $x=2$ のとき $y=-8$ で、$x=4$ のとき $y=-14$ となる1次関数の式を求めなさい。
答え
$y=-3x-2$
「直線の式を求めよ」「1次関数の式を求めよ」「1次関数であるとき、$y$ を $x$ の式で表せ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
$y=ax+b$ に $x=2,y=-8$ を代入すると
$$-8=2a+b$$
$y=ax+b$ に $x=4,y=-14$ を代入すると
$$-14=4a+b$$
こうしてできたふたつの式を連立させて解きます。引き算をすれば $b$ が消えます。
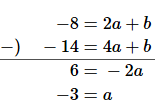
$a=-3$ を $-8=2a+b$ に代入して $b$ を求めます。
\begin{eqnarray*}
-8&=&2×(-3)+b\\
-8&=&-6+b\\
-8+6&=&b\\
-2&=&b
\end{eqnarray*}
これで $a=-3$ , $b=-2$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-3x-2$$
ところで、この問題に関してはもうひとつ、前の問題で説明した $a=\cfrac{y_2-y_1}{x_2-x_1}$ という公式を使って、まず $a$ を求めてしまう、というやり方でもいけます。どっちでもいけます。テストのときは好きなほうでやってください。
(11) $y$ が $x$ の1次関数であるとき、表のア~ウにあてはまる数をこたえなさい。また、$y$ を $x$ の式で表しなさい。
\begin{array}{c|ccccc}
\hline
x & -6 & -3 & 1 & 6 & ウ \\
\hline
y & ア & 6 & イ & 0 & -4 \\
\hline
\end{array}
答え
ア…$8$, イ…$\cfrac{10}{3}$, ウ…$12$, 式 $y=-\cfrac{2}{3}x+4$
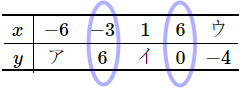 まず、$y$ を $x$ の式で表してしまいましょう。そのために、$x$ と $y$ がわかっている組を $2$ 組、見つけます。必ず $2$ 組はあるはずです。この問題の場合は、$x=-3$ のとき $y=6$, $x=6$ のとき $y=0$ というのがありますね。これで $a$ を求めることができます。$(-3, 6), (6, 0)$ だと思ってもいいです。$a$ が求まりますよね?
まず、$y$ を $x$ の式で表してしまいましょう。そのために、$x$ と $y$ がわかっている組を $2$ 組、見つけます。必ず $2$ 組はあるはずです。この問題の場合は、$x=-3$ のとき $y=6$, $x=6$ のとき $y=0$ というのがありますね。これで $a$ を求めることができます。$(-3, 6), (6, 0)$ だと思ってもいいです。$a$ が求まりますよね?
$\quad a=\cfrac{y_2-y_1}{x_2-x_1}$ を使って、
$\quad a=\cfrac{0-6}{6-(-3)}=\cfrac{-6}{9}=-\cfrac{2}{3}$
$y=-\cfrac{2}{3}x+b$ に $(6, 0)$ を代入して、
\begin{eqnarray*}
0&=&-\cfrac{2}{3}\times6+b\\
0&=&-4+b\\
4&=&b
\end{eqnarray*}
これで、式は $y=-\cfrac{2}{3}x+4$ だと求められました。あとはアとイとウをだしていきましょう。
アは $x=-6$ のときの $y$ の値のことだから、
\begin{eqnarray*}
y&=&-\cfrac{2}{3}\times(-6)+4=4+4=8
\end{eqnarray*}
イは $x=1$ のときの $y$ の値のことだから、
\begin{eqnarray*}
y=-\cfrac{2}{3}\times1+4=-\cfrac{2}{3}+\cfrac{12}{3}=\cfrac{10}{3}
\end{eqnarray*}
ウは $y=-4$ のときの $x$ の値のことだから、
\begin{eqnarray*}
-4&=&-\cfrac{2}{3}x+4 \quad(\times3)\\
-12&=&-2x+12\\
2x&=&12+12\\
2x&=&24\\
x&=&12
\end{eqnarray*}
これですべて求まりました。答えを書きましょう。
ア…$8$, イ…$\cfrac{10}{3}$, ウ…$12$, 式 $y=-\cfrac{2}{3}x+4$
(12) $y=-\cfrac{1}{3}x+4$ について、$x$ の変域が $-3 \leqq x \leqq 3$ のとき、$y$ の変域を求めなさい。
答え
$3 \leqq y \leqq 5$
「$x$ の変域が $a \leqq x \leqq b$ のとき、$y$ の変域を求めなさい。」というお決まりの問題があって、こうきかれたときは、答えの形はこうです。 $$小 \leqq y \leqq 大$$ んで、小と大にそれぞれ、小さい数と大きい数を書いておけばいいです。小さい数と大きい数っていうのは、 $-3 \leqq x \leqq 3$ の $-3$ と $3$ をそれぞれ問題の $y=-\cfrac{1}{3}x+4$ の $x$ に代入してえられる数です。じゃあまず、 $x=-3$ を $y=-\cfrac{1}{3}x+4$ に代入します。 \begin{eqnarray*} y&=&-\cfrac{1}{3}×(-3)+4\\ &=&1+4\\ &=&5\\ \end{eqnarray*} 次に、 $x=3$ を $y=-\cfrac{1}{3}x+4$ に代入します。 \begin{eqnarray*} y&=&-\cfrac{1}{3}×3+4\\ &=&-1+4\\ &=&3\\ \end{eqnarray*} これで、$5$ と $3$ というふたつの数がえられました。これを小と大にあてはめればよいです。じゃあ答えを書きましょう。$$3 \leqq y \leqq 5$$ これでOKです。ただし、 $y$ の変域をきかれたときのこのやり方は、3年生で習う「2乗に比例する関数$y=ax^2$」では通用しないから気をつけてください。
(13) 下の直線の式を求めなさい。
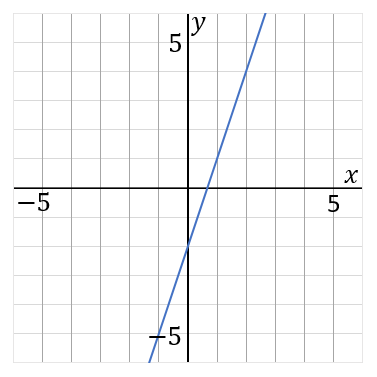
答え
$y=3x-2$
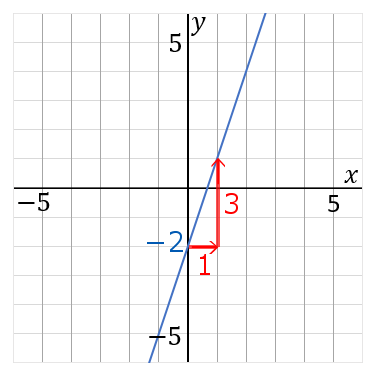
「直線の式を求めよ」「1次関数の式を求めよ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
このグラフは右に$1$歩いって縦に$3$ 歩いっています。傾き $a=\cfrac{縦}{右}$ だから、
$$a=\cfrac{3}{1}=3$$
それから、このグラフは $y$ 軸の $-2$ を通っています。切片 $b$ は $y$ 軸のどこを通っているか、ということだから、
$$b=-2$$
これで $a=3$ , $b=-2$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=3x-2$$
(14) 下の直線の式を求めなさい。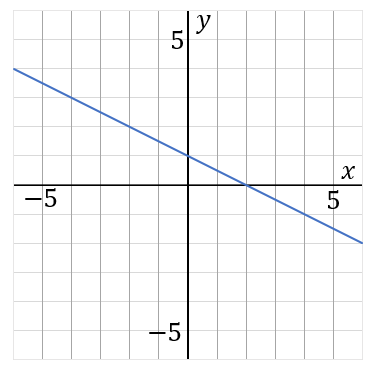
答え
$y=-\cfrac{1}{2}x+1$
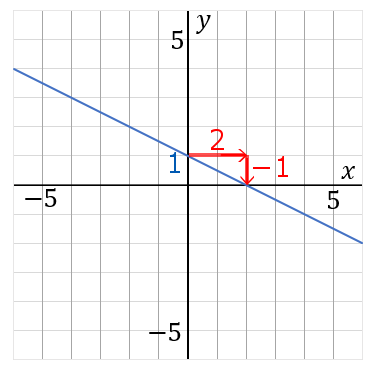
「直線の式を求めよ」「1次関数の式を求めよ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
このグラフは右に$2$歩いって縦に$-1$ 歩いっています。傾き $a=\cfrac{縦}{右}$ だから、
$$a=\cfrac{-1}{2}=-\cfrac{1}{2}$$
それから、このグラフは $y$ 軸の $1$ を通っています。切片 $b$ は $y$ 軸のどこを通っているか、ということだから、
$$b=1$$
これで $a=-\cfrac{1}{2}$ , $b=1$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-\cfrac{1}{2}x+1$$
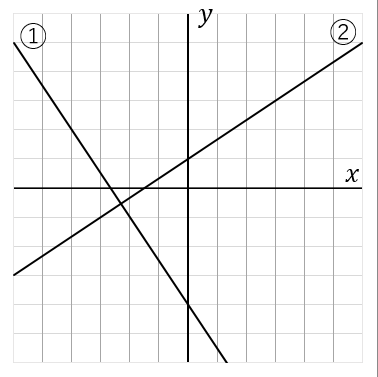
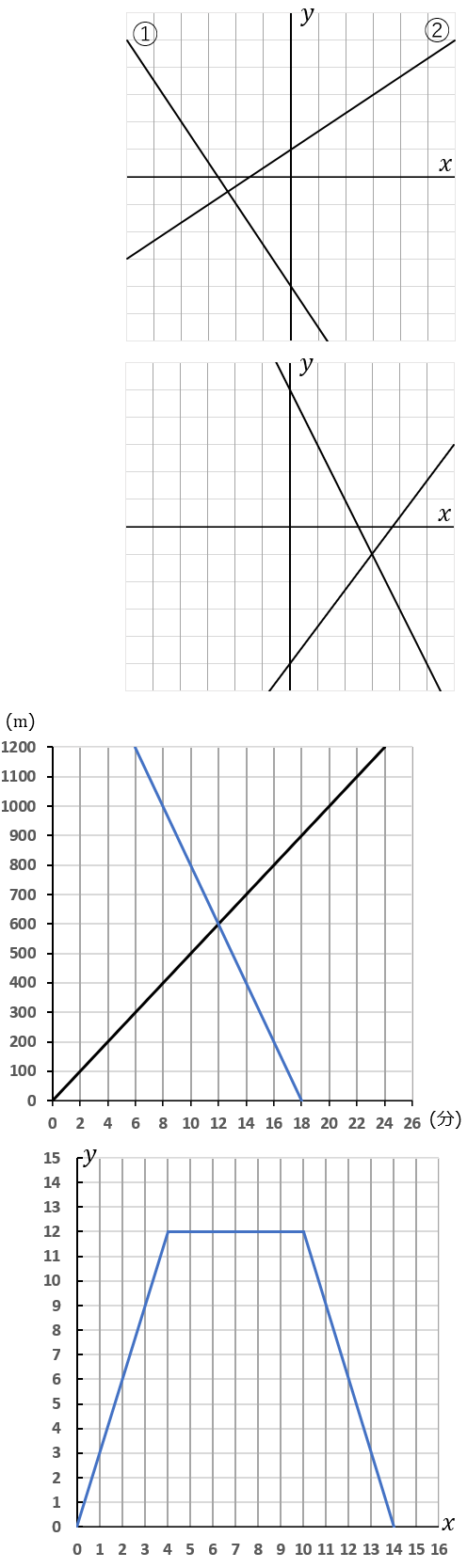
(15) 下の①,②の直線の式を求めなさい。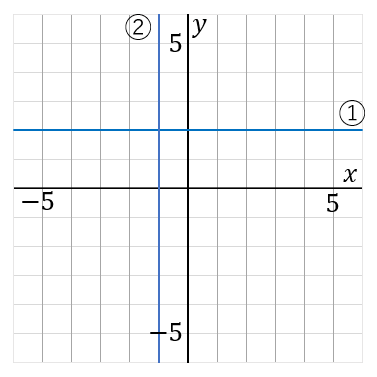
答え
① $y=2$ ② $x=-1$
① $x$軸に平行な直線のときはちょっと特別で、答えの形は $y=n$ です。この直線は $y$ 軸の $2$ を通っていて、$x$軸に平行な直線だから、答えは
$$y=2$$
② $y$ 軸に平行な直線のときもちょっと特別で、答えの形は $x=n$ です。この直線は $x$軸の $-1$ を通っていて、$y$ 軸に平行な直線だから、答えは
$$x=-1$$
(16) 次の1次関数のグラフをかきなさい。
① $y=-\cfrac{3}{2}x-4$
② $-3=2x-3y$
答え
① 傾きが $-\cfrac{3}{2}$ で切片が $-4$ のグラフです。
② このままでは傾きや切片がわかりません。こういうときは、$y$ について解きます。
\begin{eqnarray*}
-3&=&2x-3y\\
3y&=&2x+3\\
y&=&\cfrac{2}{3}x+\cfrac{3}{3}\\
y&=&\cfrac{2}{3}x+1
\end{eqnarray*}
これで傾きが $\cfrac{2}{3}$ で切片が $1$ だとわかりました。そのグラフをかきましょう。
(17) 次の連立方程式の解を、グラフをかいて求めなさい。
\begin{eqnarray*}
\left\{
\begin{array}{l}
2x+y=5\\
4x-3y=15
\end{array}
\right.
\end{eqnarray*}

答え
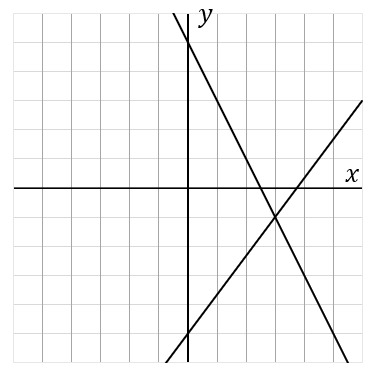 \begin{eqnarray*}
\left\{
\begin{array}{l}
x=3\\
y=-1
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*}
\left\{
\begin{array}{l}
x=3\\
y=-1
\end{array}
\right.
\end{eqnarray*}
加減法や代入法を使って解いてしまうこともできますが、それだとテストのとき点数はもらえません。グラフをかいていなければダメです。というわけでグラフをかきます。このままでは傾きや切片がわかりませんので、こういうときは、それぞれの式を $y$ について解きます。
\begin{eqnarray*}
2x+y&=&5\\
y&=&-2x+5
\end{eqnarray*}
\begin{eqnarray*}
4x-3y&=&15\\
-3y&=&-4x+15\\
3y&=&4x-15\\
y&=&\cfrac{4}{3}x-\cfrac{15}{3}\\
y&=&\cfrac{4}{3}x-5
\end{eqnarray*}
こうしてできた $2$ つの式をおなじグラフ上にかいて、その交点を座標を答えればいいです。交点の座標は点$(3, \ -1)$ ですね。$x=3, \ y=-1$ が解です。
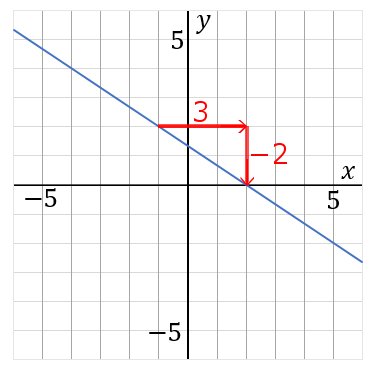
(18) 下の直線の式を求めなさい。
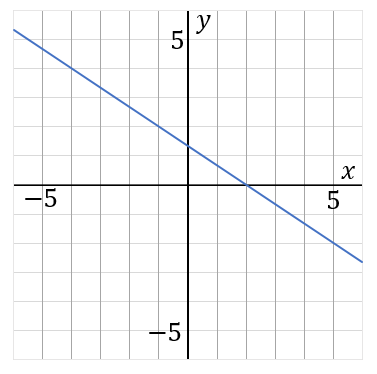
答え
$y=-\cfrac{2}{3}x+\cfrac{4}{3}$
「直線の式を求めよ」「1次関数の式を求めよ」といわれたら、答えの形は $y=ax+b$ で、 $a$ と $b$ を求めるのが目標になります。
このグラフは右に$3$歩いって縦に$-2$ 歩いっています。傾き $a=\cfrac{縦}{右}$ だから、
$$a=\cfrac{-2}{3}=-\cfrac{2}{3}$$
それから、このグラフは $y$ 軸のぴったりしたところを通っていません。こういうときの $b$ はどこかの座標を代入して計算で求めます。たとえばこのグラフは点$(2,0)$ を通っているから、$x=2,$ $y=0$ を、$y=-\cfrac{2}{3}x+b$ に代入して $b$ を求めます。
\begin{eqnarray*}
0&=&-\cfrac{2}{3}×2+b\\
0&=&-\cfrac{4}{3}+b\\
\cfrac{4}{3}&=&b\\
\end{eqnarray*}
これで $a=-\cfrac{2}{3}$ , $b=\cfrac{4}{3}$ というふうに、$a$ と $b$ が求められました。じゃあ答えを書きましょう。
$$y=-\cfrac{2}{3}x+\cfrac{4}{3}$$
今回は点$(2,0)$ を代入して $b$ を求めたけれど、$(5,-2)$でも$(-1,2)$でも$(-4,4)$でもどこでもいいです。どこをいれても $b=\cfrac{4}{3}$ になります。
(19) 2つの直線 $y=\cfrac{1}{2}x-2$ と $y=3x+3$ の交点の座標を求めなさい。
答え
$(-2,-3)$
2直線の交点の座標は連立方程式の解です。
連立方程式\begin{eqnarray*}
\left\{
\begin{array}{l}
y=\cfrac{1}{2}x-2\\
y=3x+3
\end{array}
\right.
\end{eqnarray*}
を解いて、その解がこの問題の答えです。代入法で、
(上の式の右辺)=(下の式の右辺)という式をたてて解いていきましょう。
\begin{eqnarray*}
\cfrac{1}{2}x-2&=&3x+3 \quad(両辺に\times2)\\
x-4&=&6x+6\\
x-6x&=&6+4\\
-5x&=&10\\
x&=&-2\\
\end{eqnarray*}
$y=3x+3$ に $x=-2$ を代入して $y$ を求めます。
\begin{eqnarray*}
y&=&3\times(-2)+3\\
&=&-6+3\\
&=&-3
\end{eqnarray*}
これで $x=-2$ , $y=-3$ というふうに、解が求められました。じゃあ答えを書きましょう。
$$(-2,-3)$$
この問題は「座標を求めよ」といわれているのだから、座標の書きかたで答えるようにしましょう。
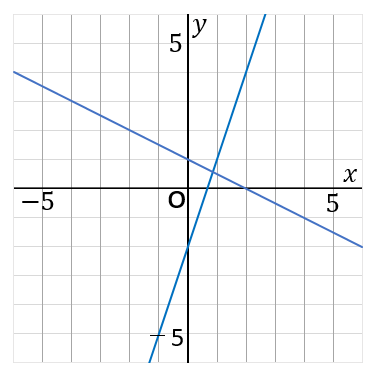
(20) 下の2つの直線の交点の座標を求めなさい。
答え
$\left(\cfrac{6}{7}, \ \cfrac{4}{7}\right)$
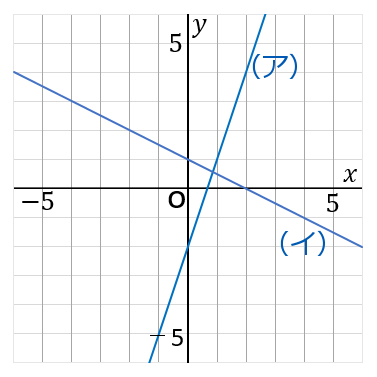
2直線の交点の座標は連立方程式の解です。まず、2つの直線の式をグラフから求めます。(ア)(イ)の直線の式はそれぞれ
$$y=3x-2\qquad{(ア)}$$
$$y=-\cfrac{1}{2}x+1\qquad{(イ)}$$
もしわからなかったら、13番と14番の問題で出題した直線なので、それを確認してください。
んで、だからこの問題に答えるには、連立方程式
\begin{eqnarray*}
\left\{
\begin{array}{l}
y=3x-2\\
y=-\cfrac{1}{2}x+1
\end{array}
\right.
\end{eqnarray*}
を解けばいいです。代入法で、
(ア)の式の右辺=(イ)の式の右辺
という式をたてて解いていきましょう。
\begin{eqnarray*}
3x-2&=&-\cfrac{1}{2}x+1\qquad(×2)\\
6x-4&=&-x+2\\
6x+x&=&2+4\\
7x&=&6\\
x&=&\cfrac{6}{7}\\
\end{eqnarray*}
$y=3x-2$ に $x=\cfrac{6}{7}$ を代入して $y$ を求めます。
\begin{eqnarray*}
y&=&3×\cfrac{6}{7}-2\\
&=&\cfrac{18}{7}-\cfrac{14}{7}\\
&=&\cfrac{4}{7}\\
\end{eqnarray*}
これで $x=\cfrac{6}{7}$ , $y=\cfrac{4}{7}$ というふうに、解が求められました。じゃあ答えを書きましょう。
$$\left(\cfrac{6}{7}, \ \cfrac{4}{7}\right)$$
この問題の答えは整数にはなりません。交点はぴったりとしたカドにはないからです。答えは分数になるはず。そう思って解いていきましょう。
このへんからちょっと難易度があがります。こりゃムリだ、というひとは、(1)番から(20)番までの問題を繰り返して、確実にできるようになりましょう。
しんどいけどやり通す、というひとはここから先へ進みましょう。がんばって!
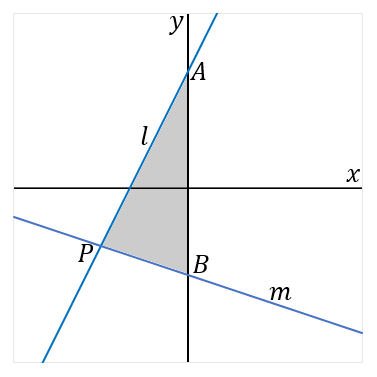 (21) 右の図で、直線 $l$ , $m$ の式はそれぞれ $y=2x+4$ , $y=-\cfrac{1}{3}x-3$ である。直線$l$ と $y$ 軸との交点を$A$ とし、直線$m$ と $y$ 軸との交点を$B$ とする。また、直線$l$ と直線$m$ との交点を$P$ とする。このとき、$\triangle PAB$の面積を求めなさい。
(21) 右の図で、直線 $l$ , $m$ の式はそれぞれ $y=2x+4$ , $y=-\cfrac{1}{3}x-3$ である。直線$l$ と $y$ 軸との交点を$A$ とし、直線$m$ と $y$ 軸との交点を$B$ とする。また、直線$l$ と直線$m$ との交点を$P$ とする。このとき、$\triangle PAB$の面積を求めなさい。
答え
$\cfrac{21}{2}$
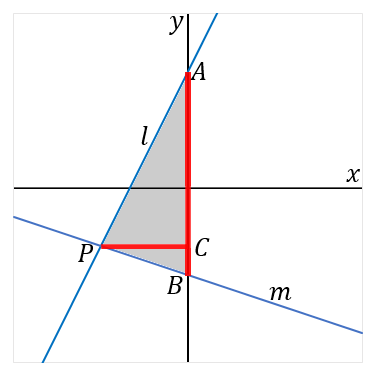
$P$を通る$AB$の垂線と$AB$との交点を$C$とします。
三角形の面積=底辺×高さ×$\cfrac{1}{2}$ 。底辺を$AB$、高さを$PC$ということにして求めていきましょう。
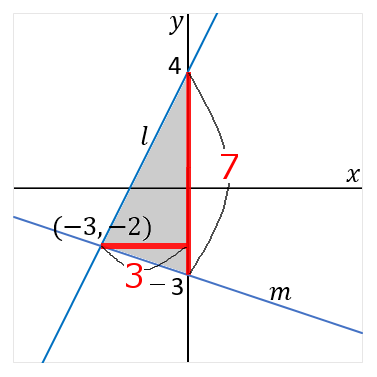
まず底辺$AB$の長さから。$A$の$y$座標は$y=2x+4$の切片だから$4$。$B$の$y$座標は$-\cfrac{1}{3}x-3$の切片だから$-3$。だから$AB=7$。
つぎに高さ$PC$。これをだすために$P$の座標を求めます。$P$は直線$l$ と直線$m$との交点だから、直線$l$ と直線$m$を連立させて解きます。
\begin{eqnarray*}
\left\{
\begin{array}{l}
y=2x+4\\
y=-\cfrac{1}{3}x-3\\
\end{array}
\right.
\end{eqnarray*}
代入法で、(上の式の右辺)=(下の式の右辺)という式をたてると、
\begin{eqnarray*}
2x+4&=&-\cfrac{1}{3}x-3\qquad(×3)\\
6x+12&=&-x-9\\
6x+x&=&-9-12\\
7x&=&-21\\
x&=&-3\\
\end{eqnarray*}
$y=2x+4$ に $x=-3$ を代入して $y$ を求めます。
 \begin{eqnarray*}
y&=&2×(-3)+4\\
&=&-6+4\\
&=&-2\\
\end{eqnarray*}
これで $P$の座標は$(-3,-2)$ というふうに求められました。高さ$PC$の長さはこれの$x$座標をみればいいから$PC=3$。
\begin{eqnarray*}
y&=&2×(-3)+4\\
&=&-6+4\\
&=&-2\\
\end{eqnarray*}
これで $P$の座標は$(-3,-2)$ というふうに求められました。高さ$PC$の長さはこれの$x$座標をみればいいから$PC=3$。
これで底辺と高さがわかりました。面積をだしましょう。
$$7×3×\cfrac{1}{2}=\cfrac{21}{2}$$
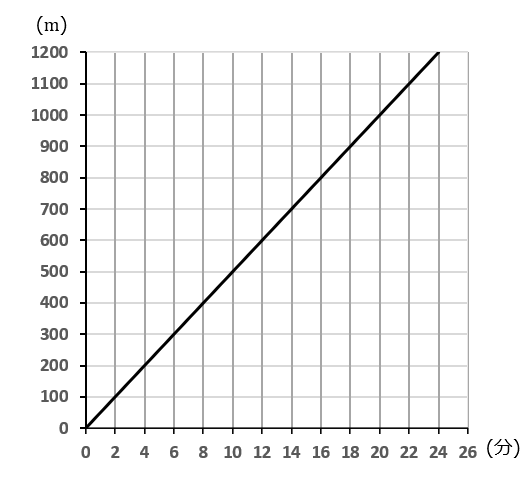
(22) 駅から $1200m$ 離れたところに学校がある。Aさんが分速 $50m$ の速さで駅から学校へ歩いた。Aさんが出発してから $6$ 分後に、Bさんが分速 $100m$ の速さで学校から駅へ自転車で走った。下のグラフは、Aさんが進んだようすを表したものである。このグラフに、Bさんが進んだようすをかきくわえなさい。また、BさんがAさんとすれちがったのは、Bさんが出発してから何分後か。
答え
$6$ 分後
〈グラフ〉
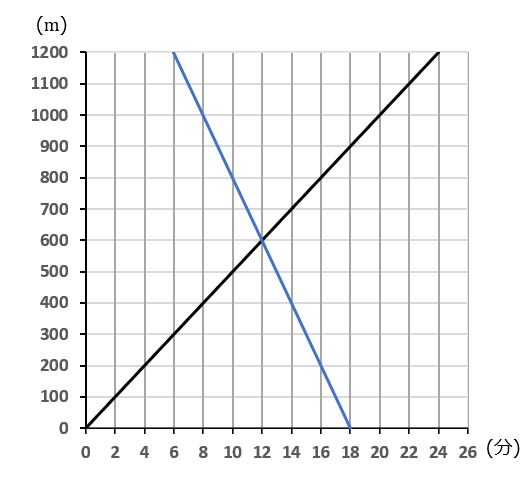
BさんはAさんが出発してから $6$ 分後に学校を出発したわけですから、点 $(6, \ 1200)$ からグラフをはじめます。
グラフをかくときは、目盛りに注意してください。$x$ 軸は $1$ 目盛りが $2$ 分です。$y$ 軸は $1$ 目盛りが $100m$ です。
Bさんの速さは分速 $100m$ なので、$2$ 分で $200m$ 進むことになります。なので、右に $1$ マスいって、下に $2$ マスいくように点をとっていきます。
〈時間〉
$2$ 直線の交点が、BさんがAさんとすれちがった地点と時間を表します。なので、すれちがったのは、Aさんが出発してから $12$ 分後です。Bさんが出発してからは、$12-6=6$ 分後です。
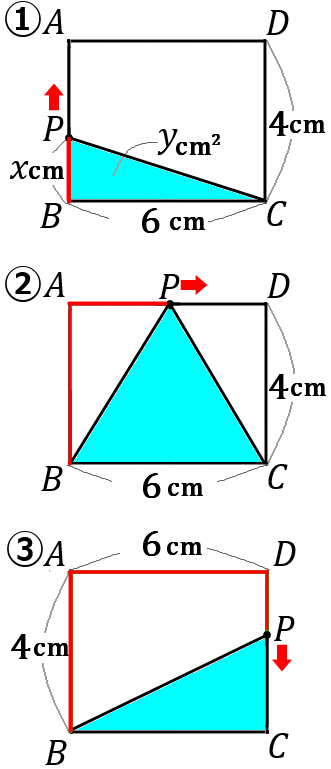 (23) 図のような長方形 $ABCD$ で、点 $P$ は辺上を点 $B$ から $A,D$ を通って $C$ まで動く。点 $P$ が辺上を点 $B$ から $xcm$ 動いたときの $\triangle PBC$ の面積を $ycm^2$ とする。
(23) 図のような長方形 $ABCD$ で、点 $P$ は辺上を点 $B$ から $A,D$ を通って $C$ まで動く。点 $P$ が辺上を点 $B$ から $xcm$ 動いたときの $\triangle PBC$ の面積を $ycm^2$ とする。
① 点 $P$ が辺 $BA$ 上にあるとき、$y$ を $x$ の式で表しなさい。また、$x$ の変域をいいなさい。
② 点 $P$ が辺 $AD$ 上にあるとき、$y$ を $x$ の式で表しなさい。また、$x$ の変域をいいなさい。
③ 点 $P$ が辺 $DC$ 上にあるとき、$y$ を $x$ の式で表しなさい。また、$x$ の変域をいいなさい。
答え
① $y=3x\qquad (0 \leqq x \leqq 4)$
② $y=12\qquad (4 \leqq x \leqq 10)$
③ $y=-3x+42\qquad (10 \leqq x \leqq 14)$
 ①〈式〉
①〈式〉三角形の面積は、底辺 $\times$ 高さ $\times\cfrac{1}{2}$ です。底辺を $BC$、高さを$PB$ ということにして、$y$ を $x$ で表します。
$BC$ の長さは $6$ です。
$P$ が動いた長さが $x$ なので、$PB$ の長さは $x$ です。
なので、三角形 $y$ の面積は、$y=6\times x \times \cfrac{1}{2}=3x$ となります。
〈変域〉
$P$ が $B$ 上にあるときは、$x=0$ です。最小値は $0$ です。$P$ が $A$ 上にきたときは、$x=4$ です。最大値は $4$ です。
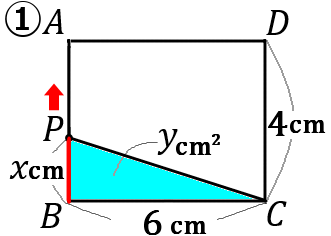
 ②〈式〉
②〈式〉$P$ から $BC$ におろした垂線と、$BC$ との交点を $E$ とします。底辺を $BC$、高さを$PE$ ということにして、$y$ を $x$ で表します。
$BC$ の長さは $6$ です。
$PE$ の長さは、$P$ がどこにあっても $4$ です。
なので、三角形 $y$ の面積は、$y=6 \times 4 \times\cfrac{1}{2}=12$ となります。
〈変域〉
$x$ の変域は、$P$ が $A$ 上にきたときは、$x=4$ です。最小値は $4$ です。$P$ が $D$ 上にきたときは、$x=4+6=10$ です。最大値は $10$ です。
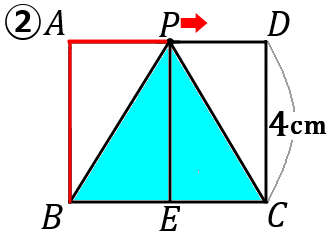
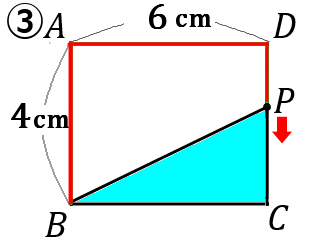 ③〈式〉
③〈式〉
底辺を $BC$、高さを$PC$ ということにして、$y$ を $x$ で表します。
$BC$ の長さは $6$ です。
$PC$ の長さは、$14-x$ です。$x$ は $P$ が動いてきた長さです。③の図の赤い線が $x$ を表しています。$BA+AD+DC$ から $x$ をひけば、$PC$ になります。なので、$PC=4+6+4-x=14-x$ です。
なので、三角形 $y$ の面積は、
\begin{eqnarray*}
y&=&6 \times (14-x) \times\cfrac{1}{2} \quad(6\times\cfrac{1}{2}を先にやってしまう)\\
&=&3(14-x)\\
&=&42-3x\\
&=&-3x+42
\end{eqnarray*}
〈変域〉
$x$ の変域は、$P$ が $D$ 上にきたときは、$x=4+6=10$ です。最小値は $10$ です。$P$ が $C$ 上にきたときは、$x=4+6+4=14$ です。最大値は $14$ です。
 (24) (23)の問題について、$x$ の変域を $0 \leqq x \leqq 14$ とするときの $x$ と $y$ の関係をグラフに表しなさい。また、$\triangle PBC$ の面積が $8cm^2$ となるときの $x$ の値を求めなさい。
(24) (23)の問題について、$x$ の変域を $0 \leqq x \leqq 14$ とするときの $x$ と $y$ の関係をグラフに表しなさい。また、$\triangle PBC$ の面積が $8cm^2$ となるときの $x$ の値を求めなさい。
答え
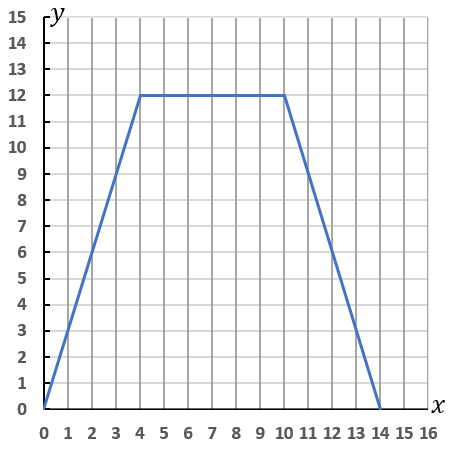 $x=\cfrac{8}{3}, \ x=\cfrac{34}{3}$
$x=\cfrac{8}{3}, \ x=\cfrac{34}{3}$
〈グラフ〉
変域が $0 \leqq x \leqq 4$ のときの式は $y=3x$ です。原点を通る直線です。点$(0, \ 0),$ $(4, \ 12)$ をとって定規でむすんでしまいましょう。線は点 $(4, \ 12)$ で終わりにしてください。その先をかいちゃダメです。
変域が $4 \leqq x \leqq 10$ のときの式は $y=12$ です。$x$ 軸に平行な直線になります。$(4, \ 12)$ から$ (10, \ 12)$ までを定規でむすんでしまいましょう。
変域が $10 \leqq x \leqq 14$ のときの式は $y=-3x+42$ です。直線です。点$(10, \ 12)$ と $(14, \ 0)$ をとって定規でむすんでしまいましょう。$x=14$ のときに面積が $0$ になるはず、と考えて点 $(14, \ 0)$ をとるわけです。
〈面積〉
グラフから、面積 $y$ が $8$ になるのは、$2$ か所あります。$P$ が $y=3x$ 上にあるときと、$y=-3x+42$ 上にあるときです。それぞれの式の $y$ に $8$ を代入して $x$ を求めればOKです。
$P$ が $y=3x$ 上にあるとき
\begin{eqnarray*}
8&=&3x\\
x&=&\cfrac{8}{3}
\end{eqnarray*}
$P$ が $y=-3x+42$ 上にあるとき
\begin{eqnarray*}
8&=&-3x+42\\
3x&=&42-8\\
3x&=&34\\
x&=&\cfrac{34}{3}
\end{eqnarray*}
(25) 次の表のようなインターネットの月額の料金プランがある。
\begin{array}{c|ccc}
\hline
& 基本料金 & 1分間の使用料 \\
\hline
Aプラン & 2000円 & 2円 \\
\hline
Bプラン & 500円 & 4円 \\
\hline
Cプラン & 0円 & 定額2500円 \\
\hline
\end{array}
① $1$か月に $x$ 分間使用したときの料金を $y$ 円として、それぞれのプランについて、$y$ を $x$ の式で表しなさい。
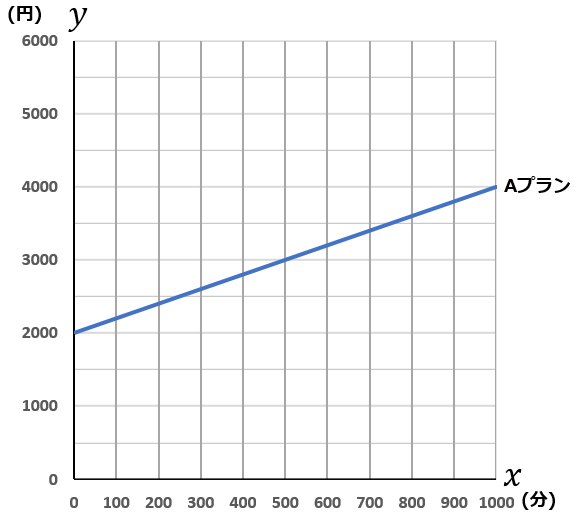
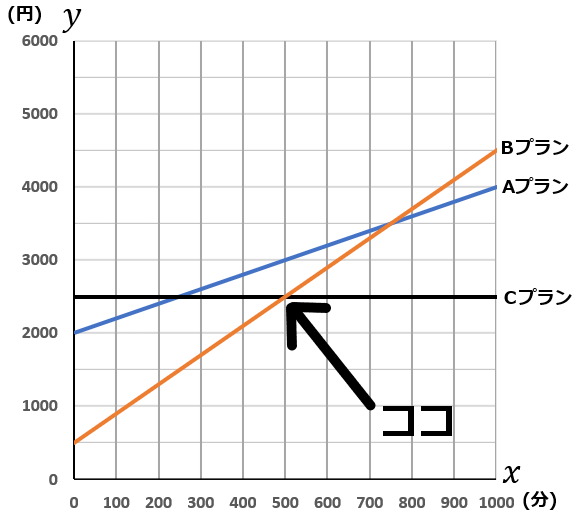
また、下のグラフは$A$プランを表したものである。このグラフに、$B$プランと$C$プランのグラフをかきくわえなさい。
② $C$ プランを利用するのがもっとも安くなるのは、何分より多く使用した場合か。
答え
①$A$プラン… $y=2x+2000$
$B$プラン… $y=4x+500$
$C$プラン… $y=2500$
②$500$分
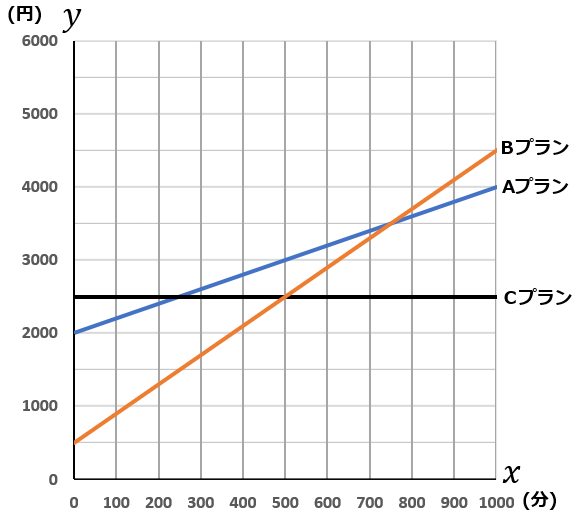
〈グラフ〉
①<式>
$A$プランは$1$分間の使用料が$2$円で基本料金が$2000$円なので、
$y=2x+2000$
$B$プランは$1$分間の使用料が$4$円で基本料金が$500$円なので、
$y=4x+500$
①$C$プランは定額$2500$円なので、
$y=2500$
<グラフ>
$A$プランは切片が$2000$で、$500$分で$1000$円かかるグラフです。右に$5$マス進んで、縦に$2$マス進んでいるのを確認しましょう。
$B$プランは切片が$500$で、$500$分で$2000$円かかるグラフです。右に$5$マス進んで、縦に$4$マス進むグラフをかきましょう。
$C$プランは切片が$2500$の横線になります。
②グラフを見て判断しましょう。$C$プランがもっとも安くなるのは、$x$が$500$のところです。
答え(中2 3章 1次関数 第3回)
 (1) $y=ax+b$, 傾き, 変化の割合, $\cfrac{xの増加量\phantom{ }}{yの増加量\phantom{ }}$,
(1) $y=ax+b$, 傾き, 変化の割合, $\cfrac{xの増加量\phantom{ }}{yの増加量\phantom{ }}$,
切片($y$ 切片), 右上がり, 右下がり
(2)① $6$
② $-2$
③ $-\cfrac{1}{3}$
(3) $y=-\cfrac{1}{4}x+5$
(4) $y=-x-3$
(5) $y=2x-5$
(6) $y=2x-10$
(7) $y=-2x-4$
(8) $y=\cfrac{1}{3}x+3$
(9) $y=x+3$
(10) $y=-3x-2$
(11) ア…$8$, イ…$\cfrac{10}{3}$, ウ…$12$, 式 $y=-\cfrac{2}{3}x+4$
(12) $3 \leqq y \leqq 5$
(13) $y=3x-2$
(14) $y=-\cfrac{1}{2}x+1$
(15) ① $y=2$ ② $x=-1$
(16) 右上図
(17) $
\left\{
\begin{array}{l}
x=3\\
y=-1
\end{array}
\right.
$
$2$ 番目の図
(18) $y=-\cfrac{2}{3}x+\cfrac{4}{3}$
(19) $(-2,-3)$
(20) $\left(\cfrac{6}{7}, \ \cfrac{4}{7}\right)$
(21) $\cfrac{21}{2}$
(22) $3$ 番目の図 $6$ 分後
(23) ① $y=3x\qquad (0 \leqq x \leqq 4)$
② $y=12\qquad (4 \leqq x \leqq 10)$
③ $y=-3x+42\qquad (10 \leqq x \leqq 14)$
(24) 右下図 $x=\cfrac{8}{3}, \ x=\cfrac{34}{3}$
(25)①$A$プラン… $y=2x+2000$
$B$プラン… $y=4x+500$
$C$プラン… $y=2500$
②$500$分
